Mechanical Properties and Weibull Scaling Laws of Unknown Spider Silks
Abstract
1. Introduction
2. Results
3. Discussion
4. Material and Methods
4.1. Spiders and Silk
4.2. Tensile Tests
4.3. Weibull Statistics
4.4. ANOVA Analysis
4.5. Effect Size (ES)
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shao, Z.; Vollrath, F. The effect of solvents on spider silk studied by mechanical testing and single-fibre Raman spectroscopy. Int. J. Biol. Macromol. 1999, 24, 295–300. [Google Scholar] [CrossRef]
- Porter, D.; Guan, J.; Vollrath, F. Spider silk: Super material or thin fibre? Adv. Mater. 2013, 25, 1275–1279. [Google Scholar] [CrossRef]
- Blamires, S.J.; Blackledge, T.A.; Tso, I.-M. Physicochemical Property Variation in Spider Silk: Ecology, Evolution, and Synthetic Production. Annu. Rev. Entomol. 2017, 62, 443–460. [Google Scholar] [CrossRef] [PubMed]
- Vollrath, F.; Porter, D. Spider silk as archetypal protein elastomer. Soft Matter 2006, 2, 377–385. [Google Scholar] [CrossRef]
- Gosline, J.; Lillie, M.; Carrington, E.; Guerette, P.; Ortlepp, C.; Savage, K. Elastic proteins: Biological roles and mechanical properties. Philos. Trans. R. Soc. B Biol. Sci. 2002, 357, 121–132. [Google Scholar] [CrossRef]
- Mirbaha, H.; Nourpanah, P.; Scardi, P.; D’incau, M.; Greco, G.; Valentini, L.; Bon, S.B.; Arbab, S.; Pugno, N. The Impact of Shear and Elongational Forces on Structural Formation of Polyacrylonitrile/Carbon Nanotubes Composite Fibers during Wet Spinning Process. Materials 2019, 12, 2797. [Google Scholar] [CrossRef]
- Dellaquila, A.; Greco, G.; Campodoni, E.; Mazzocchi, M.; Mazzolai, B.; Tampieri, A.; Pugno, N.M.; Sandri, M. Optimized production of a high-performance hybrid biomaterial: Biomineralized spider silk for bone tissue engineering. J. Appl. Polym. Sci. 2019, 137, 48739. [Google Scholar] [CrossRef]
- Yang, Y.; Greco, G.; Maniglio, D.; Mazzolai, B.; Migliaresi, C.; Pugno, N.; Motta, A. Spider (Linothele megatheloides) and silkworm (Bombyx mori) silks: Comparative physical and biological evaluation. Mater. Sci. Eng. C 2020, 107, 110197. [Google Scholar] [CrossRef] [PubMed]
- Tahir, H.M.; Zahra, K.; Zaheer, A.; Samiullah, K. Spider silk: An excellent biomaterial for medical science and industry. Punjab Univ. J. Zool. 2017, 32, 143–154. [Google Scholar]
- Salehi, S.; Koeck, K.; Scheibel, T. Spider Silk for Tissue Engineering Applications. Molecules 2020, 25, 737. [Google Scholar] [CrossRef]
- Vollrath, F.; Knight, D.P. Liquid crystal spinning of spider silk. Nature 2001, 410, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Greco, G.; Pantano, M.F.; Mazzolai, B.; Pugno, N.M. Imaging and mechanical characterization of different junctions in spider orb webs. Sci. Rep. 2019, 9, 5776. [Google Scholar] [CrossRef] [PubMed]
- Madsen, B.; Shao, Z.Z.; Vollrath, F. Variability in the mechanical properties of spider silks on three levels: Interspecific, intraspecific and intraindividual. Int. J. Biol. Macromol. 1999, 24, 301–306. [Google Scholar] [CrossRef]
- Wolff, J.O.; Gorb, S.N. Attachment Structures and Adhesive Secretions in Arachnids. Comparative Contact Mechanics; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Opell, B.D.; Clouse, M.E.; Andrews, S.F. Elastic modulus and toughness of orb spider glycoprotein glue. PLoS ONE 2018, 13, e0196972. [Google Scholar] [CrossRef] [PubMed]
- Wolff, J.O.; Řezáč, M.; Krejčí, T.; Gorb, S.N. Hunting with sticky tape: Functional shift in silk glands of araneophagous ground spiders (Gnaphosidae). J. Exp. Biol. 2017, 220, 2250–2259. [Google Scholar] [CrossRef] [PubMed]
- Basu, A. Advances in Silk Science and Technology; The Textile Institute: Cambridge, UK, 2015. [Google Scholar]
- Foelix, R. Biology of Spiders; Oxford University Press: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Denny, M.W. the Physical Properties of Spider’s Silk and Their Role in the Design of Orb-Webs. J. Exp. Biol. 1976, 65, 483–506. [Google Scholar]
- Perez-Rigueiro, J. The effect of spinning forces on spider silk properties. J. Exp. Biol. 2005, 208, 2633–2639. [Google Scholar] [CrossRef]
- Prez-Rigueiro, J.; Elices, M.; Llorca, C.V. Tensile properties of Argiope trifasciata drag line silk obtained from the spider’s web. J. Appl. Polym. Sci. 2001, 82, 2245–2251. [Google Scholar] [CrossRef]
- Agnarsson, I.; Dhinojwala, A.; Sahni, V.; Blackledge, T.A. Spider silk as a novel high performance biomimetic muscle driven by humidity. J. Exp. Biol. 2009, 212, 1990–1994. [Google Scholar] [CrossRef]
- Pogozelski, E.M.; Becker, W.L.; See, B.D.; Kieffer, C.M. Mechanical testing of spider silk at cryogenic temperatures. Int. J. Biol. Macromol. 2011, 48, 27–31. [Google Scholar] [CrossRef]
- Shao, Z.; Vollrath, F. The effect of solvents on the contraction and mechanical properties of spider silk. Polymer 1999, 40, 1799–1806. [Google Scholar] [CrossRef]
- Yazawa, K.; Malay, A.D.; Masunaga, H.; Norma-Rashid, Y.; Numata, K. Simultaneous effect of strain rate and humidity on the structure and mechanical behavior of spider silk. Commun. Mater. 2020, 1, 10. [Google Scholar] [CrossRef]
- Vollrath, F.; Madsen, B.; Shao, Z. The effect of spinning conditions on the mechanics of a spider’s dragline silk. Proc. R. Soc. B Biol. Sci. 2001, 268, 2339–2346. [Google Scholar] [CrossRef] [PubMed]
- Pugno, N.M.; Ruoff, R.S. Quantized fracture mechanics. Philos. Mag. 2004, 84, 2829–2845. [Google Scholar] [CrossRef]
- Carpinteri, A.; Pugno, N. Are scaling laws on strength of solids related to mechanics or to geometry? Nat. Mater. 2005, 4, 421–423. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Pugno, N.; Sapora, A. Strength of hierarchical materials. Microsyst. Technol. 2009, 15, 27–31. [Google Scholar] [CrossRef]
- Rinne, H. The Weibull Distribution. A Handbook; Taylor & Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Weibull, W. A Statistical Theory of the Strength of Materials. Ingeniorsvetenskapsakademiens 1939, 151, 1–45. [Google Scholar]
- Perez-Rigueiro, J. The influence of anaesthesia on the tensile properties of spider silk. J. Exp. Biol. 2006, 209, 320–326. [Google Scholar] [CrossRef]
- Ortlepp, C.S.; Gosline, J.M. Consequences of forced silking. Biomacromolecules 2004, 5, 727–731. [Google Scholar] [CrossRef]
- Blackledge, T.A. Quasistatic and continuous dynamic characterization of the mechanical properties of silk from the cobweb of the black widow spider Latrodectus hesperus. J. Exp. Biol. 2005, 208, 1937–1949. [Google Scholar] [CrossRef]
- Schneider, C.A.; Rasband, W.S.; Eliceri, K.W. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Pasquet, A.; Toscani, C.; Anotaux, M. Influence of aging on brain and web characteristics of an orb web spider. J. Ethol. 2018, 36, 85–91. [Google Scholar] [CrossRef] [PubMed]
- Work, R.W. Dimensions, Birefringences, and Force-Elongation Behavior of Major and Minor Ampullate Silk Fibers from Orb-Web-Spinning Spiders—The Effects of Wetting on these Properties. Text. Res. J. 1977, 47, 650–662. [Google Scholar] [CrossRef]
- Edmonds, D.T.; Vollrath, F. The Contribution of Atmospheric Water Vapour to the Formation and Efficiency of a Spider’s Capture Web. Proc. R. Soc. B Biol. Sci. 1992, 248, 145–148. [Google Scholar]
- Barbero, E.; Fernandez-Saez, J.; Navarro, C. Statistical analysis of the mechanical properties of composite materials. Compos. Part B Eng. 2000, 31, 375–381. [Google Scholar] [CrossRef]
- Dirikolu, M.; Aktas, A.; Birgoren, B. Statistical analysis of fracture strength of composite materials using Weibull distribution. Turk. J. Eng. Environ. Sci. 2002, 26, 45–48. [Google Scholar]
- Peterlik, H. The validity of Weibull estimators. J. Mater. Sci. 1995, 30, 1972–1976. [Google Scholar] [CrossRef]
- Sullivan, G.M.; Feinn, R. Using Effect Size—Or Why the P Value Is Not Enough. J. Grad. Med. Educ. 2012, 4, 279–282. [Google Scholar] [CrossRef]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1988. [Google Scholar]
- Sawilowsky, S.S. New Effect Size Rules of Thumb. J. Mod. Appl. Stat. Methods 2009, 8, 597–599. [Google Scholar] [CrossRef]
- Swanson, B.O.; Blackledge, T.A.; Beltrán, J.; Hayashi, C.Y. Variation in the material properties of spider dragline silk across species. Appl. Phys. A Mater. Sci. Process. 2006, 82, 213–218. [Google Scholar] [CrossRef]
- Swanson, B.O.; Anderson, S.P.; DiGiovine, C.; Ross, R.N.; Dorsey, J.P. The evolution of complex biomaterial performance: The case of spider silk. Integr. Comp. Biol. 2009, 49, 21–31. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Agnarsson, I.; Kuntner, M.; Blackledge, T.A. Bioprospecting finds the toughest biological material: Extraordinary silk from a giant riverine orb spider. PLoS ONE 2010, 5, e11234. [Google Scholar] [CrossRef] [PubMed]
- Greco, G.; Wolff, J.; Pugno, N.M. Strong and tough silk for resilient attachment discs: The mechanical properties of piriform silk, in the spider Cupiennius salei (Keyserling, 1877). Front. Mater. 2020, 7, 138. [Google Scholar] [CrossRef]
- Sahni, V.; Blackledge, T.A.; Dhinojwala, A. Viscoelastic solids explain spider web stickiness. Nat. Commun. 2010, 1, 19. [Google Scholar] [CrossRef] [PubMed]
- Ortlepp, C.; Gosline, J.M. The scaling of safety factor in spider draglines. J. Exp. Biol. 2008, 211, 2832–2840. [Google Scholar] [CrossRef] [PubMed]
- Eberhard, W.G. Physical properties of sticky spirals and their connections: Sliding connections in ORB webs. J. Nat. Hist. 1976, 10, 481–488. [Google Scholar] [CrossRef]
- Keten, S.; Buehler, M.J. Nanostructure and molecular mechanics of spider dragline silk protein assemblies. J. R. Soc. Interface 2010, 7, 1709–1721. [Google Scholar] [CrossRef]
- Nova, A.; Keten, S.; Pugno, N.M.; Redaelli, A.; Buehler, M.J. Molecular and nanostructural mechanisms of deformation, strength and toughness of spider silk fibrils. Nano Lett. 2010, 10, 2626–2634. [Google Scholar] [CrossRef]
- Asakura, T.; Miller, T. Biotechnology of Silk; Springer: Dordrecht, The Netherlands, 2014. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are available from the authors. |
| Species | Nr. Samples | Strain at Break (mm/mm) | Strength (MPa) | Young’s Modulus (GPa) | Toughness Modulus (MJ/m3) | Scale Parameter b (MPa) | Shape Parameter (c) |
|---|---|---|---|---|---|---|---|
| Araneus diadematus | 16 | 0.25 ± 0.09 | 655 ± 286 | 8.5 ± 4.9 | 267 ± 164 | 949 | 2.56 |
| Ancylometes bogotensis | 15 | 0.24 ± 0.08 | 897 ± 441 | 21.8 ± 9.9 | 191 ± 175 | 1112 | 2.01 |
| Ceratogyrus marshalli | 15 | 0.17 ± 0.15 | 163 ± 158 | 2.6 ± 2.1 | 14 ± 11 | 236 | 1.16 |
| Cupiennius salei | 36 | 0.29 ± 0.15 | 253 ± 217 | 3.5 ± 2.8 | 37 ± 35 | 859 | 2.35 |
| Grammostola rosea | 15 | 0.17 ± 0.15 | 13 ± 9 | 3.0 ± 2.2 | 26 ± 16 | 42 | 1.58 |
| Linothele fallax | 15 | 0.27 ± 0.16 | 110 ± 86 | 5.0 ± 4.3 | 21 ± 20 | 127 | 1.22 |
| Nuctenea umbratica | 15 | 0.21 ± 0.06 | 1199 ± 725 | 10.2 ± 4.2 | 138 ± 81 | 1693 | 2.35 |
| Phoneutria fera | 15 | 0.32 ± 0.19 | 936 ± 544 | 27.2 ± 13 | 202 ± 141 | 1191 | 3.14 |
| Zygiella x-notata | 15 | 0.19 ± 0.07 | 283 ± 137 | 5.0 ± 2.6 | 36 ± 25 | 597 | 2.19 |
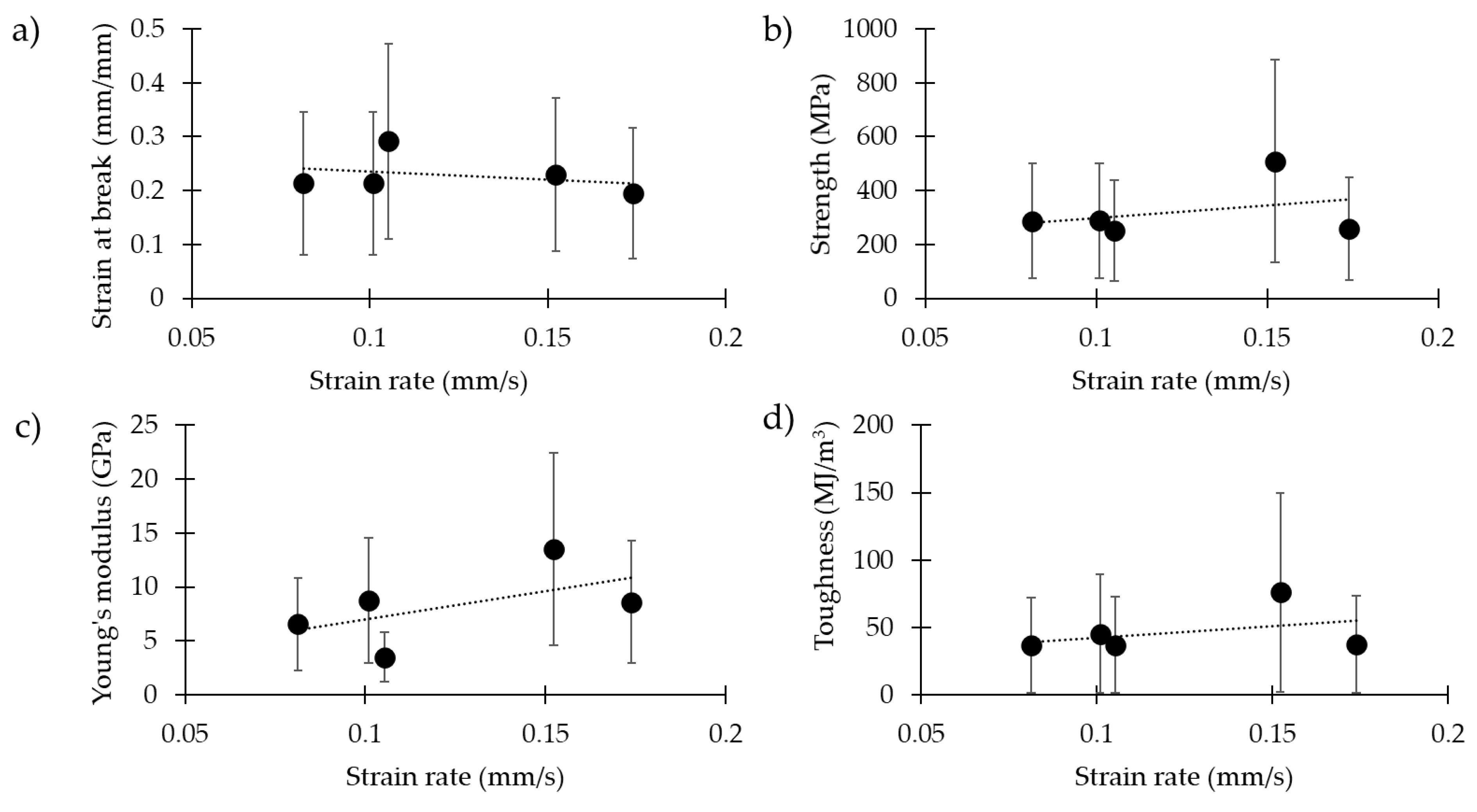
| Strain Rate (mm/s) | Nr. Samples | Diameter (μm) | Strain at Break (mm/mm) | Strength (MPa) | Young’s Modulus (GPa) | Toughness Modulus (MJ/m3) |
|---|---|---|---|---|---|---|
| 0.08 | 33 | 3.5 ± 1.5 | 0.21 ± 0.15 | 288 ± 241 | 6.6 ± 3.9 | 36 ± 41 |
| 0.10 | 37 | 4.0 ± 1.2 | 0.21 ± 0.12 | 289 ± 218 | 8.8 ± 6.5 | 45 ± 46 |
| 0.11 | 36 | 3.3 ± 0.9 | 0.29 ± 0.15 | 253 ± 217 | 3.5 ± 2.8 | 37 ± 35 |
| 0.15 | 31 | 3.0 ± 1.6 | 0.23 ± 0.17 | 510 ± 311 | 13.5 ± 6.7 | 76 ± 63 |
| 0.17 | 35 | 3.9 ± 1.5 | 0.20 ± 0.11 | 259 ± 168 | 8.6 ± 5.4 | 37 ± 36 |
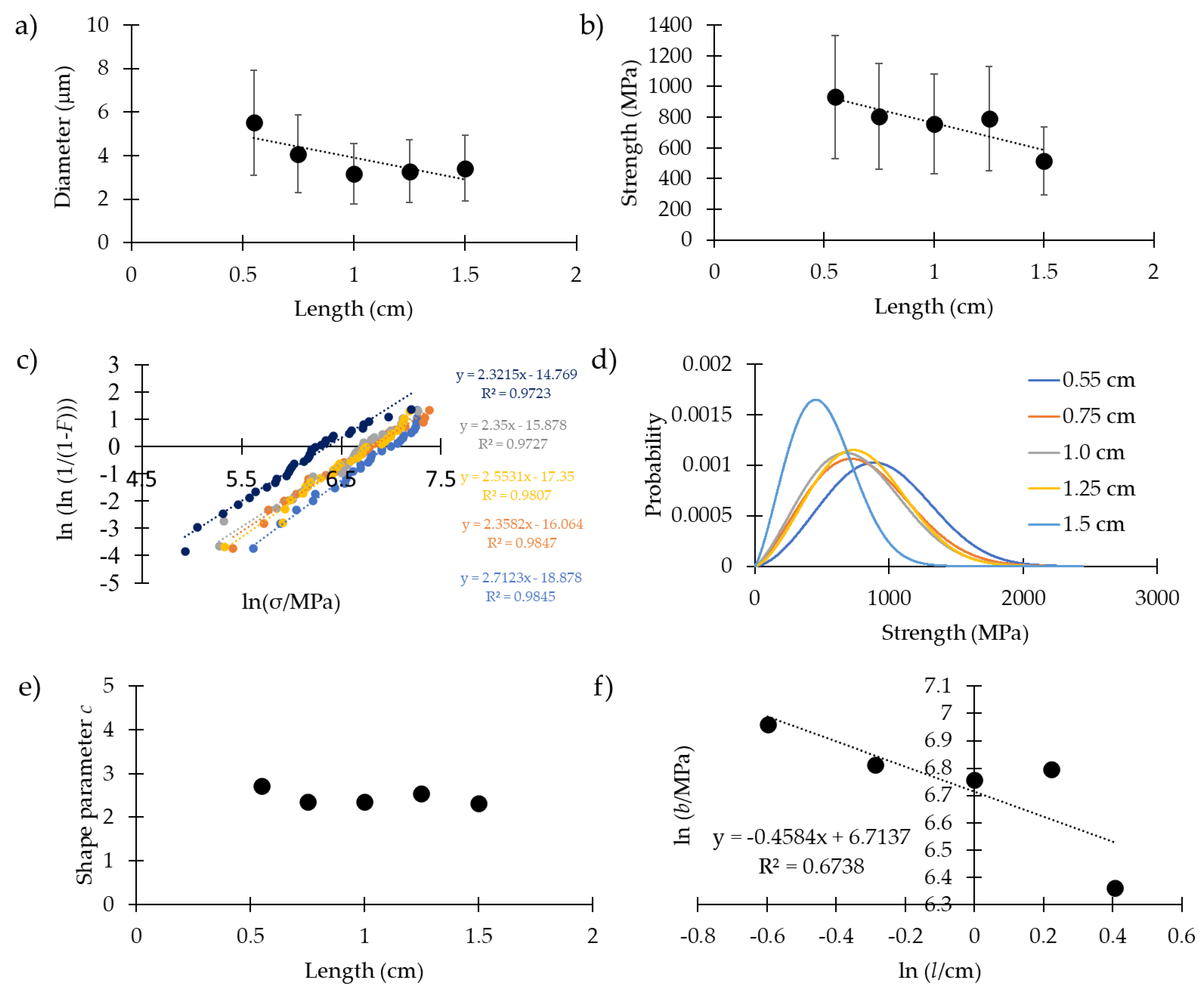
| Length (cm) | Nr. Samples | Diameter (μm) | Strain at Break (mm/mm) | Young’s Modulus (GPa) | Toughness Modulus (MJ/m3) | Strength (MPa) | Shape Parameter c | Scale Parameter b (MPa) |
|---|---|---|---|---|---|---|---|---|
| 0.55 | 29 | 5.5 ± 2.9 | 0.23 ± 0.11 | 8.0 ± 4.1 | 39 ± 40 | 932 ± 345 | 2.7 (3.10) | 1054 (1044) |
| 0.75 | 29 | 4.1 ± 1.6 | 0.20 ± 0.15 | 7.6 ± 5.3 | 45 ± 41 | 805 ± 371 | 2.4 (2.4) | 909 (910) |
| 1.0 | 27 | 3.2 ± 1.2 | 0.25 ± 0.14 | 6.1 ± 3.8 | 60 ± 43 | 754 ± 315 | 2.4 (2.7) | 860 (849) |
| 1.25 | 28 | 3.3 ± 1.9 | 0.22 ± 0.10 | 7.1 ± 4.2 | 51 ± 45 | 790 ± 317 | 2.6 (2.8) | 894 (889) |
| 1.5 | 33 | 3.4 ± 1.4 | 0.21 ± 0.17 | 7.5 ± 2.5 | 64 ± 39 | 515 ± 260 | 2.3 (2.1) | 579 (583) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Greco, G.; Pugno, N.M. Mechanical Properties and Weibull Scaling Laws of Unknown Spider Silks. Molecules 2020, 25, 2938. https://doi.org/10.3390/molecules25122938
Greco G, Pugno NM. Mechanical Properties and Weibull Scaling Laws of Unknown Spider Silks. Molecules. 2020; 25(12):2938. https://doi.org/10.3390/molecules25122938
Chicago/Turabian StyleGreco, Gabriele, and Nicola M. Pugno. 2020. "Mechanical Properties and Weibull Scaling Laws of Unknown Spider Silks" Molecules 25, no. 12: 2938. https://doi.org/10.3390/molecules25122938
APA StyleGreco, G., & Pugno, N. M. (2020). Mechanical Properties and Weibull Scaling Laws of Unknown Spider Silks. Molecules, 25(12), 2938. https://doi.org/10.3390/molecules25122938







