Abstract
Cryo-electron microscopy (cryo-EM) has now become a widely used technique for structure determination of macromolecular complexes. For modeling molecular structures from density maps of different resolutions, many algorithms have been developed. These algorithms can be categorized into rigid fitting, flexible fitting, and de novo modeling methods. It is also observed that machine learning (ML) techniques have been increasingly applied following the rapid progress of the ML field. Here, we review these different categories of macromolecule structure modeling methods and discuss their advances over time.
1. Introduction
Cryo-electron microscopy (cryo-EM) has now become a widely used technique for determining biological macromolecular structures. Recent developments of microscopy instruments, as well as progress in image processing algorithms, have drastically improved the resolution that can be achieved by cryo-EM [1,2,3]. These advances in cryo-EM have led to the increase in the number of solved structures, particularly those which were obtained at near-atomic resolution [4,5,6,7]. According to the statistics of the Electron Microscopy Data Bank (EMDB), the public repository for electron microscopy maps, there have been 2234 maps deposited in 2019 at the time of writing, about 3.5 times the 640 maps deposited in 2015 [8]. Among these deposited maps, maps at 4 Å resolution or better increased more drastically, from 114 in 2015 to 1089 maps in 2019, which is a 9.6-fold increase.
The advances in cryo-EM have certainly had a strong impact on the software developed to model molecular structures from cryo-EM maps. Structure modeling methods can be roughly classified into rigid-body fitting, flexible fitting, and de novo modeling methods. Among them, rigid fitting methods were the first to appear in literature (Figure 1). A rigid fitting method places a high-resolution structure into a low resolution EM density map. As EM map resolutions have improved, flexible fitting algorithms have emerged, which aim to consider conformational changes of rigidly fitted structures in cryo-EM maps to improve the agreement of the structures and EM maps. Recently, with an increase of need partly due to the drastic improvement of map resolution revolution, de novo modeling algorithms have started trending. De novo modeling methods benefit from the higher level of details in density, which provide information to trace protein main chain in principle without the need for known structures. Figure 1 summarizes publications of these three categories of modeling methods.
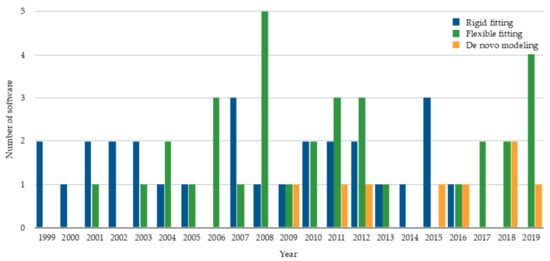
Figure 1.
The number of rigid fitting, flexible fitting, and de novo modeling software published per year. The statistics are based on publication. The plot shows 28 rigid fitting methods [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36], 33 flexible fitting methods
[37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69], and 8 de novo modeling methods [70,71,72,73,74,75,76,77].
This review is intended to cover the developments of macromolecular modeling methods and the emergence of machine learning in cryo-EM analysis. The review is structured as follows: we first review the three categories of modeling methods, rigid fitting, flexible fitting, and de novo modeling methods, in this order. Then, we discuss methods that use machine learning approaches, which are emerging in recent years in the cryo-EM structure modeling field.
2. Rigid Fitting Methods
In rigid body fitting, high resolution atomic models which are derived from X-ray crystallography, Nuclear Magnetic Resonance (NMR) spectroscopy, or protein prediction are fitted into a cryo-EM map. One of the earliest rigid fitting methods is EMfit developed by Rossmann et al. in 2001 [12]. In EMfit, a high-resolution structure is placed manually into a specific position in the EM map. Then, a 3-D rotational search is applied to find the best orientation. After that, EMfit optimizes the initial fitting by performing local rotational and translational steps. In general, rigid-body fitting methods search for the best placement of an atomic model in a density map. Search algorithms that have been used for rigid fitting include Fast Fourier transform-based (FFT) [14,32,35], grid-threading Monte Carlo (GTMC) [16], spherical harmonic-based search [20], and geometric hashing [27]. FFT is a fast search scheme that accelerates the 3-D translational search [14]. HermiteFit speeds up the rotation step in the FFT by representing densities as three-dimensional orthogonal Hermite functions and performing rotation in the Hermite space [32]. Fast polar Fourier search is a variation of FFT, which is based on non-uniform SO(3) Fourier Transforms [35]. Its principal advantage is the ability to search efficiently and uniformly over a set of samples of the conformational space. GTMC combines grid search and Monte Carlo sampling [16]. GTMC divides the search space into grid points and uses Monte Carlo to find local maxima near the grid points to identify the global maximum. ADP_EM is a spherical harmonic-based (SH) method which applies exhaustive translational scanning and accelerates the rotational search by representing densities as SH functions [20]. Geometric hashing identifies a set of possible transformations which are stored in a fast-searchable hash map [27]. Later, the set of transformations is searched to find the best fit.
While the methods above exhaustively scan a density map for possible placements, there are methods that use other techniques to fit atomic models into density maps. One of these methods is gmfit, which converts atomic models and a 3-D density map to Gaussian mixture models (GMMs) [23,78]. Then, gmfit generates a random set of initial configurations and applies steepest-descent local searches using gradients and torques of the energy function for fitting. Pintilie et al. presented a rigid fitting protocol [25] which uses a map segmentation method, Segger [79]. Segger is based on the immersive watershed method, which sorts voxels of EM map in descending order based on their density values and assigns a voxel to a new region if it is not adjacent to another region, otherwise it is added to its adjacent region. After segmenting the EM map, Segger groups the segments using scale-space filtering [80], which moves local maxima representing regions to local density maxima in the smoothed EM maps using steepest ascent and groups regions of points converging to the same local maximum. Then, atomic models are fitted into resulted regions [25]. EMLZerD docks protein components and generates a set of different conformations. Then, docking models are ranked based on the overall shape similarity with the cryo-EM map using 3-D Zernike descriptors [30]. γ-TEMPy uses vector quantization to identify feature points in a density map, which are centers of density clusters, using a neural gas clustering technique [33]. After identifying feature points which represent the positions where atomic models can fit, γ-TEMPy applies genetic algorithm to generate different conformations.
Evaluating the quality of fitting atomic models into EM density maps can be done using different scoring functions. The scores include mutual information [33,81] and cross-correlation (CC) coefficient, which is the most widely used score. CC has been used in different forms such as density CC [25,27] which takes into account all density values, Laplacian-filtered CC [81,82], which considers only EM map contours that represent the surface of the structures, and core-weighted CC function [16] in which a core is the part where the density is least likely to be changed by other components. In addition to CC, evolutionary information such as interface conservation can be used to evaluate a set of fitted models based on the fact that interface residues are conserved higher than non-interface residue [83]. Also, surface-based scores such as normal vector score (NVA), which computes the difference in angle between the normal vectors of EM maps, and the chamfer distance score (CDAgdt), which calculates the average distance between closest surface points of two EM maps [81,82]. Another possible score is skeleton–secondary structure score that depends on matching the skeleton of detected secondary structures of the density map with the secondary structure units of the atomic model [35].
3. Flexible Fitting Methods
In many cases, the available conformation of component biomolecules, e.g., proteins, could be different from what the map represents for various reasons such as different functional states of a complex. Thus, flexible fitting methods are applied to change the fitted structure to conform to the EM map. Flexible fitting approaches are categorized into five major categories. These categories are normal mode analysis-based methods, molecular dynamics-based methods, geometric simulation methods, methods using structural variability of protein superfamilies, and methods guided by α-helix correspondences.
Normal mode analysis was one of the first techniques used for flexible fitting. Normal mode analysis (NMA) is a technique used to explore the natural vibrational motion of a structure [84,85]. NMA has been applied in flexible fitting in various ways. NMFF-EM is one of the NMA methods which considers only low-frequency normal modes that represent collective low-energy global motions of the biological structure. It deforms the all-atom or Cα structure iteratively along low-frequency normal modes and optimizes the overall cross-correlation between the deformed structure and the EM map [39,86]. Another NMA method, mENM, uses all normal modes, which allows it to capture both local and global structural changes, computed for a two-bead-per-residue protein representation [54]. iMODFIT uses NMA in internal coordinates (torsional space), which offers a reasonable and efficient way to search the conformational space [60].
In addition to NMA methods, molecular dynamics (MD)-based methods are well established in the field of flexible fitting. The strength of MD simulations is the use of well-established force fields, which preserves physical correctness during fitting. MDFF is an MD-based flexible fitting, which applies MD simulation that incorporates the EM density as an external potential to the molecular mechanics force field and derives the structure towards the target density [49]. There are different variations of MD-based fitting including adding biased potentials such as cross-correlation between the model and the density map [50] and symmetry information of structure [55] to enhance the fitting results. Another MD approach uses coarse-grained representation, particularly GO-model of the molecule instead of all atoms [53]. REMDFit runs MD with a number of fitting trials with different force constants to obtain sufficient conformational sampling, which are shown to be valuable especially for lower resolution EM maps [62].
Besides MD, geometric simulation is also used for flexible fitting. Geometric simulation fitting approaches change the starting structure to conform to the density map while keeping rigid bodies such as secondary structures identified early, intact during the entire simulation which maintains valid local geometry and stereochemistry [47]. Another category of flexible fitting methods uses the structural variability of protein domains of a given superfamily, according to structural databases such as CATH, to guide the fitting [42,45]. The last category of flexible fitting is α-helix correspondence-based fitting which does not require initial rigid fitting. This fitting is instead guided by the correspondence between α-helices predicted in the density map and in the model, which reduces the fitting time [63]. Overall, these different flexible fitting approaches change the conformation of a fitted structure into an EM map to improve the fit to the map. These flexible fitting methods are aimed at not only small but also at substantial domain motions, that can have a large root–mean–square deviation (RMSD) of over 15 Å.
Rigid fitting methods fit atomic structures into EM maps of intermediate to low resolution, while flexible fitting improves the quality of the fitting into intermediate resolution EM maps by performing conformational change to the atomic structure to align with the EM map structure [87,88]. The main advantage of fitting methods is that models can be built with relatively inexpensive computational cost. On the other hand, modeling is only possible when the structure is available.
4. De Novo Modeling Methods
Recent years have witnessed a drastic increase in the number of maps determined at a resolution of 3 to 5 Å. This is a frustrating resolution, where a part of structures can be observed in a map but difficult to build a structure model with conventional tools that are originally designed for X-ray crystallography. De novo modeling methods use maps in this resolution range, aimed at situations where known structures are not available for rigid or flexible fitting. De novo modeling tools build a full atom model or a main-chain trace without using a template structure. There are six tools that belong to this category, EM-Fold [70], Gorgon [71], Rosetta [73,89], Pathwalking [72,74], Phenix [75,77], and MAINMAST [76,90]. The methods discussed below are summarized in Table 1.

Table 1.
Strengths and limitations of de novo methods.
EM-Fold is designed for predicting structures of α-helical proteins from intermediate resolution EM maps [70]. First, density rods in EM map are identified manually and different secondary structure prediction methods are used to detect α-helices from the protein sequence. Then, EM-Fold places consensus predicted α-helices into the density rods using a simulated annealing Monte Carlo Metropolis search algorithm, refines the placement, and ranks the generated models. Finally, side-chains and loops are built for highest ranked models using Rosetta. Gorgon is an interactive visualization software which provides several computational tools for modeling near-atomic proteins, including tools for calculating density skeleton and matching secondary structure elements (SSE) predicted in sequence to SSE in a density map [71].
Rosetta is a software suite for modeling, predicting, and analyzing protein structures. Rosetta includes de novo modeling for cryo-EM, which consists of three main steps [73]. First, sliding a 9-residue window on the sequence and collecting representative structural fragments from databases. Second, evaluating the fragments using a 4-term score function which includes density correlation, overlap, closability, and clash terms, then finding a set of fragments that optimizes the score function using Monte Carlo with simulated annealing. These two steps are run iteratively until 70% of the sequence is covered. RosettaES overcomes the 70% covering limitation by iteratively sampling individual missing segments and combining them using a Monte Carlo assembly method [89]. Last, density-guided sampling and all-atom refinement are used to complete the partial model.
Another de novo tool, Pathwalking, is included in the EMAN package. The Pathwalking method builds a protein Cα model from an EM map using the travel salesman problem (TSP) in the following steps [74]. First, it places pseudo-atoms in the high-density regions in the density map and then applying the K-means clustering to their positions, where K is the number of amino acid residues. Next, an initial path in the EM maps is detected by a TSP solver. After that, a path refinement step is applied iteratively, identifying secondary structure elements, fixing them, and reseeding the pseudo-atoms based on that.
Phenix, a software suite for molecular structure modeling for X-ray crystallography, cryo-EM, and other methods, has a de novo modeling tool, phenix.map_to_model. Phenix.map_to_model is composed of four main steps [75]. It begins with sharpening density map to maximize its details using phenix.auto_sharpen [91]. Then, the density map is segmented to extract a unique set of connected density regions that are above an automatically determined density threshold. After that, a number of model building methods are applied to each type of macromolecule that is inferred using the phenix.guess_chain_types_from_sequences tool. Alternatively, the phenix.trace_and_build tool developed recently could be used for protein modeling [77]. Last, a model is assembled by combining structure fragments using phenix.combine_models tool, then refined using phenix.real_space_refine tool [92].
MAINMAST (MAINchin Model trAcing from Spanning Tree) is a de novo modeling method, which was recently developed by our group [76]. MAINMAST provides a set of models with their confidence score. The procedure is fully automated and does not require any external known structures. The MAINMAST algorithm consists of six steps as shown in Figure 2. The first step is identifying local points with high density in the EM map using the mean shift method, which performs local clustering of density points. Next, identified points are connected into a minimum spanning tree (MST). Then, the MST structure is refined using a tabu search, which generates a pool of alternative trees. After that, the protein sequence is mapped onto the longest path of each MST using the Smith–Waterman dynamic programming algorithm. MSTs are ranked based on a threading (sequence-structure matching) score, which evaluates the fit of the amino acid sequence of the protein to a path in a tree. The last two steps are constructing a full-atom model for the top few hundred trees using PULCHRA [93], then refining them using MDFF [49]. The models are finally evaluated and ranked by the MDFF score. The confidence score for each local region in a model is computed as the fraction of models that have the local structure.
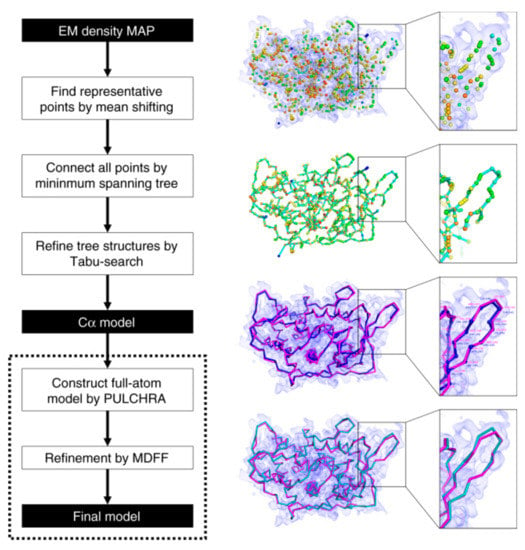
Figure 2.
Schematic flow diagram of the MAINMAST algorithm. The cryo-EM density map shown on the right is of structural protein 5 of cytoplasmic polyhedrosis virus solved at a 2.9 Å resolution (EMD-6374). This figure was adapted from the MAINMAST paper [76].
In general, de novo modeling methods need further development and have room for improvement. One promising strategy could be to incorporate techniques developed for protein structure prediction methods.
5. Machine Learning Approaches
In this section, we discuss emerging applications of ML in structure modeling for cryo-EM. ML has been actively used in many bioinformatics domains. Particularly, recently deep learning has been successfully applied to various tasks in protein sequence and structure analyses. Naturally, we have started to observe deep learning applied in software for cryo-EM, particularly in single particle picking and secondary structure prediction.
A critical step for constructing a high resolution 3-D cryo-EM map is the picking of single-particle two-dimensional (2-D) projections from thousands of 2-D micrographs. Many methods have been developed to automate the particle extraction process. ML methods applied include unsupervised clustering approaches, i.e., k-means, fuzzy c-means (FCM), and intensity-based clustering (IBC) that is used in AutoCryoPicker [94]. Recently, deep learning using convolutional neural networks (CNN) have been applied in DeepPicker [95], DeepEM [96], Deep Consensus [97], E2boxer.py procedure in the EMAN2 package [98,99], and PIXER [100].
Another task in cryo-EM where ML can be effectively applied is protein structure identification in medium to low resolution (5–10 Å) maps. At this range of the resolution, some fragments of secondary structure elements (SSE), α-helices and β-sheets are barely visible, but ML can significantly improve identification. RENNSH is a method which identifies α-helices in a density map by applying nested K-nearest neighbors (KNN) classifiers with spherical harmonic descriptors [101,102]. SSELearner, uses another classification method, support vector machines (SVM), to identify both α-helices and β-sheets in EM maps [103]. In addition to conventional machine learning techniques, very recently deep learning has been used for secondary structure prediction in EM maps. Deep learning, in particular 3-D CNN, turned out to be very suitable for identifying secondary structures from cryo-EM maps [104].
Our group has developed Emap2sec, a deep learning-based method, which uses 3-D CNN for detecting secondary structures of a protein (α-helix, β-sheets, and other structures) in cryo-EM maps of 5 to 10 Å [101]. Emap2sec first scans a cryo-EM map with a voxel of size 11 Å. Emap2sec consists of a two-phase stacked network architecture. The first phase outputs probability values for an input voxel to have α-helix, β-sheets, and other structures, through a network with convolutional layers, a maximum-pooling layer, fully connected layers, and a softmax layer. The second phase network takes the probability values from the first phase as an input and outputs the final refined probabilities through five fully connected layers followed by a softmax layer. The purpose of the second phase is to smooth the predictions of the first phase by incorporating predictions of neighboring voxels. Emap2sec was tested on both simulated and experimental cryo-EM maps and shown to outperform existing methods. Examples of emap2sec results on two experimental maps are visualized in Figure 3. The methods discussed above are summarized in Table 2.
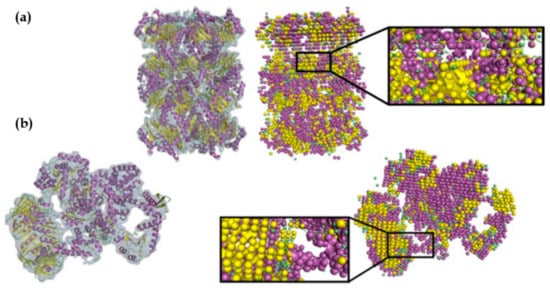
Figure 3.
Emap2sec applied on two experimental maps. Density maps and their fitted protein structures are shown on the left and the secondary structure detection by Emap2sec is shown on the right. Spheres in magenta, yellow, and green show detected α-helices, β-strands, and other structures, respectively. (a) Archaeal 20S proteasome (EMD-1733 of resolution 6.8 Å; PDB 3C91). (b) Eschirichia coli replicative DNA polymerase complex (EMD-3201 of resolution 8.34 Å; PDB 5FKU). This figure was adapted from the EMap2sec paper [101].

Table 2.
Strengths and limitations of SSE detection methods.
6. Conclusions
Cryo-electron microscopy is now a well-established technique for determining the structure of macromolecular complexes. At the beginning of cryo-electron microscopy, reconstructed EM images were limited to intermediate-to-low resolution, thus fitting methods of high-resolution structures into EM maps were developed. Over time, advances in cryo-electron technology enabled obtaining higher resolution EM maps, hence de novo modeling methods emerged which provided high resolution images without the need of extra resources.
New software will be required as the cryo-EM field further progresses. Two areas are expected to make substantial progress in coming years. First, as the resolution of cryo-EM improves, the study of macromolecular conformational dynamics will become possible, which requires new development of the software that enables it [87]. Macromolecules may have discrete or continuous conformational states [105]. These different conformational states, which may exist in the same sample, will need new computational approaches to be classified and extracted from a series of 3-D maps [106,107]. Second, it is highly expected that cryo-electron tomography (cryo-ET), which can analyze biological assemblies in their native cellular environment, will become a focus of studies in structural biology [108]. Recent technical advances such as focused ion beam [109] allow producing higher resolution tomograms, which would accelerate the development of cryo-ET methods.
Structural biology using cryo-EM/ET has entered an exciting era where many new experimental and computational methods are developed and synergize to produce unprecedented pictures and movies of molecules, cells, and tissues.
Author Contributions
Conceptualization, D.K.; investigation, E.A.; resources, D.K.; data curation, E.A..; writing—original draft preparation, E.A..; writing—review and editing, D.K.; supervision, D.K.; project administration, D.K.; funding acquisition, E.A. and D.K. All authors have read and agreed to the published version of the manuscript.
Funding
E.A. received a fellowship from Umm Al-Qura University, Saudi Arabia. This work was partly supported by the National Institutes of Health (R01GM123055), the National Science Foundation (DMS1614777, CMMI1825941, and MCB1925643) and the Purdue Institute for Drug Discovery.
Acknowledgments
The authors are grateful to Charles Christoffer for proofreading the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, Y. Single-Particle Cryo-EM at Crystallographic Resolution. Cell 2015, 161, 450–457. [Google Scholar] [CrossRef] [PubMed]
- Nogales, E. The development of cryo-EM into a mainstream structural biology technique. Nat. Methods 2016, 13, 24. [Google Scholar] [CrossRef] [PubMed]
- Glaeser, R.M. How good can single-particle cryo-EM become? What remains before it approaches its physical limits? Annu. Rev. Biophys. 2019, 48, 45–61. [Google Scholar]
- Kuhlbrandt, W. Biochemistry. The resolution revolution. Science 2014, 343, 1443–1444. [Google Scholar] [CrossRef] [PubMed]
- Henderson, R. Overview and future of single particle electron cryomicroscopy. Arch. Biochem. Biophys. 2015, 581, 19–24. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Guo, F.; Wang, F.; Li, T.C.; Jiang, W. 2.9 A Resolution Cryo-EM 3D Reconstruction of Close-Packed Virus Particles. Structure 2016, 24, 319–328. [Google Scholar] [CrossRef] [PubMed]
- Herzik, M.A., Jr.; Wu, M.; Lander, G.C. Achieving better-than-3-A resolution by single-particle cryo-EM at 200 keV. Nat. Methods 2017, 14, 1075–1078. [Google Scholar] [CrossRef]
- Spainhour, J.C.G.; Janech, M.G.; Ramakrishnan, V. A study of the properties of Gaussian mixture model for stable isotope standard quantification in MALDI-TOF MS. Commun. Stat. Simul. Comput. 2019, 48, 1637–1650. [Google Scholar] [CrossRef]
- Volkmann, N.; Hanein, D. Quantitative fitting of atomic models into observed densities derived by electron microscopy. J. Struct. Biol. 1999, 125, 176–184. [Google Scholar] [CrossRef]
- Wriggers, W.; Milligan, R.A.; McCammon, J.A. Situs: A package for docking crystal structures into low-resolution maps from electron microscopy. J. Struct. Biol. 1999, 125, 185–195. [Google Scholar] [CrossRef]
- Roseman, A.M. Docking structures of domains into maps from cryo-electron microscopy using local correlation. Acta Cryst. D Biol. Cryst. 2000, 56, 1332–1340. [Google Scholar] [CrossRef] [PubMed]
- Rossmann, M.G.; Bernal, R.; Pletnev, S.V. Combining electron microscopic with x-ray crystallographic structures. J. Struct. Biol. 2001, 136, 190–200. [Google Scholar] [CrossRef] [PubMed]
- Jiang, W.; Baker, M.L.; Ludtke, S.J.; Chiu, W. Bridging the information gap: Computational tools for intermediate resolution structure interpretation. J. Mol. Biol. 2001, 308, 1033–1044. [Google Scholar] [CrossRef] [PubMed]
- Chacon, P.; Wriggers, W. Multi-resolution contour-based fitting of macromolecular structures. J. Mol. Biol. 2002, 317, 375–384. [Google Scholar] [CrossRef] [PubMed]
- Navaza, J.; Lepault, J.; Rey, F.A.; Alvarez-Rua, C.; Borge, J. On the fitting of model electron densities into EM reconstructions: A reciprocal-space formulation. Acta Cryst. D Biol. Cryst. 2002, 58, 1820–1825. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Milne, J.L.; Borgnia, M.J.; Rostapshov, A.V.; Subramaniam, S.; Brooks, B.R. A core-weighted fitting method for docking atomic structures into low-resolution maps: Application to cryo-electron microscopy. J. Struct. Biol. 2003, 141, 63–76. [Google Scholar] [CrossRef]
- Kovacs, J.A.; Chacon, P.; Cong, Y.; Metwally, E.; Wriggers, W. Fast rotational matching of rigid bodies by fast Fourier transform acceleration of five degrees of freedom. Acta Cryst. D Biol. Cryst. 2003, 59, 1371–1376. [Google Scholar] [CrossRef]
- Ceulemans, H.; Russell, R.B. Fast fitting of atomic structures to low-resolution electron density maps by surface overlap maximization. J. Mol. Biol. 2004, 338, 783–793. [Google Scholar] [CrossRef]
- Topf, M.; Baker, M.L.; John, B.; Chiu, W.; Sali, A. Structural characterization of components of protein assemblies by comparative modeling and electron cryo-microscopy. J. Struct. Biol. 2005, 149, 191–203. [Google Scholar] [CrossRef]
- Garzon, J.I.; Kovacs, J.; Abagyan, R.; Chacon, P. ADP_EM: Fast exhaustive multi-resolution docking for high-throughput coverage. Bioinformatics 2007, 23, 427–433. [Google Scholar] [CrossRef]
- Birmanns, S.; Wriggers, W. Multi-resolution anchor-point registration of biomolecular assemblies and their components. J. Struct. Biol. 2007, 157, 271–280. [Google Scholar] [CrossRef] [PubMed]
- Lasker, K.; Dror, O.; Shatsky, M.; Nussinov, R.; Wolfson, H.J. EMatch: Discovery of high resolution structural homologues of protein domains in intermediate resolution cryo-EM maps. IEEE/ACM Trans. Comput. Biol. Bioinform. 2007, 4, 28–39. [Google Scholar] [CrossRef]
- Kawabata, T. Multiple subunit fitting into a low-resolution density map of a macromolecular complex using a gaussian mixture model. Biophys. J. 2008, 95, 4643–4658. [Google Scholar] [CrossRef] [PubMed]
- Lasker, K.; Topf, M.; Sali, A.; Wolfson, H.J. Inferential optimization for simultaneous fitting of multiple components into a CryoEM map of their assembly. J. Mol. Biol. 2009, 388, 180–194. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Pintilie, G.D.; Zhang, J.; Goddard, T.D.; Chiu, W.; Gossard, D.C. Quantitative analysis of cryo-EM density map segmentation by watershed and scale-space filtering, and fitting of structures by alignment to regions. J. Struct. Biol. 2010, 170, 427–438. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Vasishtan, D.; Xu, M.; Topf, M.; Alber, F. A fast mathematical programming procedure for simultaneous fitting of assembly components into cryoEM density maps. Bioinformatics 2010, 26, 261–268. [Google Scholar] [CrossRef]
- Woetzel, N.; Lindert, S.; Stewart, P.L.; Meiler, J. BCL::EM-Fit: Rigid body fitting of atomic structures into density maps using geometric hashing and real space refinement. J. Struct. Biol. 2011, 175, 264–276. [Google Scholar] [CrossRef][Green Version]
- Birmanns, S.; Rusu, M.; Wriggers, W. Using Sculptor and Situs for simultaneous assembly of atomic components into low-resolution shapes. J. Struct. Biol. 2011, 173, 428–435. [Google Scholar] [CrossRef]
- De Vries, S.J.; Zacharias, M. ATTRACT-EM: A new method for the computational assembly of large molecular machines using cryo-EM maps. PLoS ONE 2012, 7, 49733. [Google Scholar] [CrossRef]
- Esquivel-Rodriguez, J.; Kihara, D. Fitting multimeric protein complexes into electron microscopy maps using 3D Zernike descriptors. J. Phys. Chem. B 2012, 116, 6854–6861. [Google Scholar] [CrossRef]
- Hoang, T.V.; Cavin, X.; Ritchie, D.W. gEMfitter: A highly parallel FFT-based 3D density fitting tool with GPU texture memory acceleration. J. Struct. Biol. 2013, 184, 348–354. [Google Scholar] [CrossRef] [PubMed]
- Derevyanko, G.; Grudinin, S. HermiteFit: Fast-fitting atomic structures into a low-resolution density map using three-dimensional orthogonal Hermite functions. Acta Cryst. D Biol. Cryst. 2014, 70, 2069–2084. [Google Scholar] [CrossRef] [PubMed]
- Pandurangan, A.P.; Vasishtan, D.; Alber, F.; Topf, M. gamma-TEMPy: Simultaneous Fitting of Components in 3D-EM Maps of Their Assembly Using a Genetic Algorithm. Structure 2015, 23, 2365–2376. [Google Scholar] [CrossRef] [PubMed]
- Van Zundert, G.C.P.; Melquiond, A.S.J.; Bonvin, A. Integrative Modeling of Biomolecular Complexes: HADDOCKing with Cryo-Electron Microscopy Data. Structure 2015, 23, 949–960. [Google Scholar] [CrossRef]
- Bettadapura, R.; Rasheed, M.; Vollrath, A.; Bajaj, C. PF2fit: Polar Fast Fourier Matched Alignment of Atomistic Structures with 3D Electron Microscopy Maps. PLoS Comput. Biol. 2015, 11, 1004289. [Google Scholar] [CrossRef][Green Version]
- Kuzu, G.; Keskin, O.; Nussinov, R.; Gursoy, A. PRISM-EM: Template interface-based modelling of multi-protein complexes guided by cryo-electron microscopy density maps. Acta Cryst. D Struct. Biol. 2016, 72, 1137–1148. [Google Scholar] [CrossRef]
- Wriggers, W.; Birmanns, S. Using situs for flexible and rigid-body fitting of multiresolution single-molecule data. J. Struct. Biol. 2001, 133, 193–202. [Google Scholar] [CrossRef]
- Chen, J.Z.; Furst, J.; Chapman, M.S.; Grigorieff, N. Low-resolution structure refinement in electron microscopy. J. Struct. Biol. 2003, 144, 144–151. [Google Scholar] [CrossRef]
- Tama, F.; Miyashita, O.; Brooks, C.L., 3rd. Normal mode based flexible fitting of high-resolution structure into low-resolution experimental data from cryo-EM. J. Struct. Biol. 2004, 147, 315–326. [Google Scholar] [CrossRef]
- Delarue, M.; Dumas, P. On the use of low-frequency normal modes to enforce collective movements in refining macromolecular structural models. Proc. Natl. Acad. Sci. USA 2004, 101, 6957–6962. [Google Scholar] [CrossRef]
- Hinsen, K.; Reuter, N.; Navaza, J.; Stokes, D.L.; Lacapere, J.J. Normal mode-based fitting of atomic structure into electron density maps: Application to sarcoplasmic reticulum Ca-ATPase. Biophys. J. 2005, 88, 818–827. [Google Scholar] [CrossRef] [PubMed]
- Velazquez-Muriel, J.A.; Valle, M.; Santamaria-Pang, A.; Kakadiaris, I.A.; Carazo, J.M. Flexible fitting in 3D-EM guided by the structural variability of protein superfamilies. Structure 2006, 14, 1115–1126. [Google Scholar] [CrossRef] [PubMed]
- Suhre, K.; Navaza, J.; Sanejouand, Y.H. NORMA: A tool for flexible fitting of high-resolution protein structures into low-resolution electron-microscopy-derived density maps. Acta Cryst. D Biol. Cryst. 2006, 62, 1098–1100. [Google Scholar] [CrossRef] [PubMed]
- Topf, M.; Baker, M.L.; Marti-Renom, M.A.; Chiu, W.; Sali, A. Refinement of protein structures by iterative comparative modeling and CryoEM density fitting. J. Mol. Biol. 2006, 357, 1655–1668. [Google Scholar] [CrossRef] [PubMed]
- Velazquez-Muriel, J.A.; Carazo, J.M. Flexible fitting in 3D-EM with incomplete data on superfamily variability. J. Struct. Biol. 2007, 158, 165–181. [Google Scholar] [CrossRef] [PubMed]
- Topf, M.; Lasker, K.; Webb, B.; Wolfson, H.; Chiu, W.; Sali, A. Protein structure fitting and refinement guided by cryo-EM density. Structure 2008, 16, 295–307. [Google Scholar] [CrossRef]
- Jolley, C.C.; Wells, S.A.; Fromme, P.; Thorpe, M.F. Fitting low-resolution cryo-EM maps of proteins using constrained geometric simulations. Biophys. J. 2008, 94, 1613–1621. [Google Scholar] [CrossRef]
- Tan, R.K.; Devkota, B.; Harvey, S.C. YUP.SCX: Coaxing atomic models into medium resolution electron density maps. J. Struct. Biol. 2008, 163, 163–174. [Google Scholar] [CrossRef]
- Trabuco, L.G.; Villa, E.; Mitra, K.; Frank, J.; Schulten, K. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure 2008, 16, 673–683. [Google Scholar] [CrossRef]
- Orzechowski, M.; Tama, F. Flexible fitting of high-resolution x-ray structures into cryoelectron microscopy maps using biased molecular dynamics simulations. Biophys. J. 2008, 95, 5692–5705. [Google Scholar] [CrossRef]
- Siebert, X.; Navaza, J. UROX 2.0: An interactive tool for fitting atomic models into electron-microscopy reconstructions. Acta Cryst. D Biol. Cryst. 2009, 65, 651–658. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.; Cheng, L.; Fang, Q.; Zhou, Z.H.; Honig, B. Building and refining protein models within cryo-electron microscopy density maps based on homology modeling and multiscale structure refinement. J. Mol. Biol. 2010, 397, 835–851. [Google Scholar] [CrossRef] [PubMed]
- Grubisic, I.; Shokhirev, M.N.; Orzechowski, M.; Miyashita, O.; Tama, F. Biased coarse-grained molecular dynamics simulation approach for flexible fitting of X-ray structure into cryo electron microscopy maps. J. Struct. Biol. 2010, 169, 95–105. [Google Scholar] [CrossRef] [PubMed]
- Zheng, W. Accurate flexible fitting of high-resolution protein structures into cryo-electron microscopy maps using coarse-grained pseudo-energy minimization. Biophys. J. 2011, 100, 478–488. [Google Scholar] [CrossRef] [PubMed]
- Chan, K.Y.; Gumbart, J.; McGreevy, R.; Watermeyer, J.M.; Sewell, B.T.; Schulten, K. Symmetry-restrained flexible fitting for symmetric EM maps. Structure 2011, 19, 1211–1218. [Google Scholar] [CrossRef] [PubMed]
- Whitford, P.C.; Ahmed, A.; Yu, Y.; Hennelly, S.P.; Tama, F.; Spahn, C.M.; Onuchic, J.N.; Sanbonmatsu, K.Y. Excited states of ribosome translocation revealed through integrative molecular modeling. Proc. Natl. Acad. Sci. USA 2011, 108, 18943–18948. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Schroder, G.F. Real-space refinement with DireX: From global fitting to side-chain improvements. Biopolymers 2012, 97, 687–697. [Google Scholar] [CrossRef]
- Vashisth, H.; Skiniotis, G.; Brooks, C.L., 3rd. Using enhanced sampling and structural restraints to refine atomic structures into low-resolution electron microscopy maps. Structure 2012, 20, 1453–1462. [Google Scholar] [CrossRef]
- Ahmed, A.; Whitford, P.C.; Sanbonmatsu, K.Y.; Tama, F. Consensus among flexible fitting approaches improves the interpretation of cryo-EM data. J. Struct. Biol. 2012, 177, 561–570. [Google Scholar] [CrossRef][Green Version]
- Lopez-Blanco, J.R.; Chacon, P. iMODFIT: Efficient and robust flexible fitting based on vibrational analysis in internal coordinates. J. Struct. Biol. 2013, 184, 261–270. [Google Scholar] [CrossRef]
- Singharoy, A.; Teo, I.; McGreevy, R.; Stone, J.E.; Zhao, J.; Schulten, K. Molecular dynamics-based refinement and validation for sub-5 A cryo-electron microscopy maps. Elife 2016, 5. [Google Scholar] [CrossRef] [PubMed]
- Miyashita, O.; Kobayashi, C.; Mori, T.; Sugita, Y.; Tama, F. Flexible fitting to cryo-EM density map using ensemble molecular dynamics simulations. J. Comput. Chem. 2017, 38, 1447–1461. [Google Scholar] [CrossRef] [PubMed]
- Dou, H.; Burrows, D.W.; Baker, M.L.; Ju, T. Flexible Fitting of Atomic Models into Cryo-EM Density Maps Guided by Helix Correspondences. Biophys. J. 2017, 112, 2479–2493. [Google Scholar] [CrossRef] [PubMed]
- Croll, T.I. ISOLDE: A physically realistic environment for model building into low-resolution electron-density maps. Acta Cryst. D Struct. Biol. 2018, 74, 519–530. [Google Scholar] [CrossRef]
- Kovacs, J.A.; Galkin, V.E.; Wriggers, W. Accurate flexible refinement of atomic models against medium-resolution cryo-EM maps using damped dynamics. BMC Struct. Biol. 2018, 18, 12. [Google Scholar] [CrossRef]
- Kim, D.N.; Moriarty, N.W.; Kirmizialtin, S.; Afonine, P.V.; Poon, B.; Sobolev, O.V.; Adams, P.D.; Sanbonmatsu, K. Cryo_fit: Democratization of flexible fitting for cryo-EM. J. Struct. Biol. 2019, 208, 1–6. [Google Scholar] [CrossRef]
- Kidmose, R.T.; Juhl, J.; Nissen, P.; Boesen, T.; Karlsen, J.L.; Pedersen, B.P. Namdinator – automatic molecular dynamics flexible fitting of structural models into cryo-EM and crystallography experimental maps. IUCrJ 2019, 6, 526–531. [Google Scholar] [CrossRef]
- Mori, T.; Kulik, M.; Miyashita, O.; Jung, J.; Tama, F.; Sugita, Y. Acceleration of cryo-EM Flexible Fitting for Large Biomolecular Systems by Efficient Space Partitioning. Structure 2019, 27, 161–174. [Google Scholar] [CrossRef]
- Igaev, M.; Kutzner, C.; Bock, L.V.; Vaiana, A.C.; Grubmuller, H. Automated cryo-EM structure refinement using correlation-driven molecular dynamics. Elife 2019, 8. [Google Scholar] [CrossRef]
- Lindert, S.; Staritzbichler, R.; Wotzel, N.; Karakas, M.; Stewart, P.L.; Meiler, J. EM-fold: De novo folding of alpha-helical proteins guided by intermediate-resolution electron microscopy density maps. Structure 2009, 17, 990–1003. [Google Scholar] [CrossRef]
- Baker, M.L.; Abeysinghe, S.S.; Schuh, S.; Coleman, R.A.; Abrams, A.; Marsh, M.P.; Hryc, C.F.; Ruths, T.; Chiu, W.; Ju, T. Modeling protein structure at near atomic resolutions with Gorgon. J. Struct. Biol. 2011, 174, 360–373. [Google Scholar] [CrossRef] [PubMed]
- Baker, M.R.; Rees, I.; Ludtke, S.J.; Chiu, W.; Baker, M.L. Constructing and validating initial Calpha models from subnanometer resolution density maps with pathwalking. Structure 2012, 20, 450–463. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.Y.; Kudryashev, M.; Li, X.; Egelman, E.H.; Basler, M.; Cheng, Y.; Baker, D.; DiMaio, F. De novo protein structure determination from near-atomic-resolution cryo-EM maps. Nat. Methods 2015, 12, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Baldwin, P.R.; Ludtke, S.J.; Baker, M.L. De Novo modeling in cryo-EM density maps with Pathwalking. J. Struct. Biol. 2016, 196, 289–298. [Google Scholar] [CrossRef]
- Terwilliger, T.C.; Adams, P.D.; Afonine, P.V.; Sobolev, O.V. A fully automatic method yielding initial models from high-resolution cryo-electron microscopy maps. Nat. Methods 2018, 15, 905–908. [Google Scholar] [CrossRef]
- Terashi, G.; Kihara, D. De novo main-chain modeling for EM maps using MAINMAST. Nat. Commun. 2018, 9, 1618. [Google Scholar] [CrossRef]
- Terwilliger, T.C.; Adams, P.D.; Afonine, P.V.; Sobolev, O.V. Cryo-EM map interpretation and protein model-building using iterative map segmentation. Protein Sci. 2019, 1, 1–13. [Google Scholar] [CrossRef]
- Kawabata, T. Gaussian-input Gaussian mixture model for representing density maps and atomic models. J. Struct. Biol. 2018, 203, 1–16. [Google Scholar] [CrossRef]
- Vincent, L.; Soille, P. Watersheds in digital spaces: An efficient algorithm based on immersion simulations. IEEE Trans. Pattern Anal. Mach. 1991, 13, 583–598. [Google Scholar] [CrossRef]
- Witkin, A. Scale-space filtering: A new approach to multi-scale description. IEEE Int. Conf. Acoust. SpeechSignal Process. (ICASSP) 1983, 9, 150–153. [Google Scholar]
- Vasishtan, D.; Topf, M. Scoring functions for cryoEM density fitting. J. Struct. Biol. 2011, 174, 333–343. [Google Scholar] [CrossRef] [PubMed]
- Joseph, A.P.; Lagerstedt, I.; Patwardhan, A.; Topf, M.; Winn, M. Improved metrics for comparing structures of macromolecular assemblies determined by 3D electron-microscopy. J. Struct. Biol. 2017, 199, 12–26. [Google Scholar] [CrossRef] [PubMed]
- Joseph, A.P.; Swapna, L.S.; Rakesh, R.; Srinivasan, N. Use of evolutionary information in the fitting of atomic level protein models in low resolution cryo-EM map of a protein assembly improves the accuracy of the fitting. J. Struct. Biol. 2016, 195, 294–305. [Google Scholar] [CrossRef] [PubMed]
- Go, N.; Noguti, T.; Nishikawa, T. Dynamics of a small globular protein in terms of low-frequency vibrational modes. Proc. Natl. Acad. Sci. USA 1983, 80, 3696–3700. [Google Scholar] [CrossRef] [PubMed]
- Tama, F.; Sanejouand, Y.H. Conformational change of proteins arising from normal mode calculations. Protein Eng. 2001, 14, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Tama, F.; Miyashita, O.; Brooks, C.L., 3rd. Flexible multi-scale fitting of atomic structures into low-resolution electron density maps with elastic network normal mode analysis. J. Mol. Biol. 2004, 337, 985–999. [Google Scholar] [CrossRef]
- Malhotra, S.; Trager, S.; Dal Peraro, M.; Topf, M. Modelling structures in cryo-EM maps. Curr. Opin. Struct. Biol. 2019, 58, 105–114. [Google Scholar] [CrossRef]
- Kim, D.N.; Sanbonmatsu, K.Y. Tools for the cryo-EM gold rush: Going from the cryo-EM map to the atomistic model. Biosci. Rep. 2017, 37. [Google Scholar] [CrossRef]
- Frenz, B.; Walls, A.C.; Egelman, E.H.; Veesler, D.; DiMaio, F. RosettaES: A sampling strategy enabling automated interpretation of difficult cryo-EM maps. Nat. Methods 2017, 14, 797–800. [Google Scholar] [CrossRef]
- Terashi, G.; Kihara, D. De novo main-chain modeling with MAINMAST in 2015/2016 EM Model Challenge. J. Struct. Biol. 2018, 204, 351–359. [Google Scholar] [CrossRef]
- Terwilliger, T.C.; Sobolev, O.V.; Afonine, P.V.; Adams, P.D. Automated map sharpening by maximization of detail and connectivity. Acta Cryst. D Struct. Biol. 2018, 74, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Afonine, P.V.; Poon, B.K.; Read, R.J.; Sobolev, O.V.; Terwilliger, T.C.; Urzhumtsev, A.; Adams, P.D. Real-space refinement in PHENIX for cryo-EM and crystallography. Acta Cryst. D Struct. Biol. 2018, 74, 531–544. [Google Scholar] [CrossRef] [PubMed]
- Rotkiewicz, P.; Skolnick, J. Fast procedure for reconstruction of full-atom protein models from reduced representations. J. Comput. Chem. 2008, 29, 1460–1465. [Google Scholar] [CrossRef] [PubMed]
- Al-Azzawi, A.; Ouadou, A.; Tanner, J.J.; Cheng, J. AutoCryoPicker: An unsupervised learning approach for fully automated single particle picking in Cryo-EM images. BMC Bioinform. 2019, 20, 326. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Gong, H.; Liu, G.; Li, M.; Yan, C.; Xia, T.; Li, X.; Zeng, J. DeepPicker: A deep learning approach for fully automated particle picking in cryo-EM. J. Struct. Biol. 2016, 195, 325–336. [Google Scholar] [CrossRef]
- Zhu, Y.; Ouyang, Q.; Mao, Y. A deep convolutional neural network approach to single-particle recognition in cryo-electron microscopy. BMC Bioinform. 2017, 18, 348. [Google Scholar] [CrossRef]
- Sanchez-Garcia, R.; Segura, J.; Maluenda, D.; Carazo, J.M.; Sorzano, C.O.S. Deep Consensus, a deep learning-based approach for particle pruning in cryo-electron microscopy. IUCrJ 2018, 5, 854–865. [Google Scholar] [CrossRef]
- Chen, M.; Dai, W.; Sun, S.Y.; Jonasch, D.; He, C.Y.; Schmid, M.F.; Chiu, W.; Ludtke, S.J. Convolutional neural networks for automated annotation of cellular cryo-electron tomograms. Nat. Methods 2017, 14, 983–985. [Google Scholar] [CrossRef]
- Bell, J.M.; Chen, M.; Durmaz, T.; Fluty, A.C.; Ludtke, S.J. New software tools in EMAN2 inspired by EMDatabank map challenge. J. Struct. Biol. 2018, 204, 283–290. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Z.; Chen, Y.; Han, R.; Liu, Z.; Sun, F.; Zhang, F. PIXER: An automated particle-selection method based on segmentation using a deep neural network. BMC Bioinform. 2019, 20, 41. [Google Scholar] [CrossRef]
- Maddhuri Venkata Subramaniya, S.R.; Terashi, G.; Kihara, D. Protein secondary structure detection in intermediate-resolution cryo-EM maps using deep learning. Nat. Methods 2019, 16, 911–917. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Reisert, M.; Burkhardt, H. RENNSH: A novel alpha-helix identification approach for intermediate resolution electron density maps. IEEE/ACM Trans. Comput. Biol. Bioinform. 2012, 9, 228–239. [Google Scholar] [CrossRef] [PubMed]
- Si, D.; Ji, S.; Nasr, K.A.; He, J. A machine learning approach for the identification of protein secondary structure elements from electron cryo-microscopy density maps. Biopolymers 2012, 97, 698–708. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Si, D.; Zeng, T.; Ji, S.; He, J. Deep Convolutional Neural Networks for Detecting Secondary Structures in Protein Density Maps from Cryo-Electron Microscopy. Proc. IEEE Int. Conf. Bioinform. Biomed. 2016, 2016, 41–46. [Google Scholar] [CrossRef]
- Sorzano, C.O.S.; Jimenez, A.; Mota, J.; Vilas, J.L.; Maluenda, D.; Martinez, M.; Ramirez-Aportela, E.; Majtner, T.; Segura, J.; Sanchez-Garcia, R.; et al. Survey of the analysis of continuous conformational variability of biological macromolecules by electron microscopy. Acta Cryst. F Struct. Biol. Commun. 2019, 75, 19–32. [Google Scholar] [CrossRef] [PubMed]
- Frank, J.; Ourmazd, A. Continuous changes in structure mapped by manifold embedding of single-particle data in cryo-EM. Methods 2016, 100, 61–67. [Google Scholar] [CrossRef] [PubMed]
- Haselbach, D.; Komarov, I.; Agafonov, D.E.; Hartmuth, K.; Graf, B.; Dybkov, O.; Urlaub, H.; Kastner, B.; Luhrmann, R.; Stark, H. Structure and Conformational Dynamics of the Human Spliceosomal B(act) Complex. Cell 2018, 172, 454–464. [Google Scholar] [CrossRef]
- Hutchings, J.; Zanetti, G. Fine details in complex environments: The power of cryo-electron tomography. Biochem. Soc. Trans. 2018, 46, 807–816. [Google Scholar] [CrossRef]
- Schaffer, M.; Mahamid, J.; Engel, B.D.; Laugks, T.; Baumeister, W.; Plitzko, J.M. Optimized cryo-focused ion beam sample preparation aimed at in situ structural studies of membrane proteins. J. Struct. Biol. 2017, 197, 73–82. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).