How to Measure and Calculate Equivalent Series Resistance of Electric Double-Layer Capacitors
Abstract
1. Introduction
2. Fundamentals of the EIS and GCD Methods
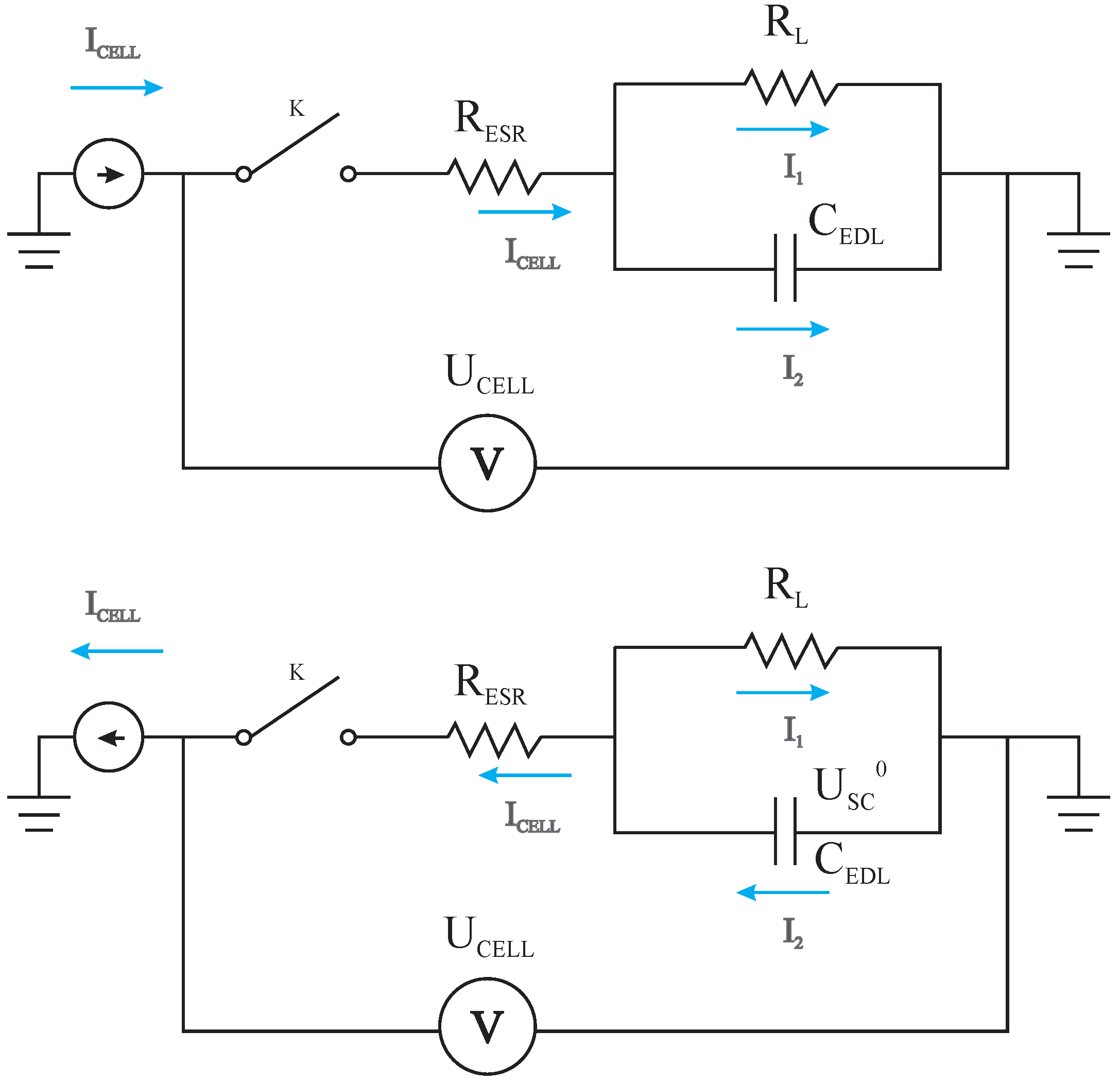
3. Theoretical Electric Response of the GCD Curves Using the Canonic Equivalent Circuit Model
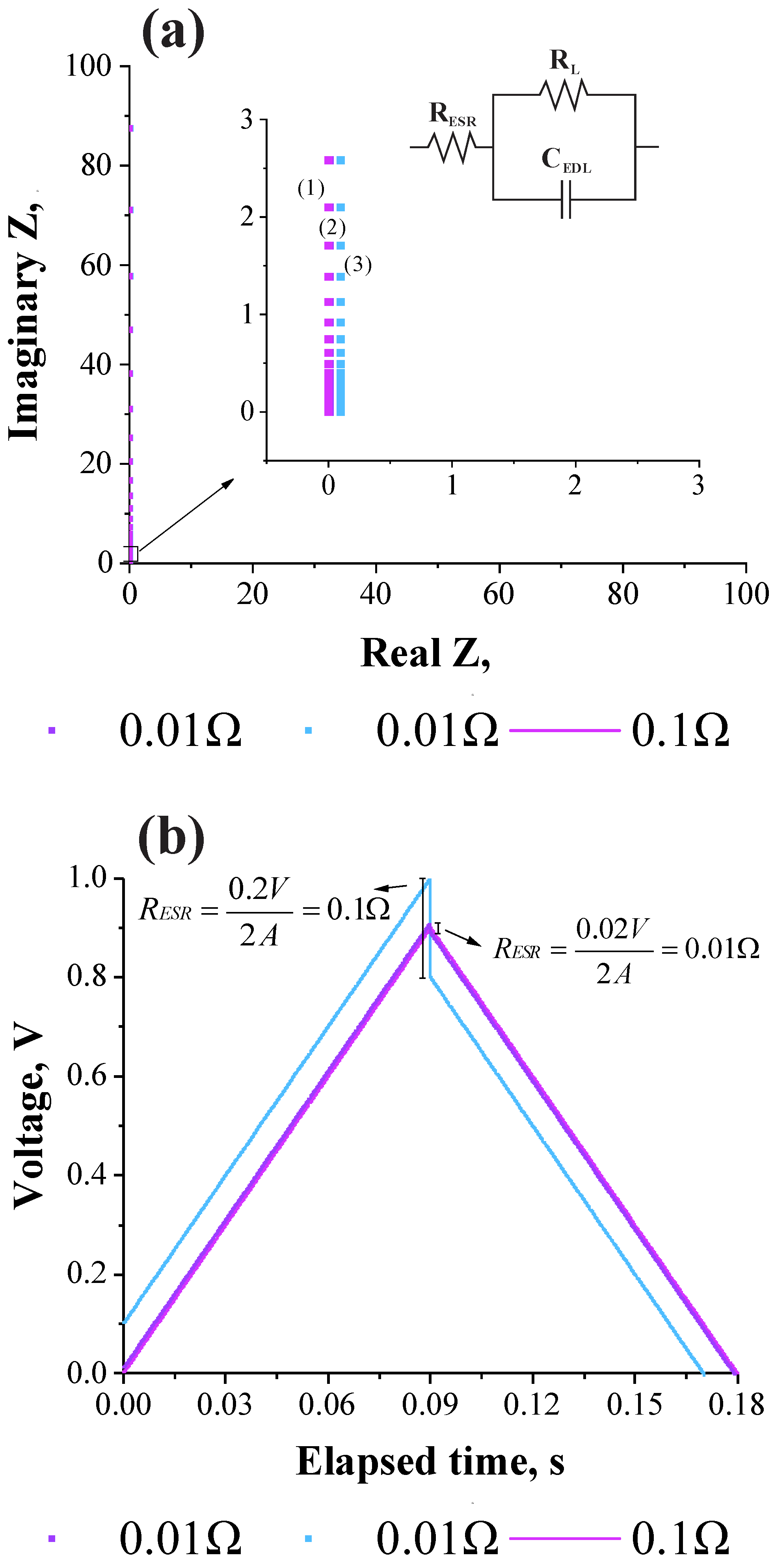
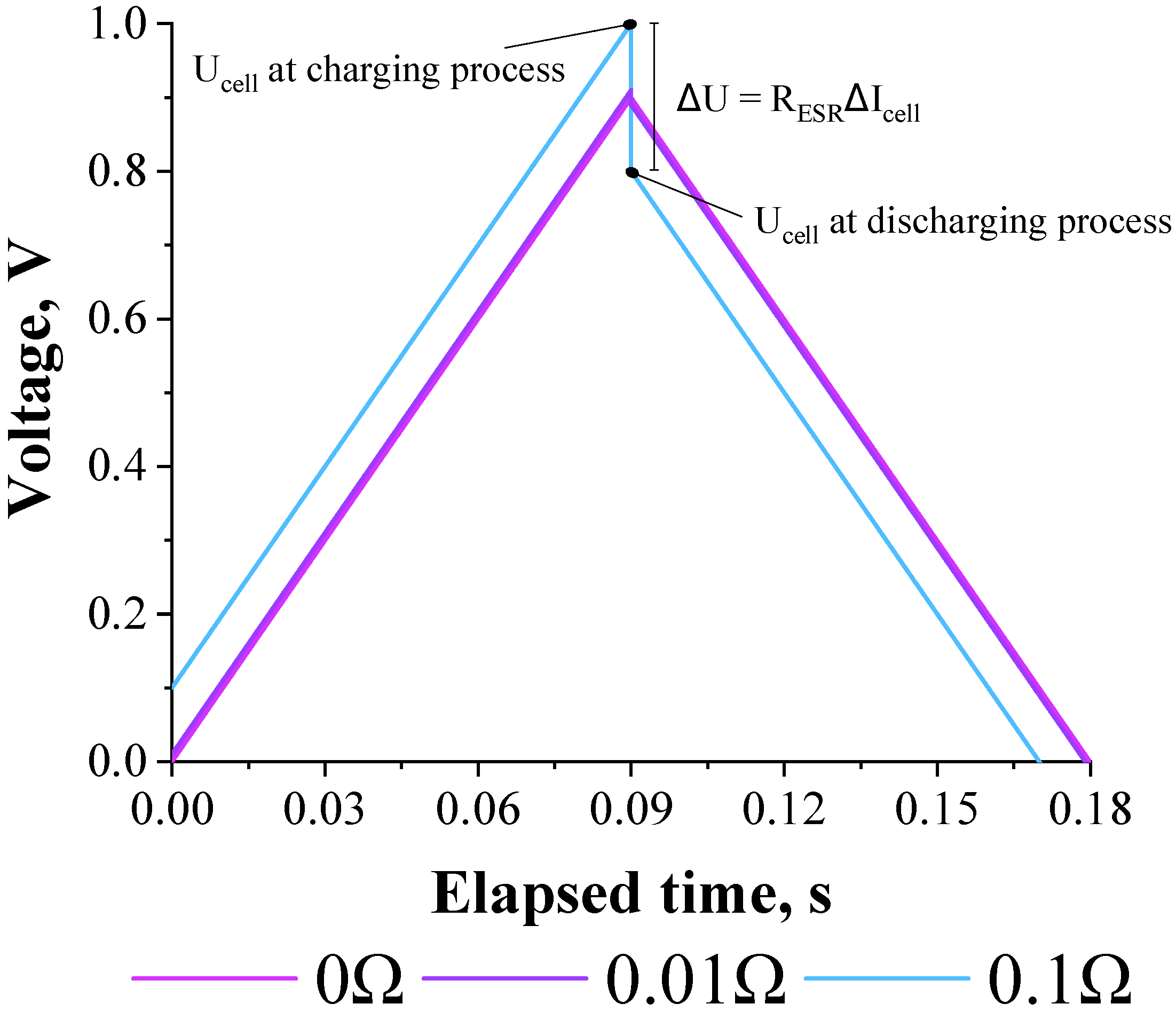
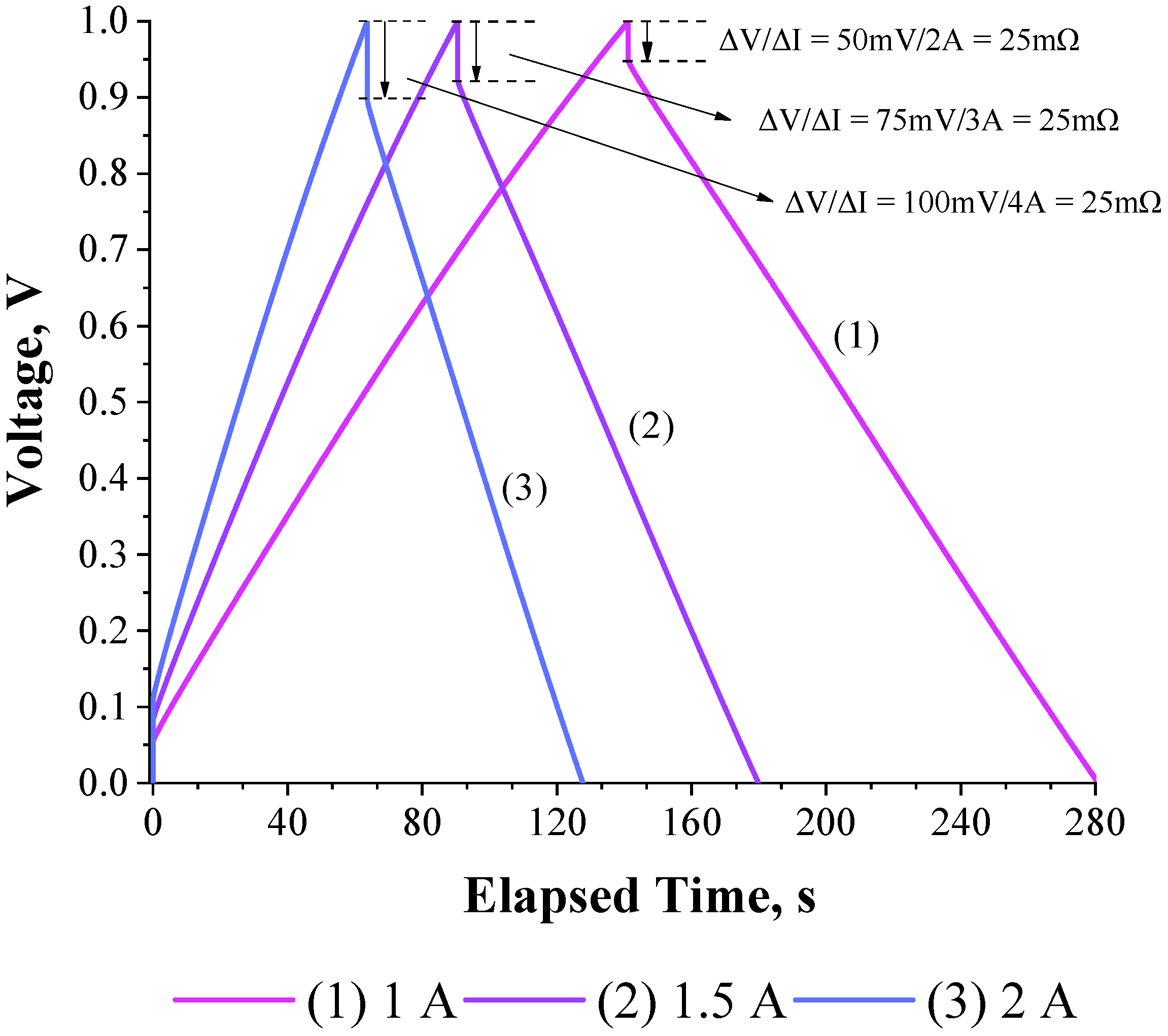
3.1. Deriving the Theoretical Formula for the Equivalent Series Resistance
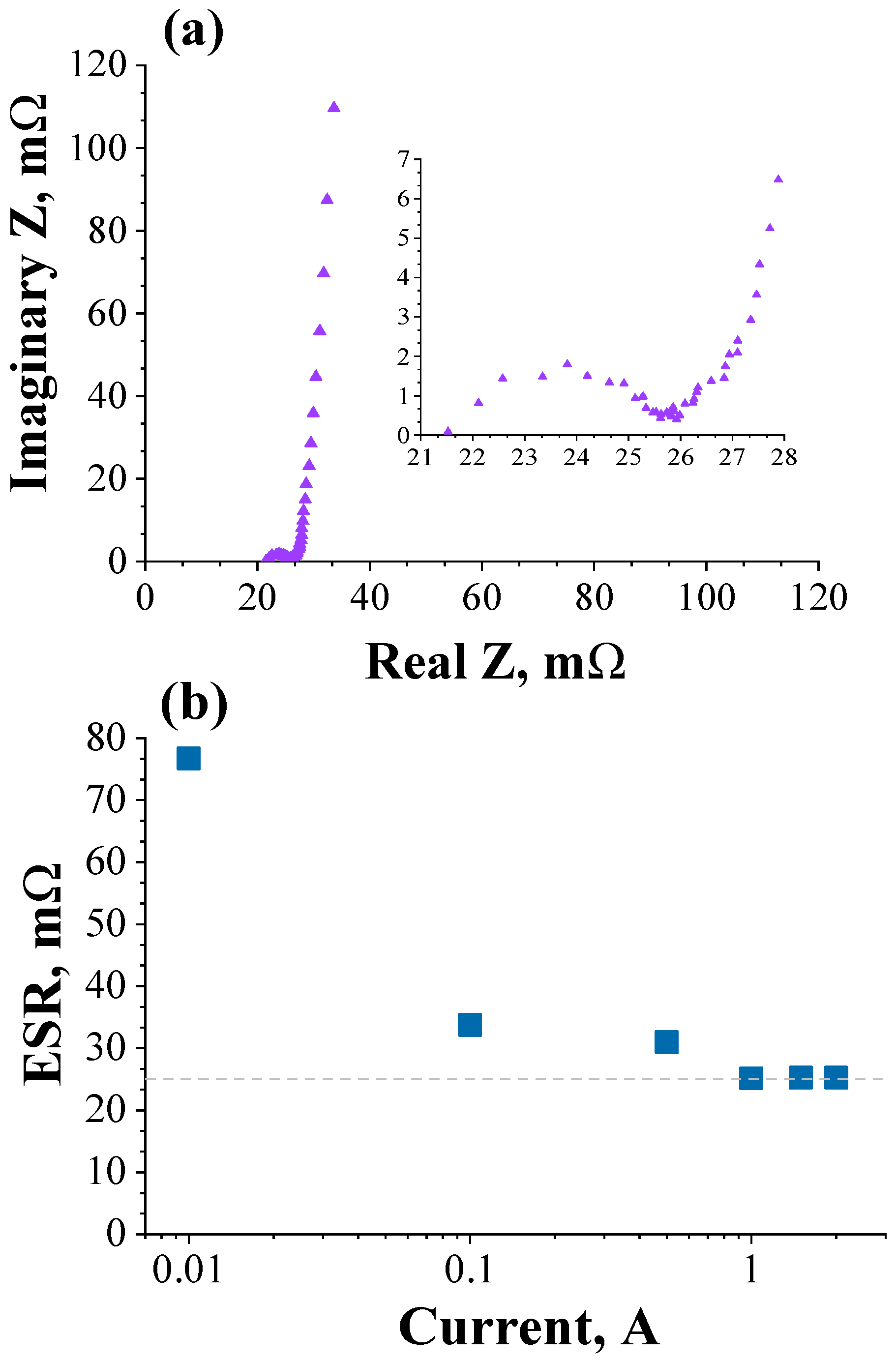
3.2. Validation of the Theoretical Expression Obtained for the Equivalent Series Resistance Using a Commercial Supercapacitor of 200 F
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yu, A.; Chabot, V.; Zhang, J. Electrochemical Supercapacitors for Energy Storage and Delivery: Fundamentals and Applications, 1st ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Lu, M.; Beguin, F.; Frackowiak, E. Supercapacitors: Materials, Systems, and Applications, 1st ed.; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Vicentini, R.; Costa, L.H.; Nunes, W.; Boas, O.V.; Soares, D.M.; Alves, T.A.; Real, C.; Bueno, C.; Peterlevitz, A.C.; Zanin, H. Direct growth of mesoporous Carbon on aluminum foil for supercapacitors devices. J. Mater. Sci. Mater. Electron. 2018, 29, 10573–10582. [Google Scholar] [CrossRef]
- Conway, B.E. Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications; Plenum Press: New York, NY, USA, 1999. [Google Scholar]
- Taberna, P.L.; Simon, P.; Fauvarque, J.F. Electrochemical Characteristics and Impedance Spectroscopy Studies of Carbon-Carbon Supercapacitors. J. Electrochem. Soc. 2003, 150, A292–A300. [Google Scholar] [CrossRef]
- Taberna, P.L.; Portet, C.; Simon, P. Electrode surface treatment and electrochemical impedance spectroscopy study on carbon/carbon supercapacitors. Appl. Phys. A 2006, 82, 639–646. [Google Scholar] [CrossRef]
- Basri, N.H.; Dolah, B.N.M. Physical and electrochemical properties of supercapacitor electrodes derived from carbon nanotube and biomass carbon. Int. J. Electrochem. Sci. 2013, 8, 257–273. [Google Scholar]
- Niu, Z.; Zhou, W.; Chen, J.; Feng, G.; Li, H.; Ma, W.; Li, J.; Dong, H.; Ren, Y.; Zhao, D.; et al. Compact-designed supercapacitors using free-standing single-walled carbon nanotube films. Environ. Sci. 2011, 4, 1440–1446. [Google Scholar] [CrossRef]
- Wang, Y.; Shi, Z.; Huang, Y.; Ma, Y.; Wang, C.; Chen, M.; Chen, Y. Supercapacitor Devices Based on Graphene Materials. J. Phys. Chem. C 2009, 113, 13103–13107. [Google Scholar] [CrossRef]
- Boukhalfa, S.; Evanoff, K.; Yushin, G. Atomic layer deposition of vanadium oxide on carbon nanotubes for high-power supercapacitor electrodes. Environ. Sci. 2012, 5, 6872–6879. [Google Scholar] [CrossRef]
- Giorgi, A.; Mastragostino, M.; Soavi, F.; Di Fabio, A. Carbon-Poly(3-methylthiophene) Hybrid Supercapacitors. J. Electrochem. Soc. 2001, 148, A845–A850. [Google Scholar]
- Caporali, S.; Soavi, F.; Balducci, A.; Bardi, U.; Mastragostino, M. Ionic liquids for hybrid supercapacitors. Electrochem. Commun. 2004, 6, 566–570. [Google Scholar]
- Futaba, D.N.; Hata, K.; Yamada, T.; Hiraoka, T.; Hayamizu, Y.; Kakudate, Y.; Tanaike, O.; Hatori, H.; Yumura, M.; Iijima, S. Shape-engineerable and highly densely packed single-walled carbon nanotubes and their application as super-capacitor electrodes. Nat. Mater. 2006, 5, 987–994. [Google Scholar] [CrossRef] [PubMed]
- Gualous, H.; Bouquain, D.; Berthon, A.; Kauffmann, J. Experimental study of supercapacitor serial resistance and capacitance variations with temperature. J. Source 2003, 123, 86–93. [Google Scholar] [CrossRef]
- Keskinen, J.; Sivonen, E.; Jussila, S.; Bergelin, M.; Johansson, M.; Vaari, A.; Smolander, M. Printed supercapacitors on paperboard substrate. Electrochim. Acta 2012, 85, 302–306. [Google Scholar] [CrossRef]
- Zhong, Y.; Zhang, J.; Li, G.; Liu, A. Research on Energy Efficiency of Supercapacitor Energy Storage System. In Proceedings of the 2006 International Conference on Power System Technology, Chongqing, China, 22–16 October 2006; IEEE: Chongqing, China, 2006; pp. 1–4. [Google Scholar]
- Lasia, A. Electrochemical Impedance Spectroscopy and its Applications. Mod. Asp. Electrochem. 2002, 32, 143–248. [Google Scholar]
- Liu, X.; Pickup, P.G. Ru oxide supercapacitors with high loadings and high power and energy densities. J. Source 2008, 176, 410–416. [Google Scholar] [CrossRef]
- Shaijumon, M.M.; Ou, F.S.; Ci, L.; Ajayan, P.M. Synthesis of hybrid nanowire arrays and their application as high power supercapacitor electrodes. Chem. Commun. 2008, 2373–2375. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Wei, T.; Shao, B.; Ma, F.; Fan, Z.; Zhang, M.; Zheng, C.; Shang, Y.; Qian, W.; Wei, F. Electrochemical properties of graphene nanosheet/carbon black composites as electrodes for supercapacitors. Carbon 2010, 48, 1731–1737. [Google Scholar] [CrossRef]
- Blomquist, N.; Wells, T.; Andres, B.; Bäckström, J.; Forsberg, S.; Olin, H. Metal-free supercapacitor with aqueous electrolyte and low-cost carbon materials. Sci. Rep. 2017, 7, 39836. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Yu, Z.; Neff, D.; Zhamu, A.; Jang, B.Z. Graphene-Based Supercapacitor with an Ultrahigh Energy Density. Nano Lett. 2010, 10, 4863–4868. [Google Scholar] [CrossRef] [PubMed]
- Onsager, L. Deviations from Ohm’s law in weak electrolytes. J. Chem. Phys. 1934, 2, 599–615. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vicentini, R.; Da Silva, L.M.; Cecilio Junior, E.P.; Alves, T.A.; Nunes, W.G.; Zanin, H. How to Measure and Calculate Equivalent Series Resistance of Electric Double-Layer Capacitors. Molecules 2019, 24, 1452. https://doi.org/10.3390/molecules24081452
Vicentini R, Da Silva LM, Cecilio Junior EP, Alves TA, Nunes WG, Zanin H. How to Measure and Calculate Equivalent Series Resistance of Electric Double-Layer Capacitors. Molecules. 2019; 24(8):1452. https://doi.org/10.3390/molecules24081452
Chicago/Turabian StyleVicentini, Rafael, Leonardo Morais Da Silva, Edson Pedro Cecilio Junior, Thayane Almeida Alves, Willian Gonçalves Nunes, and Hudson Zanin. 2019. "How to Measure and Calculate Equivalent Series Resistance of Electric Double-Layer Capacitors" Molecules 24, no. 8: 1452. https://doi.org/10.3390/molecules24081452
APA StyleVicentini, R., Da Silva, L. M., Cecilio Junior, E. P., Alves, T. A., Nunes, W. G., & Zanin, H. (2019). How to Measure and Calculate Equivalent Series Resistance of Electric Double-Layer Capacitors. Molecules, 24(8), 1452. https://doi.org/10.3390/molecules24081452





