Distinct Difference in Sensitivity of NIR vs. IR Bands of Melamine to Inter-Molecular Interactions with Impact on Analytical Spectroscopy Explained by Anharmonic Quantum Mechanical Study
Abstract
1. Introduction
2. Results and Discussion
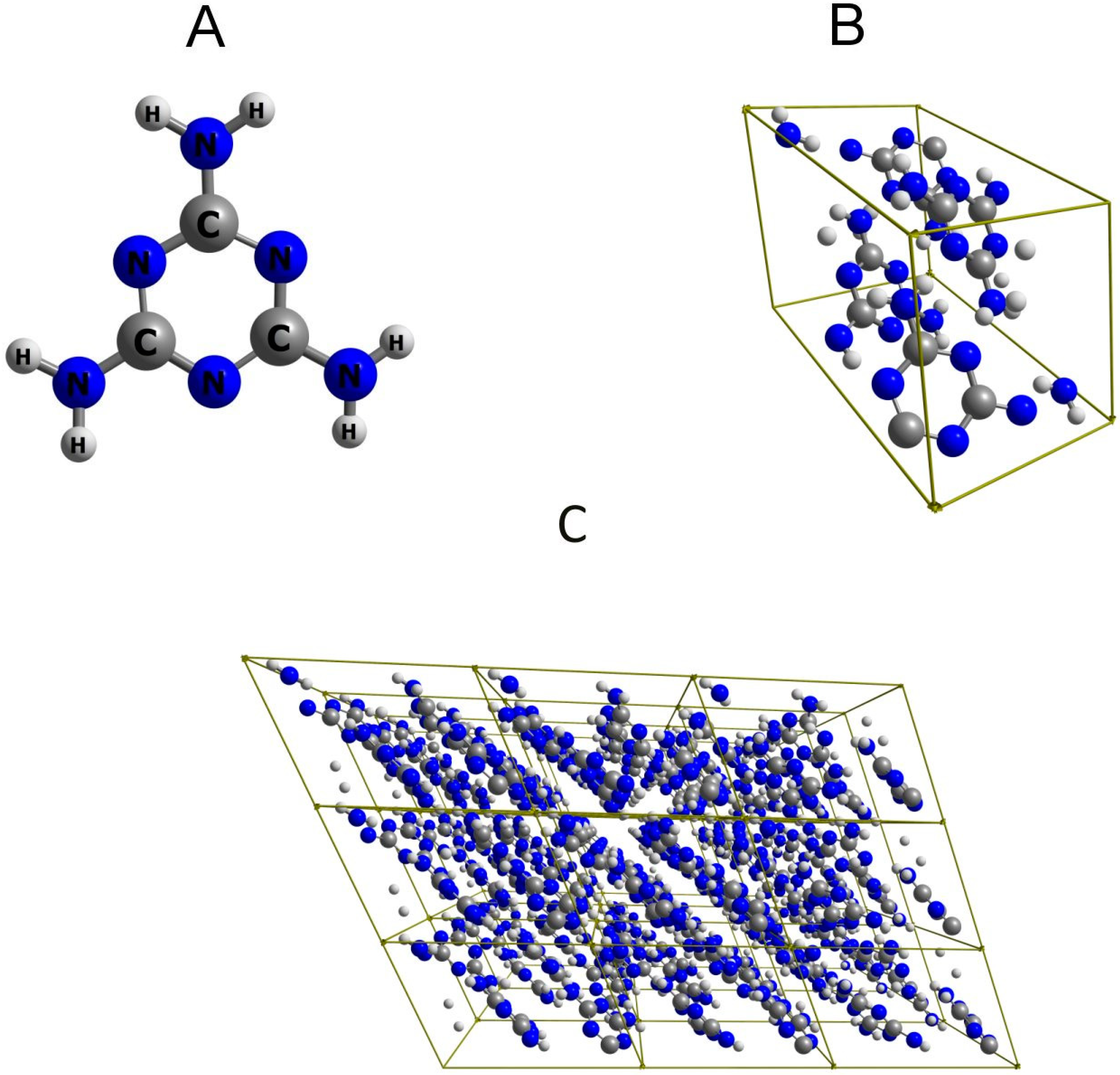
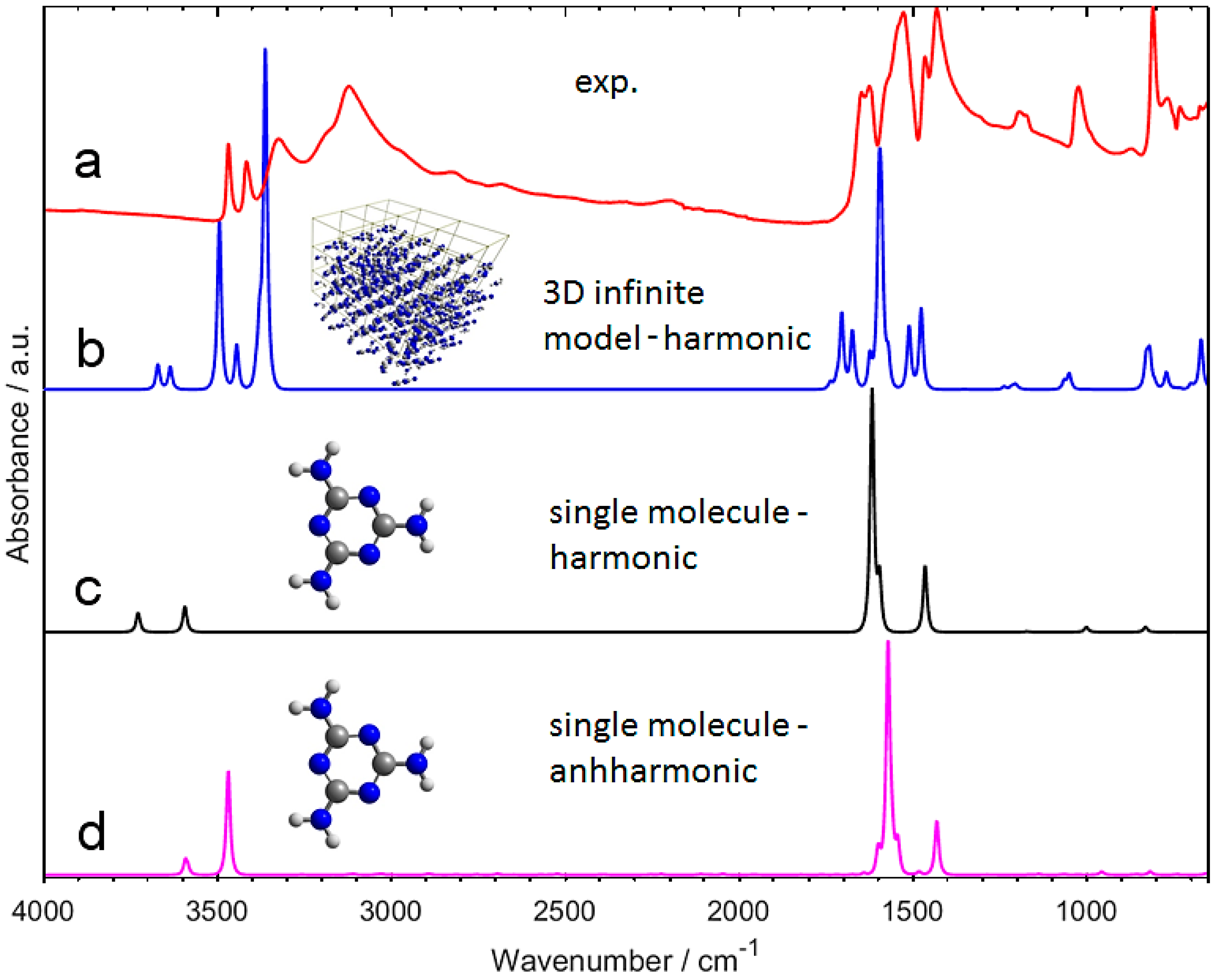
2.1. Experimental and Simulated IR Spectra of Crystalline Melamine
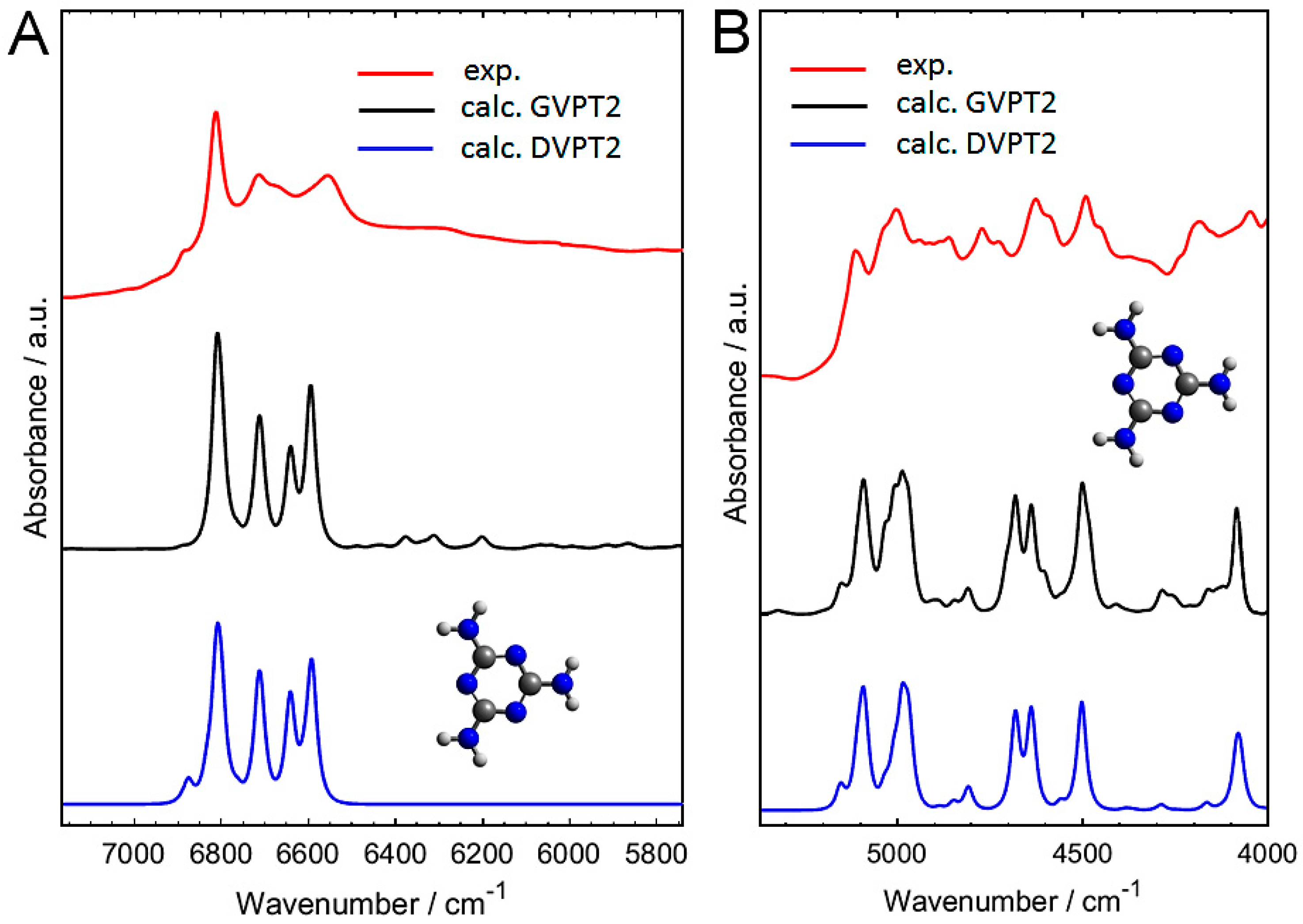
2.2. Experimental and Simulated NIR Spectra of Crystalline Melamine
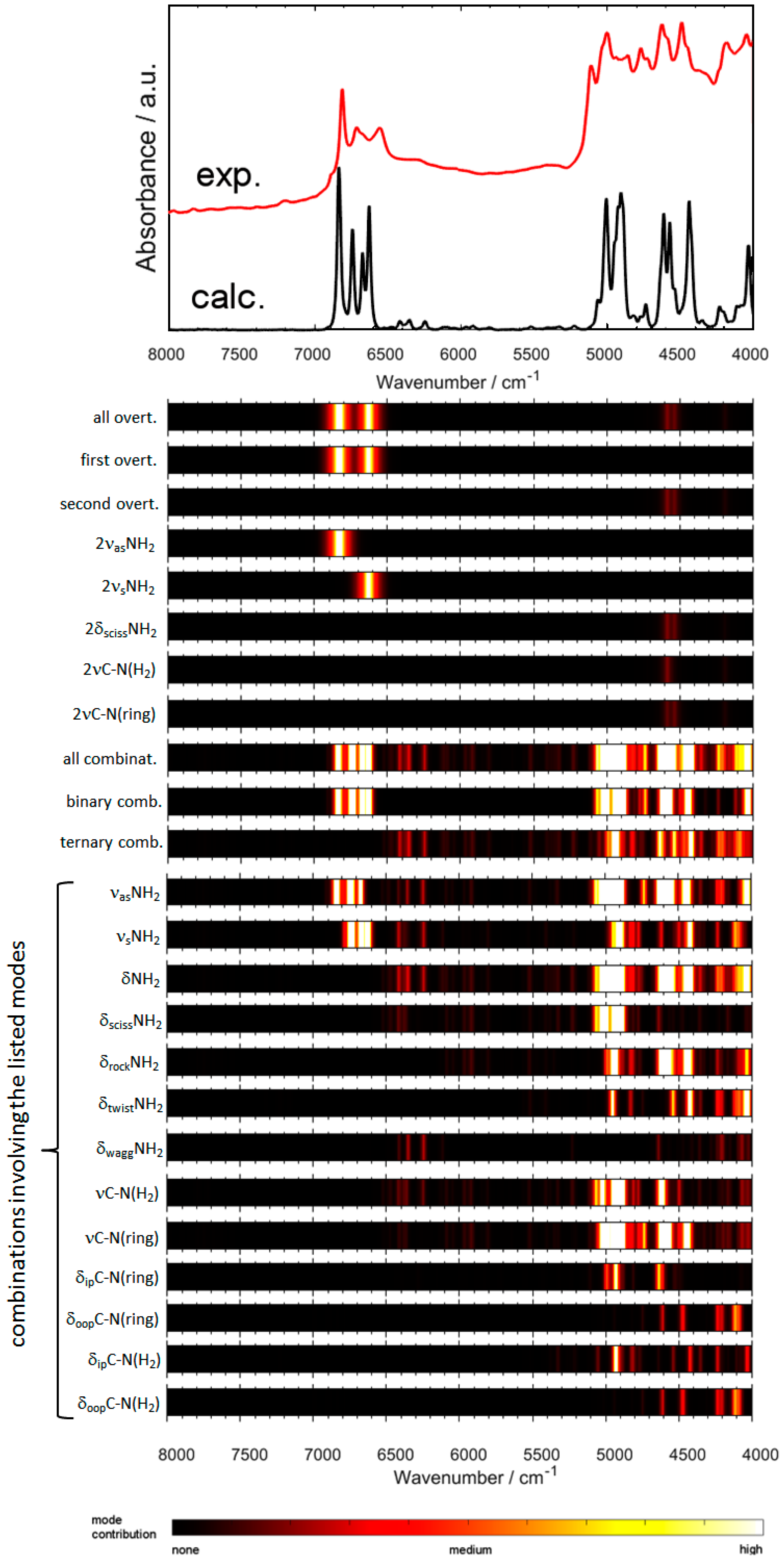
2.3. An In-Depth Analysis of the Origin of NIR Bands of Crystalline Melamine
2.4. The Relationships Between IR and NIR Bands, and the Structural Features of Crystalline Melamine
2.5. New Insights on the Quantitative Analytical Spectroscopy of Melamine
3. Materials and Methods
3.1. Experimental
3.2. Quantum Mechanical Calculations
3.2.1. IR spectrum Calculation in 3D Periodic Approximation
3.2.2. Anharmonic Calculation of NIR Spectra
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Deim, H.; Matthias, G.; Wagner, R.A. Amino Resins. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Weinheim, Germany, 2012. [Google Scholar]
- Ogawa, A. Effect of a melamine resin admixture on the properties of concrete. Concr. J. (Tokyo 1963) 1973, 11, 12–21. [Google Scholar] [CrossRef]
- Ashford, R.D. (Ed.) Ashford’s Dictionary of Industrial Chemicals, 3rd ed.; Wavelength Publications Ltd.: London, UK, 2011; p. 5713. [Google Scholar]
- Zhong, Y.; Jaidann, M.; Zhang, Y.; Zhang, G.; Liu, H.; Ionescu, M.; Li, R.; Sun, X.; Abou-Rachid, H.; Lussier, L.-S. Synthesis of high nitrogen doping of carbon nanotubes and modeling the stabilization of filled DAATO@CNTs (10,10) for nanoenergetic materials. J. Phys. Chem. Solids 2010, 71, 134–139. [Google Scholar] [CrossRef]
- Hauck, R.D.; Stephenson, H.F. Nitrification of triazine nitrogen. Fertilizer Nitrogen Sources 1964, 12, 147–151. [Google Scholar] [CrossRef]
- Chow, C.-Y. Number of Melamine-Sickened Children Revised up Five-Fold; South China Morning Post: Hong Kong, China, 2 December 2008; p. A9. [Google Scholar]
- Ng, T.-W. Lawyers Warned to Shun Milk Suits; South China Morning Post: Hong Kong, China, 23 September 2008; p. A2, Archived from the original on 6 February 2009. [Google Scholar]
- Pei, X.; Tandon, A.; Alldrick, A.; Giorgi, L.; Huang, W.; Yang, R. The China melamine milk scandal and its implications for food safety regulation. Food Policy 2011, 6, 412–420. [Google Scholar] [CrossRef]
- Cantor, S.L.; Gupta, A.; Khan, M.A. Analytical methods for the evaluation of melamine contamination. J. Pharm. Sci. 2014, 103, 539–544. [Google Scholar] [CrossRef] [PubMed]
- Henn, R.; Kirchler, C.G.; Grossgut, M.E.; Huck, C.W. Comparison of sensitivity to artificial spectral errors and multivariate LOD in NIR spectroscopy—Determining the performance of miniaturizations on melamine in milk powder. Talanta 2017, 166, 109–118. [Google Scholar] [CrossRef] [PubMed]
- De Benedictis, L.; Huck, C.W. New approach to optimise near-infrared spectra with design of experiments and determination of milk compounds as influence factors for changing milk over time. Food Chem. 2016, 212, 552–560. [Google Scholar] [CrossRef] [PubMed]
- Charlebois, S.; Schwab, A.; Henn, R.; Huck, C.W. An exploratory study for measuring consumer perception towards mislabelled food products and influence on self-authentication intentions. Trends Food Sci. Technol. 2016, 50, 211–218. [Google Scholar] [CrossRef]
- Near-Infrared Spectroscopy in Food Science and Technology; Ozaki, Y., McClure, W.F., Christy, A.A., Eds.; Wiley-Interscience: Hoboken, NJ, USA, 2007. [Google Scholar]
- Su, W.-H.; Arvanitoyannis, I.-S.; Sun, D.-W. Chapter: 18 Trends in Food Authentication. In Modern Techniques for Food Authentication, 2nd ed.; Sun, D.-W., Ed.; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Marini, F. (Ed.) Chemometrics in Food Chemistry, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 28. [Google Scholar]
- Ozaki, Y.; Huck, C.W.; Beć, K.B. Near infrared spectroscopy and its applications. In Molecular and Laser Spectroscopy; Gupta, V.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Huck, C.W. Infrared Spectroscopy in Near-Infrared/Infrared Bioanalysis Including Imaging; John Wiley & Sons, Encyclopedia of Analytical Chemistry: Hoboken, NJ, USA, 2016. [Google Scholar]
- Ciurczak, E.W.; Drennen, J.K., III. Pharmaceutical and Medical Applications of Near-Infrared Spectroscopy; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Chalmers, J.M.; Griffiths, P.R. (Eds.) Handbook of Vibrational Spectroscopy; John Wiley & Sons: Hoboken, NJ, USA, 2002; Volume 1. [Google Scholar]
- Herberholz, L.; Kolomiets, O.; Siesler, H.W. Quantitative analysis by a portable near infrared spectrometer: Can it replace laboratory instrumentation for in situ analysis? NIR News 2010, 21, 1–8. [Google Scholar] [CrossRef]
- Henn, R.; Schwab, A.; Huck, C.W. Evaluation of benchtop versus portable near-infrared spectroscopic method combined with multivariate approaches for the fast and simultaneous quantitative analysis of main sugars in syrup formulations. Food Contr. 2016, 68, 97–104. [Google Scholar] [CrossRef]
- SCiO—Pocket molecular sensor. Available online: https://www.consumerphysics.com/scio-for-consumers/ (accessed on 10 April 2019).
- Saranwong, S.; Kawano, S.; Ikehata, A.; Noguchi, G.; Park, S.; Sashida, K.; Okura, T.; Haff, R. Development of a low-cost NIR instrument for minced meat analysis: Part 1—Spectrophotometer and sample presentations. Am. J. Agric. Sci. Technol. 2013, 2, 61–68. [Google Scholar] [CrossRef]
- Huck, C.W. Near-infrared (NIR) spectroscopy in natural product research. In Handbook of Chemical and Biological Plant Analytical Methods; Hostettman, K., Chen, S., Marston, A., Stuppner, H., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Siesler, H.W. Near-Infrared Spectra, Interpretation. In Encyclopedia of Spectroscopy and Spectrometry (Third Edition); Lindon, J.C., Tranter, G.E., Koppenaal, D.W., Eds.; Academic Press: Oxford, UK, 2017. [Google Scholar]
- Weyer, L.G.; Lo, S.C. Spectra-structure correlations in the near-infrared. In Handbook of Vibrational Spectroscopy; Chalmers, J.M., Griffiths, P.R., Eds.; Wiley: Chichester, UK, 2002; Volume 3. [Google Scholar]
- Beć, K.B.; Grabska, J.; Ozaki, Y.; Hawranek, J.P.; Huck, C.W. Influence of non-fundamental modes on mid-infrared spectra of aliphatic ethers. A fully anharmonic DFT study. J. Phys. Chem. A 2017, 121, 1412–1424. [Google Scholar] [CrossRef] [PubMed]
- Łydżba-Kopczyńska, B.I.; Beć, K.B.; Tomczak, J.; Hawranek, J.P. Optical constants of liquid pyrrole in the infrared. J. Mol. Liq. 2012, 172, 34–40. [Google Scholar] [CrossRef]
- Beć, K.B.; Hawranek, J.P. Vibrational analysis of liquid n-butylmethylether. Vib. Spectrosc. 2013, 64, 164–171. [Google Scholar] [CrossRef]
- Beć, K.B.; Kwiatek, A.; Hawranek, J.P. Vibrational analysis of neat liquid tert-butylmethylether. J. Mol. Liq. 2014, 196, 26–31. [Google Scholar] [CrossRef]
- Beć, K.B.; Grabska, J.; Ozaki, Y. Advances in anharmonic methods and their applications to vibrational spectroscopies. In Frontiers of Quantum Chemistry; Wójcik, M.J., Nakatsuji, H., Kirtman, B., Ozaki, Y., Eds.; Springer: Singapore, 2017. [Google Scholar]
- Beć, K.B.; Grabska, J.; Huck, C.W.; Ozaki, Y. Quantum mechanical simulation of NIR spectra. In Applications in Physical and Analytical Chemistry; Ozaki, Y., Wójcik, M.J., Popp, J., Eds.; Wiley: Hoboken, NJ, USA, 2019; in press. [Google Scholar]
- Beć, K.B.; Futami, Y.; Wójcik, M.J.; Ozaki, Y. A spectroscopic and theoretical study in the near-infrared region of low concentration aliphatic alcohols. Phys. Chem. Chem. Phys. 2016, 18, 13666–13682. [Google Scholar] [CrossRef]
- Grabska, J.; Ishigaki, M.; Beć, K.B.; Wójcik, M.J.; Ozaki, Y. Structure and near-infrared spectra of saturated and unsaturated carboxylic acids. An insight from anharmonic DFT calculations. J. Phys. Chem. A 2017, 121, 3437–3451. [Google Scholar] [CrossRef]
- Grabska, J.; Beć, K.B.; Ishigaki, M.; Wójcik, M.J.; Ozaki, Y. Spectra-structure correlations of saturated and unsaturated medium-chain fatty acids. Near-infrared and anharmonic DFT study of hexanoic acid and sorbic acid. Spectrochim. Acta A 2017, 185, 35–44. [Google Scholar] [CrossRef]
- Grabska, J.; Beć, K.B.; Ishigaki, M.; Huck, C.W.; Ozaki, Y. NIR spectra simulations by anharmonic DFT-saturated and unsaturated long-chain fatty acids. J. Phys. Chem. B 2018, 122, 6931–6944. [Google Scholar] [CrossRef]
- Beć, K.B.; Grabska, J.; Kirchler, C.G.; Huck, C.W. NIR spectra simulation of thymol for better understanding of the spectra forming factors, phase and concentration effects and PLS regression features. J. Mol. Liq. 2018, 268, 895–902. [Google Scholar] [CrossRef]
- Kirchler, C.G.; Pezzei, C.K.; Beć, K.B.; Mayr, S.; Ishigaki, M.; Ozaki, Y.; Huck, C.W. Critical evaluation of spectral information of benchtop vs. portable near-infrared spectrometers: Quantum chemistry and two-dimensional correlation spectroscopy for a better understanding of PLS regression models of the rosmarinic acid content in Rosmarini folium. Analyst 2017, 142, 455–464. [Google Scholar]
- Kirchler, C.G.; Pezzei, C.K.; Beć, K.B.; Henn, R.; Ishigaki, M.; Ozaki, Y.; Huck, C.W. Critical evaluation of NIR and ATR-IR spectroscopic quantifications of rosmarinic acid in rosmarini folium supported by quantum chemical calculations. Planta Med. 2017, 83, 1076–1084. [Google Scholar] [CrossRef]
- Mircescu, N.E.; Oltean, M.; Chis, V.; Leopold, N. FTIR, FT-Raman, SERS and DFT study on melamine. Vib. Spectrosc. 2012, 62, 165–171. [Google Scholar] [CrossRef]
- Yuan, X.; Luo, K.; Zhang, K.; He, J.; Zhao, Y.; Yu, D. Combinatorial vibration-mode assignment for the FTIR spectrum of crystalline melamine: A strategic approach toward theoretical IR vibrational calculations of triazine-based compounds. J. Phys. Chem. A 2016, 120, 7427–7433. [Google Scholar] [CrossRef]
- Lu, C.; Xiang, B.; Hao, G.; Xu, J.; Wang, Z.; Chen, C. Rapid detection of melamine in milk powder by near infrared spectroscopy. J. Near Infrared Spectrosc. 2009, 17, 59–67. [Google Scholar] [CrossRef]
- Balabin, R.M.; Smirnov, S.V. Melamine detection by mid- and near-infrared (MIR/NIR) spectroscopy: A quick and sensitive method for dairy products analysis including liquid milk, infant formula, and milk powder. Talanta 2011, 85, 562–568. [Google Scholar] [CrossRef]
- Abbas, O.; Lecler, B.; Dardenne, P.; Baeten, V. Detection of melamine and cyanuric acid in feed ingredients by near infrared spectroscopy and chemometrics. J. Near Infrared Spectrosc. 2013, 21, 183–194. [Google Scholar] [CrossRef]
- Haughey, S.A.; Galvin-King, P.; Malechaux, A.; Elliott, C.T. The use of handheld near-infrared reflectance spectroscopy (NIRS) for the proximate analysis of poultry feed and to detect melamine adulteration of soya bean meal. Anal. Methods 2015, 7, 181–186. [Google Scholar] [CrossRef]
- Lim, J.; Kim, G.; Mo, C.; Kim, M.S.; Chao, K.; Qin, J.; Fu, X.; Baek, I.; Cho, B.-K. Detection of melamine in milk powders using near-infrared hyperspectral imaging combined with regression coefficient of partial least square regression model. Talanta 2016, 151, 183–191. [Google Scholar] [CrossRef]
- Boczar, M.; Boda, Ł.; Wójcik, M.J. Theoretical modeling of infrared spectra of hydrogen-bonded crystals of salicylic acid. Spectrochim. Acta A 2006, 64, 757–760. [Google Scholar] [CrossRef]
- Flakus, H.T.; Chelmecki, M. Infrared spectra of the hydrogen bond in benzoic acid crystals: Temperature and polarization effects. Spectrochim. Acta A 2002, 58, 179–196. [Google Scholar] [CrossRef]
- Hanuza, J.; Godlewska, P.; Kucharska, E.; Ptak, M.; Kopacz, M.; Mączka, M.; Hermanowicz, K.; Macalik, L. Molecular structure and vibrational spectra of quercetin and quercetin-5′-sulfonic acid. Vib. Spectrosc. 2017, 88, 94–105. [Google Scholar] [CrossRef]
- Kucharska, E.; Bryndal, I.; Lis, T.; Lorenc, J.; Hanuza, J. Influence of methyl and nitro group substitutions on the structure and vibrational characteristics of the hydrazo-bridge in 6,6′-dimethyl-3,3′,5,5′-tetranitro-2,2′-hydrazobipyridine. Vib. Spectrosc. 2016, 83, 70–77. [Google Scholar] [CrossRef]
- Latouche, C.; Barone, V. Computational chemistry meets experiments for explaining the behavior of bibenzyl: A thermochemical and spectroscopic (Infrared, Raman, and NMR) investigation. J. Chem. Theory Comput. 2014, 10, 5586–5592. [Google Scholar] [CrossRef]
- Vazart, F.; Latouche, C.; Cimino, P.; Barone, V. Accurate infrared (IR) spectra for molecules containing the C≡N moiety by anharmonic computations with the double hybrid B2PLYP density functional. J. Chem. Theory Comput. 2015, 11, 4364–4369. [Google Scholar] [CrossRef]
- Beć, K.B.; Huck, C.W. Breakthrough potential in near-infrared spectroscopy: Spectra simulation. A review of recent developments. Front. Chem. 2019, 7, 48. [Google Scholar] [CrossRef]
- Bloino, J.; Baiardi, A.; Biczysko, M. Aiming at an accurate prediction of vibrational and electronic spectra for medium-to-large molecules: An overview. Int. J. Quantum Chem. 2016, 116, 1543–1574. [Google Scholar] [CrossRef]
- Grabska, J.; Czarnecki, M.A.; Beć, K.B.; Ozaki, Y. Spectroscopic and quantum mechanical calculation study of the effect of isotopic substitution on NIR spectra of methanol. J. Phys. Chem. A 2017, 121, 7925–7936. [Google Scholar] [CrossRef]
- Chen, Y.; Morisawa, Y.; Futami, Y.; Czarnecki, M.A.; Wang, H.-S.; Ozaki, Y. Combined IR/NIR and density functional theory calculations analysis of the solvent effects on frequencies and intensities of the fundamental and overtones of the C=O stretching vibrations of acetone and 2-hexanone. J. Phys. Chem. A 2014, 118, 2576–2583. [Google Scholar] [CrossRef]
- Workman, J., Jr.; Weyer, L. Practical Guide and Spectral Atlas for Interpretive Near-Infrared Spectroscopy, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Grabska, J.; Beć, K.B.; Ozaki, Y.; Huck, C.W. Temperature drift of conformational equilibria of butyl alcohols studied by near-infrared spectroscopy and fully anharmonic DFT. J. Phys. Chem. A 2017, 121, 1950–1961. [Google Scholar] [CrossRef]
- Dovesi, R.; Saunders, V.R.; Roetti, C.; Orlando, R.; Zicovich-Wilson, C.M.; Pascale, F.; Civalleri, B.; Doll, K.; Harrison, N.M.; Bush, I.J.; et al. CRYSTAL09 User’s Manual; University of Torino: Torino, Italy, 2009. [Google Scholar]
- Cambridge Structural Database. CSD Entry: MELAMI05. Available online: https://www.ccdc.cam.ac.uk/structures/search?id=doi:10.5517/cc7yptn&sid=DataCite (accessed on 10 April 2019).
- Kooijman, H.; Beijer, F.H.; Sijbesma, R.P.; Meijer, E.W.; Spek, A.L. CCDC 237082: Experimental Crystal Structure Determination. CSD Commun. 2004. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Gatti, C.; Saunders, V.R.; Roetti, C. Crystal-field effects on the topological properties of the electron-density in molecular-crystals. The case of urea. J. Chem. Phys. 1994, 101, 10686–10696. [Google Scholar] [CrossRef]
- Yoshida, H.; Ehara, A.; Matsuura, H. Density functional vibrational analysis using wavenumber-linear scale factors. Chem. Phys. Lett. 2000, 325, 477–483. [Google Scholar] [CrossRef]
- Beć, K.B.; Wójcik, M.J.; Nakajima, T. Quantum chemical calculations of basic molecules: Alcohols and carboxylic acids. NIR News 2016, 27, 15–21. [Google Scholar] [CrossRef]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef]
- Barone, V.; Cimino, P.; Stendardo, E. Development and validation of the B3LYP/N07D computational model for structural parameter and magnetic tensors of large free radicals. J. Chem. Theory Comput. 2008, 4, 751–764. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Hawranek, J.P. On the numerical description of asymmetric absorption bands. Acta Phys. Pol. B 1971, 40, 811–814. [Google Scholar]
- MATLAB. The MathWorks, Inc.: Natick, MA, USA. Available online: https://www.mathworks.com/products/matlab.html (accessed on 10 April 2019).
Sample Availability: Sample of the compound melamine is available from the authors. |
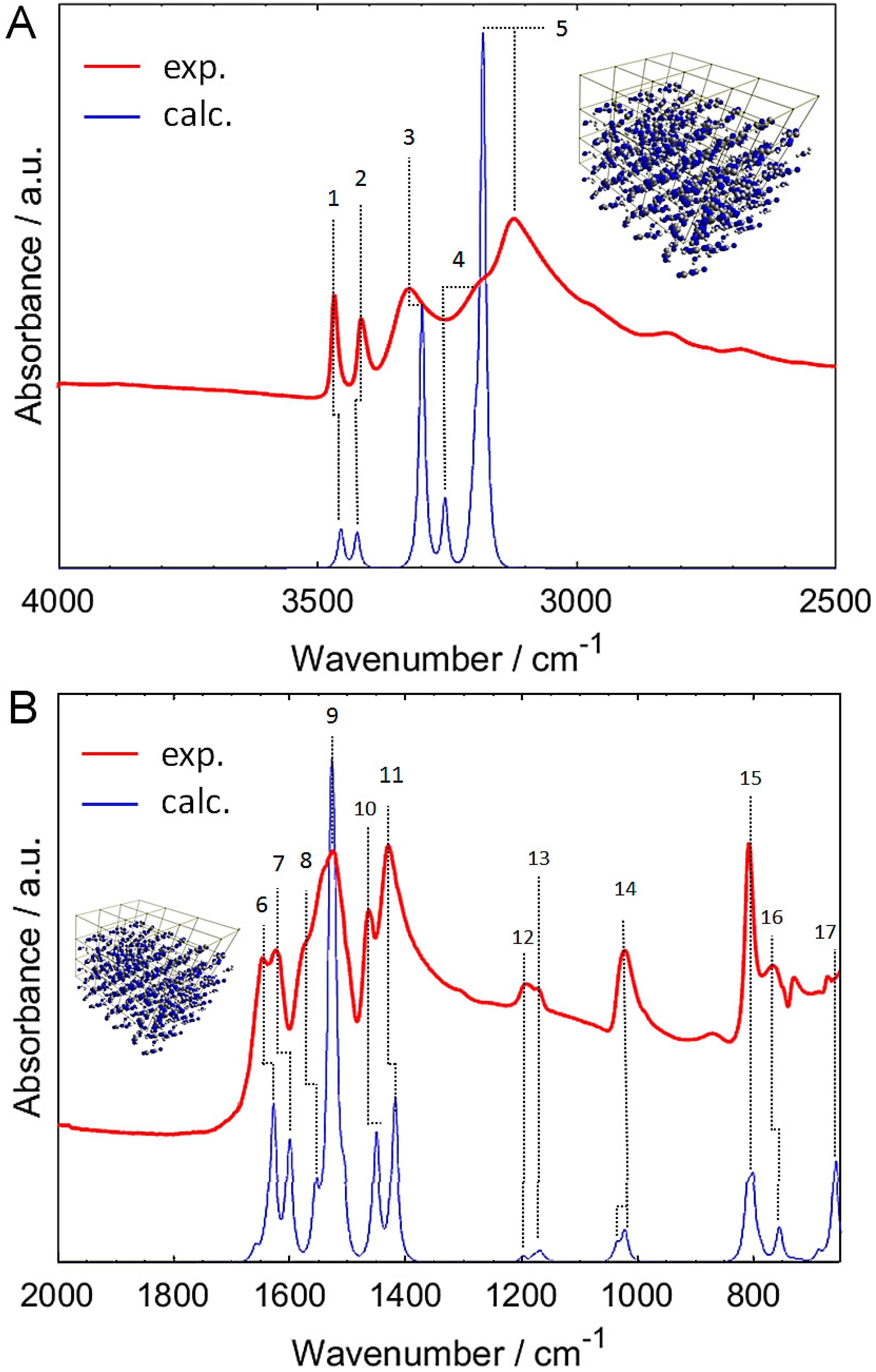
| Band Number | Wavenumber/cm−1 | Assignment | ||
|---|---|---|---|---|
| Experimental | Scaled Calc. | Non-Scaled Calc. | ||
| 1 | 3468 | 3454 | 3669 | νasNH2 |
| 2 | 3416 | 3423 | 3634 | νasNH2 |
| 3 | 3324 | 3296 | 3491 | νasNH2 |
| 4 | ~3188 | 3252 | 3441 | νasNH2 |
| 5 | 3121.7 | 3179 | 3360 | νsNH2 |
| 6 | 1647.7 | 1627 | 1705 | δscissNH2 |
| 7 | 1624.9 | 1599 | 1675 | δscissNH2 |
| 8 | ~1574 | 1553 | 1624 | δscissNH2; δipring |
| 9 | 1527.7 | 1528 1523 | 1597 1591 | δscissNH2; δrockNH2; δipring δrockNH2; δipring |
| 10 | 1465.6 | 1449 | 1511 | δscissNH2; νC-N(H2) |
| 11 | 1431.6 | 1417 | 1476 | νC-N(H2); δipring |
| 12 | 1194.3 | 1197 | 1238 | δrockNH2 |
| 13 | 1173.5 | 1177 1167 | 1217 1206 | δrockNH2 |
| 14 | 1024.1 | 1035 1021 | 1066 1051 | δrockNH2; δipring δrockNH2; νC-N(H2); δipring |
| 15 | 810.1 | 811 801 | 830 819 | δoopring; δtwistNH2 δwaggNH2 |
| 16 | 768.4 | 755 | 771 | δtwistNH2 |
| 17 | 674.5 | 661 | 673 | δwaggNH2 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grabska, J.; Beć, K.B.; Kirchler, C.G.; Ozaki, Y.; Huck, C.W. Distinct Difference in Sensitivity of NIR vs. IR Bands of Melamine to Inter-Molecular Interactions with Impact on Analytical Spectroscopy Explained by Anharmonic Quantum Mechanical Study. Molecules 2019, 24, 1402. https://doi.org/10.3390/molecules24071402
Grabska J, Beć KB, Kirchler CG, Ozaki Y, Huck CW. Distinct Difference in Sensitivity of NIR vs. IR Bands of Melamine to Inter-Molecular Interactions with Impact on Analytical Spectroscopy Explained by Anharmonic Quantum Mechanical Study. Molecules. 2019; 24(7):1402. https://doi.org/10.3390/molecules24071402
Chicago/Turabian StyleGrabska, Justyna, Krzysztof B. Beć, Christian G. Kirchler, Yukihiro Ozaki, and Christian W. Huck. 2019. "Distinct Difference in Sensitivity of NIR vs. IR Bands of Melamine to Inter-Molecular Interactions with Impact on Analytical Spectroscopy Explained by Anharmonic Quantum Mechanical Study" Molecules 24, no. 7: 1402. https://doi.org/10.3390/molecules24071402
APA StyleGrabska, J., Beć, K. B., Kirchler, C. G., Ozaki, Y., & Huck, C. W. (2019). Distinct Difference in Sensitivity of NIR vs. IR Bands of Melamine to Inter-Molecular Interactions with Impact on Analytical Spectroscopy Explained by Anharmonic Quantum Mechanical Study. Molecules, 24(7), 1402. https://doi.org/10.3390/molecules24071402









