PLS Subspace-Based Calibration Transfer for Near-Infrared Spectroscopy Quantitative Analysis
Abstract
:1. Introduction
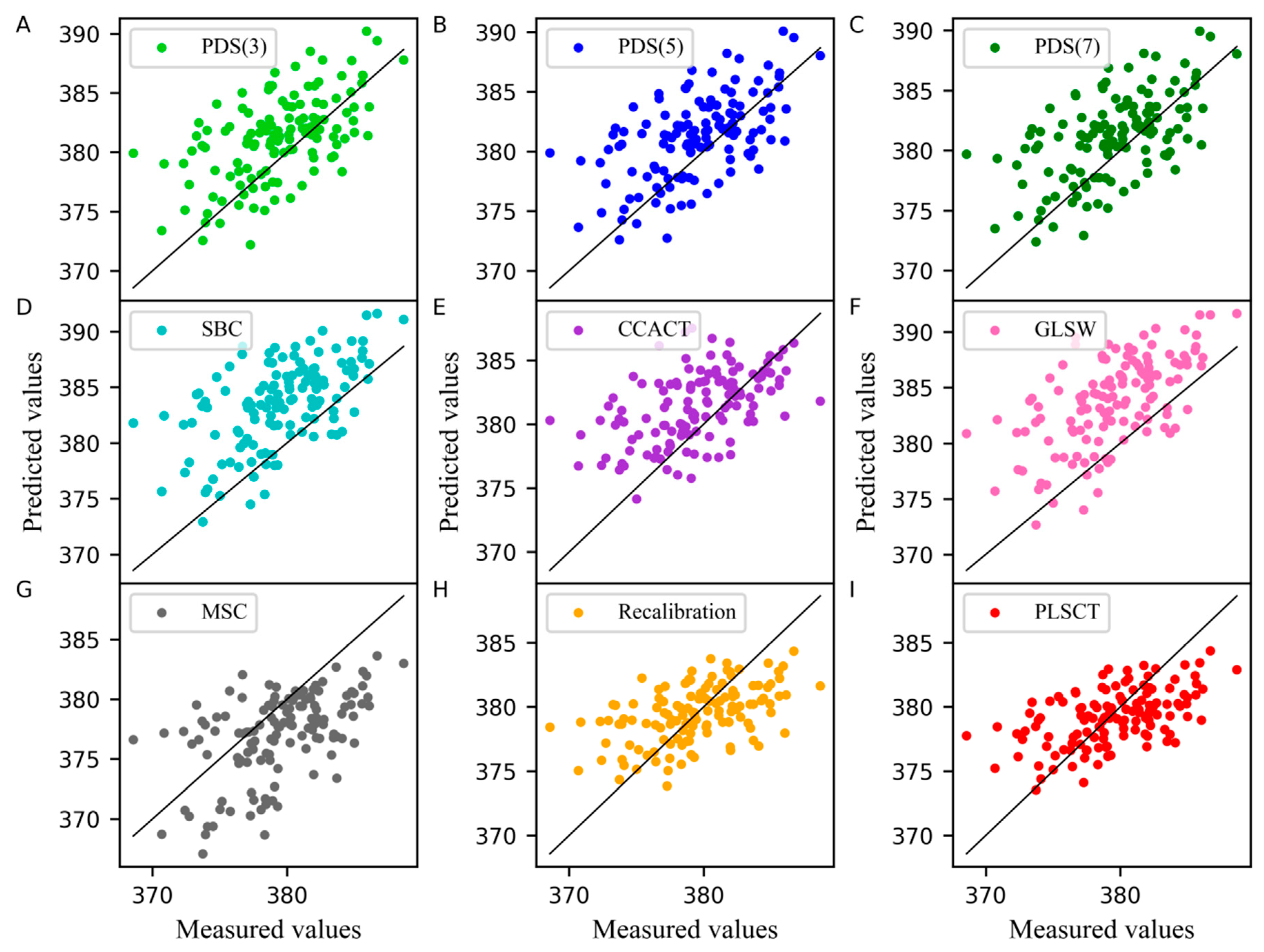
2. Results and Discussion
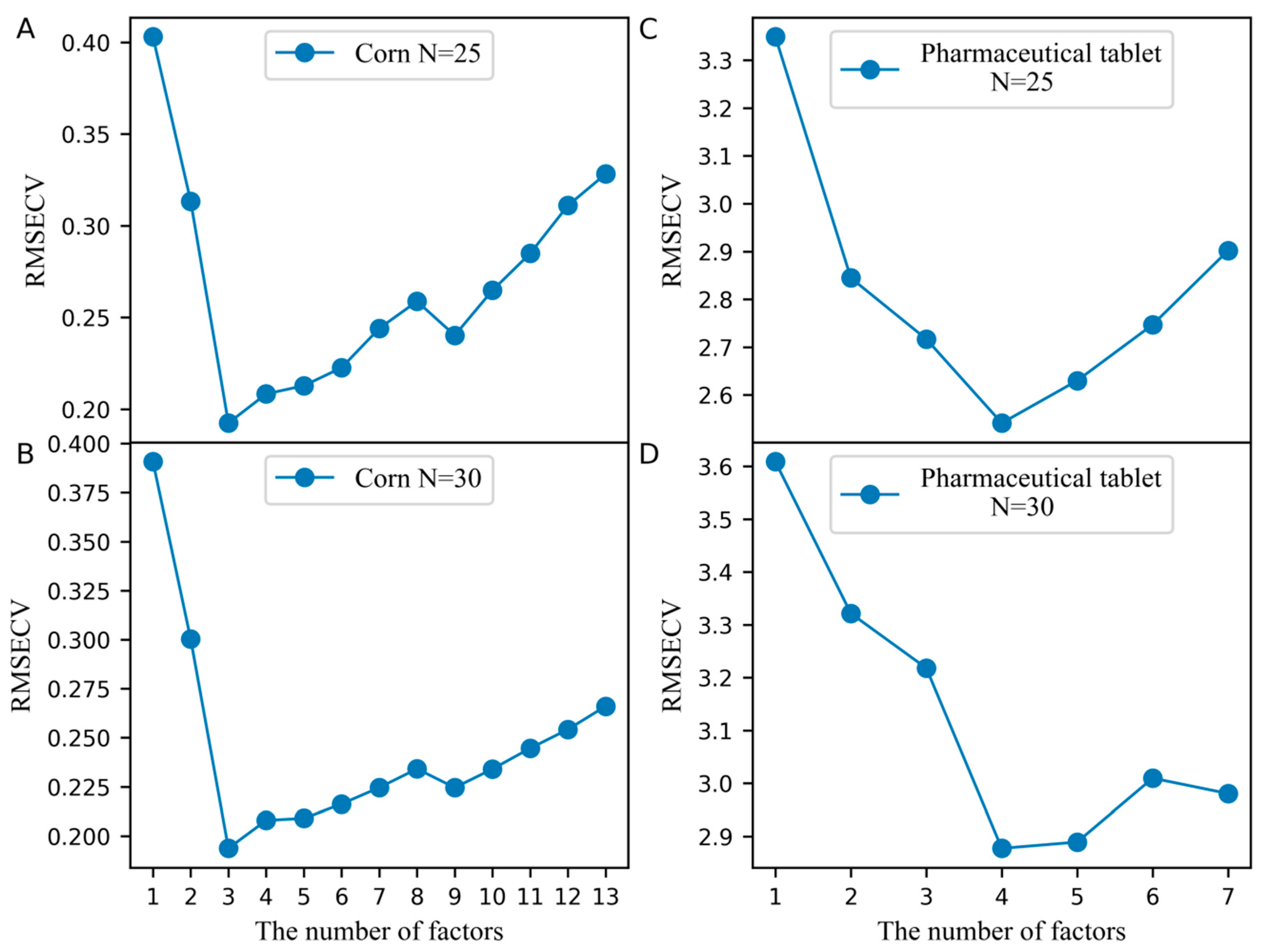
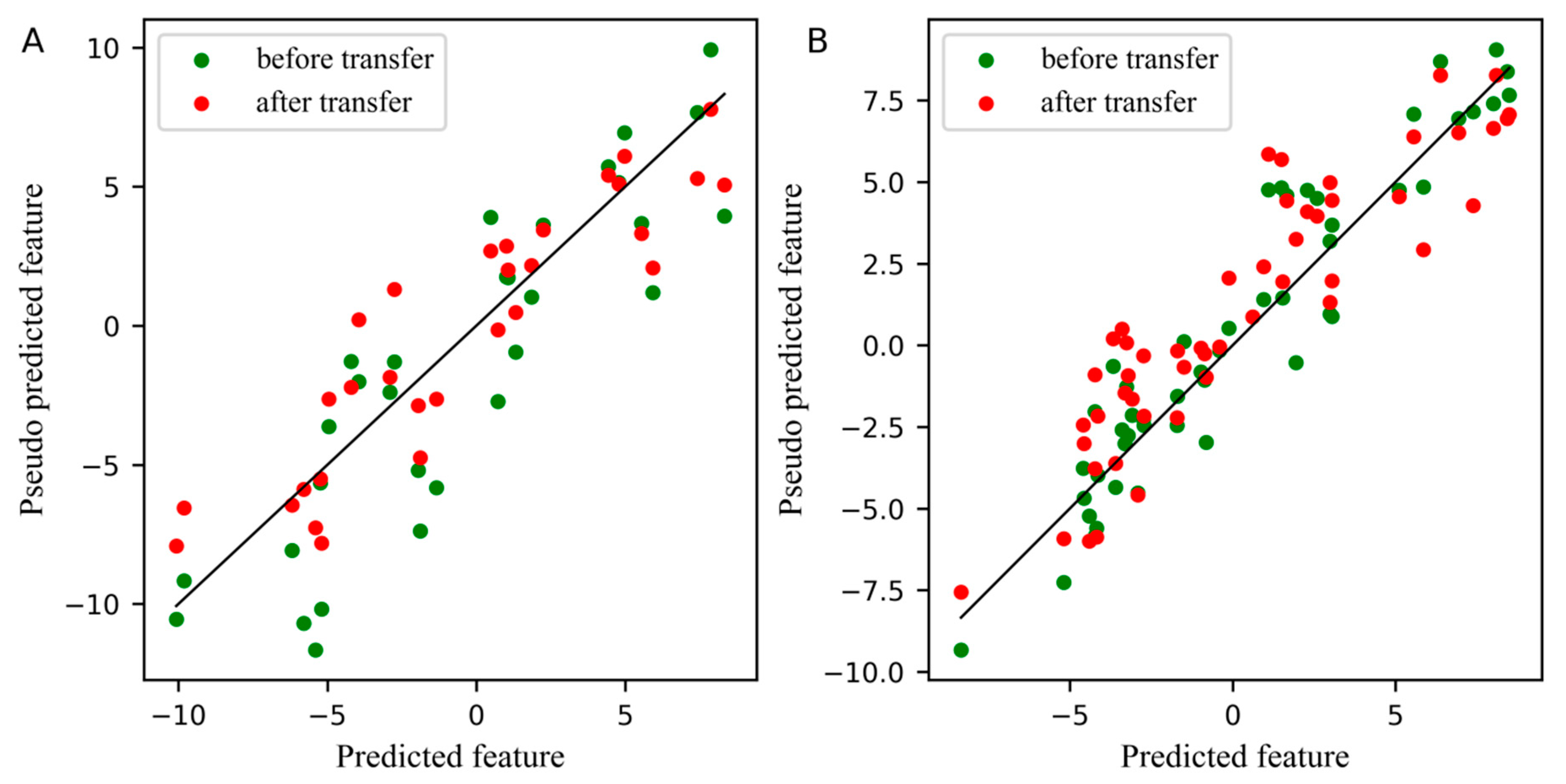
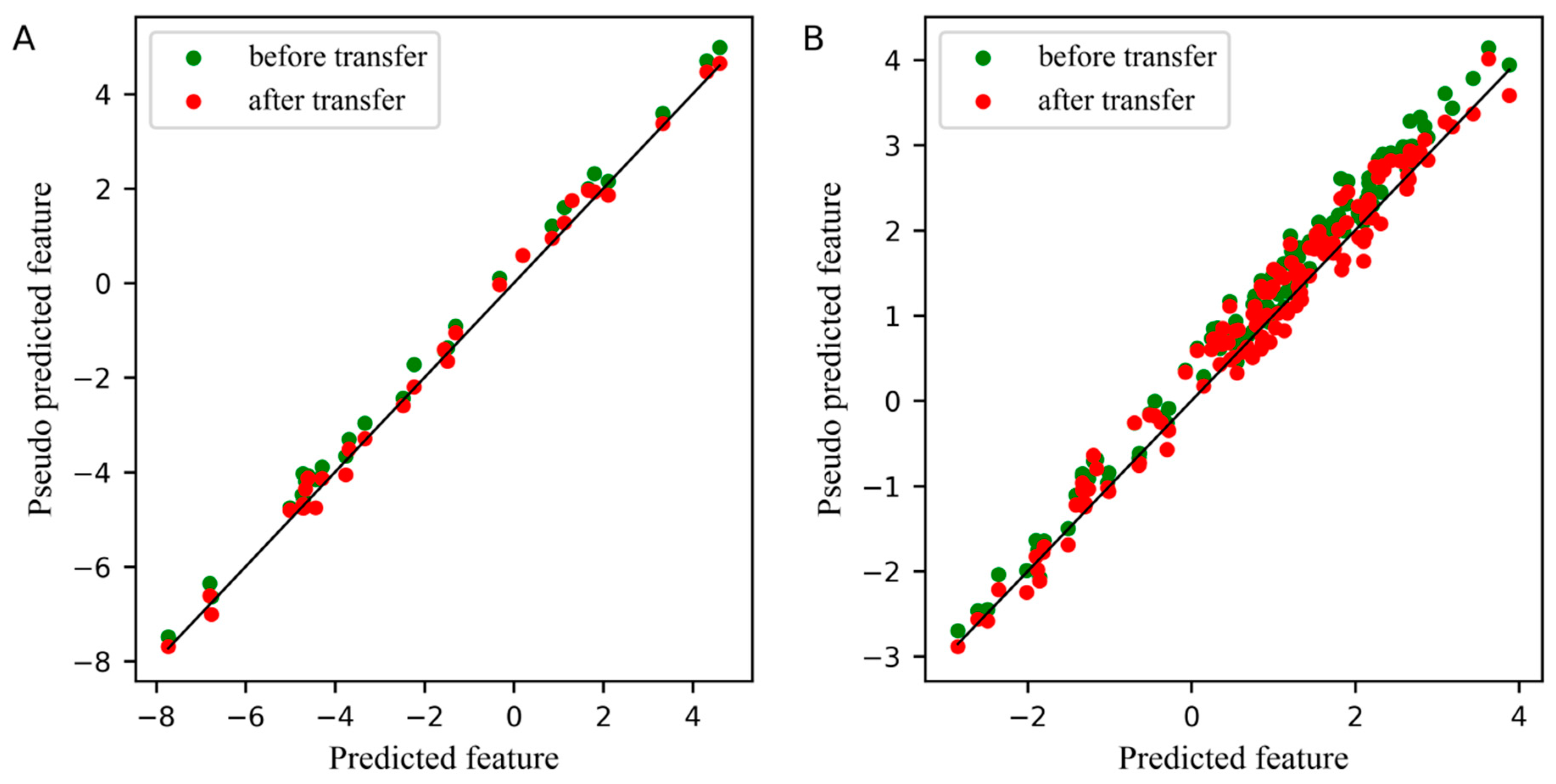
2.1. The Analysis of the Corn Dataset
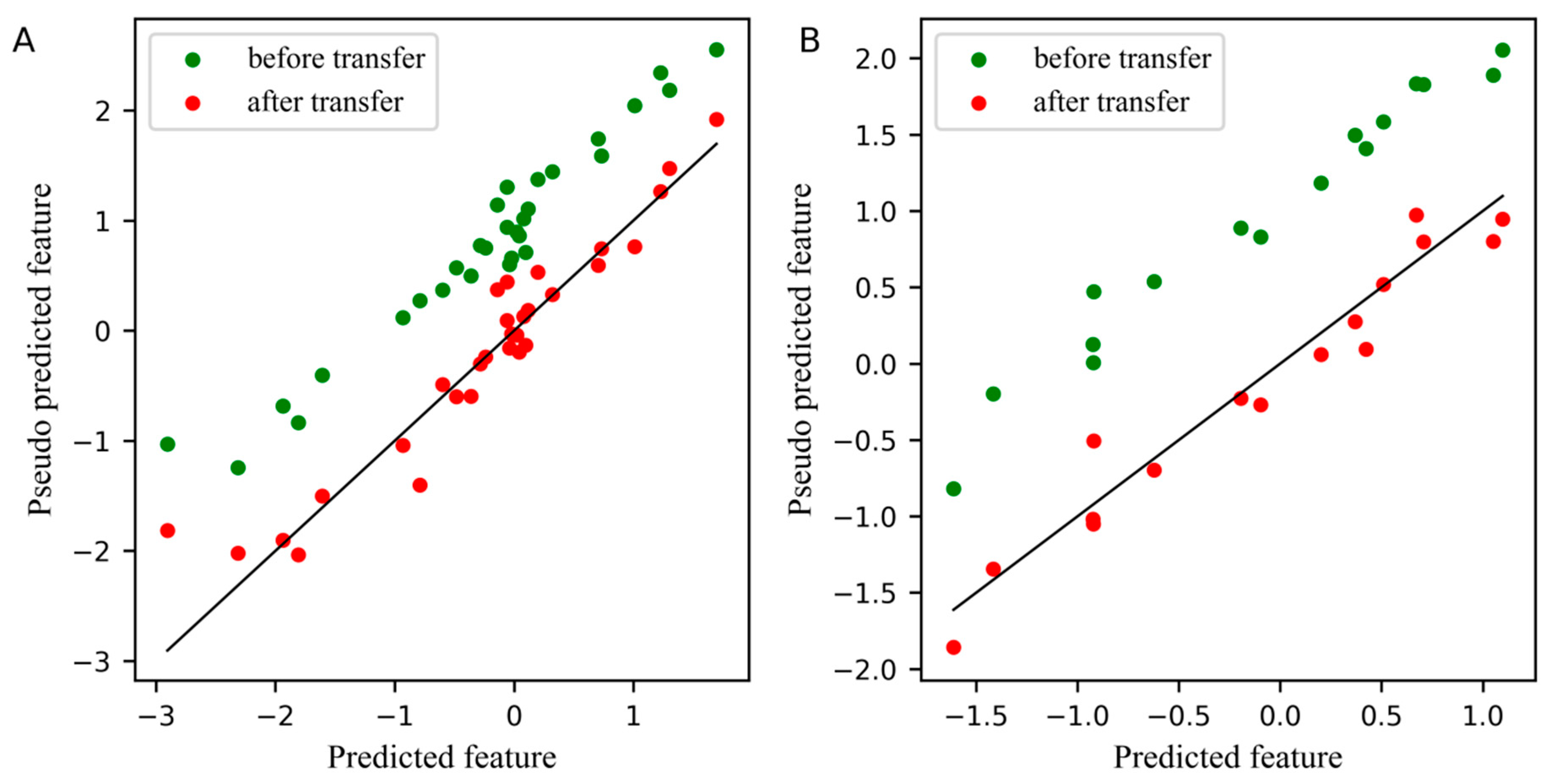
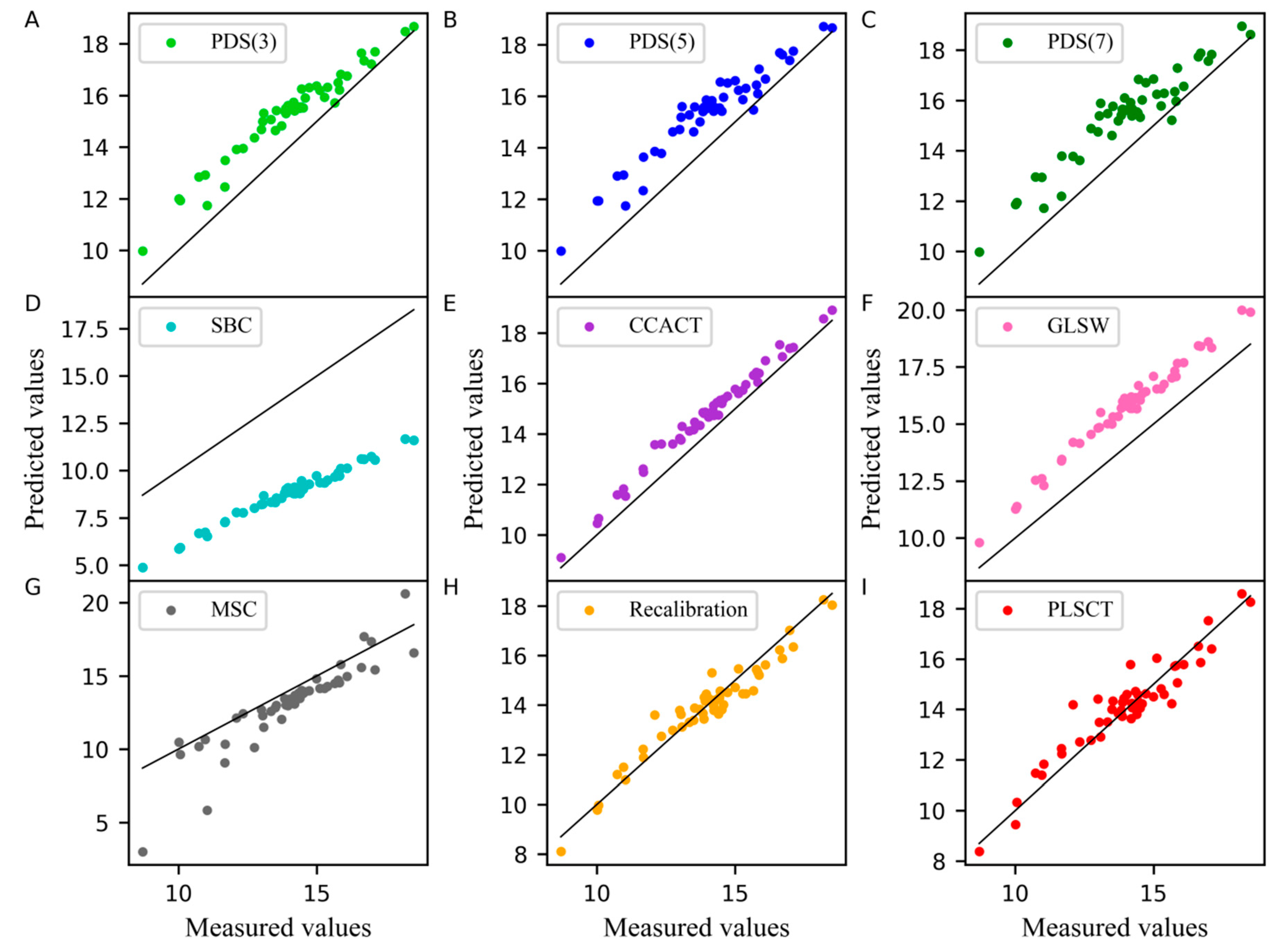
2.2. The Analysis of the Wheat Dataset
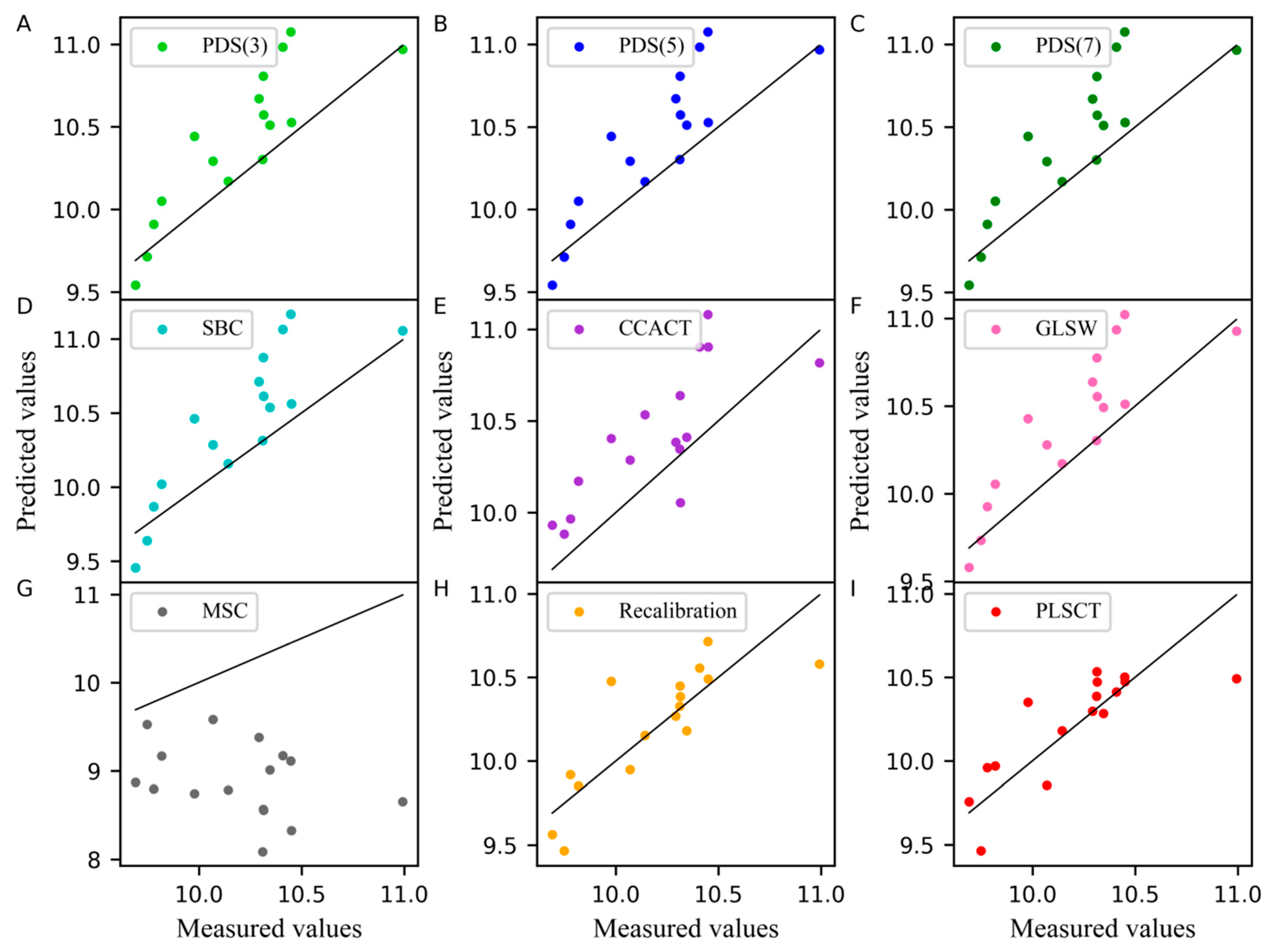
2.3. The Analysis of the Pharmaceutical Tablet Dataset
3. Materials and Methods
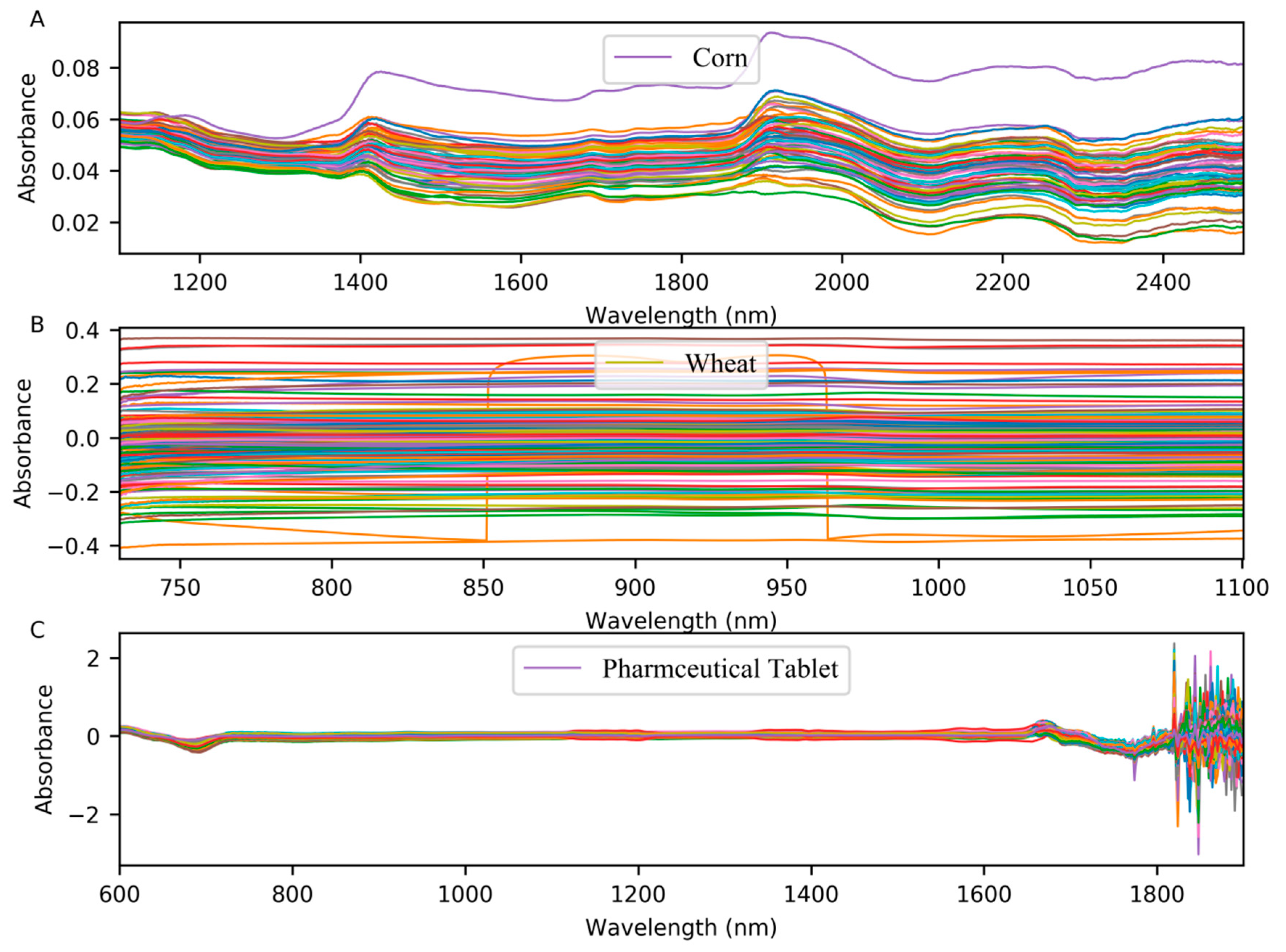
3.1. Dataset Description
3.1.1. Corn Dataset
3.1.2. Wheat Dataset
3.1.3. Pharmaceutical Tablet Dataset
3.2. Dataset Division
3.3. Determination of the Optimal Parameters
3.4. Model Performance Evaluation
3.5. Calibration Transfer Method
3.5.1. Notation
3.5.2. Overview of PLS
3.5.3. Proposed PLSCT method
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| PDS | SBC | CCACT | GLSW | MSC | PLSCT | Recalibration2 2 | Recalibration 3 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| W 1 = 3 | W 1 = 5 | W 1 = 7 | ||||||||
| Corn dataset | ||||||||||
| N = 5 | 0.4142 | 0.4336 | 0.4354 | 0.5370 | 0.2411 | 0.4056 | 1.4302 | 0.1991 | 0.3538 | 0.2085 |
| N = 10 | 0.3753 | 0.3617 | 0.3729 | 0.4440 | 0.2545 | 0.3696 | 1.4302 | 0.1980 | 0.2237 | |
| N = 15 | 0.3507 | 0.3495 | 0.3357 | 0.4307 | 0.3663 | 0.3535 | 1.4302 | 0.2127 | 0.2425 | |
| N = 20 | 0.3440 | 0.3440 | 0.3440 | 0.3900 | 0.2841 | 0.3208 | 1.4302 | 0.2087 | 0.2379 | |
| N = 25 | 0.3373 | 0.3372 | 0.3366 | 0.3720 | 0.3528 | 0.3106 | 1.4302 | 0.2082 | 0.2314 | |
| N = 30 | 0.3136 | 0.3135 | 0.3135 | 0.3511 | 0.3245 | 0.2921 | 1.4302 | 0.2038 | 0.2230 | |
| Wheat dataset | ||||||||||
| N = 5 | 8.2434 | 9.1587 | 8.4226 | 14.3731 | 1.6248 | 4.0835 | 1.5160 | 1.8478 | 2.7176 | 0.5308 |
| N = 10 | 8.5844 | 9.3534 | 10.8927 | 10.5310 | 1.2496 | 3.5824 | 1.5160 | 0.8588 | 2.2233 | |
| N = 15 | 2.1373 | 2.8513 | 3.2012 | 8.7159 | 1.5315 | 2.9205 | 1.5160 | 1.8280 | 1.3985 | |
| N = 20 | 1.9586 | 2.0927 | 2.2380 | 7.0482 | 0.9688 | 2.4743 | 1.5160 | 1.8263 | 0.4520 | |
| N = 25 | 1.5656 | 1.6480 | 1.7445 | 6.1945 | 1.0437 | 1.9804 | 1.5160 | 0.6850 | 2.3661 | |
| N = 30 | 1.3694 | 1.4468 | 1.5366 | 5.2635 | 0.7735 | 1.7085 | 1.5160 | 0.6604 | 2.2000 | |
| Pharmaceutical tablet dataset | ||||||||||
| N = 5 | 4.7971 | 4.2899 | 4.4594 | 5.9983 | 4.1302 | 6.5988 | 4.2482 | 3.3202 | 5.8027 | 3.3160 |
| N = 10 | 4.1431 | 4.0098 | 4.0444 | 5.4720 | 4.1112 | 5.6721 | 4.2482 | 3.5821 | 5.5904 | |
| N = 15 | 3.9698 | 3.8314 | 3.8347 | 5.7069 | 3.9357 | 6.2284 | 4.2482 | 3.3834 | 5.8043 | |
| N = 20 | 3.9787 | 3.8789 | 3.9190 | 5.2838 | 3.8979 | 5.6511 | 4.2482 | 3.2794 | 5.0811 | |
| N = 25 | 3.9263 | 3.8416 | 3.7789 | 5.2514 | 4.0549 | 5.4809 | 4.2482 | 3.2765 | 4.9428 | |
| N = 30 | 3.8499 | 3.7931 | 3.7590 | 5.3699 | 3.8703 | 5.5354 | 4.2482 | 3.2195 | 4.2267 | |
| PLSCT | ||||
|---|---|---|---|---|
| Corn | Wheat | Pharmaceutical Tablet | ||
| PDS(3) 1 | h (%) 2 | 35.00575 | 51.77389 | 16.3743 |
| p3 | 0.00717 | 3.17 × | 3.2 × | |
| PDS(5) 1 | h (%) | 34.99841 | 54.35396 | 15.12146 |
| p | 0.00717 | 2.23 × | 1.78 × | |
| PDS(7) 1 | h (%) | 34.98937 | 57.02112 | 14.35178 |
| p | 0.00717 | 2.23 × | 1.2 × | |
| SBC | h (%) | 41.95097 | 87.45319 | 40.04516 |
| p | 0.011286 | 7.56 × | 4.84 × | |
| CCACT | h (%) | 37.18537 | 42.18862 | 16.81376 |
| p | 0.004455 | 0.001161 | 4.37 × | |
| GLSW | h (%) | 30.21822 | 61.34526 | 41.83697 |
| p | 0.00717 | 8.53 × | 6.82 × | |
| MSC | h (%) | 85.7502 | 56.43832 | 24.21448 |
| p | 0.000531 | 1.57 × | 1.51 × | |
| Recalibration2 | h (%) | 8.610493 | 69.98222 | 23.82937 |
| p | 0.017378 | 0.000231 | 3.05 × | |
| Recalibration | h (%) | 2.26298 | −24.4164 | 2.908651 |
| p | 0.876722 | 9.06 × | 0.000198 | |
References
- Roggo, Y.; Chalus, P.; Maurer, L.; Lema-Martinez, C.; Edmond, A.; Jent, N. A review of near infrared spectroscopy and chemometrics in pharmaceutical technologies. J. Pharm. Biomed. Anal. 2007, 44, 683–700. [Google Scholar] [CrossRef]
- Kumar, M.; Bhatia, R.; Rawal, R.K. Applications of Various Analytical Techniques in Quality Control of Pharmaceutical Excipients. J. Pharm. Biomed. Anal. 2018, 157, 122–136. [Google Scholar] [CrossRef] [PubMed]
- Martinez, J.C.; Guzmán-Sepúlveda, J.R.; Bolañoz Evia, G.R.; Córdova, T.; Guzmán-Cabrera, R. Enhanced Quality Control in Pharmaceutical Applications by Combining Raman Spectroscopy and Machine Learning Techniques. Int. J. Thermophys. 2018, 39, 79. [Google Scholar] [CrossRef]
- Heesang, A.; Hyerin, S.; Dong-Myeong, S.; Kyujung, K.; Jong-ryul, C. Emerging optical spectroscopy techniques for biomedical applications—A brief review of recent progress. Appl. Spectrosc. Rev. 2017, 53, 264–278. [Google Scholar] [CrossRef]
- Morris, R.E.; Hammond, M.H.; Cramer, J.A.; Johnson, K.J.; Giordano, B.C.; Kramer, K.E.; Rose-Pehrsson, S.L. Rapid fuel quality surveillance through chemometric modeling of near-infrared spectra. Energy Fuels 2009, 23, 1610–1618. [Google Scholar] [CrossRef]
- López, A.; Arazuri, S.; García, I.; Mangado, J.S.; Jarén, C. A review of the application of near-infrared spectroscopy for the analysis of potatoes. J. Agric. Food Chem. 2013, 61, 5413–5424. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Hierro, J.M.; Valverde, J.; Villacreces, S.; Reilly, K.; Gaffney, M.; González-Miret, M.L.; Heredia, F.J.; Downey, G. Feasibility study on the use of visible–near-infrared spectroscopy for the screening of individual and total glucosinolate contents in Broccoli. J. Agric. Food Chem. 2012, 60, 7352–7358. [Google Scholar] [CrossRef]
- Cen, H.; He, Y. Theory and application of near infrared reflectance spectroscopy in determination of food quality. Trends Food Sci. Technol. 2007, 18, 72–83. [Google Scholar] [CrossRef]
- Huang, H.; Yu, H.; Xu, H.; Ying, Y. Near infrared spectroscopy for on/in-line monitoring of quality in foods and beverages:a review. J. Food Eng. 2008, 87, 303–313. [Google Scholar] [CrossRef]
- Lukacs, M.; Bazar, G.; Pollner, B.; Henn, R.; Kirchler, C.G.; Huck, C.W.; Kovacs, Z. Near infrared spectroscopy as an alternative quick method for simultaneous detection of multiple adulterants in whey protein-based sports supplement. Food Control 2018, 94, 331–340. [Google Scholar] [CrossRef]
- Geladi, P.; Kowalski, B.R. Partial least-squares regression: A tutorial. Anal. Chim. Acta 1986, 185, 1–17. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Næs, T.; Martens, H. Principal component regression in NIR analysis: View-points, background details and selection of components. J. Chemom. 1988, 2, 155–167. [Google Scholar] [CrossRef]
- Geladi, P.; Esbensen, K. Regression on multivariate images: Principal component regression for modeling, prediction and visual diagnostic tools. J. Chemom. 1991, 5, 97–111. [Google Scholar] [CrossRef]
- Wang, Y.; Veltkamp, D.J.; Kowalski, B.R. Multivariate instrument standardization. Anal. Chem. 1991, 63, 2750–2756. [Google Scholar] [CrossRef]
- Bouveresse, E.; Massart, D. Improvement of the piecewise direct standardisation procedure for the transfer of NIR spectra for multivariate calibration. Chemom. Intell. Lab. Syst. 1996, 32, 201–213. [Google Scholar] [CrossRef]
- Wise, B.M.; Martens, H.; Høy, M.; Bro, R.; Brockhoff, P.B. Calibration transfer by generalized least squares. 2001. Available online: http://www.eigenvector.com/Docs/GLS_Standardization.pdf (accessed on 31 March 2019).
- Wise, B.M.; Martens, H.; Høy, M. Generalized least squares for calibration transfer. Available online: http://www.eigenvector.com/Docs/GLS_Calibration_Trans.pdf (accessed on 22 October).
- Bouveresse, E.; Hartmann, C.; Massart, D.L.; Last, I.R.; Prebble, K.A. Standardization of Near-Infrared Spectrometric Instruments. Anal. Chem. 1996, 68, 982–990. [Google Scholar] [CrossRef]
- Fan, W.; Liang, Y.; Yuan, D.; Wang, J. Calibration model transfer for near-infrared spectra based on canonical correlation analysis. Anal. Chim. Acta 2008, 623, 22–29. [Google Scholar] [CrossRef]
- Kramer, K.E.; Morris, R.E.; Rose-Pehrsson, S.L. Comparison of two multiplicative signal correction strategies for calibration transfer without standards. Chemom. Intell. Lab. Syst. 2008, 92, 33–43. [Google Scholar] [CrossRef]
- Blank, T.B.; Sum, S.T.; Brown, S.D.; Monfre, S.L. Transfer of near-infrared multivariate calibrations without standards. Anal. Chem. 1996, 68, 2987–2995. [Google Scholar] [CrossRef]
- Wold, S.; Antti, H.; Lindgren, F.; Öhman, J. Orthogonal signal correction of near infrared spectra. Chemom. Intell. Lab. Syst. 1998, 44, 175–185. [Google Scholar] [CrossRef]
- Sjöblom, J.; Svensson, O.; Josefson, M.; Kullberg, H.; Wold, S. An evaluation of orthogonal signal correction applied to calibration transfer of near infrared spectra. Chemom. Intell. Lab. Syst. 1998, 44, 229–244. [Google Scholar] [CrossRef]
- Pan, S.J.; Tsang, I.; Kwok, J.; Yang, Q. Domain adaptation via transfer component analysis. IEEE Trans. Neural Netw. 2011, 22, 199–210. [Google Scholar] [CrossRef] [PubMed]
- Schölkopf, B.; Smola, A.; Müller, K.R. Kernel principal component analysis. Artificial Neural Networks—ICANN’97 1997, 583–588. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biometrics Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Haaland, D.M.; Thomas, E.V. Partial Least-Squares Methods for Spectral Analyses. 1. Relation to Other Quantitative Calibration Methods and the Extraction of Qualitative Information. Anal. Chem. 1988, 60, 1193–1202. [Google Scholar] [CrossRef]
Sample Availability: Samples are not available from the authors. |
| Instrument | Methods | LVs | RMSEP |
|---|---|---|---|
| Corn | Calibration 1 | 13 | 0.010156 |
| Direct transfer 2 | 1.41931 | ||
| Recalibration 3 | 5 | 0.208522 | |
| Wheat | Calibration 1 | 12 | 0.258014 |
| Direct transfer 2 | 0.85131 | ||
| Recalibration 3 | 8 | 0.530799 | |
| Pharmaceutical tablet | Calibration 1 | 7 | 3.123115 |
| Direct transfer 2 | 4.514284 | ||
| Recalibration 3 | 2 | 3.31598 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yu, J.; Shan, P.; Zhao, Z.; Jiang, X.; Gao, S. PLS Subspace-Based Calibration Transfer for Near-Infrared Spectroscopy Quantitative Analysis. Molecules 2019, 24, 1289. https://doi.org/10.3390/molecules24071289
Zhao Y, Yu J, Shan P, Zhao Z, Jiang X, Gao S. PLS Subspace-Based Calibration Transfer for Near-Infrared Spectroscopy Quantitative Analysis. Molecules. 2019; 24(7):1289. https://doi.org/10.3390/molecules24071289
Chicago/Turabian StyleZhao, Yuhui, Jinlong Yu, Peng Shan, Ziheng Zhao, Xueying Jiang, and Shuli Gao. 2019. "PLS Subspace-Based Calibration Transfer for Near-Infrared Spectroscopy Quantitative Analysis" Molecules 24, no. 7: 1289. https://doi.org/10.3390/molecules24071289
APA StyleZhao, Y., Yu, J., Shan, P., Zhao, Z., Jiang, X., & Gao, S. (2019). PLS Subspace-Based Calibration Transfer for Near-Infrared Spectroscopy Quantitative Analysis. Molecules, 24(7), 1289. https://doi.org/10.3390/molecules24071289






