The Good, the Bad, and the Ugly: “HiPen”, a New Dataset for Validating (S)QM/MM Free Energy Simulations
Abstract
1. Introduction
2. Results
3. Discussion
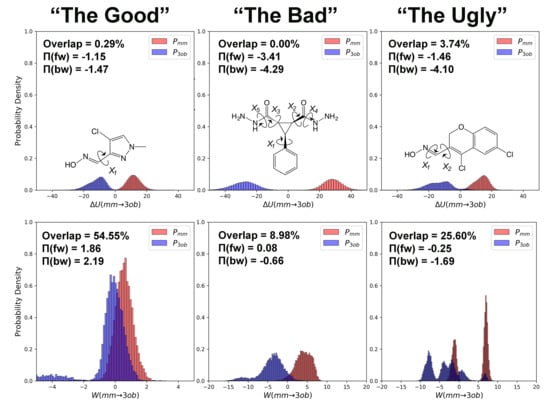
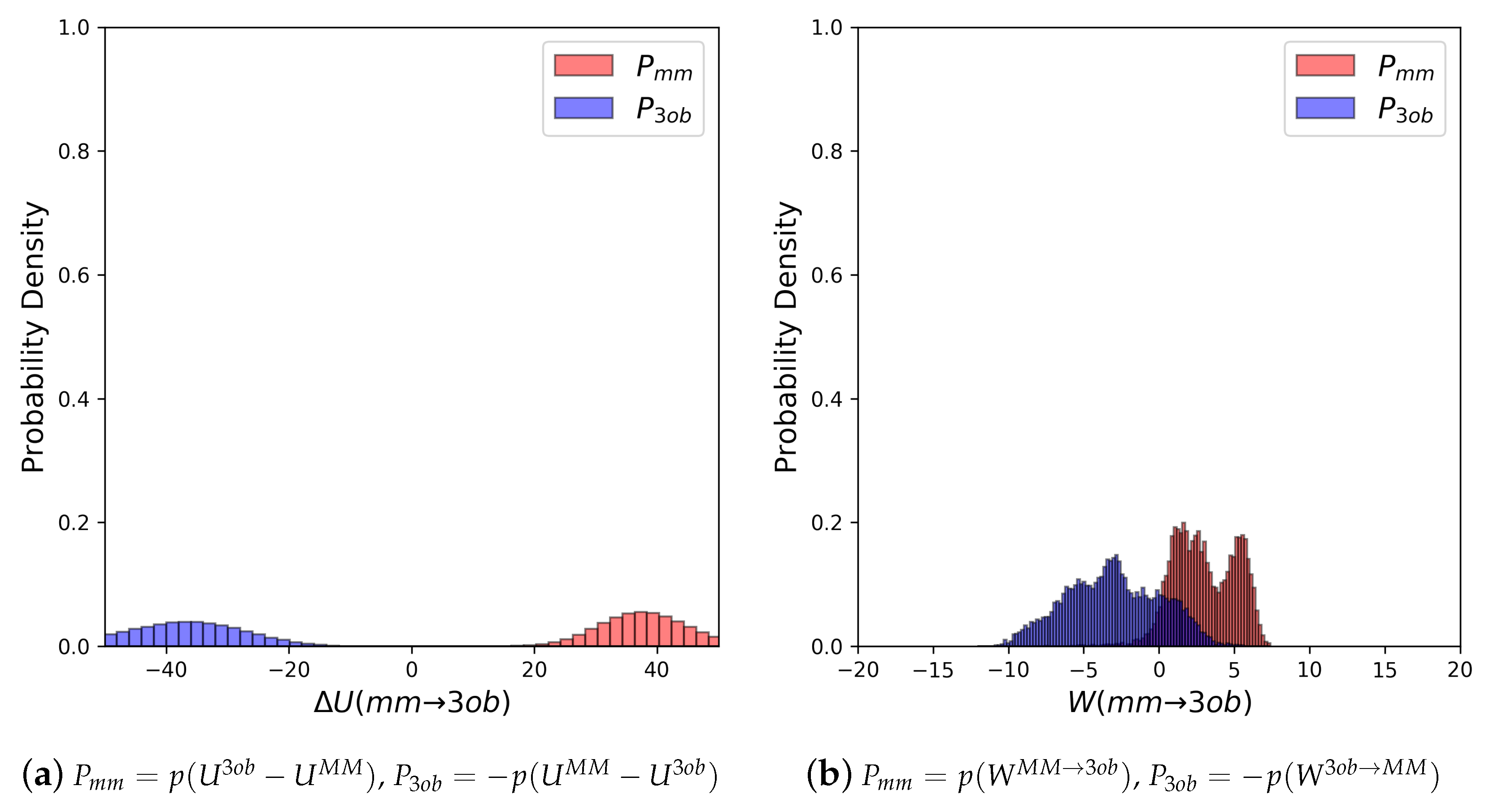
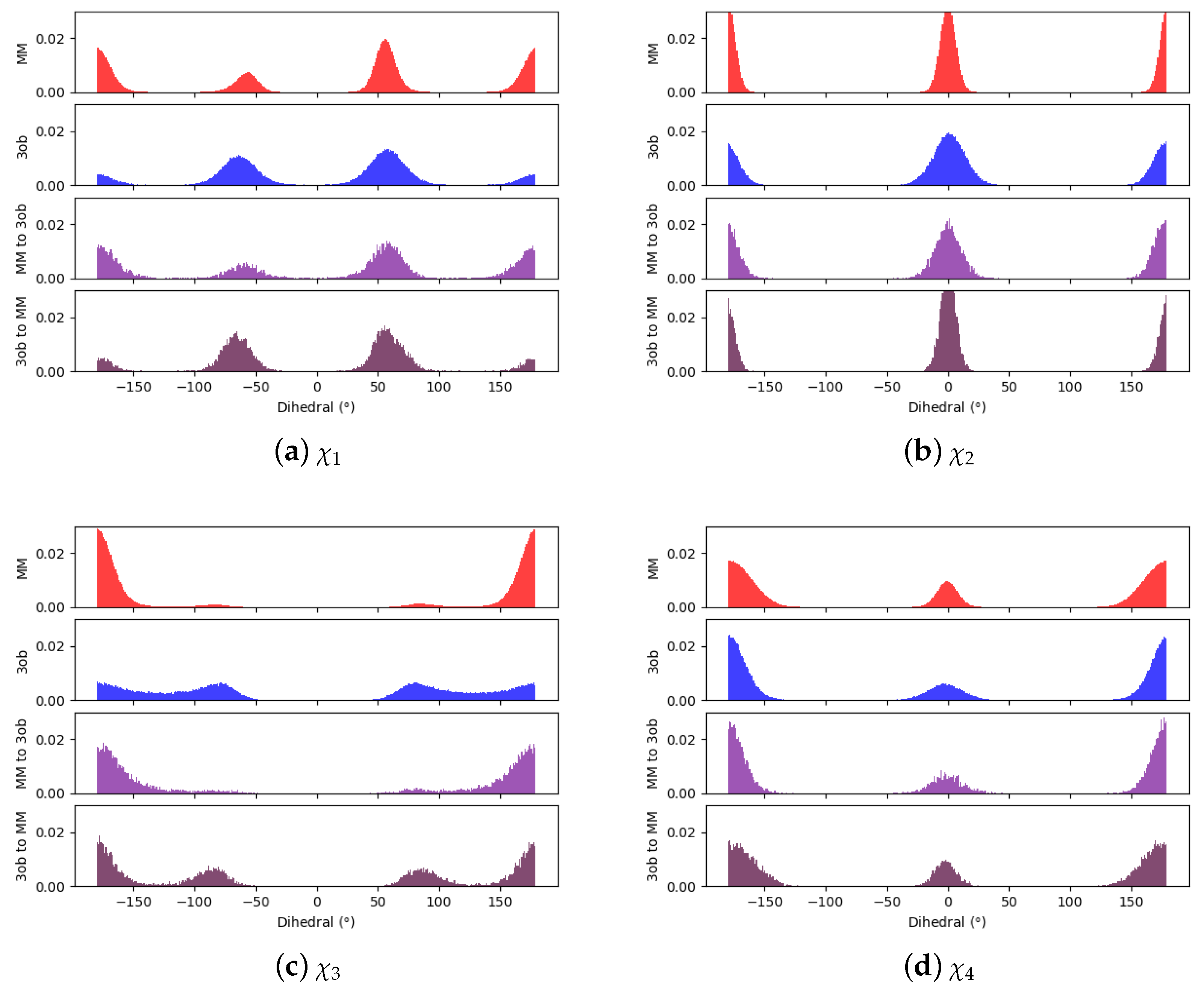
3.1. The Good
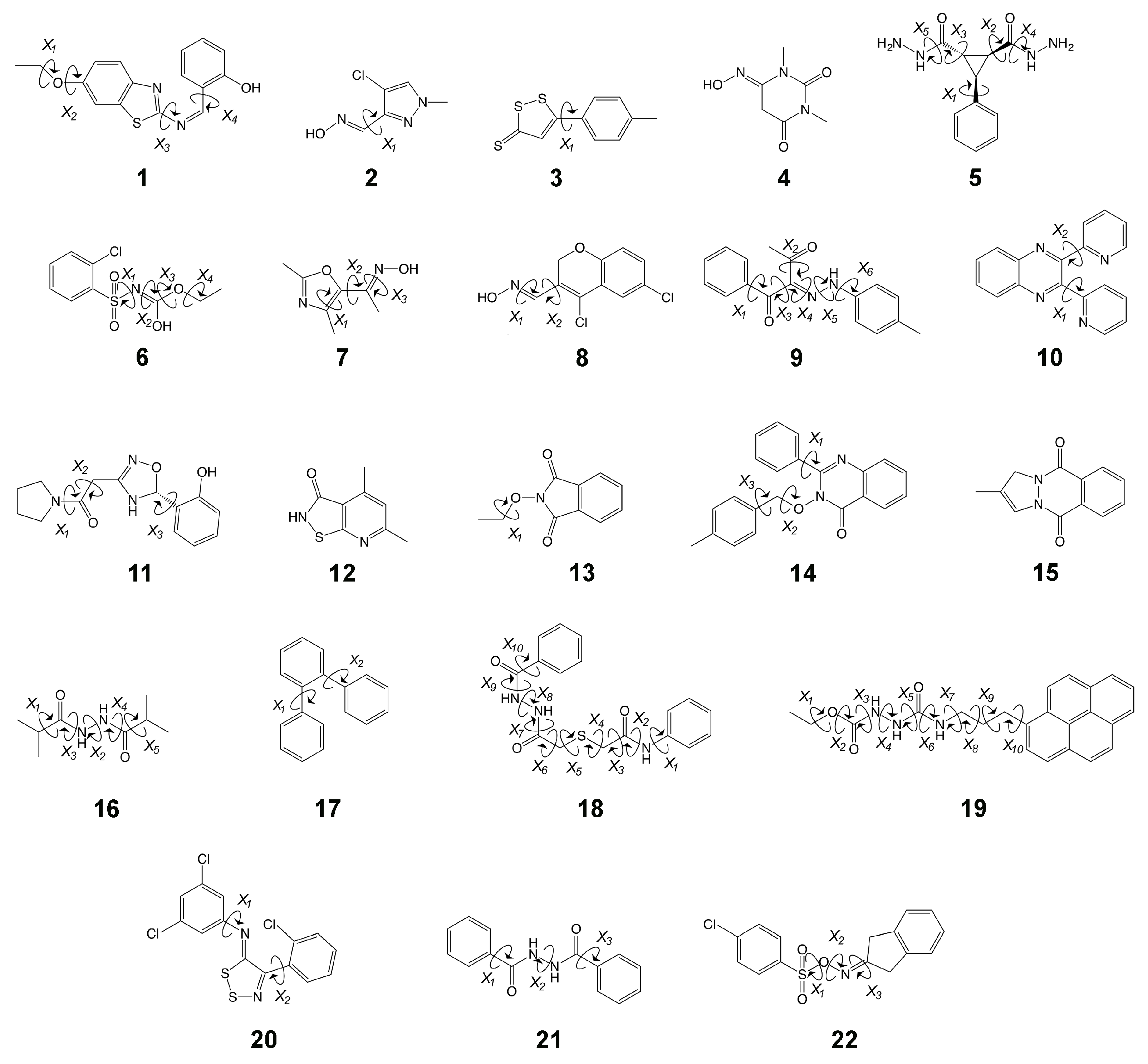
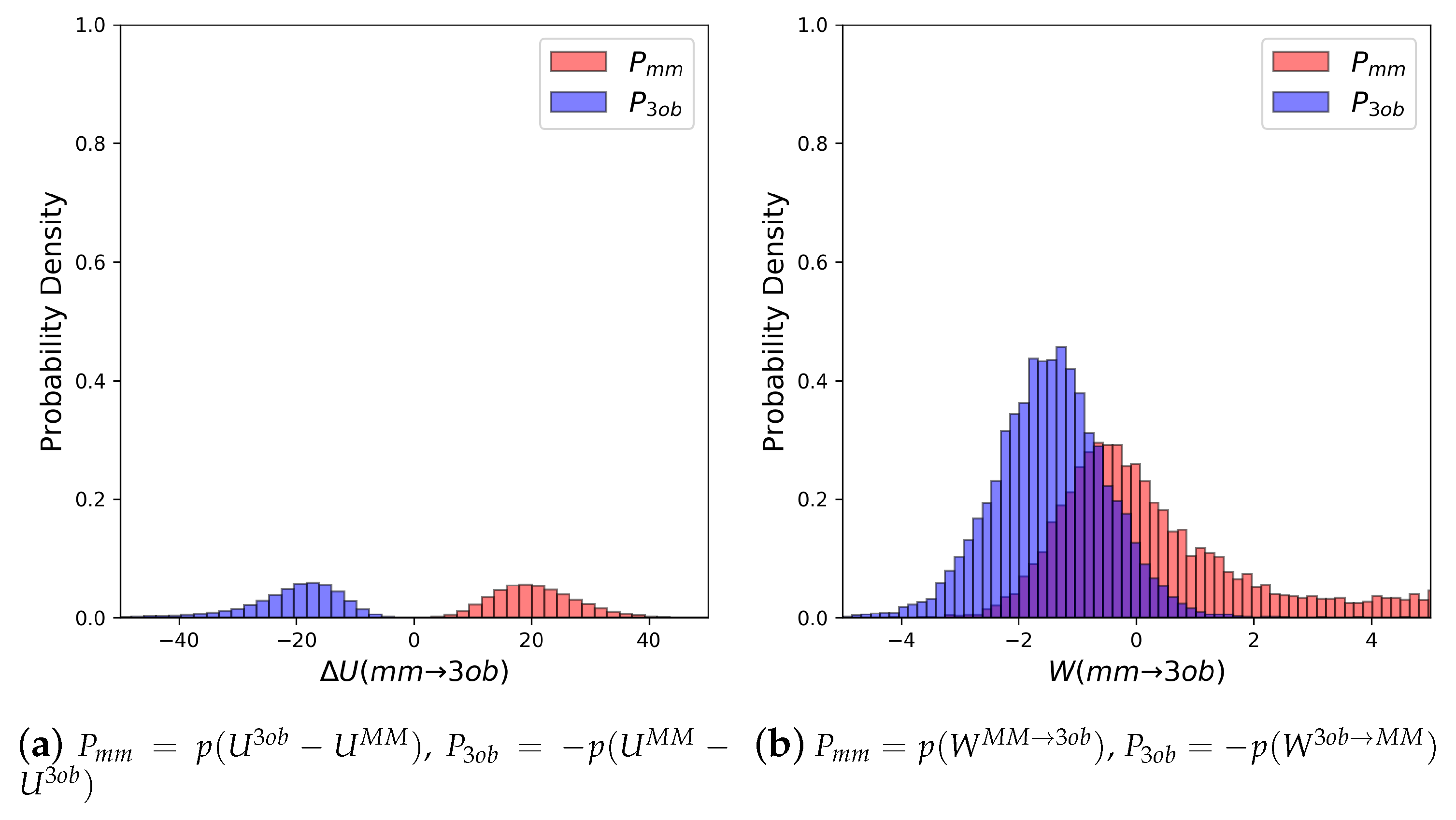
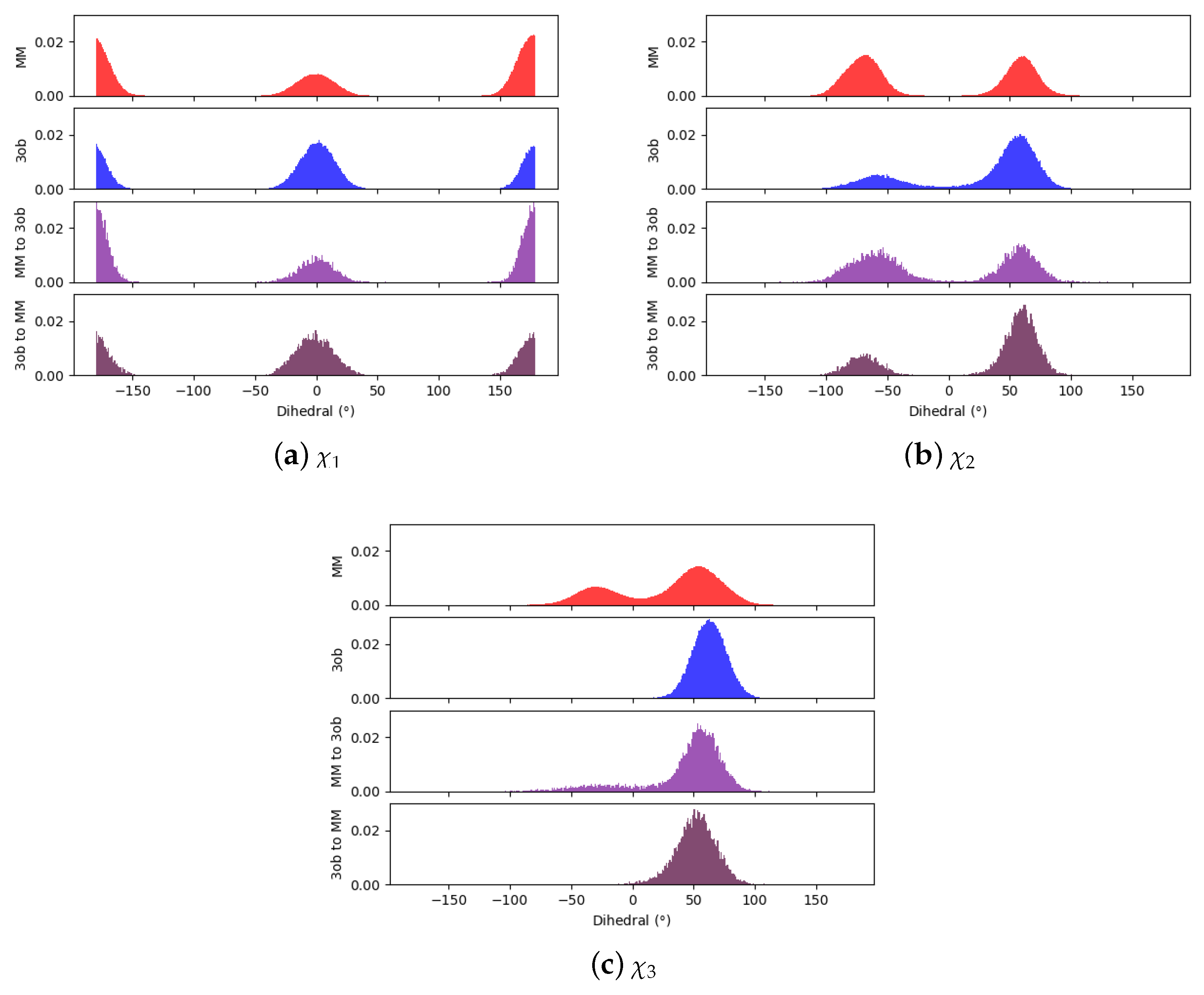
3.1.1. Molecule 2
3.1.2. Molecule 11
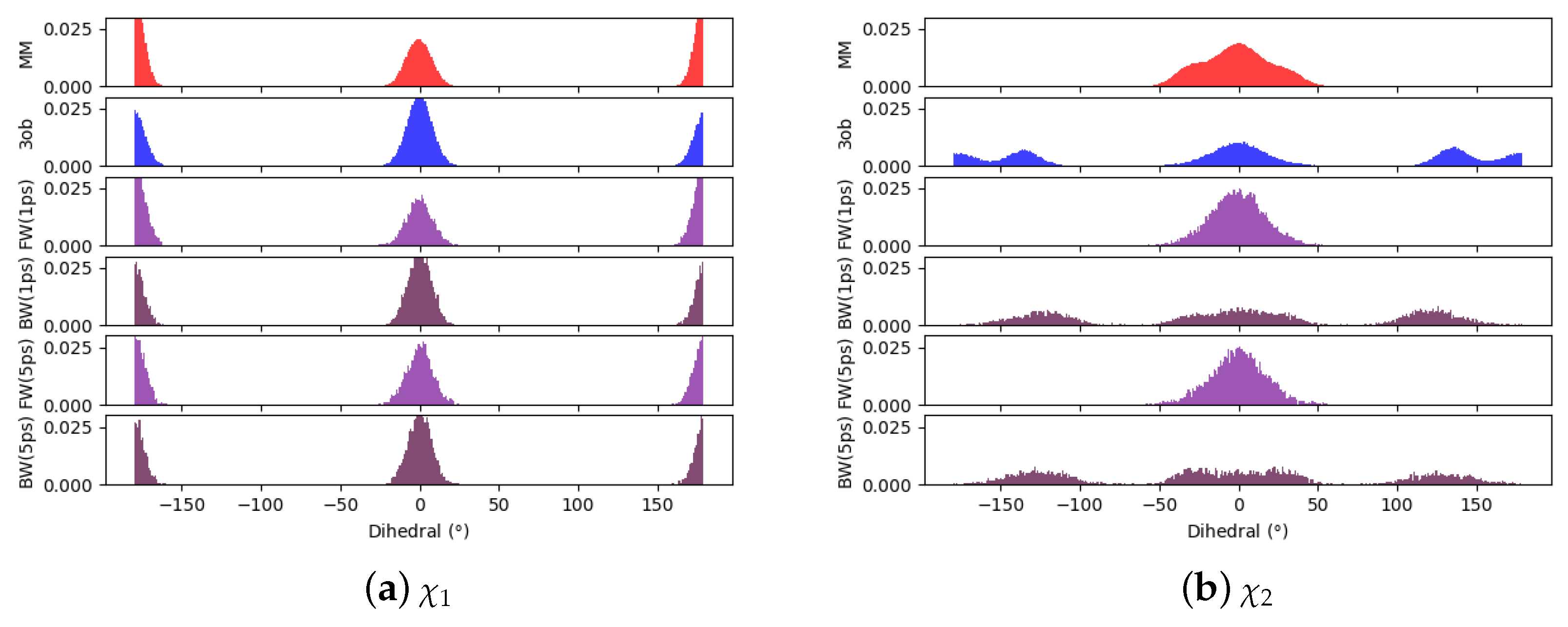
3.2. The Bad
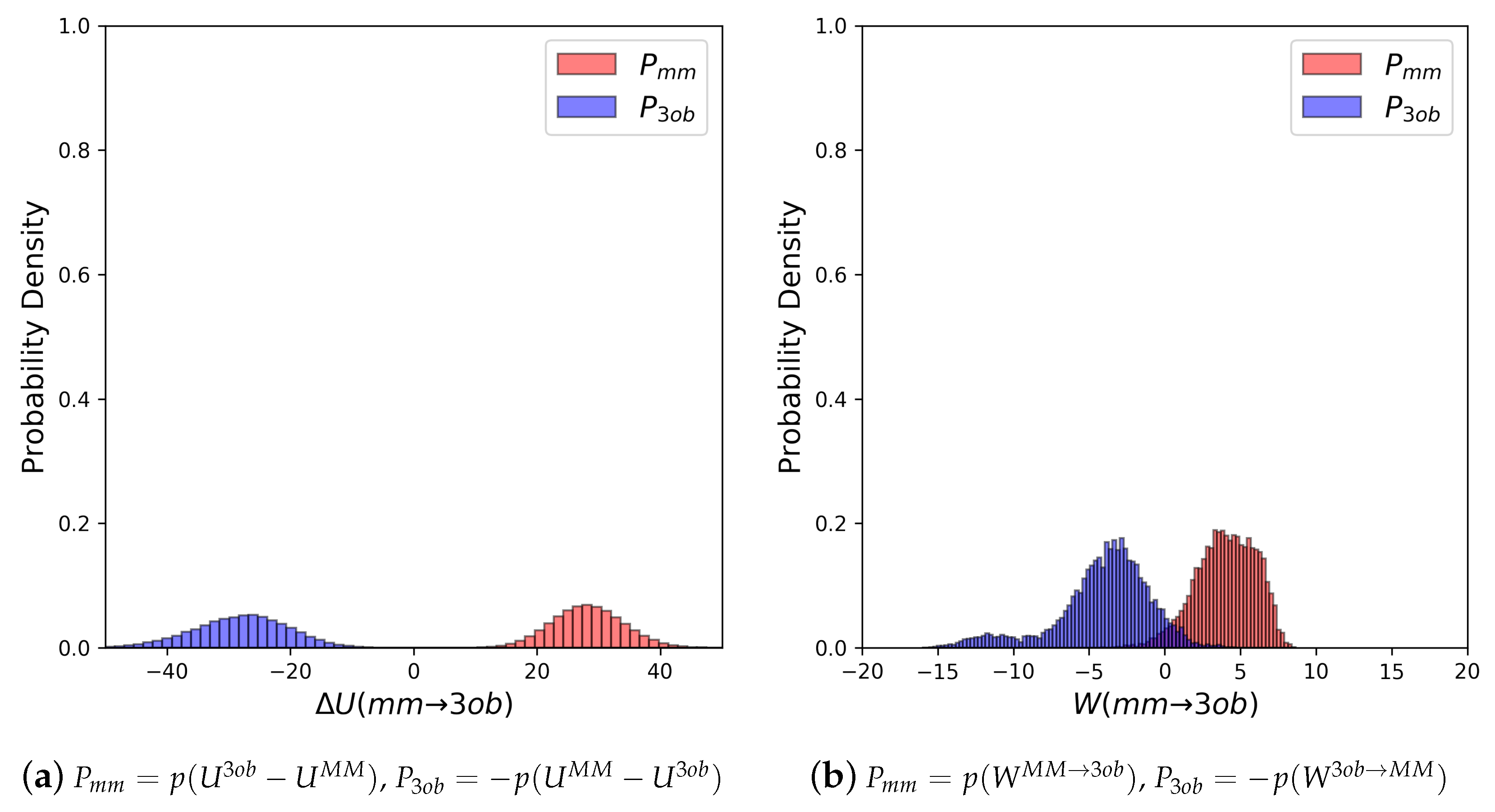
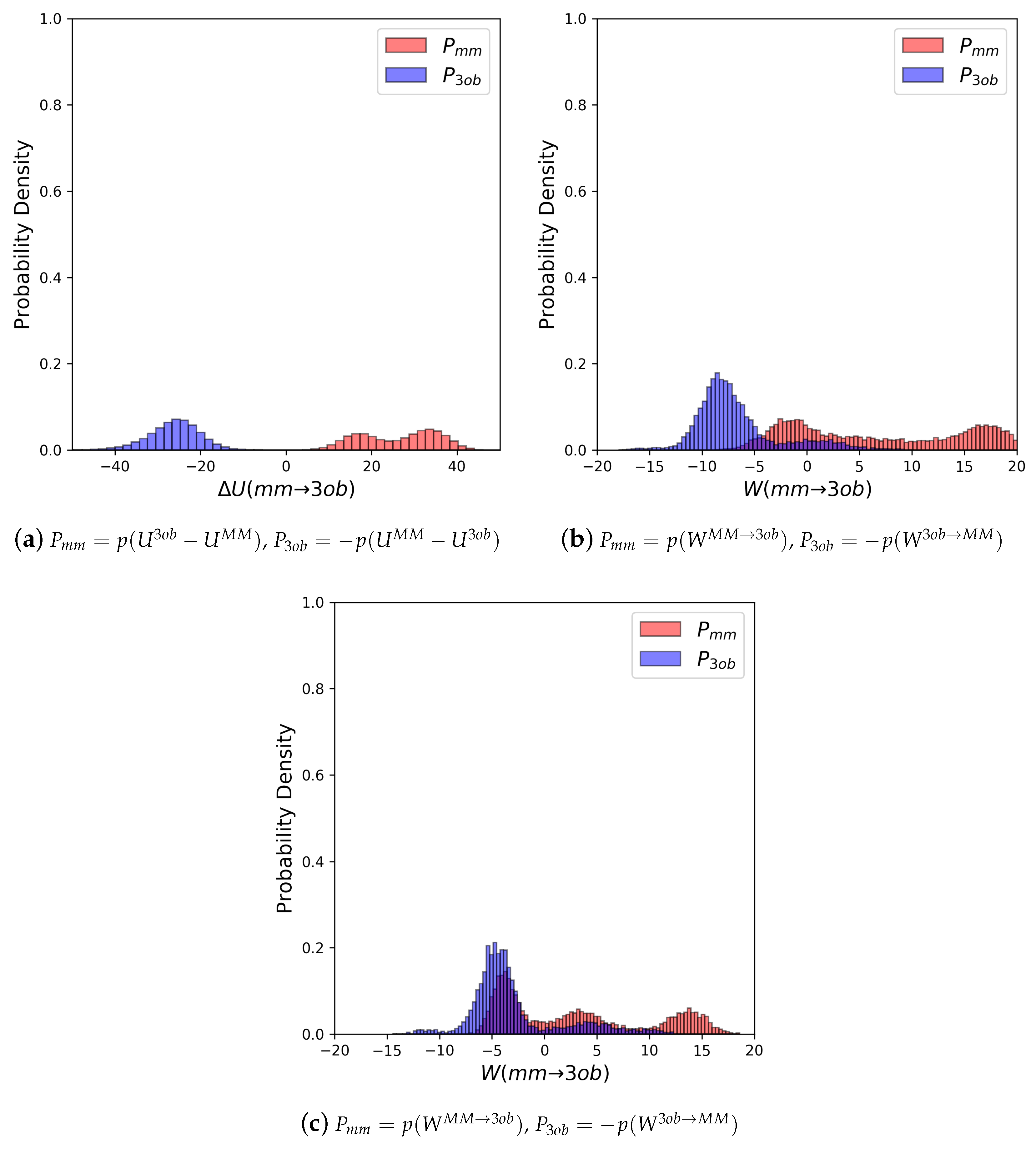
3.2.1. Molecule 5
3.2.2. Molecule 6
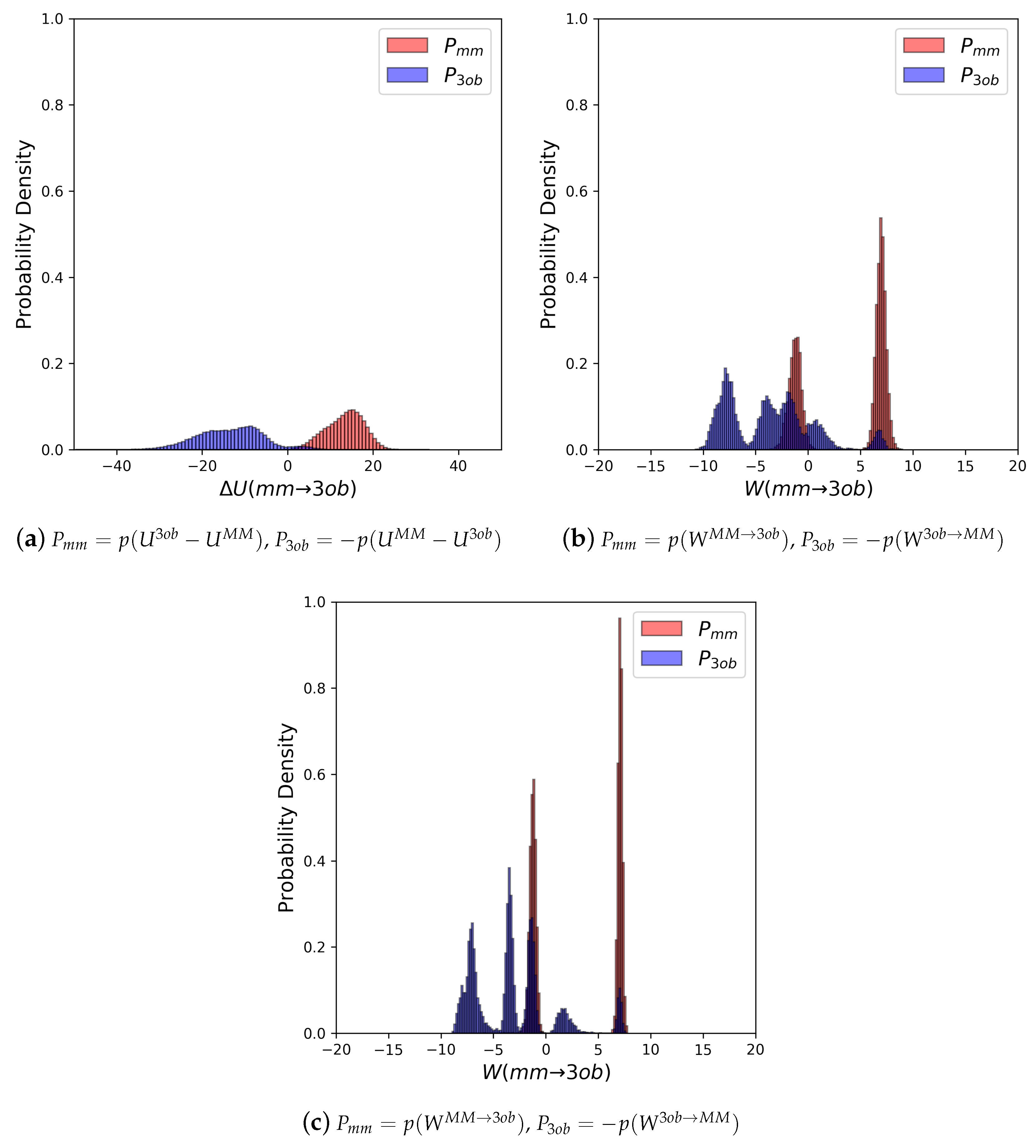
3.3. The Ugly
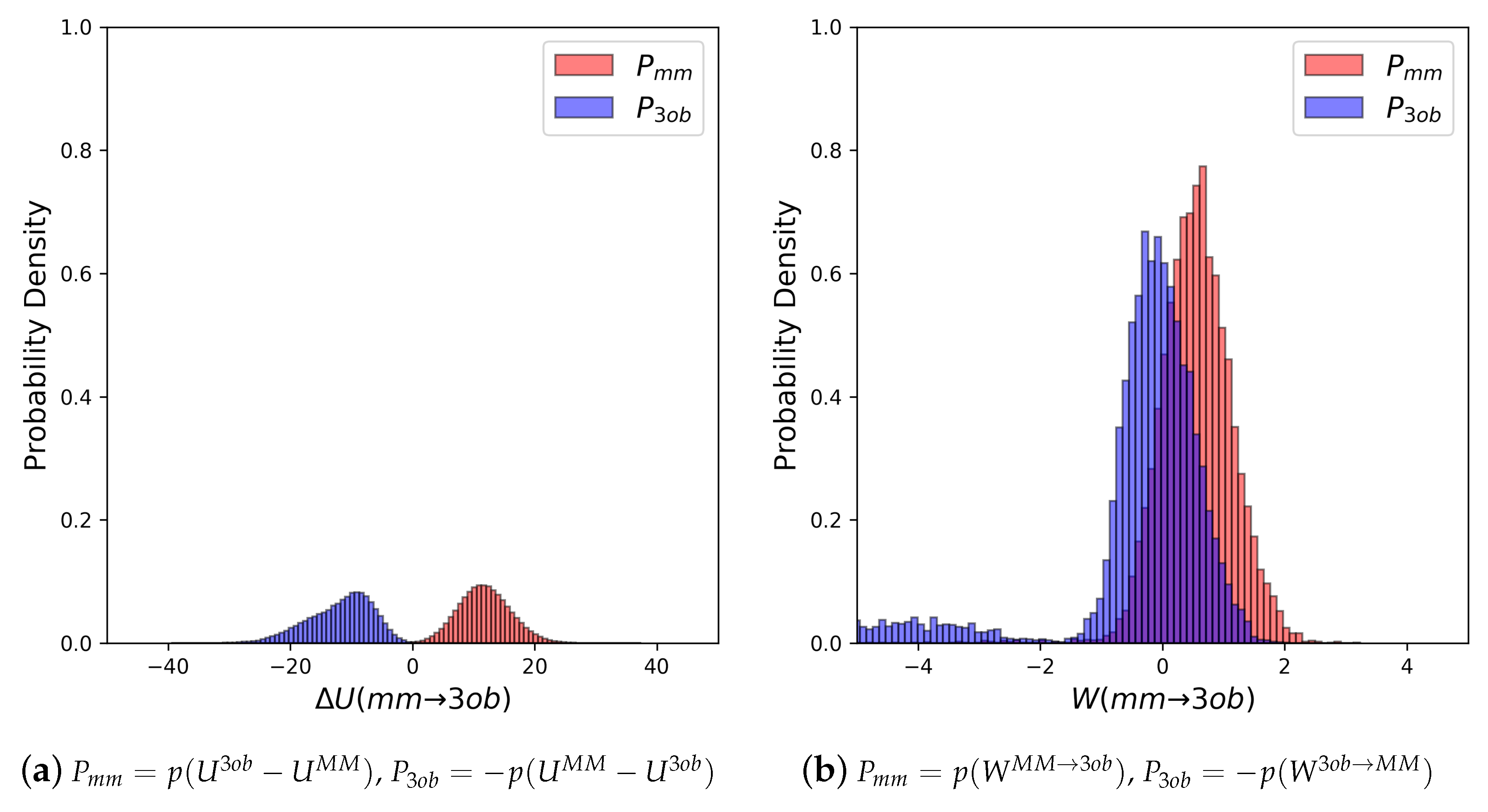
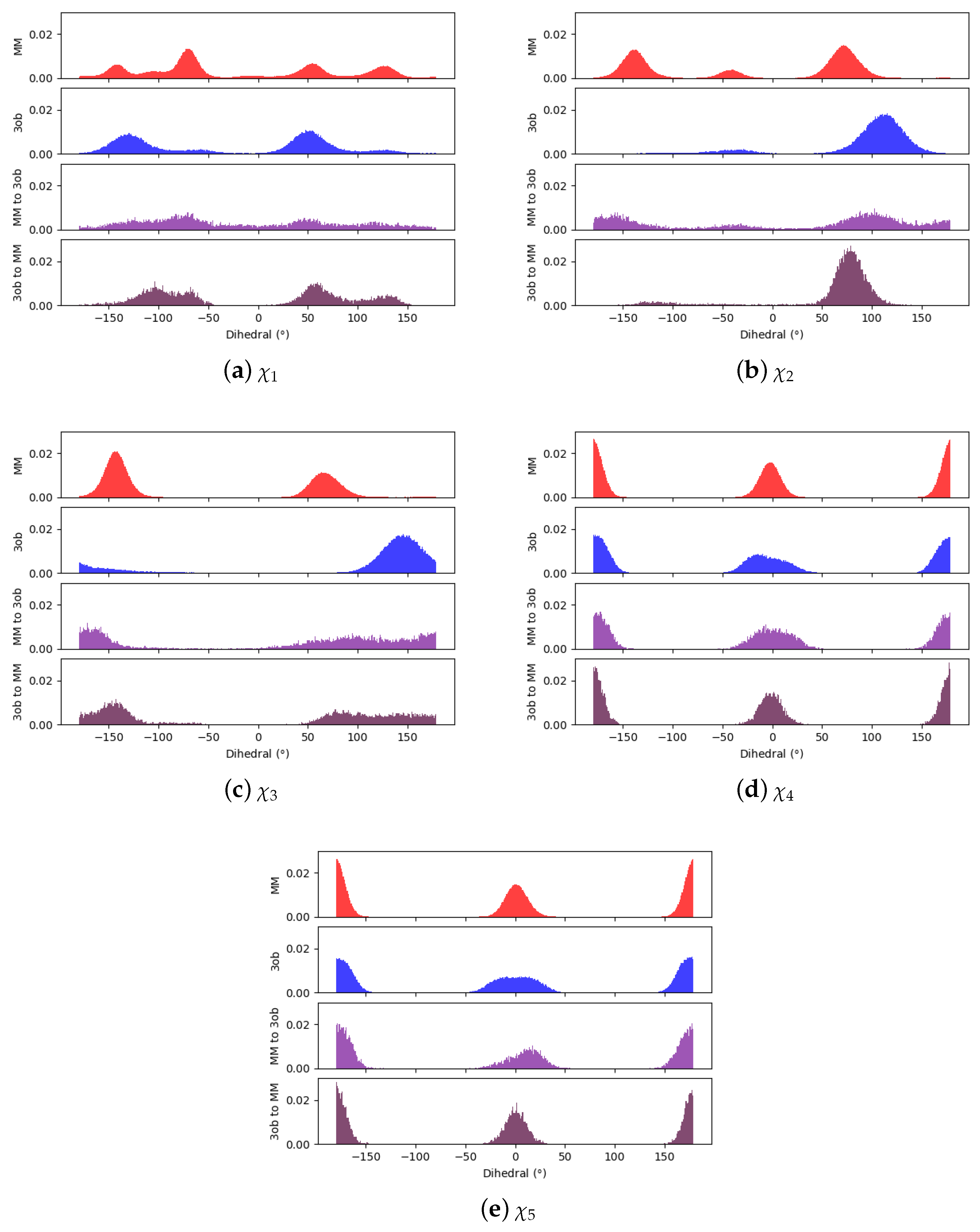
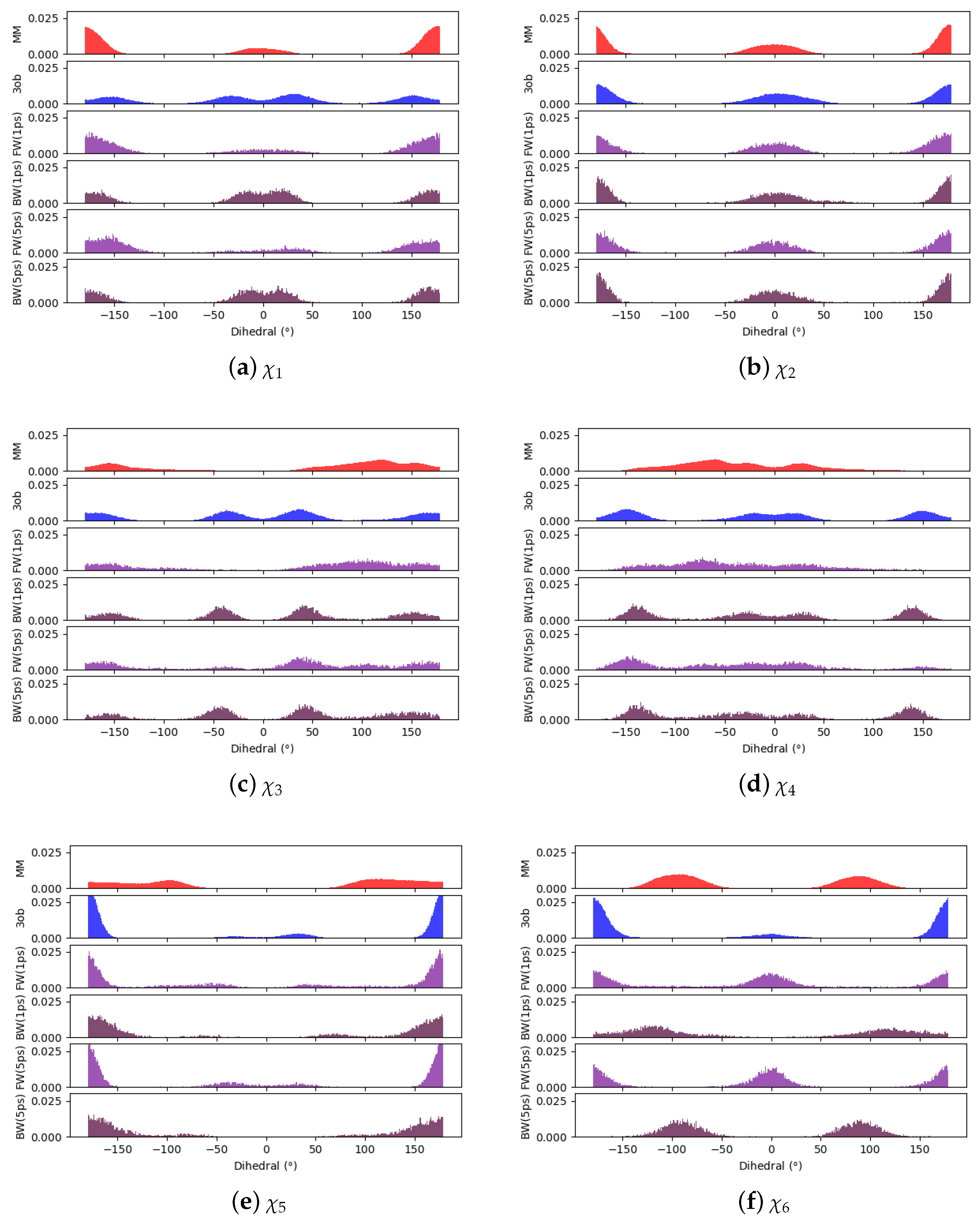
3.3.1. Molecule 8
3.3.2. Molecule 9
4. Materials and Methods
4.1. Equilibrium Simulations
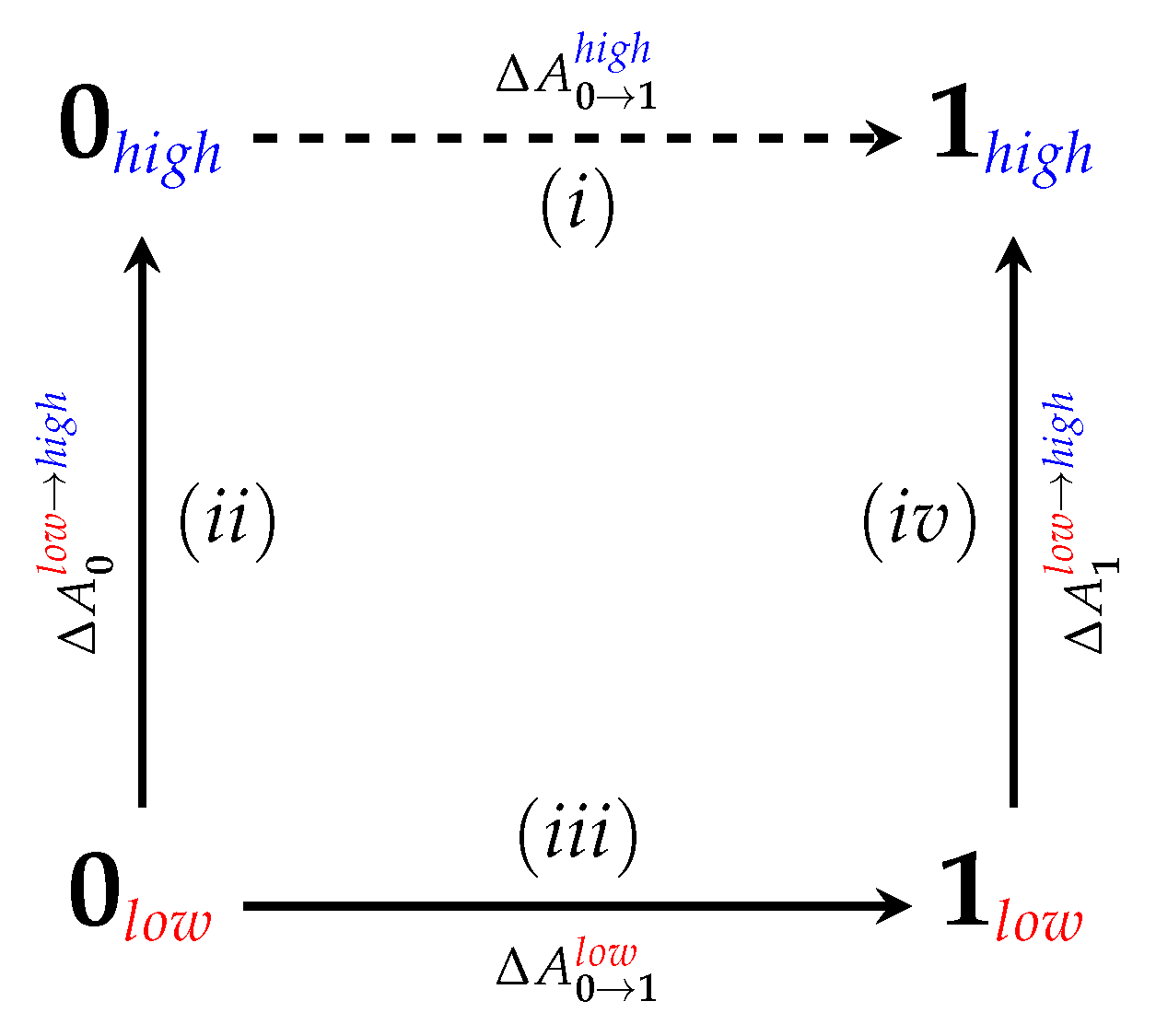
4.2. Nonequilibrium “Switching” Simulations
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MM | Molecular Mechanics |
| QM | Quantum Mechanics |
| SQM | Semiempirical Quantum Mechanics |
| QM/MM | Quantum Mechanical/Molecular Mechanical hybrid methods |
| SQM/MM | Semiempirical Quantum Mechanical/Molecular Mechanical hybrid methods |
| FEP | Free Energy Perturbation |
| BAR | Bennett’s Acceptance Ratio |
| JAR | Jarzynski’s equation |
| CRO | Crooks’ equation |
References
- Kästner, J.; Senn, H.M.; Thiel, S.; Otte, N.; Thiel, W. QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling: Application to an Enzymatic Reaction. J. Chem. Theory Comput. 2006, 2, 452–461. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.; Cui, Q.; Min, D.; Li, H. QM/MM Alchemical Free Energy Simulations: Challenges and Recent Developments. Annu. Rep. Comput. Chem. 2010, 6, 51–62. [Google Scholar]
- Lu, X.; Fang, D.; Ito, S.; Okamoto, Y.; Ovchinnikov, V.; Cui, Q. QM/MM free energy simulations: Recent progress and challenges. Mol. Simul. 2016, 42, 1056–1078. [Google Scholar] [CrossRef] [PubMed]
- Rathore, R.S.; Sumakanth, M.; Reddy, M.S.; Reddanna, P.; Rao, A.A.; Erion, M.D.; Reddy, M.R. Advances in Binding Free Energies Calculations: QM/MM—Based Free Energy Perturbation Method for Drug Design. Curr. Pharm. Des. 2017, 19, 4674–4686. [Google Scholar] [CrossRef]
- Ryde, U.; Söderhjelm, P. Ligand-Binding Affinity Estimates Supported by Quantum-Mechanical Methods. Chem. Rev. 2016, 116, 5520–5566. [Google Scholar] [CrossRef] [PubMed]
- Olsson, M.A.; Ryde, U. Comparison of QM/MM Methods To Obtain Ligand–Binding Free Energies. J. Chem. Theory Comput. 2017, 13, 2245–2253. [Google Scholar] [CrossRef] [PubMed]
- Kearns, F.L.; Hudson, P.S.; Boresch, S.; Woodcock, H.L. Chapter Four—Methods for Efficiently and Accurately Computing Quantum Mechanical Free Energies for Enzyme Catalysis. Methods Enzymol. 2016, 577, 75–104. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Xia, X. A priori evaluation of aqueous polarization effects through Monte Carlo QM-MM simulations. Science 1992, 258, 631–635. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; Luque, F.J.; Orozco, M. Induced dipole moment and atomic charges based on average electrostatic potentials in aqueous solution. J. Chem. Phys. 1993, 98, 2975. [Google Scholar] [CrossRef]
- Gao, J.; Freindorf, M. Hybrid ab Initio QM/MM Simulation of N-Methylacetamide in Aqueous Solution. J. Phys. Chem. A 1997, 101, 3182–3188. [Google Scholar] [CrossRef]
- Luzhkov, V.; Warshel, A. Microscopic models for quantum mechanical calculations of chemical processes in solutions: LD/AMPAC and SCAAS/AMPAC calculations of solvation energies. J. Comput. Chem. 1992, 13, 199–213. [Google Scholar] [CrossRef]
- Wesolowski, T.; Warshel, A. Ab Initio Free Energy Perturbation Calculations of Solvation Free Energy Using the Frozen Density Functional Approach. J. Phys. Chem. 1994, 98, 5183–5187. [Google Scholar] [CrossRef]
- Zheng, Y.J.; Merz, K.M. Mechanism of the human carbonic anhydrase II-catalyzed hydration of carbon dioxide. J. Am. Chem. Soc. 1992, 114, 10498–10507. [Google Scholar] [CrossRef]
- Beutler, T.C.; Mark, A.E.; van Schaik, R.C.; Gerber, P.R.; van Gunsteren, W.F. Avoiding Singularities and Numerical Instabilities in Free Energy Calculations Based on Molecular Simulations. Chem. Phys. Lett. 1994, 222, 529–539. [Google Scholar] [CrossRef]
- Zacharias, M.; Straatsma, T.P.; McCammon, J.A. Separation-Shifted Scaling, a New Scaling Method for {Lennard}-{Jones} Interactions in Thermodynamic Integration. J. Chem. Phys. 1994, 100, 9025–9031. [Google Scholar] [CrossRef]
- Zwanzig, R. High—Temperature Equation of State by a Perturbation Method. I. Nonpolar Gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Bennett, C.H. Efficient estimation of free energy differences from Monte Carlo data. J. Comput. Phys. 1976, 22, 245–268. [Google Scholar] [CrossRef]
- Shirts, M.R.; Chodera, J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008, 129, 124105. [Google Scholar] [CrossRef] [PubMed]
- Lee, T.S.; Radak, B.K.; Pabis, A.; York, D.M. A new maximum likelihood approach for free energy profile construction from molecular simulations. J. Chem. Theory Comput. 2013, 9, 153–164. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Heimdal, J.; Ryde, U. Convergence of QM/MM free-energy perturbations based on molecular-mechanics or semiempirical simulations. Phys. Chem. Chem. Phys. 2012, 14, 12592. [Google Scholar] [CrossRef] [PubMed]
- König, G.; Hudson, P.S.; Boresch, S.; Woodcock, H.L.; König, G.; Hudson, P.S.; Boresch, S.; Woodcock, H.L. Multiscale free energy simulations: An efficient method for connecting classical MD simulations to QM or QM/MM free energies using Non-Boltzmann Bennett reweighting schemes. J. Chem. Theory Comput. 2014, 10, 1406–1419. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Cabedo Martinez, A.I.; Criddle, M.P.; Essex, J.W. Extensive all-atom Monte Carlo sampling and QM/MM corrections in the SAMPL4 hydration free energy challenge. J. Comput. Aided Mol. Des. 2014, 28, 187–200. [Google Scholar] [CrossRef] [PubMed]
- Cave-Ayland, C.; Skylaris, C.K.; Essex, J.W. Direct Validation of the Single Step Classical to Quantum Free Energy Perturbation. J. Phys. Chem. B 2015, 119, 1017–1025. [Google Scholar] [CrossRef] [PubMed]
- König, G.; Brooks, B.R. Correcting for the free energy costs of bond or angle constraints in molecular dynamics simulations. Biochim. Biophys. Acta Gen. Subj. 2015, 1850, 932–943. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.S.; White, J.K.; Kearns, F.L.; Hodoscek, M.; Boresch, S.; Lee Woodcock, H. Efficiently computing pathway free energies: New approaches based on chain-of-replica and Non-Boltzmann Bennett reweighting schemes. Biochim. Biophys. Acta 2015, 1850, 944–953. [Google Scholar] [CrossRef] [PubMed]
- Sampson, C.; Fox, T.; Tautermann, C.S.; Woods, C.; Skylaris, C.K. A “Stepping Stone” Approach for Obtaining Quantum Free Energies of Hydration. J. Phys. Chem. B 2015, 119, 7030–7040. [Google Scholar] [CrossRef]
- Ryde, U. How Many Conformations Need To Be Sampled To Obtain Converged QM/MM Energies? The Curse of Exponential Averaging. J. Chem. Theory Comput. 2017, 13, 5745–5752. [Google Scholar] [CrossRef]
- Pohorille, A.; Jarzynski, C.; Chipot, C. Good Practices in Free-Energy Calculations. J. Phys. Chem. B 2010, 114, 10235–10253. [Google Scholar] [CrossRef]
- Shirts, M.R.; Mobley, D.L. An introduction to best practices in free energy calculations. Methods Mol. Biol. 2013, 924, 271–311. [Google Scholar] [PubMed]
- Hudson, P.S.; Boresch, S.; Rogers, D.M.; Woodcock, H.L. Accelerating QM/MM Free Energy Computations via Intramolecular Force Matching. J. Chem. Theory Comput. 2018, 14, 6327–6335. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.S.; Woodcock, H.L.; Boresch, S. Use of Nonequilibrium Work Methods to Compute Free Energy Differences Between Molecular Mechanical and Quantum Mechanical Representations of Molecular Systems. J. Phys. Chem. Lett. 2015, 6, 4850–4856. [Google Scholar] [CrossRef] [PubMed]
- Kearns, F.L.; Hudson, P.S.; Woodcock, H.L.; Boresch, S. Computing converged free energy differences between levels of theory via nonequilibrium work methods: Challenges and opportunities. J. Comput. Chem. 2017, 38, 1376–1388. [Google Scholar] [CrossRef] [PubMed]
- Ercolessi, F.; Adams, J.B. Interatomic Potentials from First-Principles Calculations: The Force-Matching Method. Europhys. Lett. 1994, 26, 583–588. [Google Scholar] [CrossRef]
- Maurer, P.; Laio, A.; Hugosson, H.W.; Colombo, M.C.; Rothlisberger, U. Automated Parametrization of Biomolecular Force Fields from Quantum Mechanics/Molecular Mechanics (QM/MM) Simulations through Force Matching. J. Chem. Theory Comput. 2007, 3, 628–639. [Google Scholar] [CrossRef]
- Izvekov, S.; Parrinello, M.; Burnham, C.J.; Voth, G.A. Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: A new method for force-matching. J. Chem. Phys. 2004, 120, 10896–10913. [Google Scholar] [CrossRef]
- Zhou, Y.; Pu, J. Reaction Path Force Matching: A New Strategy of Fitting Specific Reaction Parameters for Semiempirical Methods in Combined QM/MM Simulations. J. Chem. Theory Comput. 2014, 10, 3038–3054. [Google Scholar] [CrossRef]
- Zhou, Y.; Ojeda-May, P.; Nagaraju, M.; Pu, J. Chapter Eight—Toward Determining ATPase Mechanism in ABC Transporters: Development of the Reaction Path-Force Matching QM/MM Method. Methods Enzymol. 2016, 577, 185–212. [Google Scholar] [CrossRef]
- Kroonblawd, M.P.; Pietrucci, F.; Saitta, A.M.; Goldman, N. Generating Converged Accurate Free Energy Surfaces for Chemical Reactions with a Force-Matched Semiempirical Model. J. Chem. Theory Comput. 2018, 14, 2207–2218. [Google Scholar] [CrossRef]
- Csányi, G.; Albaret, T.; Payne, M.C.; De Vita, A. “Learn on the Fly”: A Hybrid Classical and Quantum-Mechanical Molecular Dynamics Simulation. Phys. Rev. Lett. 2004, 93, 175503. [Google Scholar] [CrossRef] [PubMed]
- Akin-Ojo, O.; Song, Y.; Wang, F. Developing ab initio quality force fields from condensed phase quantum-mechanics/molecular-mechanics calculations through the adaptive force matching method. J. Chem. Phys. 2008, 129, 64108. [Google Scholar] [CrossRef] [PubMed]
- Akin-Ojo, O.; Wang, F. The quest for the best nonpolarizable water model from the adaptive force matching method. J. Comput. Chem. 2010, 32, 453–462. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Akin-Ojo, O.; Pinnick, E.; Song, Y. Approaching post-Hartree–Fock quality potential energy surfaces with simple pair-wise expressions: Parameterising point-charge-based force fields for liquid water using the adaptive force matching method. Mol. Simul. 2011, 37, 591–605. [Google Scholar] [CrossRef]
- Pinnick, E.R.; Calderon, C.E.; Rusnak, A.J.; Wang, F. Achieving fast convergence of ab initio free energy perturbation calculations with the adaptive force-matching method. Theor. Chem. Acc. 2012, 131, 1146. [Google Scholar] [CrossRef]
- Li, J.; Wang, F. Pairwise-additive force fields for selected aqueous monovalent ions from adaptive force matching. J. Chem. Phys. 2015, 143, 194505. [Google Scholar] [CrossRef]
- Wang, L.P.; Voorhis, T.V. Communication: Hybrid ensembles for improved force matching. J. Chem. Phys. 2010, 133, 231101. [Google Scholar] [CrossRef]
- Wang, L.P.; Chen, J.; Voorhis, T.V. Systematic Parametrization of Polarizable Force Fields from Quantum Chemistry Data. J. Chem. Theory Comput. 2012, 9, 452–460. [Google Scholar] [CrossRef]
- Wang, L.P.; McKiernan, K.A.; Gomes, J.; Beauchamp, K.A.; Head-Gordon, T.; Rice, J.E.; Swope, W.C.; Martíinez, T.J.; Pande, V.S. Building a More Predictive Protein Force Field: A Systematic and Reproducible Route to AMBER-FB15. J. Phys. Chem. B 2017, 121, 4023–4039. [Google Scholar] [CrossRef]
- Li, P.; Jia, X.; Pan, X.; Shao, Y.; Mei, Y. Accelerated Computation of Free Energy Profile at ab Initio Quantum Mechanical/Molecular Mechanics Accuracy via a Semi-Empirical Reference Potential. I. Weighted Thermodynamics Perturbation. J. Chem. Theory Comput. 2018, 14, 5583–5596. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium Equality for Free Energy Differences. Phys. Rev. Lett. 1997, 78, 2690–2693. [Google Scholar] [CrossRef]
- Crooks, G.E. Path-ensemble averages in systems driven far from equilibrium. Phys. Rev. E 2000, 61, 2361–2366. [Google Scholar] [CrossRef]
- Pevzner, Y.; Frugier, E.; Schalk, V.; Caflisch, A.; Woodcock, H.L. Fragment-Based Docking: Development of the CHARMMing Web User Interface as a Platform for Computer-Aided Drug Design. J. Chem. Inf. Model. 2014, 54, 2612–2620. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) I: Bond and perception and atom typing. J. Chem. Inf. Model. 2012, 52, 3144–3154. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Raman, E.P.; MacKerell, A.D., Jr. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of bonded parameters and partial atomic charges. J. Chem. Inf. Model. 2012, 52, 3155–3168. [Google Scholar] [CrossRef] [PubMed]
- Vanommeslaeghe, K.; Hatcher, E.; Acharya, C.; Kundu, S.; Zhong, S.; Shim, J.; Darian, E.; Guvench, O.; Lopes, P.; Vorobyov, I.; et al. CHARMM general force field: A force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields. J. Comput. Chem. 2010, 31, 671–690. [Google Scholar] [CrossRef]
- Maybridge HitFinderTM (14,400 Compounds). 2018. Available online: https://www.maybridge.com/portal/alias__Rainbow/lang__en-US/tabID__229/DesktopDefault.aspx (accessed on 30 June 2018).
- Mardirossian, N.; Head-Gordon, M. Mapping the genome of meta-generalized gradient approximation density functionals: The search for B97M-V. J. Chem. Phys. 2015, 142, 074111. [Google Scholar] [CrossRef]
- Manzer, S.; Horn, P.R.; Mardirossian, N.; Head-Gordon, M. Fast, accurate evaluation of exact exchange: The occ-RI-K algorithm. J. Chem. Phys. 2015, 143, 024113. [Google Scholar] [CrossRef] [PubMed]
- Mardirossian, N.; Head-Gordon, M. ωB97M-V: A combinatorially optimized, range-separated hybrid, meta-GGA density functional with VV10 nonlocal correlation. J. Chem. Phys. 2016, 144, 214110. [Google Scholar] [CrossRef]
- Mao, Y.; Horn, P.R.; Mardirossian, N.; Head-Gordon, T.; Skylaris, C.K.; Head-Gordon, M. Approaching the basis set limit for DFT calculations using an environment-adapted minimal basis with perturbation theory: Formulation, proof of concept, and a pilot implementation. J. Chem. Phys. 2016, 145, 044109. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Survival of the most transferable at the top of Jacob’s ladder: Defining and testing the ωB97M(2) double hybrid density functional. J. Chem. Phys. 2018, 148, 241736. [Google Scholar] [CrossRef]
- Wang, Y.; Verma, P.; Jin, X.; Truhlar, D.G.; He, X. Revised M06 density functional for main-group and transition-metal chemistry. Proc. Natl. Acad. Sci. USA 2018, 115, 10257–10262. [Google Scholar] [CrossRef]
- Wang, Y.; Jin, X.; Yu, H.S.; Truhlar, D.G.; He, X. Revised M06-L functional for improved accuracy on chemical reaction barrier heights, noncovalent interactions, and solid-state physics. Proc. Natl. Acad. Sci. USA 2017, 114, 8487–8492. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.S.; He, X.; Li, S.L.; Truhlar, D.G. MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions. Chem. Sci. 2016, 7, 5032–5051. [Google Scholar] [CrossRef] [PubMed]
- Taylor, D.E.; Ángyán, J.G.; Galli, G.; Zhang, C.; Gygi, F.; Hirao, K.; Song, J.W.; Rahul, K.; Anatole von Lilienfeld, O.; Podeszwa, R.; et al. Blind test of density-functional-based methods on intermolecular interaction energies. J. Chem. Phys. 2016, 145, 124105. [Google Scholar] [CrossRef] [PubMed]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Peverati, R.; Truhlar, D.G. Quest for a universal density functional: The accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos. Trans. A Math Phys. Eng. Sci. 2014, 372, 20120476. [Google Scholar] [CrossRef]
- Goldey, M.; Head-Gordon, M. Attenuating Away the Errors in Inter- and Intramolecular Interactions from Second-Order Møller–Plesset Calculations in the Small Aug-cc-pVDZ Basis Set. J. Phys. Chem. Lett. 2012, 3, 3592–3598. [Google Scholar] [CrossRef]
- Huang, Y.; Goldey, M.; Head-Gordon, M.; Beran, G.J.O. Achieving High-Accuracy Intermolecular Interactions by Combining Coulomb-Attenuated Second-Order Møller–Plesset Perturbation Theory with Coupled Kohn–Sham Dispersion. J. Chem. Theory Comput. 2014, 10, 2054–2063. [Google Scholar] [CrossRef]
- Goldey, M.; Head-Gordon, M. Separate Electronic Attenuation Allowing a Spin-Component-Scaled Second-Order Møller–Plesset Theory to Be Effective for Both Thermochemistry and Noncovalent Interactions. J. Phys. Chem. B 2014, 118, 6519–6525. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Grimme, S. Accurate Modeling of Organic Molecular Crystals by Dispersion-Corrected Density Functional Tight Binding (DFTB). J. Phys. Chem. Lett. 2014, 5, 1785–1789. [Google Scholar] [CrossRef]
- Cui, Q.; Elstner, M. Density functional tight binding: Values of semi-empirical methods in an ab initio era. Phys. Chem. Chem. Phys. 2014, 16, 14368–14377. [Google Scholar] [CrossRef] [PubMed]
- Loeffler, H.H.; Bosisio, S.; Matos, G.D.R.; Suh, D.; Roux, B.; Mobley, D.L.; Michel, J. Reproducibility of Free Energy Calculations across Different Molecular Simulation Software Packages. J. Chem. Theory Comput. 2018, 14, 5567–5582. [Google Scholar] [CrossRef] [PubMed]
- Geballe, M.T.; Skillman, A.G.; Nicholls, A.; Guthrie, J.P.; Taylor, P.J. The SAMPL2 blind prediction challenge: Introduction and overview. J. Comp. Aided Mol. Des. 2010, 24, 259–279. [Google Scholar] [CrossRef] [PubMed]
- Geballe, M.T.; Guthrie, J.P. The SAMPL3 blind prediction challenge: Transfer energy overview. J. Comp. Aided Mol. Des. 2012, 26, 489–496. [Google Scholar] [CrossRef]
- Bannan, C.C.; Burley, K.H.; Chiu, M.; Shirts, M.R.; Gilson, M.K.; Mobley, D.L. Blind Prediction of Cyclohexane–Water Distribution Coefficients from the SAMPL5 Challenge. J. Comput. Aided Mol. Des. 2016, 30, 927–944. [Google Scholar] [CrossRef]
- Boresch, S.; Woodcock, H.L. Convergence of single-step free energy perturbation. Mol. Phys. 2017, 115, 1200–1213. [Google Scholar] [CrossRef]
- Wu, D.; Kofke, D.A. Phase-space overlap measures. I. Fail-safe bias detection in free energies calculated by molecular simulation. J. Chem. Phys. 2005, 123, 54103. [Google Scholar] [CrossRef]
- Wood, R.H.; Muhlbauer, W.C.F.; Thompson, P.T. Systematic errors in free energy perturbation calculations due to a finite sample of configuration space: Sample-size hysteresis. J. Phys. Chem. 1991, 95, 6670–6675. [Google Scholar] [CrossRef]
- Wu, D.; Kofke, D.A. Model for Small-Sample Bias of Free-Energy Calculations Applied to {{Gaussian}}-Distributed Nonequilibrium Work Measurements. J. Chem. Phys. 2004, 121, 8742–8747. [Google Scholar] [CrossRef]
- Dai, H.; Ge, S.; Li, G.; Chen, J.; Shi, Y.; Ye, L.; Ling, Y. Synthesis and bioactivities of novel pyrazole oxime derivatives containing a 1,2,3-thiadiazole moiety. Biol. Med. Chem. Lett. 2016, 26, 4504–4507. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Wang, J.L.; Dang, D.B.; Zheng, Y.N. Synthesis, crystal structures and luminescent properties of two one-dimensional cadmium(II) coordination polymers generated from polydentate Schiff-base ligand. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2012, 97, 105–110. [Google Scholar] [CrossRef] [PubMed]
- Abd-Ellah, H.S.; Abdel-Aziz, M.; Shoman, M.E.; Beshr, E.A.; Kaoud, T.S.; Ahmed, A.S.F. Novel 1,3,4-oxadiazole/oxime hybrids: Synthesis, docking studies and investigation of anti-inflammatory, ulcerogenic liability and analgesic activities. Biol. Chem. 2016, 69, 48–63. [Google Scholar] [CrossRef] [PubMed]
- Ichimaru, Y.; Saito, H.; Uchiyama, T.; Metori, K.; Tabata, K.; Suzuki, T.; Miyairi, S. Indirubin 3′-(O-oxiran- 2-ylmethyl)oxime: A novel anticancer agent. Biol. Med. Chem. Lett. 2015, 25, 1403–1406. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Sha, S.; Wang, K.; Zhang, Y.H.; Liu, Y.D.; Ju, G.D.; Wang, B.; Zhu, H.L. Discovery of Chromeno[4,3-c] pyrazol-4(2H)-one Containing Carbonyl or Oxime Derivatives as Potential, Selective Inhibitors PI3Kα. Chem. Pharm. Bull. 2016, 64, 1576–1581. [Google Scholar] [CrossRef]
- Brooks, B.R.; Brooks, C.L., III; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Irwin, J.J.; Sterling, T.; Mysinger, M.M.; Bolstad, E.S.; Coleman, R.G. ZINC: A Free Tool to Discover Chemistry for Biology. J. Chem. Inf. Model. 2012, 52, 1757–1768. [Google Scholar] [CrossRef]
- Woodcock, H.L.; Miller, B.T.; Hodoscek, M.; Okur, A.; Larkin, J.D.; Ponder, J.W.; Brooks, B.R. MSCALE: A General Utility for Multiscale Modeling. J. Chem. Theory Comput. 2011, 7, 1208–1219. [Google Scholar] [CrossRef] [PubMed]
- Dellago, C.; Hummer, G. Computing Equilibrium Free Energies Using Non-Equilibrium Molecular Dynamics. Entropy 2013, 16, 41–61. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds are not available from the authors. |
| ZINC ID | CGenFF Penalties | Offset (kcal/mol) | |||
|---|---|---|---|---|---|
| Param | Charge | ||||
| 1 | 00061095 | 36/21 | 432.10 | 200.99 | 29,000 |
| 2 | 00077329 | 16/10 | 378.50 | 347.24 | 15,000 |
| 3 | 00079729 | 18/13 | 683.00 | 207.72 | 17,000 |
| 4 | 00086442 | 21/12 | 312.50 | 283.62 | 19,000 |
| 5 | 00087557 | 31/17 | 378.50 | 347.31 | 25,000 |
| 6 | 00095858 | 25/16 | 567.90 | 361.40 | 25,000 |
| 7 | 00107550 | 21/11 | 378.50 | 347.29 | 16,000 |
| 8 | 00107778 | 22/15 | 378.50 | 347.29 | 21,000 |
| 9 | 00123162 | 34/21 | 385.50 | 217.28 | 29,000 |
| 10 | 00133435 | 34/22 | 470.50 | 27.14 | 28,000 |
| 11 | 00138607 | 36/20 | 336.00 | 261.56 | 29,000 |
| 12 | 00140610 | 20/12 | 449.00 | 214.90 | 17,000 |
| 13 | 00164361 | 23/14 | 424.00 | 194.49 | 20,000 |
| 14 | 00167648 | 44/26 | 436.50 | 226.60 | 35,000 |
| 15 | 00169358 | 26/16 | 540.40 | 142.16 | 22,000 |
| 16 | 01755198 | 28/12 | 329.00 | 21.11 | 19,000 |
| 17 | 01867000 | 32/18 | 470.50 | 5.82 | 22,000 |
| 18 | 03127671 | 41/24 | 329.00 | 25.20 | 34,000 |
| 19 | 04344392 | 52/29 | 329.00 | 24.78 | 40,000 |
| 20 | 04363792 | 28/21 | 698.00 | 185.49 | 28,000 |
| 21 | 06568023 | 30/18 | 329.00 | 21.60 | 25,000 |
| 22 | 33381936 | 33/21 | 545.50 | 395.62 | 30,000 |
| FEP (fw) | FEP (bw) | BAR | Overlap (%) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hyst | Hyst | Hyst | ||||||||||||||
| 1 | −301.11 | 4.08 | 5.29 | −282.47 | 7.89 | −3.14 | 305.82 | 1.87 | 2.02 | 322.87 | 7.30 | −3.29 | −303.34 | −0.15 | 3.15 | 0.04 |
| 2 | −255.52 | 0.19 | 0.51 | −245.10 | 4.29 | −1.15 | 258.88 | 0.29 | 0.60 | 268.72 | 5.28 | −1.47 | −256.87 | −0.05 | 0.11 | 0.28 |
| 3 | −412.88 | 0.35 | 0.65 | −402.47 | 3.49 | −1.17 | 416.38 | 0.54 | 0.78 | 428.26 | 4.86 | −2.06 | −414.19 | −0.01 | 0.01 | 0.12 |
| 4 | −254.51 | 0.43 | 0.69 | −239.09 | 5.66 | −2.43 | 259.24 | 0.51 | 0.84 | 269.67 | 4.34 | −1.64 | −256.34 | 0.00 | 0.03 | 0.06 |
| 5 | −589.94 | 2.30 | 2.38 | −570.06 | 5.78 | −3.41 | 604.61 | 2.25 | 2.49 | 626.49 | 7.84 | −4.29 | −596.97 | 0.48 | 0.25 | 0.00 |
| 6 | −109.58 | 2.58 | 2.59 | −86.31 | 7.14 | −4.07 | 130.57 | 4.83 | 4.41 | 162.27 | 10.42 | −6.04 | −118.33 | 0.56 | 2.35 | 0.00 |
| 7 | −992.13 | 0.33 | 0.67 | −982.02 | 3.94 | −1.06 | 994.96 | 4.83 | 12.05 | 1011.88 | 19.05 | −3.26 | −993.15 | 0.21 | 0.49 | 0.28 |
| 8 | −994.00 | 4.16 | 4.03 | −982.45 | 4.39 | −1.46 | 988.29 | 9.09 | 5.74 | 1009.22 | 7.77 | −4.10 | −992.02 | 1.03 | 14.08 | 3.72 |
| 9 | −447.42 | 2.99 | 3.12 | −423.12 | 9.04 | −4.27 | 451.15 | 8.94 | 4.93 | 475.54 | 6.40 | −4.77 | −449.44 | 1.02 | 5.61 | 0.02 |
| 10 | −336.30 | 0.84 | 0.99 | −320.41 | 5.46 | −2.54 | 341.91 | 0.31 | 0.72 | 352.24 | 4.10 | −1.61 | −337.98 | 0.11 | 0.07 | 0.04 |
| 11 | −460.25 | 1.37 | 1.30 | −441.09 | 7.09 | −3.26 | 464.90 | 1.43 | 1.15 | 482.37 | 8.89 | −3.38 | −461.88 | 0.11 | 0.07 | 0.02 |
| 12 | −70.74 | 2.17 | 1.31 | −54.33 | 4.82 | −2.66 | 84.97 | 0.85 | 1.21 | 115.59 | 11.07 | −5.86 | −77.20 | 0.25 | 0.02 | 0.00 |
| 13 | −556.49 | 2.79 | 1.67 | −547.25 | 5.39 | −3.27 | 571.83 | 1.37 | 1.32 | 587.80 | 5.62 | −3.28 | −567.59 | 0.18 | 0.15 | 0.01 |
| 14 | −80.28 | 0.79 | 0.97 | −65.97 | 4.62 | −2.17 | 85.55 | 0.78 | 0.77 | 100.32 | 6.15 | −2.89 | −82.62 | 0.12 | 0.10 | 0.03 |
| 15 | −406.76 | 0.18 | 0.46 | −398.31 | 3.39 | −0.56 | 408.29 | 0.32 | 0.54 | 419.87 | 5.52 | −2.04 | −407.59 | 0.02 | 0.00 | 0.51 |
| 16 | −633.17 | 1.32 | 1.57 | −621.65 | 4.28 | −1.45 | 638.22 | 2.26 | 2.73 | 664.09 | 8.08 | −5.12 | −636.14 | 0.72 | 0.68 | 0.05 |
| 17 | −673.11 | 0.21 | 0.55 | −664.21 | 3.29 | −0.70 | 672.67 | −0.13 | 0.71 | 682.01 | 3.11 | −1.71 | −673.41 | −0.03 | 0.01 | 0.69 |
| 18 | −518.20 | 1.82 | 1.80 | −501.32 | 5.34 | −2.76 | 525.15 | 4.99 | 4.91 | 551.31 | 9.84 | −5.09 | −520.79 | 0.90 | 3.94 | 0.10 |
| 19 | −879.27 | 3.54 | 2.13 | −857.72 | 6.10 | −3.74 | 892.96 | 1.86 | 2.43 | 918.55 | 9.50 | −4.99 | −885.39 | 0.51 | 0.21 | 0.00 |
| 20 | −691.39 | 3.08 | 4.83 | −676.22 | 6.43 | −2.37 | 713.26 | 0.83 | 1.34 | 753.13 | 14.99 | −7.29 | −702.33 | 0.83 | 1.13 | 0.00 |
| 21 | −70.62 | 2.52 | 1.58 | −59.20 | 3.66 | −1.43 | 69.86 | 1.10 | 1.30 | 87.37 | 8.66 | −3.39 | −69.33 | 0.25 | 0.84 | 0.37 |
| 22 | −177.51 | 0.73 | 0.97 | −165.15 | 4.25 | −1.68 | 181.81 | 0.82 | 1.04 | 213.38 | 37.01 | −6.02 | −179.19 | 0.14 | 0.22 | 0.07 |
| JAR (fw) | JAR (bw) | CRO | Overlap (%) | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hyst | Hyst | Hyst | W | |||||||||||||
| 1 | −305.97 | 2.92 | 3.87 | −299.85 | 5.07 | −0.80 | 300.95 | 0.47 | 0.39 | 302.15 | 1.97 | 1.60 | −301.61 | 0.53 | 4.44 | 32.71 |
| 2 | −272.53 | 0.21 | 0.48 | −271.48 | 0.60 | 1.86 | 271.88 | 0.13 | 0.48 | 272.59 | 1.59 | 2.19 | −271.84 | 0.09 | 0.08 | 53.89 |
| 3 | −408.69 | 0.00 | 0.03 | −408.18 | 0.90 | 2.40 | 408.63 | 0.00 | 0.05 | 409.03 | 0.63 | 2.57 | −408.66 | 0.00 | 0.00 | 56.68 |
| 4 | −271.25 | 0.00 | 0.03 | −271.10 | 0.41 | 3.02 | 271.15 | 0.00 | 0.02 | 271.31 | 0.49 | 3.00 | −271.20 | 0.00 | 0.00 | 79.52 |
| 5 | −539.16 | 0.58 | 0.98 | −535.17 | 1.98 | 0.08 | 537.50 | 2.26 | 2.71 | 543.25 | 3.18 | −0.66 | −538.78 | 0.36 | 0.37 | 8.76 |
| 6 | −143.51 | 3.69 | 2.10 | −137.78 | 2.08 | −0.65 | 138.57 | 1.46 | 2.12 | 143.83 | 3.12 | −0.47 | −140.17 | 0.41 | 1.70 | 23.95 |
| 7 | −999.40 | 0.42 | 0.69 | −998.41 | 0.69 | 1.91 | 998.80 | 1.37 | 2.82 | 1000.98 | 3.29 | 1.03 | −999.02 | 0.42 | 0.28 | 44.88 |
| 8 | −995.50 | 3.54 | 3.79 | −990.77 | 4.06 | −0.25 | 989.35 | 6.99 | 4.61 | 998.13 | 4.05 | −1.69 | −995.41 | 0.90 | 9.68 | 24.92 |
| 8 (5 ps) | −995.88 | 2.90 | 3.74 | −991.48 | 4.16 | −0.18 | 989.36 | 7.05 | 3.29 | 997.91 | 3.78 | −1.71 | −995.87 | 0.68 | 1.60 | 27.70 |
| 9 | −426.22 | 1.72 | 1.95 | −414.69 | 8.21 | −2.48 | 415.08 | 7.74 | 5.19 | 428.09 | 4.12 | −2.87 | −423.89 | 0.91 | 8.28 | 22.83 |
| 9 (5 ps) | −426.53 | −0.28 | 1.04 | −419.30 | 7.09 | −1.24 | 412.65 | 9.23 | 5.75 | 425.23 | 4.45 | −2.95 | −425.45 | 1.22 | 6.82 | 60.27 |
| 10 | −285.45 | 0.02 | 0.15 | −284.78 | 0.82 | 2.25 | 285.36 | 0.00 | 0.03 | 286.22 | 1.18 | 2.03 | −285.41 | 0.01 | 0.00 | 46.14 |
| 11 | −510.05 | 0.02 | 0.17 | −507.81 | 2.93 | 0.99 | 509.50 | 0.23 | 0.41 | 510.72 | 0.96 | 1.68 | −509.92 | 0.03 | 0.01 | 44.12 |
| 12 | −81.64 | 0.00 | 0.03 | −81.37 | 0.55 | 2.78 | 81.48 | 0.00 | 0.03 | 81.77 | 0.63 | 2.73 | −81.56 | 0.00 | 0.00 | 72.35 |
| 13 | −558.93 | 0.00 | 0.02 | −558.82 | 0.36 | 3.13 | 558.80 | 0.00 | 0.01 | 558.91 | 0.36 | 3.12 | −558.86 | 0.00 | 0.00 | 84.07 |
| 14 | −61.10 | 0.00 | 0.05 | −60.35 | 0.91 | 2.08 | 60.95 | −0.01 | 0.09 | 61.75 | 0.99 | 1.97 | −61.03 | 0.02 | 0.00 | 45.35 |
| 15 | −408.64 | 0.00 | 0.02 | −408.50 | 0.39 | 2.63 | 408.56 | 0.00 | 0.00 | 408.70 | 0.42 | 3.03 | −408.59 | 0.01 | 0.00 | 76.59 |
| 16 | −604.94 | 1.73 | 2.59 | −600.37 | 2.46 | −0.55 | 599.77 | 2.54 | 0.82 | 607.38 | 4.70 | −1.37 | −602.79 | 0.52 | 2.78 | 33.53 |
| 17 | −672.92 | 0.00 | 0.02 | −672.79 | 0.38 | 3.08 | 672.88 | 0.00 | 0.01 | 673.01 | 0.41 | 3.07 | −672.90 | 0.00 | 0.00 | 76.92 |
| 18 | −533.65 | 2.30 | 2.30 | −527.81 | 2.42 | −0.69 | 529.28 | 2.69 | 3.09 | 536.11 | 5.43 | −1.05 | −530.42 | 0.61 | 3.72 | 26.08 |
| 19 | −912.05 | 4.65 | 3.21 | −904.31 | 3.36 | −1.53 | 906.22 | 0.00 | 0.81 | 909.91 | 3.03 | 0.05 | −907.05 | 0.45 | 1.40 | 25.82 |
| 20 | −704.48 | 2.63 | 4.45 | −699.99 | 4.35 | −0.18 | 697.46 | 5.67 | 3.51 | 706.31 | 2.49 | −1.72 | −704.26 | 0.77 | 7.32 | 13.21 |
| 21 | −55.94 | 1.36 | 1.40 | −53.45 | 1.12 | 0.82 | 53.51 | −0.02 | 0.04 | 54.19 | 1.09 | 2.05 | −53.70 | 0.09 | 0.53 | 60.60 |
| 22 | −172.40 | 6.19 | 3.39 | −162.42 | 1.51 | −2.45 | 165.24 | 0.37 | 0.78 | 171.36 | 7.48 | −0.80 | −165.13 | 0.11 | 0.20 | 9.71 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kearns, F.L.; Warrensford, L.; Boresch, S.; Woodcock, H.L. The Good, the Bad, and the Ugly: “HiPen”, a New Dataset for Validating (S)QM/MM Free Energy Simulations. Molecules 2019, 24, 681. https://doi.org/10.3390/molecules24040681
Kearns FL, Warrensford L, Boresch S, Woodcock HL. The Good, the Bad, and the Ugly: “HiPen”, a New Dataset for Validating (S)QM/MM Free Energy Simulations. Molecules. 2019; 24(4):681. https://doi.org/10.3390/molecules24040681
Chicago/Turabian StyleKearns, Fiona L., Luke Warrensford, Stefan Boresch, and H. Lee Woodcock. 2019. "The Good, the Bad, and the Ugly: “HiPen”, a New Dataset for Validating (S)QM/MM Free Energy Simulations" Molecules 24, no. 4: 681. https://doi.org/10.3390/molecules24040681
APA StyleKearns, F. L., Warrensford, L., Boresch, S., & Woodcock, H. L. (2019). The Good, the Bad, and the Ugly: “HiPen”, a New Dataset for Validating (S)QM/MM Free Energy Simulations. Molecules, 24(4), 681. https://doi.org/10.3390/molecules24040681