Transport and Optical Gaps in Amorphous Organic Molecular Materials
Abstract
1. Introduction
2. Methods and Numerical Computations
2.1. General Considerations
2.2. Specific Procedures
3. Results
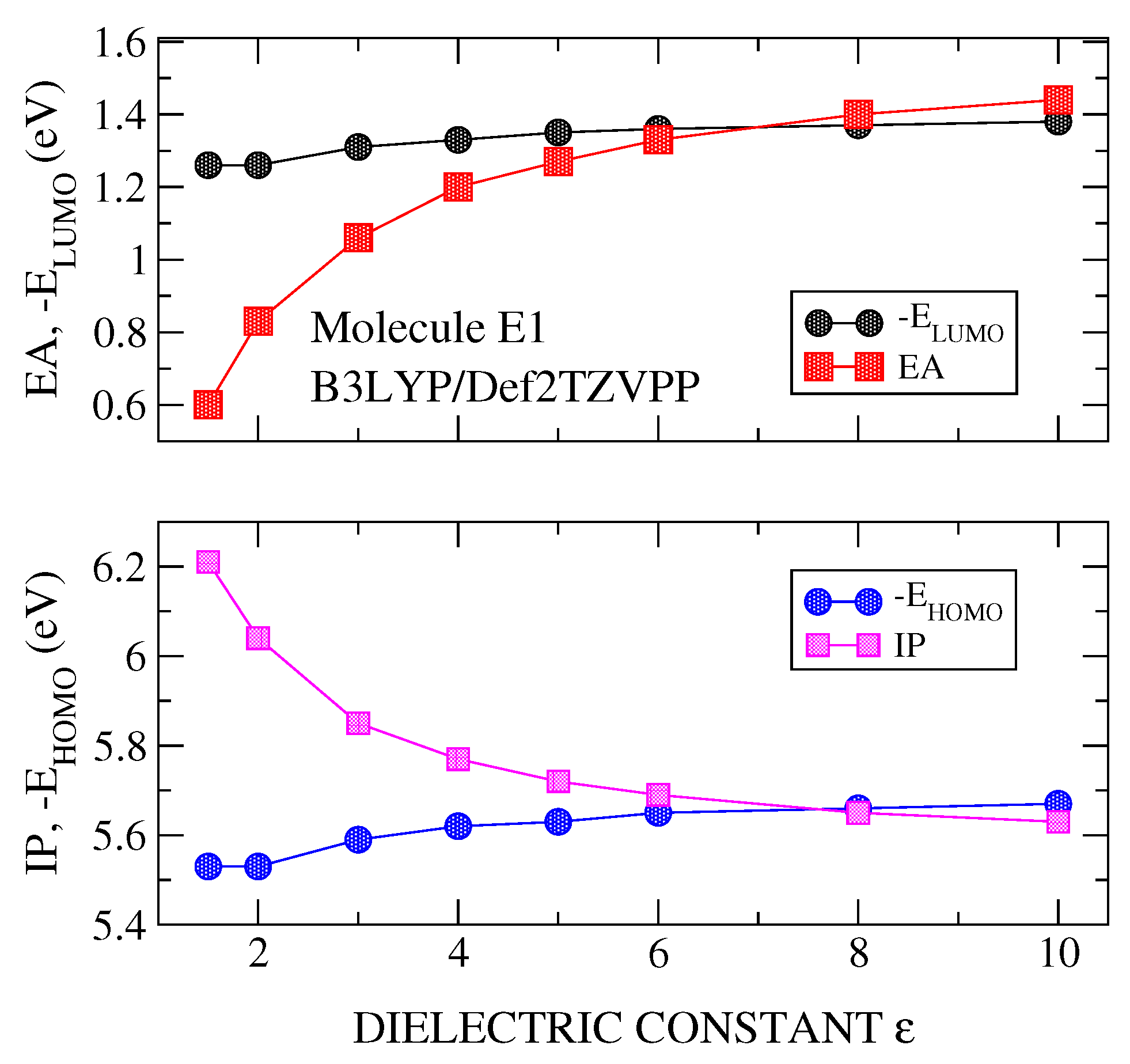
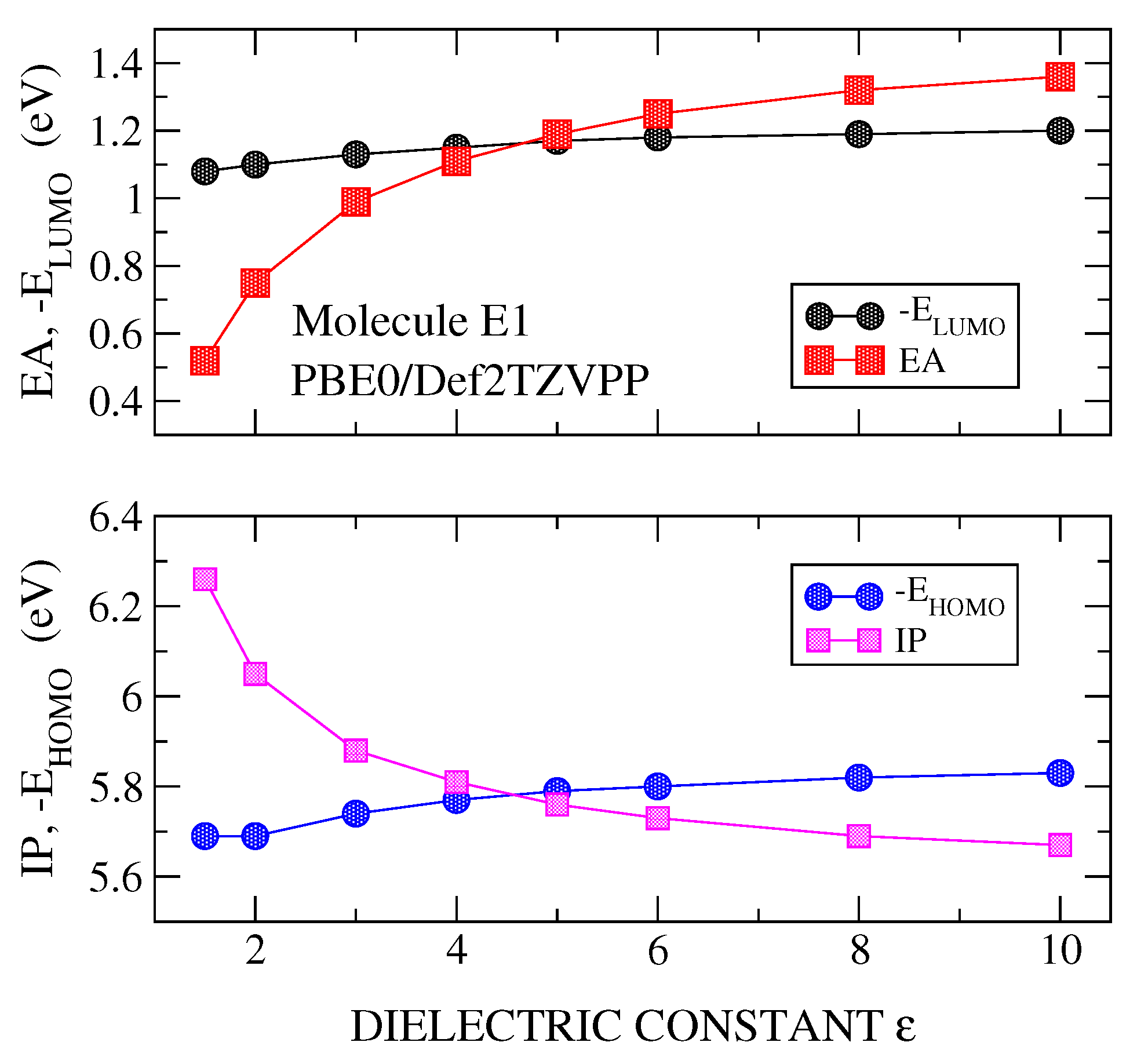
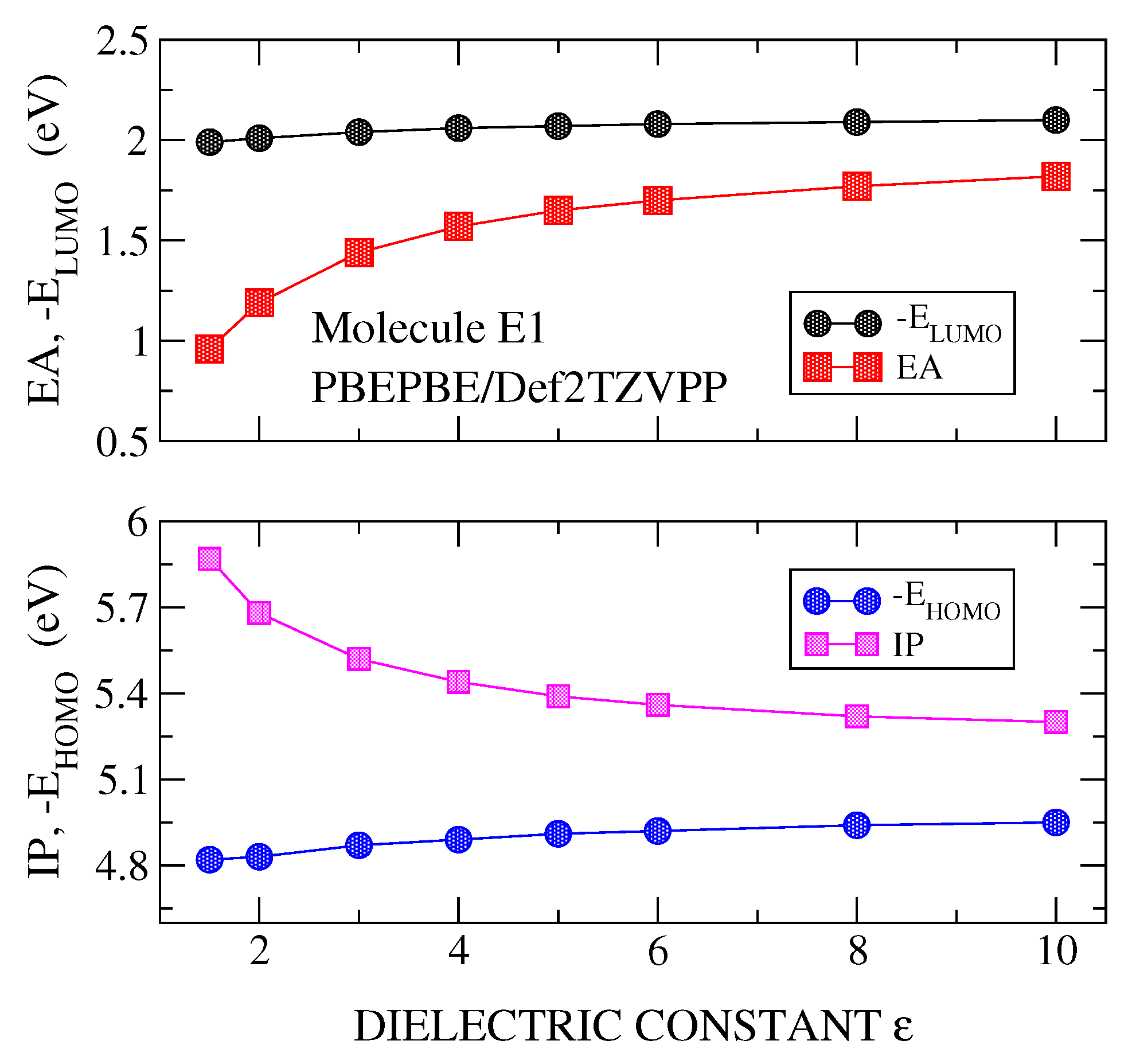
3.1. Transport Gap
3.2. Optical Gap and Exciton Binding Energies
4. Concluding Remarks
- Calculation of the ground state wave-function and the excitation energy within time independent DFT framework and using high performance combinations of a functional/basis set.
- Incorporate the extended character of the system implemented in the present work by means of a polarized continuum model.
- Our results reveal the importance of considering the exact exchange energy in the calculation of the optimal value of .
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AOM | Amorphous organic materials |
| B3LYP | Hybrid BLYP functional |
| BLYP | Becke-Lee-Yang-Parr exchange correlation functional |
| CAM-B3LYP | Long-range-corrected version of B3LYP functional |
| CT | Charge transferred |
| DFT | Density functional theory |
| EA | Electron affinity |
| GEDT | Global electron density transfer |
| GGA | Generalized gradient approximation |
| G | Fundamental gap |
| G | Transport gap |
| G | Optical gap |
| HOMO | Highest occupied molecular orbital |
| IP | Ionization potential |
| LC-PBE | Long-range-corrected PBE functional |
| LUMO | Lowest unoccupied molecular orbital |
| OLED | Organic light-emitting diode |
| PCM | Polarizable continuum medium |
| PBEPBE | Perdew, Burke and Ernzerhof exchange correlation functional |
| PBE0 | Hybrid PBEPBE functional |
| TD-DFT | Time-dependent DFT |
| HCTH | The -dependent Handy’s functional |
References
- Shirota, Y.; Kageyama, H. Charge carrier transporting molecular materials and their applications in devices. Chem. Rev. 2007, 107, 953–1010. [Google Scholar] [CrossRef] [PubMed]
- Brédas, J.L. Mind the gap! Mater. Horiz. 2014, 1, 17–19. [Google Scholar] [CrossRef]
- Louis, E.; San-Fabián, E.; Díaz-García, M.A.; Chiappe, G.; Vergés, J.A. Are electron affinity and ionization potential intrinsic parameters to predict the electron or hole acceptor character of amorphous molecular materials? J. Phys. Chem. Lett. 2017, 8, 2445–2449. [Google Scholar] [CrossRef] [PubMed]
- Hernández-Verdugo, E.; Sancho-García, J.C.; San-Fabián, E. The application of TD-DFT to excited states of a family of TPD molecules interesting for optoelectronic use. Theor. Chem. Acc. 2017, 136, 77. [Google Scholar] [CrossRef]
- Becke, A.D. Communication: Optical gap in polyacetylene from a simple quantum chemistry exciton model. J. Chem. Phys. 2018, 149, 081102. [Google Scholar] [CrossRef] [PubMed]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. [Google Scholar] [CrossRef]
- Blase, X.; Attaccalite, C.; Olevano, V. First-principles GW calculations for fullerenes, porphyrins, phtalocyanine, and other molecules of interest for organic photovoltaic applications. Phys. Rev. B 2011, 83, 115103. [Google Scholar] [CrossRef]
- Faber, C.; Boulanger, P.; Attaccalite, C.; Duchemin, I.; Blase, X. Excited states properties of organic molecules: From density functional theory to the GW and Bethe-Salpeter Green’s function formalisms. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2014, 372, 20130271. [Google Scholar] [CrossRef]
- Jacquemin, D.; Duchemin, I.; Blase, X. Is the Bethe–Salpeter formalism accurate for excitation energies? Comparisons with TD-DFT, CASPT2, and EOM-CCSD. J. Phys. Chem. Lett. 2017, 8, 1524–1529. [Google Scholar] [CrossRef]
- Lange, M.F.; Berkelbach, T.C. On the relation between equation-of-motion coupled-cluster theory and the GW approximation. J. Chem. Theory Comput. 2018, 14, 4224–4236. [Google Scholar] [CrossRef]
- Li, J.; D’Avino, G.; Duchemin, I.; Beljonne, D.; Blase, X. Accurate description of charged excitations in molecular solids from embedded many-body perturbation theory. Phys. Rev. B 2018, 97, 035108. [Google Scholar] [CrossRef]
- Duchemin, I.; Jacquemin, D.; Blase, X. Combining the GW formalism with the polarizable continuum model: A state-specific non-equilibrium approach. J. Chem. Phys. 2016, 144, 164106. [Google Scholar] [CrossRef] [PubMed]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D.01.; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Berleb, S.; Brütting, W.; Paasch, G. Interfacial charges and electric field distribution in organic hetero-layer light-emitting devices. Org. Electron. 2000, 1, 41–47. [Google Scholar] [CrossRef]
- Koopmans, T. Über die zuordnung von wellenfunktionen und eigenwerten zu den einzelnen elektronen eines atoms. Physica 1934, 1, 104–113. [Google Scholar] [CrossRef]
- Janak, J.F. Proof that in density-functional theory. Phys. Rev. B 1978, 18, 7165–7168. [Google Scholar] [CrossRef]
- Perdew, J.P.; Parr, R.G.; Levy, M.; Balduz, J.L. Density-functional theory for fractional particle number: Derivative discontinuities of the energy. Phys. Rev. Lett. 1982, 49, 1691–1694. [Google Scholar] [CrossRef]
- Perdew, J.P.; Levy, M. Physical content of the exact kohn-sham orbital energies: Band gaps and derivative discontinuities. Phys. Rev. Lett. 1983, 51, 1884–1887. [Google Scholar] [CrossRef]
- Jones, R.O.; Gunnarsson, O. The density functional formalism, its applications and prospects. Rev. Mod. Phys. 1989, 61, 689–746. [Google Scholar] [CrossRef]
- Levy, M.; Perdew, J.P.; Sahni, V. Exact differential equation for the density and ionization energy of a many-particle system. Phys. Rev. A 1984, 30, 2745–2748. [Google Scholar] [CrossRef]
- Baerends, E.J. Density functional approximations for orbital energies and total energies of molecules and solids. J. Chem. Phys. 2018, 149, 054105. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Ryno, S.; Zhong, C.; Ravva, M.K.; Sun, Z.; Körzdörfer, T.; Brédas, J.L. Ionization energies, electron affinities, and polarization energies of organic molecular crystals: Quantitative estimations from a polarizable continuum model (PCM)-tuned range-separated density functional approach. J. Chem. Theory Comput. 2016, 12, 2906–2916. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Brédas, J.L.; Coropceanu, V. Description of the charge transfer states at the pentacene/C60 interface: Combining range-separated hybrid functionals with the polarizable continuum model. J. Phys. Chem. Lett. 2016, 7, 2616–2621. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Egger, D.A.; Brédas, J.L.; Kronik, L.; Coropceanu, V. Effect of solid-state polarization on charge-transfer excitations and transport Levels at organic interfaces from a screened range-separated hybrid functional. J. Phys. Chem. Lett. 2017, 8, 3277–3283. [Google Scholar] [CrossRef] [PubMed]
- Nayak, P.K.; Periasamy, N. Calculation of electron affinity, ionization potential, transport gap, optical band gap and exciton binding energy of organic solids using ‘solvation’ model and DFT. Org. Electron. 2009, 10, 1396–1400. [Google Scholar] [CrossRef]
- Tsiper, E.V.; Soos, Z.G. Charge redistribution and polarization energy of organic molecular crystals. Phys. Rev. B 2001, 64, 195124. [Google Scholar] [CrossRef]
- Yoshida, H.; Yamada, K.; Tsutsumi, J.; Sato, N. Complete description of ionization energy and electron affinity in organic solids: Determining contributions from electronic polarization, energy band dispersion, and molecular orientation. Phys. Rev. B 2015, 92, 075145. [Google Scholar] [CrossRef]
- Li, J.; Duchemin, I.; Roscioni, O.M.; Friederich, P.; Anderson, M.; Da Como, E.; Kociok-Köhn, G.; Wenzel, W.; Zannoni, C.; Beljonne, D.; et al. Host dependence of the electron affinity of molecular dopants. Mater. Horiz. 2019, 6, 107–114. [Google Scholar] [CrossRef]
- Schwenn, P.; Burn, P.; Powell, B. Calculation of solid state molecular ionisation energies and electron affinities for organic semiconductors. Org. Electron. 2011, 12, 394–403. [Google Scholar] [CrossRef]
- Madigan, C.; Bulović, V. Exciton energy disorder in polar amorphous organic thin films: Monte Carlo calculations. Phys. Rev. B 2007, 75, 081403. [Google Scholar] [CrossRef]
- Meredith, P.; Bettinger, C.J.; Irimia-Vladu, M.; Mostert, A.B.; Schwenn, P.E. Electronic and optoelectronic materials and devices inspired by nature. Rep. Prog. Phys. 2013, 76, 034501. [Google Scholar] [CrossRef]
- D’Avino, G.; Muccioli, L.; Castet, F.; Poelking, C.; Andrienko, D.; Soos, Z.G.; Cornil, J.; Beljonne, D. Electrostatic phenomena in organic semiconductors: Fundamentals and implications for photovoltaics. J. Phy. Condens. Matter 2016, 28, 433002. [Google Scholar] [CrossRef] [PubMed]
- Stein, T.; Kronik, L.; Baer, R. Reliable prediction of charge transfer excitations in molecular complexes using time-dependent density functional theory. J. Am. Chem. Soc. 2009, 131, 2818–2820. [Google Scholar] [CrossRef]
- Refaely-Abramson, S.; Sharifzadeh, S.; Govind, N.; Autschbach, J.; Neaton, J.B.; Baer, R.; Kronik, L. Quasiparticle spectra from a nonempirical optimally tuned range-separated hybrid density functional. Phys. Rev. Lett. 2012, 109, 226405. [Google Scholar] [CrossRef] [PubMed]
- Kronik, L.; Stein, T.; Refaely-Abramson, S.; Baer, R. Excitation gaps of finite-sized systems from optimally tuned range-separated hybrid functionals. J. Chem. Theory Comput. 2012, 8, 1515–1531. [Google Scholar] [CrossRef] [PubMed]
- Haitao, S.; Jochen, A. Influence of the delocalization error and applicability of optimal functional tuning in density functional calculations of nonlinear optical properties of organic donor-acceptor chromophores. Chem. Phys. Chem. 2013, 14, 2450–2461. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Erratum: Generalized gradient approximation made simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef]
- Becke, A.D. Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
- Ernzerhof, M.; Scuseria, G.E. Assessment of the Perdew-Burke-Ernzerhof exchange-correlation functional. J. Chem. Phys. 1999, 110, 5029–5036. [Google Scholar] [CrossRef]
- Boese, A.D.; Handy, N.C. New exchange-correlation density functionals: The role of the kinetic-energy density. J. Chem. Phys. 2002, 116, 9559–9569. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Scuseria, G.E. Assessment of a long-range corrected hybrid functional. J. Chem. Phys. 2006, 125, 234109. [Google Scholar] [CrossRef]
- Tsuneda, T.; Song, J.W.; Suzuki, S.; Hirao, K. On Koopmans’ theorem in density functional theory. J. Chem. Phys. 2010, 133, 174101. [Google Scholar] [CrossRef]
- Perdew, J.P.; Yang, W.; Burke, K.; Yang, Z.; Gross, E.K.U.; Scheffler, M.; Scuseria, G.E.; Henderson, T.M.; Zhang, I.Y.; Ruzsinszky, A.; et al. Understanding band gaps of solids in generalized Kohn-Sham theory. Proc. Natl. Acad. Sci. USA 2017, 114, 2801–2806. [Google Scholar] [CrossRef] [PubMed]
- Runge, E.; Gross, E.K.U. Density-functional theory for time-dependent systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar] [CrossRef]
- Casida, M.E. Time-dependent density-functional theory for molecules and molecular solids. Theochem-J. Mol. Struct. 2009, 914, 3–18. [Google Scholar] [CrossRef]
- Ullrich, C.A. Time-Dependent Density-Functional Theory: Concepts and Applications; Oxford University Press: Oxford, UK, 2011; p. 536. [Google Scholar]
- Marques, M.A.L.; Maitra, N.T.; Nogueira, F.M.S.; Gross, E.K.U.; Rubio, A. (Eds.) Fundamentals of Time-Dependent Density Functional Theory; Springer: Berlin, Germany, 2012. [Google Scholar]
- Cammi, R.; Mennucci, B. Linear response theory for the polarizable continuum model. Chem. Phys. 1999, 110, 9877–9886. [Google Scholar] [CrossRef]
- Lucke, A.; Ankerhold, J. Dissipative wave-packet dynamics and electron transfer. Chem. Phys. 2001, 115, 4696–4707. [Google Scholar] [CrossRef]
- Shelton, D.P. Ferroelectric domains in nitrobenzene-nitromethane solutions measured by hyper-Rayleigh scattering. Chem. Phys. 2006, 124, 124509. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, S.; Tatewaki, H.; Watanabe, Y. Gaussian-type function set without prolapse for the Dirac-Fock-Roothaan equation (II): Hg80 through Lr103. Chem. Phys. 2006, 125, 054106. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G.; Guido, C.A.; Mennucci, B.; Scalmani, G.; Frisch, M.J. Practical computation of electronic excitation in solution: Vertical excitation model. Chem. Sci. 2011, 2, 2143–2161. [Google Scholar] [CrossRef]
- Jmol. An Open-Source Java Viewer for Chemical Structures in 3D. Available online: http://www.jmol.org (accessed on 8 February 2019).
- Allouche, A.R. Gabedit—A graphical user interface for computational chemistry softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef]
- Schaftenaar, G.; Noordik, J. Molden: A pre- and post-processing program for molecular and electronic structures. J. Comput.-Aided Mol. Des. 2000, 14, 123–134. [Google Scholar] [CrossRef]
- Lipparini, F.; Scalmani, G.; Mennucci, B.; Cancés, E.; Caricato, M.; Frisch, M.J. A variational formulation of the polarizable continuum model. J. Chem. Phys. 2010, 133, 014106. [Google Scholar] [CrossRef] [PubMed]
- Le Bahers, T.; Adamo, C.; Ciofini, I. A qualitative index of spatial extent in charge-transfer excitations. J. Chem. Theory Comput. 2011, 7, 2498–2506. [Google Scholar] [CrossRef]
- Bässler, H.; Köhler, A. Charge transport in organic semiconductors. In Unimolecular and Supramolecular Electronics I: Chemistry and Physics Meet at Metal-Molecule Interfaces; Metzger, R.M., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–65. [Google Scholar]
- Turkowski, V.; Din, N.U.; Rahman, T.S. Time-dependent density-functional theory and excitons in bulk and two-dimensional semiconductors. Computation 2017, 5, 39. [Google Scholar] [CrossRef]
- Duchemin, I.; Guido, C.A.; Jacquemin, D.; Blase, X. The Bethe–Salpeter formalism with polarisable continuum embedding: Reconciling linear-response and state-specific features. Chem. Sci. 2018, 9, 4430–4443. [Google Scholar] [CrossRef] [PubMed]
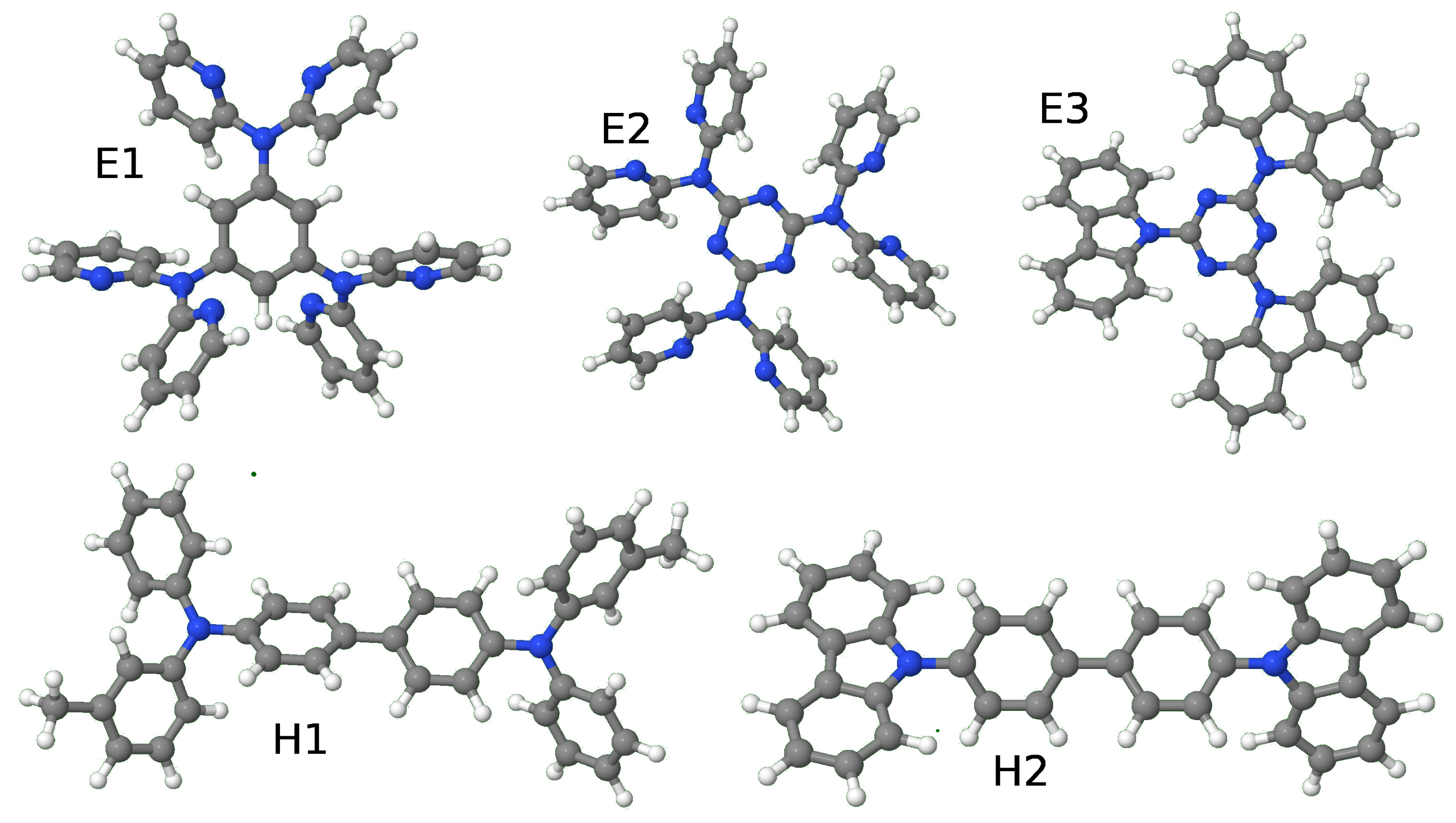
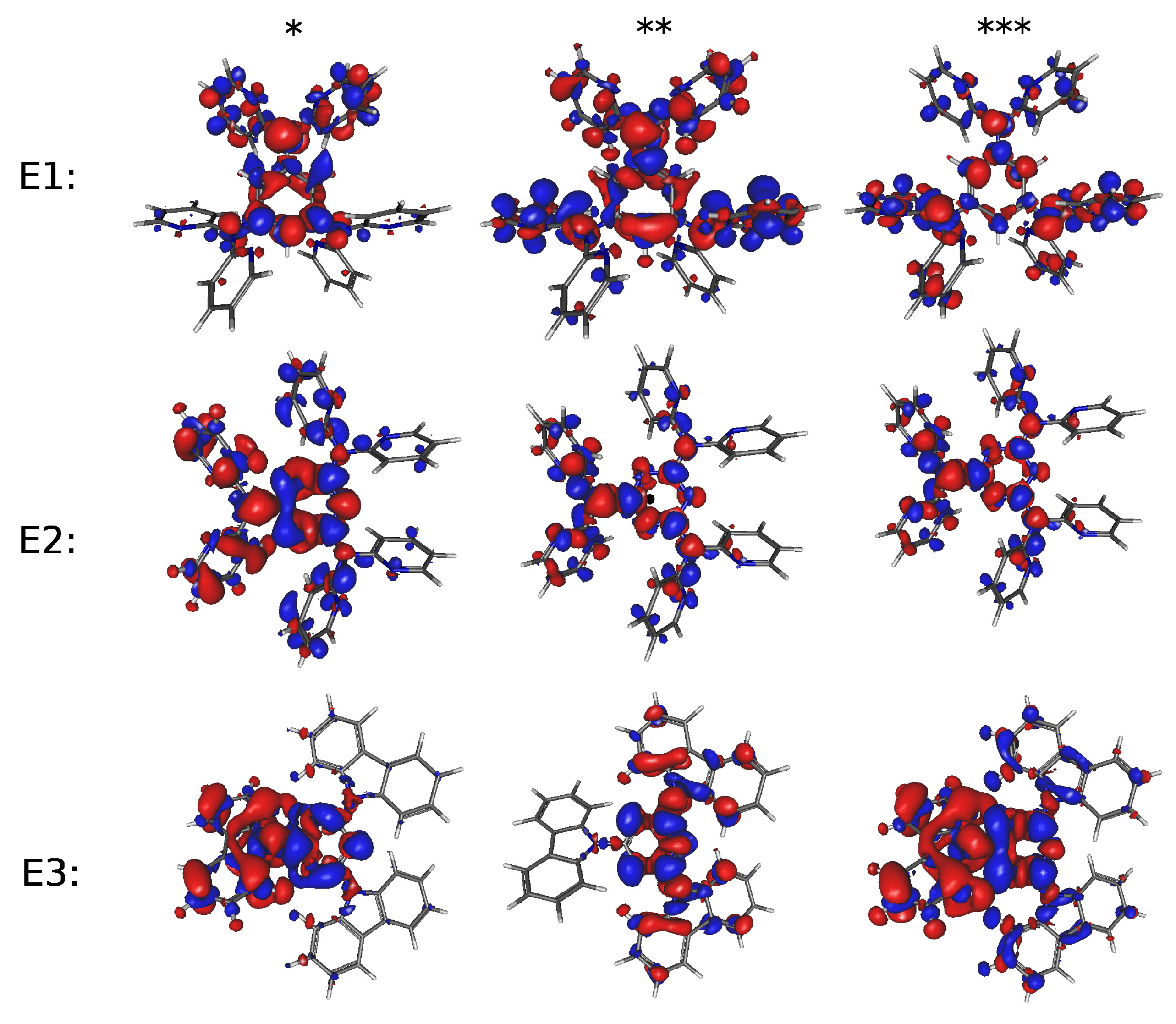
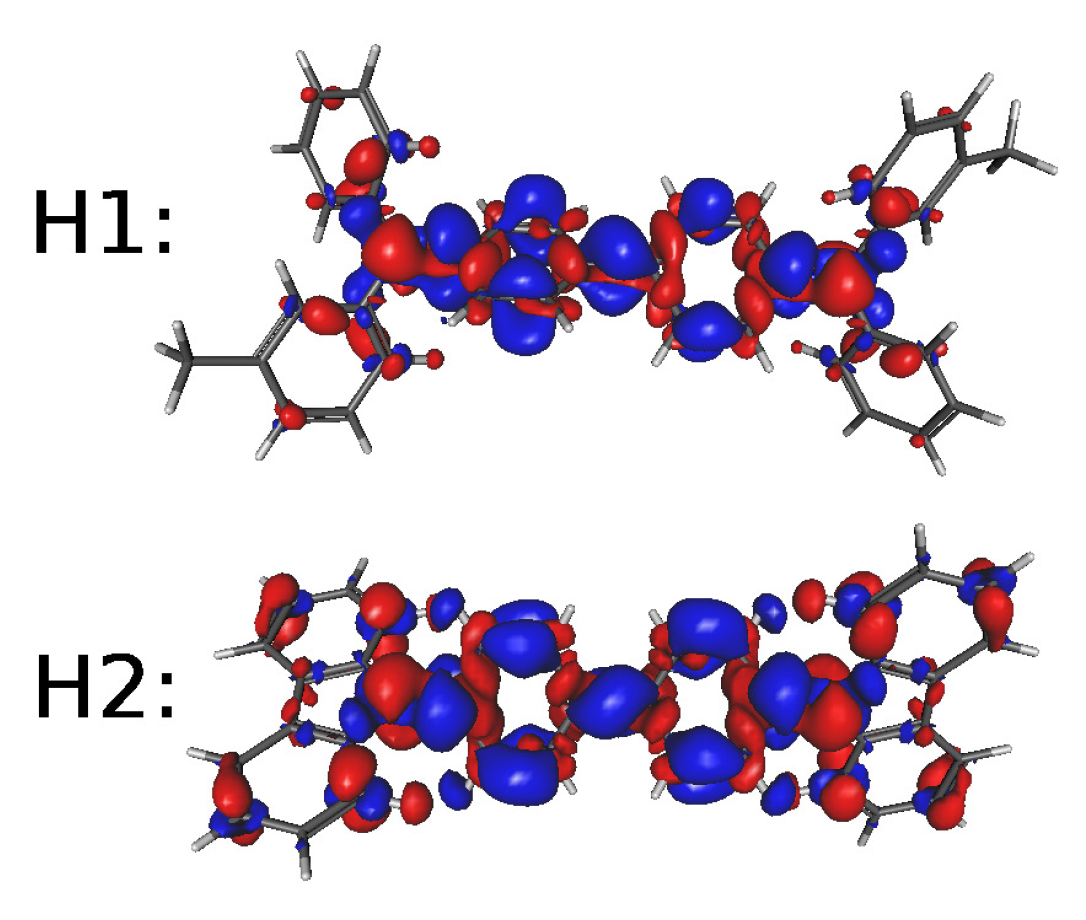
| Molecule | E1 | E2 | E3 | H1 | H2 | |||||
| Functional/Basis Set | IP | IP | IP | IP | IP | |||||
| B3LYP/Def2TZVPP | 7.8 | 5.66 | 9.4 | 6.40 | 9.0 | 6.14 | 8.0 | 5.07 | 8.0 | 5.70 |
| PBE0/Def2TZVPP | 4.6 | 5.78 | 4.8 | 6.55 | 5.0 | 6.36 | 4.7 | 5.22 | 4.8 | 5.86 |
| PBE0/Def2TZV | 4.7 | 5.81 | 4.8 | 6.55 | 5.2 | 6.39 | 4.8 | 5.22 | 5.0 | 5.88 |
| PBE0/Def2SV | 4.9 | 5.79 | 4.8 | 6.55 | 5.5 | 6.39 | 5.0 | 5.25 | 5.2 | 5.91 |
| Molecule | E1 | E2 | E3 | H1 | H2 | |||||
| Functional/Basis Set | EA | EA | EA | EA | EA | |||||
| B3LYP/Def2TZVPP | 7.2 | 1.36 | 8.1 | 1.37 | 8.2 | 1.78 | 8.1 | 1.28 | 8.4 | 1.52 |
| PBE0/Def2TZVPP | 4.7 | 1.16 | 4.8 | 1.13 | 4.4 | 1.59 | 4.6 | 1.12 | 4.9 | 1.38 |
| PBE0/Def2TZV | 4.7 | 1.10 | 4.8 | 1.19 | 4.8 | 1.69 | 4.8 | 1.02 | 5.2 | 1.29 |
| PBE0/Def2SV | 5.0 | 1.08 | 5.1 | 1.12 | 5.0 | 1.64 | 5.0 | 1.12 | 5.6 | 1.43 |
| No. | Molecule | (eV) | Oscillator Strength |
|---|---|---|---|
| E1 | 1,3,5-tris(phenyl-2-pyridylamino)benzene | 3.745 | 0.024 |
| 3.891 | 0.094 | ||
| 3.944 | 0.211 | ||
| 4.026 | 0.023 | ||
| E2 | 2,4,6-tris[di(2-pyridyl)-amino]-1,3,5-triazine | 4.480 | 0.207 |
| 4.511 | 0.352 | ||
| 4.525 | 0.226 | ||
| 4.646 | 0.092 | ||
| E3 | 2,4,6-tris(carbazolo)-1,3,5-triazine (TRZ2) | 3.911 | 0.326 |
| 4.023 | 0.011 | ||
| 4.040 | 0.421 | ||
| 4.149 | 0.015 | ||
| H1 | N,N′-Bis(3-methylphenyl)-N,N′-diphenylbenzidine (TPD) | 3.405 | 1.122 |
| 3.655 | 0.000 | ||
| 3.738 | 0.025 | ||
| 3.910 | 0.001 | ||
| H2 | 4,4′-di(N-carbazolyl)biphenyl (CBP) | 3.772 | 0.714 |
| 3.974 | 0.000 | ||
| 3.999 | 0.093 | ||
| 4.018 | 0.000 |
| Molecule | Excited State | (eV) | Oscillator Strength |
|---|---|---|---|
| E1 | 2 | 3.807 | 0.116 |
| E2 | 2 | 4.505 | 0.354 |
| E3 | 1 | 3.752 | 0.301 |
| H1 | 1 | 3.373 | 1.109 |
| H2 | 1 | 3.604 | 0.632 |
| Molecule | IP | IP | EA | ||||||
|---|---|---|---|---|---|---|---|---|---|
| E1 | 5.09 | 3.45 | 1.64 | 4.62 | 5.78 | 1.16 | 4.62 | 3.81 | 0.81 |
| E2 | 5.07 | 3.72 | 1.35 | 4.80 | 6.56 | 1.14 | 5.42 | 4.50 | 0.92 |
| E3 | 6.0 | 3.4 | 2.60 | 4.72 | 6.37 | 1.56 | 4.81 | 3.75 | 1.06 |
| H1 | 5.50 | 3.2 | 2.3 | 4.65 | 5.23 | 1.13 | 4.1 | 3.37 | 0.73 |
| H2 | 6.3 | 3.1 | 3.2 | 4.88 | 5.87 | 1.39 | 4.48 | 3.60 | 0.88 |
| Molecule | Excited State | (Electron-Charge) | (Å) | (Debye) |
|---|---|---|---|---|
| E1 | 2 | 0.768 | 1.915 | 7.068 |
| E2 | 2 | 0.472 | 0.571 | 1.293 |
| E3 | 1 | 0.832 | 2.400 | 9.597 |
| H1 | 1 | 0.572 | 0.396 | 1.088 |
| H2 | 1 | 0.857 | 0.014 | 0.056 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
San-Fabián, E.; Louis, E.; Díaz-García, M.A.; Chiappe, G.; Vergés, J.A. Transport and Optical Gaps in Amorphous Organic Molecular Materials. Molecules 2019, 24, 609. https://doi.org/10.3390/molecules24030609
San-Fabián E, Louis E, Díaz-García MA, Chiappe G, Vergés JA. Transport and Optical Gaps in Amorphous Organic Molecular Materials. Molecules. 2019; 24(3):609. https://doi.org/10.3390/molecules24030609
Chicago/Turabian StyleSan-Fabián, Emilio, Enrique Louis, María A. Díaz-García, Guillermo Chiappe, and José A. Vergés. 2019. "Transport and Optical Gaps in Amorphous Organic Molecular Materials" Molecules 24, no. 3: 609. https://doi.org/10.3390/molecules24030609
APA StyleSan-Fabián, E., Louis, E., Díaz-García, M. A., Chiappe, G., & Vergés, J. A. (2019). Transport and Optical Gaps in Amorphous Organic Molecular Materials. Molecules, 24(3), 609. https://doi.org/10.3390/molecules24030609







