3.1. Isolated Monomers
Prior to the study of the halogen-bonded complexes, an exploration of the properties of the halogen molecules was carried out. The calculated and experimental interatomic distances of the isolated XY molecules are gathered in
Table 1. Experimental geometries are available for all the diatomic molecules save for the At derivatives. The calculated values are in good agreement with the experimental ones, the largest error being 0.01 Å. The calculated and experimental distances show an almost perfect linear correlation (R
2 = 0.9997,
n = 10).
The MEP of these molecules, in agreement with the expected polar flattering already explained in the introduction, presents two σ-holes along the X-Y bond associated with the two atoms (
Table 1). In
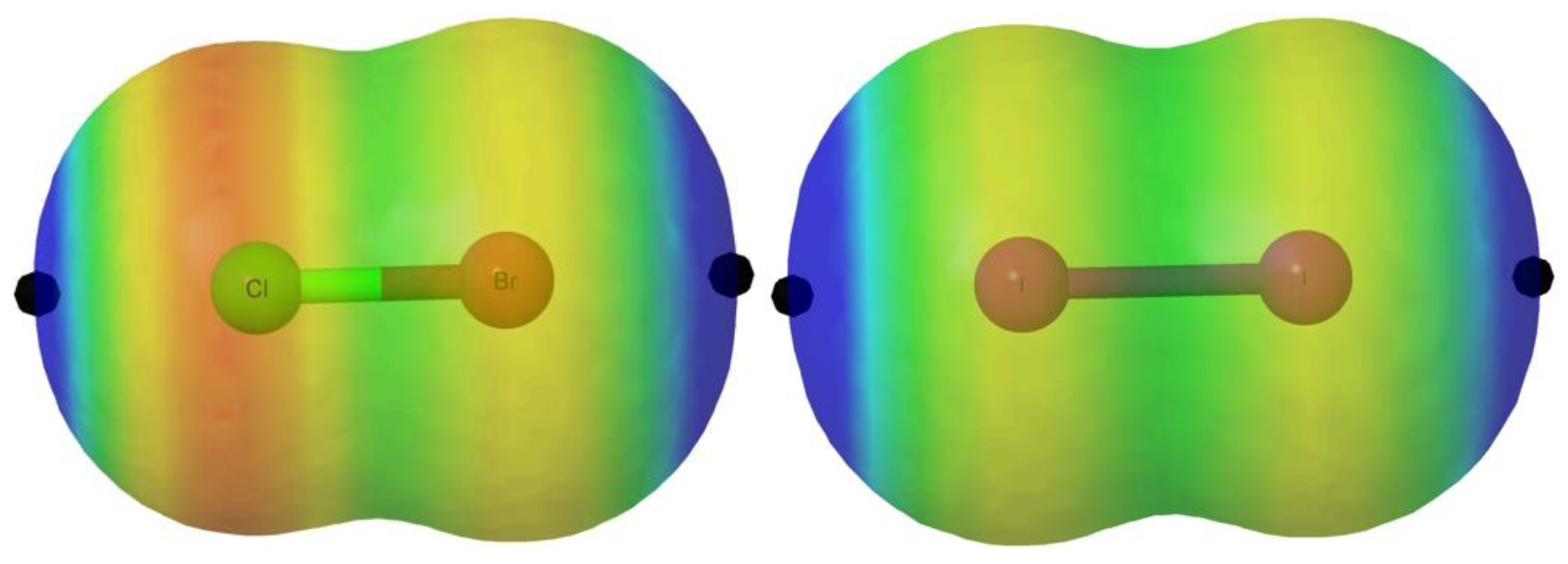
Figure 2, we illustrate the MEP for the particular cases of ClBr and I
2 as representative examples, for which the halo of the lone pairs is easily visualized in red color whereas the σ-hole is markedly blue.
These holes are maxima of the MEP and exhibit positive values. It is important to emphasize, however, that, as already reported in the literature [
42], σ-holes do not always present positive MEP values. Indeed, within the systems studied in this work, some of the F derivatives show local maxima with negative values of the MEP. In all cases, the largest σ-hole is associated with the heavier of the two atoms (Y from now on) because of its larger polarizability. For a given Y atom, the value of the σ-hole decreases as the size of X increases, which is associated with a smaller electron withdrawing ability of X. In a series of compounds with the same Y, the changes in the values of the σ-holes follow the changes in the atomic radius of the X atom. Indeed, for Y = At, the largest gap in the value of the σ-hole (0.04 a.u.) is observed on going from F to Cl, with an increase in the atomic radius of 50 pm [
43]. Going from Cl to Br, the decrease found in the σ-hole was reduced to 0.012 a.u., with an increase in the atomic radius of only 12 pm. Going from Br to I, the gap between their atomic radii slightly increased (25 pm) and, concomitantly, the gap in the values of the σ-hole (0.017 a.u.) also increased. This finding confirms that the size effects along the periodic table are particularly important when going from the first to the second period. For a given X, the σ-hole increased as the size of the Y atom did, following the increase of the polarizability of the latter. For instance, in the series F
2, FCl, FBr, FI, FAt, the values of the σ-hole increased from 0.0211 a.u. to 0.1310 a.u. (see
Table 1).
The nuclear quadrupole coupling constants (NQCC) of the isolated dihalogen molecules are gathered in
Table 2. The calculated parameters are in good agreement with the experimental ones.
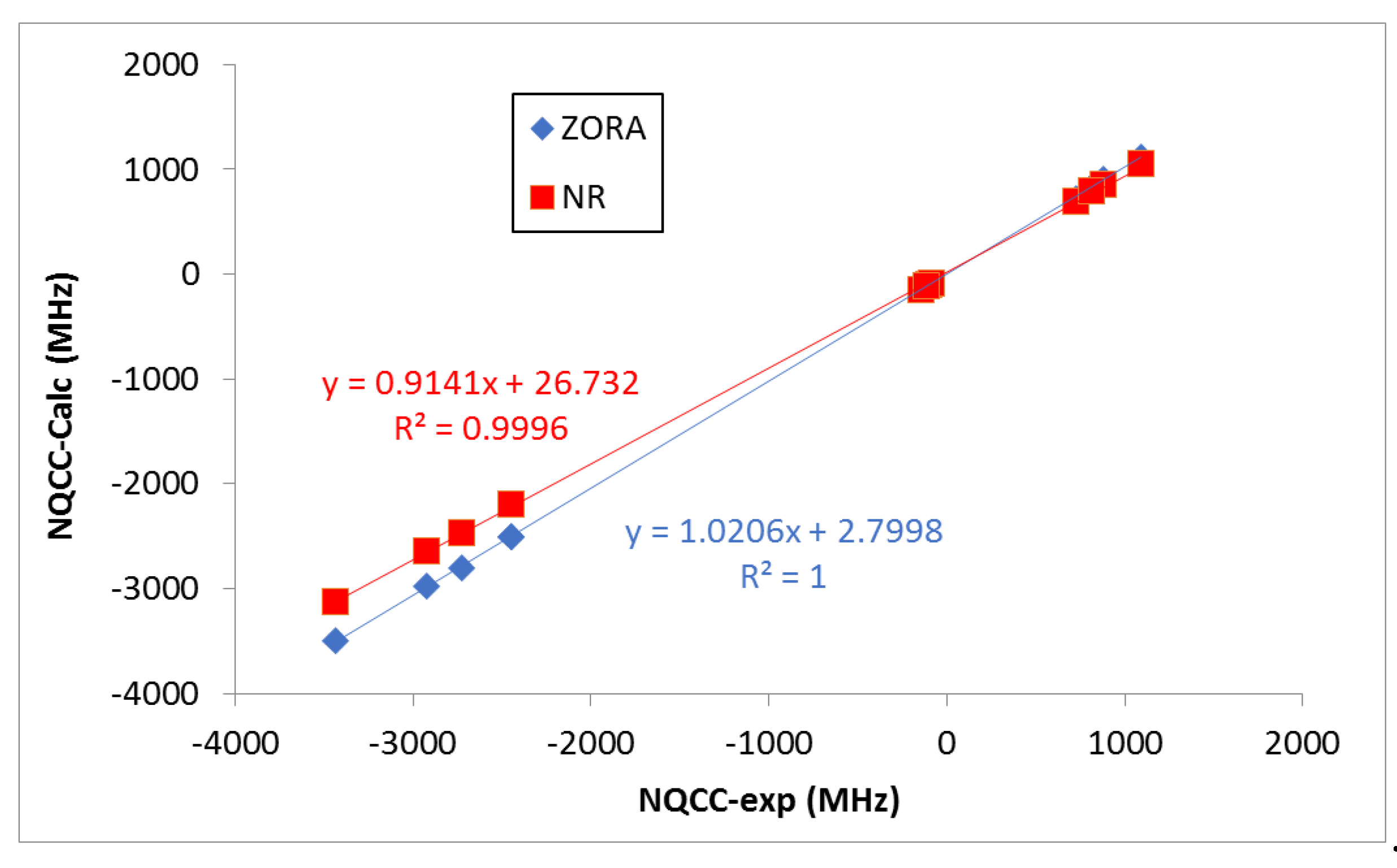
It should be noted, however, that the deviations of the NR calculated values with respect to the experimental ones are larger than those obtained when relativistic effects are accounted for (ZORA). As expected, the heavier the halogen atom, the larger the effect. This is seen more clearly when looking at the correlations shown in
Figure 3. Indeed, ZORA results present a slightly better R
2 value, a slope closer to 1.0, and an intercept value closer to 0.0 (
Figure 3). Negative NQCC values were obtained for the
35Cl,
127I and
210At nucleus, while positive ones were obtained for the
79Br nucleus (as observed in experiments). The positive and negative values of NQCC are associated with the effective shape (prolate and oblate, respectively) of the equivalent ellipsoid of the nuclear charge distribution [
46,
47]. The absolute average values for each nucleus increased steadily with its size. For a given X (or Y), the NQCC values decreased in absolute value as the size of Y (or X) does.
3.2. Dissociation Energies
Once the properties of the XY molecules were analyzed, we proceeded to study their complexes. The dissociation energies (De) of the XY: Base binary complexes are reported in
Table 3. The values ranged between 5.6 kJ·mol
−1 for the F
2:PH
3 and F
2:SH
2 complexes and 97.7 kJ·mol
−1 for the FAt: NH
3 complex. Among the trends observed in
Table 3, it is interesting to notice that for a given Y atom and base, De was smaller as the size of X increased. The largest difference between two consecutive Xs is between F and Cl. Concerning the base, the general trend is NH
3 > PH
3 > SH
2 > H
2O with only two exceptions: The F
2:OH
2 complex that is slightly more stable than the corresponding PH
3 and SH
2 ones, and FCl:PH
3 that is also slightly more stable than FCl: NH
3.
The dissociation energies listed in
Table 3 can be fitted using Equation (2) proposed by Legon and Millen that relates these energies with a nucleophilic parameter characterizing the bases,
Nb, and an electrophilic parameter characterizing the Lewis acids,
Ea [
17,
48,
49].
where the constant c has a value of 1.00 kJ·mol
−1 to preserve the units of the equation.
In the present case, we have four
Nb values and 15
Ea values to be fitted, so a total of 60 possible combinations. The simultaneous fitting of the nucleophilicities and electrophilicities is done by means of Equation (3).
where the values of
xi and
xj are 1.0 when the corresponding Lewis base or Lewis acid is present in the complex, and 0.0 if it is absent.
The fitted values for each base and acid are given in
Table 4. The fitted equation presents a R
2 value of 0.988 and an average unsigned error of 1.7 kJ·mol
−1, the largest error (7.8 kJ·mol
−1) being found for the FCl:PH
3 complex. It is known that this complex has a significant ion-pair character F
−···ClPH
3+ and, as a consequence, an enhanced De [
50], which explains this large deviation. Removing the two worst-fitted values (FCl:PH
3 and FBr:PH
3), the correlation parameter improved significantly up to R
2 = 0.994 with an average error of 1.3 kJ·mol
−1.
The
Nb and
Ea values obtained for the set of compounds studied here are compared, in
Table 4, with others reported in the literature.
Nb values in [
17] are averaged among 250 complexes including hydrogen bonds, tetrel bonds, pnictogen bonds, chalcogen bonds, and halogen bonds. It is interesting to notice that PH
3 and SH
2 are stronger nucleophiles in halogen bonds than in the rest of the interactions studied in [
17]. The same happened in the hydrogen bonds used to fit Equation (2) in [
48]. In order to verify whether this increase in the
Nb values is due to the presence of the iodine and astatine derivatives not included in [
17], we did a new fitting excluding the derivatives of these two elements. The new results of
Nb for PH
3 and SH
2 were indeed smaller (6.45 and 4.08, respectively), but the decrease is not significant and the same effect was also observed for the other bases, NH
3 and H
2O (new values 7.25 and 3.67, respectively) not affected by a significant change with respect to the values in [
17]. With respect to the
Ea values for the dihalogen molecules, they are similar to those reported in [
17] since both cases correspond to halogen bonds, though calculated at a slightly different computational level.
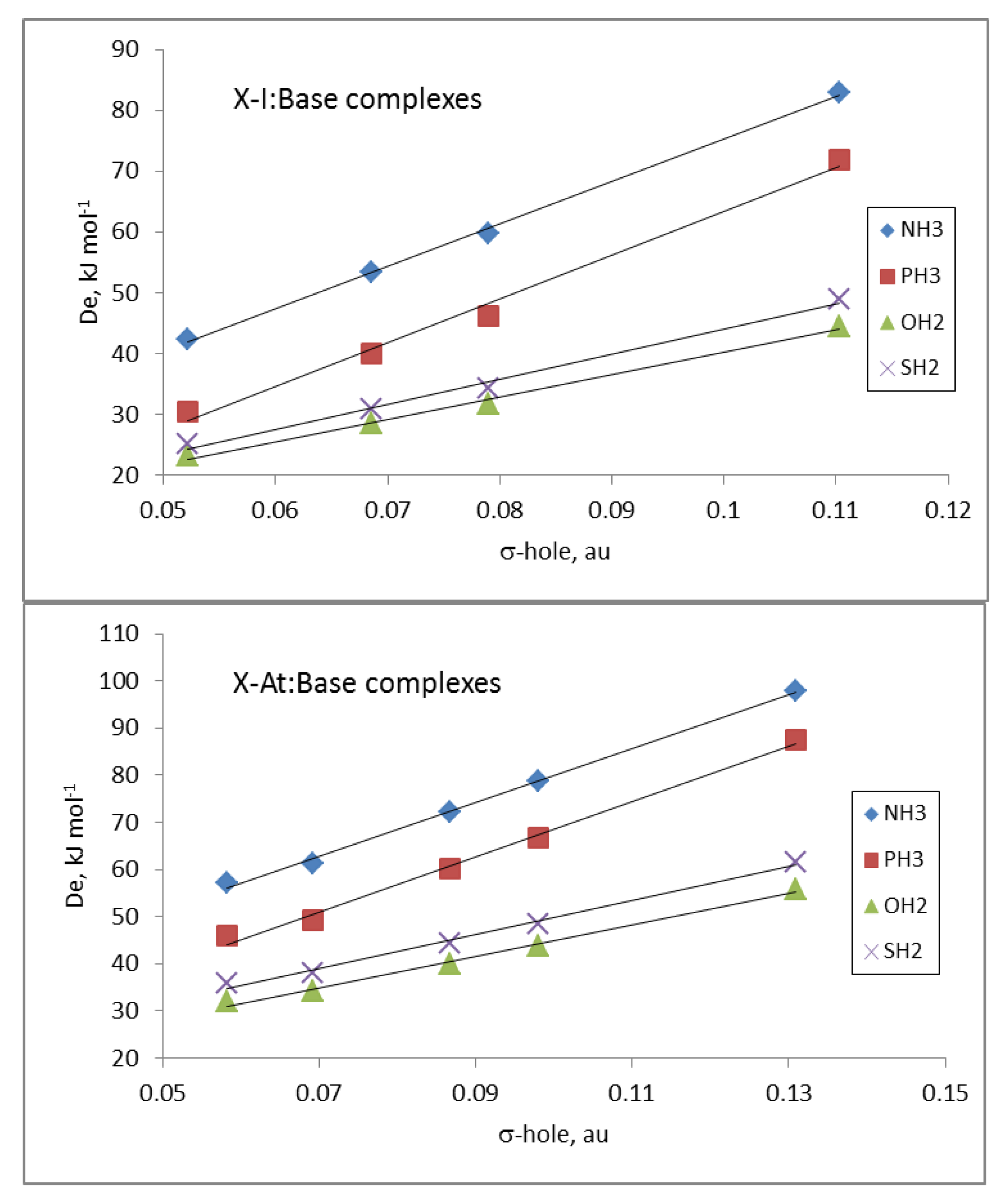
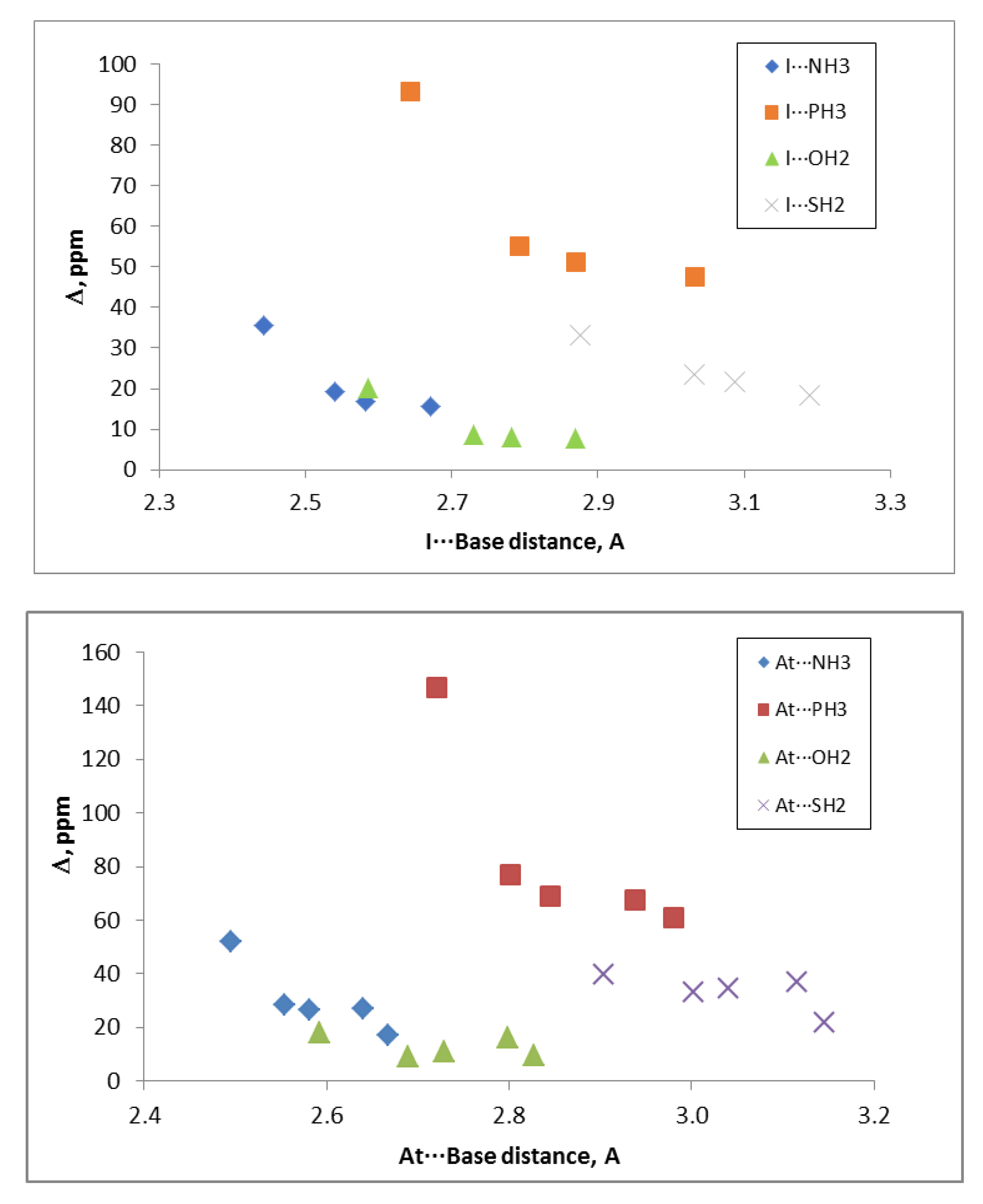
The electrostatic nature of these halogen-bonded complexes can be confirmed by comparing the
De values of all the complexes of a given base with the corresponding σ-hole values associated with the Y atom in the isolated dihalogen molecule (
Table 1). Linear correlations between the
De and σ-hole values, with R
2 between 0.89 and 0.92, were obtained for the complexes with each base. These results clearly improved if the complexes were separated in groups attending to the nature of the Y atom and the base involved in the interaction. Thus, in
Figure 4, the relationships for the complexes with iodine and astatine are depicted, showing a linear behavior with R
2 > 0.99. These results strongly indicate that other component in addition to electrostatics should be taken into account for a fine-tuning of the estimation of the De.
A more detailed analysis of interaction energy was carried out by means of the energy decomposition analysis (
Table S1 of the Supporting Information). The results show that the two attractive terms (Pauli and orbital) are important in the stabilization of the complexes, being percentage contributions between 34% and 67% depending on the base and nature of the Y atom, with minimal influence of the X one. The exception to this trend is the FCl:PH
3 complex, where the electrostatic contribution was only 22% and the orbital one 78%. In all the cases, for a given Y atom, the absolute value of the attractive contributions (Pauli, electrostatic and orbitals) decreased as the size of the X atom increased. This is due to the two facts; on the one hand, when X increased, the polarization of Y was smaller, and then the sigma-hole on Y was less deep; and on the other hand, the intermolecular distance increased. For a given X atom, the absolute value of the Pauli and electrostatic contributions increased as the size of Y increases. The FY:PH
3 complexes are an exception to this rule.
3.3. Halogen Bond Distances
Table 5 collects the halogen bond distances for the whole set of 60 complexes, comparing the MP2/aug-cc-pVTZ values with the experimental ones available in the literature [
13,
46,
47,
48]. The halogen bond distance for the 16 halogen-bonded complexes experimentally known were reasonably well reproduced by our calculations (R
2 = 0.98), especially considering that the experimental values included the ZPE effect on the geometry that is not included in the calculations of the optimized geometries. Thus, the calculated values were always shorter than experimental ones in average (0.14 Å).
The calculated halogen bond distances show that in all cases, for a given Y atom and the same base, the distance increased along with the X size because, as mentioned above, the σ-hole at the Y atom became shallower. In general, the distances for the same XY molecule followed the trend NH
3 < H
2O < PH
3 < SH
2, except in three cases: The F
2: PH
3 complex showed a slightly larger distance than the F
2:SH
2, and the FBr:PH
3 and ClBr:PH
3 distances were shorter than the corresponding one with H
2O. Interestingly, as shown in
Table 6, linear correlations R
2 > 0.92 were found between the dissociation energies and the halogen bond distances for the complexes with same Y atom and base. The cases of XF and XCl are not included because the number of points is not sufficient.
3.5. NQCC
The NQCC values of the halogen atoms XY in the binary complexes calculated with the ZORA Hamiltonian are gathered in
Table 9. Remember that
19F has no NQCC. Significant variations of this parameter were observed for both nuclei X and Y upon complexation. In the case of X, positive variations with respect to the corresponding value in the isolated XY molecules (see
Table 2) were observed for the
35Cl,
127I, and
210At nuclei while negative variations were found for the
79Br one. Thus, the absolute values of the binary complexes were, from 7 to 831 MHz, smaller than the ones in the isolated XY molecules. For a given Y and base, the variation in absolute value followed the sequence Cl < Br < I < At. For a given XY molecule, the variation of the NQCC of X, with respect to the base, was larger in NH
3 and PH
3 than SH
2, the complexes with H
2O being the ones with the smallest variations.
In the case of Y, the variation was more negative (or less positive) as the size of the X atom increased for 35Cl and 127I, while for 79Br and 210At nuclei, the reverse trend was observed.
Recently, a relationship has been explored between the variation of the NQCC of the dihalogen molecules isolated and in complexes and the charge redistribution using the Townes–Dailey model [
53]. Similar results have been obtained from the theoretical charge distribution obtained within the atoms in molecules methodology [
54].