Surface Persistence of Trace Level Deposits of Highly Energetic Materials
Abstract
1. Introduction
2. Materials and Methods
2.1. Reagents
2.2. Synthesis of TATP
2.3. Instrumentation
2.4. Sublimation Study by Thermal Analysis
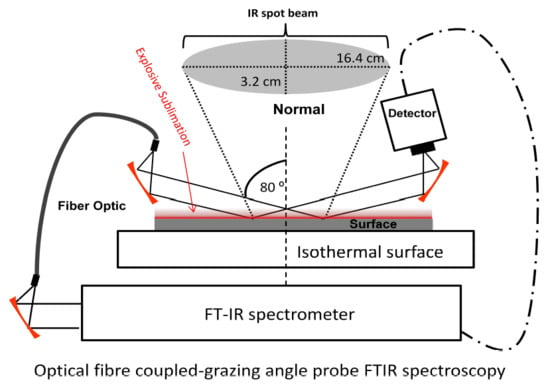
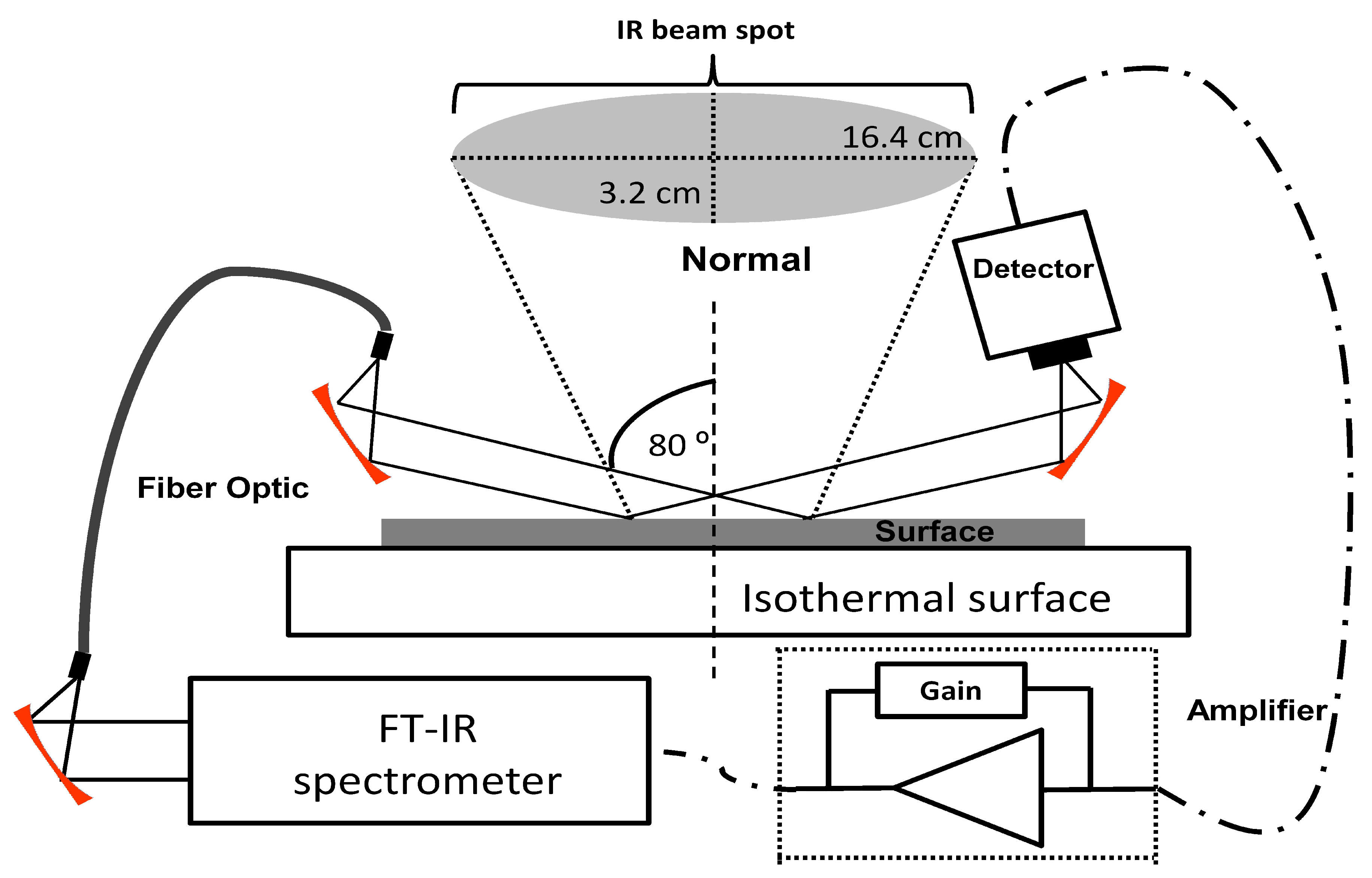
2.5. Sublimation Study by GAP
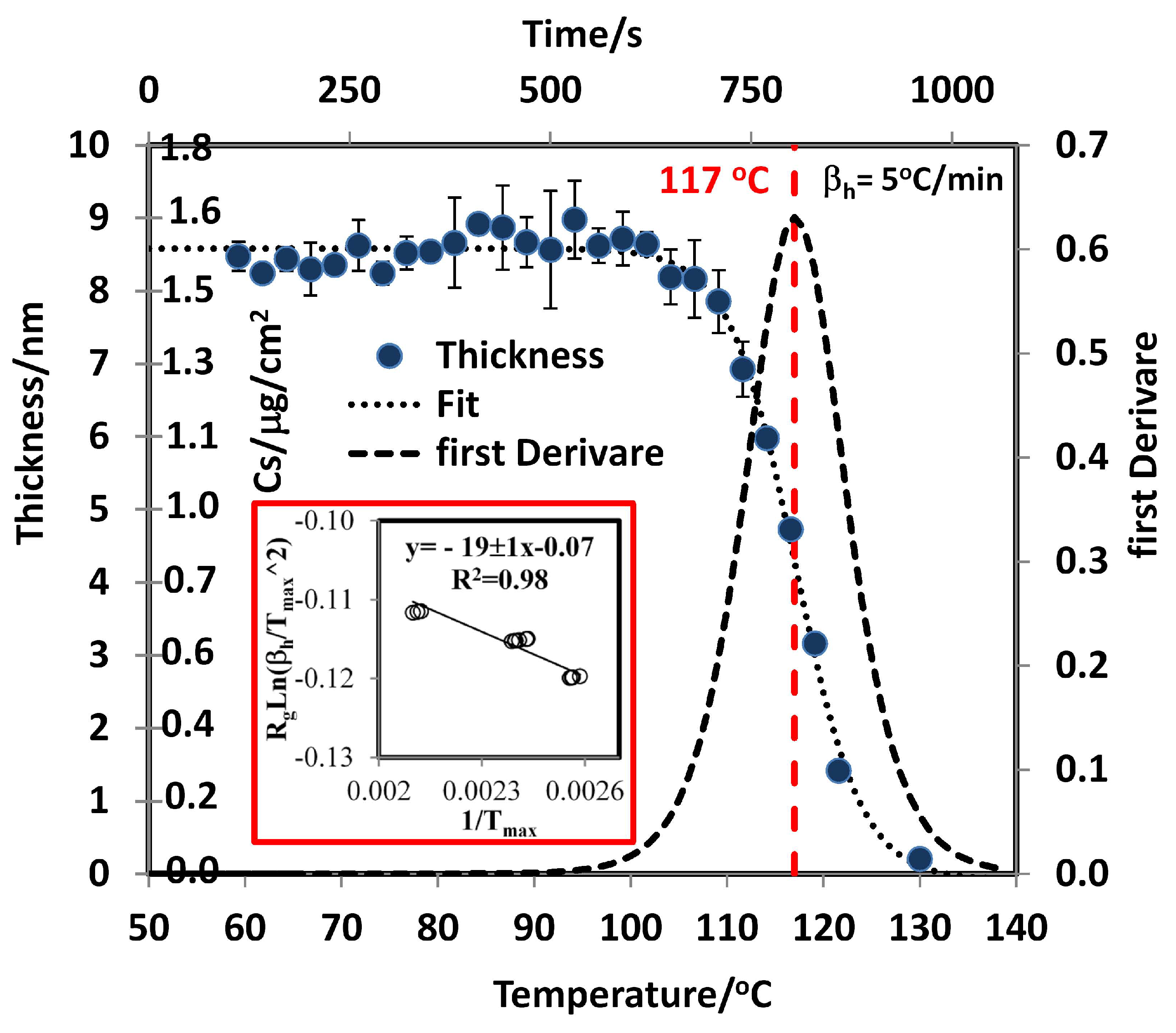
2.6. Desorption Energy
3. Results and Discussion
3.1. Spectroscopic Signatures
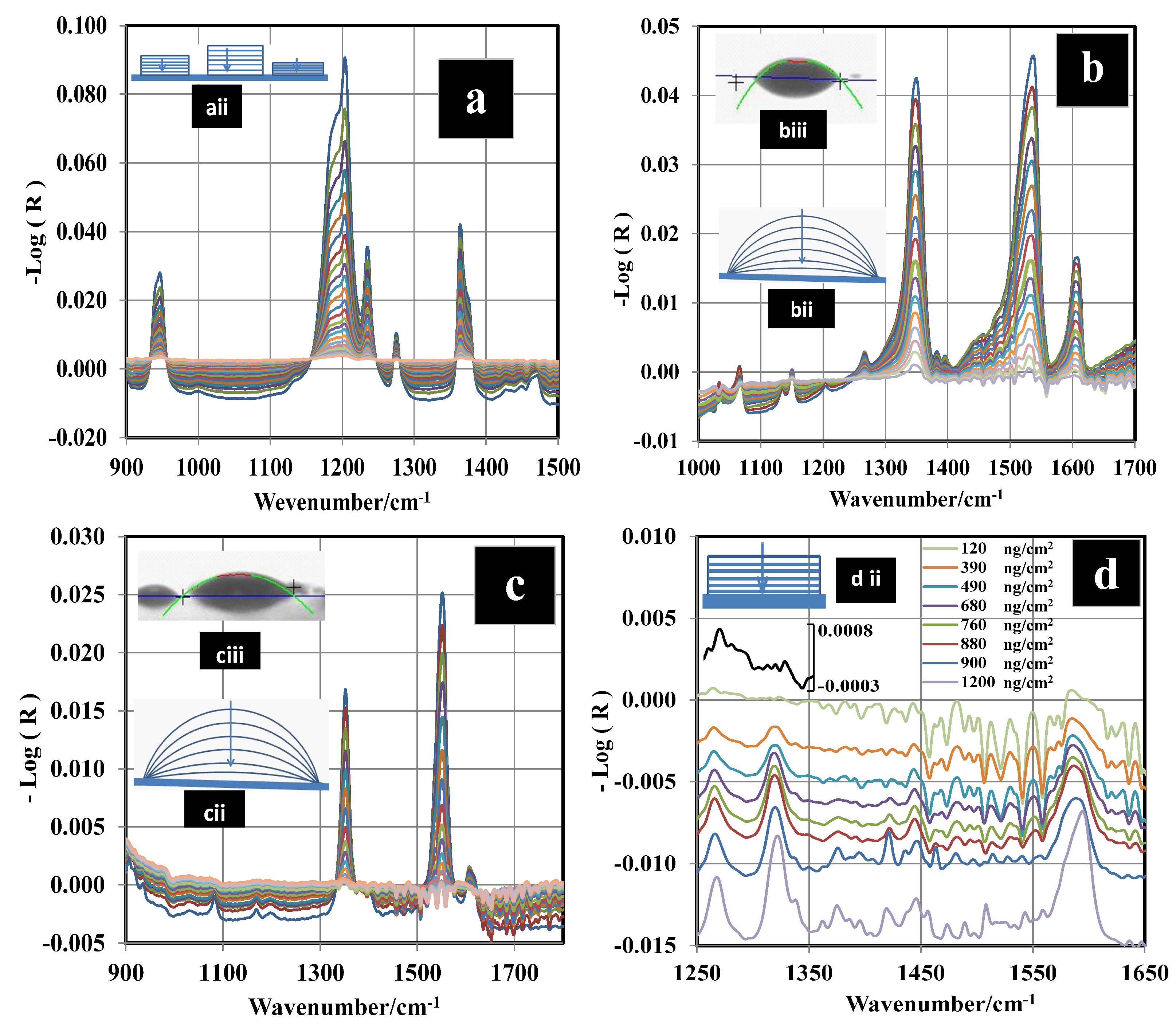
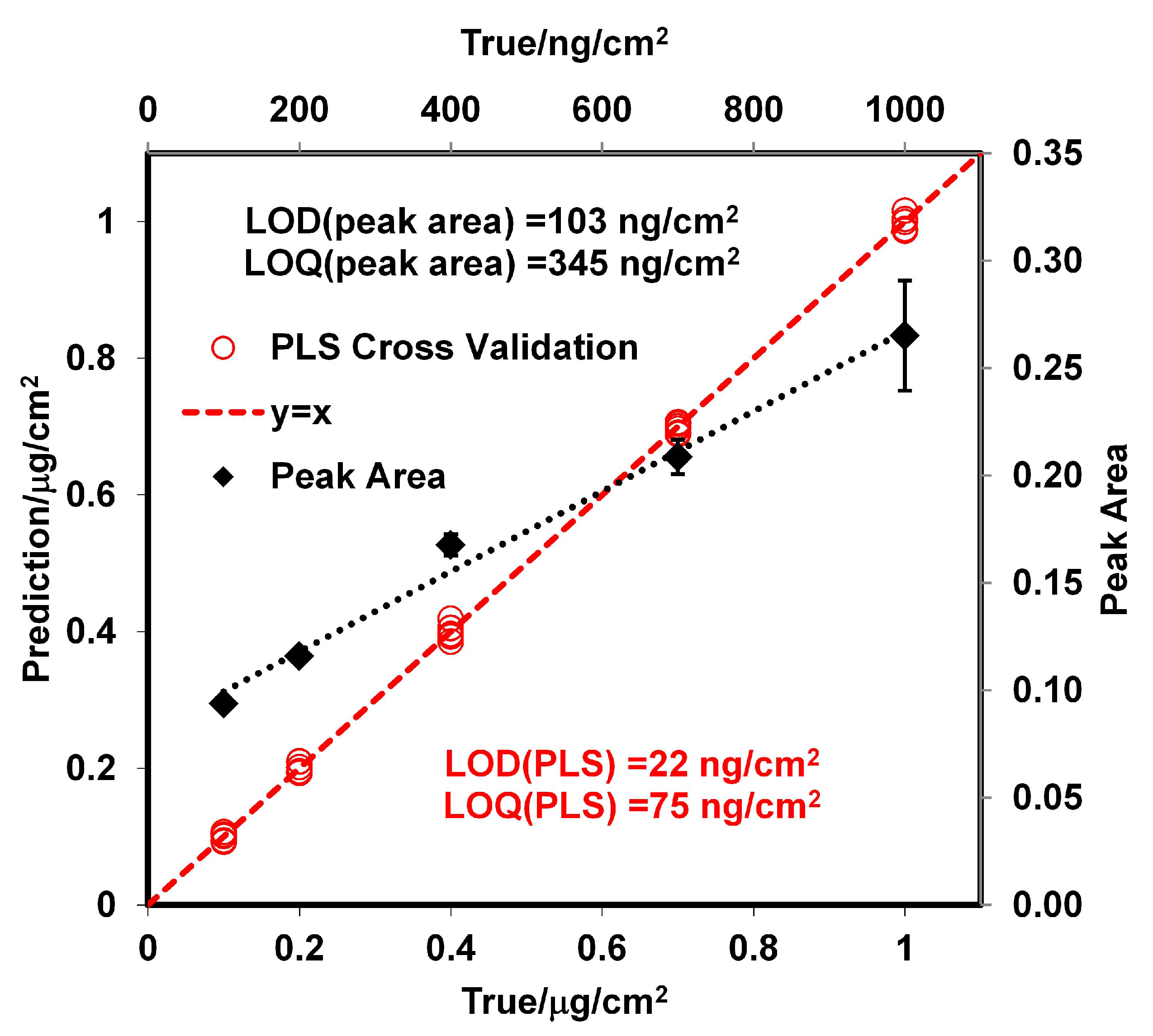
3.2. Determination of Surface Concentration and Thickness for RDX
3.3. GAP vs. GAO Measurements for RDX
3.4. Sublimation Enthalpies and Desorption Energies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| GAP | grazing angle probe fiber-optic |
| GAO | grazing-angle objective |
| HEM | highly energetic material |
| TGA | thermogravimetric analysis |
| TDS | thermal desorption spectroscopy |
| TPM | temperature-programmed method |
| TATP | triacetone triperoxide |
| DNT | 2,4-dinitrotoluene |
| TNT | 2,4,6-trinitrotoluene |
| SS | stainless steel |
| desorption energy | |
| enthalpy of sublimation | |
| difference between the heat capacity | |
| SNRs | signal-to-noise ratios |
| MCT | mercury cadmium telluride |
| CA | contact angle |
| CLS | classical least squares |
| limit of detection | |
| PLS | Partial least squares regression |
| VN | Vector normalization |
| HPLC | high-performance liquid chromatography |
References
- Mamo, S.K.; Gonzalez-Rodriguez, J. Development of a Molecularly Imprinted Polymer-Based Sensor for the Electrochemical Determination of Triacetone Triperoxide (TATP). Sensors 2014, 14, 23269–23282. [Google Scholar] [CrossRef] [PubMed]
- Walter, M.A.; Panne, U.; Weller, M.G. A Novel Immunoreagent for the Specific and Sensitive Detection of the Explosive Triacetone Triperoxide (TATP). Biosensors 2011, 1, 93–106. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.P.; Fernández, M.J.; Fontecha, J.L.; Matatagui, D.; Sayago, I.; Horrillo, M.C.; Gracia, I. Nanocrystalline Tin Oxide Nanofibers Deposited by a Novel Focused Electrospinning Method. Application to the Detection of TATP Precursors. Sensors 2014, 14, 24231–24243. [Google Scholar] [CrossRef] [PubMed]
- Lü, X.; Hao, P.; Xie, G.; Duan, J.; Gao, L.; Liu, B. A Sensor Array Realized by a Single Flexible TiO2/POMs Film to Contactless Detection of Triacetone Triperoxide. Sensors 2019, 19, 915. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Wu, Z.; Duan, H.; Jia, D. Detection of Triacetone Triperoxide (TATP) Precursors with an Array of Sensors Based on MoS2/RGO Composites. Sensors 2019, 19, 1281. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Phan, D.N.; Nguyen, D.C.; Do, V.T.; Bach, L.G. The Chemical Compatibility and Adhesion of Energetic Materials with Several Polymers and Binders: An Experimental Study. Polymers 2018, 10, 1396. [Google Scholar] [CrossRef] [PubMed]
- Trofimov, V.A.; Varentsova, S.A. A Possible Way for the Detection and Identification of Dangerous Substances in Ternary Mixtures Using THz Pulsed Spectroscopy. Sensors 2019, 19, 2365. [Google Scholar] [CrossRef] [PubMed]
- Manley, P.V.; Sagan, V.; Fritschi, F.B.; Burken, J.G. Remote Sensing of Explosives-Induced Stress in Plants: Hyperspectral Imaging Analysis for Remote Detection of Unexploded Threats. Remote Sens. 2019, 11, 1827. [Google Scholar] [CrossRef]
- Herrera-Chacon, A.; Campos, I.; Bottone, L.; Valle, M.d. Molecularly Imprinted Polymers for TNT Analogues. Development of Electrochemical TNT Biosensors. Proceedings 2017, 1, 731. [Google Scholar] [CrossRef]
- Charles, P.T.; Wadhwa, V.; Kouyate, A.; Mesa-Donado, K.J.; Adams, A.A.; Deschamps, J.R.; Kusterbeck, A.W. A High Aspect Ratio Bifurcated 128-Microchannel Microfluidic Device for Environmental Monitoring of Explosives. Sensors 2018, 18, 1568. [Google Scholar] [CrossRef]
- Marchisio, A.; Tulliani, J.M. Semiconducting Metal Oxides Nanocomposites for Enhanced Detection of Explosive Vapors. Ceramics 2018, 1, 98–119. [Google Scholar] [CrossRef]
- Zarejousheghani, M.; Lorenz, W.; Vanninen, P.; Alizadeh, T.; Cämmerer, M.; Borsdorf, H. Molecularly Imprinted Polymer Materials as Selective Recognition Sorbents for Explosives: A Review. Polymers 2019, 11, 888. [Google Scholar] [CrossRef] [PubMed]
- Attard, G.; Barnes, C. Surface; Oxford Science Publications: New York, NY, USA, 1998. [Google Scholar]
- Galleano, M.; Boveris, A.; Puntarulo, S. Understanding the Clausius–Clapeyron Equation by Employing an Easily Adaptable Pressure Cooker. J. Chem. Educ. 2008, 85, 276. [Google Scholar] [CrossRef]
- Sladkov, I.B.; Nedoshivina, M.S. On the accuracy of calculation by the Clapeyron-Clausius equation. Russ. J. Appl. Chem. 2001, 74, 390–393. [Google Scholar] [CrossRef]
- Velasco, S.; Román, F.L.; White, J.A. On the Clausius–Clapeyron vapor pressure equation. J. Chem. Educ. 2009, 86, 106–111. [Google Scholar] [CrossRef]
- Yarwood, J.L.; Le Croissette, D.H. Vapour pressure measurements of bromine. Vacuum 1951, 1, 37–38. [Google Scholar] [CrossRef]
- Pikal, M.; Lukes, A. Knudsen Vapor Pressure Measurements on Pure Materials and Solutions Dispersed in Porous Media: Molded Nitroglycerin Tablets. J. Pharm. Sci. 1976, 65, 1269–1277. [Google Scholar] [CrossRef]
- Elder, J.P. Sublimation measurements of pharmaceutical compounds by isothermal thermogravivletry. J. Therm. Anal. 1997, 49, 897–905. [Google Scholar] [CrossRef]
- Jones, D.; Lightfoot, P.; Fouchard, R.; Kwok, Q. Thermal properties of DMNB, a detection agent for explosives. Thermochim. Acta 2002, 388, 159–173. [Google Scholar] [CrossRef]
- Chatterjee, K.; Dollimore, D.; Alexander, K.S. Calculation of vapor pressure curves for hydroxy benzoic acid derivatives using thermogravimetry. Thermochim. Acta 2002, 392–393, 107–117. [Google Scholar] [CrossRef]
- Ramirez, M.; Pacheco-Londoño, L.; Peña Quevedo, A.; Hernández-Rivera, S. Characterization of peroxide-based explosives by thermal analysis—Art. no. 62012B. Proc. SPIE 2006, 6201, 62012B–620111A. [Google Scholar] [CrossRef]
- Stefanov, A.; Stibor, A.; Dominguez-Clarimon, A.; Arndt, M. Sublimation enthalpy of dye molecules measured using fluorescence. J. Chem. Phys. 2004, 121, 6935–6940. [Google Scholar] [CrossRef] [PubMed]
- Mehta, N.; Goenaga-Polo, J.; Hernández-Rivera, S.P.; Hernández, D.; Thomson, M.A.; Melling, P.J. Development of an In-Situ Spectroscopic Method for Cleaning Validation Using Mid-IR Fiber Optics. Spectroscopy 2003, 18, 14. [Google Scholar]
- Hamilton, M.L.; Perston, B.B.; Harland, P.W.; Williamson, B.E.; Thomson, M.A.; Melling, P.J. Grazing-Angle Fiber-Optic IRRAS for in Situ Cleaning Validation. Org. Process Res. Dev. 2005, 9, 337–343. [Google Scholar] [CrossRef]
- Primera-Pedrozo, O.; Pacheco-Londono, L.; De la Torre-Quintana, L.; Hernández-Rivera, S.; Thomas Chamberlain, R.; Lareau, R. Use of fiber-optic coupled FT-IR in detection of explosives on surfaces. Proc. SPIE 2004, 5403, 237–245. [Google Scholar] [CrossRef]
- Casperson, L.W. Grazing reflection of Gaussian beams. Appl. Opt. 1999, 38, 554–562. [Google Scholar] [CrossRef] [PubMed]
- Verdeyen, J.T. Laser Electronics, 1st ed.; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1981. [Google Scholar]
- Mansfield, E.; Kar, A.; Quinn, T.P.; Hooker, S.A. Quartz Crystal Microbalances for Microscale Thermogravimetric Analysis. Anal. Chem. 2010, 82, 9977–9982. [Google Scholar] [CrossRef] [PubMed]
- Price, D.M. Volatilisation, evaporation and vapour pressure studies using a thermobalance. J. Therm. Anal. Calorim. 2001, 64, 315–322. [Google Scholar] [CrossRef]
- Langmuir, I. The vapor pressure of metallic tungsten. Phys. Rev. 1913, 2, 329–342. [Google Scholar] [CrossRef]
- Price, D.M.; Hawkins, M. Calorimetry of two disperse dyes using thermogravimetry. Thermochim. Acta 1998, 315, 19–24. [Google Scholar] [CrossRef]
- Colomina, M.; Jimenez, P.; Turrion, C. Vapour pressures and enthalpies of sublimation of naphthalene and benzoic acid. J. Chem. Thermodyn. 1982, 14, 779–784. [Google Scholar] [CrossRef]
- Ribeiro da Silva, M.A.V.; Monte, M.J.S.; Santos, L.M.N.B.F. The design, construction, and testing of a new Knudsen effusion apparatus. J. Chem. Thermodyn. 2006, 38, 778–787. [Google Scholar] [CrossRef]
- Oura, K.; Lifshits, V.G.; Saranin, A.A.; Zotov, A.V.; Katayama, M. Surface Science: An Introduction; Springer: Berlin, Germany, 2003. [Google Scholar]
- Redhead, P.A. Thermal desorption of gases. Vacuum 1962, 12, 203–211. [Google Scholar] [CrossRef]
- Tolstoy, V.P.; Chernyshova, I.V.; Skryshevsky, V.A. Handbook of Infrared Spectroscopy of Ultrathin Films; Wiley-Interscience: Hoboken, NJ, USA, 2003. [Google Scholar]
- Buttigieg, G.A.; Knight, A.K.; Denson, S.; Pommier, C.; Bonner Denton, M. Characterization of the explosive triacetone triperoxide and detection by ion mobility spectrometry. Forensic Sci. Int. 2003, 135, 53–59. [Google Scholar] [CrossRef]
- Brauer, B.; Dubnikova, F.; Zeiri, Y.; Kosloff, R.; Gerber, R.B. Vibrational spectroscopy of triacetone triperoxide (TATP): Anharmonic fundamentals, overtones and combination bands. Spectrochim. Acta-Part A Mol. Biomol. Spectrosc. 2008, 71, 1438–1445. [Google Scholar] [CrossRef] [PubMed]
- Alzate, L.F.; Ramos, C.M.; Hernandez, N.M.; Hernandez, S.P.; Mina, N. The vibrational spectroscopic signature of TNT in clay minerals. Vib. Spectrosc. 2006, 42, 357–368. [Google Scholar] [CrossRef]
- Ortiz-Rivera, W.; Pacheco-Londoño, L.; Castro, J.; Felix-Rivera, H.; Hernendez-Rivera, S. Vibrational Spectroscopy Standoff Detection of Threat Chemicals. Proc. SPIE 2011, 8031, 803129. [Google Scholar] [CrossRef]
- Pacheco-Londoño, L.; Ortiz-Rivera, W.; Primera-Pedrozo, O.; Hernandez-Rivera, S. Vibrational spectroscopy standoff detection of explosives. Anal. Bioanal. Chem. 2009, 395, 323–335. [Google Scholar] [CrossRef]
- Infante-Castillo, R.; Pacheco-Londoño, L.C.; Hernandez-Rivera, S.P. Monitoring the α to β solid-solid phase transition of RDX with Raman spectroscopy: A theoretical and experimental study. J. Mol. Struct. 2010, 970, 51–58. [Google Scholar] [CrossRef]
- Infante-Castillo, R.; Pacheco-Londoño, L.; Hernandez-Rivera, S.P. Vibrational spectra and structure of RDX and its 13C- and 15N-labeled derivatives: A theoretical and experimental study. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2010, 76, 137–141. [Google Scholar] [CrossRef]
- Torres, P.; Mercado, L.; Cotte, I.; Hernandez, S.P.; Mina, N.; Santana, A.; Chamberlain, R.T.; Lareau, R.; Castro, M.E. Vibrational Spectroscopy Study of β and α RDX Deposits. J. Phys. Chem. B 2004, 108, 8799–8805. [Google Scholar] [CrossRef]
- Figueroa-Navedo, A.M.; Ruiz-Caballero, J.L.; Pacheco-Londoño, L.C.; Hernandez-Rivera, S.P. Characterization of α- and β-RDX Polymorphs in Crystalline Deposits on Stainless Steel Substrates. Cryst. Growth Des. 2016, 16, 3631–3638. [Google Scholar] [CrossRef]
- Ruiz-Caballero, J.L.; Aparicio-Bolaño, J.A.; Figueroa-Navedo, A.M.; Pacheco-Londoño, L.C.; Hernandez-Rivera, S.P. Optical Properties of β-RDX Thin Films Deposited on Gold and Stainless Steel Substrates Calculated from Reflection–Absorption Infrared Spectra. Appl. Spectrosc. 2017, 71, 1990–2000. [Google Scholar] [CrossRef] [PubMed]
- Ruiz-Caballero, J.L.; Blanco-Riveiro, L.A.; Ramirez-Marrero, I.A.; Perez-Almodovar, L.A.; Colon-Mercado, A.M.; Castro-Suarez, J.R.; Pacheco-Londoño, L.C.; Hernandez-Rivera, S.P. Enhanced RDX Detection Studies on Various Types of Substrates via Tunable Quantum Cascade Laser Spectrometer Coupled with Grazing Angle Probe. IOP Conf. Ser. Mater. Sci. Eng. 2019, 519, 012007. [Google Scholar] [CrossRef]
- Wold, S.; Sjöströma, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Mardia, J.K.V.; Kent, J.T.; Biby, J.M. Chemometrics: Statistic and Computer Application in Analytical Chemistry; Academic Press: London, UK, 1980. [Google Scholar]
- Otto, M. Chemometrics: Statistic and Computer Application in Analytical Chemistry; Wiley-VCH: Weinheim, Germany, 1999. [Google Scholar]
- Brereton. Chemometrics: Data Analysis for the Laboratory and Chemical Plant; John Wiley & Sons, Ltd.: Chichester, UK, 2003. [Google Scholar]
- Beebe, K.R.; Pell, R.J.; Seasholtz, M.B. Chemometrics. A Pactricla Guide; John Wiley & Sons, Inc.: New York, NY, USA, 1998. [Google Scholar]
- Primera-Pedrozo, O.; Soto-Feliciano, Y.; Pacheco-Londoño, L.; Hernandez-Rivera, S. Detection of High Explosives Using Reflection Absorption Infrared Spectroscopy with Fiber Coupled Grazing Angle Probe/FTIR. Sens. Imaging Int. J. 2009, 10, 1–13. [Google Scholar] [CrossRef]
- Primera-Pedrozo, O.; Soto-Feliciano, Y.; Pacheco-Londoño, L.; Hernandez-Rivera, S. High Explosives Mixtures Detection Using Fiber Optics Coupled: Grazing Angle Probe/Fourier Transform Reflection Absorption Infrared Spectroscopy. Sens. Imaging Int. J. 2008, 9, 27–40. [Google Scholar] [CrossRef]
- Galán-Freyle, N.J.; Pacheco-Londoño, L.C.; Figueroa-Navedo, A.M.; Hernandez-Rivera, S.P. Standoff Detection of Highly Energetic Materials Using Laser-Induced Thermal Excitation of Infrared Emission. Appl. Spectrosc. 2015, 69, 535–544. [Google Scholar] [CrossRef]
- Wrable-Rose, M.; Primera-Pedrozo, O.M.; Pacheco-Londoño, L.C.; Hernandez-Rivera, S.P. Preparation of TNT, RDX and ammonium nitrate standards on gold-on-silicon surfaces by thermal inkjet technology. Sens. Imaging 2010, 11, 147–169. [Google Scholar] [CrossRef]
- Thumanu, K.; Tanthanuch, W.; Lorthongpanich, C.; Heraud, P.; Parnpai, R. FTIR microspectroscopic imaging as a new tool to distinguish chemical composition of mouse blastocyst. J. Mol. Struct. 2009, 933, 104–111. [Google Scholar] [CrossRef]
- Faber, N.M.; Bro, R. Standard error of prediction for multiway PLS-1. Background and a simulation study. Chemom. Intell. Lab. Syst. 2002, 61, 133–149. [Google Scholar] [CrossRef]
- Felipe-Sotelo, M.; Cal-Prieto, M.J.; Ferre, J.; Boque, R.; Andrade, J.M.; Carlosena, A. Linear PLS regression to cope with interferences of major concomitants in the determination of antimony by ETAAS. J. Anal. At. Spectrom. 2006, 21, 61–68. [Google Scholar] [CrossRef]
- Galan-Freyle, N.J.; Pacheco-Londoño, L.C.; Roman-Ospino, A.D.; Hernandez-Rivera, S.P. Applications of Quantum Cascade Laser Spectroscopy in the Analysis of Pharmaceutical Formulations. Appl. Spectrosc. 2016, 70, 1511–1519. [Google Scholar] [CrossRef]
- Pacheco-Londoño, L.C.; Galán-Freyle, N.J.; Figueroa-Navedo, A.M.; Infante-Castillo, R.; Ruiz-Caballero, J.L.; Hernández-Rivera, S.P. Quantum cascade laser back-reflection spectroscopy at grazing-angle incidence using the fast Fourier transform as a data preprocessing algorithm. J. Chemom. 2019, 33, e3167. [Google Scholar] [CrossRef]
- Pacheco-Londoño, L.C.; Aparicio-Bolaño, J.A.; Galan-Freyle, N.J.; Roman-Ospino, A.D.; Ruiz-Caballero, J.L.; Hernandez-Rivera, S.P. Classical Least Squares-Assisted Mid-Infrared (MIR) Laser Spectroscopy Detection of High Explosives on Fabrics. Appl. Spectrosc. 2019, 73, 17–29. [Google Scholar] [CrossRef]
- IUPAC. Erratum: International union of pure and applied chemistry analytical chemistry division commission on spectrochemical and other optical procedures for analysis nomenclature, symbols, units and their usage in spectrochemical analysis - II. Data interpretation (Analytical Chemistry (1976) 48 (1424)). Anal. Chem. 1976, 48, 2293. [Google Scholar]
- Goldberg, I.G.; Swift, J.A. New Insights into the Metastable β Form of RDX. Cryst. Growth Des. 2012, 12, 1040–1045. [Google Scholar] [CrossRef]
- Verevkin, S.P. Enthalpy of sublimation of dibenzofuran: A redetermination. Phys. Chem. Chem. Phys. 2003, 5, 710–712. [Google Scholar] [CrossRef]
- Bevington, P.R.; Robinson, D.K. Data Reduction and Error Analysis for the Physical Sciences, 3rd ed.; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Hibbert, D.B. The uncertainty of a result from a linear calibration. Analyst 2006, 131, 1273–1278. [Google Scholar] [CrossRef]
- Damour, P.L.; Freedman, A.; Wormhoudt, J. Knudsen Effusion Measurement of Organic Peroxide Vapor Pressures. Propellants Explos. Pyrotech. 2010, 35, 514–520. [Google Scholar] [CrossRef]
- Felix-Rivera, H.; Ramirez-Cedeño, M.L.; Sanchez-Cuprill, R.A.; Hernandez-Rivera, S.P. Triacetone triperoxide thermogravimetric study of vapor pressure and enthalpy of sublimation in 303–338 K temperature range. Thermochim. Acta 2011, 514, 37–43. [Google Scholar] [CrossRef]
- Oxley, J.C.; Smith, J.L.; Shinde, K.; Moran, J. Determination of the Vapor Density of Triacetone Triperoxide (TATP) Using a Gas Chromatography Headspace Technique. Propellants Explos. Pyrotech. 2005, 30, 127–130. [Google Scholar] [CrossRef]
- Oxley, J.C.; Smith, J.L.; Luo, W.; Brady, J. Determining the Vapor Pressures of Diacetone Diperoxide (DADP) and Hexamethylene Triperoxide Diamine (HMTD). Propellants Explos. Pyrotech. 2009, 34, 539–543. [Google Scholar] [CrossRef]
- Dunayevskiy, I.; Tsekoun, A.; Prasanna, M.; Go, R.; Patel, C.K.N. High-sensitivity detection of triacetone triperoxide (TATP) and its precursor acetone. Appl. Opt. 2007, 46, 6397–6404. [Google Scholar] [CrossRef] [PubMed]
- Espinosa-Fuentes, E.; Castro-Suarez, J.; Meza-Payares, D.; Pacheco-Londono, L.; Hernández-Rivera, S. Sublimation enthalpy of homemade peroxide explosives using a theoretically supported nonlinear equation. J. Therm. Anal. Calorim. 2015, 119, 681–688. [Google Scholar] [CrossRef]
- Harris, N.J.; Lammertsma, K. Ab Initio Density Functional Computations of Conformations and Bond Dissociation Energies for Hexahydro-1,3,5-trinitro-1,3,5-triazine. J. Am. Chem. Soc. 1997, 119, 6583–6589. [Google Scholar] [CrossRef]
- Rice, B.M.; Chabalowski, C.F. Ab Initio and Nonlocal Density Functional Study of 1,3,5-Trinitro-s-triazine (RDX) Conformers. J. Phys. Chem. A 1997, 101, 8720–8726. [Google Scholar] [CrossRef]
- Vladimiroff, T.; Rice, B.M. Reinvestigation of the Gas-Phase Structure of RDX Using Density Functional Theory Predictions of Electron-Scattering Intensities. J. Phys. Chem. A 2002, 106, 10437–10443. [Google Scholar] [CrossRef]
- Lenchitz, C.; Velicky, R.W. Vapor pressure and heat of sublimation of three nitrotoluenes. J. Chem. Eng. Data 1970, 15, 401–403. [Google Scholar] [CrossRef]
- Pella, P.A. Generator for producing trace vapor concentrations of 2,4,6-trinitrotoluene, 2,4-dinitrotoluene, and ethylene glycol dinitrate for calibrating explosives vapor detectors. Anal. Chem. 1976, 48, 1632–1637. [Google Scholar] [CrossRef]
- Lenchitz, C.; Velicky, R.W.; Silvestro, G.; Schlosberg, L.P. Thermodynamic properties of several nitrotoluenes. J. Chem. Thermodyn. 1971, 3, 689–692. [Google Scholar] [CrossRef]
- Edwards, G. The vapour pressure of 2 : 4 : 6-trinitrotoluene. Trans. Faraday Soc. 1950, 46, 423–427. [Google Scholar] [CrossRef]
- Dionne, B.C.; Rounbehler, D.P.; Achter, E.K.; Hobbs, J.R.; Fine, D.H. Vapor pressure of explosives. J. Energ. Mater. 1986, 4, 447–472. [Google Scholar] [CrossRef]
- Gershanik, A.P.; Zeiri, Y. Sublimation Rate of TNT Microcrystals in Air. J. Phys. Chem. A 2010, 114, 12403–12410. [Google Scholar] [CrossRef] [PubMed]
- Eiceman, G.A.; Preston, D.; Tiano, G.; Rodriguez, J.; Parmeter, J.E. Quantitative calibration of vapor levels of TNT, RDX, and PETN using a diffusion generator with gravimetry and ion mobility spectrometry. Talanta 1997, 45, 57–74. [Google Scholar] [CrossRef]
- Leggett, D.C. Vapor pressure of 2,4,6-trinitrotoluene by a gas chromatographic headspace technique. J. Chromatogr. A 1977, 133, 83–90. [Google Scholar] [CrossRef]
- Hikal, W.M.; Weeks, B.L. Sublimation kinetics and diffusion coefficients of TNT, PETN, and RDX in air by thermogravimetry. Talanta 2014, 125, 24–28. [Google Scholar] [CrossRef]
- Hikal, W.M.; Paden, J.T.; Weeks, B.L. Thermo-optical determination of vapor pressures of TNT and RDX nanofilms. Talanta 2011, 87, 290–294. [Google Scholar] [CrossRef]
- Mu, R.; Ueda, A.; Liu, Y.C.; Wu, M.; Henderson, D.O.; Lareau, R.T.; Chamberlain, R.T. Effects of interfacial interaction potential on the sublimation rates of TNT films on a silica surface examined by QCM and AFM techniques. Surf. Sci. 2003, 530, L293–L296. [Google Scholar] [CrossRef]
- Chickos, J.S.; Acree, W.E. Enthalpies of Sublimation of Organic and Organometallic Compounds. 1910–2001. J. Phys. Chem. Ref. Data 2002, 31, 537–698. [Google Scholar] [CrossRef]
- Cundall, R.B.; Frank Palmer, T.; Wood, C.E.C. Vapour pressure measurements on some organic high explosives. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1978, 74, 1339–1345. [Google Scholar] [CrossRef]
- Pella, P.A. Measurement of the vapor pressures of tnt, 2,4-dnt, 2,6-dnt, and egdn. J. Chem. Thermodyn. 1977, 9, 301–305. [Google Scholar] [CrossRef]
- Jones, A.H. Sublimation Pressure Data for Organic Compounds. J. Chem. Eng. Data 1960, 5, 196–200. [Google Scholar] [CrossRef]
- Hikal, W.M.; Weeks, B.L. Non-Isothermal Sublimation Kinetics of 2,4,6-Trinitrotoluene (TNT) Nanofilms. Molecules 2019, 24, 1163. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.J.; Weeks, B.L. Investigation of Size-Dependent Sublimation Kinetics of 2,4,6-Trinitrotoluene (TNT) Micro-Islands Using In Situ Atomic Force Microscopy. Molecules 2019, 24, 1895. [Google Scholar] [CrossRef] [PubMed]
- Rosen, J.M.; Dickinson, C. Vapor pressures and heats of sublimation of some high-melting organic explosives. J. Chem. Eng. Data 1969, 14, 120–124. [Google Scholar] [CrossRef]
- Gershanik, A.P.; Zeiri, Y. Sublimation Rate of Energetic Materials in Air: RDX and PETN. Propellants Explos. Pyrotech. 2012, 37, 207–214. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
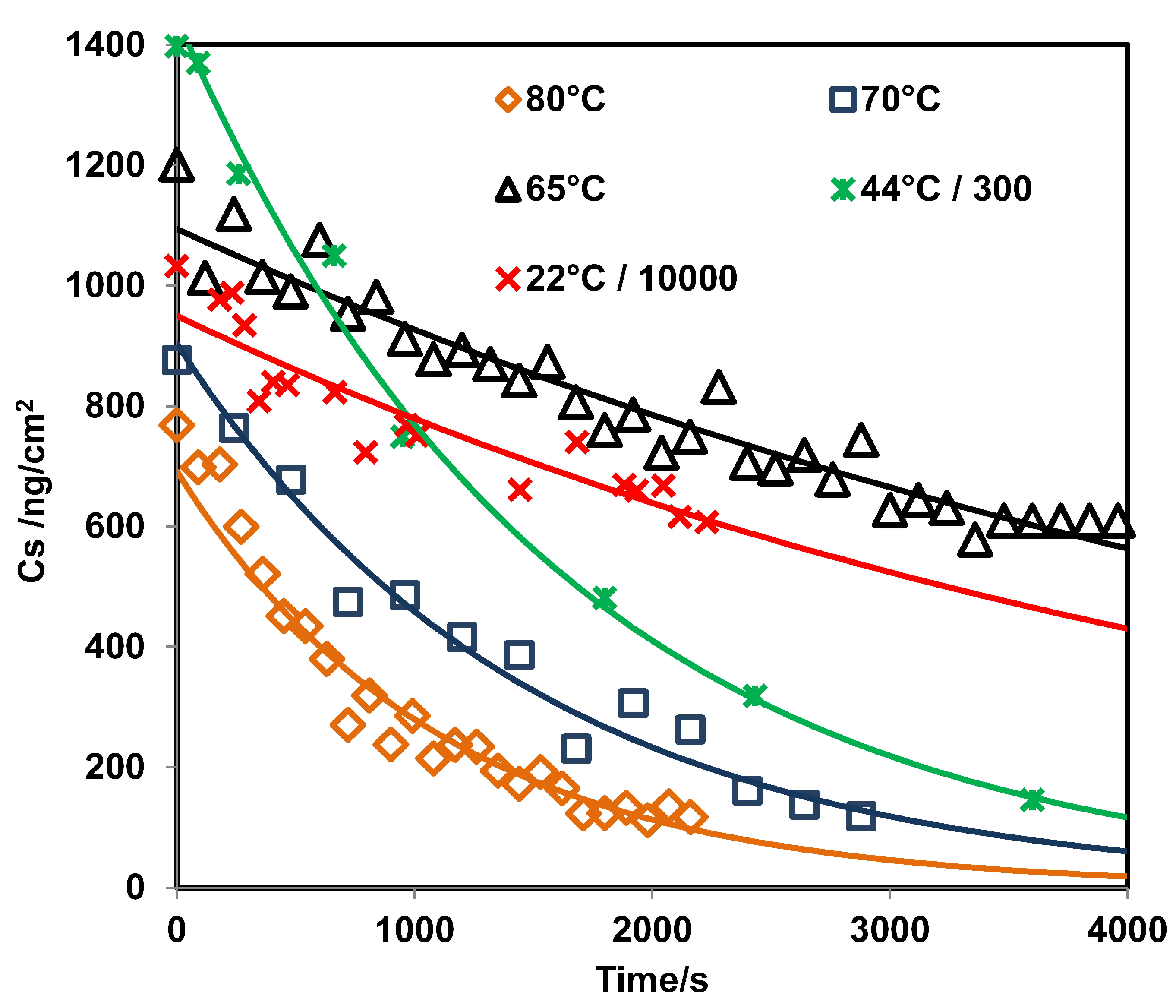

| Exp | HEM | Range of T | /C | R | |
|---|---|---|---|---|---|
| GAP | TATP | 14–33 | 20.9 | 144 ± 14 | 0.997 |
| TGA_1 | TATP | 20–65 | 37.5 | 83 ± 5 | 0.999 |
| TGA_2 | TATP | 22–64 | 44.0 | 87 ± 3 | 1.000 |
| TGA_3 | TATP | 21–63 | 37.8 | 86 ± 2 | 1.000 |
| GAP | 2,4-DNT | 23–35 | 36.0 | 94 ± 5 | 0.986 |
| TGA | 2,4-DNT | 25–75 | 46.6 | 94 ± 2 | 0.998 |
| GAP | TNT | 40–70 | 55.0 | 111 ± 6 | 0.998 |
| TGA | TNT | 40–65 | 52.5 | 95 ± 3 | 0.997 |
| GAP | RDX | 22–80 | 56.2 | 153 ± 5 | 0.998 |
| TGA | RDX | 55–125 | 90.0 | 99 ± 3 | 0.987 |
| TPM | RDX | U/kJ/mol | /C/min | /C | |
| = 19 ± 1 | 5 | 117 ± 2 | |||
| 10 | 142 ± 3 | ||||
| 20 | 200 ± 3 |
| Molecule | for GAP | for TGA | for TGA_2 | for TGA_3 |
|---|---|---|---|---|
| TATP | 104 ± 15 | 99 ± 6 | 107 ± 3 | 102 ± 3 |
| 2,4-DNT | 103 ± 11 | 100 ± 5 | ||
| TNT | 117 ± 31 | 120 ± 9 | ||
| RDX | 165 ± 22 for -RDX | 112 ± 20 for -RDX | ||
| Molecule | for GAP | for TGA | for TGA_2 | for TGA_3 |
| TATP | 8.6 ± 0.9 | 1.21 ± 0.09 | 1.50 ± 0.04 | 1.24 ± 0.04 |
| 2,4-DNT | 1.1 ± 0.9 | 0.3 ± 0.2 | ||
| TNT | 0.3 ± 1.0 | 0.9 ± 0.3 | ||
| RDX | 0.4 ± 0.7 | 0.2 ± 0.3 |
| in C | N of T | in kJ/mol·K | in kJ/mol | |
|---|---|---|---|---|
| GAP | 20.9 | 19 | 8.6 ± 0.9 | 142 ± 14 |
| TGA_1 | 37.5 | 14 | 1.21 ± 0.09 | 83 ± 5 |
| TGA_2 | 44 | 42 | 1.50 ± 0.04 | 87 ± 2 |
| TGA_3 | 37.8 | 88 | 1.24 ± 0.03 | 85 ± 2 |
| Damour et al., 2010 [69] | 14.3 | 27 | 0 | 86.2 ± 1 |
| Ramirez et al., 2006 [22] | 50.0 | 7 | 0.75 ± 0.08 | 85.8 |
| Felix et al., 2011 [70] | 50.0 | 8 | - | 72.1 |
| Oxley et al., 2005 [71] | 40 | 6 | 0.3 ± 0.5 | 109 |
| Oxley et al., 2009 [72] | 32.2 | 7 | 0.6 ± 0.7 | 73 |
| Dunayevskiy et al., 2007 [73] | 0 | - | - | 81.3 |
| Espinosa-Fuentes et al., 2015 [74] | 46 | 32 | 1.5 | 103.8 ± 0.2 |
| HEM | Autor | /C | |
|---|---|---|---|
| DNT | This work from GAP | 36 | 94 ± 5 |
| DNT | This work from TGA | 46.6 | 94 ± 2 |
| DNT | Lenchitz 1970 [78] | 64 | 98.3 ± 2.5 |
| DNT | Lenchitz 1970 [78] | 25 | 99.6 ± 2.5 |
| DNT | Felix et al., 2011 [70] | 52.4 | 96.2 |
| DNT | Pella 1976 [79] | 37 | 95.80 ± 1.25 |
| DNT | Lenchitz 1971 [80] | – | 99.6 ± 1.3 |
| TNT | This work from GAP | 55 | 111 ± 6 |
| TNT | This work from TGA | 52.5 | 95 ± 3 |
| TNT | Edwards 1950 [81] | – | 118.4 |
| TNT | Dionne et al., 1986 [82] | 25 | 113 |
| TNT | Gershanik et al., 2010 [83] | 40 | 97 ± 7 |
| TNT | Oxley et al., 2005 [71] | 36 | 137 |
| TNT | Eiceman et al., 1997 [84] | 114.5 | 87 |
| TNT | Leggett 1977 [85] | 26 | 141.1 ± 0.2 |
| TNT | Hikal et al., 2014 [86] | 67.5 | 95.9 ± 1 |
| TNT | Hikal et al., 2011 [87] | – | 100.2 |
| TNT | Mu et al., 2003 [88] | 32.5 | 131 |
| TNT | Chickos et al., 2002 [89] | 35 | 112.4 |
| TNT | Cundall et al., 1978 [90] | 25 | 113.2 ± 1.5 |
| TNT | Felix et al., 2011 [70] | 54.8 | 106.8 |
| TNT | Pella 1977 [91] | – | 99.2 ± 2.0 |
| TNT | Lenchitz 1971 [80] | 25 | 104.6 ± 1.7 |
| TNT | Lenchitz 1970 [78] | 65 | 103.3 ± 2.5 |
| TNT | Jones 1960 [92] | – | 118.4 ± 4.2 |
| TNT | Hikal 2019 [93] | 55 | 105.9 ± 1.4 |
| TNT | Hikal 2019 [93] | 55 | 102.1 ± 2.7 |
| TNT | Hikal 2019 [93] | 55 | 105.8 ± 1.6 |
| TNT | Lee 2019 [94] | 18.5 | 104.4 ± 2.4 |
| RDX | This work from GAP | 56.2 | 150 ± 5 |
| RDX | This work from TGA | 90 | 99 ± 3 |
| RDX | Rosen et al., 1969 [95] | – | 130.2 |
| RDX | Gershanik et al., 2012 [96] | 65 | 115 - 134 |
| RDX | Eiceman et al., 1997 [84] | 130 | 115 |
| RDX | Hikal et al., 2011 [87] | – | 128 |
| RDX | Hikal et al., 2014 [86] | 120 | 130 ± 2 |
| RDX | Cundall et al., 1978 [90] | 25 | 134.3 |
| RDX | Felix et al., 2011 [70] | 92 | 99.5 |
| RDX | Chickos et al., 2002 [89] | – | 112.5 ± 0.8 |
| RDX | Rosen et al., 1969 [95] | 77 | 130.1 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacheco-Londoño, L.C.; Ruiz-Caballero, J.L.; Ramírez-Cedeño, M.L.; Infante-Castillo, R.; Gálan-Freyle, N.J.; Hernández-Rivera, S.P. Surface Persistence of Trace Level Deposits of Highly Energetic Materials. Molecules 2019, 24, 3494. https://doi.org/10.3390/molecules24193494
Pacheco-Londoño LC, Ruiz-Caballero JL, Ramírez-Cedeño ML, Infante-Castillo R, Gálan-Freyle NJ, Hernández-Rivera SP. Surface Persistence of Trace Level Deposits of Highly Energetic Materials. Molecules. 2019; 24(19):3494. https://doi.org/10.3390/molecules24193494
Chicago/Turabian StylePacheco-Londoño, Leonardo C., José L. Ruiz-Caballero, Michael L. Ramírez-Cedeño, Ricardo Infante-Castillo, Nataly J. Gálan-Freyle, and Samuel P. Hernández-Rivera. 2019. "Surface Persistence of Trace Level Deposits of Highly Energetic Materials" Molecules 24, no. 19: 3494. https://doi.org/10.3390/molecules24193494
APA StylePacheco-Londoño, L. C., Ruiz-Caballero, J. L., Ramírez-Cedeño, M. L., Infante-Castillo, R., Gálan-Freyle, N. J., & Hernández-Rivera, S. P. (2019). Surface Persistence of Trace Level Deposits of Highly Energetic Materials. Molecules, 24(19), 3494. https://doi.org/10.3390/molecules24193494