Molecular Dynamics Gives New Insights into the Glucose Tolerance and Inhibition Mechanisms on β-Glucosidases
Abstract
1. Introduction
2. Results
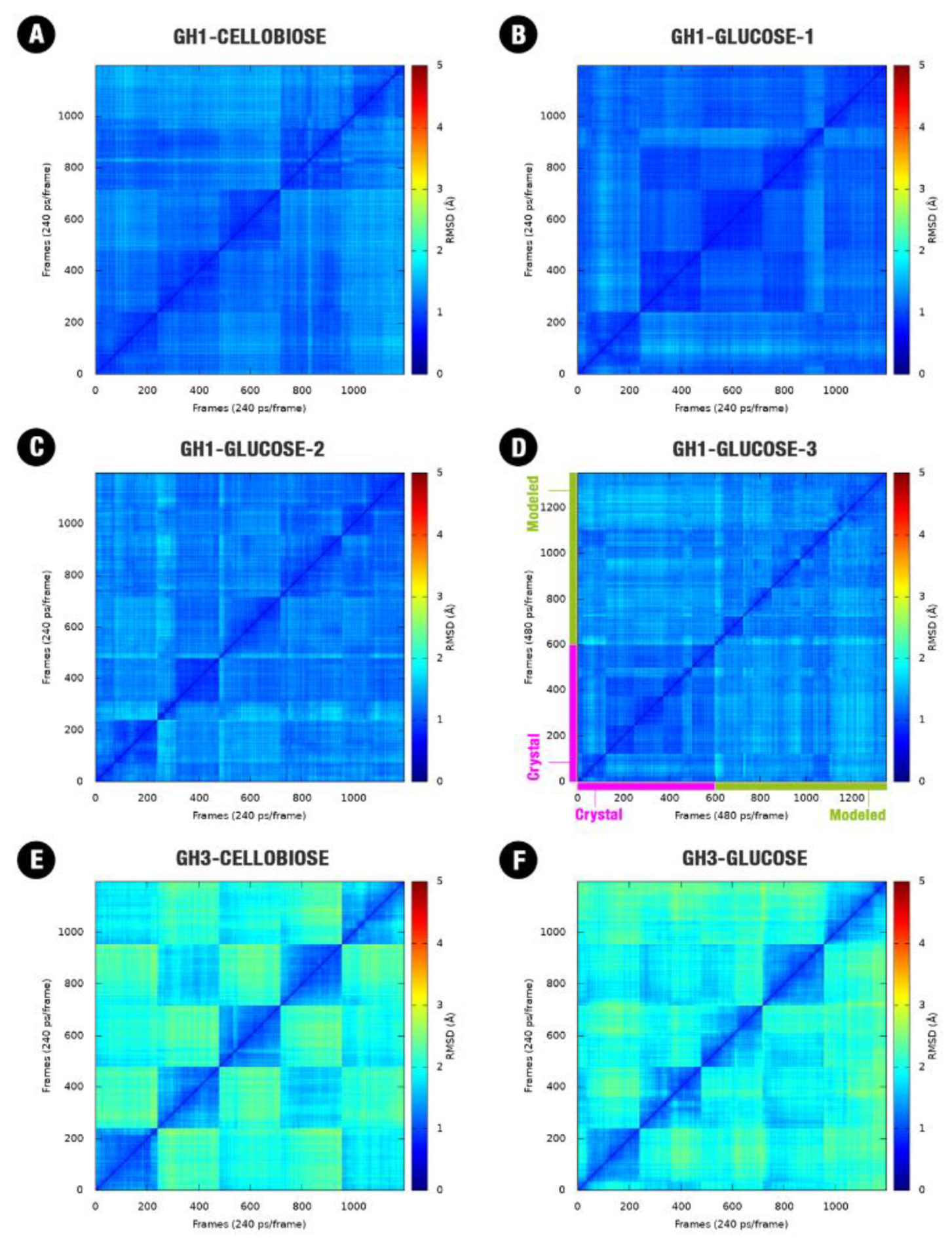
2.1. Equilibration and Conformational Sampling from the MD Sets
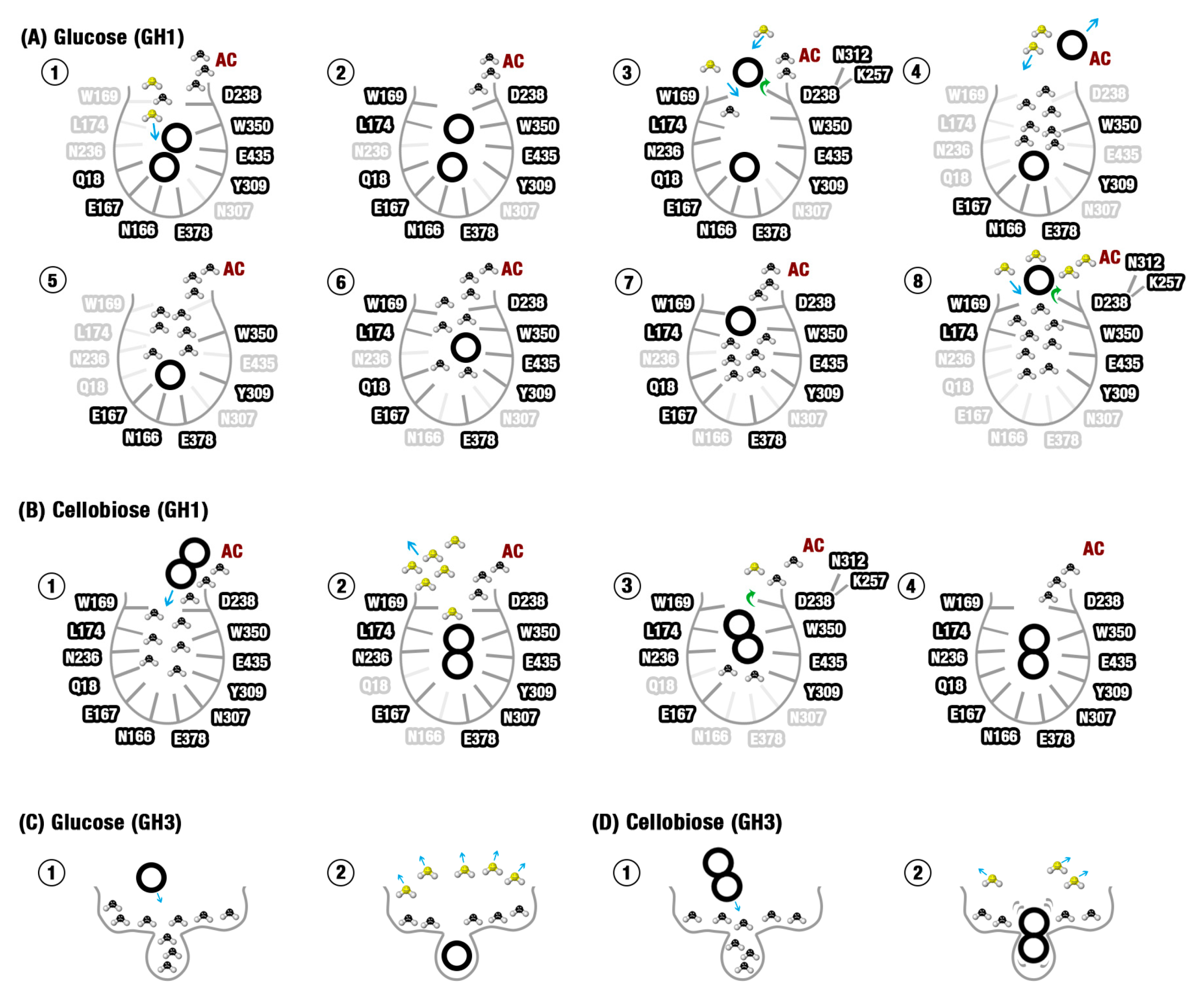
2.2. MD Shows Glucose Releasing for HiBG (GH1)
2.3. APBS vs. GIST vs. Ligand Fitting: Differences on the Electrostatic Distribution, Water Activity and Stereochemical Adjustments Around the Active Sites of Hibg and Aabg and Ligand Dynamics
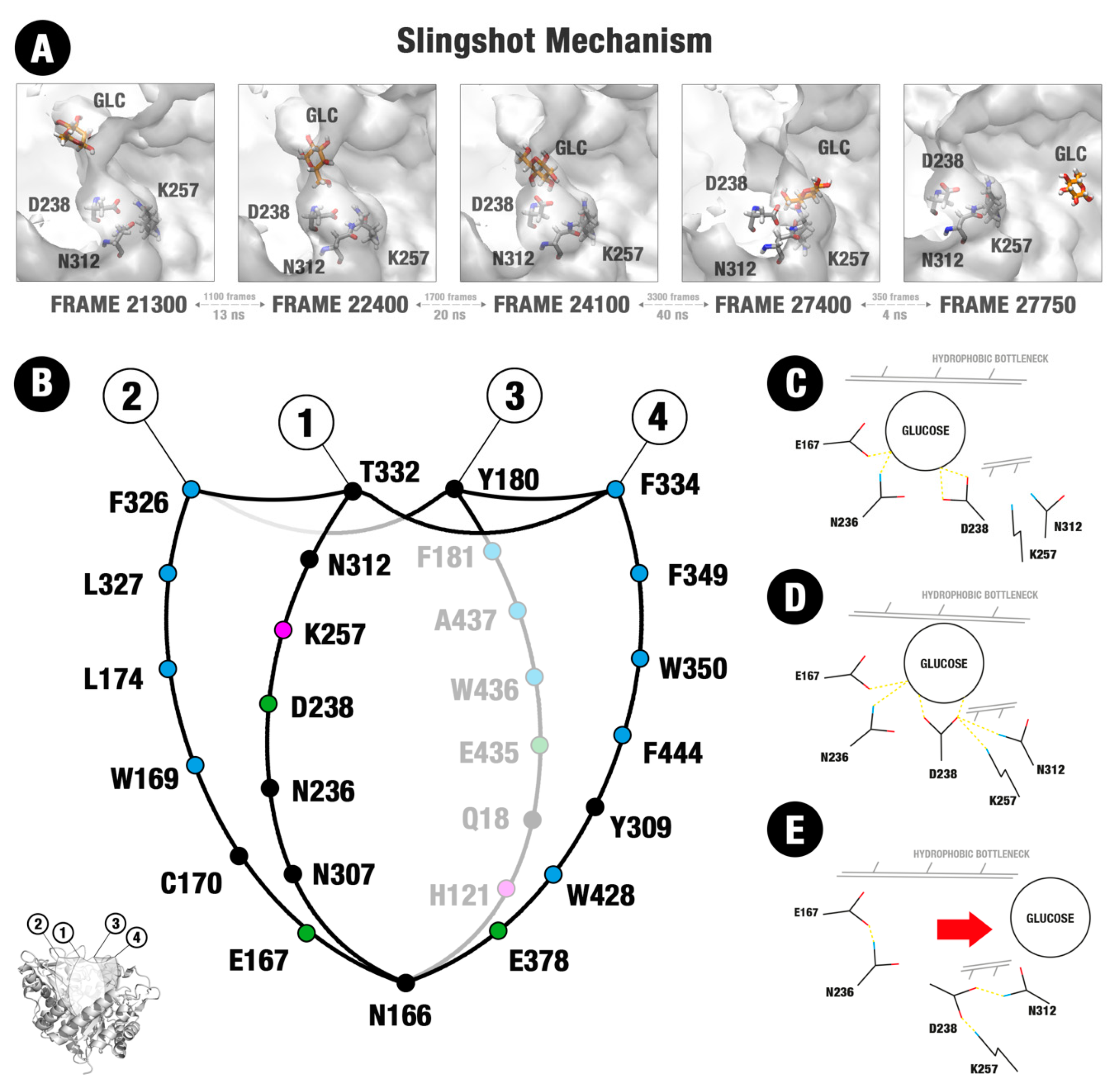
2.4. Evidence of the Participation of the D238 Residue and Neighborhood on the Glucose Catapulting Outside the GH1 Enzyme
3. Discussion
3.1. Tolerance and Inhibition are Dependent on a Set of Topological and Physical-Chemical Distinctions Between the Respective GH1 and GH3 Active Sites
3.2. The High Mobility of Glucose Inside the GH1 Active Site, Corroboration with the Sparse Electronic Density of HiBG
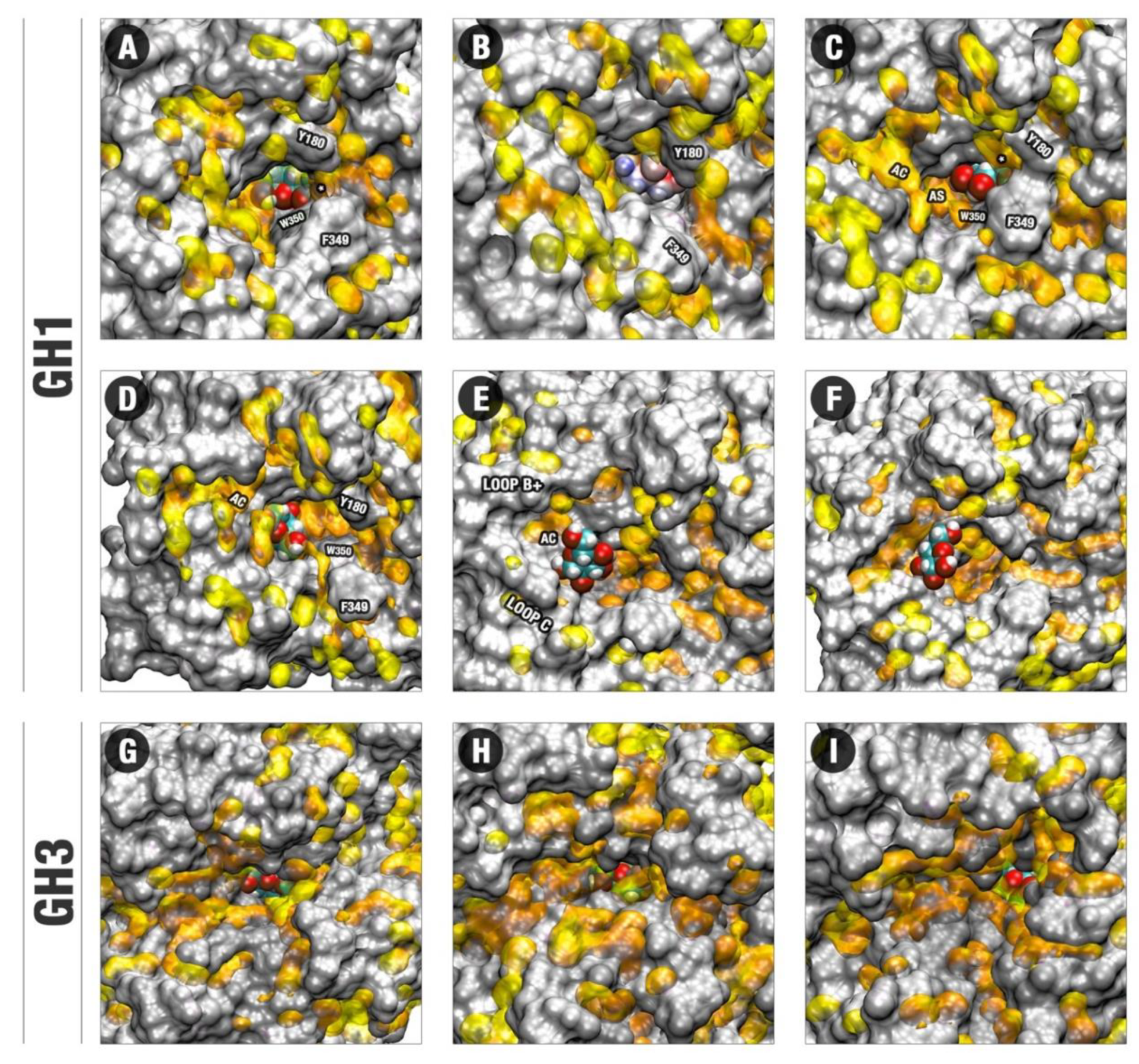
3.3. The Importance of the Hydrophobic Subsites at the Exit and the Water Activity Modulation on The Glucose Withdrawal
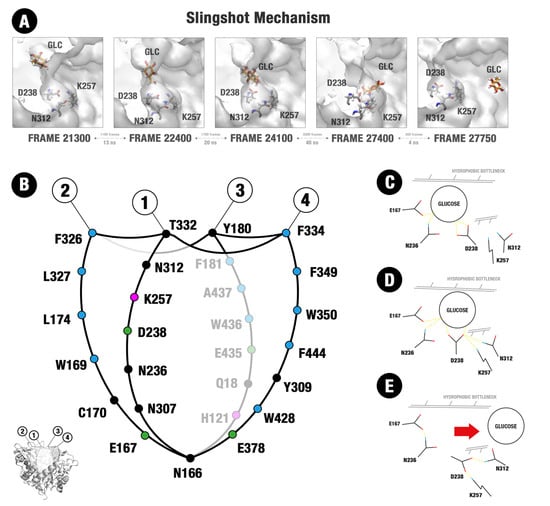
3.4. The Importance of an Allosteric Site/Channel and a Slingshot Mechanism for the Glucose Withdrawal
4. Materials and Methods
4.1. Protein and Ligand Structures
4.2. Molecular Dynamics Simulations
4.3. MD Trajectories Analysis
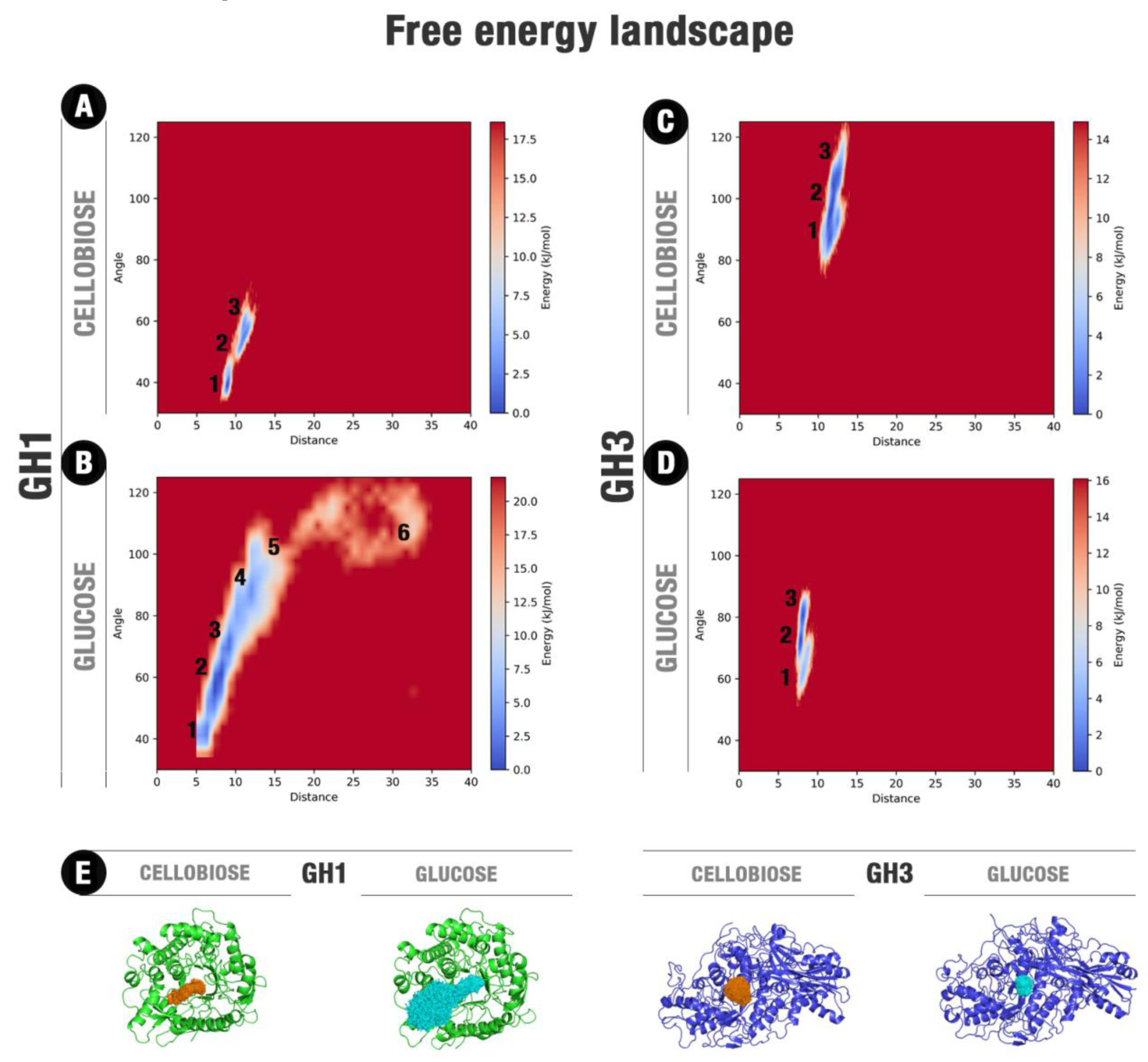
4.4. Ligand–Protein Free Energy Landscape Estimations
4.5. Poisson–Boltzmann Surface Area
4.6. Grid Inhomogeneous Solvation Theory Analyses
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Swangkeaw, J.; Vichitphan, S.; Butzke, C.E.; Vichitphan, K. Characterization of β-glucosidases from Hanseniaspora sp. and Pichia anomala with potentially aroma-enhancing capabilities in juice and wine. World J. Microbiol. Biotechnol. 2010, 27, 423–430. [Google Scholar] [CrossRef]
- Cota, J.; Corrêa, T.L.R.; Damásio, A.R.L.; Diogo, J.A.; Hoffmam, Z.B.; Garcia, W.; Oliveira, L.C.; Prade, R.A.; Squina, F.M. Comparative analysis of three hyperthermophilic GH1 and GH3 family members with industrial potential. New Biotechnol. 2015, 32, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Mariano, D.C.B.; Leite, C.; Santos, L.H.S.; Marins, L.F.; Machado, K.S.; Werhli, A.V.; Lima, L.H.F.; de Melo-Minardi, R.C. Characterization of glucose-tolerant β-glucosidases used in biofuel production under the bioinformatics perspective: A systematic review. Genet. Mol. Res. 2017, 16, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Singhania, R.R.; Patel, A.K.; Sukumaran, R.K.; Larroche, C.; Pandey, A. Role and significance of beta-glucosidases in the hydrolysis of cellulose for bioethanol production. Bioresour. Technol. 2013, 127, 500–507. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Singh, S.; Singh, O.V. Bioconversion of lignocellulosic biomass: Biochemical and molecular perspectives. J. Ind. Microbiol. Biotechnol. 2008, 35, 377–391. [Google Scholar] [CrossRef] [PubMed]
- Cairns, J.R.K.; Esen, A. β-Glucosidases. Cell. Mol. Life Sci. 2010, 67, 3389–3405. [Google Scholar] [CrossRef] [PubMed]
- Béguin, P.; Aubert, J.P. The biological degradation of cellulose. FEMS Microbiol. Rev. 1994, 13, 25–58. [Google Scholar] [CrossRef]
- Teugjas, H.; Väljamäe, P. Selecting β-glucosidases to support cellulases in cellulose saccharification. Biotechnol. Biofuels 2013, 6, 105. [Google Scholar] [CrossRef]
- Yang, F.; Yang, X.; Li, Z.; Du, C.; Wang, J.; Li, S. Overexpression and characterization of a glucose-tolerant β-glucosidase from T. aotearoense with high specific activity for cellobiose. Appl. Microbiol. Biotechnol. 2015, 99, 8903–8915. [Google Scholar] [CrossRef]
- Zhao, L.; Pang, Q.; Xie, J.; Pei, J.; Wang, F.; Fan, S. Enzymatic properties of Thermoanaerobacterium thermosaccharolyticum β-glucosidase fused to Clostridium cellulovorans cellulose binding domain and its application in hydrolysis of microcrystalline cellulose. BMC Biotechnol. 2013, 13, 101. [Google Scholar] [CrossRef]
- Chamoli, S.; Kumar, P.; Navani, N.K.; Verma, A.K. Secretory expression, characterization and docking study of glucose-tolerant β-glucosidase from B. subtilis. Int. J. Biol. Macromol. 2016, 85, 425–433. [Google Scholar] [CrossRef] [PubMed]
- de Giuseppe, P.O.; Souza, T.; de, A.C.B.; Souza, F.H.M.; Zanphorlin, L.M.; Machado, C.B.; Ward, R.J.; Jorge, J.A.; dos Furriel, R.P.M.; Murakami, M.T. Structural basis for glucose tolerance in GH1 β-glucosidases. Acta Crystallogr. D Biol. Crystallogr. 2014, 70, 1631–1639. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, X.; Yin, Q.; Fang, W.; Fang, Z.; Wang, X.; Zhang, X.; Xiao, Y. A mechanism of glucose tolerance and stimulation of GH1 β-glucosidases. Sci. Rep. 2015, 5, 17296. [Google Scholar] [CrossRef] [PubMed]
- Pei, J.; Pang, Q.; Zhao, L.; Fan, S.; Shi, H. Thermoanaerobacterium thermosaccharolyticum β-glucosidase: A glucose-tolerant enzyme with high specific activity for cellobiose. Biotechnol Biofuels 2012, 5, 1–10. [Google Scholar] [CrossRef]
- Guo, B.; Amano, Y.; Nozaki, K. Improvements in Glucose Sensitivity and Stability of Trichoderma reesei β-Glucosidase Using Site-Directed Mutagenesis. PLoS ONE 2016, 11, e0147301. [Google Scholar] [CrossRef] [PubMed]
- Cao, L.; Wang, Z.; Ren, G.; Kong, W.; Li, L.; Xie, W.; Liu, Y. Engineering a novel glucose-tolerant β-glucosidase as supplementation to enhance the hydrolysis of sugarcane bagasse at high glucose concentration. Biotechnol. Biofuels 2015, 8. [Google Scholar] [CrossRef] [PubMed]
- Uchima, C.A.; Tokuda, G.; Watanabe, H.; Kitamoto, K.; Arioka, M. Heterologous expression and characterization of a glucose-stimulated β-glucosidase from the termite Neotermes koshunensis in Aspergillus oryzae. Appl. Microbiol. Biotechnol. 2011, 89, 1761–1771. [Google Scholar] [CrossRef]
- Souza, F.H.M.; Nascimento, C.V.; Rosa, J.C.; Masui, D.C.; Leone, F.A.; Jorge, J.A.; Furriel, R.P.M. Purification and biochemical characterization of a mycelial glucose- and xylose-stimulated β-glucosidase from the thermophilic fungus Humicola insolens. Process Biochem. 2010, 45, 272–278. [Google Scholar] [CrossRef]
- Souza, F.H.M.; Inocentes, R.F.; Ward, R.J.; Jorge, J.A.; Furriel, R.P.M. Glucose and xylose stimulation of a β-glucosidase from the thermophilic fungus Humicola insolens: A kinetic and biophysical study. J. Mol. Catal. B Enzym. 2013, 94, 119–128. [Google Scholar] [CrossRef]
- Crespim, E.; Zanphorlin, L.M.; de Souza, F.H.M.; Diogo, J.A.; Gazolla, A.C.; Machado, C.B.; Figueiredo, F.; Sousa, A.S.; Nóbrega, F.; Pellizari, V.H.; et al. A novel cold-adapted and glucose-tolerant GH1 β-glucosidase from Exiguobacterium antarcticum B7. Int. J. Biol. Macromol. 2016, 82, 375–380. [Google Scholar] [CrossRef]
- Meleiro, L.P.; Salgado, J.C.S.; Maldonado, R.F.; Alponti, J.S.; Zimbardi, A.L.R.L.; Jorge, J.A.; Ward, R.J.; Furriel, R.P.M. A Neurospora crassa ß-glucosidase with potential for lignocellulose hydrolysis shows strong glucose tolerance and stimulation by glucose and xylose. J. Mol. Catal. B Enzym. 2015, 122, 131–140. [Google Scholar] [CrossRef]
- Salgado, J.C.S.; Meleiro, L.P.; Carli, S.; Ward, R.J. Glucose tolerant and glucose stimulated β-glucosidases-A review. Bioresour. Technol. 2018, 267, 704–713. [Google Scholar] [CrossRef] [PubMed]
- Jabbour, D.; Klippel, B.; Antranikian, G. A novel thermostable and glucose-tolerant β-glucosidase from Fervidobacterium islandicum. Appl. Microbiol. Biotechnol. 2012, 93, 1947–1956. [Google Scholar] [CrossRef] [PubMed]
- Pang, P.; Cao, L.; Liu, Y.; Xie, W.; Wang, Z. Structures of a glucose-tolerant β-glucosidase provide insights into its mechanism. J. Struct. Biol. 2017, 198, 154–162. [Google Scholar] [CrossRef] [PubMed]
- Mariano, D.C.B.; Santos, L.H.; Machado, K.D.S.; Werhli, A.V.; de Lima, L.H.F.; de Melo-Minardi, R.C. A Computational Method to Propose Mutations in Enzymes Based on Structural Signature Variation (SSV). Int. J. Mol. Sci. 2019, 20, 333. [Google Scholar] [CrossRef] [PubMed]
- Breves, R.; Bronnenmeier, K.; Wild, N.; Lottspeich, F.; Staudenbauer, W.L.; Hofemeister, J. Genes encoding two different beta-glucosidases of Thermoanaerobacter brockii are clustered in a common operon. Appl. Environ. Microbiol. 1997, 63, 3902–3910. [Google Scholar]
- Chen, W.; Enck, S.; Price, J.L.; Powers, D.L.; Powers, E.T.; Wong, C.-H.; Dyson, H.J.; Kelly, J.W. The Structural and Energetic Basis of Carbohydrate Aromatic Packing Interactions in Proteins. J. Am. Chem. Soc. 2013, 135, 9877–9884. [Google Scholar] [CrossRef] [PubMed]
- Duff, M.R.; Howell, E.E. Thermodynamics and solvent linkage of macromolecule-ligand interactions. Methods San Diego Calif 2015, 76, 51–60. [Google Scholar] [CrossRef]
- Geronimo, I.; Ntarima, P.; Piens, K.; Gudmundsson, M.; Hansson, H.; Sandgren, M.; Payne, C.M. Kinetic and molecular dynamics study of inhibition and transglycosylation in Hypocrea jecorina family 3 β-glucosidases. J. Biol. Chem. 2019, 294, 3169–3180. [Google Scholar] [CrossRef]
- Bergmann, J.C.; Costa, O.Y.A.; Gladden, J.M.; Singer, S.; Heins, R.; D’haeseleer, P.; Simmons, B.A.; Quirino, B.F. Discovery of two novel β-glucosidases from an Amazon soil metagenomic library. FEMS Microbiol. Lett. 2014, 351, 147–155. [Google Scholar] [CrossRef]
- Spiwok, V. CH/π Interactions in Carbohydrate Recognition. Molecules 2017, 22, 1038. [Google Scholar] [CrossRef] [PubMed]
- Matsuzawa, T.; Jo, T.; Uchiyama, T.; Manninen, J.A.; Arakawa, T.; Miyazaki, K.; Fushinobu, S.; Yaoi, K. Crystal structure and identification of a key amino acid for glucose tolerance, substrate specificity, and transglycosylation activity of metagenomic β-glucosidase Td2F2. FEBS J. 2016, 283, 2340–2353. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, K.; Sumitani, J.-I.; Nam, Y.-W.; Nishimaki, T.; Tani, S.; Wakagi, T.; Kawaguchi, T.; Fushinobu, S. Crystal structures of glycoside hydrolase family 3 β-glucosidase 1 from Aspergillus aculeatus. Biochem. J. 2013, 452, 211–221. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Anandakrishnan, R.; Aguilar, B.; Onufriev, A.V. H++ 3.0: Automating pK prediction and the preparation of biomolecular structures for atomistic molecular modeling and simulations. Nucleic Acids Res. 2012, 40, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Betz, R.M.; Cerutti, D.S. Proceedings of the AMBER 16; University of California: San Francisco, CA, USA, 2016. [Google Scholar]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [PubMed]
- Kirschner, K.N.; Yongye, A.B.; Tschampel, S.M.; González-Outeiriño, J.; Daniels, C.R.; Foley, B.L.; Woods, R.J. GLYCAM06: A generalizable biomolecular force field. Carbohydrates. J. Comput. Chem. 2008, 29, 622–655. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Ben-Shalom, I.Y.; Brozell, S.R. Proceedings of the AMBER 18; University of California: San Francisco, CA, USA, 2018. [Google Scholar]
- Nguyen, C.N.; Kurtzman Young, T.; Gilson, M.K. Grid inhomogeneous solvation theory: Hydration structure and thermodynamics of the miniature receptor cucurbit [7] uril. J. Chem. Phys. 2012, 137, 044101. [Google Scholar] [CrossRef]
- Seeber, M.; Cecchini, M.; Rao, F.; Settanni, G.; Caflisch, A. Wordom: A program for efficient analysis of molecular dynamics simulations. Bioinforma. Oxf. Engl. 2007, 23, 2625–2627. [Google Scholar] [CrossRef]
- Wallace, A.C.; Laskowski, R.A.; Thornton, J.M. LIGPLOT: A program to generate schematic diagrams of protein-ligand interactions. Protein Eng. 1995, 8, 127–134. [Google Scholar] [CrossRef]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef] [PubMed]
- Stock, G.; Jain, A.; Riccardi, L.; Nguyen, P.H. Exploring the Energy Landscape of Small Peptides and Proteins by Molecular Dynamics Simulations. In Protein and Peptide Folding, Misfolding, and Non-Folding; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; pp. 55–77. ISBN 978-1-118-18337-3. [Google Scholar]
- Dolinsky, T.J.; Nielsen, J.E.; McCammon, J.A.; Baker, N.A. PDB2PQR: An automated pipeline for the setup of Poisson–Boltzmann electrostatics calculations. Nucleic Acids Res. 2004, 32, 665–667. [Google Scholar] [CrossRef] [PubMed]
- Baker, N.A.; Sept, D.; Joseph, S.; Holst, M.J.; McCammon, J.A. Electrostatics of nanosystems: Application to microtubules and the ribosome. Proc. Nat. Acad. Sci. USA 2001, 98, 10037–10041. [Google Scholar] [CrossRef] [PubMed]
- Jurrus, E.; Engel, D.; Star, K.; Monson, K.; Brandi, J.; Felberg, L.E.; Brookes, D.H.; Wilson, L.; Chen, J.; Liles, K.; et al. Improvements to the APBS biomolecular solvation software suite. Protein Sci. 2018, 27, 112–128. [Google Scholar] [CrossRef] [PubMed]
- Unni, S.; Huang, Y.; Hanson, R.M.; Tobias, M.; Krishnan, S.; Li, W.W.; Nielsen, J.E.; Baker, N.A. Web servers and services for electrostatics calculations with APBS and PDB2PQR. J. Comput. Chem. 2011, 32, 1488–1491. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Nguyen, C.N.; Cruz, A.; Gilson, M.K.; Kurtzman, T. Thermodynamics of Water in an Enzyme Active Site: Grid-Based Hydration Analysis of Coagulation Factor Xa. J. Chem. Theory Comput. 2014, 10, 2769–2780. [Google Scholar] [CrossRef]
- Schauperl, M.; Podewitz, M.; Waldner, B.J.; Liedl, K.R. Enthalpic and Entropic Contributions to Hydrophobicity. J. Chem. Theory Comput. 2016, 12, 4600–4610. [Google Scholar] [CrossRef]
- Schauperl, M.; Podewitz, M.; Ortner, T.S.; Waibl, F.; Thoeny, A.; Loerting, T.; Liedl, K.R. Balance between hydration enthalpy and entropy is important for ice binding surfaces in Antifreeze Proteins. Sci. Rep. 2017, 7, 11901. [Google Scholar] [CrossRef]
- Schauperl, M.; Czodrowski, P.; Fuchs, J.E.; Huber, R.G.; Waldner, B.J.; Podewitz, M.; Kramer, C.; Liedl, K.R. Binding Pose Flip Explained via Enthalpic and Entropic Contributions. J. Chem. Inf. Model. 2017, 57, 345–354. [Google Scholar] [CrossRef]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics; Academic Press: Cambridge, MA, USA, 2011; ISBN 978-0-12-382189-8. [Google Scholar]
- Ramsey, S.; Nguyen, C.; Salomon-Ferrer, R.; Walker, R.C.; Gilson, M.K.; Kurtzman, T. Solvation thermodynamic mapping of molecular surfaces in AmberTools: GIST. J. Comput. Chem. 2016, 37, 2029–2037. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not available. |


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, L.S.C.; Mariano, D.C.B.; Rocha, R.E.O.; Kraml, J.; Silveira, C.H.d.; Liedl, K.R.; de Melo-Minardi, R.C.; Lima, L.H.F.d. Molecular Dynamics Gives New Insights into the Glucose Tolerance and Inhibition Mechanisms on β-Glucosidases. Molecules 2019, 24, 3215. https://doi.org/10.3390/molecules24183215
Costa LSC, Mariano DCB, Rocha REO, Kraml J, Silveira CHd, Liedl KR, de Melo-Minardi RC, Lima LHFd. Molecular Dynamics Gives New Insights into the Glucose Tolerance and Inhibition Mechanisms on β-Glucosidases. Molecules. 2019; 24(18):3215. https://doi.org/10.3390/molecules24183215
Chicago/Turabian StyleCosta, Leon Sulfierry Corrêa, Diego César Batista Mariano, Rafael Eduardo Oliveira Rocha, Johannes Kraml, Carlos Henrique da Silveira, Klaus Roman Liedl, Raquel Cardoso de Melo-Minardi, and Leonardo Henrique Franca de Lima. 2019. "Molecular Dynamics Gives New Insights into the Glucose Tolerance and Inhibition Mechanisms on β-Glucosidases" Molecules 24, no. 18: 3215. https://doi.org/10.3390/molecules24183215
APA StyleCosta, L. S. C., Mariano, D. C. B., Rocha, R. E. O., Kraml, J., Silveira, C. H. d., Liedl, K. R., de Melo-Minardi, R. C., & Lima, L. H. F. d. (2019). Molecular Dynamics Gives New Insights into the Glucose Tolerance and Inhibition Mechanisms on β-Glucosidases. Molecules, 24(18), 3215. https://doi.org/10.3390/molecules24183215