Zn2+ Interaction with Amyloid-B: Affinity and Speciation
Abstract
:1. Introduction
2. Zn2+ Interaction with Amyloid-β
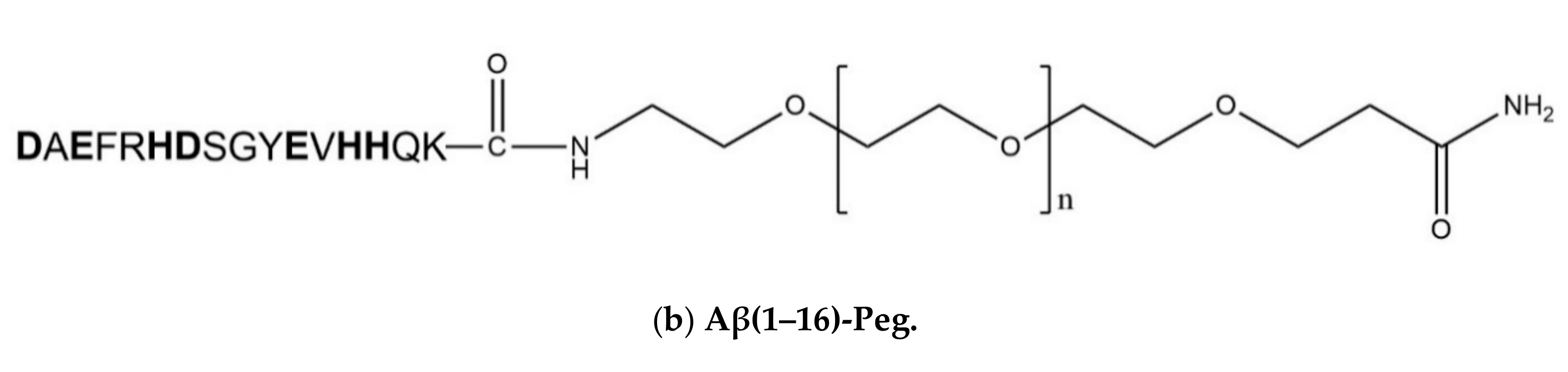
2.1. Aβ(1–16)-Peg
2.2. Zn2+ in Alzheimer’s Disease
3. Zn2+ Affinity for Aβ
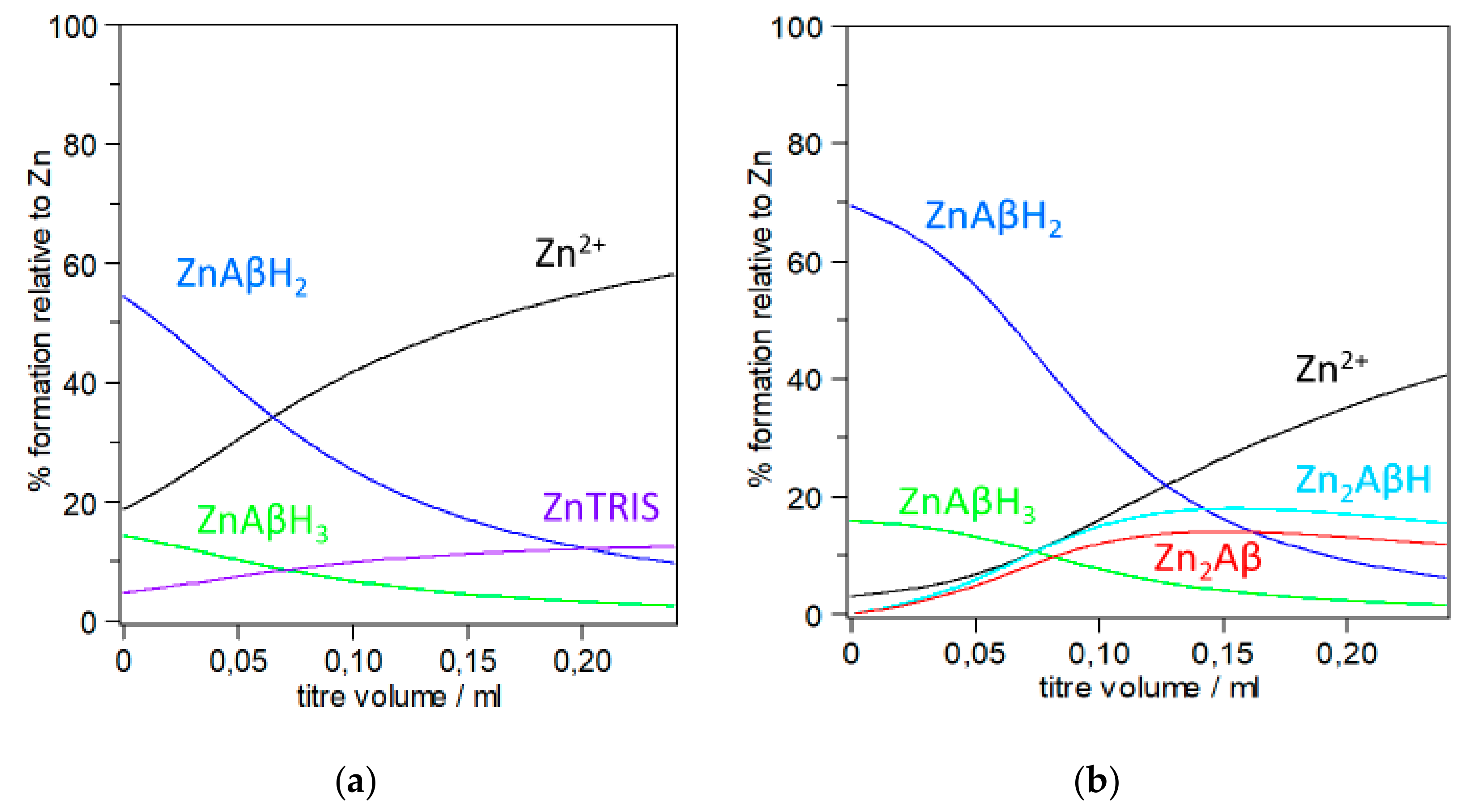
3.1. Stability Constant and Speciation
3.2. Main Techniques Employed to Determine the Binding Constant
3.2.1. Potentiometry
3.2.2. Calorimetry
3.2.3. Spectroscopy
3.2.4. NMR
3.2.5. Other Techniques
3.3. Use of Speciation Data
4. Concluding Remarks
Funding
Conflicts of Interest
References
- World Alzheimer Report 2018. Available online: https://www.alz.co.uk/research/WorldAlzheimerReport2018.pdf (accessed on 13 May 2019).
- Dementia statistics. Available online: https://www.alz.co.uk/research/statistics (accessed on 13 May 2019).
- Frequently Asked Questions. Available online: https://www.alz.co.uk/info/faq (accessed on 13 May 2019).
- Masters, C.L.; Simms, G.; Weinman, N.A.; Multhaup, G.; McDonald, R.L.; Beyreuther, K. Amyloid plaque core protein in Alzheimer disease and Down syndrome. Proc. Natl. Acad. Sci. USA 1985, 82, 4245–4249. [Google Scholar] [CrossRef] [PubMed]
- Glenner, G.G.; Wong, C.W. Alzheimer’s disease: Initial report of the purification and characterization of a novel cerebrovascular amyloid protein. Biochem. Biophys. Res. Commun. 1984, 120, 885–890. [Google Scholar] [CrossRef]
- Mucke, L. Neuroscience: Alzheimer’s disease. Nature 2009, 461, 895–897. [Google Scholar] [CrossRef] [PubMed]
- Kuo, Y.M.; Emmerling, M.R.; Vigo-Pelfrey, C.; Kasunic, T.C.; Kirkpatric, J.B.; Murdoch, G.H.; Ball, M.J.; Rother, A.E. Water-soluble Aβ (N-40, N-42) Oligomers in Normal and Alzheimer Disease Brains. J. Biol. Chem. 1996, 271, 4077–4081. [Google Scholar] [CrossRef] [PubMed]
- Checler, F. Processing of the beta-amyloid precursor protein and its regulation in Alzheimer’s disease. J. Neurochem. 1995, 65, 1431–1444. [Google Scholar] [CrossRef] [PubMed]
- Selkoe, D.J. Alzheimer’s disease: Genes, proteins, and therapy. J. Physiol. Rev. 2001, 81, 741–766. [Google Scholar] [CrossRef]
- Rana, M.; Sharma, A.K.M. Cu and Zn interactions with Aβ peptides: Consequence of coordination on aggregation and formation of neurotoxic soluble Aβ oligomers. Metallomics 2019, 11, 64–84. [Google Scholar] [CrossRef] [PubMed]
- Jarrett, J.T.; Berger, E.P.; Lansbury, P.T. The C-Terminus of the β Protein is Critical in Amyloidogenesis. Ann. N. Y. Acad. Sci. 1993, 695, 144–148. [Google Scholar] [CrossRef]
- Hartmann, T.; Bieger, S.C.; Brühl, B.; Tienari, P.J.; Ida, N.; Allsop, D.G.; Roberts, W.C.; Masters, L.; Dotti, C.G.; Unsicker, K.; et al. Distinct sites of intracellular production for Alzheimer’s disease Aβ 40/42 amyloid peptides. Nat. Med. 1997, 3, 1016–1020. [Google Scholar] [CrossRef]
- Bibl, M.; Esselmann, H.; Mollenhauer, B.; Weniger, G.; Welge, V.; Liess, M.; Lewczuk, P.; Otto, M.; Schulz, J.B.; Trenkwalder, C.; et al. Wiltfang, J. Blood-based neurochemical diagnosis of vascular dementia: A pilot study. J. Neurochem. 2007, 103, 467–474. [Google Scholar] [CrossRef]
- Schoonenboom, N.S.; Mulder, C.; Van Kamp, G.J.; Mehta, S.P.; Scheltens, P.; Blankenstein, M.A.; Mehta, P.D. Amyloid beta 38, 40, and 42 species in cerebrospinal fluid: More of the same? Ann. Neurol. 2005, 58, 139–142. [Google Scholar] [CrossRef] [PubMed]
- Burdick, D.; Soreghan, B.; Kwon, M.; Kosmoski, J.; Knauer, M.; Henschen, A.; Yates, J.; Cotman, C.; Glabe, C. Assembly and aggregation properties of synthetic Alzheimer’s A4/beta amyloid peptide analogs. J. Biol. Chem. 1992, 267, 546–554. [Google Scholar] [PubMed]
- Jarrett, J.T.; Berger, E.P.; Lansbury, P.T., Jr. The carboxy terminus of the beta. amyloid protein is critical for the seeding of amyloid formation: Implications for the pathogenesis of Alzheimer’s disease. Biochemistry 1993, 32, 4693–4697. [Google Scholar] [CrossRef] [PubMed]
- Ricchelli, F.; Drago, D.; Filippi, B.; Tognona, G.; Zatta, P. Aluminum-triggered structural modifications and aggregation of β-amyloids. Cell. Mol. Life Sci. 2005, 62, 1724–1733. [Google Scholar] [CrossRef] [PubMed]
- Lovell, M.A.; Robertson, J.D.; Teesdale, W.J.; Campbell, J.L.; Markesbery, W.R. Copper, iron and zinc in Alzheimer’s disease senile plaques. J. Neurol. Sci. 1998, 158, 47–52. [Google Scholar] [CrossRef]
- Maynard, C.J.; Bush, A.I.; Masters, C.L.; Cappai, R.; Li, Q.X. Metals and amyloid-beta in Alzheimer’s disease. Int. J. Exp. Path. 2005, 86, 147–1159. [Google Scholar] [CrossRef] [PubMed]
- Gaggelli, E.; Janicka-Klos, A.; Jankowska, E.; Kozlowski, H.; Migliorini, C.; Molteni, E.; Valensin, D.; Valensin, G.; Wieczerzak, E. NMR Studies of the Zn2+ Interactions with Rat and Human β-Amyloid (1–28) Peptides in Water-Micelle Environment. J. Phys. Chem. B. 2008, 112, 100–109. [Google Scholar] [CrossRef]
- Religa, D.; Strozik, D.; Cherny, R.A.; Volitakis, I.; Haroutunian, V.; Winblad, B.; Naslund, J.; Bush, A.I. Elevated cortical zinc in Alzheimer disease. Neurology 2006, 67, 69–75. [Google Scholar] [CrossRef]
- Bush, A.I.; Pettingell, W.H.; Multhaup, G.; Paradis, M.D.; Vonsattel, J.P.; Gusella, J.F.; Beyreuther, K.; Masters, C.L.; Tanzi, R.E. Rapid induction of Alzheimer A beta amyloid formation by zinc. Science 1994, 265, 1464–1467. [Google Scholar] [CrossRef]
- Huang, X.; Atwood, C.S.; Moir, R.D.; Hartshorn, M.A.; Vonsatell, J.P.; Tanzi, R.E.; Bush, A.I. Zinc-induced Alzheimer’s Aβ1–40 Aggregation Is Mediated by Conformational Factors. J. Biol. Chem. 1997, 272, 26464–26470. [Google Scholar] [CrossRef]
- Morgan, D.M.; Dong, J.; Jacob, J.; Lu, K.; Apkarian, R.P.; Thiyagarajan, P.; Lynn, D.G. Metal switch for amyloid formation: Insight into the structure of the nucleus. J. Am. Chem. Soc. 2002, 124, 12644–12645. [Google Scholar] [CrossRef] [PubMed]
- Syme, C.D.; Nadal, R.C.; Rigby, S.E.J.; Viles, J.H. Copper Binding to the Amyloid-(A) Peptide Associated with Alzheimer’s Disease. J. Biol. Chem. 2004, 279, 18169–18177. [Google Scholar] [CrossRef] [PubMed]
- Faller, P.; Hureau, C. Bioinorganic chemistry of copper and zinc ions coordinated to amyloid-b peptide. Dalton Trans. 2009, 1080–1094. [Google Scholar] [CrossRef] [PubMed]
- Haass, C.; Selkoe, D.J. Soluble protein oligomers in neurodegeneration: Lessons from the Alzheimer’s amyloid beta-peptide. Nat. Rev. Mol. Cell Biol. 2007, 8, 101–112. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Kim, J.I.; Na, S.; Eom, K. Metal ions affect the formation and stability of amyloid β aggregates at multiple length scales. Phys.Chem.Chem.Phys. 2018, 20, 8951–8961. [Google Scholar] [CrossRef] [PubMed]
- Yoshiike, Y.; Tanemura, K.; Murayama, O.; Akagi, T.; Murayama, M.; Sato, S.; Sun, X.; Tanaka, N.; Takashima, A. New Insights on How Metals Disrupt Amyloid β-Aggregation and Their Effects on Amyloid-β Cytotoxicity. J. Biol. Chem. 2001, 276, 32293–32299. [Google Scholar] [CrossRef] [PubMed]
- Abelein, A.; Graslund, A.; Danielsson, J. Zinc as chaperone-mimicking agent for retardation ofamyloidβpeptide fibril formation. Proc. Natl. Acad. Sci. USA 2015, 112, 5407–5412. [Google Scholar] [CrossRef] [PubMed]
- Lim, K.H.; Kim, Y.K.; Chang, Y.-T. Investigations of the Molecular Mechanism of Metal-Induced Aβ (1−40) Amyloidogenesis. Biochemistry 2007, 46, 13523–13532. [Google Scholar] [CrossRef]
- Mannini, B.; Habchi, J.; Chia, S.K.R.; Ruggeri, F.S.; Perni, M.; Knowles, T.P.J.; Dobson, C.M.; Vendruscolo, M. Stabilization and characterization of cytotoxic Aβ40 oligomers isolated from an aggregation reaction in the presence of zinc ions. ACS Chem Neurosci. 2018, 9, 2959–2971. [Google Scholar] [CrossRef]
- Arena, G.; Pappalardo, G.; Sovago, I.; Rizzarelli, E. Copper(II) interaction with amyloid-β: Affinity and speciation. Coord. Chem. Rev. 2012, 256, 3–12. [Google Scholar] [CrossRef]
- Damante, C.A.; Osz, K.; Nagy, Z.; Pappalardo, G.; Grasso, G.; Impellizzeri, G.; Rizzarelli, E.; Sóvágó, I. Metal Loading Capacity of Aβ N-Terminus: A Combined Potentiometric and Spectroscopic Study of Zinc(II) Complexes with Aβ(1–16), Its Short or Mutated Peptide Fragments and Its Polyethylene Glycol-ylated Analogue. Inorg. Chem. 2009, 48, 10405–10415. [Google Scholar] [CrossRef]
- Kozin, S.A.; Zirah, S.; Rebuffat, S.; Hoa, G.H.B.; Debey, P. Zinc Binding to Alzheimer’s Aβ(1–16) Peptide Results in Stable Soluble Complex. Biochem. Biophys. Res. Commun. 2001, 285, 959–964. [Google Scholar] [CrossRef] [PubMed]
- Mekmouche, Y.; Coppel, Y.; Hochgrafe, K.; Guiloreau, L.; Talmard, C.; Mazarguil, H.; Faller, P. Characterization of the ZnII Binding to the Peptide Amyloid-β1–16 linked to Alzheimer’s Disease. ChemBioChem 2005, 6, 1663–1671. [Google Scholar] [CrossRef] [PubMed]
- Damante, C.A.; Osz, K.; Nagy, Z.; Pappalardo, G.; Grasso, G.; Impellizzeri, G.; Rizzarelli, E.; Sóvágó, I. The Metal Loading Ability of β-Amyloid N-Terminus: A Combined Potentiometric and Spectroscopic Study of Copper(II) Complexes with β-Amyloid(1–16), Its Short or Mutated Peptide Fragments, and Its Polyethylene Glycol (PEG)-ylated Analogue. Inorg. Chem. 2008, 47, 9669–9683. [Google Scholar] [CrossRef] [PubMed]
- Vallee, B.L.; Falchuk, K.H. Zinc and gene expression. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 1981, 294, 185–197. [Google Scholar] [CrossRef] [PubMed]
- Coleman, J.E. Zinc proteins: Enzymes, storage proteins, transcription factors, and replication proteins. Annu Rev. Biochem. 1992, 61, 897–946. [Google Scholar] [CrossRef] [PubMed]
- Foster, M.; Samman, S. Zinc and redox signaling: Perturbations associated with cardiovascular disease and diabetes mellitus. Antioxid. Redox Signal. 2010, 13, 1549–1573. [Google Scholar] [CrossRef]
- Takeda, A. Zinc homeostasis and functions of zinc in the brain. BioMetals 2001, 14, 343–351. [Google Scholar] [CrossRef]
- Cuajungco, M.P.; Lees, G.J. Zinc and Alzheimer’s disease: Is there a direct link? Brain. Res. Rev. 1997, 23, 219–236. [Google Scholar] [CrossRef]
- Frederickson, C.J.; Bush, A.I. Synaptically released zinc: Physiological functions and pathological effects. BioMetals 2001, 14, 353–366. [Google Scholar] [CrossRef]
- Cherny, R.A.; Legg, J.T.; McLean, C.A.; Fairlie, D.P.; Huang, X.; Atwood, C.S.; Beyreuther, K.; Tanzi, R.E.; Masters, C.L.; Bush, A.I. Aqueous dissolution of Alzheimer’s disease Abeta amyloid deposits by biometal depletion. J. Biol Chem. 1999, 274, 23223–23228. [Google Scholar] [CrossRef] [PubMed]
- Lovell, M.A.; Xie, C.; Markeshery, W.R. Protection against amyloid beta peptide toxicity by zinc. Brain Res. 1999, 823, 88–95. [Google Scholar] [CrossRef]
- Bishop, G.M.; Robinson, S.R. The amyloid paradox: Amyloid-beta-metal complexes can be neurotoxic and neuroprotective. Brain Pathol. 2004, 14, 448–452. [Google Scholar] [CrossRef] [PubMed]
- Moreira, P.; Pereira, C.; Santos, M.S.; Oliveira, C. Effect of zinc ions on the cytotoxicity induced by the amyloid beta-peptide. Antioxid. Redox Signaling 2000, 2, 317–325. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.J.; Lin, H.; Lal, R. Fresh and nonfibrillar amyloid beta protein(1–40) induces rapid cellular degeneration in aged human fibroblasts: Evidence for AbetaP-channel-mediated cellular toxicity. FASEB J. 2000, 14, 1244–1254. [Google Scholar] [CrossRef] [PubMed]
- Cuajungco, M.P.; Goldstein, L.E.; Nunomura, A.; Smith, M.A.; Lim, J.T.; Atwood, C.S.; Huang, X.; Farrag, Y.W.; Perry, G.; Bush, A.I. Evidence that the β-Amyloid Plaques of Alzheimer’s Disease Represent the Redox-silencing and Entombment of Aβ by Zinc. J. Biol. Chem. 2000, 275, 19439–19442. [Google Scholar] [CrossRef]
- Garai, K.; Sahoo, B.; Kaushalya, S.K.; Desai, R.; Maiti, S. Zinc Lowers Amyloid-β Toxicity by Selectively Precipitating Aggregation Intermediates. Biochemistry 2007, 46, 10655–10663. [Google Scholar] [CrossRef]
- Gaggelli, E.; Kozlowski, H.; Valensin, D.; Valensin, G. Copper homeostasis and neurodegenerative disorders (Alzheimer’s, prion, and Parkinson’s diseases and amyotrophic lateral sclerosis). Chem. Rev. 2006, 106, 1995–2044. [Google Scholar] [CrossRef]
- Kowalik-Jankowska, T.; Ruta, M.; Wisniewska, K.; Lankiewicz, L. Coordination abilities of the 1-16 and 1-28 fragments of beta-amyloid peptide towards copper(II) ions: A combined potentiometric and spectroscopic study. J. Inorg. Biochem. 2003, 95, 270–282. [Google Scholar] [CrossRef]
- Arena, G.; Bindoni, M.; Cardile, V.; Maccarrone, G.; Riello, M.C.; Rizzarelli, E.; Sciuto, S.J. Cytotoxic and cytostatic activity of copper(II) complexes. Importance of the speciation for the correct interpretation of the in vitro biological results. Inorg. Biochem. 1993, 50, 31–45. [Google Scholar] [CrossRef]
- Kozlowski, H.; Łuczkowski, M.; Remelli, M. Prion proteins and copper ions. Biological and chemical controversies. Dalton Trans. 2010, 39, 6371–6385. [Google Scholar] [CrossRef] [PubMed]
- Copper complex species within a fragment of the N-terminal repeat region in opossum PrP protein. Dalton Trans. 2010, 40, 2441–2450.
- Travaglia, A.; Arena, G.; Fattorusso, R.; Isernia, C.; La Mendola, D.; Malgieri, G.; Nicoletti, V.G.; Rizzarelli, E. The inorganic perspective of nerve growth factor: Interactions of Cu2+ and Zn2+ with the N-terminus fragment of nerve growth factor encompassing the recognition domain of the TrkA receptor. Chem. Eur. J. 2011, 17, 3726–3738. [Google Scholar] [CrossRef] [PubMed]
- Talmard, C.; Bouzan, A.; Faller, P. Zinc Binding to Amyloid-â: Isothermal Titration Calorimetry and Zn Competition Experiments with Zn Sensors. Biochemistry 2007, 46, 13658–13666. [Google Scholar] [CrossRef] [PubMed]
- Ayton, S.; Belaidi, A.A.; Lei, P.; Bush, A.I. Targeting Transition Metals for Neuroprotection in Alzheimer’s Disease. In Neuroprotection in Alzheimer’s Disease; Gozes, I., Ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2017; Chapter 10; pp. 193–215. [Google Scholar] [CrossRef]
- Magyar, J.S.; Godwin, H.A. Spectropotentiometric analysis of metal binding to structural zinc-binding sites: Accounting quantitatively for pH and metal ion buffering effects. Anal. Biochem. 2003, 320, 39–54. [Google Scholar] [CrossRef]
- Outten, C.E.; O’Halloran, T.V. Femtomolar sensitivity of metalloregulatory proteins controlling zinc homeostasis. Science 2001, 292, 2488–2492. [Google Scholar] [CrossRef] [PubMed]
- Arena, G.; Sgarlata, C. Modern Calorimetry: An Invaluable Tool in Supramolecular Chemistry. In Comprehensive Supramolecular Chemistry II; Atwood, J.L., Gokel, G.W., Barbour, L.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; Volume 2. [Google Scholar] [CrossRef]
- Bush, A.I.; Pettingell, W.H.D.; Paradis, M.; Tanzi, R.E. Modulation of A beta adhesiveness and secretase site cleavage by zinc. J. Biol. Chem. 1994, 269, 12152–12158. [Google Scholar] [PubMed]
- Clements, A.; Allsop, D.; Walsh, D.M.; Williams, C.H. Aggregation and metal-binding properties of mutant forms of the amyloid A beta peptide of Alzheimer’s disease. J. Neurochem. 1996, 66, 740–747. [Google Scholar] [CrossRef]
- Garzon-Rodriguez, W.; Yatsimirsky, A.K.; Glabe, C.G. Binding of Zn(II), Cu(II), and Fe(II) ions to Alzheimer’s A beta peptide studied by fluorescence. Bioorg. Med. Chem. Lett. 1999, 9, 2243–2248. [Google Scholar] [CrossRef]
- Danielsson, J.; Pierattelli, R.; Banci, L.; Graslund, A. High-resolution NMR studies of the zinc-binding site of the Alzheimer’s amyloid b-peptide. FEBS J. 2007, 274, 46–59. [Google Scholar] [CrossRef]
- Tõugu, V.; Karafin, A.; Palumaa, P. Binding of zinc(II) and copper(II) to the full-length Alzheimer’s amyloid-b peptide. J. Neurochem. 2008, 104, 1249–1259. [Google Scholar] [CrossRef] [PubMed]
- Noel, S.; Bustos Rodriguez, S.; Sayen, S.; Guillon, E.; Faller, P.; Hureau, C. Use of a new water-soluble Zn sensor to determine Zn affinity for the amyloid-β peptide and relevant mutants. Metallomics 2014, 6, 1220–1222. [Google Scholar] [CrossRef] [PubMed]
- Nancollas, G.H.; Tomson, M.B. Guidelines for the determination of stability constants. Pure Appl. Chem. 1982, 54, 2675–2692. [Google Scholar] [CrossRef]
- Sokolowska, M.; Bal, W. Cu(II) complexation by ‘non-coordinating’ N-2-hydroxyethylpiperazine-N’-2-ethanesulfonic acid (HEPES buffer). J. Inorg. Biochem. 2005, 99, 1653–1660. [Google Scholar] [CrossRef] [PubMed]
- Zawisza, I.; Rozga, M.; Bal, W. Affinity of copper and zinc ions to proteins and peptides related to neurodegenerative conditions (Aβ, APP, α-synuclein, PrP). Coord. Chem. Rev. 2012, 256, 2297–2307. [Google Scholar] [CrossRef]
- Atwood, C.S.; Scarpa, R.C.; Huang, X.; Moir, R.D.; Jones, W.D.; Fairlie, D.P.; Tanzi, R.E.; Bush, A.I. Characterization of copper interactions with alzheimer amyloid beta peptides: Identification of an attomolar-affinity copper binding site on amyloid beta1-42. J. Neurochem. 2000, 75, 1219–1233. [Google Scholar] [CrossRef] [PubMed]
- Margerum, D.W.; Dukes, G.R. Kinetics and mechanisms of metal-ion and proton-transfer reactions. In Metal. Ions in Biological Systems; Sigel, H., Ed.; Dekker: New York, NY, USA, 1974; Volume 1, pp. 158–207. [Google Scholar]
- Arena, G.; La Mendola, D.; Pappalardo, G.; Sovago, I.; Rizzarelli, E. Interactions of Cu2+ with prion family peptide fragments: Considerations on affinity, speciation and coordination. Coord. Chem. Rev. 2012, 256, 2202–2218. [Google Scholar] [CrossRef]
- Santoro, A.; Wezynfeld, N.E.; Stefaniak, E.; Pomorski, A.; Płonka, D.; Krezel, A.; Bal, W.; Faller, P. Cu transfer from amyloid-β4–16 to metallothionein-3: the role of the neurotransmitter glutamate and metallothionein-3 Zn(II)-load states. Chem. Commun. 2018, 54, 12634–12637. [Google Scholar] [CrossRef]
- Gans, P.; Sabatini, A.; Vacca, A. Investigation of equilibria in solution. Determination of equilibrium constants with the HYPERQUAD suite of programs. Talanta 1996, 43, 1739–1753. [Google Scholar] [CrossRef]
- Schwarzenbach, G. Die Komplexometrische Titration, 2nd ed.Oberostendorf, Germany, 1956. [Google Scholar]
- Irving, H. Complexometric Titration; Methuen & Co.: London, UK, 1957. [Google Scholar]
- Flaschka, H.A. EDTA Titrations; Pergamon Press: London, UK, 1959. [Google Scholar]
- Harris, D. Quantitative Chemical Analysis, 6th ed.; W.H. Freeman & Co.: New York, NY, USA, 2003. [Google Scholar]
- Alberty, A.R. Recommendations for nomenclature and tables in biochemical thermodynamics (IUPAC Recommendations 1994). Pure Appl. Chem. 1994, 66, 1641–1666. [Google Scholar] [CrossRef]
- Pettit, L.D.; Hefford, R.J. Stereoselectivity in the metal complexes of aminoacids and dipeptides. In Metal Ions in Biological Systems; Sigel, H., Ed.; Marcel Dekker: New York, NY, USA, 1979; Volume 9, pp. 174–209. [Google Scholar]
- Zékány, L.; Nagypál, I. Computational Methods for the Determination of Formation Constants; Leggett, D.J., Ed.; Plenum Press: New York, NY, USA, 1985; pp. 291–355. [Google Scholar]
- Faller, P.; Hureau, C.; Dorlet, P.; Hellwige, P.; Coppel, Y.; Collin, F.; Alies, B. Methods and techniques to study the bioinorganic chemistry of metal–peptide complexes linked to neurodegenerative diseases. Coord. Chem. Rev. 2012, 256, 2381–2396. [Google Scholar]
- Johnson, R.A.; Manley, O.; Spuches, A.M.; Grossoehme, N.E. Dissecting ITC data of metal ions binding to ligands and proteins. Biochim. et Biophysica. Acta. 2016, 1860, 892–901. [Google Scholar] [CrossRef] [PubMed]
- Velazquez Campoy, A.; Freire, E. ITC in the post-genomic era…? Priceless. Biophys. Chem. 2005, 115, 115–124. [Google Scholar] [CrossRef] [PubMed]
- Hansen, L.D.; Fellingham, G.W.; Russell, D.J. Simultaneous determination of equilibrium constants and enthalpy changes by titration calorimetry: Methods, instruments, and uncertainties. Anal. Biochem. 2011, 409, 220–229. [Google Scholar] [CrossRef]
- Demarse, N.A.; Quinn, C.F.; Eggett, D.L.; Russell, D.J.; Hansen, L.D. Calibration of nanowatt isothermal titration calorimeters with overflow reaction vessels. Anal. Biochem. 2011, 417, 247–255. [Google Scholar] [CrossRef]
- Wiseman, T.; Williston, S.; Brandts, J.F.; Lint, L.N. Rapid measurement of binding constants and heats of binding using a new titration calorimeter. Anal. Biochem. 1989, 179, 131–137. [Google Scholar] [CrossRef]
- Turnbull, W.B.; Daranas, A.H. On the value of c: Can low affinity systems be studied by isothermal titration calorimetry? J. Am. Chem. Soc. 2003, 125, 14859–14866. [Google Scholar] [CrossRef] [PubMed]
- Tellinghuisen, J. Isothermal titration calorimetry at very low c. Anal. Biochem. 2008, 373, 395–397. [Google Scholar] [CrossRef] [PubMed]
- Arena, G.; Gans, P.; Sgarlata, C. HypCal, a general-purpose computer program for the determination of standard reaction enthalpy and binding constant values by means of calorimetry. Anal. Bioanal. Chem. 2016, 408, 6413–6422. [Google Scholar] [CrossRef] [PubMed]
- Bolles, T.F.; Drago, R.S. A Calorimetric Procedure for Determining Free Energies, Enthalpies, and Entropies for the Formation of Acid-Base Adducts. J. Am. Chem. Soc. 1965, 87, 5015–5019. [Google Scholar] [CrossRef]
- Sgarlata, C.; Arena, G.; Longo, E.; Zhang, D.; Yang, Y.; Bartsch, R.A. Heavy metal separation with polymer inclusion membranes. J. Membr. Sci. 2008, 323, 444–451. [Google Scholar] [CrossRef]
- Specfit, Spectrum Software Associates, Chapel Hill, NC. Available online: http://www.kingkongsci.co.uk/specfitglobalanalysis.htm (accessed on 13 May 2019).
- Smirnova, J.; Zhukova, L.; Witkiewicz-Kucharczyk, A.; Kopera, E.; Olędzki, J.; Wysłouch-Cieszyńska, A.; Palumaa, P.; Hartwig, A.; Bal, W. Quantitative electrospray ionization mass spectrometry of zinc finger oxidation: The reaction of XPA zinc finger with H2O2. Anal. Biochem. 2007, 369, 226–231. [Google Scholar] [CrossRef] [PubMed]
- Martell, A.E.; Smith, R.M. Critical Stability Constants; Volume 6 (Second Supplement); Plenum Press: New York, NY, USA, 1989. [Google Scholar]
- Protonic Software. Available online: http://www.hyperquad.co.uk/hyss.htm (accessed on 13 May 2019).
- Maret, W. Analyzing free zinc(II) ion concentrations in cell biology with fluorescent chelating molecules. Metallomics 2015, 7, 202–211. [Google Scholar] [CrossRef] [PubMed]
- Brecher, K. A guide for the perplexed. Nature 1979, 278, 215–218. [Google Scholar] [CrossRef]



| Aβ Fragment a | Kd (μM) | pH | T (°C) | Conc. (μM) | Method | Buffer | Background Salt | Ref. |
|---|---|---|---|---|---|---|---|---|
| 1–40 | 5/0.1 | 7.4 | 20 | - | Radioact. Sat.bind. | TRIS (20mM) | 0.1 M NaCl + 1mM MnCl2 | 62 |
| 1–40 | 3.5 | 7.4 | 20 | - | Radioact. Sat.bind. | TRIS (50mM) | 1 M KCl | 63 |
| 1–40 | 300 | 7.4 | n.s.b | 3 | Tyr. fl. | TRIS/HEPES (10 mM) | 0.1 M NaCl | 64 |
| 1–42 | 57 | 7.4 | n.s.b | 3 | Tyr. fl. | TRIS (10 mM) | 0.1 M NaCl | 64 |
| 1–28 | 1.1 | 7.2 | 20 | 10 | Tyr. fl. Zn/Cu Compet. | Phosphate (10 mM) | none | 65 |
| 1–40 | 1.2 | 7.2 | 20 | 50 | NMR | Phosphate (10 mM) | none | 65 |
| 1–28 | 6.6 | 7.2 | 20 | 10 | Tyr. fl. Zn/Cu Compet. | HEPES (10 mM) | none | 65 |
| 1–16 | 22/71 c,d | 7.4 | 25 | 20/140 c | ITC | HEPES/TRIS (20 mM) e | 0.1 M NaCl | 57 |
| 1–28 | 10/30 c,d | 7.4 | 25 | 20/140 c | ITC | HEPES/TRIS (20 mM) e | 0.1 M NaCl | 57 |
| 1–40 | 7/3 c | 7.4 | 25 | 10/70 c | ITC | HEPES/TRIS e (20 mM) e | 0.1 M NaCl | 57 |
| 1–16 | 14 | 7.4 | n.s.b | 10 | Fl. Zincon Compet. | HEPES (20 mM) | 0.1 M NaCl | 57 |
| 1–28 | 12 | 7.4 | n.s.b | 10 | Fl. Zincon Compet. | HEPES (20 mM) | 0.1 M NaCl | 57 |
| 1–40/1–42 | 7/7 | 7.4 | n.s. b | 10 | Fl. Zincon Compet. | HEPES (20 mM) | 0.1 M NaCl | 57 |
| 1–40 | 65 | 7.4 | n.s. b | 4 | Tyr. fl. | HEPES (20 mM) | 0.1 M NaCl | 66 |
| 1–42 | 91 | 7.4 | n.s. b | 4 | Tyr. fl. | HEPES (20 mM) | 0.1 M NaCl | 66 |
| 1–40 | 60 | 7.4 | n.s. b | 4 | Tyr. fl. | TRIS (10 mM) | 0.1 M NaCl | 66 |
| 1–40 | 184 | 7.4 | n.s. b | 4 | Tyr. fl. | TRIS (100 mM) | 0.1 M NaCl | 66 |
| 1–40 | 11/2 f | 7.3 | n.s. b | 12 | Fl. Zincon Compet. | HEPES (50 mM) | 0.1 M NaCl | 66 |
| 1–16-PEG | - g | - | 25 | 1–4 (×103) | Potentiometry | No Buffer | 0.2 M KCl | 34 |
| 1–16 | 9 | 7.1 | 25 | - h | UV-Vis Compet.h | HEPES (50 mM) | none | 67 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arena, G.; Rizzarelli, E. Zn2+ Interaction with Amyloid-B: Affinity and Speciation. Molecules 2019, 24, 2796. https://doi.org/10.3390/molecules24152796
Arena G, Rizzarelli E. Zn2+ Interaction with Amyloid-B: Affinity and Speciation. Molecules. 2019; 24(15):2796. https://doi.org/10.3390/molecules24152796
Chicago/Turabian StyleArena, Giuseppe, and Enrico Rizzarelli. 2019. "Zn2+ Interaction with Amyloid-B: Affinity and Speciation" Molecules 24, no. 15: 2796. https://doi.org/10.3390/molecules24152796
APA StyleArena, G., & Rizzarelli, E. (2019). Zn2+ Interaction with Amyloid-B: Affinity and Speciation. Molecules, 24(15), 2796. https://doi.org/10.3390/molecules24152796






