Spectra–Structure Correlations in Isotopomers of Ethanol (CX3CX2OX; X = H, D): Combined Near-Infrared and Anharmonic Computational Study
Abstract
1. Introduction
2. Results and Discussion
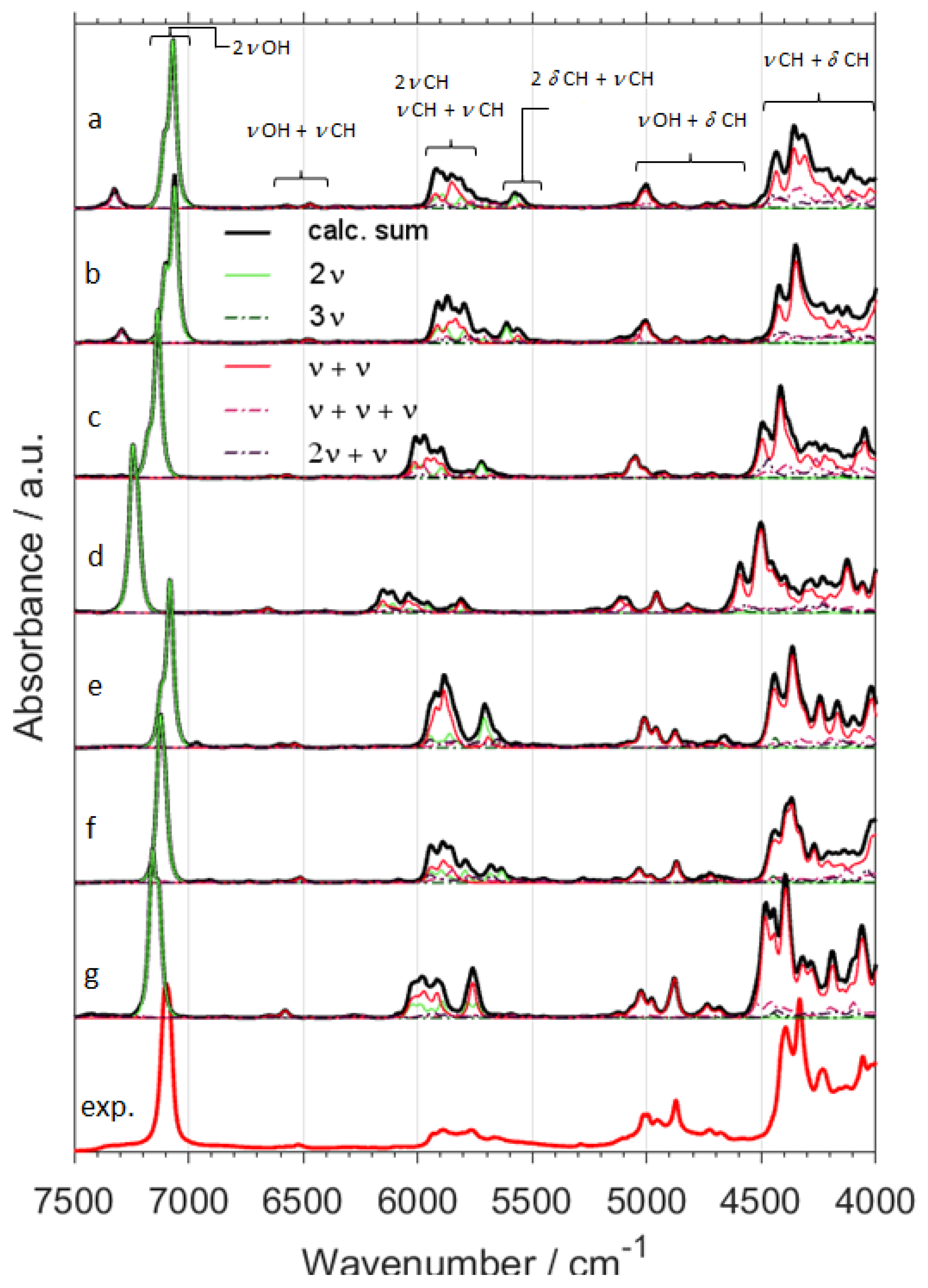
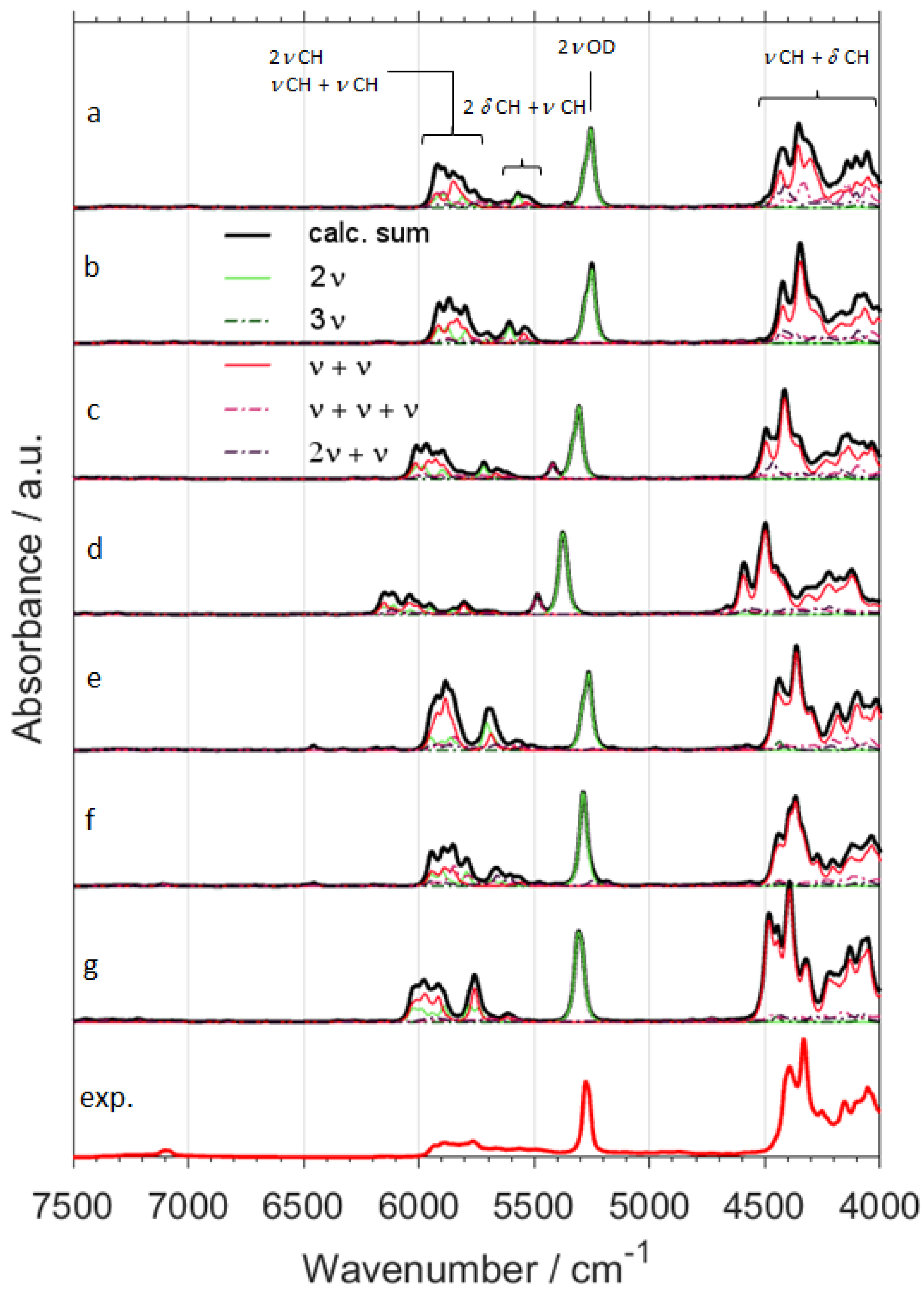
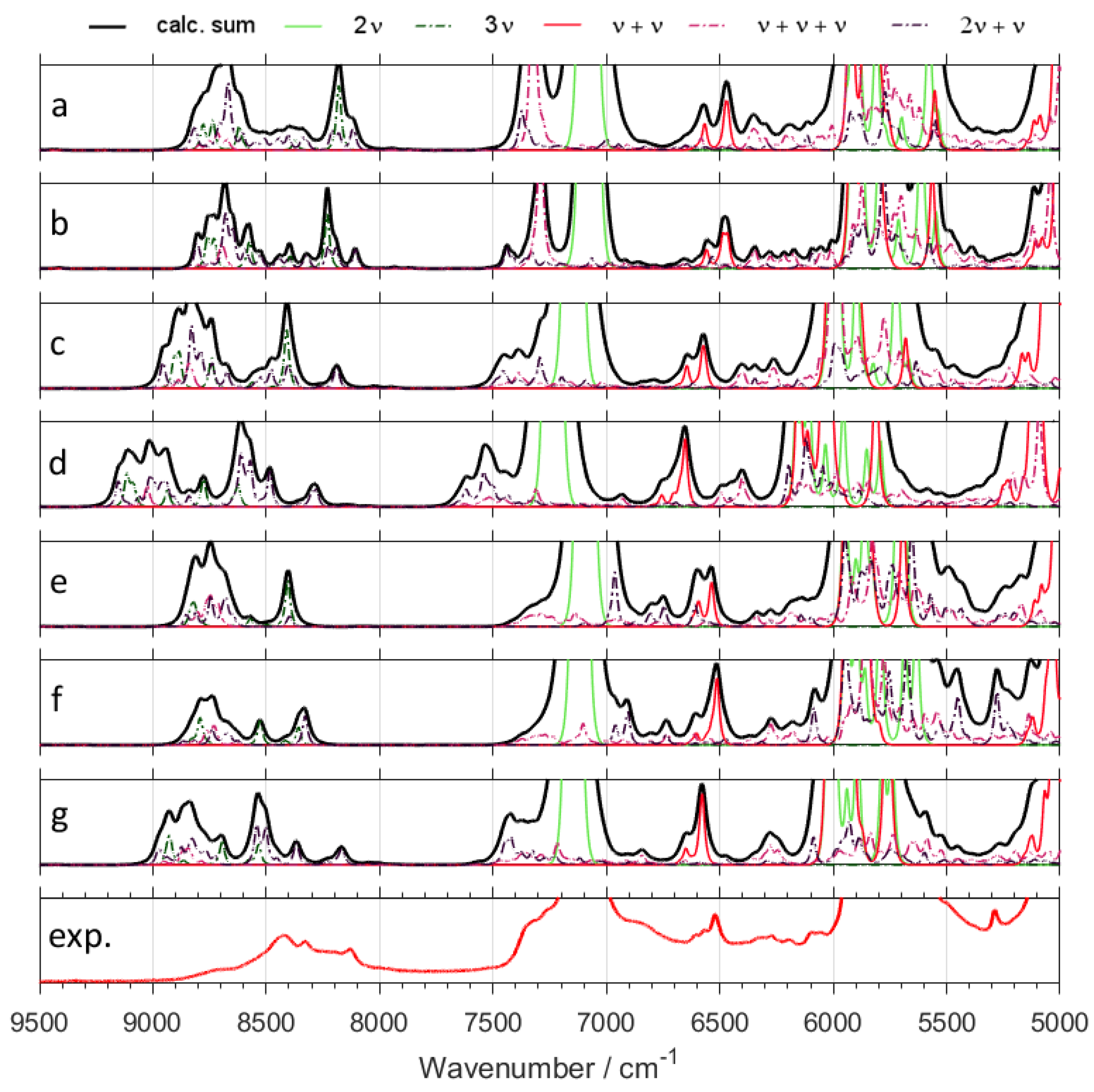
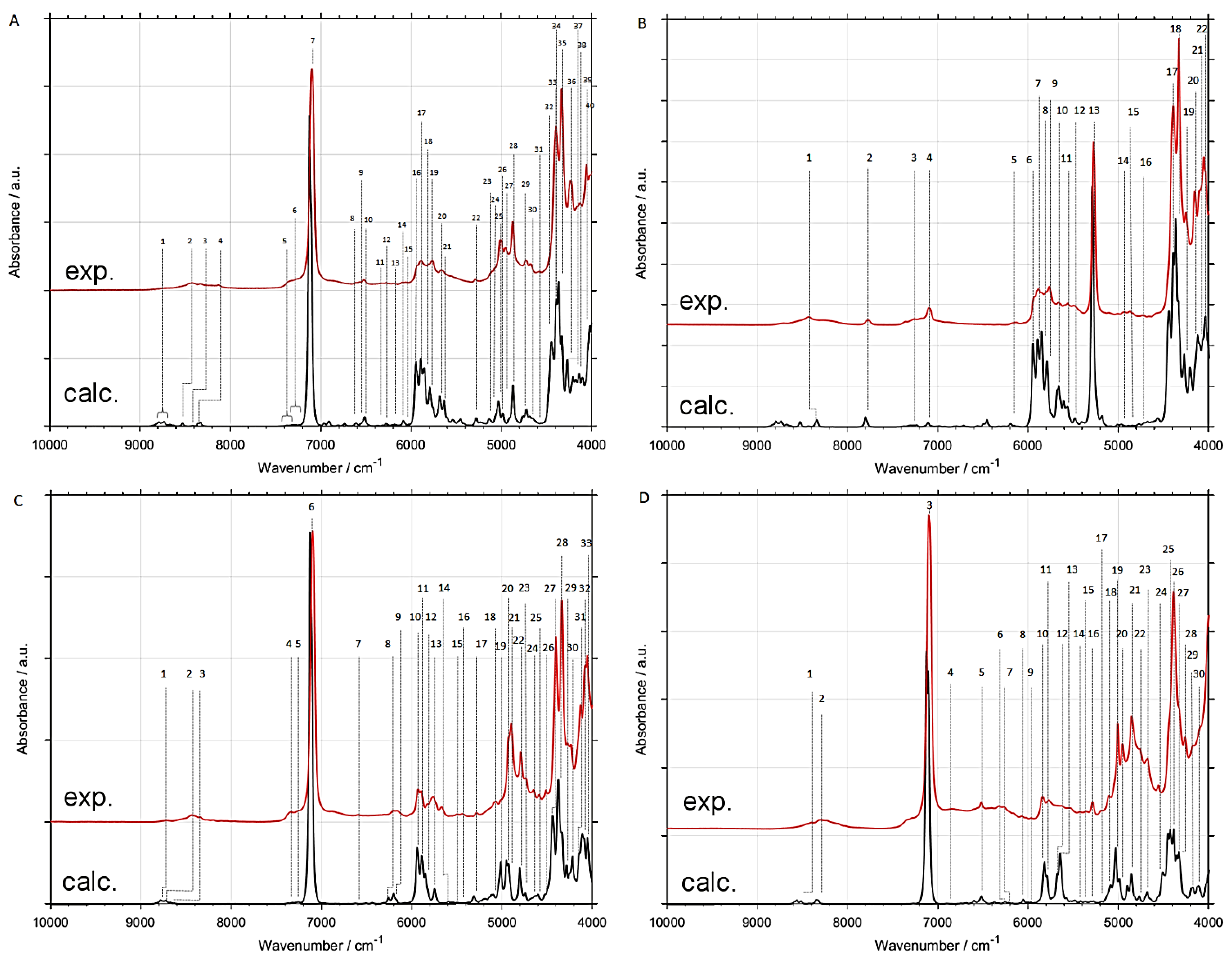
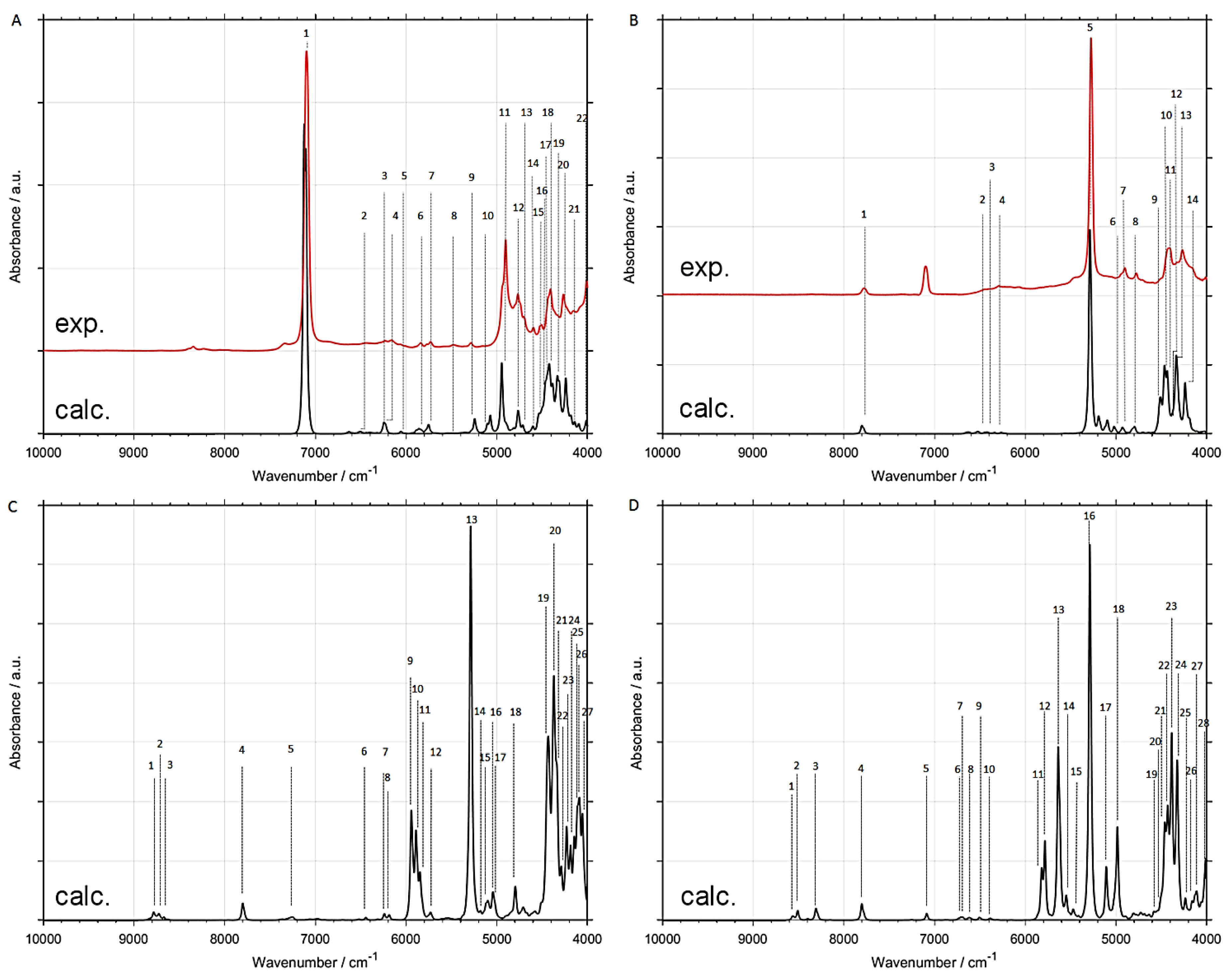
2.1. Accuracy of Reproduction of NIR Spectra by Selected Approaches
2.2. Origins of NIR Bands of CX3CX2OX (X = H, D)
3. Experimental and Computational Methods
3.1. Materials and Spectroscopic Measurements
3.2. Computational Procedures
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Siesler, H.W.; Ozaki, Y.; Kawata, S.; Heise, H.M. (Eds.) Near-Infrared Spectroscopy; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Beć, K.B.; Grabska, J.; Ozaki, Y. Advances in anharmonic methods and their applications to vibrational spectroscopies. In Frontiers of Quantum Chemistry; Wójcik, M.J., Nakatsuji, H., Kirtman, B., Ozaki, Y., Eds.; Springer: Singapore, 2017. [Google Scholar]
- Beć, K.B.; Grabska, J.; Huck, C.W.; Ozaki, Y. Quantum mechanical simulation of NIR spectra. In Applications in Physical and Analytical Chemistry; Ozaki, Y., Wójcik, M.J., Popp, J., Eds.; Wiley: Hoboken, NJ, USA, 2019; in press. [Google Scholar]
- Ozaki, Y.; Huck, C.W.; Beć, K.B. Near infrared spectroscopy and its applications. In Molecular and Laser Spectroscopy; Gupta, V.P., Ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Siesler, H.W. Near-infrared spectra, interpretation. In Encyclopedia of Spectroscopy and Spectrometry, 3rd ed.; Lindon, J.C., Tranter, G.E., Koppenaal, D.W., Eds.; Academic Press: Oxford, UK, 2017. [Google Scholar]
- Workman, J., Jr.; Weyer, L. Practical Guide and Spectral Atlas for Interpretive Near-Infrared Spectroscopy, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Beć, K.B.; Hawranek, J.P. Vibrational analysis of liquid n-butylmethylether. Vib. Spectrosc. 2013, 64, 164–171. [Google Scholar] [CrossRef]
- Beć, K.B.; Kwiatek, A.; Hawranek, J.P. Vibrational analysis of neat liquid tert-butylmethylether. J. Mol. Liq. 2014, 196, 26–31. [Google Scholar] [CrossRef]
- Kirchler, C.G.; Pezzei, C.K.; Beć, K.B.; Henn, R.; Ishigaki, M.; Ozaki, Y.; Huck, C.W. Critical evaluation of NIR and ATR-IR spectroscopic quantifications of rosmarinic acid in rosmarini folium supported by quantum chemical calculations. Planta Med. 2017, 83, 1076–1084. [Google Scholar] [CrossRef] [PubMed]
- Beć, K.B.; Huck, C.W. Breakthrough potential in near-infrared spectroscopy: Spectra simulation. A review of recent developments. Front. Chem. 2019, 7, 1–22. [Google Scholar] [CrossRef] [PubMed]
- Bozzolo, G.; Plastino, A. Generalized anharmonic oscillator: A simple variational approach. Phys. Rev. D 1981, 24, 3113–3117. [Google Scholar]
- Gribov, L.A.; Prokof’eva, N.I. Variational solution of the problem of anharmonic vibrations of molecules in the central force field. J. Struct. Chem. 2015, 56, 752–754. [Google Scholar] [CrossRef]
- Bowman, J.M. Self-consistent field energies and wavefunctions for coupled oscillators. J. Chem. Phys. 1978, 68, 608–610. [Google Scholar] [CrossRef]
- Gerber, R.B.; Chaban, G.M.; Brauer, B.; Miller, Y. Theory and Applications of Computational Chemistry: The First 40 Years; Elsevier: Amsterdam, The Netherlands, 2005; pp. 165–193. [Google Scholar]
- Jung, J.O.; Gerber, R.B. Vibrational wave functions and spectroscopy of (H2O)n, n = 2, 3, 4, 5: Vibrational self-consistent field with correlation corrections. J. Chem. Phys. 1996, 105, 10332–10348. [Google Scholar] [CrossRef]
- Norris, L.S.; Ratner, M.A.; Roitberg, A.E.; Gerber, R.B. Møller–Plesset perturbation theory applied to vibrational problems. J. Chem. Phys. 1996, 105, 11261–11267. [Google Scholar] [CrossRef]
- Monteiro, J.G.S.; Barbosa, A.G.H. VSCF calculations for the intra- and intermolecular vibrational modes of the water dimer and its isotopologs. Chem. Phys. 2016, 479, 81–90. [Google Scholar] [CrossRef]
- Barone, V.; Biczysko, M.; Bloino, J.; Borkowska-Panek, M.; Carnimeo, I.; Panek, P. Toward Anharmonic Computations of Vibrational Spectra for Large Molecular Systems. Int. J. Quantum Chem. 2012, 112, 2185–2200. [Google Scholar] [CrossRef]
- Beć, K.B.; Futami, Y.; Wójcik, M.J.; Nakajima, T.; Ozaki, Y. Spectroscopic and computational study of acetic acid and its cyclic dimer in the near-infrared region. J. Phys. Chem. A 2016, 120, 6170–6183. [Google Scholar] [CrossRef]
- Grabska, J.; Ishigaki, M.; Beć, K.B.; Wójcik, M.J.; Ozaki, Y. Structure and near-infrared spectra of saturated and unsaturated carboxylic acids. An insight from anharmonic DFT calculations. J. Phys. Chem. A 2017, 121, 3437–3451. [Google Scholar] [CrossRef]
- Grabska, J.; Beć, K.B.; Ishigaki, M.; Wójcik, M.J.; Ozaki, Y. Spectra-structure correlations of saturated and unsaturated medium-chain fatty acids. Near-infrared and anharmonic DFT study of hexanoic acid and sorbic acid. Spectrochim. Acta A 2017, 185, 35–44. [Google Scholar] [CrossRef] [PubMed]
- Grabska, J.; Beć, K.B.; Ishigaki, M.; Huck, C.W.; Ozaki, Y. NIR spectra simulations by anharmonic DFT-saturated and unsaturated long-chain fatty acids. J. Phys. Chem. B 2018, 122, 6931–6944. [Google Scholar] [CrossRef] [PubMed]
- Biczysko, M.; Bloino, J.; Carnimeo, I.; Panek, P.; Barone, V. Fully ab initio IR spectra for complex molecular systems from perturbative vibrational approaches: Glycine as a test case. J. Mol. Struct. 2012, 1009, 74–82. [Google Scholar] [CrossRef]
- Biczysko, M.; Bloino, J.; Brancato, G.; Cacelli, I.; Cappelli, C.; Ferretti, A.; Lami, A.; Monti, S.; Pedone, A.; Prampolini, G.; et al. Integrated computational approaches for spectroscopic studies of molecular systems in the gas phase and in solution: Pyrimidine as a test case. Theor. Chem. Acc. 2012, 131, 1201–1220. [Google Scholar] [CrossRef]
- Beć, K.B.; Karczmit, D.; Kwaśniewicz, M.; Ozaki, Y.; Czarnecki, M.A. Overtones of νC≡N vibration as a probe of structure of liquid CH3CN, CD3CN and CCl3CN. Combined IR, NIR, and Raman spectroscopic studies with anharmonic DFT calculations. J. Phys. Chem. A 2019, 123, 4431–4442. [Google Scholar] [CrossRef]
- Grabska, J.; Beć, K.B.; Kirchler, C.G.; Ozaki, Y.; Huck, C.W. Distinct Difference in Sensitivity of NIR vs. IR Bands of Melamine to Inter-Molecular Interactions with Impact on Analytical Spectroscopy Explained by Anharmonic Quantum Mechanical Study. Molecules 2019, 24, 1402. [Google Scholar] [CrossRef]
- Beć, K.B.; Grabska, J.; Czarnecki, M.A. Spectra-structure correlations in NIR region: Spectroscopic and anharmonic DFT study of n-hexanol, cyclohexanol and phenol. Spectrochim. Acta A 2018, 197, 176–184. [Google Scholar] [CrossRef]
- Beć, K.B.; Grabska, J.; Kirchler, C.G.; Huck, C.W. NIR spectra simulation of thymol for better understanding of the spectra forming factors, phase and concentration effects and PLS regression features. J. Mol. Liq. 2018, 268, 895–902. [Google Scholar] [CrossRef]
- Beć, K.B.; Futami, Y.; Wójcik, M.J.; Ozaki, Y. A spectroscopic and theoretical study in the near-infrared region of low concentration aliphatic alcohols. Phys. Chem. Chem. Phys. 2016, 18, 13666–13682. [Google Scholar] [CrossRef]
- Grabska, J.; Beć, K.B.; Ozaki, Y.; Huck, C.W. Temperature drift of conformational equilibria of butyl alcohols studied by near-infrared spectroscopy and fully anharmonic DFT. J. Phys. Chem. A 2017, 121, 1950–1961. [Google Scholar] [CrossRef]
- Pele, L.; Gerber, R.B. On the mean accuracy of the separable VSCF approximation for large molecules. J. Phys. Chem. C 2010, 114, 20603–20608. [Google Scholar]
- Otaki, H.; Yagi, K.; Ishiuchi, S.; Fujii, M.; Sugita, Y. Anharmonic Vibrational Analyses of Pentapeptide Conformations Explored with Enhanced Sampling Simulations. J. Phys. Chem. B 2016, 120, 10199–10213. [Google Scholar] [CrossRef]
- Yagi, K.; Otaki, H.; Li, P.-C.; Thomsen, B.; Sugita, Y. Weight Averaged Anharmonic Vibrational Calculations: Applications to Polypeptide, Lipid Bilayers, and Polymer Materials; Ozaki, Y., Wójcik, M.J., Popp, J., Eds.; Wiley: Hoboken, NJ, USA, 2019; in press. [Google Scholar]
- Yagi, K.; Yamada, K.; Kobayashi, C.; Sugita, Y. Anharmonic Vibrational Analysis of Biomolecules and Solvated Molecules Using Hybrid QM/MM Computations. J. Chem. Theory Comput. 2019, 15, 1924–1938. [Google Scholar] [CrossRef]
- Gonjo, T.; Futami, Y.; Morisawa, Y.; Wójcik, M.J.; Ozaki, Y. Hydrogen bonding effects on the wavenumbers and absorption intensities of the OH fundamental and the first, second and third overtones of phenol and 2,6-dihalogenated phenols studied by visible/near-infrared/infrared spectroscopy and density functional theory calculations. J. Phys. Chem. A 2011, 115, 9845–9853. [Google Scholar]
- Futami, Y.; Ozaki, Y.; Hamada, Y.; Wójcik, M.J.; Ozaki, Y. Solvent dependence of absorption intensities and wavenumbers of the fundamental and first overtone of NH stretching vibration of pyrrole studied by near-infrared/infrared spectroscopy and DFT calculations. J. Phys. Chem. A 2011, 115, 1194–1198. [Google Scholar] [CrossRef]
- Kuenzer, U.; Sorarù, J.-A.; Hofer, T.S. Pushing the limit for the grid-based treatment of Schrödinger’s equation: A sparse Numerov approach for one, two and three dimensional quantum problems. Phys. Chem. Chem. Phys. 2016, 18, 31521–31533. [Google Scholar] [CrossRef]
- Kuenzer, U.; Klotz, M.; Hofer, T.S. Probing vibrational coupling via a grid-based quantum approach-an efficient strategy for accurate calculations of localized normal modes in solid-state systems. J. Comput. Chem. 2018, 39, 2196–2209. [Google Scholar] [CrossRef]
- Kuenzer, U.; Hofer, T.S. A four-dimensional Numerov approach and its application to the vibrational eigenstates of linear triatomic molecules—The interplay between anharmonicity and inter-mode coupling. Chem. Phys. 2019, 520, 88–89. [Google Scholar]
- Wu, P.; Siesler, H.W. The diffusion of alcohols and water in polyamide 11: A study by FTNIR-spectroscopy. Macromol. Symp. 1999, 143, 323–336. [Google Scholar] [CrossRef]
- Grabska, J.; Czarnecki, M.A.; Beć, K.B.; Ozaki, Y. Spectroscopic and quantum mechanical calculation study of the effect of isotopic substitution on NIR spectra of methanol. J. Phys. Chem. A 2017, 121, 7925–7936. [Google Scholar]
- Wang, L.; Ishiyama, T.; Morita, A. Theoretical investigation of C−H vibrational spectroscopy. 1. Modeling of methyl and methylene groups of ethanol with different conformers. J. Phys. Chem. A 2017, 121, 6687–6700. [Google Scholar] [CrossRef]
- Wang, L.; Ishiyama, T.; Morita, A. Theoretical investigation of C−H vibrational spectroscopy. 2. Unified assignment method of IR, Raman, and sum frequency generation spectra of ethanol. J. Phys. Chem. A 2017, 121, 6701–6712. [Google Scholar]
- Bloino, J.; Baiardi, A.; Biczysko, M. Aiming at an accurate prediction of vibrational and electronic spectra for medium-to-large molecules: An overview. Int. J. Quantum Chem. 2016, 116, 1543–1574. [Google Scholar]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar]
- Fornaro, T.; Biczysko, M.; Monti, S.; Barone, V. Dispersion corrected DFT approaches for anharmonic vibrational frequency calculations: Nucleobases and their dimers. Phys. Chem. Chem. Phys. 2014, 16, 10112–10128. [Google Scholar]
- Matczak, P.; Wojtulewski, S. Performance of Møller-Plesset second-order perturbation theory and density functional theory in predicting the interaction between stannylenes and aromatic molecules. J. Mol. Model. 2015, 21, 41. [Google Scholar] [CrossRef]
- Kirchler, C.G.; Pezzei, C.K.; Beć, K.B.; Mayr, S.; Ishigaki, M.; Ozaki, Y.; Huck, C.W. Critical evaluation of spectral information of benchtop vs. portable near-infrared spectrometers: Quantum chemistry and two-dimensional correlation spectroscopy for a better understanding of PLS regression models of the rosmarinic acid content in Rosmarini folium. Analyst 2017, 142, 455–464. [Google Scholar]
- Czarnecki, M.A. Effect of temperature and concentration on self-association of octan-1-ol studied by two-dimensional Fourier transform near-infrared correlation spectroscopy. J. Phys. Chem. A 2000, 104, 6356–6361. [Google Scholar] [CrossRef]
- Czarnecki, M.A. Two-dimensional correlation analysis of the second overtone of the ν(OH) mode of octan-1-ol in the pure liquid phase. Appl. Spectrosc. 2000, 54, 1767–1770. [Google Scholar] [CrossRef]
- Czarnecki, M.A.; Czarnik-Matusewicz, B.; Ozaki, Y.; Iwahashi, M. Resolution enhancement and band assignments for the first overtone of OH(D) stretching modes of butanols by two-dimensional near-infrared correlation spectroscopy. 3. Thermal dynamics of hydrogen bonding in butan-1-(ol-d) and 2-methylpropan-2-(ol-d) in the pure liquid states. J. Phys. Chem. A 2000, 104, 4906–4911. [Google Scholar]
- Czarnecki, M.A.; Maeda, H.; Ozaki, Y.; Suzuki, M.; Iwahashi, M. Resolution enhancement and band assignments for the first overtone of OH stretching mode of butanols by two-dimensional near-infrared correlation spectroscopy. Part I: Sec-butanol. Appl. Spectrosc. 1998, 52, 994–1000. [Google Scholar] [CrossRef]
- Czarnecki, M.A.; Morisawa, Y.; Futami, Y.; Ozaki, Y. Advances in molecular structure and interaction studies using near-infrared spectroscopy. Chem. Rev. 2015, 115, 9707–9744. [Google Scholar] [CrossRef]
- Umer, M.; Kopp, W.A.; Leonhard, K. Efficient yet accurate approximations for ab initio calculations of alcohol cluster thermochemistry. J. Chem. Phys. 2015, 143, 214306. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, S.L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic interaction of a solute with a continuum. A direct utilization of ab initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Barone, V. Anharmonic vibrational properties by a fully automated second-order perturbative approach. J. Chem. Phys. 2005, 122, 014108. [Google Scholar] [CrossRef]
- Barone, V.; Biczysko, M.; Bloino, J. Fully anharmonic IR and Raman spectra of medium-size molecular systems: Accuracy and interpretation. Phys. Chem. Chem. Phys. 2014, 16, 1759–1787. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 16, Revision A.03; Gaussian, Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Bloino, J.; Biczysko, M. IR and Raman Spectroscopies beyond the Harmonic Approximation: The Second-Order Vibrational Perturbation Theory Formulation. In Reference Module in Chemistry, Molecular Sciences and Chemical Engineering; Reedijk, J., Ed.; Elsevier: Waltham, MA, USA, 2015. [Google Scholar]
- McQuarrie, D.A. Statistical Mechanics; Harper & Row: New York, NY, USA, 1976. [Google Scholar]
- Robertson, M.B.; Klein, P.G.; Ward, I.M.; Packer, K.J. NMR study of the energy difference and population of the gauche and trans conformations in solid polyethylene. Polymer 2001, 42, 1261–1264. [Google Scholar] [CrossRef]
- Martin, J.M.L.; Van Alsenoy, C. GAR2PED; University of Antwerp: Antwerp, Belgium, 1995. [Google Scholar]
- Pulay, P.; Fogarasi, G.; Pang, F.; Boggs, J.E. Systematic ab initio gradient calculation of molecular geometries, force constants, and dipole moment derivatives. J. Am. Chem. Soc. 1979, 101, 2550–2560. [Google Scholar] [CrossRef]
- MATLAB; The MathWorks, Inc.: Natick, MA, USA, 2016.
Sample Availability: Samples of the compounds (CH3CH2OD, CH3CD2OH, CD3CH2OH, CD3CD2OH, CD3CD2OD) are available from the authors. |

| Assignment | Exp. | Calculated | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MP2/aVTZ + CPCM | Diff. | B2PLYP-GD3BJ/def2-TZVP + CPCM | Diff. | B2PLYP-GD3BJ/SNST + CPCM | Diff. | MP2/6-31G(d,p) + CPCM | Diff. | B2PLYP-GD3BJ/6-31G(d,p) + CPCM | Diff. | B3LYP-GD3BJ/6-31G(d,p) + CPCM | Diff. | B3LYP-GD3BJ/6-31G(d,p) | Diff. | ||
| CH3CH2OH | |||||||||||||||
| 2νOH | 7099 | 7157 | 58 | 7125 | 26 | 7081 | −18 | 7243 | 144 | 7134 | 35 | 7061 | −38 | 7096 | −3 |
| νsCH2 + νOH | 6520.4 | 6578 | 57.6 | 6513 | −7.4 | 6536 | 15.6 | 6654 | 133.6 | 6576 | 55.6 | 6477 | -43.4 | 6472 | −48.4 |
| 2δas’CH3 + νOH | 5886.1 | 5980 | 93.9 | 5889 | 2.9 | 5922 | 35.9 | 6111 | 224.9 | 5970 | 83.9 | 5871 | −15.1 | 5892 | 5.9 |
| 2νasCH2 | 5765.7 | 5897 | 131.3 | 5790 | 24.3 | 5864 | 98.3 | 5957 | 191.3 | 5898 | 132.3 | 5797 | 31.3 | 5812 | 46.3 |
| 2νsCH2; 2νsCH3 + δsCH3 | 5665.1 | 5759 | 93.9 | 5681 | 15.9 | 5708 | 42.9 | 5812 | 146.9 | 5722 | 56.9 | 5611 | −54.1 | 5768 | 102.9 |
| [δwaggCH2, δsCH3] + νOH | 5013.8 | 5026 | 12.2 | 5029 | 15.2 | 5012 | −1.8 | 5114 | 100.2 | 5049 | 35.2 | 5040 | 26.2 | 5019 | 5.2 |
| [δtwistCH2, δipCOH, δwaggCH2] + νOH | 4954.2 | 4978 | 23.8 | 4979 | 24.8 | 4959 | 4.8 | 5003 | 48.8 | 5009 | 54.8 | 5008 | 53.8 | 5003 | 48.8 |
| δipCOH + νOH | 4873 | 4881 | 8 | 4868 | −5 | 4877 | 4 | 4958 | 85 | 4926 | 53 | 4874 | 1 | 4883 | 10 |
| δsCH3 + νas’CH3 | 4394.8 | 4448 | 53.2 | 4366 | −28.8 | 4443 | 48.2 | 4592 | 197.2 | 4473 | 78.2 | 4424 | 29.2 | 4436 | 41.2 |
| [δoopCOH, τCC] + νOH | 4333.5 | 4395 | 61.5 | 4331 | −2.5 | 4364 | 30.5 | 4502 | 168.5 | 4416 | 82.5 | 4353 | 19.5 | 4357 | 23.5 |
| RMSE | 70.0 | RMSE | 18.1 | RMSE | 40.8 | RMSE | 153.1 | RMSE | 72.2 | RMSE | 35.0 | RMSE | 44.6 | ||
| CH3CH2OD | |||||||||||||||
| 2νasCH3 | 5885.2 | 5978 | 92.8 | 5895 | 9.8 | 5921 | 35.8 | 6114 | 228.8 | 5967 | 81.8 | 5871 | −14.2 | 5894 | 8.8 |
| 2νasCH2 | 5765.6 | 5917 | 151.4 | 5788 | 22.4 | 5862 | 96.4 | 6007 | 241.4 | 5896 | 130.4 | 5799 | 33.4 | 5815 | 49.4 |
| 2νOD | 5277.1 | 5312 | 34.9 | 5289 | 11.9 | 5265 | −12.1 | 5378 | 100.9 | 5306 | 28.9 | 5250 | −27.1 | 5255 | −22.1 |
| δscissCH2 + νasCH2 | 4393.7 | 4445 | 51.3 | 4397 | 3.3 | 4439 | 45.3 | 4592 | 198.3 | 4493 | 99.3 | 4422 | 28.3 | 4424 | 30.3 |
| [δsCH3, δwaggCH2] + νasCH3 | 4331.8 | 4392 | 60.2 | 4364 | 32.2 | 4364 | 32.2 | 4500 | 168.2 | 4415 | 83.2 | 4349 | 17.2 | 4355 | 23.2 |
| [δrockCH2, δrockCH3] + νsCH2 | 4054.1 | 4057 | 2.9 | 4037 | −17.1 | 4020 | −34.1 | 4122 | 67.9 | 4036 | −18.1 | 4068 | 13.9 | 4058 | 3.9 |
| RMSE | 80.6 | RMSE | 18.6 | RMSE | 50.0 | RMSE | 179.4 | RMSE | 83.3 | RMSE | 23.6 | RMSE | 27.3 | ||
| Peak Number | νExp | νCalc | Assignment (Major Contribution) |
|---|---|---|---|
| 1 | 8718.0 | 8739 | 2νasCH2 + νasCH3 |
| 2 | 8430.0 | 8526 | 3νasCH2 |
| 3 | 8329.0 | 8416 | 3νsCH2 |
| 4 | 8131.0 | 8329 | 2νsCH2 + νasCH2 |
| 5 | 7400–7300 | 7400–7300 | δsCH3 + νasCH3 + νas’CH3 [δas’CH3, δasCH3] + νasCH3 + νas’CH3 δscissCH2 + νasCH2 + νas’CH3 [δrockCH2, δrockCH3] + νasCH2 + νOH |
| 6 | 7300–7200 | 7300–7200 | δtwistCH2 + νasCH3 + νas’CH3 δsCH3 + νsCH3 + νas’CH3 [δasCH3, δas’CH3] + νsCH3 + νasCH3 [δasCH3, δas’CH3] + νsCH3 + νas’CH3 |
| 7 | 7099.0 | 7125 | 2νOH |
| 8 | 6610.0 | 6609 | νsCH3 + νOH |
| 9 | 6565.0 | 6540 | 2δasCH3 + νOH |
| 10 | 6520.4 | 6513 | νsCH2 + νOH |
| 11 | 6331.0 | 6314 | 2δtwistCH2 + νOH |
| 12 | 6271.8 | 6275 | δipCOH + δwaggCH2 + νOH |
| 13 | 6193.0 | 6178 | [τCC, δoopCOH] + νasCH3 + νas’CH3 |
| 14 | 6063.0 | 6085 | 2δipCOH + νOH |
| 15 | 6051.0 | 6021 | [νCC, δipCOH] + δtwistCH2 + νOH |
| 16 | 5936.0 | 5948 | 2νas’CH3, νasCH3 + νas’CH3 |
| 17 | 5886.1 | 5889 | 2δas’CH3 + νOH |
| 18 | 5809.0 | 5846 | [δasCH3, δas’CH3] + δscissCH2 + νasCH2 |
| 19 | 5765.7 | 5790 | 2νasCH2 |
| 20 | 5665.1 | 5681 | 2νsCH2; 2νsCH3 + δsCH3 |
| 21 | 5634.0 | 5632 | δipCOH + δwaggCH2 + νsCH3 |
| 22 | 5287.6 | 5277 | δipOH + δCCO +νOH |
| 23 | 5111.0 | 5128 | δscissCH2+ νOH |
| 24 | 5071.0 | 5118 | [δasCH3, δas’CH3] + νOH |
| 25 | 5013.8 | 5029 | [δwaggCH2, δsCH3] + νOH |
| 26 | 4996.2 | ||
| 27 | 4954.2 | 4979 | [δtwistCH2, δipCOH, δwaggCH2] + νOH |
| 28 | 4873.0 | 4868 | δipCOH + νOH |
| 29 | 4724.3 | 4763 | δsCH3 + 2[δasCH3, δas’CH3] |
| 30 | 4677.0 | 4726 | [νCO, δrock’CH3] + νOH |
| 31 | 4582.9 | 4648 | [δoopCOH, τCC] + δas’CH3 + νsCH3 |
| 32 | 4454.0 | 4450 | 3δscissCH2 |
| 33 | 4409.0 | 4396 | δscissCH2 + νasCH2 |
| 34 | 4394.8 | 4366 | δsCH3 + νas’CH3 |
| 35 | 4333.5 | 4331 | [δoopCOH, τCC] + νOH |
| 36 | 4232.6 | 4269 | δtwistCH2 + νas’CH3 |
| 37 | 4162.0 | 4177 | δipCOH + νsCH2 |
| 38 | 4131.7 | 4137 | δtwistCH2 + νsCH2 |
| 39 | 4057.4 | 4020 | [δrockCH2, δrockCH3] + νsCH2 |
| 40 | 4024.0 | 3997 | [νCO, δrock’CH3] + νasCH2 |
| Peak Number | νexp | νcalc | Assignment (Major Contribution) |
|---|---|---|---|
| 1 | 8428.0 | 8334 | 2νsCH2 + νasCH2 |
| 2 | 7777.5 | 7796 | 3νOD |
| 3 | 7260.0 | 7227 | δtwistCH2 + νasCH3 + νas’CH3 |
| 4 | 7099.1 | 7112 | δas’CH3 + νsCH2 + νasCH2 |
| 5 | 6133.4 | 6200 | τCC + νasCH3 + νas’CH3 |
| 6 | 5935.0 | 5946 | 2νas’CH3 |
| 7 | 5885.2 | 5895 | 2νasCH3 |
| 8 | 5850.0 | 5847 | [δasCH3, δas’CH3] + δscissCH2 + νasCH2 |
| 9 | 5765.6 | 5788 | 2νasCH2 |
| 10 | 5665.7 | 5669 | 2δwaggCH2 + νsCH2 |
| 11 | 5564.3 | 5559 | νOD + νsCH2 |
| 12 | 5494.3 | 5498 | νasCH2 + δtwistCH2 + δwaggCH2 |
| 13 | 5277.1 | 5289 | 2νOD |
| 14 | 4947.0 | 4963 | [δrockCH2, δrockCH3] + δtwistCH2 + νsCH2 |
| 15 | 4873.0 | 4846 | [δrockCH2, δrockCH3] + [δrockCH2, δrockCH3] + νsCH2 |
| 16 | 4720.8 | 4717 | [νCO, δrock’CH3, δipCOD] + [δrock’CH3, δipCOD, δscissCH2CO] +νOD |
| 17 | 4393.7 | 4397 | δscissCH2 + νasCH2 |
| 18 | 4331.8 | 4364 | [δsCH3, δwaggCH2] +νasCH3 |
| 19 | 4253.4 | 4275 | δtwistCH2 + νas’CH3 |
| 20 | 4155.1 | 4127 | [δrock’CH3, δipCOD, δscissCH2CO] +νasCH3 |
| 21 | 4105.0 | 4063 | [δrock’CH3, δipCOD, δscissCH2CO] + νsCH3 |
| 22 | 4054.1 | 4037 | [δrockCH2, δrockCH3] + δsCH2 |
| Peak Number | νexp | νcalc | Assignment (Major Contribution) |
|---|---|---|---|
| 1 | 8717.0 | 8788 | 3νasCH3 |
| 2 | 8434.1 | 8728 | νsCH3 + νasCH3 + νas’CH3 |
| 3 | 8337.0 | 8665 | 2νsCH3 + νasCH3 |
| 4 | 7345.0 | 7324 | [δrockCD2, δtwist CD2] + νas’CH3 + νOH |
| 5 | 7251.0 | 7255 | [δasCH3, δas’CH3] + νsCH3 + νasCH3 |
| 6 | 7098.2 | 7126 | 2νOH |
| 7 | 6590.4 | 6618 | νas’CH3 + νOH |
| 8 | 6205.8 | 6257 | 2δipCOH + νOH |
| 9 | 6158.0 | 6198 | 2δipCOH + νOH |
| 10 | 5929.9 | 5943 | 2νasCH3 |
| 11 | 5895.4 | 5892 | 2νas’CH3 |
| 12 | 5828.0 | 5844 | νsCH3 + νas’CH3 |
| 13 | 5763.8 | 5744 | νsCD2 + νOH |
| 14 | 5669.1 | 5595 | νsCH3 + 2νasCH3 |
| 15 | 5449.0 | 5496 | δrockCH3 + δsCH3 + νas’CH3 |
| 16 | 5439.4 | 5449 | δscissCD2CO + 2νasCH3 |
| 17 | 5282.0 | 5309 | νasCD2 + 2[δasCH3, δas’CH3] |
| 18 | 5070.1 | 5094 | νsCD2 + νasCH3 |
| 19 | 5017.0 | 5018 | [τCC, δoop COH] + 2[δasCH3, δas’CH3] |
| 20 | 4927.0 | 4954 | δipCOH + νOH |
| 21 | 4898.3 | 4930 | δipCOH + νOH |
| 22 | 4792.1 | 4806 | [νCO, δwaggCD2] + νOH |
| 23 | 4737.2 | 4744 | δscissCD2 + νOH |
| 24 | 4650.2 | 4641 | [νCC, δrock’CH3] + νOH |
| 25 | 4591.7 | 4600 | [νCO, δwaggCD2] + νOH |
| 26 | 4513.3 | 4525 | δipCOH + νOH |
| 27 | 4404.6 | 4437 | [δasCH3, δas’CH3] + νas’CH3 |
| 28 | 4338.0 | 4373 | δsCH3 + νas’CH3 |
| 29 | 4275.7 | 4285 | δipCOH + νasCH3 |
| 30 | 4238.1 | 4218 | νsCD2 + νasCD2 |
| 31 | 4129.6 | 4147 | [νCO, δwaggCD2] + νas’CH3 |
| 32 | 4079.7 | 4117 | δrockCH3 + νasCH3 |
| 33 | 4056.2 | 4052 | δrockCH3 + νsCH3, δscissCD2CO + νOH |
| Peak Number | νexp | νcalc | Assignment (Major Contribution) |
|---|---|---|---|
| 1 | 8405.0 | 8511 | 3νasCH2 |
| 2 | 8307.6 | 8323 | 2νsCH2 + νasCH2 |
| 3 | 7098.5 | 7124 (t) 7100 (g) | 2νOH |
| 4 | 6841.1 | 6897 | [νCO, δas’CD3] + νsCH2 + νasCH2 |
| 5 | 6517.6 | 6510 | νsCH2 + νOH |
| 6 | 6324.0 | 6261 | [δipCOH, δtwistCH2] + δwaggCH2 + νOH |
| 7 | 6268.0 | 6111 | [δrock’CD3, νCC] + νas’CD3 + νOH |
| 8 | 6070.4 | 6059 | 2[δipCOH, δtwistCH2] + νOH |
| 9 | 5966.3 | 5966 | [δsCD3, νCC] + δwaggCH2 + νOH |
| 10 | 5839.1 | 5825 | 2νasCH2 |
| 11 | 5772.1 | 5793 | 2νasCH2 |
| 12 | 5628.0 | 5686 | 2νsCH2 |
| 13 | 5533.0 | 5641 | 2νsCH2 |
| 14 | 5427.9 | 5419 | 2δtwistCH2 + νasCH2 |
| 15 | 5358.0 | 5367 | [νCO, δas’CD3] + νsCD3 + νas’CD3 |
| 16 | 5286.8 | 5287 | δsCD3 + δtwistCH2 + νasCH2 |
| 17 | 5190.0 | 5188 | 2[δsCD3, νCC] + νsCH2 |
| 18 | 5102.7 | 5084 | δoopCOH + 2δwaggCH2 |
| 19 | 5007.1 | 5028 | δwaggCH2 + νOH |
| 20 | 4955.8 | 4987 | [δtwistCH2, δipCOH, δwaggCH2] + νOH |
| 21 | 4853.8 | 4853 | [δipCOH, δtwistCH2] + νOH |
| 22 | 4764.7 | 4768 | [δsCD3, νCC] + νOH |
| 23 | 4676.7 | 4676 | νCO + νOH |
| 24 | 4558.4 | 4511 | δas’CD3 + [δtwistCH2, δipCOH] + νas’CD3 |
| 25 | 4443.0 | 4429 | δscissCH2 + νasCH2 |
| 26 | 4390.5 | 4390 | δscissCH2 + νasCH2 |
| 27 | 4329.0 | 4356 | δscissCH2 + νsCH2 |
| 28 | 4263.8 | 4332 | δscissCH2 + νsCH2 |
| 29 | 4174.6 | 4180 | 2[δtwistCH2, δipCOH, δwaggCH2] + δscissCH2 |
| 30 | 4100.0 | 4107 | τCC + δoopCOH + νOH |
| Peak Number | νexp | νcalc | Assignment (Major Contribution) |
|---|---|---|---|
| 1 | 7099.0 | 7126 (t) 7102 (g) | 2νOH |
| 2 | 6444.0 | 6495 | νsCD2 + [νasCD2, νasCD3] + [νas’CD3, νasCD2] |
| 3 | 6232.1 | 6244 | 2δipCOH +νOH |
| 4 | 6162.9 | 6224 | 2[νCC, δwaggCD2] + νOH |
| 5 | 6063.0 | 6059 | [δscissCD2, νCO] + [νCC, δwaggCD2] + νOH |
| 6 | 5838.3 | 5861 | [νasCD2, νasCD3] + νOH |
| 7 | 5732.3 | 5746 | [δrockCD2, δrockCD3] + [δsCD3, δwaggCD2] + νOH |
| 8 | 5478.7 | 5488 | [νCC, δwaggCD2] + νsCD3 + [νasCD2, νasCD3] |
| 9 | 5285.8 | 5247 | νsCD3 + νasCD2 + νCO |
| 10 | 5160.0 | 5103 | [δtwistCD2, δrockCD3, δrockCD2] + 2[νCC, δwaggCD2] |
| 11 | 4903.7 | 4947 | δipCOH + νOH |
| 12 | 4769.2 | 4766 | [δscissCD2, νCO] + νOH |
| 13 | 4701.4 | 4714 | [δas’CD3, δasCD3] + νOH |
| 14 | 4598.4 | 4604 | [νCO, δwaggCD2] + νOH |
| 15 | 4525.0 | 4539 | [δtwistCD2, δrockCD3, δrockCD2] + δipCOH + [νas’CD3, νasCD2] |
| 16 | 4506.9 | 4499 | 2δscissCD2CO + νasCD3 |
| 17 | 4430.0 | 4447 | [νasCD2, νasCD3] +νasCD3, 2[νas’CD3, νasCD2] |
| 18 | 4409.6 | 4420 | [νasCD2, νasCD3] + [νas’CD3, νasCD2] |
| 19 | 4332.0 | 4334 | 2νasCD2 |
| 20 | 4267.4 | 4235 | [νsCD2, νsCD3] + νasCD2 |
| 21 | 4156.8 | 4140 | 2δoopCOH +νOH |
| 22 | 4013.0 | 4012 | δscissCD2CO +νOH |
| Peak Number | νExp | νCalc | Assignment (Major Contribution) |
|---|---|---|---|
| 1 | 7771.0 | 7799 | 3νOD |
| 2 | 6468.0 | 6525 | νsCD3 + [νas’CD3, νasCD2] + νasCD3 |
| 3 | 6450.0 | 6447 | 3νasCD2 |
| 4 | 6290.1 | 6267 | 2νsCD2 + νasCD2 |
| 5 | 5276.0 | 5289 | 2νOD |
| 6 | 4948.0 | 5020 | [νCO, δtwistCD2] + 2[δscissCD2, νCO] |
| 7 | 4902.2 | 4929 | [δtwistCD2, δrockCD2] + 2[δscissCD2, νCO] |
| 8 | 4779.2 | 4795 | νsCD2 + νOD |
| 9 | 4509.0 | 4510 | [δasCD3, δas’CD3] + [νCC, δwaggCD2] +νasCD3 |
| 10 | 4437.4 | 4465 | 2νas’CD3, νasCD3 + νas’CD3 |
| 11 | 4409.3 | 4434 | 2νasCD3, νasCD2 + νas’CD3 |
| 12 | 4325.2 | 4381 | 2[δscissCD2, νCO] + νsCD3 |
| 13 | 4269.5 | 4337 | 2νasCD2 |
| 14 | 4170.2 | 4241 | [νsCD2, νsCD3] + νasCD2 |
| Peak Number | νCalc | Assignment (Major Contribution) |
|---|---|---|
| 1 | 8781 | 3νas’CH3 |
| 2 | 8722 | νsCH3 + νasCH3 + νas’CH3 |
| 3 | 8666 | 2νsCH3 + νasCH3, 2νsCH3 + νas’CH3 |
| 4 | 7802 | 3νOD |
| 5 | 7257 | [δasCH3, δas’CH3] + νsCH3 + νasCH3 |
| 6 | 6445 | 3νasCD2 |
| 7 | 6188 | τCC + νasCH3 + νas’CH3 |
| 8 | 5943 | 2νasCH3, νasCH3 + νas’CH3 |
| 9 | 5890 | 2[δas’CH3, δasCH3] + νas’CH3, 2νas’CH3 |
| 10 | 5845 | νsCH3 + νasCH3 |
| 11 | 5728 | 2δsCH3 + νasCH3 |
| 12 | 5288 | 2νOD |
| 13 | 5182 | νasCD2 + νas’CH3 |
| 14 | 5120 | νasCD2 + νsCH3 |
| 15 | 5097 | νsCD2 + νasCH3 |
| 16 | 5046 | τCC + 2[δasCH3,δas’CH3] |
| 17 | 4796 | δoopCOD + 2[δas’CH3,δasCH3] |
| 18 | 4434 | τCC + [δwaggCD2,νCC] + νas’CH3 |
| 19 | 4372 | δsCH3 +νasCH3, δsCH3 +νas’CH3 |
| 20 | 4341 | 2νasCD2 |
| 21 | 4289 | τCC + δscissCD2 + [δscissCD2,νCO] |
| 22 | 4233 | νsCD2 + νasCD2 |
| 23 | 4190 | 2νsCD2, [δwaggCD2, νCC] + νasCH3 |
| 24 | 4149 | [δscissCD2, νCO] + νasCH3, [δscissCD2, νCO] +νas’CH3 |
| 25 | 4113 | δrockCH3 + νas’CH3 |
| 26 | 4089 | [δscissCD2, νCO] + νsCH3 |
| 27 | 4056 | δrockCH3 + νsCH3 |
| Peak Number | νcalc | Assignment (Major Contribution) |
|---|---|---|
| 1 | 8560 | 3νasCH2, 2νsCH2 + νasCH2 |
| 2 | 8508 | 3νasCH2 |
| 3 | 8305 | 2νsCH2 + νasCH2 |
| 4 | 7802 | 3νOD |
| 5 | 7088 | δscissCH2 + νsCH2 + νasCH2 |
| 6 | 6736 | δrockCH2 + νsCH2 + νasCH2 |
| 7 | 6706 | [νCO, δas’CD3] + νsCH2 + νasCH2 |
| 8 | 6614 | 3νas’CD3 |
| 9 | 6505 | νsCD3 +νasCD3 +νas’CD3 |
| 10 | 6382 | 2νsCD3 + νasCD3, 2νsCD3 + νas’CD3 |
| 11 | 5821 | [δoopCOD, τCC] + νasCH2 + νsCH2 |
| 12 | 5785 | 2νasCH2, δwaggCH2 + δscissCH2 + νasCH2 |
| 13 | 5638 | 2νsCH2, νsCH2 + νasCH2 |
| 14 | 5547 | νOD + νsCH2 |
| 15 | 5473 | δrockCH2 + δscissCH2 + νasCH2 |
| 16 | 5288 | 2νOD |
| 17 | 5106 | [τCC, δoopCOD] + 2δwaggCH2 |
| 18 | 4986 | 2[νCC, δsCD3] + νOD |
| 19 | 4585 | δrock’CD3 + 2δwaggCH2 |
| 20 | 4503 | [τCC, δoopCOD] + δwaggCH2 + νasCH2 |
| 21 | 4459 | 2νasCD3 |
| 22 | 4431 | [δas’CD3, νCO] + [νCC, δsCD3] + νas’CD3 |
| 23 | 4385 | δscissCH2 + νasCH2 |
| 24 | 4324 | 2νas’CD3, δscissCH2 + νsCH2 |
| 25 | 4237 | δwaggCH2 + νsCH2 |
| 26 | 4167 | δtwistCH2 + νasCH2 |
| 27 | 4112 | δtwistCH2 + νsCH2 |
| 28 | 4015 | [δrockCD3, δrockCH2] + δrockCH2 + νas’CD3 |
| 10,000–4000 cm−1 | |||||
| 2νx | 3νx | νx + νy | νx + νy + νz | 2νx + νy | |
| CH3CH2OH | 26.1 | 1.7 | 47.0 | 14.3 | 10.9 |
| CH3CH2OD | 18.0 | 2.2 | 51.2 | 17.4 | 11.1 |
| CH3CD2OH | 35.8 | 1.7 | 41.5 | 11.8 | 9.2 |
| CD3CH2OH | 40.9 | 1.2 | 32.6 | 15.1 | 10.1 |
| CD3CD2OH | 46.0 | 0.3 | 23.7 | 15.8 | 14.2 |
| CD3CD2OD | 43.1 | 2.0 | 19.2 | 17.8 | 17.9 |
| CH3CD2OD | 27.9 | 3.2 | 44.7 | 15.0 | 9.2 |
| CD3CH2OD | 36.0 | 2.5 | 35.5 | 10.8 | 15.2 |
| 10,000–7500 cm−1 | |||||
| 2νx | 3νx | νx + νy | νx + νy + νz | 2νx + νy | |
| CH3CH2OH | 0.0 | 39.7 | 0.0 | 22.3 | 38.0 |
| CH3CH2OD | 0.0 | 55.5 | 0.0 | 15.4 | 29.1 |
| CH3CD2OH | 0.0 | 43.9 | 0.0 | 30.5 | 25.6 |
| CD3CH2OH | 0.0 | 66.9 | 0.0 | 1.4 | 31.7 |
| CD3CD2OH | 0.0 | 0.0 | 0.0 | 43.0 | 57.0 |
| CD3CD2OD | 0.0 | 100.0 | 0.0 | 0.0 | 0.0 |
| CH3CD2OD | 0.0 | 69.9 | 0.0 | 16.7 | 13.4 |
| CD3CH2OD | 0.0 | 76.3 | 0.0 | 0.5 | 23.2 |
| 7500–4000 cm−1 | |||||
| 2νx | 3νx | νx + νy | νx + νy + νz | 2νx + νy | |
| CH3CH2OH | 26.5 | 1.2 | 47.6 | 14.2 | 10.5 |
| CH3CH2OD | 18.4 | 1.0 | 52.4 | 17.5 | 10.7 |
| CH3CD2OH | 36.0 | 1.4 | 41.8 | 11.7 | 9.1 |
| CD3CH2OH | 41.4 | 0.4 | 33.0 | 15.3 | 9.9 |
| CD3CD2OH | 46.0 | 0.3 | 23.7 | 15.8 | 14.2 |
| CD3CD2OD | 43.7 | 0.5 | 19.5 | 18.0 | 18.2 |
| CH3CD2OD | 28.4 | 2.0 | 45.5 | 15.0 | 9.1 |
| CD3CH2OD | 37.0 | 0.5 | 36.4 | 11.1 | 15.0 |
| Sample | Purity | D Atom Content | Other Remarks | |
|---|---|---|---|---|
| 1 | CH3CH2OD | 99% | ≥99.5% | |
| 2 | CH3CD2OH | 99% | 98% | |
| 3 | CD3CH2OH | 99% | 99% | |
| 4 | CD3CD2OH | 99% | 99.5% | |
| 5 | CD3CD2OD | >99% | ≥99.5% | anhydrous |
| 6 | CCl4 | >99% | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beć, K.B.; Grabska, J.; Huck, C.W.; Czarnecki, M.A. Spectra–Structure Correlations in Isotopomers of Ethanol (CX3CX2OX; X = H, D): Combined Near-Infrared and Anharmonic Computational Study. Molecules 2019, 24, 2189. https://doi.org/10.3390/molecules24112189
Beć KB, Grabska J, Huck CW, Czarnecki MA. Spectra–Structure Correlations in Isotopomers of Ethanol (CX3CX2OX; X = H, D): Combined Near-Infrared and Anharmonic Computational Study. Molecules. 2019; 24(11):2189. https://doi.org/10.3390/molecules24112189
Chicago/Turabian StyleBeć, Krzysztof B., Justyna Grabska, Christian W. Huck, and Mirosław A. Czarnecki. 2019. "Spectra–Structure Correlations in Isotopomers of Ethanol (CX3CX2OX; X = H, D): Combined Near-Infrared and Anharmonic Computational Study" Molecules 24, no. 11: 2189. https://doi.org/10.3390/molecules24112189
APA StyleBeć, K. B., Grabska, J., Huck, C. W., & Czarnecki, M. A. (2019). Spectra–Structure Correlations in Isotopomers of Ethanol (CX3CX2OX; X = H, D): Combined Near-Infrared and Anharmonic Computational Study. Molecules, 24(11), 2189. https://doi.org/10.3390/molecules24112189









