Abstract
Curved (non-planar) aromatic compounds have attracted significant research attention in the fields of basic chemistry and materials science. The contribution of the quinoidal structure in the curved π-conjugated structures has been proposed to be the key for materials functions. In this study, the curve effect on the quinoidal contribution was investigated in Kekulé-type singlet diradicals (S-DR1-4) as a sensitive probe for quinoidal structures in curved π-conjugated molecules. The quinoidal contribution in S-DR1-4 was found to increase with increasing the curvature of the curved structure, which was quantitatively analyzed using NBO analysis and the natural orbital occupation numbers computed by the CASSCF method. The curve effect on the singlet-triplet energy gap was examined by the CASPT2 method. The singlet-triplet energy gaps for the highly π-conjugated diradicals were determined for the first time using the CASPT2 method. Substantial quinoidal contribution was found in the curved structures of the delocalized singlet diradicals S-DR1-4, in contrast to its absence in the corresponding triplet states T-DR1-4.
1. Introduction
Curved (non-planar) aromatic compounds like fullerenes, buckybowls, and carbon nanotubes have attracted considerable attention from researchers in the fields of basic chemistry as well as materials science [1,2,3,4,5,6,7,8,9,10,11]. In general, the HOMO–LUMO energy gap of a π-conjugated molecule decreases with increasing π-conjugation, leading to red-shifted absorption spectra [12]. However, according to recent reports on cycloparaphenylenes ([n]CPPs, n being the number of benzene rings in the structure) [13,14,15,16,17,18,19], which are hoop-shaped carbon molecules, the absorption bands were blue-shifted with increasing number of benzene rings [20,21,22,23,24,25]. This has been explained by the quinoidal characteristic of CPPs having small ring size, such as [6]CPP (Figure 1a). The quinoidal character of small CPPs has been proved by Raman spectroscopic analyses [26] and size-dependent-change of emission in CPPs [27,28].
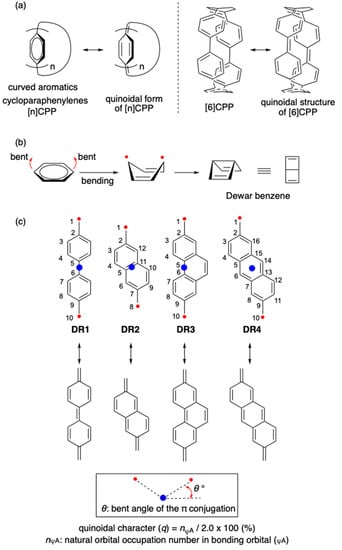
Figure 1.
(a) [n]CPPs and their quinoidal structures; (b) bent effect on the diradical character of benzene [7]; (c) curve (θ°) effect on the diradical character in DR1-4 as a sensitive probe for the quinoidal contribution (this study). The structures DR1, DR2, and DR4 were optimized in C2 symmetry. The structure DR3 was optimized in CS symmetry.
The quinoidal contribution is rationalized by the increase of diradical character in the bent structure of benzene, which is the intermediate structure for the formation of Dewar benzene [29,30,31,32] (Figure 1b). In this study, the curve effect on the quinoidal character in Kekulé-type singlet diradicals S-DR1-4 [33,34,35,36,37] is investigated to design a sensitive probe for the quinoidal contribution (q) in curved π-conjugated molecules (Figure 1c) [35,36,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55].
2. Results and Discussion
2.1. Computations for DR1
First, the curve effect on the diradical character was investigated on the 4,4′-dimethyl-1,1′-biphenyl-4,4′-diyl diradical (DR1) (Table 1, entries 1–4). The molecular structures of the singlet (S) and triplet (T) forms of DR1 were optimized to obtain C2 symmetry at the UB3LYP/6-31G(d) level of theory with Gaussian 09 (revision D.01) software (Gaussian, Inc., Wallingford, CT, USA). The broken-symmetry (BS) method [56] was used for the optimization of S-DR1 (See Supplementary Materials). The natural occupation numbers in the active orbitals were determined by the complete active-space multiconfiguration method at the CASSCF(14,14) [57]/cc-pVDZ [58] level of theory with MOLCAS 8 program package (v8.0.15-06-18) (MOLCAS, Lund, Sweden). The occupation number in orbital ψA (HOMO in the restricted Hartree-Fock (RHF) method) increased from 1.66 (θ = 0°, entry 1) to 1.80 (θ = 29°, entry 4) with increasing angle of bend (θ) in the diradical structures. The bent angles (θ) were obtained after the structural optimization of DR1 in C2 symmetry at the fixed angles of C1–C2–C6 = C10–C9–C5 = 180, 160, 140, and 135°, respectively. On the other hand, the occupation number in orbital ψB (LUMO in the RHF method) decreased from 0.35 (θ = 0°, entry 1) to 0.21 (θ = 29°, entry 4) with increasing θ. Figure 2 shows that the HOMO and LUMO orbitals correspond to the bonding and anti-bonding orbitals of the quinoid form, respectively. The quinoidal contribution (q) was given by q (%) = (nψA/2.0) × 100, nψA being the number of electrons in the HOMO orbital. The q values increased from 83 to 90 with increasing θ. The θ-dependent changes in the occupation number and q value indicates that the bonding interaction between the two phenyl-rings, leading to the formation of the quinoidal structure, increased with increasing θ. In fact, the C5–C6 distance was found to decrease from 143.0 pm (θ = 0°) to 139.6 pm (θ = 29°). The increase in quinoidal contribution was also proved by the decrease in C1–C2 bond distance and the increase in the Wiberg bond order (BO) [59] (entries 1–4). The computational results clearly indicate that the quinoidal contribution increases with increasing the extent of bending in S-DR1.

Table 1.
Curve effect, in terms of θ (°), on the natural occupation numbers in ψA (HOMO) and ψB (LUMO), quinoidal contribution (q), Wiberg bond order (BO), C1–C2 distance (pm), and singlet-triplet energy gap (ΔEST, kcal mol–1) a.
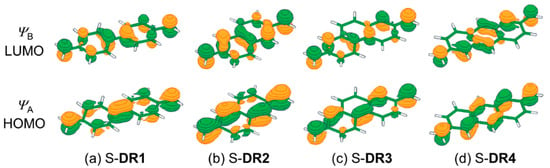
Figure 2.
The molecular orbitals ψA (HOMO) and ψB (LUMO) for (a) S-DR1, (b) S-DR2, (c) S-DR3, and (d) S-DR4.
The electronic energies of singlet ground state (11A) S- and triplet (13B) T-DR1 were computed using the complete active-space second-order multiconfigurational perturbation theory (CASPT2) [61,62], including the dynamic corrections and cc-pVDZ basis set (Table 1). Active-space CAS (14,14) encompasses all π orbitals. The MO plots and weights of the leading configurations of the CASSCF wavefunction are provided in the Supporting Information. Both S- and T-DR1 were destabilized with increasing θ, as reflected by the ΔErel,S/ΔErel,T values in Table 1. The relative energies, ΔErel,S and ΔErel,T, were calculated with respect to the singlet and triplet absolute energies, respectively, in the planar structure (θ = 0°). The singlet–triplet energy difference, ΔEST = ES − ET, increased substantially from 11.6 (θ = 0°, entry 1) to 19.3 kcal mol–1 (θ = 29°, entry 4). As judged by the curve effect on the electronic energies of S-DR1 and T-DR1, i.e., ΔErel,S/ΔErel,T, the triplet state was destabilized more significantly than the singlet one with increasing θ. For example, at θ = 29° ΔErel,S and ΔErel,T were calculated to be +21.0 and +28.7 kcal mol–1, respectively (entry 4). The curve effect on ΔEST is rationalized by the quinoidal contribution to the curved structure of the singlet state S-DR1, which stabilized the singlet state, but not the triplet state.
The quinoidal contribution in S-DR1 was also rationalized by the curve effect on the dihedral angle (θd = C4–C5–C6–C7) of the biphenyl moiety (Figure 3). The dihedral angle θd decreased to nearly 0° from 7.4° when the bent angle θ increased from 0° to 29° (Figure 3a,b). In contrast to the significant curve effect on θd, the corresponding dihedral angle was nearly the same in T-DR1 because there was no quinoidal contribution in the triplet state (Figure 3c).
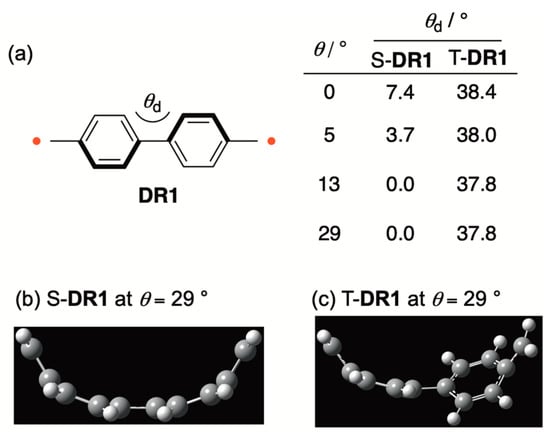
Figure 3.
(a) The curve effect on the dihedral angle (θd = C4–C5–C6–C7) in DR1; (b) the optimized structure of S-DR1 at θ = 29°; (c) the optimized structure of T-DR1 at θ = 29°.
2.2. Computations for DR2-4
Similar computations were conducted for the π-extended Kekulé-type diradicals, viz., 2,6-dimethylnaphthalene-2,6-diyl diradical (DR2) (entries 5–8), 2,7-dimethylphenanthrene-2,7-diyl diradical (DR3) (entries 9–12), and 2,6-dimethylanthracene-2,6-diyl diradical (DR4) (entries 13–16) to analyze the quinoidal contribution to the curved singlet states. As found for DR1, the quinoidal contribution (q) to the singlet state of DR2-4 increased with increasing θ (entries 5–16). For DR2, the q value increased from 88.5 to 92.5 with increasing θ. The q values for other diradicals DR3 and DR4 were also found to increase with increasing their curved character: from 79 to 93.5 for S-DR3 and from 82.5 to 91.0 for S-DR4. Consistent with the increase in quinoidal contribution, the C1–C2 bond in the singlet state became shorter than that in the triplet state, indicating that the quinoidal contribution to the singlet state increases with increasing θ. Furthermore, the Wiberg BOs of C1–C2 increased with increasing θ in DR2-4: from 1.68 to 1.76 for S-DR2, from 1.47 to 1.75 for S-DR3, and from 1.54 to 1.73 for S-DR4. As for DR1, the significant curve effect on the singlet–triplet energy gap (ΔEST) was also computed for DR2-4. The energy gap increased with increasing θ, because the destabilization with increasing θ in the triplet states T-DR2-4 were larger than those in the corresponding singlet states.
3. Conclusions
In this study, the quinoidal contributions in curved aromatic structures were quantitatively analyzed by computing the curve effect on the diradical character of DR1-4 at high-level ab initio calculations using the CASPT2/CASSCF method. The singlet-triplet energy gaps for the highly π-conjugated diradicals were determined for the first time using the CASPT2 method. The diradical character in the singlet states decreased with increasing the curve angle (θ) of the aromatic ring. In other words, the quinoidal contribution increases with increasing θ of the aromatic ring. The increases in the quinoidal contribution in the curved diradicals are consistent with the curve effect on the quinoidal character of hoop-shaped molecules, which has been intensively investigated in the last decade. The curved structure can increase the π-conjugation length with decreasing the HOMO-LUMO gap, which should be smaller than that in the planar molecules having the same number of π-electrons. The molecular design is expected to be appropriate for future soft-materials.
Supplementary Materials
The following are available online.
Author Contributions
Writing-original draft preparation, M.M.; CASPT2/CASSCF computations, I.A.; conceptualization M.A.; writing–review and editing, I.A. and M.A.
Funding
M.A. gratefully acknowledges financial support by JSPS KAKENHI (Grant No. JP17H03022). I.A. also acknowledge the Isabella cluster (http://isabella.srce.hr) at the Zagreb University Computing Center (SRCE).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Barth, W.E.; Lawton, R.G. Dibenzo[ghi,mno]fluoranthene. J. Am. Chem. Soc. 1966, 88, 380–381. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; Obrien, S.C.; Curl, R.F.; Smalley, R.E. C-60—Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Scott, L.T. Fragments of fullerenes: Novel syntheses, structures and reactions. Pure Appl. Chem. 1996, 68, 291–300. [Google Scholar] [CrossRef]
- Sakurai, H.; Daiko, T.; Hirao, T. A synthesis of sumanene, a fullerene fragment. Science 2003, 301, 1878. [Google Scholar] [CrossRef] [PubMed]
- Scott, L.T. Methods for the Chemical Synthesis of Fullerenes. Angew. Chem. Int. Ed. 2004, 43, 4994–5007. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.T.; Siegel, J.S. Aromatic molecular-bowl hydrocarbons: Synthetic derivatives, their structures, and physical properties. Chem. Rev. 2006, 106, 4843–4867. [Google Scholar] [CrossRef]
- Akasaka, T.; Osuka, A.; Fukuzumi, S.; Kandori, H.; Aso, Y. (Eds.) Chemical Science of π-Electron Systems; Springer: Tokyo, Japan, 2015. [Google Scholar]
- Nestoros, E.; Stuparu, M.C. Corannulene: A molecular bowl of carbon with multifaceted properties and diverse applications. Chem. Commun. 2018, 54, 6503–6519. [Google Scholar] [CrossRef]
- Márquez, I.R.; Castro-Ferández, S.; Millán, A.; Campaña, A.G. Synthesis of distorted nanographenes containing seven- and eight-membered carbocycles. Chem. Commun. 2018, 54, 6705–6718. [Google Scholar] [CrossRef]
- Sun, Z.; Matsuno, T.; Isobe, H. Stereoisomerism and Structures of Rigid Cylindrical Cycloarylenes. Bull. Chem. Soc. Jpn. 2018, 91, 907–921. [Google Scholar] [CrossRef]
- Meier, H.; Stalmach, U.; Kolshorn, H. Effective conjugation length and UV/vis spectra of oligomers. Acta Polym. 1997, 48, 379–384. [Google Scholar] [CrossRef]
- Kammermeier, S.; Jones, P.G.; Herges, R. Ring-Expanding Metathesis of Tetradehydro- anthracene-Synthesis and Structure of a Tubelike, Fully Conjugated Hydrocarbon. Angew. Chem. Int. Ed. 1996, 35, 2669–2671. [Google Scholar] [CrossRef]
- Kawase, T.; Kurata, H. Ball-, bowl-, and belt-shaped conjugated systems and their complexing abilities: Exploration of the concave-convex π-π interaction. Chem. Rev. 2006, 106, 5250–5273. [Google Scholar] [CrossRef] [PubMed]
- Tahara, K.; Tobe, Y. Molecular loops and belts. Chem. Rev. 2006, 106, 5274–5290. [Google Scholar] [CrossRef] [PubMed]
- Jasti, R.; Bhattacharjee, J.; Neaton, J.B.; Bertozzi, C.R. Synthesis, Characterization, and Theory of [9]-, [12]-, and [18]Cycloparaphenylene: Carbon Nanohoop Structures. J. Am. Chem. Soc. 2008, 130, 17646–17647. [Google Scholar] [CrossRef] [PubMed]
- Takaba, H.; Omachi, H.; Yamamoto, Y.; Bouffard, J.; Itami, K. Selective Synthesis of 12 Cycloparaphenylene. Angew. Chem. Int. Ed. 2009, 48, 6112–6116. [Google Scholar] [CrossRef] [PubMed]
- Yamago, S.; Watanabe, Y.; Iwamoto, T. Synthesis of 8 Cycloparaphenylene from a Square-Shaped Tetranuclear Platinum Complex. Angew. Chem. Int. Ed. 2010, 49, 757–759. [Google Scholar] [CrossRef] [PubMed]
- Omachi, H.; Matsuura, S.; Segawa, Y.; Itami, K. A Modular and Size-Selective Synthesis of n Cycloparaphenylenes: A Step toward the Selective Synthesis of n, n Single-Walled Carbon Nanotubes. Angew. Chem. Int. Ed. 2010, 49, 10202–10205. [Google Scholar] [CrossRef] [PubMed]
- Iwamoto, T.; Watanabe, Y.; Sakamoto, Y.; Suzuki, T.; Yamago, S. Selective and Random Syntheses of n Cycloparaphenylenes (n = 8–13) and Size Dependence of Their Electronic Properties. J. Am. Chem. Soc. 2011, 133, 8354–8361. [Google Scholar] [CrossRef] [PubMed]
- Segawa, Y.; Fukazawa, A.; Matsuura, S.; Omachi, H.; Yamaguchi, S.; Irle, S.; Itami, K. Combined experimental and theoretical studies on the photophysical properties of cycloparaphenylenes. Org. Biomol. Chem. 2012, 10, 5979–5984. [Google Scholar] [CrossRef]
- Wong, B.M. Optoelectronic Properties of Carbon Nanorings: Excitonic Effects from Time-Dependent Density Functional Theory. J. Phys. Chem. C 2009, 113, 21921–21927. [Google Scholar] [CrossRef] [PubMed]
- Golder, M.R.; Jasti, R. Syntheses of the Smallest Carbon Nanohoops and the Emergence of Unique Physical Phenomena. Acc. Chem. Res. 2015, 48, 557–566. [Google Scholar] [CrossRef] [PubMed]
- Darzi, E.R.; Jasti, R. The dynamic, size-dependent properties of 5–12 cycloparaphenylenes. Chem. Soc. Rev. 2015, 44, 6401–6410. [Google Scholar] [CrossRef]
- Segawa, Y.; Yagi, A.; Matsui, K.; Itami, K. Design and Synthesis of Carbon Nanotube Segments. Angew. Chem. Int. Ed. 2016, 55, 5136–5158. [Google Scholar] [CrossRef] [PubMed]
- Fujitsuka, M.; Iwamoto, T.; Kayahara, E.; Yamago, S.; Majima, T. Enhancement of the Quinoidal Character for Smaller n Cycloparaphenylenes Probed by Raman Spectroscopy. ChemPhysChem 2013, 14, 1570–1572. [Google Scholar] [CrossRef] [PubMed]
- Fujitsuka, M.; Cho, D.W.; Iwamoto, T.; Yamago, S.; Majima, T. Size-dependent fluorescence properties of n cycloparaphenylenes (n = 8–13), hoop-shaped pi-conjugated molecules. Phys. Chem. Chem. Phys. 2012, 14, 14585–14588. [Google Scholar] [CrossRef]
- Fujitsuka, M.; Lu, C.; Iwamoto, T.; Kayahara, E.; Yamago, S.; Majima, T. Properties of Triplet-Excited n Cycloparaphenylenes (n = 8–12): Excitation Energies Lower than Those of Linear Oligomers and Polymers. J. Phys. Chem. A 2014, 118, 4527–4532. [Google Scholar] [CrossRef]
- Jenneskens, L.W.; Vaneenige, E.N.; Louwen, J.N. A P-orbital axis vector (POAV) analysis of boat-shaped benzenes. New J. Chem. 1992, 16, 775–779. [Google Scholar]
- Tobe, Y. Strained N Cyclophanes. Cyclophanes 1994, 172, 1–40. [Google Scholar]
- Bickelhaupt, F. Small cyclophanes—The bent benzene business. Pure Appl. Chem. 1990, 62, 373–382. [Google Scholar] [CrossRef][Green Version]
- Dewar, M.J.S.; Wade, L.E. Study of mechanism of cope rearrangement. J. Am. Chem. Soc. 1977, 99, 4417–4424. [Google Scholar] [CrossRef]
- Thiele, J.; Balhorn, H. Ueber einen chinoïden Kohlenwasserstoff. Chem. Berichte 1904, 37, 1463–1470. [Google Scholar] [CrossRef]
- Tschichibabin, A.E. Über einige phenylierte derivate des p,p-Ditolyls. Chem. Berichte 1907, 40, 1810–1819. [Google Scholar] [CrossRef]
- Müller, E.; Pfanz, H. Über biradikaloide Terphenylderivate. Chem. Berichte 1941, 74, 1051–1074. [Google Scholar] [CrossRef]
- Müller, E.; Hermann, P. Über ein biradikaloides Quterphenylderivat. Chem. Berichte 1941, 74, 1075–1083. [Google Scholar] [CrossRef]
- Schmidt, R.; Brauer, H.-D. The Energetic Positions of the Lowest Singlet and Triplet State of the Schlenk and of the Müller Hydrocarbon. Angew. Chem. Int. Ed. Engl. 1971, 10, 506. [Google Scholar] [CrossRef]
- Doering, W.V.E.; Toscano, V.G.; Beasley, G.H. Kinetics of cope rearrangement of 1,1-dideuteriohexa-1,5-diene. Tetrahedron 1971, 27, 5299–5306. [Google Scholar] [CrossRef]
- Kolc, J.; Michl, J. Pi,Pi-Biradicaloid Hydrocarbons—Pleiadene Family. I. Photochemical Preparation from Cyclobutene Precursors. J. Am. Chem. Soc. 1973, 95, 7391–7401. [Google Scholar] [CrossRef]
- Michl, J.; Bonacickoutecky, V. Biradicals and biradicaloids—A unified view. Tetrahedron 1988, 44, 7559–7585. [Google Scholar] [CrossRef]
- Shimizu, A.; Tobe, Y. Indeno 2,1-a fluorene: An Air-Stable ortho-Quinodimethane Derivative. Angew. Chem. Int. Ed. 2011, 50, 6906–6910. [Google Scholar] [CrossRef]
- Abe, M. Diradicals. Chem. Rev. 2013, 113, 7011–7088. [Google Scholar] [CrossRef] [PubMed]
- Sun, Z.; Zeng, Z.B.; Wu, J.S. Zethrenes, Extended p-Quinodimethanes, and Periacenes with a Singlet Biradical Ground State. Acc. Chem. Res. 2014, 47, 2582–2591. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.B.; Shi, X.L.; Chi, C.Y.; Navarrete, J.T.L.; Casado, J.; Wu, J.S. Pro-aromatic and anti-aromatic π-conjugated molecules: An irresistible wish to be diradicals. Chem. Soc. Rev. 2015, 44, 6578–6596. [Google Scholar] [CrossRef] [PubMed]
- Kubo, T. Recent Progress in Quinoidal Singlet Biradical Molecules. Chem. Lett. 2015, 44, 111–122. [Google Scholar] [CrossRef]
- Frederickson, C.K.; Zalcharov, L.N.; Haley, M.M. Modulating Paratropicity Strength in Diareno-Fused Antiaromatics. J. Am. Chem. Soc. 2016, 138, 16827–16838. [Google Scholar] [CrossRef] [PubMed]
- Konishi, A.; Okada, Y.; Nakano, M.; Sugisaki, K.; Sato, K.; Takui, T.; Yasuda, M. Synthesis and Characterization of Dibenzo[a,f]pentalene: Harmonization of the Antiaromatic and Singlet Biradical Character. J. Am. Chem. Soc. 2017, 139, 15284–15287. [Google Scholar] [CrossRef] [PubMed]
- Frederickson, C.K.; Rose, B.D.; Haley, M.M. Explorations of the Indenofluorenes and Expanded Quinoidal Analogues. Acc. Chem. Res. 2017, 50, 977–987. [Google Scholar] [CrossRef] [PubMed]
- Li, S.Y.; Yuan, N.N.; Fang, Y.; Chen, C.; Wang, L.; Feng, R.; Zhao, Y.; Cui, H.Y.; Wang, X.P. Studies on the Bridge Dependence of Bis(triarylamine) Diradical Dications: Long-Range π-Conjugation and π-π Coupling Systems. J. Org. Chem. 2018, 83, 3651–3656. [Google Scholar] [CrossRef]
- Li, G.; Gopalakrishna, T.Y.; Phan, H.; Herng, T.S.; Ding, J.; Wu, J. From Open-shell Singlet Diradicaloid to Closed-Shell Global Antiaromatic Macrocycles. Angew. Chem. Int. Ed. 2018, 57, 7166–7170. [Google Scholar] [CrossRef]
- Dressler, J.J.; Teraoka, M.; Espejo, G.L.; Kishi, R.; Takamuku, S.; Gómez-Garcia, C.J.; Zakharov, L.N.; Nakano, M.; Casado, J.; Haley, M.M. Thiophene and its sulfur inhibit indenoindenodibenzothiophene diradicals from low-energy lying thermal triplets. Nat. Chem. 2018, 10, 1134–1140. [Google Scholar] [CrossRef]
- Ravat, P.; Solomek, T.; Haussinger, D.; Blacque, O.; Juricek, M. Dimethylcethrene: A Chiroptical Diradicaloid Photoswitch. J. Am. Chem. Soc. 2018, 140, 10839–10847. [Google Scholar] [CrossRef] [PubMed]
- Tokunaga, A.; Mutoh, K.; Hasegawa, T.; Abe, J. Reversible Valence Photoisomerization between Closed-Shell Quinoidal and Open-Shell Biradical Forms. J. Phys. Chem. Lett. 2018, 9, 1833–1837. [Google Scholar] [CrossRef] [PubMed]
- Rottschafer, D.; Ho, N.K.T.; Neumann, B.; Stammler, H.G.; van Gastel, M.; Andrada, D.M.; Ghadwal, R.S. N-Heterocyclic Carbene Analogues of Thiele and Chichibabin Hydrocarbons. Angew. Chem. Int. Ed. 2018, 57, 5838–5842. [Google Scholar] [CrossRef] [PubMed]
- Hansmann, M.M.; Melaimi, M.; Munz, D.; Bertrand, G.J. Modular Approach to Kekulé Diradicaloids Derived from Cyclic (Alkyl)(amino)carbenes. Am. Chem. Soc. 2018, 140, 2546–2554. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, K.; Jensen, F.; Dorigo, A.; Houk, K.N. A spin correction procedure for unrestricted Hartree-Fock and Møller-Plesset wavefunctions for singlet diradicals and polyradicals. Chem. Phys. Lett. 1988, 149, 537–542. [Google Scholar] [CrossRef]
- Hegarty, D.; Robb, M.A. Application of unitary group-methods to configuration-interaction calculations. Mol. Phys. 1979, 38, 1795–1812. [Google Scholar] [CrossRef]
- Woon, D.E.; Dunning, T.H. Gaussian-basis sets for use in correlated molecular calculations. 3. the atoms aluminum through argon. J. Chem. Phys. 1993, 98, 1358–1371. [Google Scholar] [CrossRef]
- Wiberg, K.B. Application of the Pople-Santry-Segal CNDO Method to the Cyclopropylcarbinyl and Cyclobutyl Cation and to Bicyclobutane. Tetrahedron 1966, 24, 1083–1096. [Google Scholar] [CrossRef]
- Weinhold, F.; Landis, C.R. Discovering Chemistry with Natural Bond Orbitals; Wiley: New York, NY, USA, 2012. [Google Scholar]
- Andersson, K.; Malmqvist, P.A.; Roos, B.O.; Sadlej, A.J.; Wolinski, K. 2nd-order perturbation-theory with a CASSCF reference function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar] [CrossRef]
- Andersson, K.; Malmqvist, P.A.; Roos, B.O. 2nd-order perturbation-theory with a complete active space self-consistent field reference function. J. Chem. Phys. 1992, 96, 1218–1226. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).