Abstract
The Cartesian product and join are two classical operations in graphs. Let be the degree of a vertex in line graph of a graph . The edge versions of atom-bond connectivity () and geometric arithmetic () indices of G are defined as and , respectively. In this paper, and indices for certain Cartesian product graphs (such as , and ) are obtained. In addition, and indices of certain join graphs (such as , , and ) are deduced. Our results enrich and revise some known results.
1. Introduction
The invariants based on the distance or degree of vertices in molecules are called topological indices. In theoretical chemistry, physics and graph theory, topological indices are the molecular descriptors that describe the structures of chemical compounds, and they help us to predict certain physico-chemical properties. The first topological index, Wiener index, was published in 1947 [1], and the edge version of the Wiener index was proposed by Iranmanesh et al. in 2009 [2]. Because the important effects of the topological indices are proved in chemical research, more and more topological indices are studied, including the classical atom-bond connectivity index and the geometric arithmetic index.
Let be a simple connected graph. Denote by and the vertex set and edge set of , respectively. Let , , and be a path, a cycle, a complete graph and a star, respectively, on vertices. represents edge-connecting vertices and . is an open neighborhood of vertex , i.e., . Denote by (simply ) the degree of vertex of graph , i.e., . Let or be the line graph of such that each vertex of represents an edge of and two vertices of are adjacent if and only if their corresponding edges share a common endpoint in [3]. It is known that the line graph of any graph is claw-free. Denote by the degree of edge in , which is the number of edges sharing a common endpoint with edge in , or the degree of vertex in . We denote by (or ) the set of edges with degrees and of end vertices and in (or in ), i.e., or . The distance (or for short) between and in is the length of a shortest path.
The atom-bond connectivity (ABC) index was proposed by Estrada et al. in 1998 [4]. The ABC index is defined as:
where and are the degrees of the vertices and in . Meanwhile, the edge version of the ABC index is:
where and are the degrees of the edges and , respectively, in . The recent research on edge version ABC index can be referred to Gao et al. [5].
The geometric arithmetic (GA) index was proposed by Vukicevic and Furthla in 2009 [6]. The GA index is defined as
The edge version of the GA index was proposed by Mahmiani et al. [7] and is
Recent research on the edge-version GA index can be referred to the articles [5,8,9,10,11,12,13,14,15,16]. In addition, Das [17] obtained the upper and lower bounds of the ABC index of trees. Furtula et al. [18] found the chemical trees with extremal ABC values. Fath-Tabar et al. [19] obtained some inequalities for the ABC index of a series of graph operations. Chen et al. [20] obtained some upper bounds for the ABC index of graphs with given vertex connectivity. Das and Trinajstić [21] compared the GA and ABC indices for chemical trees and molecular graphs. Xing et al. [22] gave the upper bound for the ABC index of trees with perfect matching and characterized the unique extremal tree.
Based on the results, and indices for certain Cartesian product graphs (such as , and ) are obtained. In addition, and indices of certain join graphs (such as , , and ) are deduced. Our results extend and enrich some known results [5,23,24].
2. Main Results
It is known that the Cartesian product and join operation are very complicated. In this section, we present these two classical type of graphs.
2.1. Cartesian Product Graphs
In graph theory, the Cartesian product of graphs and is a graph such that the vertex set of is the Cartesian product ; and any two vertices () and () are adjacent in if and only if either and are adjacent with in or and are adjacent with in . The graph and the line graph of are illustrated in Figure 1. In the following, we discuss the edge-version ABC and GA indices of some Cartesian product graphs.
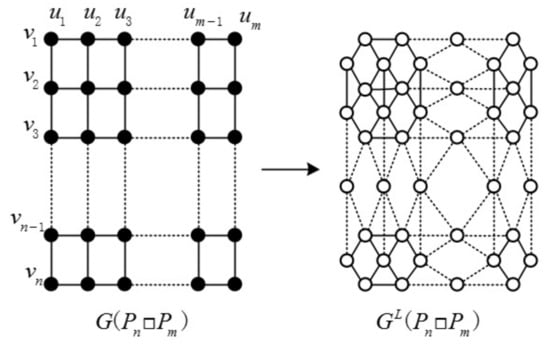
Figure 1.
and the line graph of .
Theorem 1.
If, then
Proof.
Let , we have has edges. Moreover, , , , , , , and .
By now, the proof is complete.
Theorem 2.
If, then
Proof.
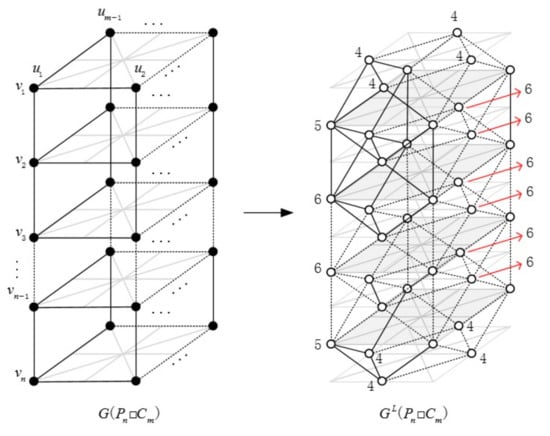
Let , we have has edges. Moreover, , , and . In Figure 2, the degrees of vertices in line graph are displayed near the corresponding vertices.

Figure 2.
and .
In the end, the proof is complete.
Theorem 3.
If, then
Proof.
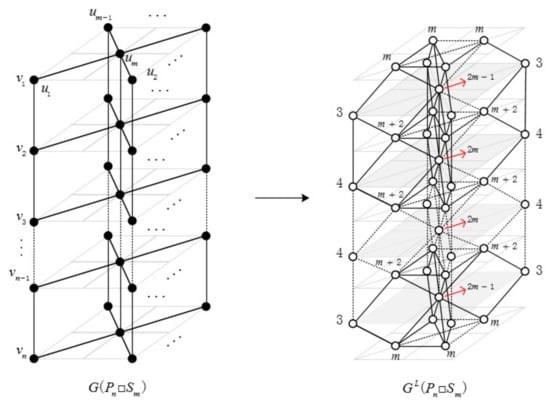
Let , we have has edges. Moreover, , , , , , , , , , , and . In Figure 3, the degrees of vertices in line graph are displayed near by the corresponding vertices.

Figure 3.
and .
Until now, the proof is complete.
2.2. Join Graph
The results of and indices of , , and , which were first established by [7], as well as the and indices of some join graphs, such as , , , and , created by , and were obtained by [5]. However, there are some problems in the calculation of the and indices of join graph in [5].
The join graph operation’s definition is given as follows: If we are given two graphs and and two vertices , , the join graph is obtained by merging and into one vertex. The certain join graphs and are illustrated in Figure 4 and Figure 5, respectively.
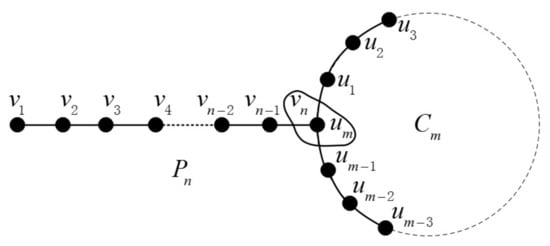
Figure 4.
The join graph of .
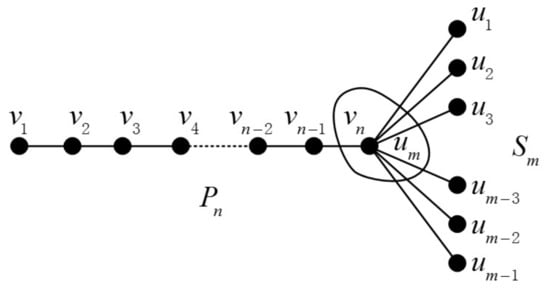
Figure 5.
The join graph of .
Theorem A is stated in [5]. However, the result is not correct. In this paper, we correct the result of Theorem A and restate it in Theorem 4 as follows:
Theorem A.
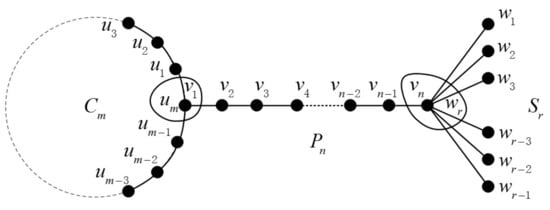
If, then
The join graph of is illustrated in Figure 6. It can be seen that is 2 and is in , so we have one edge of types and in .

Figure 6.
The join graph of .
Theorem 4.
If, then we have
Proof.
Let , we have , , , , and .
Remark: The result of is the same as that of [5], only because the . We must note .
Now the proof is complete.
Theorem 5.


Figure 7.
The join graph of .
Proof.
Let , we have and .
Now the proof is complete.
Theorem 6.
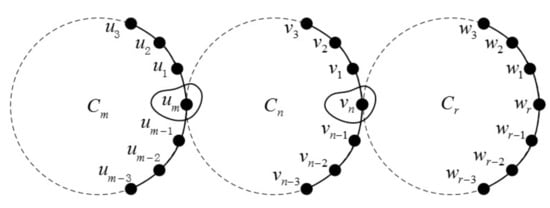

Figure 8.
The join graph of .
Proof.
Let , we have , and .
Now the proof is complete.
Theorem 7.
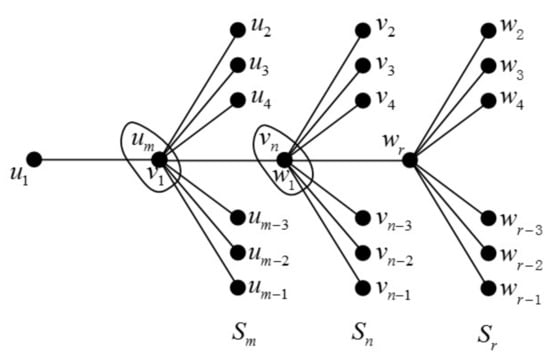

Figure 9.
The join graph of .
Proof.
Let , we have , , , , , , and .
Now the proof is complete.
3. Conclusions
The physical and chemical properties of proteins, DNAs and RNAs are very important for human disease and various approaches have been proposed to predict, validate and identify their structures and features [25,26]. Among these, topological indices were proved to be very helpful in testing the chemical properties of new chemical or physical materials such as new drugs or nanomaterials. Topological indices play an important role in studying the topological properties of chemical compounds, especially organic materials i.e., carbon containing molecular structures.
Various topological indices provide a better correlation for certain physico-chemical properties. Hence, the edge version ABC and GA indices for some special Cartesian product graphs and certain join graphs are described by graph structure analysis and a mathematical derivation method in this paper. The results of the current study also have promising prospects for applications in chemical and material engineering. The conclusions we draw here will not work for other classes of indices such as distance-based and distance adjacency-based topological indices. Thus a similar kind of study is needed for other classes of indices which might be a future direction in this area of mathematical chemistry.
Author Contributions
X.Z. contributes for conceptualization, designing the experiments and analyzed the data curation, he wrote the initial draft of the paper which were investigated and approved by Z.S. and J.-B.L. H.J. contribute for computing and performed experiments. J.-B.L. contributes for validation and formal analyzing. Z.S. contributes for supervision, funding and methodology and wrote the final draft. All authors read and approved the final version of the paper.
Funding
This work was supported by Applied Basic Research (Key Project) of the Sichuan Province under grant 2017JY0095, the key project of the Sichuan Provincial Department of Education under grant 17ZA0079 and 18ZA0118, the Soft Scientific Research Foundation of Sichuan Provincial Science and Technology Department (18RKX1048).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 7–20. [Google Scholar] [CrossRef]
- Iranmanesh, A.; Gutman, I.; Khormali, O.; Mahmiani, A. The edge versions of the wiener index. MATCH Commun. Math. Comput. Chem. 2009, 61, 663–672. [Google Scholar]
- Harary, F.; Norman, R.Z. Some properties of line digraphs. Rendiconti del Circolo Matematico di Palermo 1960, 9, 161–169. [Google Scholar] [CrossRef]
- Estrada, E.; Torres, L.; Rodriguez, L.; Gutman, I. An atom-bond connectivity index: Modelling the enthalpy of formation of Alkanes. Indian J. Chem. 1998, 37A, 849–855. [Google Scholar]
- Gao, W.; Farahani, M.; Wang, S.; Husin, M.N. On the edge-version atom-bond connectivity and geometric arithmetic indices of certain graph operations. Appl. Math. Comput. 2017, 308, 11–17. [Google Scholar] [CrossRef]
- Vukicevic, D.; Furtula, B. Topological index based on the ratios of geometric and arithmetical means of end-vertex degrees of edges. J. Math. Chem. 2009, 46, 1369–1376. [Google Scholar] [CrossRef]
- Mahmiani, A.; Khormali, O.; Iranmanesh, A. On the edge version of geometric-arithmetic index. Digest J. Nanomater. Biostruct. 2012, 7, 411–414. [Google Scholar]
- Liu, J.; Pan, X.; Yu, L.; Li, D. Complete characterization of bicyclic graphs with minimal Kirchhoff index. Discrete Appl. Math. 2016, 200, 95–107. [Google Scholar] [CrossRef]
- Liu, J.; Wang, W.; Zhang, Y.; Pan, X. On degree resistance distance of cacti. Discrete Appl. Math. 2016, 203, 217–225. [Google Scholar] [CrossRef]
- Li, X.L.; Shi, Y.T. A survey on the Randic’ index. MATCH Commun. Math. Comput. Chem. 2008, 59, 127–156. [Google Scholar]
- Randić, M. The connectivity index 25 years after. J. Mol. Graph. Modell. 2001, 20, 19–35. [Google Scholar] [CrossRef]
- Ma, J.; Shi, Y.; Wang, Z.; Yue, J. On Wiener polarity index of bicyclic networks. Sci. Rep. 2016, 6, 19066. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y. Note on two generalizations of the Randić index. Appl. Math. Comput. 2015, 265, 1019–1025. [Google Scholar] [CrossRef]
- Estes, J.; Wei, B. Sharp bounds of the Zagreb indices of k-trees. J. Comb. Optim. 2014, 27, 271–291. [Google Scholar] [CrossRef]
- Ji, S.; Wang, S. On the sharp lower bounds of Zagreb indices of graphs with given number of cut vertices. J. Math. Anal. Appl. 2018, 458, 21–29. [Google Scholar] [CrossRef]
- Zafar, S.; Nadeem, M.F.; Zahid, Z. On the edge version of geometric-arithmetic index of nanocones. Stud. Univ. Babes-Bolyai Chem. 2016, 61, 273–282. [Google Scholar]
- Das, K.C.; Trinajstić, N. Comparison between first geometric-arithmetic index and atom-bond connectivity index. Chem. Phys. Lett. 2010, 497, 149–151. [Google Scholar] [CrossRef]
- Furtula, B.; Graovac, A. Atom-bond connectivity index of trees. Discrete Appl. Math. 2009, 157, 2828–2835. [Google Scholar] [CrossRef]
- Fath-Tabar, G.H.; Vaez-Zadeh, B.; Ashrafi, A.R.; Graova, A. Some inequalities for the atom-bond connectivity index of graph operations. Discrete Appl. Math. 2011, 159, 1323–1330. [Google Scholar] [CrossRef]
- Chen, J.; Liu, J.; Guo, X. Some upper bounds for the atom-bond connectivity index of graphs. Appl. Math. Lett. 2012, 25, 1077–1081. [Google Scholar] [CrossRef]
- Das, K.C. Atom-bond connectivity index of graphs. Discrete Appl. Math. 2010, 158, 1181–1188. [Google Scholar] [CrossRef]
- Xing, R.; Zhou, B.; Du, Z. Further results on atom-bond connectivity index of trees. Discrete Appl. Math. 2010, 158, 1536–1545. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, P.; Gao, Y.; Gutman, I.; Zhang, X. On the maximum ABC index of graphs without pendent vertices. Appl. Math. Comp. 2017, 315, 298–312. [Google Scholar] [CrossRef]
- Shao, Z.; Wu, P.; Zhang, X.; Dimitrov, D.; Liu, J. On the maximum ABC index of graphs with prescribed size and without pendent vertices. IEEE Access 2018, 6, 27604–27616. [Google Scholar] [CrossRef]
- Zeng, X.; Lin, W.; Guo, M.; Zou, Q. A comprehensive overview and evaluation of circular RNA detection tools. PLoS Comput. Biol. 2017, 13, e1005420. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Liao, Y.; Liu, Y.; Zou, Q. Prediction and validation of disease genes using HeteSim Scores. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 687–695. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not available. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).