Regularized Multi-View Subspace Clustering for Common Modules Across Cancer Stages
Abstract
:1. Introduction
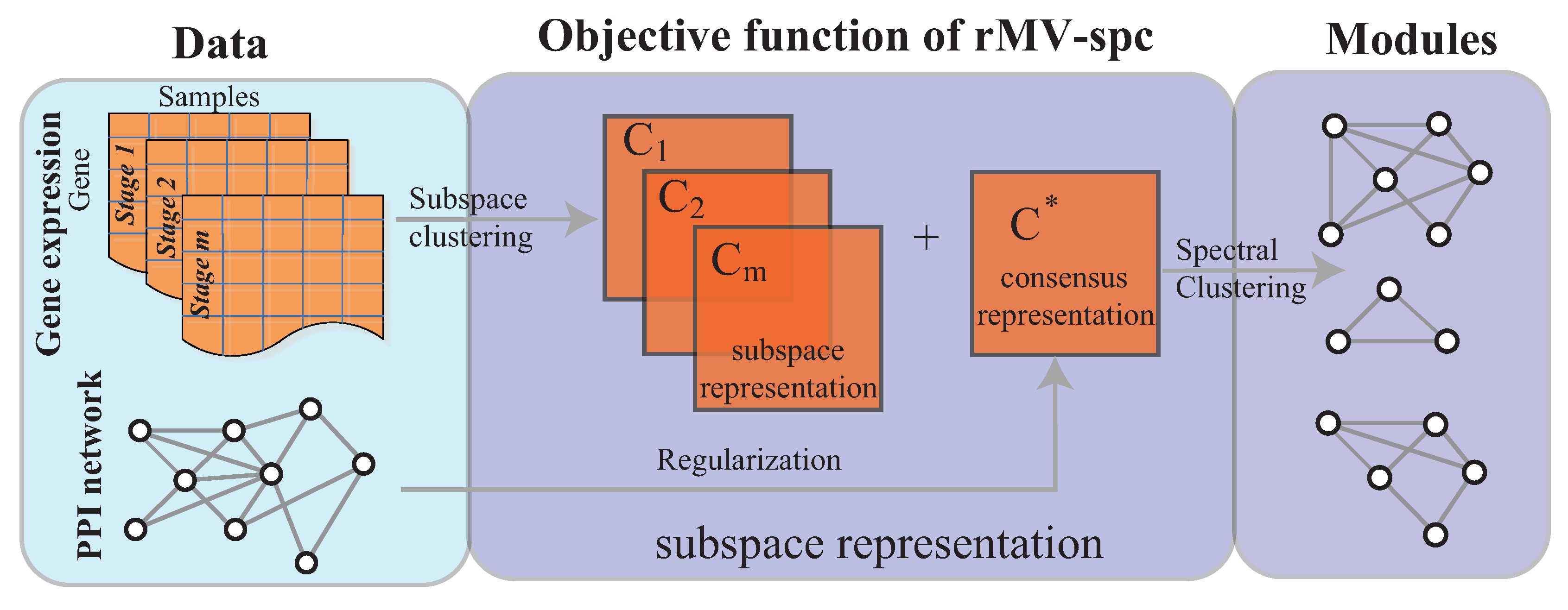
2. Methods
2.1. Preliminaries
2.2. Procedure of Algorithm
| Algorithm 1 The rMV-spc algorithm |
| Input: : Gene expression data : Protein interaction network Output: : Common modules
|
3. Materials
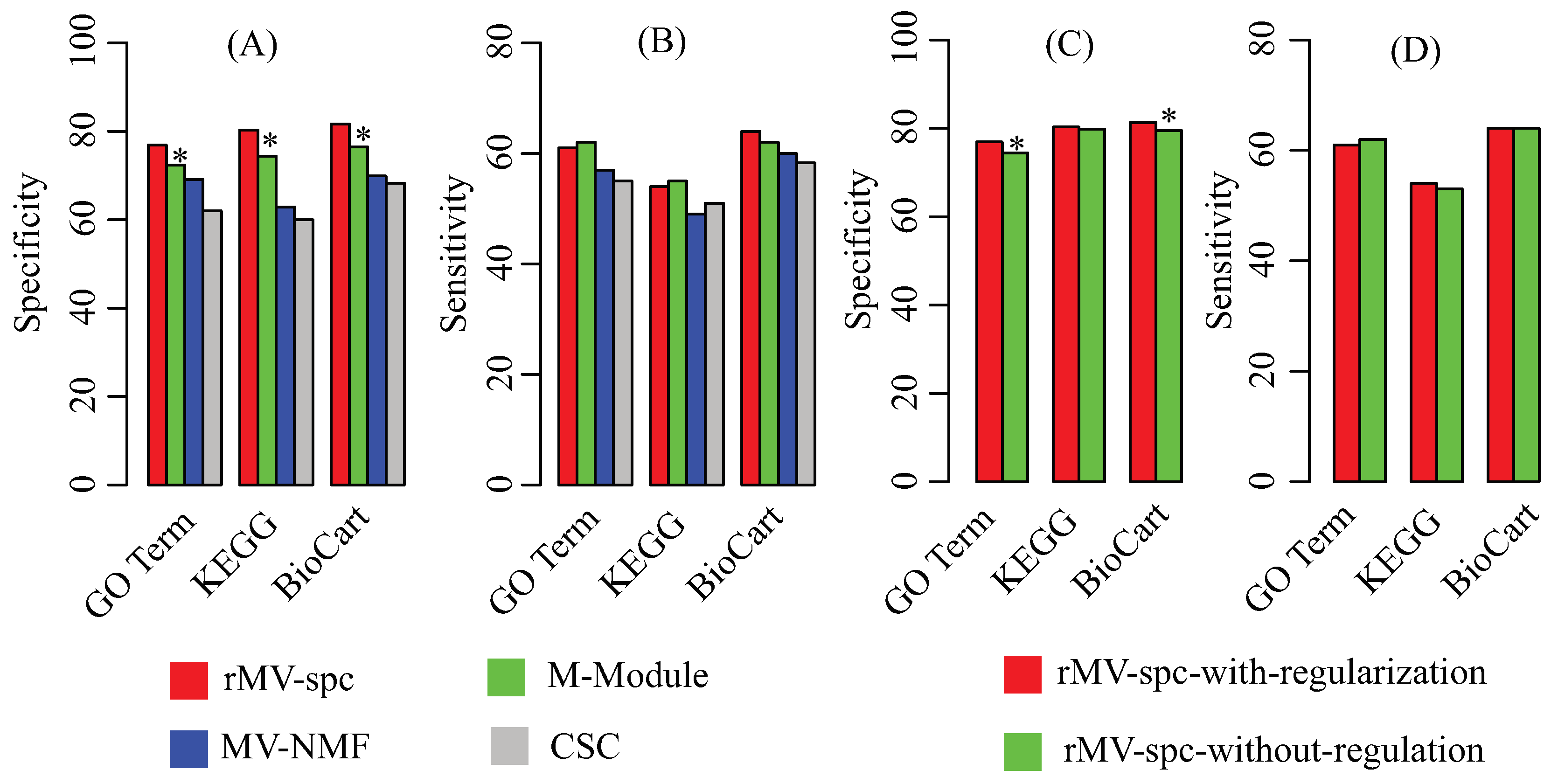
3.1. Statistical Significance of Modules
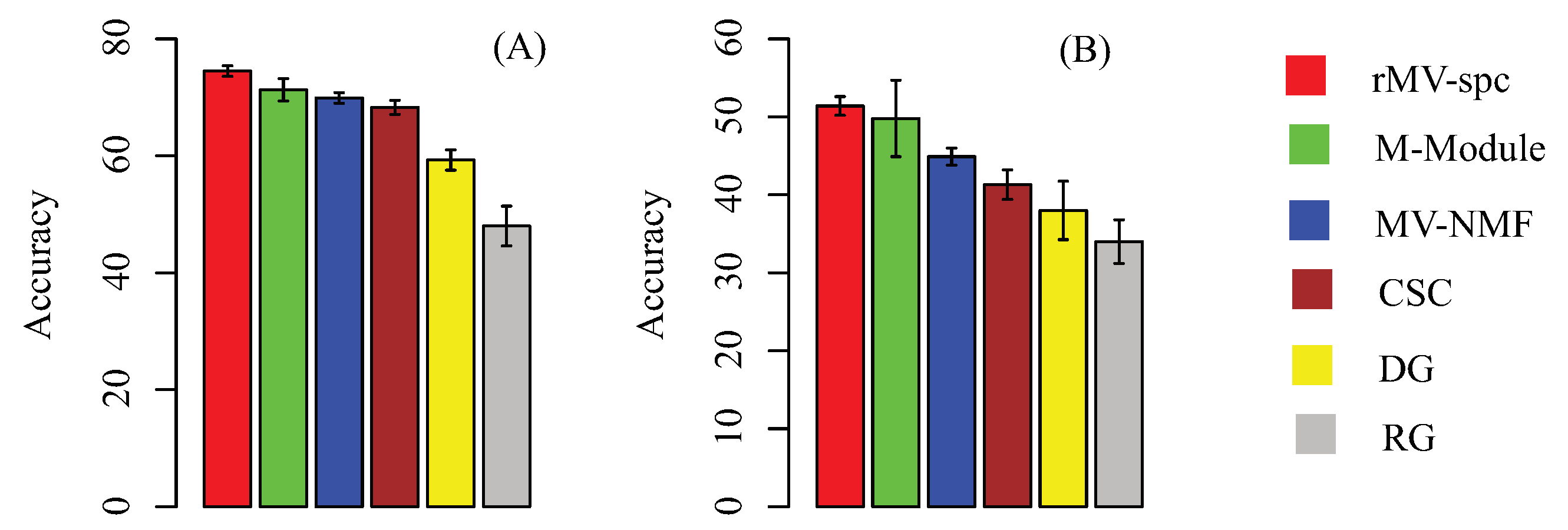
3.2. Module-Based Features for a Support Vector Machine (SVM)
3.3. Normalized Mutual Information
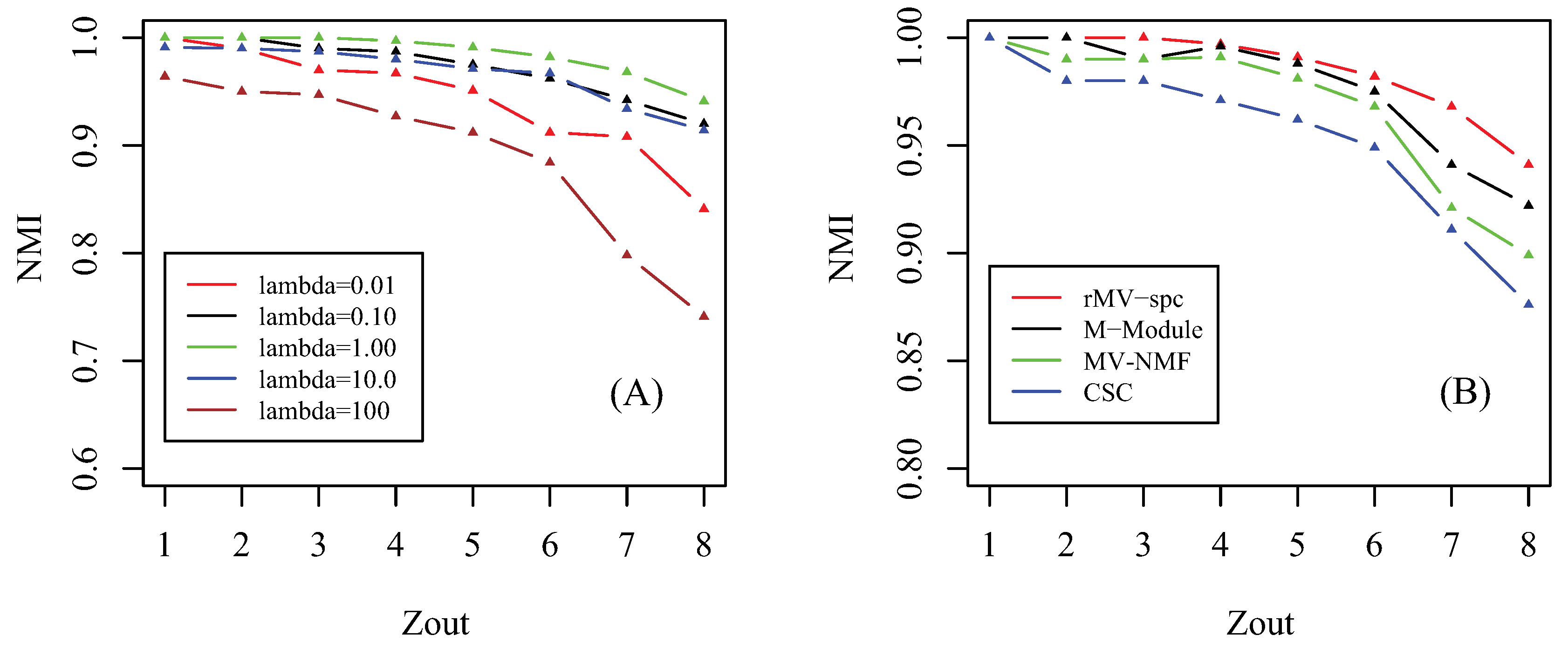
3.4. Artificial Networks
3.5. Breast Cancer Gene Expression Data
3.6. Protein Interaction Network
4. Results
4.1. Benchmarking Performance on the Artificial Networks
4.2. Benchmarking Performance on the Breast Cancer Networks
4.3. Common Modules Serve as Biomarkers to Predict Breast Cancer Stages
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Selbach, M.; Schwanhäusser, B.; Thierfelder, N.; Fang, Z.; Khanin, R.; Rajewsky, N. Widespread changes in protein synthesis induced by microRNAs. Nature 2008, 455, 58–63. [Google Scholar] [CrossRef] [PubMed]
- Lim, L.P.; Lau, N.C.; Garrett-Engele, P.; Grimson, A.; Schelter, J.M.; Castle, J.; Bartel, D.P.; Linsley, P.S.; Johnson, J.M. Microarray analysis shows that some microRNAs downregulate large numbers of target mRNAs. Nature 2005, 433, 769–773. [Google Scholar] [CrossRef] [PubMed]
- Schwanhäusser, B.; Busse, D.; Dittmar, G.; Schuchhardt, J.; Wolf, J.; Chen, W.; Selbach, M. Global quantification of mammalian gene expression control. Nature 2011, 433, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Li, F.; He, B.; Ma, X.; Yu, S.; Bhave, R.R.; Lentz, S.R.; Tan, K.; Guzman, M.L.; Zhao, C.; Xue, H.H. Prostaglandin E1 and its analog misoprostol inhibit human CML stem cell self-renewal via EP4 receptor activation and repression of AP-1. Cell Stem Cell 2017, 21, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Langfelder, P.; Horvath, S. WGCNA: An R package for weighted correlation network analysis. BMC Bioinform. 2008, 9, 559. [Google Scholar] [CrossRef] [PubMed]
- Vaquerizas, J.M.; Kummerfeld, S.K.; Teichmann, S.A.; Luscombe, N.M. A census of human transcription factors: Function, expression and evolution. Nat. Biotechnol. 2009, 10, 252–263. [Google Scholar] [CrossRef] [PubMed]
- Anastas, J.N.; Moon, R.T. WNT signaling pathways as therapeutic targets in cancer. Nat. Rev. Cancer 2013, 13, 11–26. [Google Scholar] [CrossRef] [PubMed]
- Schwikowski, B.; Uetz, P.; Fields, S. A network of protein-protein interactions in yeast. Nat. Biotechnol. 2010, 18, 1257–1261. [Google Scholar] [CrossRef] [PubMed]
- Menche, J.; Sharma, A.; Kitsak, M.; Ghiassian, S.D.; Vidal, M.; Loscalzo, J.; Barabasi, A.L. Uncovering disease-disease relationships through the incomplete interactome. Science 2015, 347, 1257601. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Lin, W.; Guo, M.; Zou, Q. A comprehensive overview and evaluation of circular RNA detection tools. PLoS Comput. Biol. 2017, 13, e1005420. [Google Scholar] [CrossRef] [PubMed]
- Tang, W.; Wan, S.; Yang, Z.; Teschendorff, A.E.; Zou, Q. Tumor origin detection with tissue-specific miRNA and DNA methylation markers. Bioinformatics 2017. [Google Scholar] [CrossRef]
- Li, P.; Guo, M.; Wang, C.; Liu, X.; Zou, Q. An overview of SNP interactions in genome-wide association studies. Brief. Funct. Genom. 2015, 14, 143–155. [Google Scholar] [CrossRef] [PubMed]
- Zeng, X.; Zhang, X.; Zou, Q. Integrative approaches for predicting microRNA function and prioritizing disease-related microRNA using biological interaction networks. Brief. Bioinform. 2016, 17, 193–203. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zeng, X.; He, Z.; Zou, Q. Inferring microRNA-disease associations by random walk on a heterogeneous network with multiple data sources. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017, 14, 905–915. [Google Scholar] [CrossRef] [PubMed]
- Wei, L.; Tang, J.; Zou, Q. Local-DPP: An Improved DNA-binding Protein Prediction Method by Exploring Local Evolutionary Information. Inf. Sci. 2017, 384, 135–144. [Google Scholar] [CrossRef]
- Taylor, I.W.; Linding, R.; Warde-Farley, D.; Liu, Y.; Pesquita, C.; Faria, D.; Bull, S.; Pawson, T.; Morris, Q.; Wrana, J.L. Dynamic modularity in protein interaction networks predicts breast cancer outcome. Nat. Biotechnol. 2009, 27, 199–204. [Google Scholar] [CrossRef] [PubMed]
- Chuang, H.Y.; Lee, E.; Liu, Y.; Lee, D.; Ideker, T. Network-based classification of breast cancer metastasis. Mol. Syst. Biol. 2007, 3, 140. [Google Scholar] [CrossRef] [PubMed]
- Spiller, D.G.; Wood, C.D.; Rand, D.A.; White, M.R.H. Measurement of single-cell dynamics. Nature 2010, 465, 736–748. [Google Scholar] [CrossRef] [PubMed]
- Lichtenberg, U.; Jensen, L.J.; Brunak, S.; Bork, P. Dynamic complex formation during the yeast cell cycle. Science 2005, 307, 724–727. [Google Scholar] [CrossRef] [PubMed]
- Gillies, R.J.; Verduco, D.; Gatenby, R.A. Evolutionary dynamics of carcinogenesis and why targeted therapy does does not work. Nature 2012, 12, 487–493. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Gao, L.; Tan, K. Modeling disease progression using dynamics of module connectivity. Bioinformatics 2014, 30, 2343–2350. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Gao, L.; Karamanlidis, G.; Gao, P.; Lee, C.F.; Garcia-Menendez, L.; Tian, R.; Tan, K. Revealing module dynamics in heart diseases by analyzing multiple differential networks. PLoS Comput. Biol. 2015, 11, e1004332. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Sun, P.; Gui, Q. Identifying condition-specific modules by clustering multiple networks. IEEE/ACM Trans. Comput. Biol. Bioinform. 2017. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Yu, L.; Wang, P.; Yang, X. Discovering DNA methylation patterns for long non-coding RNAs associated with cancer subtypes. Comput. Biol. Chem. 2017, 69, 164–170. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Tang, W.; Wang, P.; Guo, X.; Gao, L. Extracting stage-specific and dynamic modules through analyzing multiple networks associated with cancer progression. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; Yasin, U.; Gao, P.; He, B.; Ma, X.; Wang, J.; Han, S.; Tan, K. Identifying noncoding risk variants using disease-relevant regulatory networks. Nat. Commun. 2018, 9, 702. [Google Scholar] [CrossRef] [PubMed]
- Elhamifar, E.; Vidal, R. Sparse subspace clustering: Algorithm, theory, and applications. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2765–2781. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Xu, H.; Leng, C. Provable subspace clustering: When LRR meets SSC. Adv. Neural Inf. Process. Syst. 2013, 26, 64–72. [Google Scholar]
- Kumar, A.; Rai, P.; Daume, H. Co-regularized multi-view spectral clustering. Adv. Neural Inf. Process. Syst. 2011, 24, 1413–1421. [Google Scholar]
- Gao, H.; Nie, F.; Li, X.; Huang, H. Multi-view subspace clustering. IEEE Conf. Comput. Vers. 2016, 4238–4246. [Google Scholar]
- Cai, D.; He, X.; Han, J.; Huang, T.S. Graph Regularized Nonnegative Matrix Factorization for Data Representation. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1548–1560. [Google Scholar] [PubMed]
- Kim, S.J.; Koh, K.; Lustig, M.; Boyd, S.; Gorinevsky, D. An interior-point method for large-scale l1-regularized least squares. IEEE J. Sel. Top. Sign. Process. 2007, 1, 606–617. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Donoho, D.L. For Most Large Underdetermined Systems of Linear Equations the Minimal 1-norm Solution is also the Sparsest Solution. Comm. Pure Appl. Math. 2006, 59, 797–829. [Google Scholar] [CrossRef]
- Candès, E.; Tao, T. Decoding by linear programming. IEEE Trans. Inf. Theor. 2005, 51, 4203–4215. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. B Methadol. 1995, 57, 289–300. [Google Scholar]
- Danon, L.; Duch, J.; Diaz-Guileram, A.; Arenas, A. Comparing community structure identification. J. Stat. Mech. 2005, 8, P09008. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Girvan, M. Finding and evaluating community structure in networks. Phys. Rev. E 2004, 77, 026113. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Wang, C.; Gao, J.; Han, J. Multi-view clustering via joint nonnegative matrix factorization. Soc. Ind. Appl. Math. DM 2013. [Google Scholar] [CrossRef]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E 2006, 74, 036104. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Sun, P.; Wang, Y. Graph regularized nonnegative matrix factorization for temporal link prediction in dynamic networks. Phys. A 2018, 496, 121–136. [Google Scholar] [CrossRef]
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler, H.; Cherry, J.M.; Davis, A.P.; Dolinski, K.; Dwight, S.S.; Eppig, J.T. Gene ontology: Tool for the unification of biology. Nat. Genet. 2000, 25, 25–29. [Google Scholar] [CrossRef] [PubMed]
- Kanehisa, M.; Goto, M.; Sato, Y.; Furumichi, Y.; Tanabe, M. KEGG for integration and interpretation of large-scale molecular data sets. Nucleic Acids Res. 2012, 40, D109–D114. [Google Scholar] [CrossRef] [PubMed]
- Nishimura, D. BioCarta. Biotech. Softw. Internet Rep. 2001, 2, 117–120. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, E.; Ma, X. Regularized Multi-View Subspace Clustering for Common Modules Across Cancer Stages. Molecules 2018, 23, 1016. https://doi.org/10.3390/molecules23051016
Zhang E, Ma X. Regularized Multi-View Subspace Clustering for Common Modules Across Cancer Stages. Molecules. 2018; 23(5):1016. https://doi.org/10.3390/molecules23051016
Chicago/Turabian StyleZhang, Enli, and Xiaoke Ma. 2018. "Regularized Multi-View Subspace Clustering for Common Modules Across Cancer Stages" Molecules 23, no. 5: 1016. https://doi.org/10.3390/molecules23051016
APA StyleZhang, E., & Ma, X. (2018). Regularized Multi-View Subspace Clustering for Common Modules Across Cancer Stages. Molecules, 23(5), 1016. https://doi.org/10.3390/molecules23051016






