Pharmacokinetic–Pharmacodynamic Model for the Testosterone-Suppressive Effect of Leuprolide in Normal and Prostate Cancer Rats
Abstract
:1. Introduction
2. Results
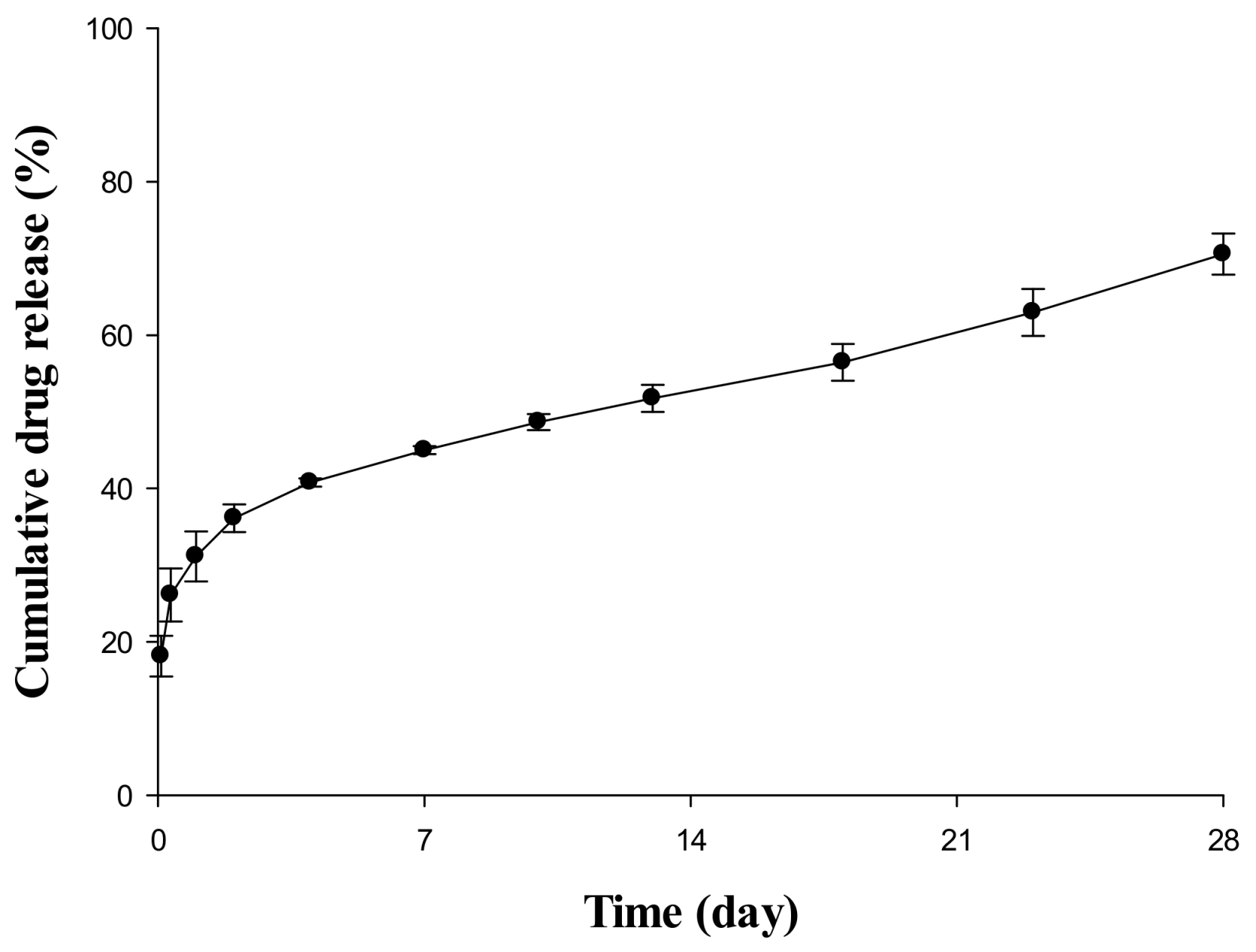
2.1. In Vitro Release Evaluation of Sustained Release (SR) Depot
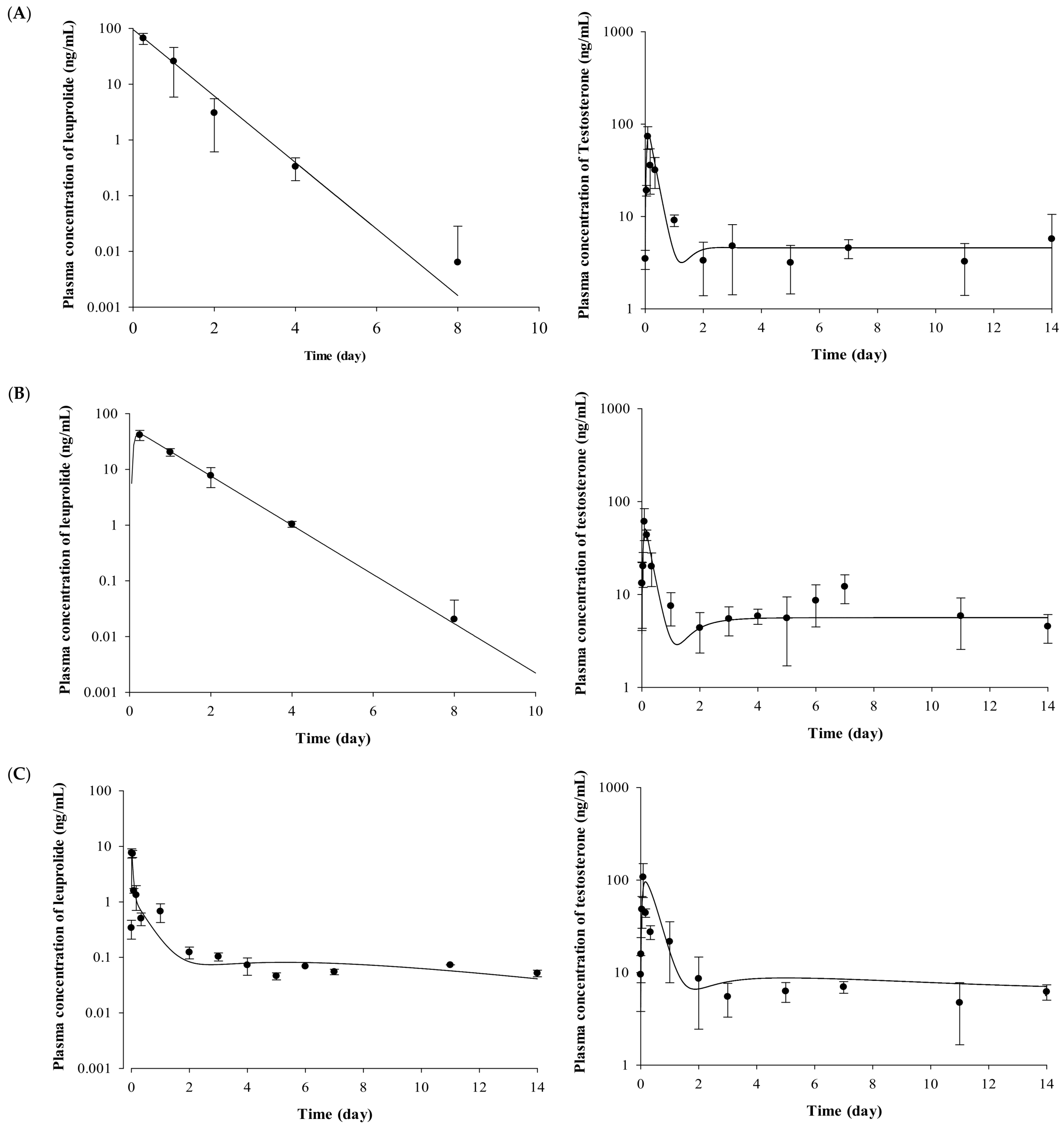
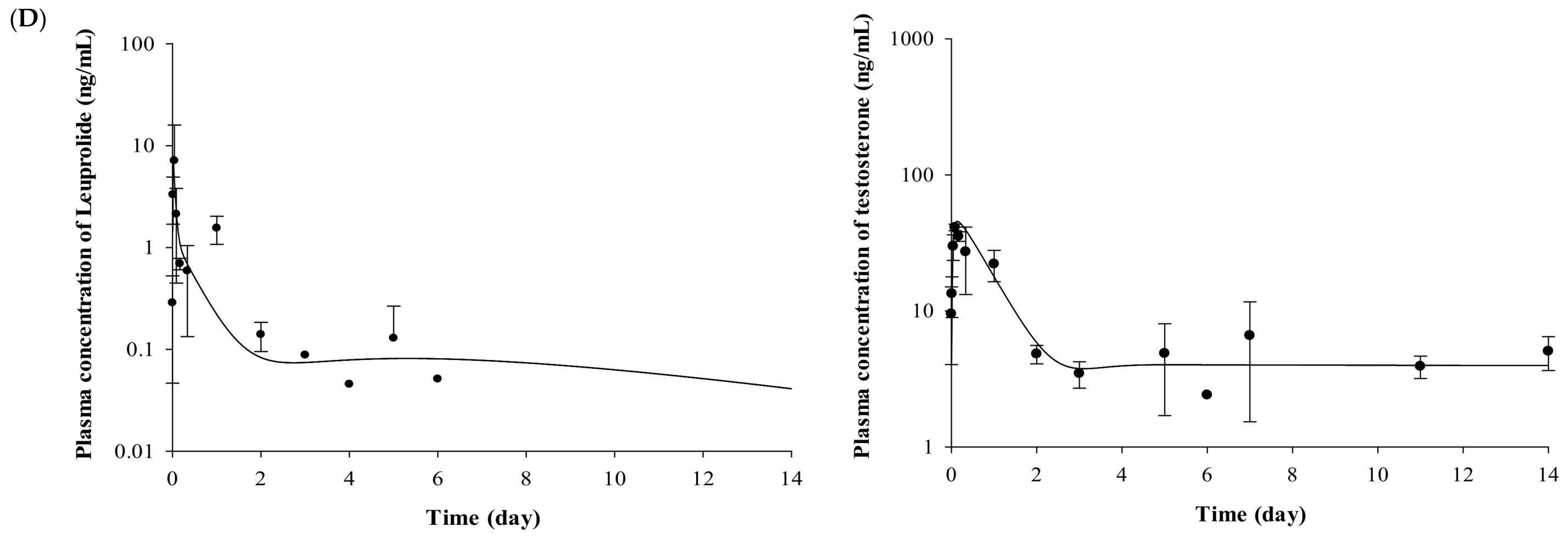
2.2. Pharmacokinetic Evaluation of Leuprolide
2.3. Pharmacodynamic Evaluation for the Testosterone-Suppressive Effect
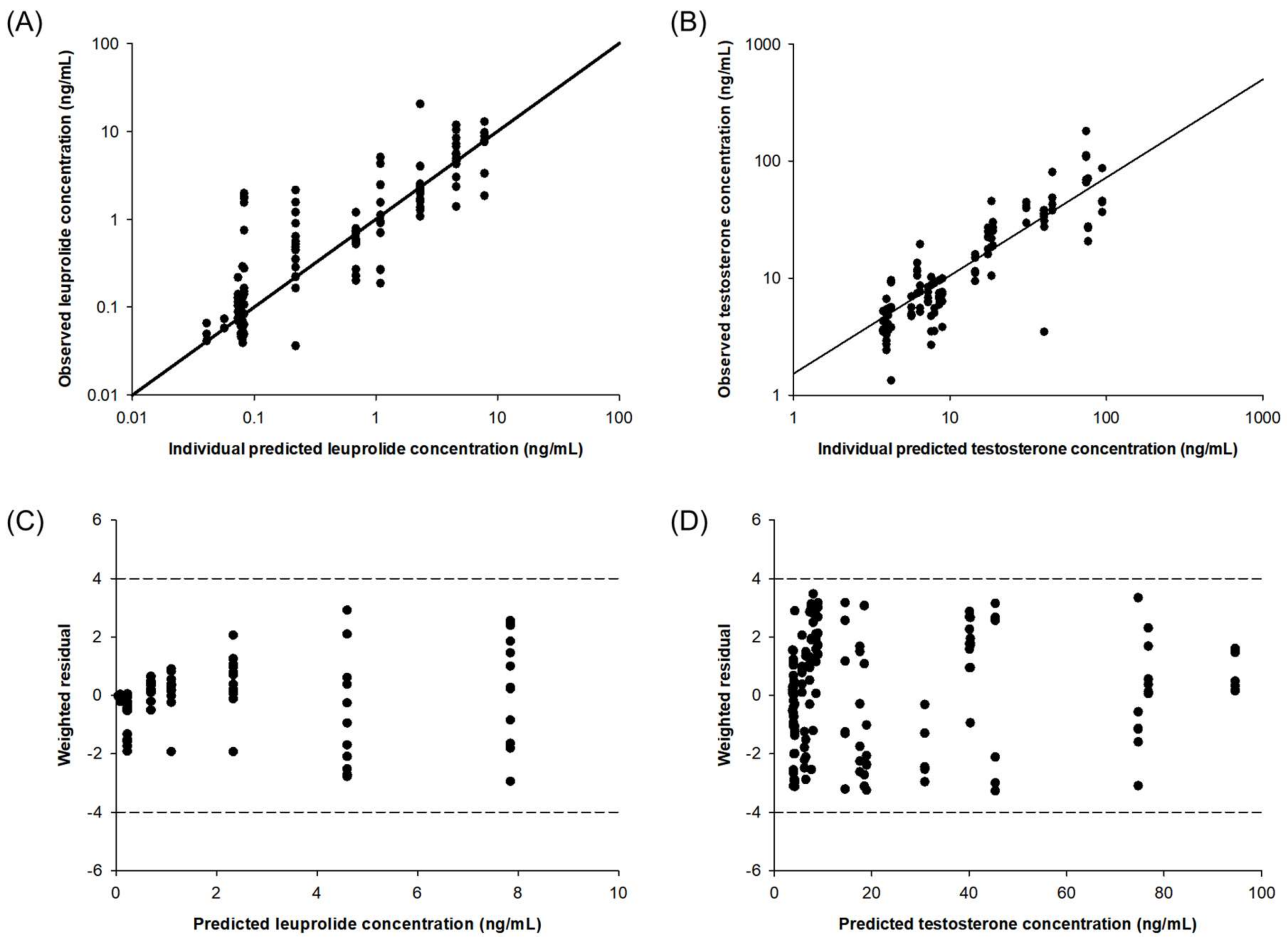
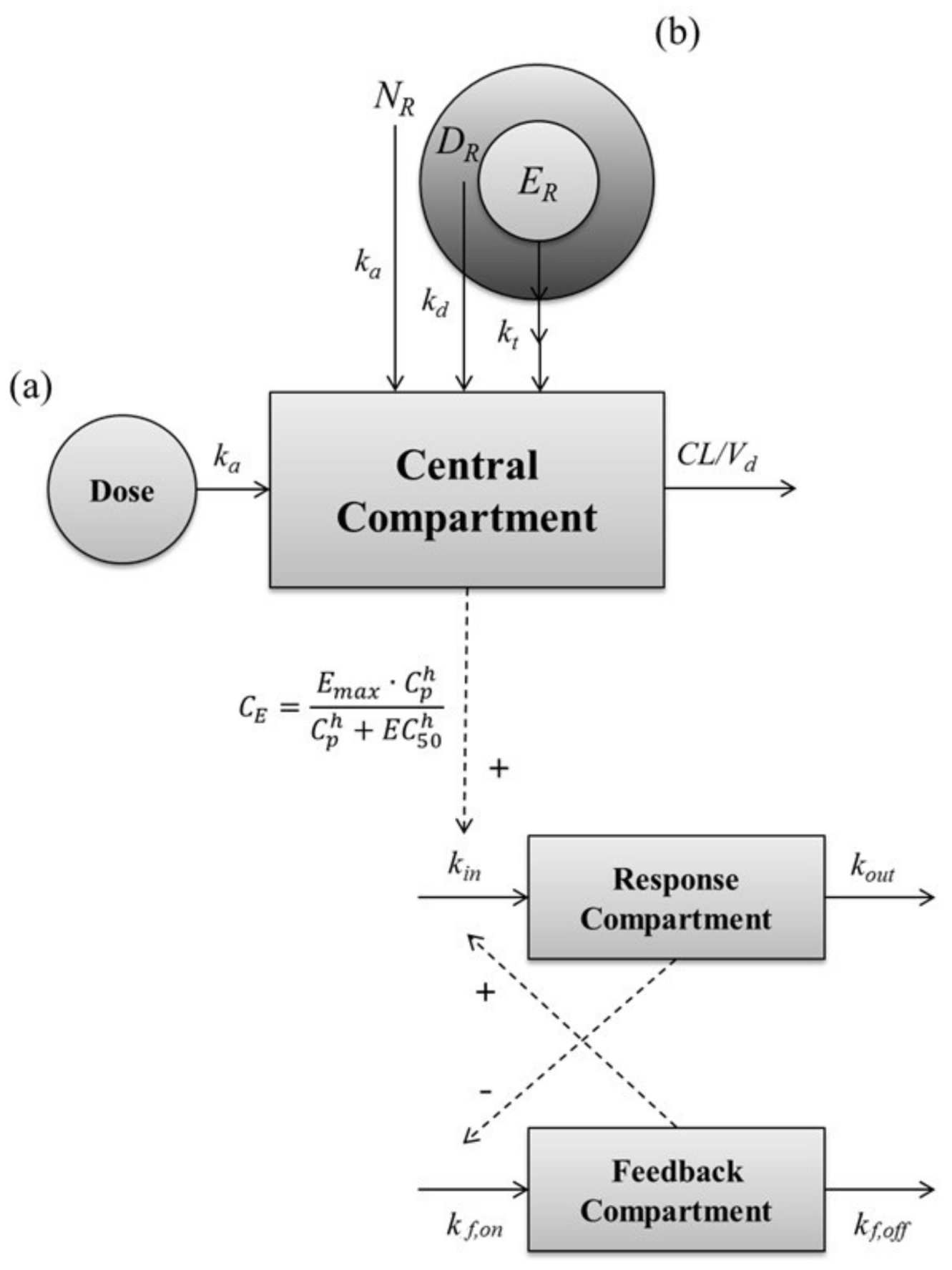
2.4. Pharmacokinetic–Pharmacodynamic (PK-PD) Modeling of Testosterone-Suppressive Effect of Leuprolide
3. Discussion
4. Materials and Methods
4.1. Chemicals and Reagents
4.2. In Vitro Release Test of SR Depot
4.3. Animals and Experimental Design
4.4. Measurement of Leuprolide in Plasma Samples
4.5. Measurement of Testosterone in Plasma Samples
4.6. Estimation of PK, PD Parameters and Data Analysis
4.7. Development and Evaluation of PK–PD Model of Leuprolide
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Gallarate, M.; Battaglia, L.; Peira, E.; Trotta, M. Peptide-loaded solid lipid nanoparticles prepared through coacervation technique. Int. J. Chem. Eng. 2011, 2011, 1–6. [Google Scholar] [CrossRef]
- Vlieghe, P.; Lisowski, V.; Martinez, J.; Khrestchatisky, M. Synthetic therapeutic peptides: Science and market. Drug Discov. Today 2010, 15, 40–56. [Google Scholar] [CrossRef] [PubMed]
- Thayer, A.M. Small firms develop better peptide drug candidates to expand this pharmaceutical class and attract big pharma partners. Improv. Pept. 2011, 89, 13–20. [Google Scholar]
- Adjei, A.; Love, S.; Johnson, E.; Diaz, G.; Greer, J.; Haviv, F.; Bush, E. Effect of formulation adjuvants on gastrointestinal absorption of leuprolide acetate. J. Drug Target. 1993, 1, 251–258. [Google Scholar] [CrossRef] [PubMed]
- Tombal, B.; Miller, K.; Boccon-Gibod, L.; Schroder, F.; Shore, N.; Crawford, E.D.; Moul, J.; Jensen, J.K.; Kold Olesen, T.; Persson, B.E. Additional analysis of the secondary end point of biochemical recurrence rate in a phase 3 trial (CS21) comparing degarelix 80 mg versus leuprolide in prostate cancer patients segmented by baseline characteristics. Eur. Urol. 2010, 57, 836–842. [Google Scholar] [CrossRef] [PubMed]
- Hintzen, F.; Perera, G.; Hauptstein, S.; Muller, C.; Laffleur, F.; Bernkop-Schnurch, A. In vivo evaluation of an oral self-microemulsifying drug delivery system (SMEDDS) for leuprorelin. Int. J. Pharm. 2014, 472, 20–26. [Google Scholar] [CrossRef] [PubMed]
- Leitner, J.M.; Corrado, M.E.; Mayr, F.B.; Spiel, A.O.; Jilma, B. The pharmacokinetics and pharmacodynamics of a new sustained-release leuprolide acetate depot compared to market references. Int. J. Clin. Pharmacol. Ther. 2008, 46, 407–414. [Google Scholar] [CrossRef] [PubMed]
- Nagaraja, N.V.; Pechstein, B.; Erb, K.; Klipping, C.; Hermann, R.; Niebch, G.; Derendorf, H. Pharmacokinetic and pharmacodynamic modeling of cetrorelix, an LH-RH antagonist, after subcutaneous administration in healthy premenopausal women. Clin. Pharmacol. Ther. 2000, 68, 617–625. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, J.; Shahnaz, G.; Perera, G.; Hintzen, F.; Sarti, F.; Bernkop-Schnurch, A. Thiolated chitosan: Development and in vivo evaluation of an oral delivery system for leuprolide. Eur. J. Pharm. Biopharm. 2012, 80, 95–102. [Google Scholar] [CrossRef] [PubMed]
- Heidenreich, A.; Pfister, D.; Thissen, A.; Piper, C.; Porres, D. Radical retropubic and perineal prostatectomy for clinically localised prostate cancer in renal transplant recipients. Arab J. Urol. 2014, 12, 142–148. [Google Scholar] [CrossRef] [PubMed]
- Jadhav, P.R.; Agerso, H.; Tornoe, C.W.; Gobburu, J.V. Semi-mechanistic pharmacodynamic modeling for degarelix, a novel gonadotropin releasing hormone (GnRH) blocker. J. Pharmacokinet. Pharmacodyn. 2006, 33, 609–634. [Google Scholar] [CrossRef] [PubMed]
- Ki, M.H.; Lim, J.L.; Ko, J.Y.; Park, S.H.; Kim, J.E.; Cho, H.J.; Park, E.S.; Kim, D.D. A new injectable liquid crystal system for one month delivery of leuprolide. J. Control. Release 2014, 185, 62–70. [Google Scholar] [CrossRef] [PubMed]
- Periti, P.; Mazzei, T.; Mini, E. Clinical Pharmacokinetics of Depot Leuprorelin. Clin. Pharm. 2002, 41, 485–504. [Google Scholar] [CrossRef] [PubMed]
- Han, J.Z.S.; Liu, W.; Leng, G.; Sun, K.; Li, Y.; Di, X. An analytical strategy to characterize the pharmacokinetics and pharmacodynamics of triptorelin in rats based on simultaneous LC-MS/MS analysis of triptorelin and endogenous testosterone in rat plasma. Anal. Bioanal. Chem. 2014, 406, 2457–2465. [Google Scholar] [CrossRef] [PubMed]
- List of Qualified Biomarkers of Biomarker Qualification Program. Available online: https://www.fda.gov/Drugs/DevelopmentApprovalProcess/DrugDevelopmentToolsQualificationProgram/BiomarkerQualificationProgram/ucm535926.htm (accessed on 2 April 2018).
- Scheff, J.D.; Almon, R.; Dubois, D.C.; Jusko, W.J.; Androulakis, I.P. Assessment of pharmacologic area under the curve when baselines are variable. Pharm. Res. 2011, 28, 1081–1089. [Google Scholar] [CrossRef] [PubMed]
- Bundgaard, C.; Larsen, F.; Jørgensen, M.; Mørk, A. Pharmacokinetic/pharmacodynamic feedback modelling of the functional corticosterone response in rats after acute treatment with escitalopram. Basic Clin. Pharmacol. Toxicol. 2007, 100, 182–189. [Google Scholar] [CrossRef] [PubMed]
- Romero, E.; Velez de Mendizabal, N.; Cendros, J.M.; Peraire, C.; Bascompta, E.; Obach, R.; Troconiz, I.F. Pharmacokinetic/pharmacodynamic model of the testosterone effects of triptorelin administered in sustained release formulations in patients with prostate cancer. J. Pharmacol. Exp. Ther. 2012, 342, 788–798. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.N.; Salem, A.H. A Semi-Mechanistic integrated pharmacokinetic/pharmacodynamic model of the testosterone effects of the gonadotropin-releasing hormone agonist leuprolide in prostate cancer patients. Clin. Pharmacokinet. 2015, 54, 963–973. [Google Scholar] [CrossRef] [PubMed]
- Bugan, I.; Karagoz, Z.; Altun, S.; Djamgoz, M.B. Gabapentin, an analgesic used against cancer-associated neuropathic pain: Effects on prostate cancer progression in an in vivo rat model. Basic Clin. Pharmacol. Toxicol. 2016, 118, 200–207. [Google Scholar] [CrossRef] [PubMed]
- Lee, D.S.; Heo, S.H.; Kim, S.J.; Lee, Y.B.; Cho, H.Y. Development of new clean-up method for UPLC–MS/MS analysis of leuprolide. J. Pharm. Investig. 2016, 47, 531–540. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
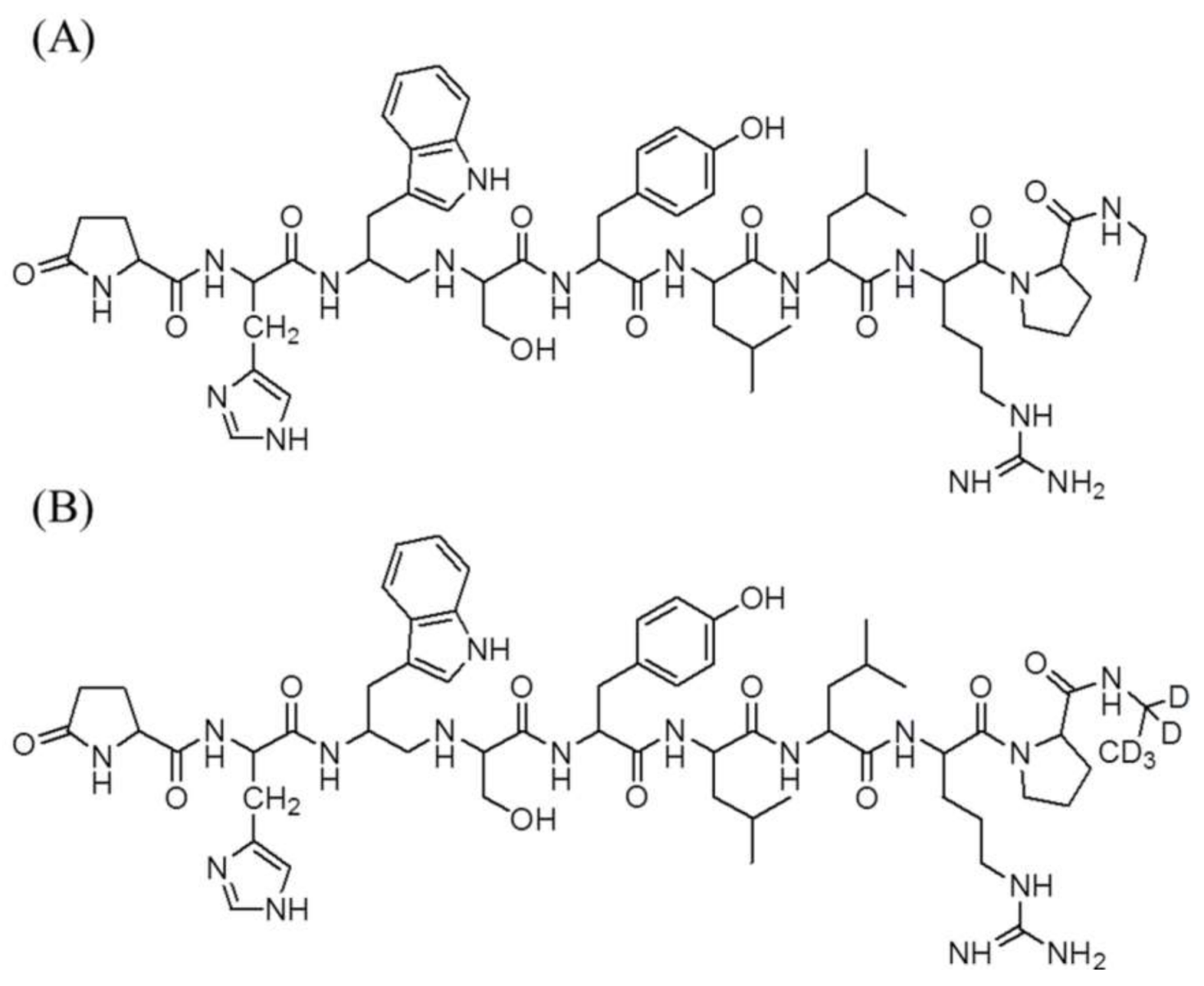
| Parameters | IV (Group 1) | SC (Group 3) |
|---|---|---|
| k (h−1) | 1.42 ± 0.24 | 1.06 ± 0.55 |
| ka (h−1) | - | 16.67 ± 2.55 |
| CL (mL/h) | 248.61 ± 35.07 | 514.46 ± 40.10 |
| Vd (mL) | 192.95 ± 54.24 | 487.40 ± 29.02 |
| Cmax (ng/mL) | 97.10 ± 13.04 a | 41.53 ± 4.61 |
| t1/2 (h) | 0.52 ± 0.10 | 0.66 ± 0.03 |
| AUC0-t (h·ng/mL) | 103.44 ± 16.93 | 51.20 ± 9.56 |
| AUC0–∞ (h·ng/mL) | 105.50 ± 17.27 | 53.33 ± 9.96 |
| F (%) | 100 | 50.6 |
| Parameters | Wistar Rats (Group 4) | Iar:COP Rats (Group 6) |
|---|---|---|
| ESn | 2 | 2 |
| NR | 0.18 ± 0.04 | 0.08 ± 0.02 |
| DR | 0.28 ± 0.07 | 0.43 ± 0.08 |
| ER | 0.54 ± 0.08 | 0.49 ± 0.08 |
| kd (h−1) | 0.08 ± 0.01 | 0.08 ± 0.01 |
| kt (h−1) | 0.0078 ± 0.0002 | 0.0193 ± 0.0083 |
| tlag,d (h) | 0.47 ± 0.09 | 0.35 ± 0.06 |
| tlag,e (h) | 3.61 ± 1.53 | 2.58 ± 0.22 |
| Group | Formulation | Routes | Animals | Positive AUEC | Negative AUEC |
|---|---|---|---|---|---|
| 1 | Leuprolide solution | IV | Wistar | 208.24 ± 52.30 | −1404.30 ± 287.31 * |
| 3 | SC | Wistar | 220.87 ± 39.56 | −775.98 ± 289.13 * | |
| 4 | SR depot | SC | Wistar | 407.91 ± 111.95 | −761.48 ± 292.02 * |
| 6 | SC | Iar:COP | 354.12 ± 78.95 | −880.28 ± 298.31 * |
| Parameters | Wistar Rats | Iar:COP Rats | ||
|---|---|---|---|---|
| Solution-IV (Group 1) | Solution-SC (Group 3) | SR-SC (Group 4) | SR-SC (Group 6) | |
| kin (h−1) | 0.68 | 0.68 | 0.68 | 0.35 |
| kout (h−1) | 0.16 | 0.16 | 0.16 | 0.06 |
| h | 2.00 ± 0.61 | 2.02 ± 0.05 | 2.00 ± 0.01 | 3.18 ± 1.27 |
| Emax | 303.77 ± 12.90 | 183.50 ± 12.87 | 380.00 ± 87.54 | 634.50 ± 144.73 * |
| EC50 (ng/mL) | 3.48 ± 1.74 | 6.17 ± 2.49 | 1.80 ± 0.57 | 3.34 ± 0.56 * |
| kf,on (h−1) | 0.29 ± 0.19 | 0.14 ± 0.03 | 0.40 ± 0.25 | 0.083 ± 0.14 |
| kf,off (h−1) | 0.059 ± 0.017 | 0.02 ± 0.014 | 0.04 ± 0.032 | 0.45 ± 0.04 |
| Group | Animal | Route | Formulation | Dose | Sampling time |
|---|---|---|---|---|---|
| 1 | Wistar | IV | Leuprolide solution | 0.1 mg/kg | 0.25, 1, 2, 4, 8 h, 1, 2, 3, 4, 5, 6, 7, 11, 14 days |
| 2 | Wistar | SC | Dispersion vehicle | 0.2 mL | 8 h, 1, 7, 14 days |
| 3 | Wistar | SC | Leuprolide solution | 0.1 mg/kg | 0.25, 1, 2, 4, 8 h, 1, 2, 3, 4, 5, 6, 7, 11, 14 days |
| 4 | Wistar | SC | Lucrin depot dispersion | 0.1 mg/kg (as leuprolide) | 0.25, 1, 2, 4, 8 h, 1, 2, 3, 4, 5, 6, 7, 11, 14 days |
| 5 | Iar:COP | SC | Dispersion vehicle | 0.2 mL | 8 h, 1, 7, 14 days |
| 6 | Iar:COP | SC | Lucrin depot dispersion | 0.1 mg/kg (as leuprolide) | 0.25, 1, 2, 4, 8 h, 1, 2, 3, 4, 5, 6, 7, 11, 14 days |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, D.-S.; Kim, S.-J.; Choi, G.-W.; Lee, Y.-B.; Cho, H.-Y. Pharmacokinetic–Pharmacodynamic Model for the Testosterone-Suppressive Effect of Leuprolide in Normal and Prostate Cancer Rats. Molecules 2018, 23, 909. https://doi.org/10.3390/molecules23040909
Lee D-S, Kim S-J, Choi G-W, Lee Y-B, Cho H-Y. Pharmacokinetic–Pharmacodynamic Model for the Testosterone-Suppressive Effect of Leuprolide in Normal and Prostate Cancer Rats. Molecules. 2018; 23(4):909. https://doi.org/10.3390/molecules23040909
Chicago/Turabian StyleLee, Dong-Seok, Sook-Jin Kim, Go-Wun Choi, Yong-Bok Lee, and Hea-Young Cho. 2018. "Pharmacokinetic–Pharmacodynamic Model for the Testosterone-Suppressive Effect of Leuprolide in Normal and Prostate Cancer Rats" Molecules 23, no. 4: 909. https://doi.org/10.3390/molecules23040909
APA StyleLee, D.-S., Kim, S.-J., Choi, G.-W., Lee, Y.-B., & Cho, H.-Y. (2018). Pharmacokinetic–Pharmacodynamic Model for the Testosterone-Suppressive Effect of Leuprolide in Normal and Prostate Cancer Rats. Molecules, 23(4), 909. https://doi.org/10.3390/molecules23040909






