Segmenting Proteins into Tripeptides to Enhance Conformational Sampling with Monte Carlo Methods
Abstract
1. Introduction
2. Results and Discussion
2.1. Implemented Move Classes and Parameter Settings
- -
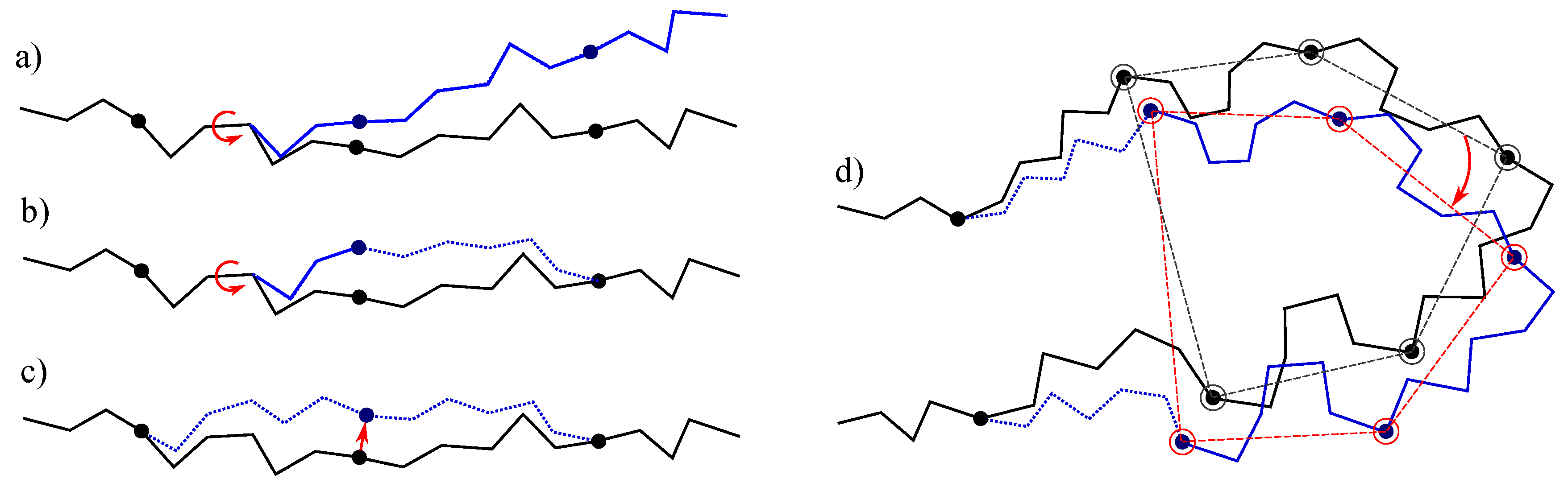
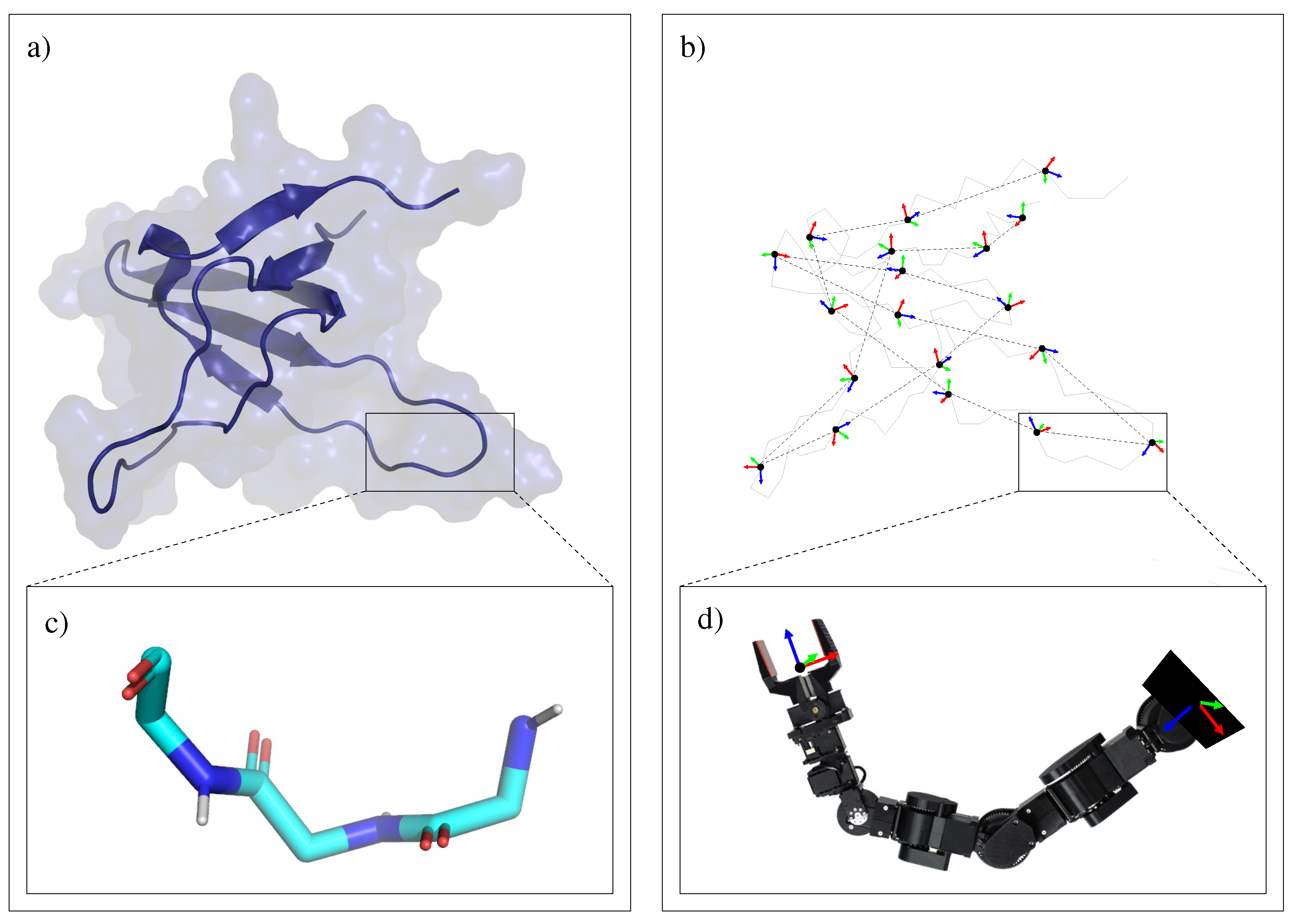
- The simplest class of trial moves, largely applied to sample the conformation of chain-like molecules, consists of perturbing a randomly selected bond torsion and then propagating the motion toward the end of the chain. Such moves, usually called pivot moves, are named here OneTorsion moves. They are illustrated in Figure 1a.
- -
- The second move class is named ConRot, since it is inspired by the concerted rotations proposed by Dodd et al. [17]. It has been implemented using the proposed tripeptide-based model as follows: an amino-acid residue is randomly selected and one of its bond torsions ( or ) is randomly perturbed; the backbone conformation of the next three residues (the next tripeptide) is modified by inverse kinematics in order to maintain fixed ends (see Section 3.2 for details). The move class is illustrated in Figure 1b.
- -
- The third move class, called OneParticle moves, corresponds to the simplest move class involving tripeptide-based particle perturbations, as described in Section 3.2, and illustrated in Figure 1c.
- -
- The last move class, called Hinge moves, corresponds to the rigid-body block moves described in Section 3.2, and illustrated in Figure 1d. The number of consecutive particles affected by the move is randomly sampled at each iteration between 3 and 10 (i.e., moves involve between 9 and 30 residues).
2.2. Test Systems
2.3. Computational Performance
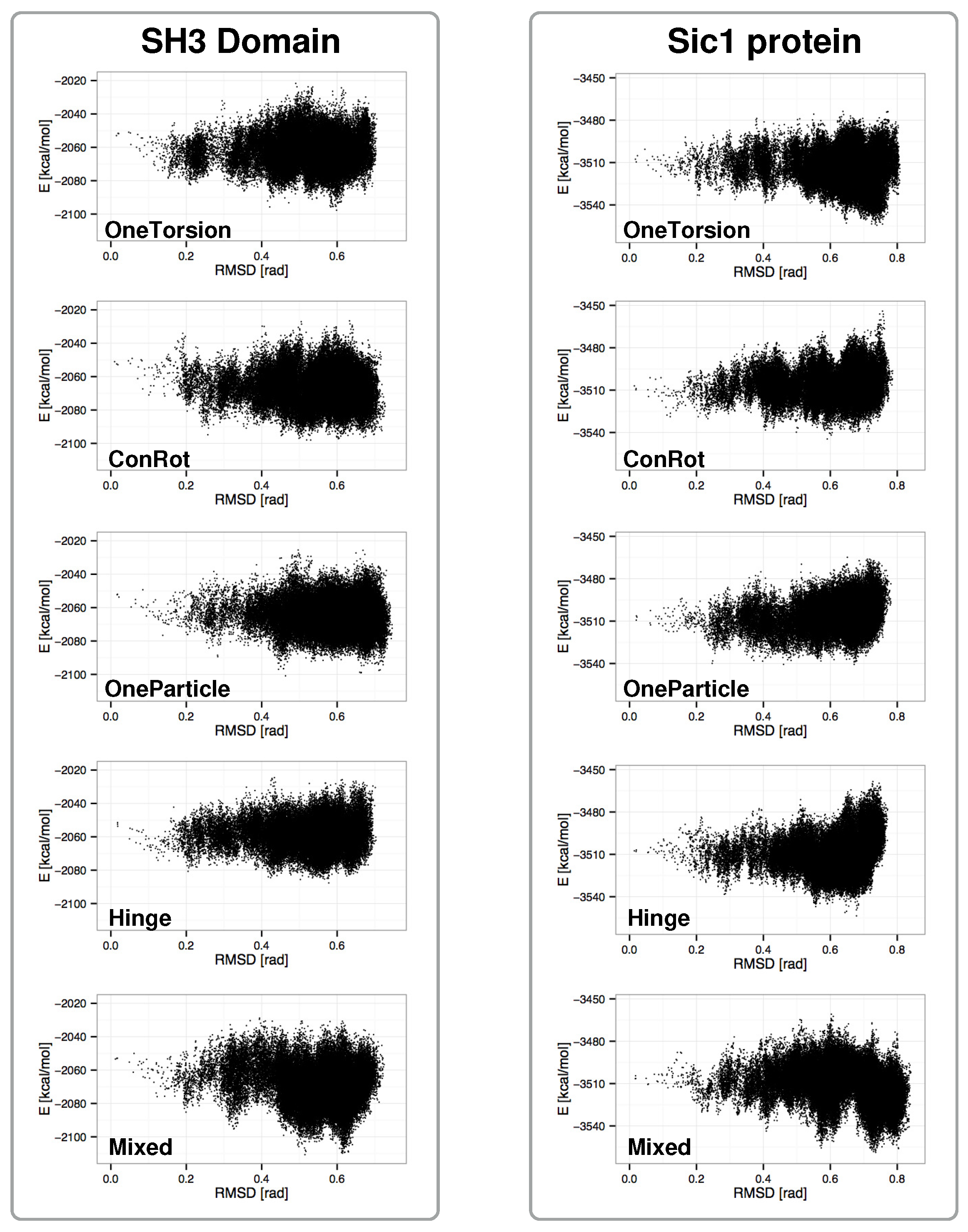
2.4. Distribution of Sampled States
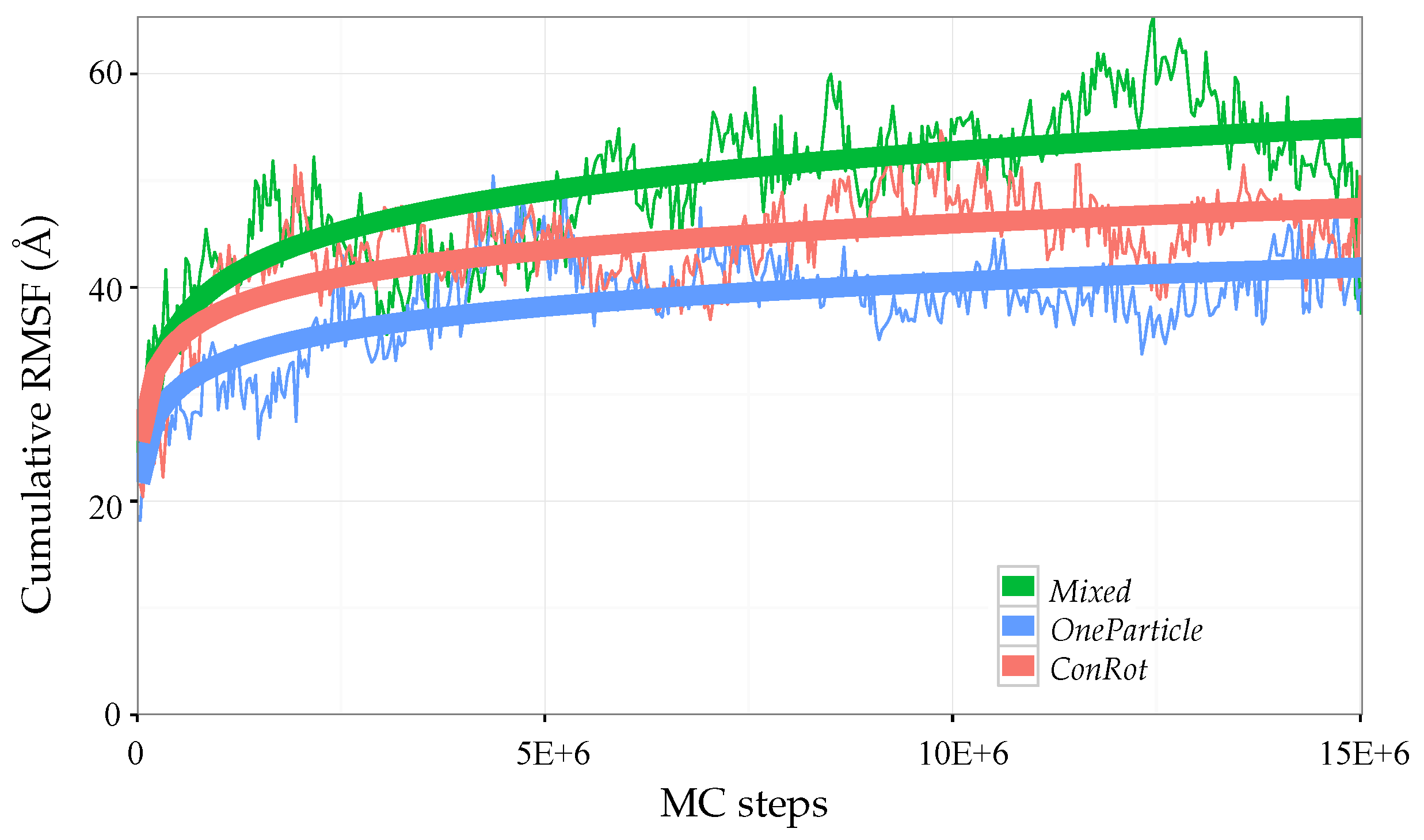
2.5. Exploration Efficiency Analysis
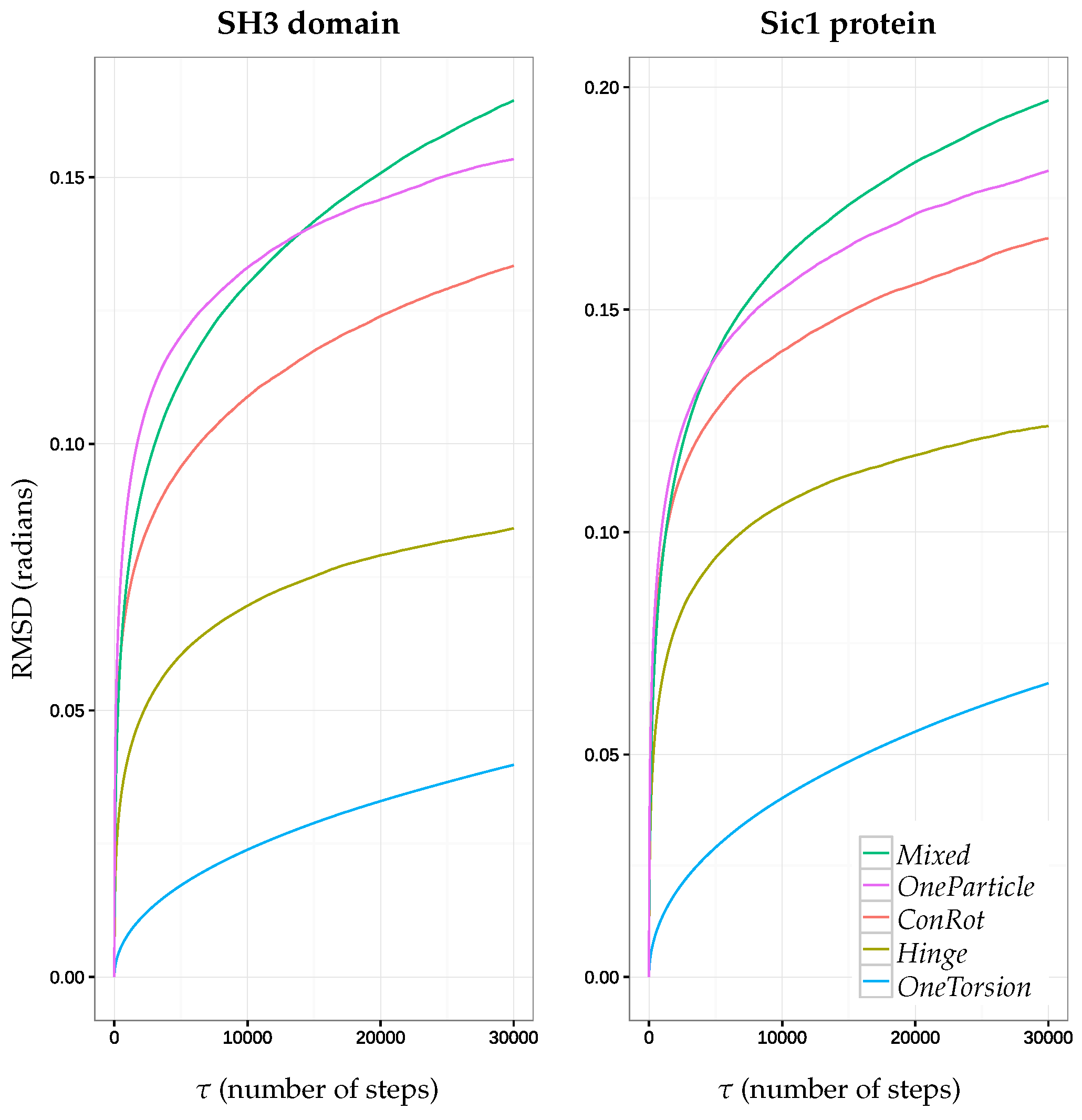
2.5.1. Time Dependent RMSD Function
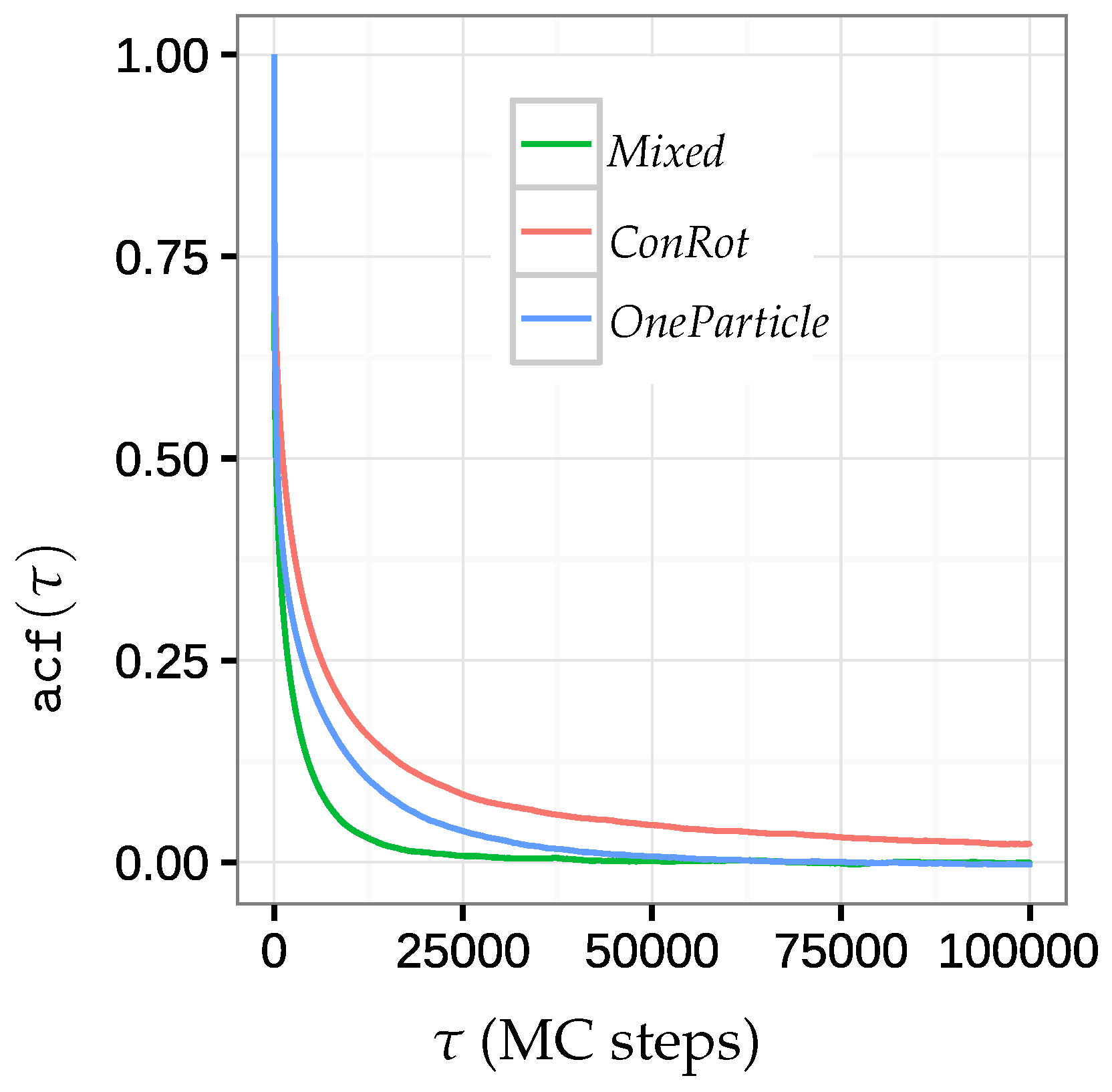
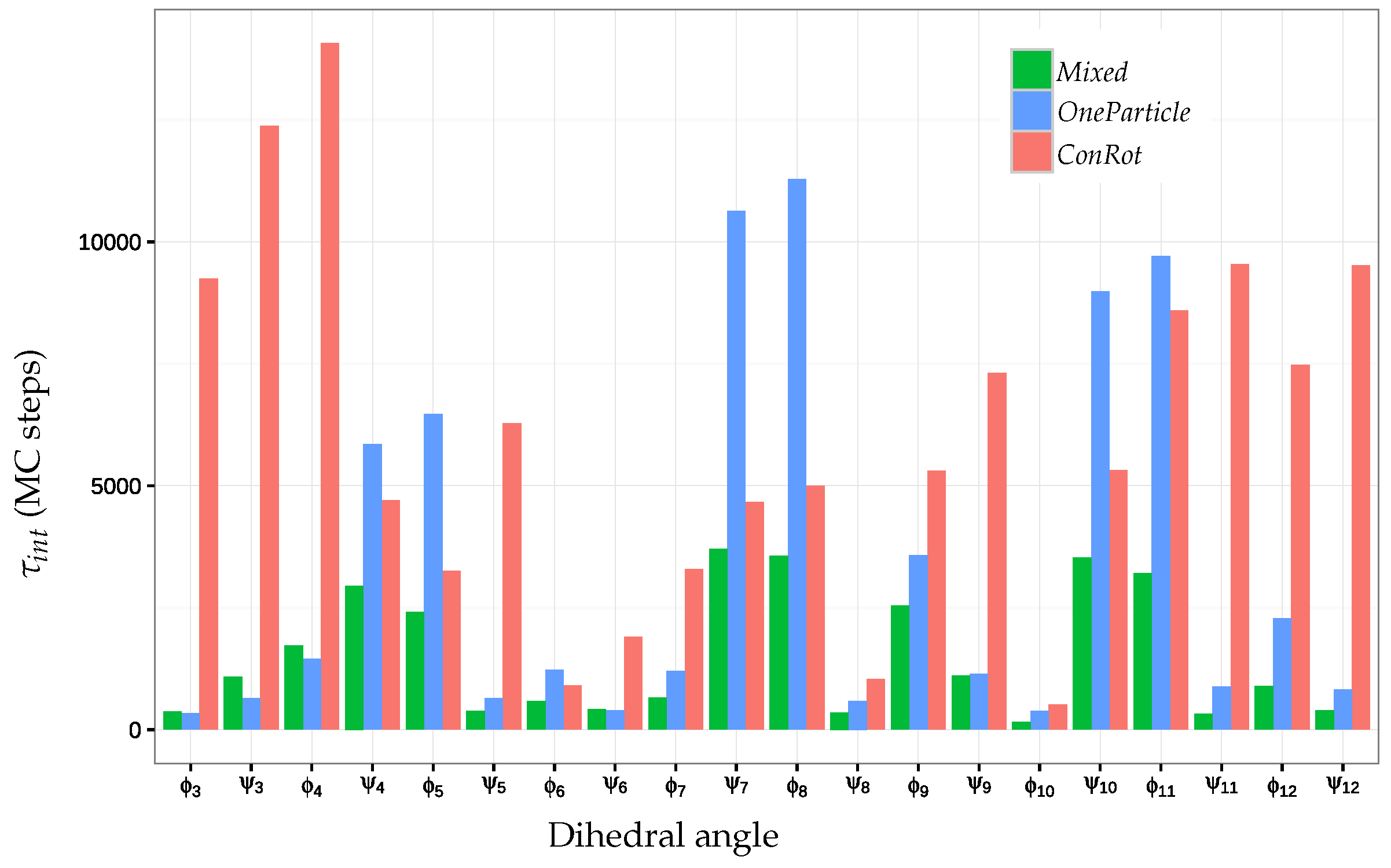
2.5.2. Autocorrelation Time
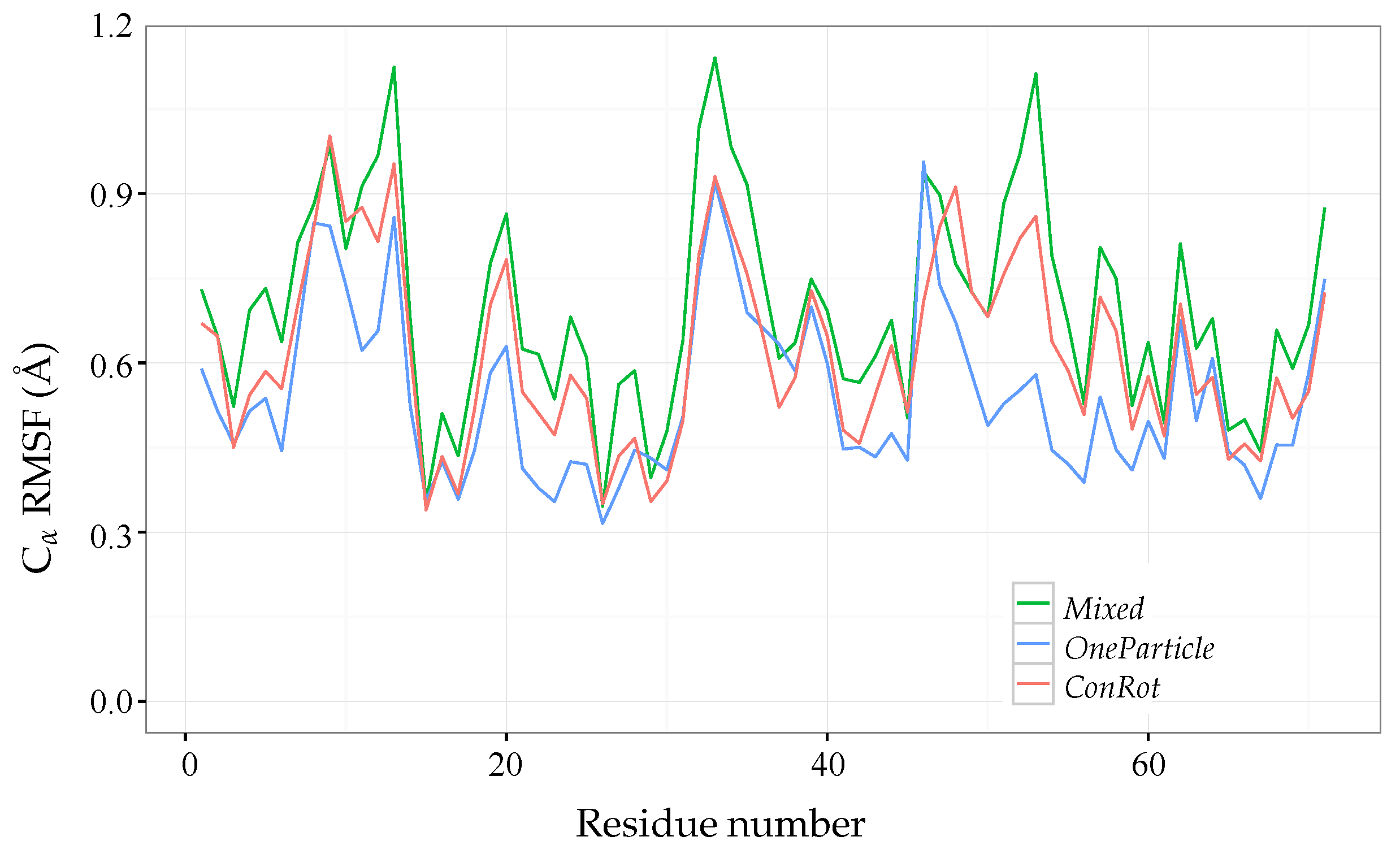
2.6. Additional Results for Ubiquitin
3. Materials and Methods
3.1. Protein Model
3.1.1. Mechanistic Model
3.1.2. Decomposition into Tripeptides
3.2. Devising Move Classes
3.2.1. Perturbing Particles
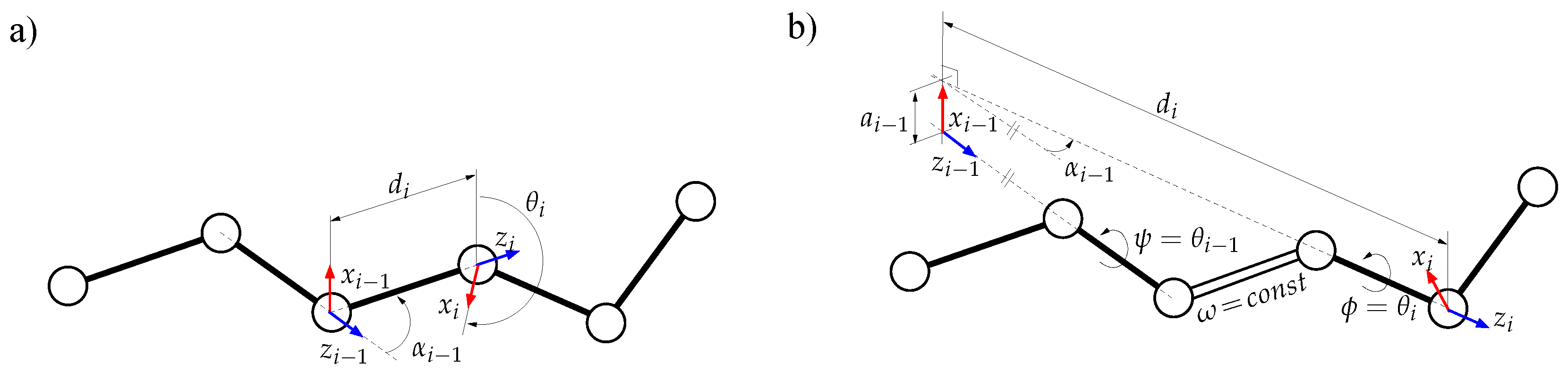
3.2.2. Solving Inverse Kinematics for a Tripeptide
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Woolfson, M.M. An Introduction to X-ray Crystallography; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kay, L.E. NMR studies of protein structure and dynamics. J. Magn. Reson. 2005, 173, 193–207. [Google Scholar] [CrossRef] [PubMed]
- Lange, O.F.; Lakomek, N.A.; Farès, C.; Schröder, G.F.; Walter, K.F.A.; Becker, S.; Meiler, J.; Grubmüller, H.; Griesinger, C.; de Groot, B.L. Recognition Dynamics Up to Microseconds Revealed from an RDC-Derived Ubiquitin Ensemble in Solution. Science 2008, 320, 1471–1475. [Google Scholar] [CrossRef] [PubMed]
- Fenwick, R.B.; van den Bedem, H.; Fraser, J.S.; Wright, P.E. Integrated description of protein dynamics from room-temperature X-ray crystallography and NMR. Proc. Natl. Acad. Sci. USA 2014, 111, E445–E454. [Google Scholar] [CrossRef] [PubMed]
- Leach, A.R. Molecular Modelling: Principles and Applications; Pearson Education: Harlow, UK, 2001. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulations: From Algorihtms to Applications; Academic Press: London, UK, 2002. [Google Scholar]
- Wales, D. Energy Landscapes: Applications to Clusters, Biomolecules and Glasses; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Donald, B.R. Algorithms in Structural Molecular Biology; The MIT Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Al-Bluwi, I.; Siméon, T.; Cortés, J. Motion Planning Algorithms for Molecular Simulations: A Survey. Comput. Sci. Rev. 2012, 6, 125–143. [Google Scholar] [CrossRef]
- Gipson, B.; Hsu, D.; Kavraki, L.; Latombe, J.C. Computational models of protein kinematics and dynamics: Beyond simulation. Ann. Rev. Anal. Chem. 2012, 5, 273–291. [Google Scholar] [CrossRef] [PubMed]
- Shehu, A.; Plaku, E. A Survey of Computational Treatments of Biomolecules by Robotics-Inspired Methods Modeling Equilibrium Structure and Dynamic. J. Artif. Intell. Res. 2016, 57, 509–572. [Google Scholar]
- Cortés, J.; Al-Bluwi, I. A Robotics Approach To Enhance Conformational Sampling Of Proteins. In Proceedings of the ASME 2012 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Chicago, IL, USA, 12–15 August 2012; Volume 4, pp. 1177–1186. [Google Scholar]
- Parsons, D.; Canny, J. Geometric Problems in Molecular Biology and Robotics. Proc. Int. Conf. Intell. Syst. Mol. Biol. 1994, 2, 322–330. [Google Scholar] [PubMed]
- Siciliano, B.; Khatib, O. (Eds.) Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Gō, N.; Scheraga, H. Ring Closure and Local Conformational Deformations of Chain Molecules. Macromolecules 1970, 3, 178–187. [Google Scholar] [CrossRef]
- Dodd, L.R.; Boone, T.D.; Theodorou, D.N. A Concerted Rotation Algorithm for Atomistic Monte Carlo Simulation of Polymer Melts and Glasses. Mol. Phys. 1993, 78, 961–996. [Google Scholar] [CrossRef]
- Leontidis, E.; de Pablo, J.J.; Laso, M.; Suter, U.W. A Critical Evaluation of Novel Algorithms for the Off-Lattice Monte Carlo Simulation of Condensed Polymer Phases. Adv. Polym. Sci. 1994, 116, 283–318. [Google Scholar]
- Wu, N.G.; Deem, M.W. Efficient Monte Carlo Methods for Cyclic Peptides. Mol. Phys. 1999, 94, 559–580. [Google Scholar] [CrossRef]
- Betancourt, M.R. Efficient Monte Carlo Trial Moves for Polypeptide Simulations. J. Chem. Phys. 2005, 123, 174905. [Google Scholar] [CrossRef] [PubMed]
- Davis, I.W.; Arendall, W.B., III; Richardson, D.C.; Richardson, J.S. The Backrub Motion: How Protein Backbone Shrugs When a Sidechain Dances. Structure 2006, 14, 265–274. [Google Scholar] [CrossRef] [PubMed]
- Bottaro, S.; Boomsma, W.; Johansson, K.E.; Andreetta, C.; Hamelryck, T.; Ferkinghoff-Borg, J. Subtle Monte Carlo Updates in Dense Molecular Systems. J. Chem. Theory Comput. 2012, 8, 695–702. [Google Scholar] [CrossRef] [PubMed]
- Vitalis, A.; Pappu, R.V. Methods for Monte Carlo Simulations of Biomacromolecules. Annu. Rep. Comput. Chem. 2009, 5, 49–76. [Google Scholar] [PubMed]
- Kollman, P.; Dixon, R.; Cornell, W.; Fox, T.; Chipot, C.; Pohorille, A. The development/application of a “minimalist” organic/biochemical molecular mechanic force field using a combination of ab initio calculations and experimental data. In Computer Simulation of Biomolecular Systems; van Gunsteren, W., Weiner, P., Wilkinson, A., Eds.; Springer: Dordrecht, The Netherlands, 1997; Volume 3, pp. 83–96. [Google Scholar]
- Bondi, A. Van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Kurochkina, N.; Guha, U. SH3 domains: Modules of protein–protein interactions. Biophys. Rev. 2013, 5, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Brocca, S.; Samalíkovà, M.; Uversky, V.N.; Lotti, M.; Vanoni, M.; Alberghina, L.; Grandori, R. Order propensity of an intrinsically disordered protein, the cyclin-dependent-kinase inhibitor Sic1. Proteins 2009, 76, 731–746. [Google Scholar] [CrossRef] [PubMed]
- Bernadó, P.; Blanchard, L.; Timmins, P.; Marion, D.; Ruigrok, R.; Blackledge, M. A structural model for unfolded proteins from residual dipolar couplings and small-angle X-ray scattering. Proc. Natl. Acad. Sci. USA 2005, 102, 17002–17005. [Google Scholar] [CrossRef] [PubMed]
- Krivov, G.G.; Shapovalov, M.V.; Dunbrack, R.L., Jr. Improved Prediction of Protein Side-chain Conformations with SCWRL4. Proteins Struct. Funct. Bioinf. 2009, 77, 778–795. [Google Scholar] [CrossRef] [PubMed]
- Ulmschneider, J.P.; Jorgensen, W.L. Monte Carlo backbone sampling for polypeptides with variable bond angles and dihedral angles using concerted rotations and a Gaussian bias. J. Chem. Phys. 2003, 118, 4261–4271. [Google Scholar] [CrossRef]
- Pickart, C.M.; Eddins, M.J. Ubiquitin: Structures, functions, mechanisms. Biochim. Biophys. Acta (BBA) Mol. Cell Res. 2004, 1695, 55–72. [Google Scholar] [CrossRef] [PubMed]
- Scott, R.; Scheraga, H. Conformational Analysis of Macromolecules. II. The Rotational Isomeric States of the Normal Hydrocarbons. J. Chem. Phys. 1966, 44, 3054–3069. [Google Scholar] [CrossRef]
- Ulmschneider, J.P.; Jorgensen, W.L. Polypeptide Folding Using Monte Carlo Sampling, Concerted Rotation, and Continuum Solvation. J. Am. Chem. Soc. 2004, 126, 1849–1857. [Google Scholar] [CrossRef] [PubMed]
- Craig, J.J. Introduction to Robotics; Addison-Wesley: Reading, MA, USA, 1989. [Google Scholar]
- Nilmeier, J.; Hua, L.; Coutsias, E.A.; Jacobson, M.P. Assessing Protein Loop Flexibility by Hierarchical Monte Carlo Sampling. J. Chem. Theory Comput. 2011, 7, 1564–1574. [Google Scholar] [CrossRef] [PubMed]
- Nilmeier, J.; Jacobson, M.P. Multiscale Monte Carlo Sampling of Protein Sidechains: Application to Binding Pocket Flexibility. J. Chem. Theory Comput. 2008, 4, 835–846. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Nilmeier, J.; Jacobson, M.P. Monte Carlo Sampling with Hierarchical Move Sets: POSH Monte Carlo. J. Chem. Theory Comput. 2009, 5, 1968–1984. [Google Scholar] [CrossRef] [PubMed]
- Wu, N.G.; Deem, M.W. Analytical Rebridging Monte Carlo: Application to cis/trans Isomerization in Proline-Containing, Cyclic Peptides. J. Chem. Phys. 1999, 111, 6625–6632. [Google Scholar] [CrossRef]
- Canutescu, A.A.; Dunbrack, R.L., Jr. Cyclic Coordinate Descent: A Robotics Algorithm for Protein Loop Closure. Protein Sci. 2003, 12, 963–972. [Google Scholar] [CrossRef] [PubMed]
- Renaud, M. A simplified inverse kinematic model calculation method for all 6R type manipulators. In Current Advances in Mechanical Design and Production VII; Hassan, M.F., Megahed, S.M., Eds.; Pergamon: New York, NY, USA, 2000; pp. 57–66. [Google Scholar]
- Renaud, M. Calcul des Modèles Géométriques Inverses des Robots Manipulateurs 6R; Rapport LAAS 06332; LAAS: Toulouse, France, 2006. [Google Scholar]
- Lee, H.Y.; Liang, C.G. A New Vector Theory for the Analysis of Spatial Mechanisms. Mech. Mach. Theory 1988, 23, 209–217. [Google Scholar] [CrossRef]
- Lee, H.Y.; Liang, C.G. Displacement Analysis of the General Spatial 7-Link 7R Mechanisms. Mech. Mach. Theory 1988, 23, 219–226. [Google Scholar]
- Manocha, D.; Canny, J.F. Efficient Inverse Kinematics for General 6R Manipulators. IEEE Trans. Robot. Autom. 1994, 10, 648–657. [Google Scholar] [CrossRef]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 3rd ed.; Johns Hopkins University Press: Baltimore, MD, USA, 1996. [Google Scholar]
- Anderson, E.; Bai, Z.; Bischof, C.; Blackford, S.; Demmel, J.; Dongarra, J.; Du Croz, J.; Greenbaum, A.; Hammarling, S.; McKenney, A.; et al. LAPACK Users’ Guide, 3rd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1999. [Google Scholar]
- Cortés, J.; Siméon, T.; Remaud-Siméon, M.; Tran, V. Geometric Algorithms for the Conformational Analysis of Long Protein Loops. J. Comput. Chem. 2004, 25, 956–967. [Google Scholar] [CrossRef] [PubMed]
- Cortés, J.; Carrión, S.; Curco, D.; Renaud, M.; Aleman, C. Relaxation of Amorphous Multichain Polymer Systems using Inverse Kinematics. Polymer 2010, 51, 4008–4014. [Google Scholar] [CrossRef]
- Dinner, A.R. Local deformations of polymers with nonplanar rigid main-chain internal coordinates. J. Comput. Chem. 2000, 21, 1132–1144. [Google Scholar] [CrossRef]
- Coutsias, E.A.; Seok, C.; Jacobson, M.P.; Dill, K.A. A Kinematic View of Loop Closure. J. Comput. Chem. 2004, 25, 510–528. [Google Scholar] [CrossRef] [PubMed]
- Mezei, M. Efficient Monte Carlo Sampling of Long Molecular Chains Using Local Moves, Tested on a Solvated Lipid Bilayer. J. Chem. Phys. 2003, 118, 3874–3879. [Google Scholar] [CrossRef]
- Okamoto, Y. Generalized-ensemble algorithms: Enhanced sampling techniques for Monte Carlo and molecular dynamics simulations. J. Mol. Graph. Model. 2004, 22, 425–439. [Google Scholar] [CrossRef] [PubMed]
- Carr, J.M.; Wales, D.J. Global optimization and folding pathways of selected alpha-helical proteins. J. Chem. Phys. 2005, 123, 234901. [Google Scholar] [CrossRef] [PubMed]
- Cortés, J.; Le, D.; Iehl, R.; Siméon, T. Simulating ligand-induced conformational changes in proteins using a mechanical disassembly method. Phys. Chem. Chem. Phys. 2010, 12, 8268–8276. [Google Scholar] [CrossRef] [PubMed]
- Mandell, D.J.; Kortemme, T. Backbone flexibility in computational protein design. Curr. Opin. Biotechnol. 2009, 20, 420–428. [Google Scholar] [CrossRef] [PubMed]
Sample Availability: Not Available. |
| OneTorsion | ConRot | OneParticle | Hinge | ||
|---|---|---|---|---|---|
| SH3 domain | 0.01 rad | 0.025 rad | 0.05 Å | 0.003 rad | 0.01 rad |
| Sic1 protein | 0.02 rad | 0.025 rad | 0.05 Å | 0.003 rad | 0.02 rad |
| Move Class | Acc. Rate | # Iterations | T | |
|---|---|---|---|---|
| SH3 domain | OneTorsion | 0.68 | 63 h | |
| ConRot | 0.56 | 51 h | ||
| OneParticle | 0.42 | 56 h | ||
| Hinge | 0.59 | 57 h | ||
| Mixed | 0.56 | 57 h | ||
| Sic1 protein | OneTorsion | 0.56 | 89 h | |
| ConRot | 0.65 | 63 h | ||
| OneParticle | 0.52 | 69 h | ||
| Hinge | 0.53 | 75 h | ||
| Mixed | 0.57 | 74 h |
| Move Class | Average | Min | Median | Max |
|---|---|---|---|---|
| ConRot | 6016 | 512 | 5315 | 14,070 |
| OneParticle | 3426 | 343 | 1215 | 11,281 |
| Mixed | 1518 | 157 | 985 | 3706 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denarie, L.; Al-Bluwi, I.; Vaisset, M.; Siméon, T.; Cortés, J. Segmenting Proteins into Tripeptides to Enhance Conformational Sampling with Monte Carlo Methods. Molecules 2018, 23, 373. https://doi.org/10.3390/molecules23020373
Denarie L, Al-Bluwi I, Vaisset M, Siméon T, Cortés J. Segmenting Proteins into Tripeptides to Enhance Conformational Sampling with Monte Carlo Methods. Molecules. 2018; 23(2):373. https://doi.org/10.3390/molecules23020373
Chicago/Turabian StyleDenarie, Laurent, Ibrahim Al-Bluwi, Marc Vaisset, Thierry Siméon, and Juan Cortés. 2018. "Segmenting Proteins into Tripeptides to Enhance Conformational Sampling with Monte Carlo Methods" Molecules 23, no. 2: 373. https://doi.org/10.3390/molecules23020373
APA StyleDenarie, L., Al-Bluwi, I., Vaisset, M., Siméon, T., & Cortés, J. (2018). Segmenting Proteins into Tripeptides to Enhance Conformational Sampling with Monte Carlo Methods. Molecules, 23(2), 373. https://doi.org/10.3390/molecules23020373