1. Introduction
The antenna is the fundamental component of transmitting and receiving radio waves in wireless communication systems, which restricts the performance and size of the wireless communication system. In order to minimize the size of the antenna and make effective use of valuable spectrum resources, it is appropriate to find better antenna materials and antenna structures in comparison to traditional microstrip antennae based on Euclidean geometry. Graphene has a unique two-dimensional planar structure, i.e., tunable thermal and electric conductivity [
1], which provides many potential engineering applications in the realm of wireless communication systems, including high-performance antennae [
2,
3,
4,
5,
6]. Additionally, the surface impedance of graphene can be adjusted macroscopically by applying bias voltage [
3,
4,
5]. Moreover, the high electrical resistance of graphene in terahertz band can inhibit the radiation side lobe of the antenna, which enables the graphene antenna to achieve directional radiation and improve the gain [
3].
Fractal geometry [
7], whose perimeter becomes larger and larger, while the area becomes smaller and smaller with fractal level increasing, can be applicable to the design of an antenna structure [
8]. Compared to traditional microstrip antennae, because of its unique self-similarity geometry, the fractal antenna has two obvious advantages. Firstly, the multifrequency performance of the electrical parameters can be obtained. Secondly, the space filling of the fractal structure makes it possible to reduce the size of some antennae [
9]. Therefore, fractal graphene may be an effective technical approach for high-performance multiband antennae with a small size. Notably, the excessive power and overheating of an electronic device will affect its service performance and lifetime. When the heat inside a high-power device cannot be released in time, the heat inside the device will cause heat accumulation and deteriorate the reliability of the device [
10]. Therefore, an antenna should take thermal transport into account to increase the reliability of the communication system. That is, it is necessary to study the thermal transportation properties of fractal graphene. Many advances in the fields of nanoelectronics and thermal management [
11,
12] have been achieved ever since the pioneering work of Novoselov et al. [
13]. The thermal conductivity of the graphene monolayer can be up to 5300
W·
m−1·
K−1 [
3,
11,
14,
15] at room temperature. Because of the strong covalent bond between carbon and carbon, graphene conducts heat through lattice vibration, i.e., phonon. Molecular dynamics (MD) is an appropriate method to study phonon vibration, which dominates the thermal transport of graphene. The thermal features of graphene sheets have been regulated through chemical doping [
16] and physical tailoring [
17]. However, graphene sheets with fractal defects have seldom been studied [
18,
19,
20].
In this work, graphene with Sierpinski carpet fractal models with different fractal levels are established, and their thermal conductivity and interfacial thermal resistances are calculated using the reverse nonequilibrium molecular dynamics method (RNEMD) method [
21]. Furthermore, the microheat flux on each atom of these fractal graphene sheets is calculated and compared with perfect graphene to verify the microscopic thermal transportation mechanism.
3. Molecular Dynamics Simulation
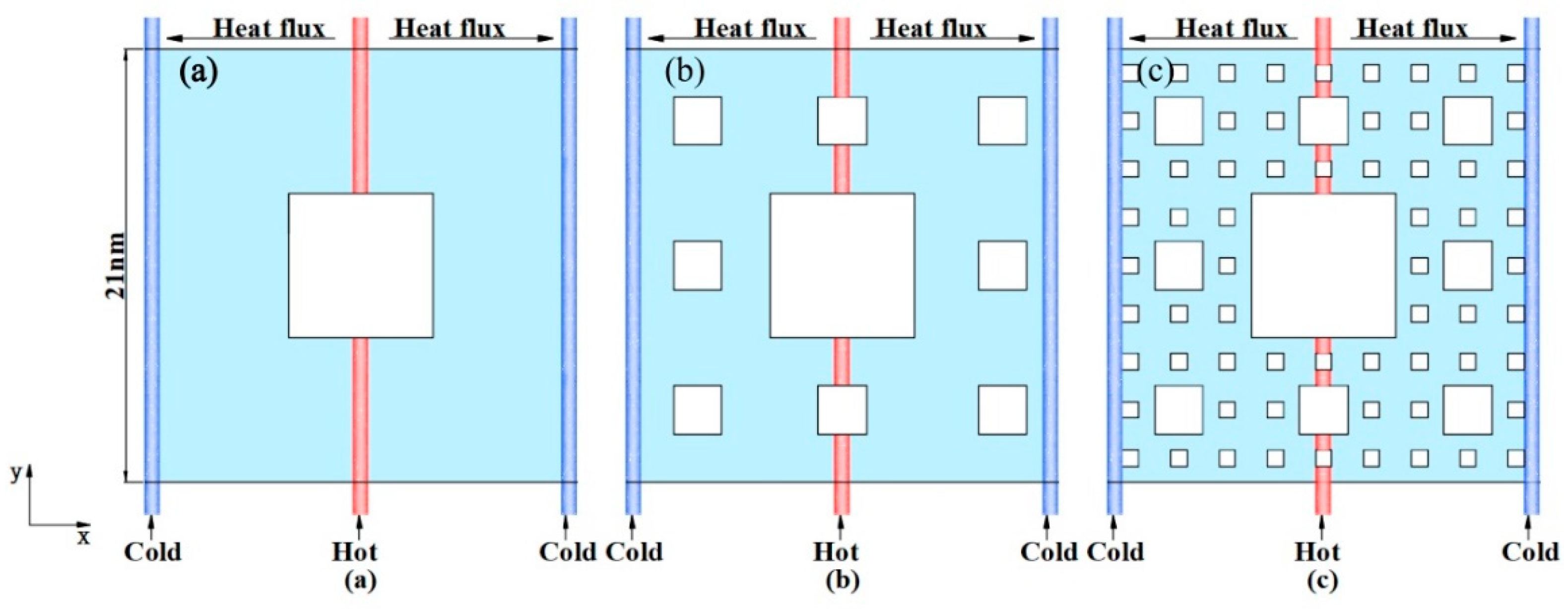
In this paper, graphene models with different fractal levels of 1, 2, and 3, and perfect graphene (gra0) have been established and studied. The chirality and size of each model are exactly the same. The chirality is Ziazag, and the side length is 21 nm. The thermal properties of graphene with different fractal levels were simulated using the RNEMD method [
21]. As shown in
Figure 1, in this work, the heat flux was imposed along the x direction to generate a temperature gradient through the Nosé–Hoover thermal bath [
22,
23]. The interaction between two carbon atoms was described by the adaptive intermolecular reactive empirical bond-order (AIREBO) potential [
24], which has been widely used to study the thermal and mechanical properties of graphene nanomaterials [
18,
25]. The simulating time step was set to be of 0.5 fs. Both the in-plane and out-plane directions were used for the periodic boundary condition. The dimension of the out-plane simulation box was set to be from –1 nm to 1 nm. Additionally, the monolayer graphene was placed in the origin position of the out-of-plane direction to avoid interaction between replicas of the monolayer graphene. Molecular dynamics were conducted using the large-scale atomic/molecular massively parallel simulator (LAMMPS) [
26]. Firstly, the energy of the system was minimized using the conjugate gradient method [
27]. Then, simulations were carried out in a NVT (constant atom number, volume, and temperature) ensemble at 300 K after 200 ps, which was long enough to reach an initial equilibrium for the system. The system was later switched to a NVE (constant atom number, volume, and energy) ensemble for 4 ns, of which 1 ns was to obtain a nonequilibrium steady state and then, 3 ns was used to produce an average temperature profile. The thermal conductivity of the graphene with fractal defects was calculated using RNEMD. The entire structural models were divided into 50 slabs along the x direction, where the 1st slab and the 50th slab were cold regions, and the 26th was a hot region. The hottest atom in the cold region periodically swaps its energy with the coldest atom in the hot region in order to achieve a temperature gradient. Here, the heat flux
Jx can be calculated by:
Jx is heat flux;
Nswap is the pair number of the atoms involved in exchange of kinetic energy in the simulation process;
tswap means the total time of exchanging atomic energy in the whole simulation process; and
vs and
vh are the velocity of the hottest atoms in the heat sink region and the coldest atoms in the heat source region, respectively. The energy was exchanged every 100 steps and the heat flow from the heat source to the heat sink reached a steady state after 1.0 ns. Then, a stable temperature gradient appeared in the model. The temperature for each slab was computed from:
Ti is the temperature of the ith slab, is the number of atoms contained in the ith slab, kB is the Boltzmann constant, and is the momentum of the j atom.
During energy exchange, the linear response of the temperature variation happens beyond the defective area, where it means interfacial thermal resistance appears. The temperature differences at jumping points, ∆T, as shown in
Figure 2 and
Figure 3, can be obtained by linearly fitting the temperature variation in each slab. In addition, the temperature distribution is linear in the central region between the heat source and heat sink, which is consistent with the temperature distribution obtained by Fourier’s heat conduction law. The thermal conductivity
κ can be calculated by the following formula:
where
A represents the cross-sectional area through the heat flux, which can be described by the width of the model to multiply the thickness of the graphene sheet. We took the thickness of the graphene sheet as 0.142 nm, the carbon–carbon bond length, which was widely adopted to calculate the thermal conductivity of graphene sheet and nanotube [
18].
The interfacial thermal resistance, also known as the Kapitza resistance, has been defined as the ratio of the temperature difference and the heat flux across the interface:
where ∆
T represents the temperature difference and
J is constant heat flux.
4. Results and Discussions
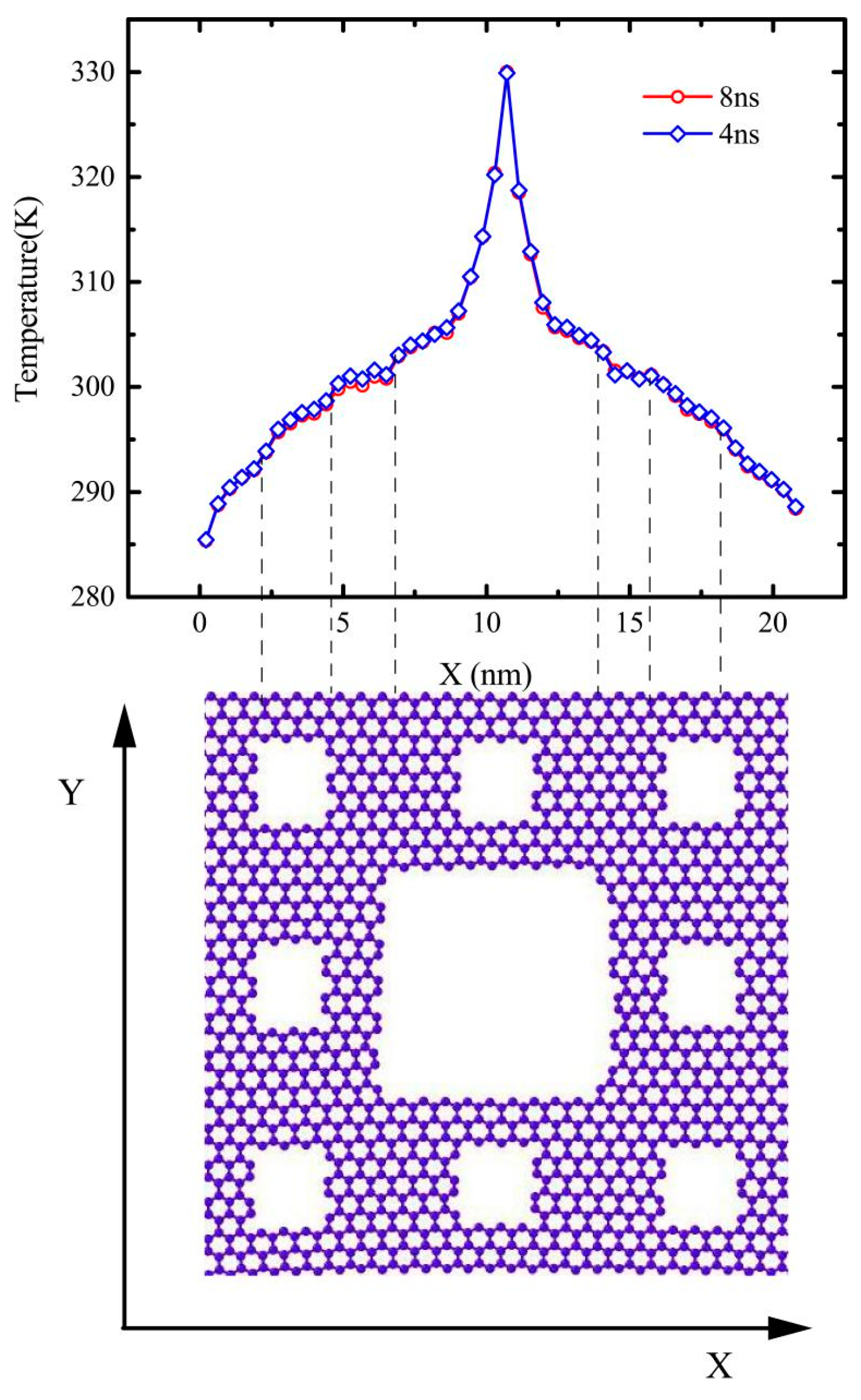
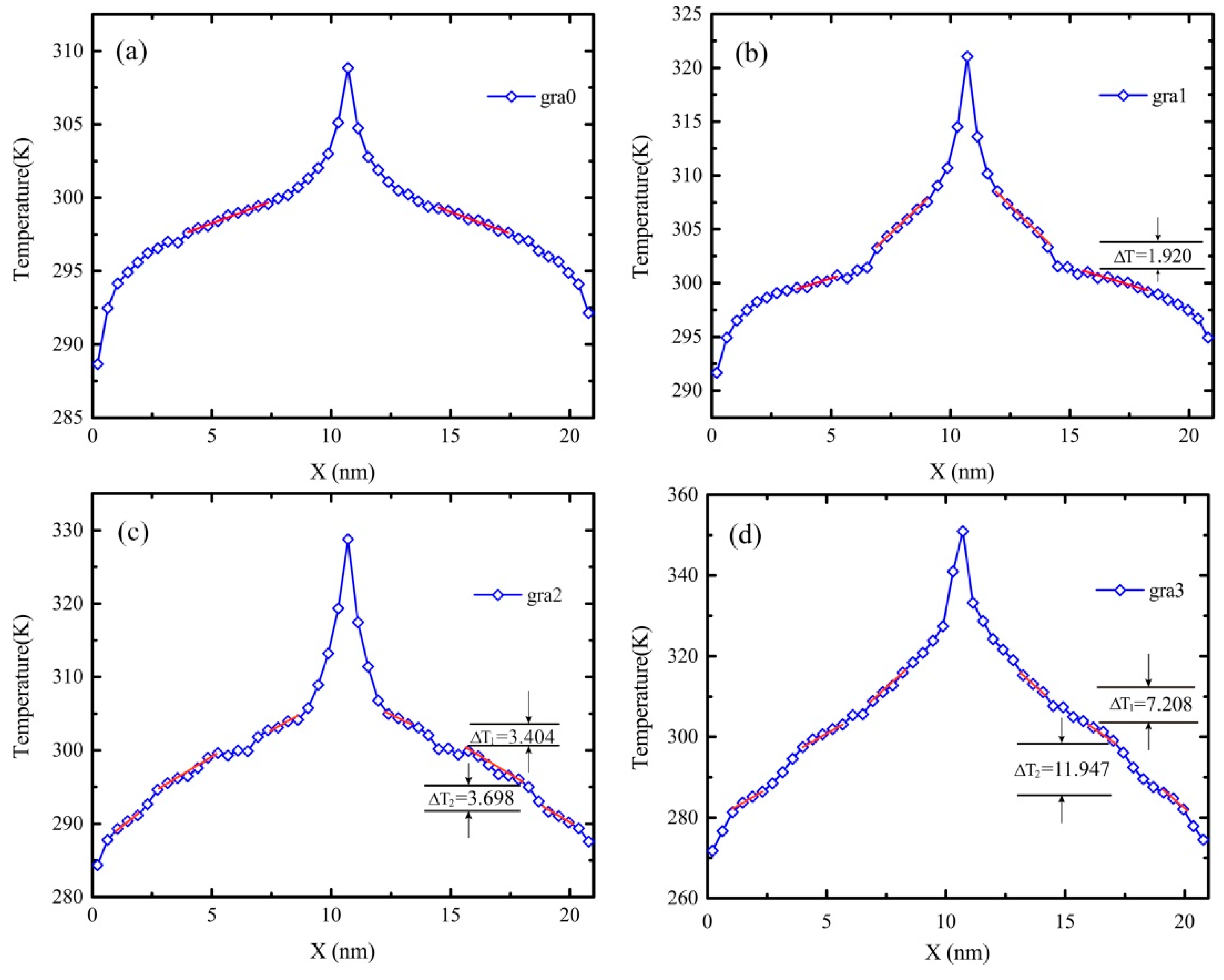
The temperature profile of gra3 seems smoother than that of the gra2, as shown in
Figure 3c,d. The reason for the roughness of the temperature profile of the gra2 may be fractal defects, which inherently affect the heat flux transfer or the insufficient time to average temperature. Therefore, we supplemented a simulation about the gra2 in same condition except that the system is running for 8 ns in a NVE ensemble, of which the 1st 4 ns that were enough to reach a nonequilibrium steady state and the 2nd 4 ns was used to average the temperature profile. As shown in
Figure 2, there is almost no difference between the temperature profiles with 8 ns and 4 ns. Therefore, the unsmoothness of temperature profiles was attributed to the fractal defects with different levels. Then, we continued this work in terms of the 4ns’ simulation time, which is sufficient to obtain accurate results.
As shown in
Figure 3, in agreement with the previous study [
28], drops were observed in the temperature profile due to the space vacancy, and they indicated the presence of interfacial thermal resistance. The jump in the temperature profile is associated with the reduction of the heat flux. Moreover, the temperature jumps near the low temperature side are larger than those near the high temperature side, which is consistent with the conclusion of a rectangular defect graphene structure [
20]. In order to decrease the error, the temperature jump values were the differences of the linear fitting data at the jump points. As shown in
Figure 3, the temperature profile of gra3 is smoother than the result of gra2. Unexpectedly, the temperature jumps of gra3 varied greatly at the same position as gra2 and the corresponding interfacial thermal resistance effect of gra3 is more obvious than those of gra2, as shown in the
Table 1. Generally, temperature jumps of a greater fractal level are bigger than those of lower fractal levels, as shown in
Figure 3 and
Table 1. That is, the biggest temperature drop occurs in the boundary or edge near defects of gra3. It seems that thermal carriers are trapped and energy is accumulated in these edge regions, but the exact physical images of heat transport at the atomic level are not clear.
In addition, the original temperatures of the systems are set to be 300 K and the energy of all simulation systems is identical. When the system is in the steady state, the stable temperature difference between heat resource and heat sink increases as the fractal level raises, which is shown in
Figure 3. The temperature difference of gra0 is 20 K and that of gra3 is 82 K. According to Equation (3), this phenomenon can be attributed to the decrease of the atom numbers of fractal graphene as the fractal level increases, while the momentum of all models is congruent.
For heterogeneous material, thermal conductivity can be evaluated by the proportion of different components [
19,
29]. Similarly, the thermal conductivity of graphene with fractal defects was evaluated by Equation (5), of which
∂T/
∂X is the average of linear fittings in the temperature profiles, as shown in
Figure 3.
Figure 4 displays the thermal conductivity of graphene with different fractal levels. The simulation results show that the thermal conductivity of the perfect graphene sheet of 21 nm × 21 nm is 164.40
W m−1 K−1, which is consistent with the result of the perfect graphene nanoribbon of 19.4 nm × 7 nm [
18], 151.60
W m−1 K−1. Additionally, the thermal conductivity of fractal graphene decreases with the increase of fractal levels. The thermal conductivity of gra1, 157.62
W m−1 K−1, is a little smaller than the value of gra0. The reduction of gra3 thermal conductivity is up to 87.5% of the gra0. As shown in
Figure 1, the structure of gra1 is similar with the gra0, except for the defect in the center; as for gra2 and gra3, the defects within interior dramatically increased further. That is, fractal defects alter the thermal transport properties of fractal graphene, but how the defects affect the thermal properties is not clear, especially at the micro level. Usually, the reason for the thermal conductivity reduction of graphene with defects lies in the three main aspects, i.e., the elongation of the real heat flux path, the overestimation of real heat flux area, and the phonon scattering at the edges. In terms of the fractal graphene model structure, the area reduction of heat flux transport is apparent.
To gain a better insight, the microheat flux on each atom was calculated by the RNEMD simulations and defined by the expression:
qi =
eivi −
Sivi, where
ei,
vi, and
Si are the energy, velocity vector, and stress tensor of each atom i, respectively [
30].
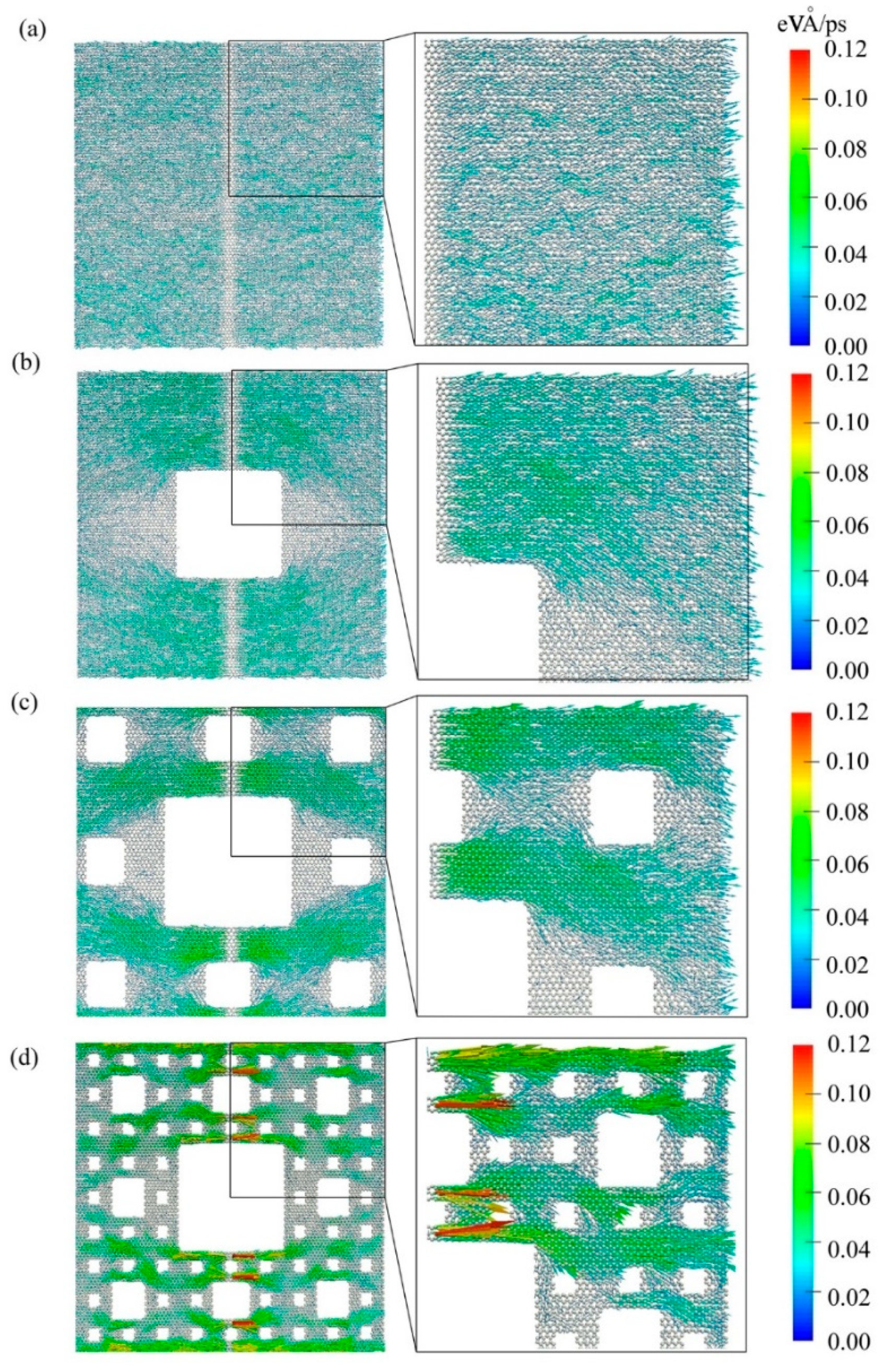
Figure 5 demonstrates vividly the elongation of the heat flux path as well as the phonon scattering in the fractal graphene. The vector arrow shows the migration direction and magnitude of the atomic heat flux. To display the atomic heat flux more clearly, the zoom in viewport is plotted at the right side, and colorful scale also shows the magnitude of the atomic heat flux, where with the color gradually turning to warm, the magnitude increases.
As shown in
Figure 5a, the colors of the atomic heat flux are relatively unvaried, which indicates the migration of the heat flux is a uniform distribution at around 0.02. Moreover, the vectors are generally oriented in the x direction, i.e., the angle of atomic heat flux vectors approaches zero degree with little fluctuations. As shown in
Figure 5b–d, with the fractal levels increasing, the color distributions of the atomic heat flux become uneven gradually, and the angles of atomic heat flux vector deviate from the x direction quickly. Furthermore, from
Figure 5a–d, some of the vector colors are deepening, which means energy is accumulated in these atoms; while others are fading, which means energy degrades in these atoms. Therefore, the temperature differences at these interfaces grow. This is in line with the enlargement of temperature differences shown in
Figure 3a–d. Notably,
Figure 5 exhibits directly the real heat flux path. Additionally, the paths of gra1, gra2, and gra3 are longer and longer than that of gra0.
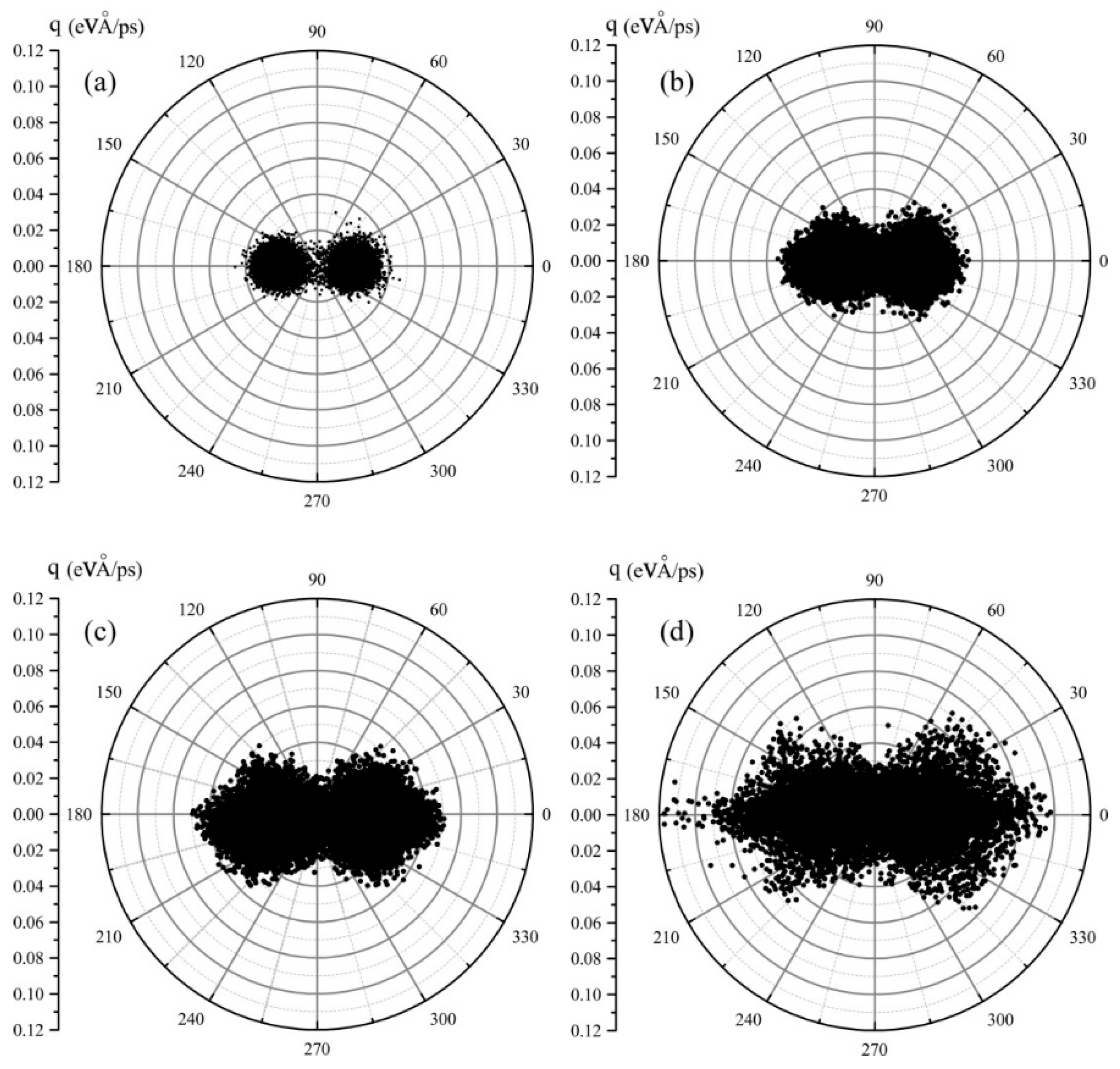
Although the heat flux transport directions are displayed with arrows at graphene with different fractal defects in
Figure 5, the magnitude and angle distribution of the atomic heat flux is perceptual. Thus, we reorganized the atomic heat flux vector data in the form of polar coordinate and replotted them in
Figure 6. It shows quantitatively the angle and magnitude distribution of the atomic vector heat flux. As shown in
Figure 6a, the angle of the atomic heat flux vector is distributed between 330 to 30 degrees and 150 to 210 degrees, symmetrically. As expected, the angle distribution range of the atomic heat flux vector is wider and wider from
Figure 6b–d. As for the shapes of the dotted vectors, from
Figure 6a–d, they evolve from two small symmetrical circles to bigger and bigger symmetrical spindles, and the area of the shapes increases with the fractal levels increasing. This implicates that the phonon or heat carriers is scattered dramatically by the defect edges with the increase of fractal levels. In fact, the direction of the atomic heat flux vector can be considered as the average phonon propagation direction. As shown in
Figure 6, the phonon scattering occurs qualitatively and quantitatively. However, it is difficult to figure out the magnitude or angle distribution of phonon scattering in statistical analysis because data points overlap in
Figure 6.
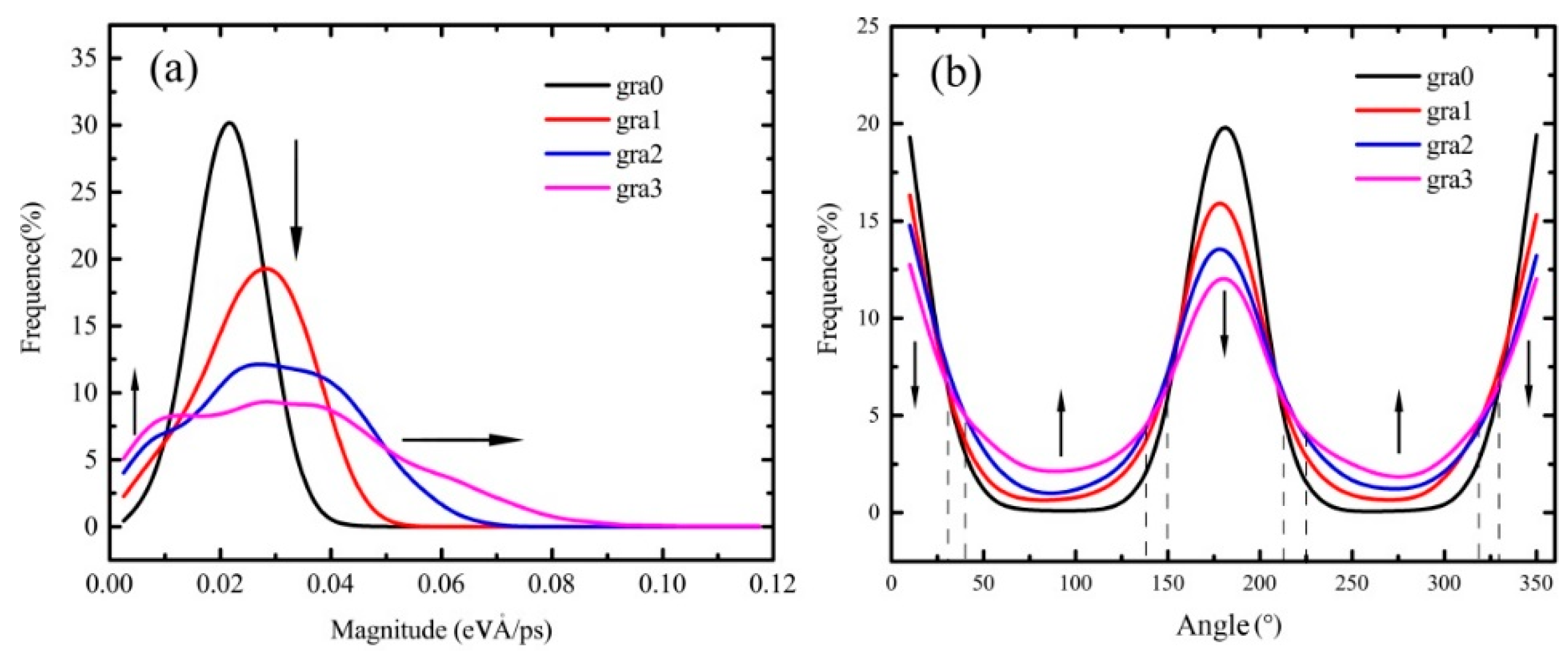
Figure 7a exhibits the magnitude distribution of the atomic heat flux vector. The peak values of frequency curves of the atomic heat flux vectors’ magnitude are diminished from gra0 to gra3 with curves flattening. That is, the number of smaller and larger magnitude values increases, while the middle magnitude value decreases. This agrees with
Figure 3. The increase of temperature difference contributes to the fractal defect, where the energy accumulation occurs. In addition, the real heat flux path elongates due to the fractal defect, as shown in
Figure 5.
Figure 7b displays the angle distribution of the atomic heat flux vector. The peak of the frequency curve of the atomic heat flux vectors’ angle diminishes from gra0 to gra3, while the two valleys rise. This indicates that the number of atomic heat flux vectors parallel to the x direction decreases due to the increase of fractal defects, which leads to the phonon scattering, i.e., the propagation direction of the atomic heat flux vector deflects, which is consistent with
Figure 5 and
Figure 6.