A Trajectory-Based Method to Explore Reaction Mechanisms
Abstract
1. Introduction
2. Method
2.1. Graph Theory
2.2. Kinetics Simulations
3. Overview of the Applications of Tsscds
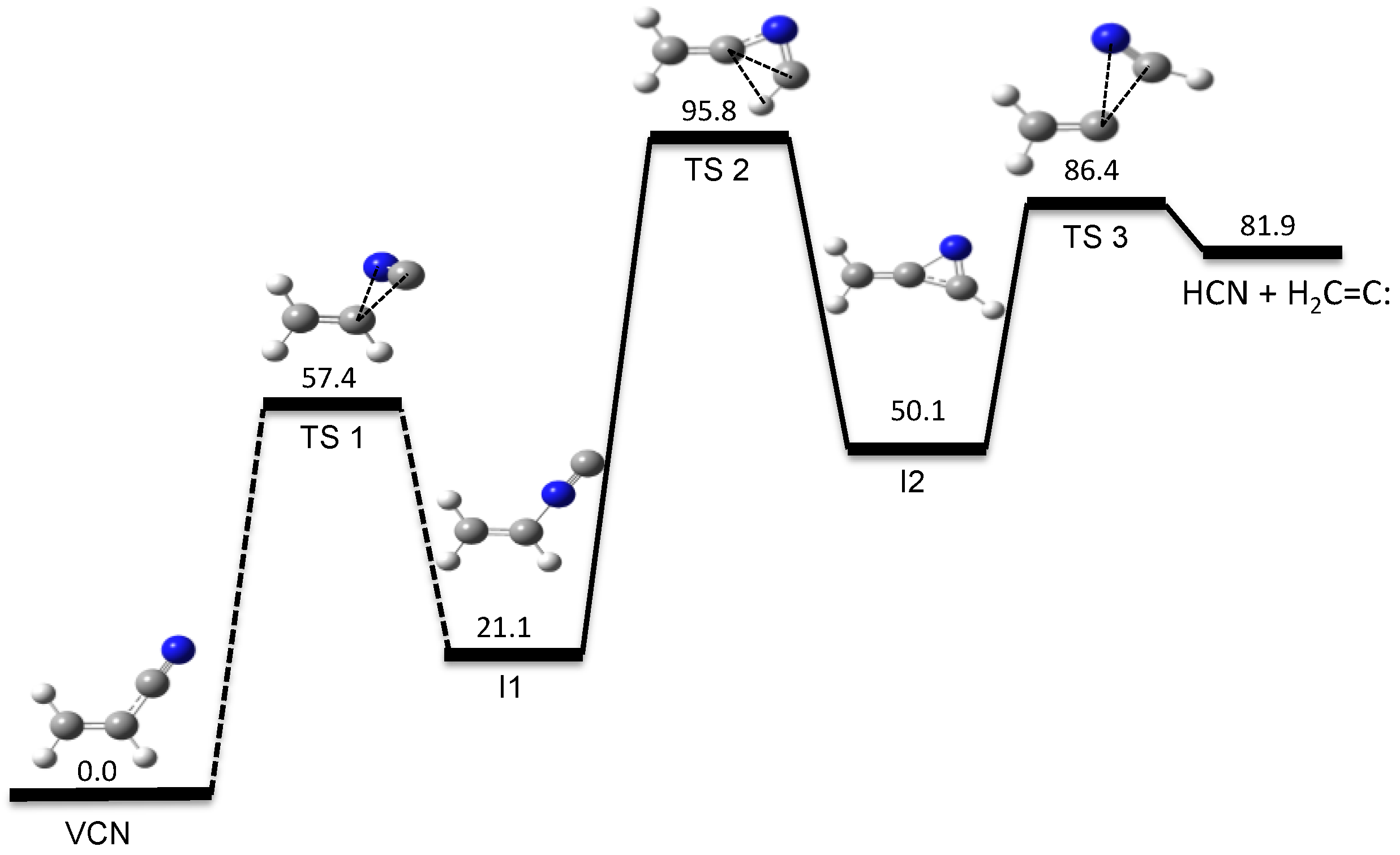
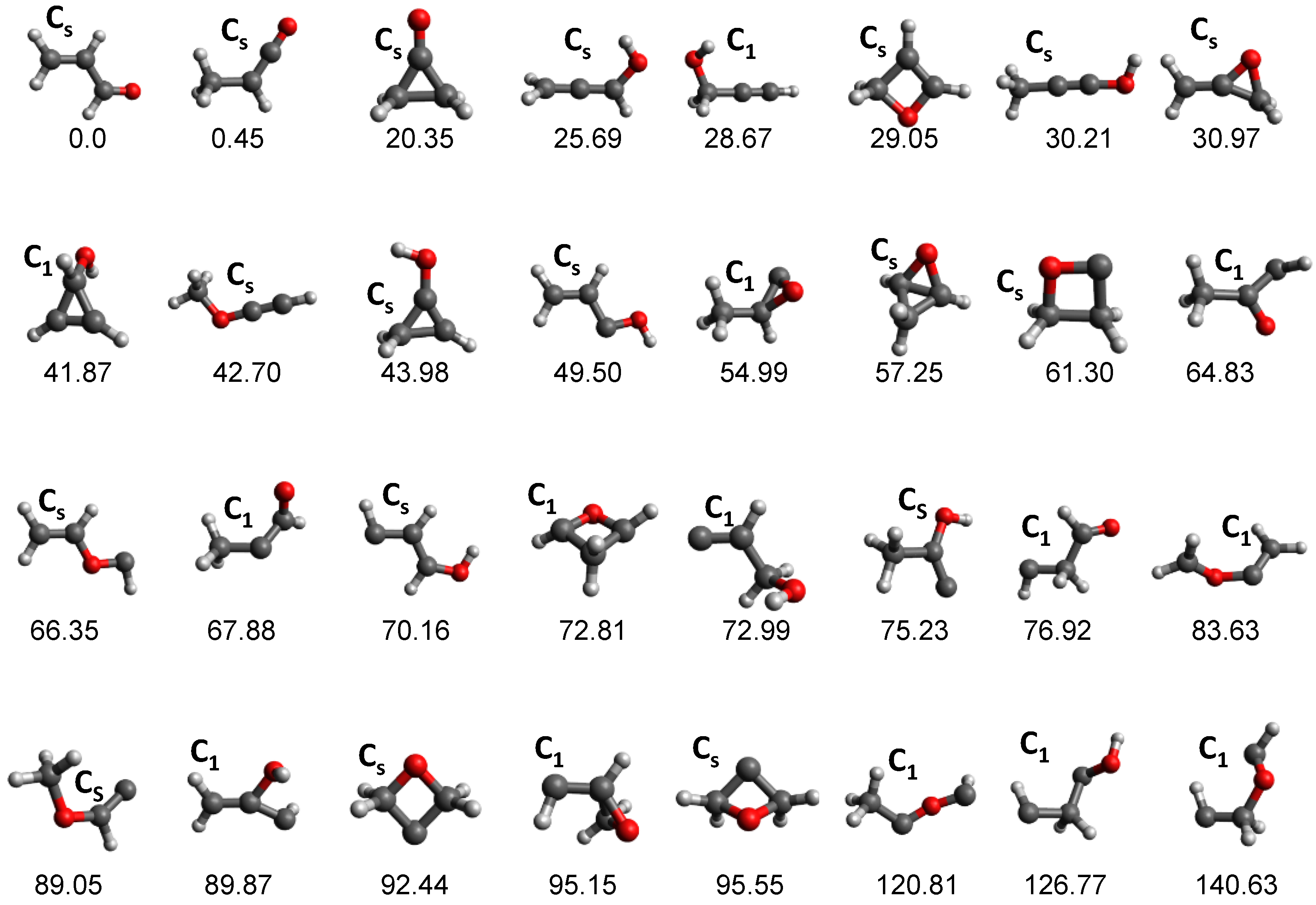
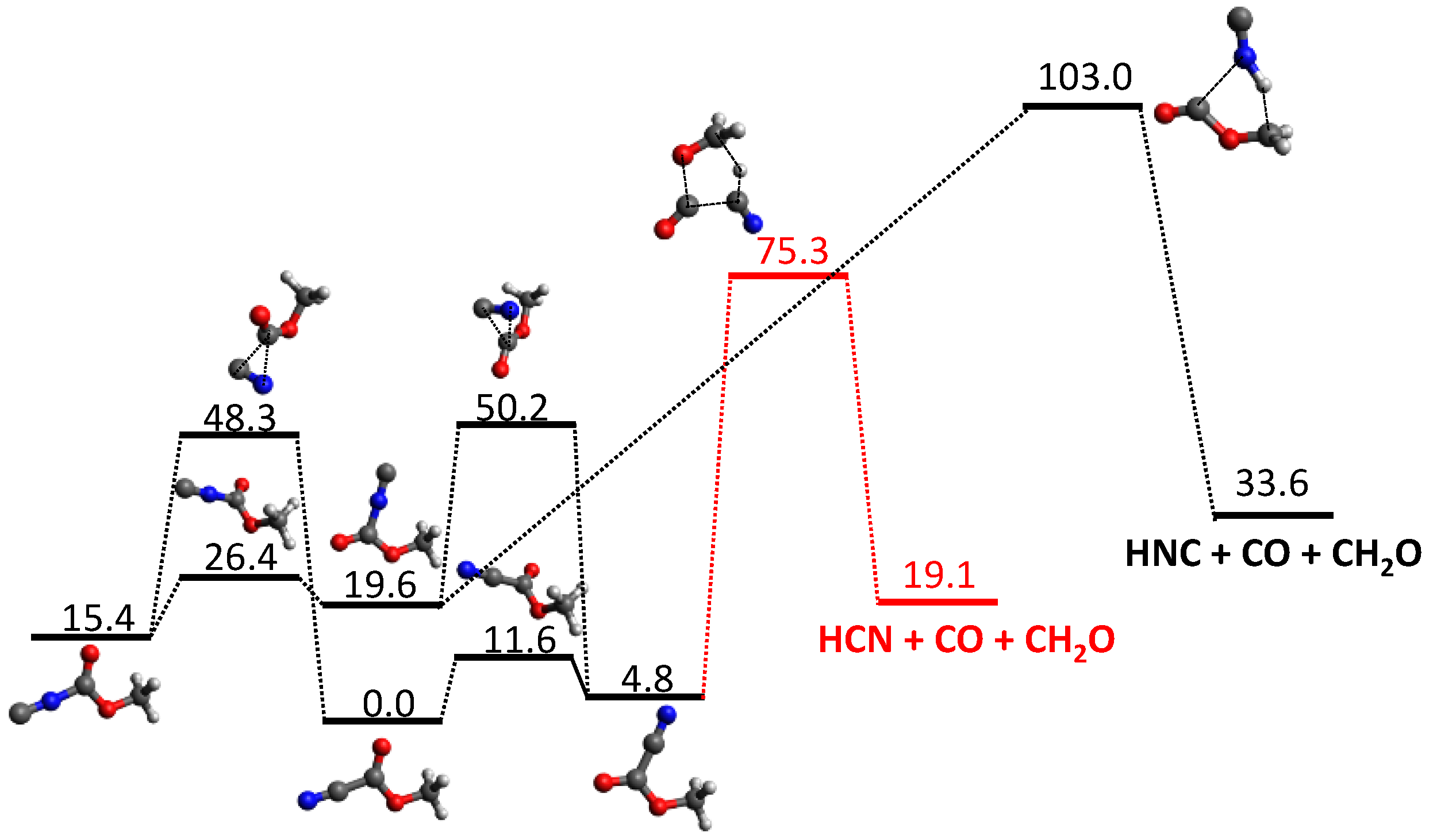
3.1. Photodissociation Dynamics
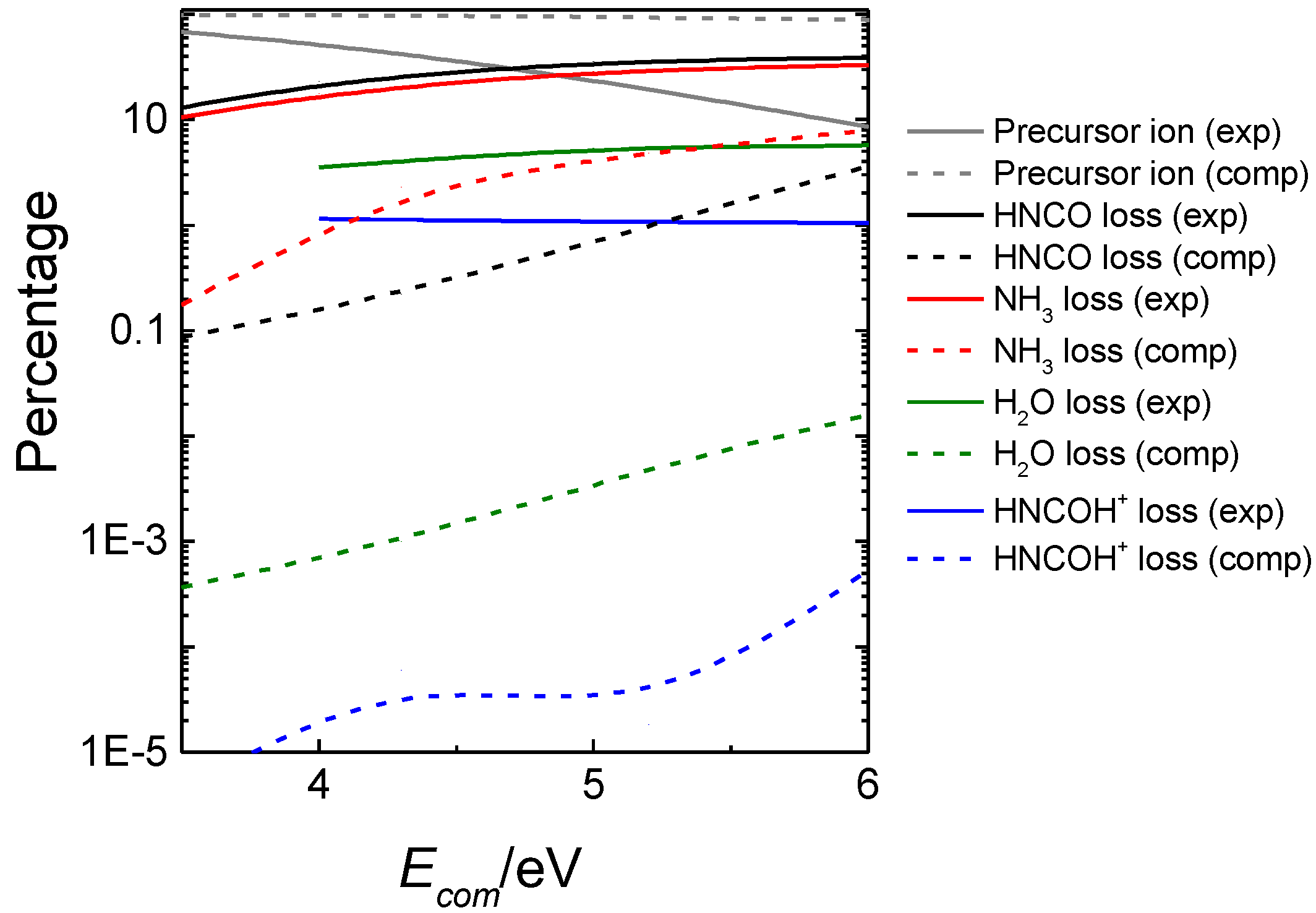
3.2. Mass Spectrometry
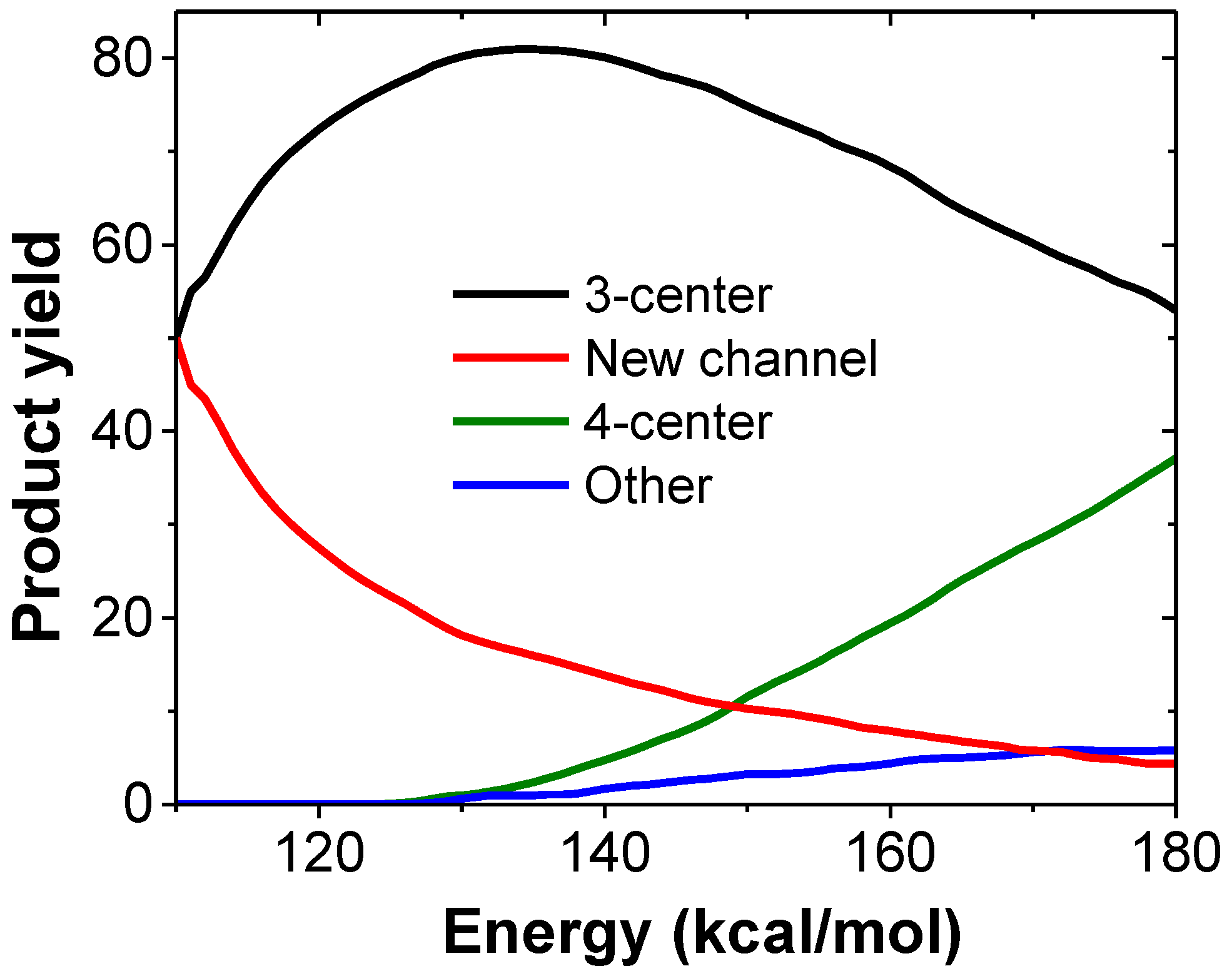
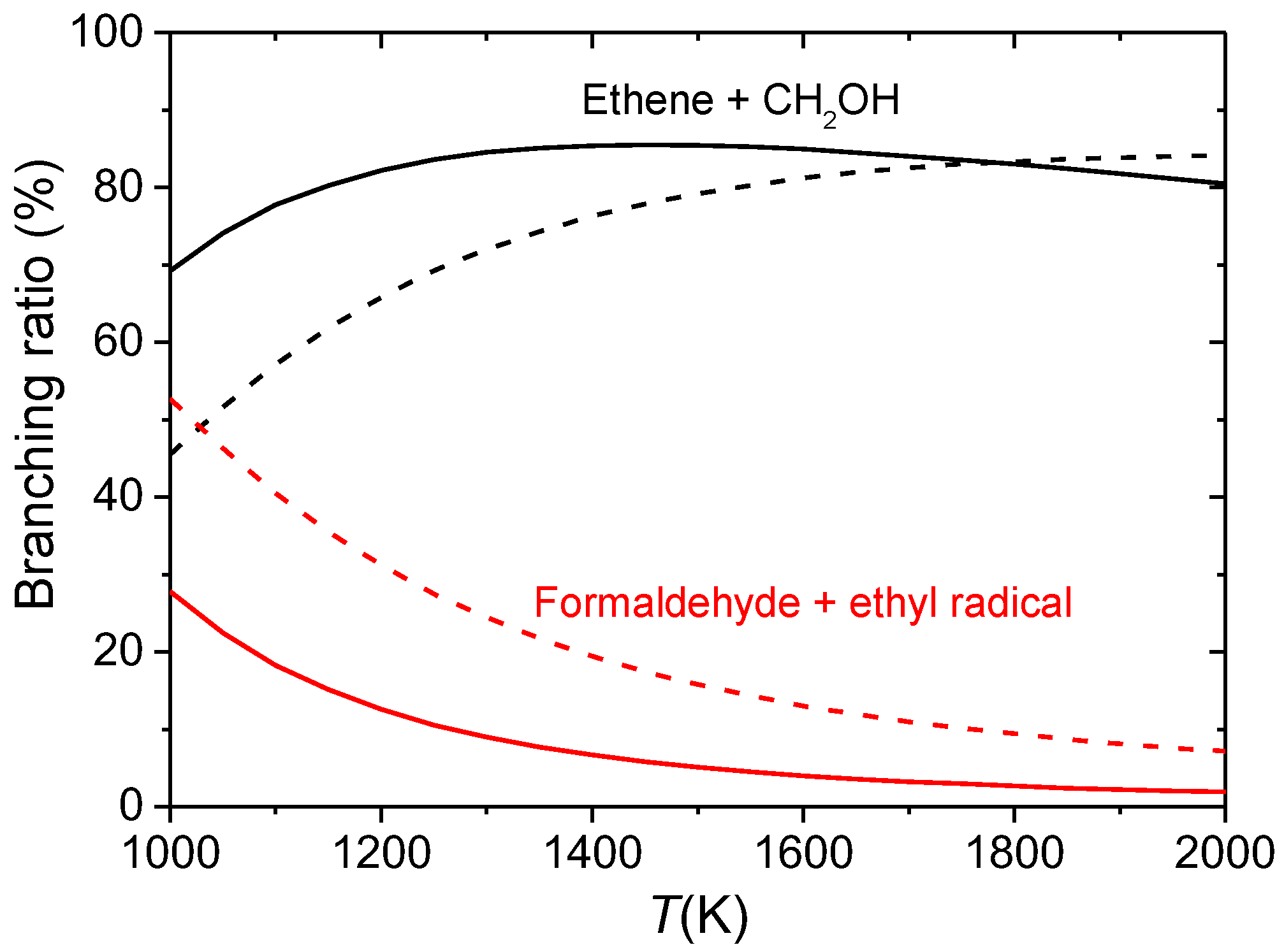
3.3. Combustion Chemistry
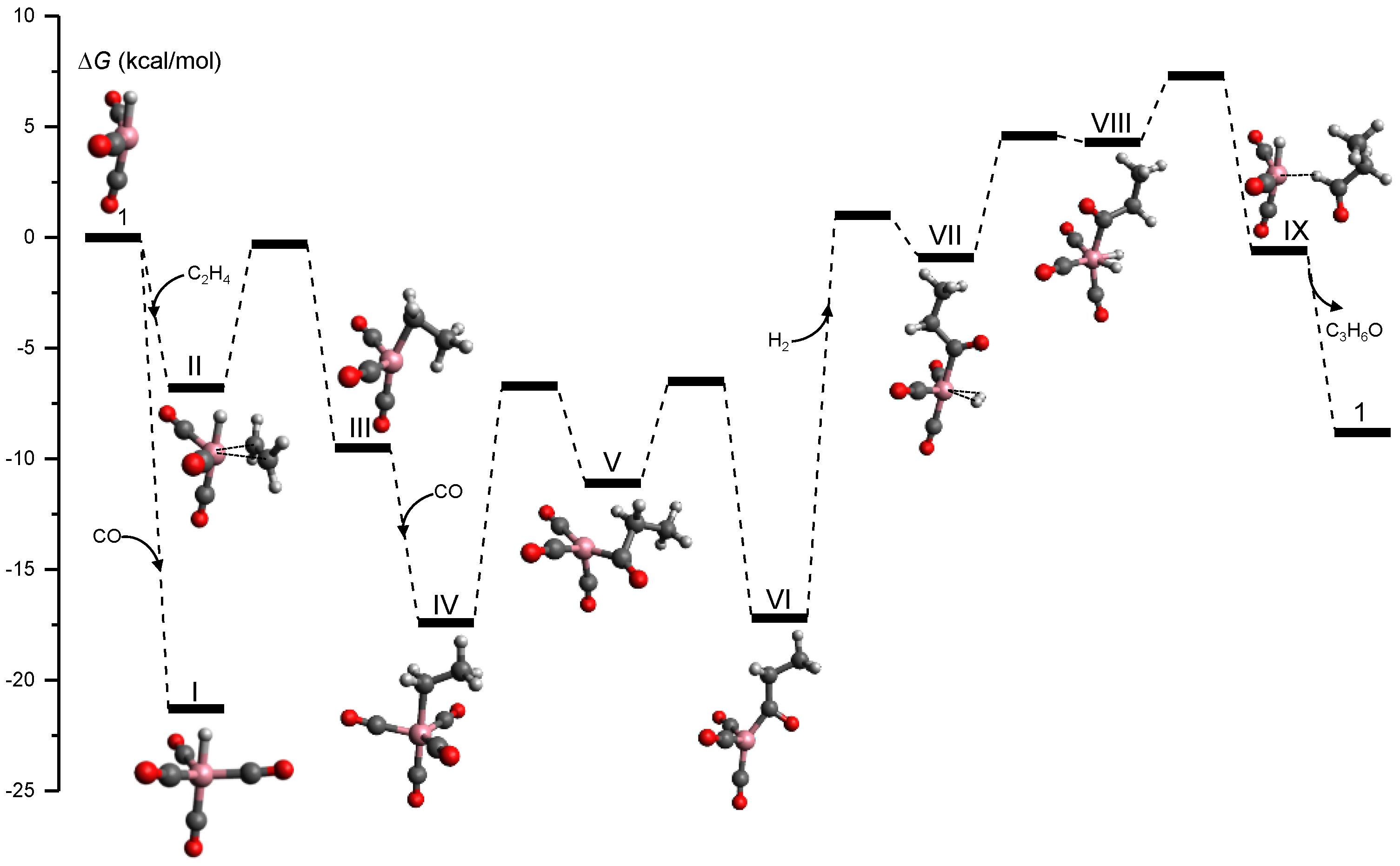
3.4. Organometallic Catalysis
4. Improvements
4.1. Use of Spectral Graph Theory to Minimize the Number of Hessian Calculations
4.2. Implementation of Knowledge-Based Mechanism Generators
4.3. Implementation of Rare-Event Acceleration MD Methods
4.4. Interface with Other Electronic Structure Codes
4.5. Reparametrization of Semiempirical Methods
4.6. Study of Condensed Phase Reactions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schlegel, H.B. Geometry optimization. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 790–809. [Google Scholar] [CrossRef]
- Davis, H.L.; Wales, D.J.; Berry, R.S. Exploring potential energy surfaces with transition state calculations. J. Chem. Phys. 1990, 92, 4308–4319. [Google Scholar] [CrossRef]
- Sun, J.Q.; Ruedenberg, K. Gradient Extremals and Steepest Descent Lines on Potential Energy Surfaces. J. Chem. Phys. 1993, 98, 9707–9714. [Google Scholar] [CrossRef]
- Tsai, C.J.; Jordan, K.D. Use of an eigenmode method to locate the stationary points on the potential energy surfaces of selected argon and water clusters. J. Phys. Chem. 1993, 97, 11227–11237. [Google Scholar] [CrossRef]
- Abashkin, Y.; Russo, N. Transition state structures and reaction profiles from constrained optimization procedure. Implementation in the framework of density functional theory. J. Chem. Phys. 1994, 100, 4477–4483. [Google Scholar] [CrossRef]
- Bondensgard, K.; Jensen, F. Gradient Extremal Bifurcation and Turning Points: An Application to the H2CO Potential Energy Surface. J. Chem. Phys. 1996, 104, 8025–8031. [Google Scholar] [CrossRef]
- Doye, J.P.K.; Wales, D.J. Surveying a potential energy surface by eigenvector-following. Z. Phys. D 1997, 40, 194–197. [Google Scholar] [CrossRef]
- Quapp, W.; Hirsch, M.; Imig, O.; Heidrich, D. Searching for Saddle Points of Potential Energy Surfaces by Following a Reduced Gradient. J. Comput. Chem. 1998, 19, 1087–1100. [Google Scholar] [CrossRef]
- Černohorský, M.; Kettou, S.; Koča, J. VADER: New Software for Exploring Interconversions on Potential Energy Surfaces. J. Chem. Inf. Comput. Sci. 1999, 39, 705–712. [Google Scholar] [CrossRef]
- Westerberg, K.M.; Floudas, C.A. Locating all transition states and studying the reaction pathways of potential energy surfaces. J. Chem. Phys. 1999, 110, 9259–9295. [Google Scholar] [CrossRef]
- Wales, D.J.; Doye, J.P.; Miller, M.A.; Mortenson, P.N.; Walsh, T.R. Energy Landscapes: From Clusters to Biomolecules. Adv. Chem. Phys. 2000, 115, 1–111. [Google Scholar]
- Irikura, K.K.; Johnson, R.D. Predicting unexpected chemical reactions by isopotential searching. J. Phys. Chem. A 2000, 104, 2191–2194. [Google Scholar] [CrossRef]
- Müller, E.M.; Meijere, A.D.; Grubmüller, H. Predicting unimolecular chemical reactions: Chemical flooding. J. Chem. Phys. 2002, 116, 897–905. [Google Scholar] [CrossRef]
- Dallos, M.; Lischka, H.; Ventura Do Monte, E.; Hirsch, M.; Quapp, W. Determination of Energy Minima and Saddle Points Using Multireference Configuration Interaction Methods in Combination with Reduced Gradient Following: The S0 surface of H2CO and the T1 and T2 surfaces of acetylene. J. Comput. Chem. 2002, 23, 576–583. [Google Scholar] [CrossRef] [PubMed]
- Baker, J.; Wolinski, K. Isomerization of stilbene using enforced geometry optimization. J. Comput. Chem. 2011, 32, 43–53. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, P.M. Automated discovery of chemically reasonable elementary reaction steps. J. Comput. Chem. 2013, 34, 1385–1392. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, P.M. Growing string method with interpolation and optimization in internal coordinates: Method and examples. J. Chem. Phys. 2013, 138, 184102. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, P. Reliable Transition State Searches Integrated with the Growing String Method. J. Chem. Theory Comput. 2013, 9, 3043–3050. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, P.M. Single-ended transition state finding with the growing string method. J. Comput. Chem. 2015, 36, 601–611. [Google Scholar] [CrossRef] [PubMed]
- Zimmerman, P.M. Navigating molecular space for reaction mechanisms: An efficient, automated procedure. Mol. Simul. 2015, 41, 43–54. [Google Scholar] [CrossRef]
- Jafari, M.; Zimmerman, P.M. Reliable and efficient reaction path and transition state finding for surface reactions with the growing string method. J. Comput. Chem. 2017, 38, 645–658. [Google Scholar] [CrossRef] [PubMed]
- Dewyer, A.L.; Zimmerman, P.M. Finding reaction mechanisms, intuitive or otherwise. Org. Biomol. Chem. 2017, 15, 501–504. [Google Scholar] [CrossRef] [PubMed]
- Rappoport, D.; Galvin, C.J.; Zubarev, D.Y.; Aspuru-Guzik, A. Complex Chemical Reaction Networks from Heuristics-Aided Quantum Chemistry. J. Chem. Theory Comput. 2014, 10, 897–907. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, B.; Mohr, S.; Amsler, M.; Goedecker, S. Minima hopping guided path search: An efficient method for finding complex chemical reaction pathways. J. Chem. Phys. 2014, 140, 214102. [Google Scholar] [CrossRef] [PubMed]
- Wales, D.J. Perspective: Insight into reaction coordinates and dynamics from the potential energy landscape. J. Chem. Phys. 2015, 142, 130901. [Google Scholar] [CrossRef] [PubMed]
- Habershon, S. Sampling reactive pathways with random walks in chemical space: Applications to molecular dissociation and catalysis. J. Chem. Phys. 2015, 143, 094106. [Google Scholar] [CrossRef] [PubMed]
- Habershon, S. Automated Prediction of Catalytic Mechanism and Rate Law Using Graph-Based Reaction Path Sampling. J. Chem. Theory Comput. 2016, 12, 1786–1798. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.-J.; Liu, Z.-P. Reaction sampling and reactivity prediction using the stochastic surface walking method. Phys. Chem. Chem. Phys. 2015, 17, 2757–2769. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-P.; McGibbon, R.T.; Pande, V.S.; Martinez, T.J. Automated Discovery and Refinement of Reactive Molecular Dynamics Pathways. J. Chem. Theory Comput. 2016, 12, 638–649. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-P.; Titov, A.; McGibbon, R.; Liu, F.; Pande, V.S.; Martínez, T.J. Discovering chemistry with an ab initio nanoreactor. Nat. Chem. 2014, 6, 1044–1048. [Google Scholar] [CrossRef] [PubMed]
- Yang, M.; Zou, J.; Wang, G.; Li, S. Automatic Reaction Pathway Search via Combined Molecular Dynamics and Coordinate Driving Method. J. Phys. Chem. A 2017, 121, 1351–1361. [Google Scholar] [CrossRef] [PubMed]
- Jacobson, L.D.; Bochevarov, A.D.; Watson, M.A.; Hughes, T.F.; Rinaldo, D.; Ehrlich, S.; Steinbrecher, T.B.; Vaitheeswaran, S.; Philipp, D.M.; Halls, M.D.; et al. Automated Transition State Search and Its Application to Diverse Types of Organic Reactions. J. Chem. Theory Comput. 2017, 13, 5780–5797. [Google Scholar] [CrossRef] [PubMed]
- Ohno, K.; Maeda, S. A Scaled Hypersphere Search Method for the Topography of Reaction Pathways on the Potential Energy Surface. Chem. Phys. Lett. 2004, 384, 277–282. [Google Scholar] [CrossRef]
- Maeda, S.; Ohno, K. Global Mapping of Equilibrium and Transition Structures on Potential Energy Surfaces by the Scaled Hypersphere Search Method: Applications to ab Initio Surfaces of Formaldehyde and Propyne Molecules. J. Phys. Chem. A 2005, 109, 5742–5753. [Google Scholar] [CrossRef] [PubMed]
- Ohno, K.; Maeda, S. Global Reaction Route Mapping on Potential Energy Surfaces of Formaldehyde, Formic Acid, and Their Metail-Substituted Analogues. J. Phys. Chem. A 2006, 110, 8933–8941. [Google Scholar] [CrossRef] [PubMed]
- Ohno, K.; Maeda, S. Automated Exploration of Reaction Channels. Phys. Scr. 2008, 78, 058122. [Google Scholar] [CrossRef]
- Maeda, S.; Morokuma, K. Communications: A systematic method for locating transition structures of A + B → X type reactions. J. Chem. Phys. 2010, 132, 241102. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Morokuma, K. Finding Reaction Pathways of Type A + B → X: Toward Systematic Prediction of Reaction Mechanisms. J. Chem. Theory Comput. 2011, 7, 2335–2345. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Ohno, K.; Morokuma, K. Systematic exploration of the mechanism of chemical reactions: The global reaction route mapping (GRRM) strategy using the ADDF and AFIR methods. Phys. Chem. Chem. Phys. 2013, 15, 3683–3701. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Taketsugu, T.; Morokuma, K. Exploring transition state structures for intramolecular pathways by the artificial force induced reaction method. J. Comput. Chem. 2014, 35, 166–173. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Harabuchi, Y.; Takagi, M.; Taketsugu, T.; Morokuma, K. Artificial Force Induced Reaction (AFIR) Method for Exploring Quantum Chemical Potential Energy Surfaces. Chem. Rec. 2016, 16, 2232–2248. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Harabuchi, Y.; Takagi, M.; Saita, K.; Suzuki, K.; Ichino, T.; Sumiya, Y.; Sugiyama, K.; Ono, Y. Implementation and performance of the artificial force induced reaction method in the GRRM17 program. J. Comput. Chem. 2017, 39, 233–250. [Google Scholar] [CrossRef] [PubMed]
- Varela, J.A.; Vazquez, S.A.; Martinez-Nunez, E. An automated method to find reaction mechanisms and solve the kinetics in organometallic catalysis. Chem. Sci. 2017, 8, 3843–3851. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Núñez, E. An automated transition state search using classical trajectories initialized at multiple minima. Phys. Chem. Chem. Phys. 2015, 17, 14912–14921. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Núñez, E. An automated method to find transition states using chemical dynamics simulations. J. Comput. Chem. 2015, 36, 222–234. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez, A.; Rodríguez-Fernández, R.; Vázquez, S.A.; Barnes, G.L.; Stewart, J.J.P.; Martínez-Núñez, E. tsscds2018: A code for automated discovery of chemical reaction mechanisms and solving the kinetics. J. Comput. Chem. 2018, 39, 1922–1930. [Google Scholar]
- Transition State Search Using Chemical Dynamics Simulations. Available online: http://forge.cesga.es/wiki/g/tsscds/HomePage (accessed on 25 October 2018).
- Broadbelt, L.J.; Stark, S.M.; Klein, M.T. Computer Generated Pyrolysis Modeling: On-the-Fly Generation of Species, Reactions, and Rates. Ind. Eng. Chem. Res. 1994, 33, 790–799. [Google Scholar] [CrossRef]
- Matheu, D.M.; Dean, A.M.; Grenda, J.M.; Green, W.H. Mechanism Generation with Integrated Pressure Dependence: A New Model for Methane Pyrolysis. J. Phys. Chem. A 2003, 107, 8552–8565. [Google Scholar] [CrossRef]
- Gao, C.W.; Allen, J.W.; Green, W.H.; West, R.H. Reaction Mechanism Generator: Automatic construction of chemical kinetic mechanisms. Comput. Phys. Commun. 2016, 203, 212–225. [Google Scholar] [CrossRef]
- Bhoorasingh, P.L.; West, R.H. Transition state geometry prediction using molecular group contributions. Phys. Chem. Chem. Phys. 2015, 17, 32173–32182. [Google Scholar] [CrossRef] [PubMed]
- Bhoorasingh, P.L.; Slakman, B.L.; Seyedzadeh Khanshan, F.; Cain, J.Y.; West, R.H. Automated Transition State Theory Calculations for High-Throughput Kinetics. J. Phys. Chem. A 2017, 121, 6896–6904. [Google Scholar] [CrossRef] [PubMed]
- Suleimanov, Y.V.; Green, W.H. Automated Discovery of Elementary Chemical Reaction Steps Using Freezing String and Berny Optimization Methods. J. Chem. Theory Comput. 2015, 11, 4248–4259. [Google Scholar] [CrossRef] [PubMed]
- Bergeler, M.; Simm, G.N.; Proppe, J.; Reiher, M. Heuristics-Guided Exploration of Reaction Mechanisms. J. Chem. Theory Comput. 2015, 11, 5712–5722. [Google Scholar] [CrossRef] [PubMed]
- Proppe, J.; Husch, T.; Simm, G.N.; Reiher, M. Uncertainty quantification for quantum chemical models of complex reaction networks. Faraday Discuss. 2016, 195, 497–520. [Google Scholar] [CrossRef] [PubMed]
- Simm, G.N.; Reiher, M. Context-Driven Exploration of Complex Chemical Reaction Networks. J. Chem. Theor. Comput. 2017, 13, 6108–6119. [Google Scholar] [CrossRef] [PubMed]
- Simm, G.N.; Reiher, M. Error-Controlled Exploration of Chemical Reaction Networks with Gaussian Processes. J. Chem. Theor. Comput. 2018, 14, 5238–5248. [Google Scholar] [CrossRef] [PubMed]
- Dewyer, A.L.; Argüelles, A.J.; Zimmerman, P.M. Methods for exploring reaction space in molecular systems. WIREs Comput. Mol. Sci. 2018, 8, e1354. [Google Scholar] [CrossRef]
- Eyring, H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. [Google Scholar] [CrossRef]
- Wigner, E. The transition state method. Trans. Faraday Soc. 1938, 34, 29–41. [Google Scholar] [CrossRef]
- Keck, J.C. Variational Theory of Reaction Rates. Adv. Chem. Phys. 1967, 13, 85–121. [Google Scholar]
- Pechukas, P. Dynamics of Molecular Collisions; Plenum: New York, NY, USA, 1976. [Google Scholar]
- Baker, J. An algorithm for the location of transition states. J. Comput. Chem. 1986, 7, 385–395. [Google Scholar] [CrossRef]
- Fukui, K. The Path of Chemical Reactions-The IRC Approach. Acc. Chem. Res. 1981, 14, 363–368. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Ferro-Costas, D.; Martínez-Núñez, E.; Rodríguez-Otero, J.; Cabaleiro-Lago, E.; Estévez, C.M.; Fernández, B.; Fernández-Ramos, A.; Vázquez, S.A. Influence of Multiple Conformations and Paths on Rate Constants and Product Branching Ratios. Thermal Decomposition of 1-Propanol Radicals. J. Phys. Chem. A 2018, 122, 4790–4800. [Google Scholar] [CrossRef] [PubMed]
- Fenard, Y.; Gil, A.; Vanhove, G.; Carstensen, H.-H.; Van Geem, K.M.; Westmoreland, P.R.; Herbinet, O.; Battin-Leclerc, F. A model of tetrahydrofuran low-temperature oxidation based on theoretically calculated rate constants. Combust. Flame 2018, 191, 252–269. [Google Scholar] [CrossRef]
- Wilhelm, M.J.; Martínez-Núñez, E.; González-Vázquez, J.; Vázquez, S.A.; Smith, J.M.; Dai, H.-L. Is Photolytic Production a Viable Source of HCN and HNC in Astrophysical Environments? A Laboratory-based Feasibility Study of Methyl Cyanoformate. Astrophys. J. 2017, 849, 15. [Google Scholar] [CrossRef]
- Perez-Soto, R.; Vazquez, S.A.; Martinez-Nunez, E. Photodissociation of acryloyl chloride at 193 nm: Interpretation of the product energy distributions, and new elimination pathways. Phys. Chem. Chem. Phys. 2016, 18, 5019–5026. [Google Scholar] [CrossRef] [PubMed]
- Vazquez, S.A.; Martinez-Nunez, E. HCN elimination from vinyl cyanide: Product energy partitioning, the role of hydrogen-deuterium exchange reactions and a new pathway. Phys. Chem. Chem. Phys. 2015, 17, 6948–6955. [Google Scholar] [CrossRef] [PubMed]
- Rossich Molina, E.; Salpin, J.-Y.; Spezia, R.; Martinez-Nunez, E. On the gas phase fragmentation of protonated uracil: A statistical perspective. Phys. Chem. Chem. Phys. 2016, 18, 14980–14990. [Google Scholar] [CrossRef] [PubMed]
- Simm, G.N.; Vaucher, A.C.; Reiher, M. Exploration of Reaction Pathways and Chemical Transformation Networks. J. Phys. Chem. A 2018. [Google Scholar] [CrossRef] [PubMed]
- Hase, W.L.; Buckowski, D.G. Monte carlo sampling of a microcanonical ensemble of classical harmonic oscillators. Chem. Phys. Lett. 1980, 74, 284–287. [Google Scholar] [CrossRef]
- Bougueroua, S.; Spezia, R.; Pezzotti, S.; Vial, S.; Quessette, F.; Barth, D.; Gaigeot, M.-P. Graph theory for automatic structural recognition in molecular dynamics simulations. J. Chem. Phys. 2018, 149, 184102. [Google Scholar] [CrossRef] [PubMed]
- Stewart, J.J.P. MOPAC2016, Stewart Computational Chemistry. Available online: http://openmopac.net (accessed on 20 October 2018).
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision A.02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Pietrucci, F.; Andreoni, W. Graph Theory Meets Ab Initio Molecule Dynamics: Atomic Structures and Transformations at the Nanoscale. Phys. Rev. Lett. 2011, 107, 085504. [Google Scholar] [CrossRef] [PubMed]
- Smith, G.; Gilbert, R.G. Theory of Unimolecular and Recombination Reactions; Blackwell Scientific Publications: Oxford, UK, 1990. [Google Scholar]
- Tarrazo-Antelo, T.; Martinez-Nunez, E.; Vazquez, S.A. Ab initio and RRKM study of the elimination of HF and HCl from chlorofluoroethylene. Chem. Phys. Lett. 2007, 435, 176–181. [Google Scholar] [CrossRef]
- Martínez-Núñez, E.; Vázquez, S. Rotational distributions of HBr in the photodissociation of vinyl bromide at 193 nm: An investigation by direct quasiclassical trajectory calculations. Chem. Phys. Lett. 2006, 425, 22–27. [Google Scholar] [CrossRef]
- Martínez-Núñez, E.; Vázquez, S. Quasiclassical trajectory calculations on the photodissociation of CF2CHCl at 193 nm: Product energy distributions for the HF and HCl eliminations. J. Chem. Phys. 2005, 122, 104316. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Núñez, E.; Vázquez, S.A.; Aoiz, F.J.; Bañares, L.; Castillo, J.F. Further investigation of the HCl elimination in the photodissociation of vinyl chloride at 193 nm: A direct MP2/6-31G(d,p) trajectory study. Chem. Phys. Lett. 2004, 386, 225–232. [Google Scholar] [CrossRef]
- Martínez-Núñez, E.; Vázquez, S. Rovibrational distributions of HF in the photodissociation of vinyl fluoride at 193 nm: A direct MP2 quasiclassical trajectory study. J. Chem. Phys. 2004, 121, 5179–5182. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Núñez, E.; Fernández-Ramos, A.; Vázquez, S.A.; JavierAoiz, F.; Bañares, L. A Direct Classical Trajectory Study of HCl Elimination from the 193 nm Photodissociation of Vinyl Chloride. J. Phys. Chem. A 2003, 107, 7611–7618. [Google Scholar] [CrossRef]
- Gonzalez-Vazquez, J.; Martinez-Nunez, E.; Fernandez-Ramos, A.; Vazquez, S.A. Dissociation of difluoroethylenes. II. Direct Classical Trajectory Study of the HF elimination from 1,2-difluoroethylene. J. Phys. Chem. A 2003, 107, 1398–1404. [Google Scholar] [CrossRef]
- Gonzalez-Vazquez, J.; Fernandez-Ramos, A.; Martinez-Nunez, E.; Vazquez, S.A. Dissociation of difluoroethylenes. I. Global potential energy surface, RRKM, and VTST calculations. J. Phys. Chem. A 2003, 107, 1389–1397. [Google Scholar] [CrossRef]
- Martínez-Núñez, E.; Estévez, C.M.; Flores, J.R.; Vázquez, S.A. Product energy distributions for the four-center HF elimination from 1,1-difluoroethylene. a direct dynamics study. Chem. Phys. Lett. 2001, 348, 81–88. [Google Scholar] [CrossRef]
- Martínez-Núñez, E.; Vázquez, S.A. Three-center vs. four-center HF elimination from vinyl fluoride: A direct dynamics study. Chem. Phys. Lett. 2000, 332, 583–590. [Google Scholar] [CrossRef]
- Homayoon, Z.; Vázquez, S.A.; Rodríguez-Fernández, R.; Martínez-Núñez, E. Ab initio and RRKM study of the HCN/HNC elimination channels from vinyl cyanide. J. Phys. Chem. A 2011, 115, 979–985. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Nunez, E.; Vazquez, S.A.; Borges, I.; Rocha, A.B.; Estevez, C.M.; Castillo, J.F.; Aoiz, F.J. On the conformational memory in the photodissociation of formic acid. J. Phys. Chem. A 2005, 109, 2836–2839. [Google Scholar] [CrossRef] [PubMed]
- Martinez-Nunez, E.; Vazquez, S.; Granucci, G.; Persico, M.; Estevez, C.M. Photodissociation of formic acid: A trajectory surface hopping study. Chem. Phys. Lett. 2005, 412, 35–40. [Google Scholar] [CrossRef]
- Chang, C.M.; Huang, Y.H.; Liu, S.Y.; Lee, Y.P.; Pombar-Perez, M.; Martinez-Nunez, E.; Vazquez, S.A. Internal energy of HCl upon photolysis of 2-chloropropene at 193 nm investigated with time-resolved Fourier-transform spectroscopy and quasiclassical trajectories. J. Chem. Phys. 2008, 129, 224301. [Google Scholar] [CrossRef] [PubMed]
- Spezia, R.; Martínez-Nuñez, E.; Vazquez, S.; Hase, W.L. Theoretical and computational studies of non-equilibrium and non-statistical dynamics in the gas phase, in the condensed phase and at interfaces. Philos. Trans. R. Soc. A 2017, 375, 20170035. [Google Scholar] [CrossRef] [PubMed]
- Tsutsumi, T.; Harabuchi, Y.; Ono, Y.; Maeda, S.; Taketsugu, T. Analyses of trajectory on-the-fly based on the global reaction route map. Phys. Chem. Chem. Phys. 2018, 20, 1364–1372. [Google Scholar] [CrossRef] [PubMed]
- Wilhelm, M.J.; Nikow, M.; Letendre, L.; Dai, H.-L. Photodissociation of vinyl cyanide at 193 nm: Nascent product distributions of the molecular elimination channels. J. Chem. Phys. 2009, 130, 044307. [Google Scholar] [CrossRef] [PubMed]
- Chin, C.-H.; Lee, S.-H. Theoretical study of isomerization and decomposition of propenal. J. Chem. Phys. 2011, 134, 044309. [Google Scholar] [CrossRef] [PubMed]
- Chaudhuri, C.; Lee, S.-H. A complete look at the multi-channel dissociation of propenal photoexcited at 193 nm: Branching ratios and distributions of kinetic energy. Phys. Chem. Chem. Phys. 2011, 13, 7312–7321. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.-W.; Scrape, P.G.; Butler, L.J.; Lee, Y.-P. Two HCl-Elimination Channels and Two CO-Formation Channels Detected with Time-Resolved Infrared Emission upon Photolysis of Acryloyl Chloride [CH2CHC(O)Cl] at 193 nm. J. Phys. Chem. A 2015, 119, 7293–7304. [Google Scholar] [CrossRef] [PubMed]
- Bauer, C.A.; Grimme, S. How to Compute Electron Ionization Mass Spectra from First Principles. J. Phys. Chem. A 2016, 120, 3755–3766. [Google Scholar] [CrossRef] [PubMed]
- Macaluso, V.; Homayoon, Z.; Spezia, R.; Hase, W.L. Threshold for shattering fragmentation in collision-induced dissociation of the doubly protonated tripeptide TIK(H+)2. Phys. Chem. Chem. Phys. 2018, 20, 19744–19749. [Google Scholar] [CrossRef] [PubMed]
- Martin-Somer, A.; Martens, J.; Grzetic, J.; Hase, W.L.; Oomens, J.; Spezia, R. Unimolecular Fragmentation of Deprotonated Diproline [Pro2-H]− Studied by Chemical Dynamics Simulations and IRMPD Spectroscopy. J. Phys. Chem. A 2018, 122, 2612–2625. [Google Scholar] [CrossRef] [PubMed]
- Homayoon, Z.; Macaluso, V.; Martin-Somer, A.; Muniz, M.C.N.B.; Borges, I.; Hase, W.L.; Spezia, R. Chemical dynamics simulations of CID of peptide ions: Comparisons between TIK(H+)2 and TLK(H+)2 fragmentation dynamics, and with thermal simulations. Phys. Chem. Chem. Phys. 2018, 20, 3614–3629. [Google Scholar] [CrossRef] [PubMed]
- Martin-Somer, A.; Spezia, R.; Yáñez, M. Gas-phase reactivity of [Ca(formamide)]2+ complex: An example of different dynamical behaviours. Philos. Trans. R. Soc. A 2017, 375, 20160196. [Google Scholar] [CrossRef] [PubMed]
- Molina, E.R.; Eizaguirre, A.; Haldys, V.; Urban, D.; Doisneau, G.; Bourdreux, Y.; Beau, J.-M.; Salpin, J.-Y.; Spezia, R. Characterization of Protonated Model Disaccharides from Tandem Mass Spectrometry and Chemical Dynamics Simulations. ChemPhysChem 2017, 18, 2812–2823. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.; Park, E.; Chung, H.; Jeanvoine, Y.; Song, K.; Spezia, R. Gas phase fragmentation mechanisms of protonated testosterone as revealed by chemical dynamics simulations. Int. J. Mass Spectrom. 2016, 407, 40–50. [Google Scholar] [CrossRef]
- Spezia, R.; Lee, S.B.; Cho, A.; Song, K. Collision-induced dissociation mechanisms of protonated penta- and octa-glycine as revealed by chemical dynamics simulations. Int. J. Mass Spectrom. 2015, 392, 125–138. [Google Scholar] [CrossRef]
- Spezia, R.; Martens, J.; Oomens, J.; Song, K. Collision-induced dissociation pathways of protonated Gly2NH2 and Gly3NH2 in the short time-scale limit by chemical dynamics and ion spectroscopy. Int. J. Mass Spectrom. 2015, 388, 40–52. [Google Scholar] [CrossRef]
- Song, K.; Spezia, R. Theoretical Mass Spectrometry, Tracing Ions with Classical Trajectories; De Gruyter: Berlin, Germany, 2018. [Google Scholar]
- Pratihar, S.; Barnes, G.L.; Laskin, J.; Hase, W.L. Dynamics of Protonated Peptide Ion Collisions with Organic Surfaces: Consonance of Simulation and Experiment. J. Phys. Chem. Lett. 2016, 7, 3142–3150. [Google Scholar] [CrossRef] [PubMed]
- Pratihar, S.; Barnes, G.L.; Hase, W.L. Chemical dynamics simulations of energy transfer, surface-induced dissociation, soft-landing, and reactive-landing in collisions of protonated peptide ions with organic surfaces. Chem. Soc. Rev. 2016, 45, 3595–3608. [Google Scholar] [CrossRef] [PubMed]
- Barnes, G.L.; Young, K.; Yang, L.; Hase, W.L. Fragmentation and reactivity in collisions of protonated diglycine with chemically modified perfluorinated alkylthiolate-self-assembled monolayer surfaces. J. Chem. Phys. 2011, 134, 094106. [Google Scholar] [CrossRef] [PubMed]
- Park, K.; Deb, B.; Song, K.; Hase, W.L. Importance of Shattering Fragmentation in the Surface-Induced Dissociation of Protonated Octaglycine. JASMS 2009, 20, 939–948. [Google Scholar] [CrossRef] [PubMed]
- Barnes, G.L.; Hase, W.L. Energy Transfer, Unfolding, and Fragmentation Dynamics in Collisions of N-Protonated Octaglycine with an H-SAM Surface. J. Am. Chem. Soc. 2009, 131, 17185–17193. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Núñez, E.; Fernández-Ramos, A.; Vázquez, S.A.; Marques, J.M.C.; Xue, M.; Hase, W.L. Quasiclassical dynamics simulation of the collision-induced dissociation of Cr (CO)6 + with Xe. J. Chem. Phys. 2005, 123, 154311. [Google Scholar] [CrossRef] [PubMed]
- Zador, J.; Jasper, A.W.; Miller, J.A. The reaction between propene and hydroxyl. Phys. Chem. Chem. Phys. 2009, 11, 11040–11053. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.-W.; Li, Z.-R.; Li, X.-Y. Kinetics and Mechanism for Formation of Enols in Reaction of Hydroxide Radical with Propene. J. Phys. Chem. A 2009, 113, 2372–2382. [Google Scholar] [CrossRef] [PubMed]
- Huynh, L.K.; Zhang, H.R.; Zhang, S.; Eddings, E.; Sarofim, A.; Law, M.E.; Westmoreland, P.R.; Truong, T.N. Kinetics of Enol Formation from Reaction of OH with Propene. J. Phys. Chem. A 2009, 113, 3177–3185. [Google Scholar] [CrossRef] [PubMed]
- El-Nahas, A.M.; Uchimaru, T.; Sugie, M.; Tokuhashi, K.; Sekiya, A. Relative reactivity and regioselectivity of halogen-substituted ethenes and propene toward addition of an OH radical or O (3P) atom: An ab initio study. THEOCHEM 2006, 770, 59–65. [Google Scholar] [CrossRef]
- Szori, M.; Fittschen, C.; Csizmadia, I.G.; Viskolcz, B. Allylic H-Abstraction Mechanism: The Potential Energy Surface of the Reaction of Propene with OH Radical. J. Chem. Theor. Comput. 2006, 2, 1575–1586. [Google Scholar] [CrossRef] [PubMed]
- Díaz-Acosta, I.; Alvarez-Idaboy, J.R.; Vivier-Bunge, A. Mechanism of the OH-propene-O2 reaction: An ab initio study. Int. J. Chem. Kinet. 1999, 31, 29–36. [Google Scholar] [CrossRef]
- Alvarez-Idaboy, J.R.; Díaz-Acosta, I.; Vivier-Bunge, A. Energetics of mechanism of OH-propene reaction at low pressures in inert atmosphere. J. Comput. Chem. 1998, 19, 811–819. [Google Scholar] [CrossRef]
- Ferro-Costas, D.; Cordeiro, M.N.D.S.; Truhlar, D.G.; Fernández-Ramos, A. Q2DTor: A program to treat torsional anharmonicity through coupled pair torsions in flexible molecules. Comput. Phys. Commun. 2018, 232, 190–205. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Isaacson, A.D.; Garret, G.C. Theory of Chemical Reaction Dynamics; Baer, M., Ed.; CRC: Boca Raton, FL, USA, 1985; Volume 4, p. 65. [Google Scholar]
- Schwarz, H. Chemistry with Methane: Concepts Rather than Recipes. Angew. Chem. Int. Ed. 2011, 50, 10096–10115. [Google Scholar] [CrossRef] [PubMed]
- Bao, J.L.; Truhlar, D.G. Variational transition state theory: Theoretical framework and recent developments. Chem. Soc. Rev. 2017, 46, 7548–7596. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Zheng, J.; Truhlar, D.G. Multi-structural variational transition state theory. Kinetics of the 1,4-hydrogen shift isomerization of the pentyl radical with torsional anharmonicity. Chem. Sci. 2011, 2, 2199–2213. [Google Scholar] [CrossRef]
- Bao, J.L.; Meana-Pañeda, R.; Truhlar, D.G. Multi-path variational transition state theory for chiral molecules: The site-dependent kinetics for abstraction of hydrogen from 2-butanol by hydroperoxyl radical, analysis of hydrogen bonding in the transition state, and dramatic temperature dependence of the activation energy. Chem. Sci. 2015, 6, 5866–5881. [Google Scholar] [PubMed]
- Yu, T.; Zheng, J.; Truhlar, D.G. Multipath Variational Transition State Theory: Rate Constant of the 1,4-Hydrogen Shift Isomerization of the 2-Cyclohexylethyl Radical. J. Phys. Chem. A 2012, 116, 297–308. [Google Scholar] [CrossRef] [PubMed]
- Meana-Pañeda, R.; Fernández-Ramos, A. Accounting for conformational flexibility and torsional anharmonicity in the H + CH3CH2OH hydrogen abstraction reactions: A multi-path variational transition state theory study. J. Chem. Phys. 2014, 140, 174303. [Google Scholar] [CrossRef] [PubMed]
- Sperger, T.; Sanhueza, I.A.; Schoenebeck, F. Computation and Experiment: A Powerful Combination to Understand and Predict Reactivities. Acc. Chem. Res. 2016, 49, 1311–1319. [Google Scholar] [CrossRef] [PubMed]
- Peng, Q.; Paton, R.S. Catalytic Control in Cyclizations: From Computational Mechanistic Understanding to Selectivity Prediction. Acc. Chem. Res. 2016, 49, 1042–1051. [Google Scholar] [CrossRef] [PubMed]
- Sperger, T.; Sanhueza, I.A.; Kalvet, I.; Schoenebeck, F. Computational Studies of Synthetically Relevant Homogeneous Organometallic Catalysis Involving Ni, Pd, Ir, and Rh: An Overview of Commonly Employed DFT Methods and Mechanistic Insights. Chem. Rev. 2015, 115, 9532–9586. [Google Scholar] [CrossRef] [PubMed]
- Rush, L.E.; Pringle, P.G.; Harvey, J.N. Computational Kinetics of Cobalt-Catalyzed Alkene Hydroformylation. Angew. Chem. Int. Ed. 2014, 53, 8672–8676. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Morokuma, K. Toward Predicting Full Catalytic Cycle Using Automatic Reaction Path Search Method: A Case Study on HCo(CO)3-Catalyzed Hydroformylation. J. Chem. Theor. Comput. 2012, 8, 380–385. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Choi, S.; Kim, W.Y. Efficient Basin-Hopping Sampling of Reaction Intermediates through Molecular Fragmentation and Graph Theory. J. Chem. Theory Comput. 2014, 10, 2419–2426. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Kim, J.W.; Kim, Z.; Kim, W.Y. Efficient prediction of reaction paths through molecular graph and reaction network analysis. Chem. Sci. 2018, 9, 825–835. [Google Scholar] [CrossRef] [PubMed]
- Heck, R.F.; Breslow, D.S. The Reaction of Cobalt Hydrotetracarbonyl with Olefins. J. Am. Chem. Soc. 1961, 83, 4023–4027. [Google Scholar] [CrossRef]
- Gholap, R.V.; Kut, O.M.; Bourne, J.R. Hydroformylation of propylene using an unmodified cobalt carbonyl catalyst: A kinetic study. Ind. Eng. Chem. Res. 1992, 31, 1597–1601. [Google Scholar] [CrossRef]
- Booth, J.; Vazquez, S.; Martínez-Núñez, E.; Marks, A.; Rodgers, J.; Glowacki, D.R.; Shalashilin, D.V. Recent Applications of Boxed Molecular Dynamics: A Simple Multiscale Technique for Atomistic Simulations. Philos. Trans. R. Soc. A 2014, 372, 20130384. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Núñez, E.; Shalashilin, D.V. Acceleration of classical mechanics by phase space constraints. J. Chem. Theor. Comput. 2006, 2, 912. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.J.; Amabilino, S.; O’Connor, M.; Shalishilin, D.V.; Glowacki, D.R. Adaptively Accelerating Reactive Molecular Dynamics Using Boxed Molecular Dynamics in Energy Space. J. Chem. Theor. Comput. 2018, 14, 4541–4552. [Google Scholar] [CrossRef] [PubMed]
- Larsen, A.H.; Mortensen, J.J.; Blomqvist, J.; Castelli, I.E.; Christensen, R.; Dułak, M.; Friis, J.; Groves, M.N.; Hammer, B.; Hargus, C.; et al. The atomic simulation environment—A Python library for working with atoms. J. Phys. Condens. Matter 2017, 29, 273002. [Google Scholar] [CrossRef] [PubMed]
- Valiev, M.; Bylaska, E.J.; Govind, N.; Kowalski, K.; Straatsma, T.P.; Van Dam, H.J.J.; Wang, D.; Nieplocha, J.; Apra, E.; Windus, T.L.; et al. NWChem: A comprehensive and scalable open-source solution for large scale molecular simulations. Comput. Phys. Commun. 2010, 181, 1477–1489. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Christensen, A.S.; Kubař, T.; Cui, Q.; Elstner, M. Semiempirical Quantum Mechanical Methods for Noncovalent Interactions for Chemical and Biochemical Applications. Chem. Rev. 2016, 116, 5301–5337. [Google Scholar] [CrossRef] [PubMed]
- Rodríguez-Fernández, R.; Pereira, F.B.; Marques, J.M.C.; Martínez-Núñez, E.; Vázquez, S.A. GAFit: A general-purpose, user-friendly program for fitting potential energy surfaces. Comput. Phys. Commun. 2017, 217, 89–98. [Google Scholar] [CrossRef]
- Nogueira, J.J.; Sánchez-Coronilla, A.; Marques, J.M.C.; Hase, W.L.; Martínez-Núñez, E.; Vázquez, S.A. Intermolecular potentials for simulations of collisions of SiNCS+ and (CH3)2SiNCS+ ions with fluorinated self-assembled monolayers. Chem. Phys. 2012, 399, 193–204. [Google Scholar] [CrossRef]
- Pratihar, S.; Kohale, S.C.; Vázquez, S.A.; Hase, W.L. Intermolecular Potential for Binding of Protonated Peptide Ions with Perfluorinated Hydrocarbon Surfaces. J. Phys. Chem. B 2014, 118, 5577–5588. [Google Scholar] [CrossRef] [PubMed]
- Semiempirical Molecular Orbital Models Based on the Neglect of Diatomic Differential Overlap Approximation. Available online: https://arxiv.org/abs/1806.06147 (accessed on 20 October 2018).
- Thomas, H.B.; Hennemann, M.; Kibies, P.; Hoffgaard, F.; Güssregen, S.; Hessler, G.; Kast, S.M.; Clark, T. The hpCADD NDDO Hamiltonian: Parametrization. J. Chem. Inf. Model. 2017, 57, 1907–1922. [Google Scholar] [CrossRef] [PubMed]
- Brooks, B.R.; Brooks, C.L.; Mackerell, A.D., Jr.; Nilsson, L.; Petrella, R.J.; Roux, B.; Won, Y.; Archontis, G.; Bartels, C.; Boresch, S.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef] [PubMed]
- Hase, W.L.; Bolton, K.; Sainte Claire, P.D.; Duchovic, R.J.; Hu, X.; Komornicki, A.; Li, G.; Lim, K.F.; Lu, D.-H.; Peslherbe, G.H.; et al. Venus05: A General Chemical Dynamics Computer Program; Bloomington: Bloomington, IN, USA, 2004. [Google Scholar]


| Channel | Chin et al. [96] | Tsscds | Exp [97] |
|---|---|---|---|
| H2O | 0.01 | 0.03 | 0.07 |
| CH2O | 0.65 | 0.20 | 0.07 |
| H2 | 0.09 | 0.19 | 0.00 |
| CO | 1.00 | 1.00 | 1.00 |
| H2 + CO + HCCH | 6.82 | 1.49 | 1.10 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vázquez, S.A.; Otero, X.L.; Martinez-Nunez, E. A Trajectory-Based Method to Explore Reaction Mechanisms. Molecules 2018, 23, 3156. https://doi.org/10.3390/molecules23123156
Vázquez SA, Otero XL, Martinez-Nunez E. A Trajectory-Based Method to Explore Reaction Mechanisms. Molecules. 2018; 23(12):3156. https://doi.org/10.3390/molecules23123156
Chicago/Turabian StyleVázquez, Saulo A., Xose L. Otero, and Emilio Martinez-Nunez. 2018. "A Trajectory-Based Method to Explore Reaction Mechanisms" Molecules 23, no. 12: 3156. https://doi.org/10.3390/molecules23123156
APA StyleVázquez, S. A., Otero, X. L., & Martinez-Nunez, E. (2018). A Trajectory-Based Method to Explore Reaction Mechanisms. Molecules, 23(12), 3156. https://doi.org/10.3390/molecules23123156