A QM/MM Derived Polarizable Water Model for Molecular Simulation
Abstract
1. Introduction
2. Methods
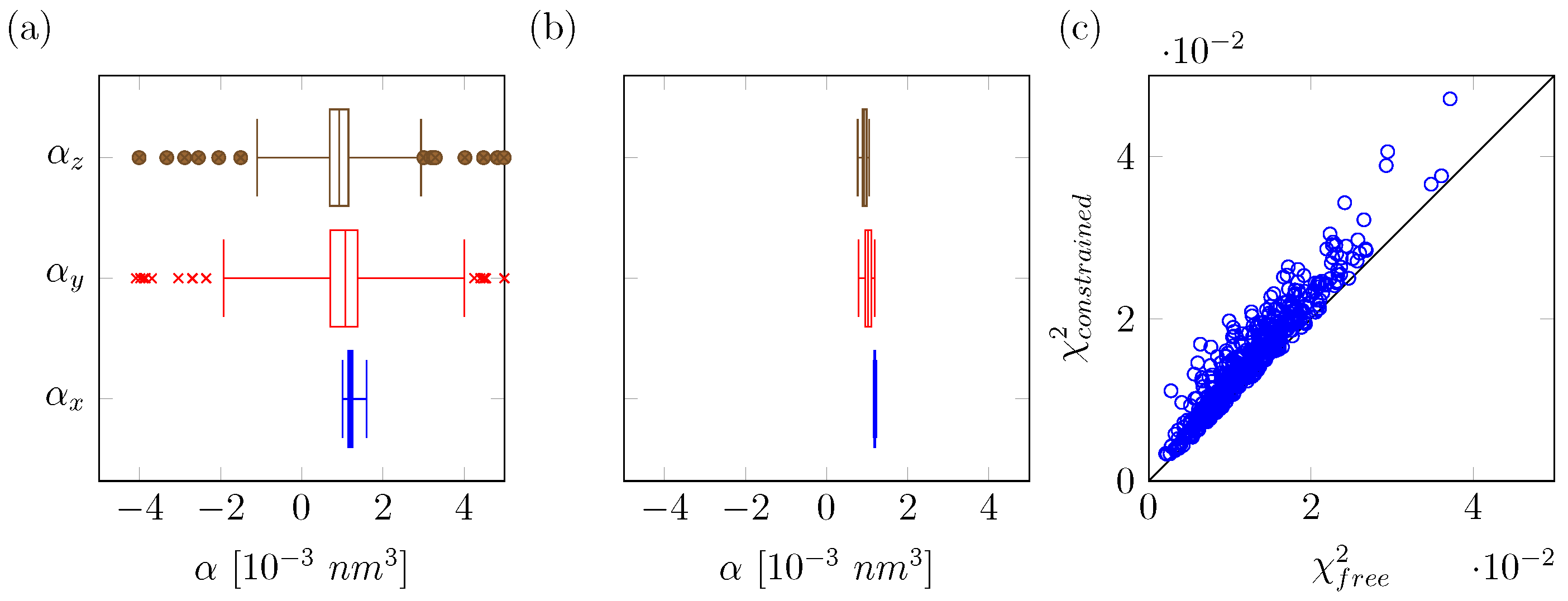
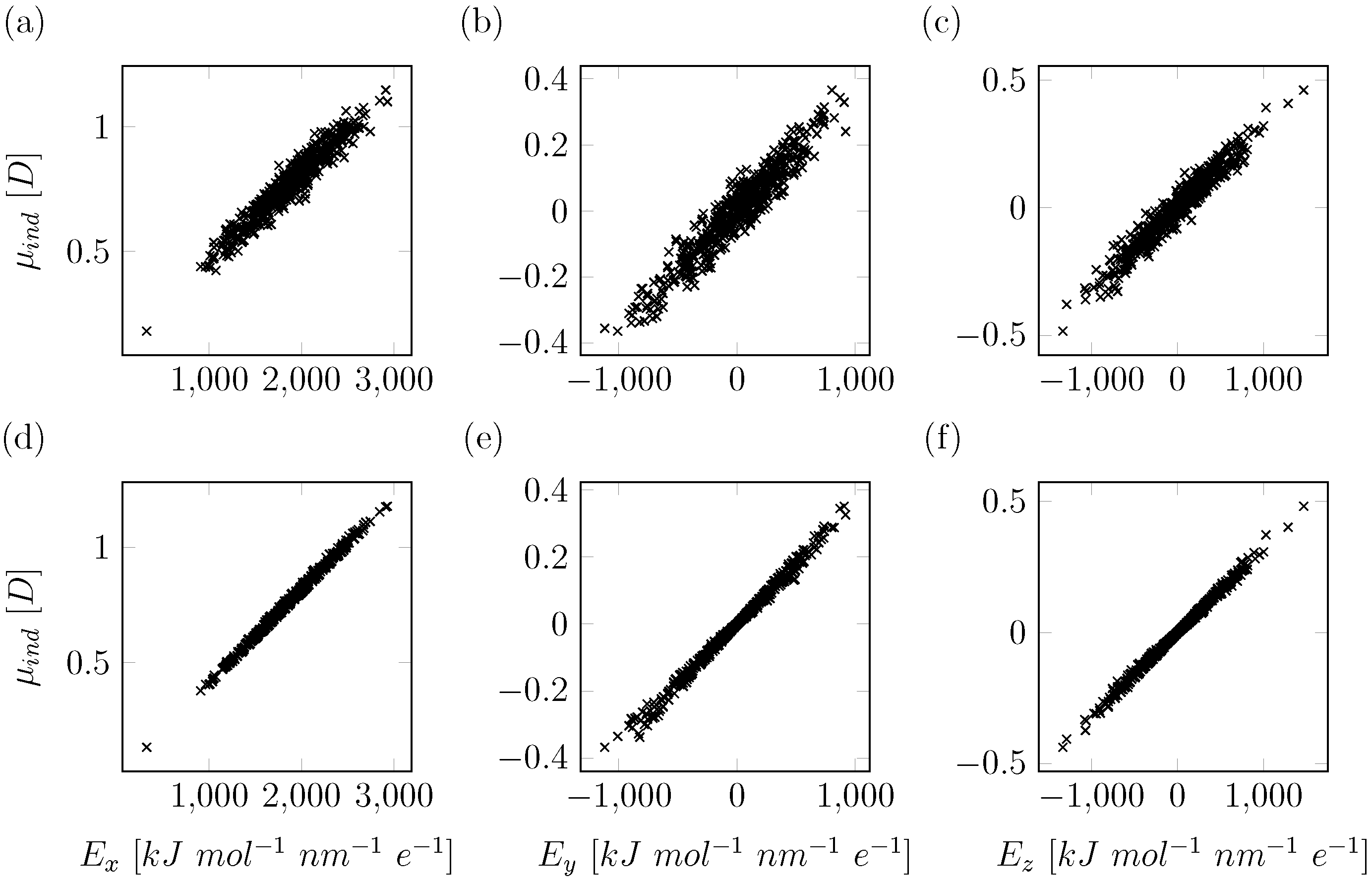
2.1. Computational Details for QM/MM Based Polarizability Fitting
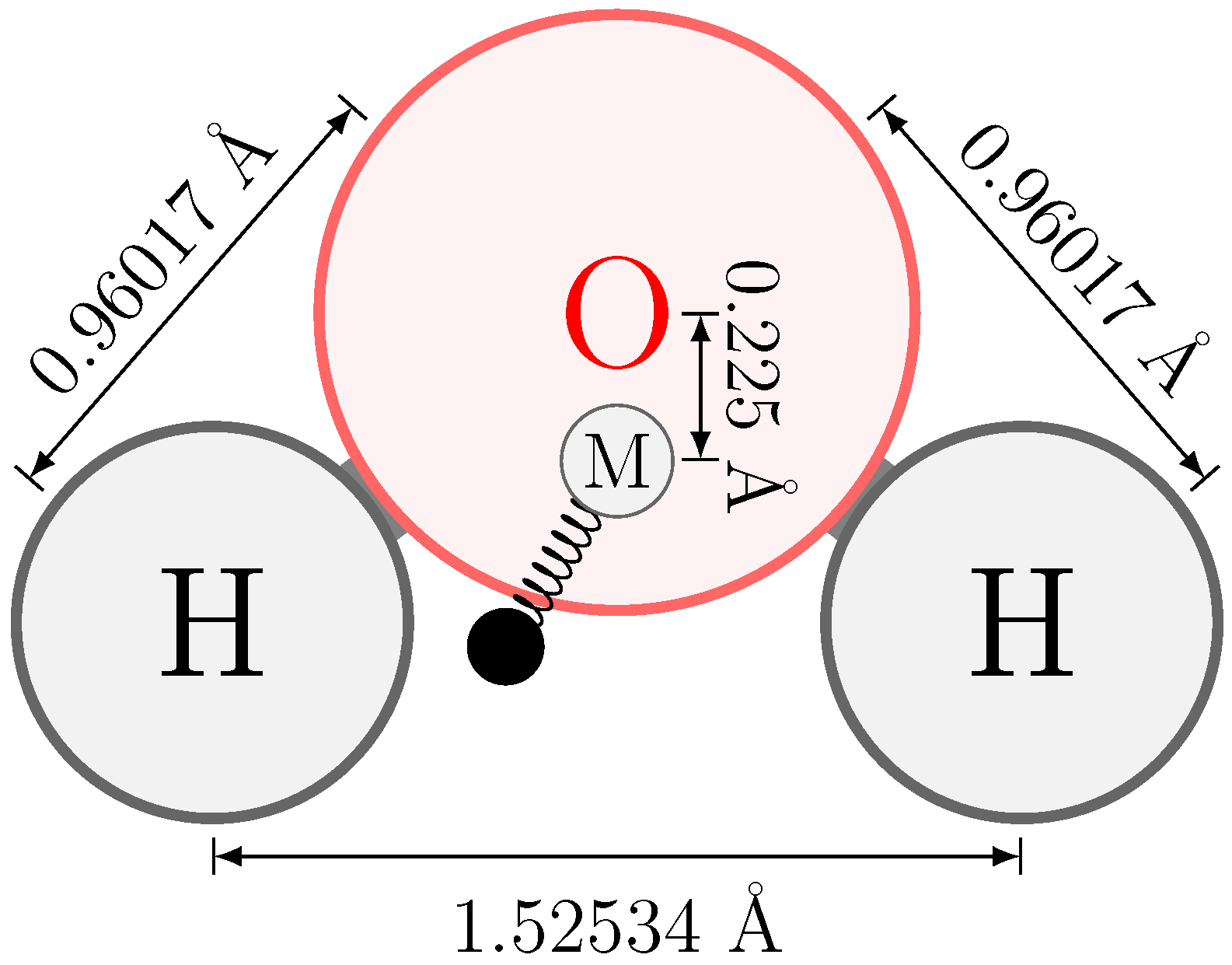
2.2. Electrostatic Model
2.3. Dispersion Calculations
2.4. Pure-Liquid MD Simulations
2.5. Pure-Liquid Property Analysis
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Weingarth, M.; Van Der Cruijsen, E.A.; Ostmeyer, J.; Lievestro, S.; Roux, B.; Baldus, M. Quantitative analysis of the water occupancy around the selectivity filter of a K+ channel in different gating modes. J. Am. Chem. Soc. 2014, 136, 2000–2007. [Google Scholar] [CrossRef] [PubMed]
- Bellissent-Funel, M.C.; Hassanali, A.; Havenith, M.; Henchman, R.; Pohl, P.; Sterpone, F.; Van Der Spoel, D.; Xu, Y.; Garcia, A.E. Water determines the structure and dynamics of proteins. Chem. Rev. 2016, 116, 7673–7697. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zheng, W.; Mittal, J. Balanced protein–water interactions improve properties of disordered proteins and non-specific protein association. J. Chem. Theory Comput. 2014, 10, 5113–5124. [Google Scholar] [CrossRef] [PubMed]
- Visscher, K.M.; Kastritis, P.L.; Bonvin, A.M. Non-interacting surface solvation and dynamics in protein–protein interactions. Proteins Struct. Funct. Bioinform. 2015, 83, 445–458. [Google Scholar] [CrossRef] [PubMed]
- Qin, Y.; Wang, L.; Zhong, D. Dynamics and mechanism of ultrafast water–protein interactions. Proc. Natl. Acad. Sci. USA 2016, 113, 8424–8429. [Google Scholar] [CrossRef] [PubMed]
- Guillot, B. A reappraisal of what we have learnt during three decades of computer simulations on water. J. Mol. Liquids 2002, 101, 219–260. [Google Scholar] [CrossRef]
- Yu, W.; Lopes, P.E.; Roux, B.; MacKerell, A.D. Six-site polarizable model of water based on the classical Drude oscillator. J. Chem. Phys. 2013, 138, 034508. [Google Scholar] [CrossRef] [PubMed]
- Bachmann, S.J.; van Gunsteren, W.F. An improved simple polarisable water model for use in biomolecular simulation. J. Chem. Phys. 2014, 141, 22D515. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; van Gunsteren, W.F.; Hermans, J. Interaction models for water in relation to protein hydration. In Intermolecular Forces, Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry Held in Jerusalem, Israel, 13–16 April 1981; Pullman, B., Ed.; Springer: Dordrecht, The Netherlands, 1981; pp. 331–342. [Google Scholar]
- Burnham, C.J.; Li, J.; Xantheas, S.S.; Leslie, M. The parametrization of a Thole-type all-atom polarizable water model from first principles and its application to the study of water clusters (n = 2–21) and the phonon spectrum of ice Ih. J. Chem. Phys. 1999, 110, 4566–4581. [Google Scholar] [CrossRef]
- Lamoureux, G.; MacKerell, A.; Roux, B. A simple polarizable model of water based on classical Drude oscillators. J. Chem. Phys. 2003, 119, 5185–5197. [Google Scholar] [CrossRef]
- Yu, H.; Van Gunsteren, W.F. Charge-on-spring polarizable water models revisited: From water clusters to liquid water to ice. J. Chem. Phys. 2004, 121, 9549–9564. [Google Scholar] [CrossRef] [PubMed]
- Horn, H.W.; Swope, W.C.; Pitera, J.W.; Madura, J.D.; Dick, T.J.; Hura, G.L.; Head-Gordon, T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. [Google Scholar] [CrossRef] [PubMed]
- Abascal, J.L.; Vega, C. A potential model for the study of ices and amorphous water: TIP4P/Ice. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef] [PubMed]
- Lamoureux, G.; Harder, E.; Vorobyov, I.V.; Roux, B.; MacKerell, A.D. A polarizable model of water for molecular dynamics simulations of biomolecules. Chem. Phys. Lett. 2006, 418, 245–249. [Google Scholar] [CrossRef]
- Yu, H.; Hansson, T.; Van Gunsteren, W.F. Development of a simple, self-consistent polarizable model for liquid water. J. Chem. Phys. 2003, 118, 221–234. [Google Scholar] [CrossRef]
- Wang, L.P.; Head-Gordon, T.; Ponder, J.W.; Ren, P.; Chodera, J.D.; Eastman, P.K.; Martinez, T.J.; Pande, V.S. Systematic improvement of a classical molecular model of water. J. Phys. Chem. B 2013, 117, 9956–9972. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Wang, L.P.; Wang, Q.; Pande, V.S.; Ren, P. United polarizable multipole water model for molecular mechanics simulation. J. Chem. Phys. 2015, 143, 014504. [Google Scholar] [CrossRef] [PubMed]
- Mohebifar, M.; Johnson, E.R.; Rowley, C.N. Evaluating Force-Field London Dispersion Coefficients Using the Exchange-Hole Dipole Moment Model. J. Chem. Theory Comput. 2017, 13, 6146–6157. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef] [PubMed]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, 4758–4766. [Google Scholar] [CrossRef] [PubMed]
- Johnson, E.R.; Becke, A.D. A post-Hartree-Fock model of intermolecular interactions: Inclusion of higher-order corrections. J. Chem. Phys. 2006, 124, 174104. [Google Scholar] [CrossRef] [PubMed]
- Visscher, K.M.; Geerke, D.P. Deriving force-field parameters from first principles using a polarizable and higher-order dispersion model. 2018. submitted. [Google Scholar]
- Vosmeer, C.R.; Rustenburg, A.S.; Rice, J.E.; Horn, H.W.; Swope, W.C.; Geerke, D.P. QM/MM-based fitting of atomic polarizabilities for use in condensed-phase biomolecular simulation. J. Chem. Theory Comput. 2012, 8, 3839–3853. [Google Scholar] [CrossRef] [PubMed]
- Vosmeer, C.R.; Kiewisch, K.; Keijzer, K.; Visscher, L.; Geerke, D.P. A comparison between QM/MM and QM/QM based fitting of condensed-phase atomic polarizabilities. Phys. Chem. Chem. Phys. 2014, 16, 17857–17862. [Google Scholar] [CrossRef] [PubMed]
- Fonseca Guerra, C.; Snijders, J.G.; te Velde, G.; Baerends, E.J. Towards an order-N DFT method. Theor. Chem. Acc. 1998, 99, 391–403. [Google Scholar] [CrossRef]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Baerends, E.J.; Ziegler, T.; Atkins, A.J.; Autschbach, J.; Baseggio, O.; Bashford, D.; Bérces, A.; Bickelhaupt, F.M.; Bo, C.; Boerrigter, P.M.; et al. ADF 2018, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands. Available online: https://www.scm.com (accessed on 29 November 2018).
- Berendsen, H.J.; Postma, J.P.; Van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Barker, J.A.; Watts, R.O. Monte Carlo studies of the dielectric properties of water-like models. Mol. Phys. 1973, 26, 789–792. [Google Scholar] [CrossRef]
- Tironi, I.G.; Sperb, R.; Smith, P.E.; van Gunsteren, W.F. A generalized reaction field method for molecular dynamics simulations. J. Chem. Phys. 1995, 102, 5451. [Google Scholar] [CrossRef]
- Fernández, D.P.; Mulev, Y.; Goodwin, A.R.H.; Sengers, J.M.H.L. A database for the static dielectric constant of water and steam. J. Phys. Chem. Ref. Data 1995, 24, 33–70. [Google Scholar] [CrossRef]
- Ryckaert, J.P.; Ciccotti, G.; Berendsen, H.J. Numerical integration of the cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J. Comput. Phys. 1977, 23, 327–341. [Google Scholar] [CrossRef]
- Richards, F.M. Areas, volumes, packing, and protein structure. Annu. Rev. Biophys. Bioeng. 1977, 6, 151–176. [Google Scholar] [CrossRef] [PubMed]
- Connolly, M.L. Analytical molecular surface calculation. J. Appl. Crystallogr. 1983, 16, 548–558. [Google Scholar] [CrossRef]
- Connolly, M.L. The molecular surface package. J. Mol. Graph. 1993, 11, 139–141. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Gordon, M.S.; Schmidt, M.W. Advances in electronic structure theory: GAMESS a decade later. In Theory and Applications of Computational Chemistry; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Nertherlands, 2005; pp. 1167–1189. [Google Scholar]
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Drude, P. The Theory of Optics; Longmans, Green and CO: New York, NY, USA, 1902; p. 592. [Google Scholar]
- Straatsma, T.P.; Mccammon, J.A. Molecular dynamics simulations with interaction potentials including polarization development of a noniterative method and application to water. Mol. Simul. 1990, 5, 181–192. [Google Scholar] [CrossRef]
- Geerke, D.P.; van Gunsteren, W.F. On the calculation of atomic forces in classical simulation using the charge-on-spring method to explicitly treat electronic polarization. J. Chem. Theory Comput. 2007, 3, 2128–2137. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Oppenheimer, R. Zur quantentheorie der molekeln. Ann. Phys. 1927, 389, 457–484. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Kendall, R.A.; Dunning, T.H.; Harrison, R.J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Bultinck, P.; Van Alsenoy, C.; Ayers, P.W.; Carbó-Dorca, R. Critical analysis and extension of the Hirshfeld atoms in molecules. J. Chem. Phys. 2007, 126, 144111. [Google Scholar] [CrossRef] [PubMed]
- Heidar-Zadeh, F.; Ayers, P.W.; Verstraelen, T.; Vinogradov, I.; Vöhringer-Martinez, E.; Bultinck, P. Information-theoretic approaches to atoms-in-molecules: Hirshfeld family of partitioning schemes. J. Phys. Chem. A 2018, 122, 4219–4245. [Google Scholar] [CrossRef] [PubMed]
- Verstraelen, T.; Tecmer, P.; Heidar-Zadeh, F.; González-Espinoza, C.E.; Chan, M.; Kim, T.D.; Boguslawski, K.; Fias, S.; Vandenbrande, S.; Berrocal, D.; et al. HORTON 2.1.0. 2017. Available online: http://theochem.github.com/horton/ (accessed on 1 April 2018).
- Kannemann, F.O.; Becke, A.D. van der Waals interactions in density-functional theory: Intermolecular complexes. J. Chem. Theory Comput. 2010, 6, 1081–1088. [Google Scholar] [CrossRef]
- Becke, A.D.; Johnson, E.R. Exchange-hole dipole moment and the dispersion interaction: High-order dispersion coefficients. J. Chem. Phys. 2006, 124, 014104. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D.; Johnson, E.R. Exchange-hole dipole moment and the dispersion interaction revisited. J. Chem. Phys. 2007, 127, 154108. [Google Scholar] [CrossRef] [PubMed]
- Otero-De-La-Roza, A.; Johnson, E.R. Non-covalent interactions and thermochemistry using XDM-corrected hybrid and range-separated hybrid density functionals. J. Chem. Phys. 2013, 138, 204109. [Google Scholar] [CrossRef] [PubMed]
- Mitroy, J.; Bromley, M.W. Higher-order Cn dispersion coefficients for hydrogen. Phys. Rev. A At. Mol. Opt. Phys. 2005, 71, 11–15. [Google Scholar]
- Christen, M.; Hünenberger, P.H.; Bakowies, D.; Baron, R.; Bürgi, R.; Geerke, D.P.; Heinz, T.N.; Kastenholz, M.A.; Kräutler, V.; Oostenbrink, C.; et al. The GROMOS software for biomolecular simulation: GROMOS05. J. Comput. Chem. 2005, 26, 1719–1751. [Google Scholar] [CrossRef] [PubMed]
- Schmid, N.; Christ, C.D.; Christen, M.; Eichenberger, A.P.; Van Gunsteren, W.F. Architecture, implementation and parallelisation of the GROMOS software for biomolecular simulation. Comput. Phys. Commun. 2012, 183, 890–903. [Google Scholar] [CrossRef]
- Eichenberger, A.P.; Allison, J.R.; Dolenc, J.; Geerke, D.P.; Horta, B.A.; Meier, K.; Oostenbrink, C.; Schmid, N.; Steiner, D.; Wang, D.; et al. GROMOS++ software for the analysis of biomolecular simulation trajectories. J. Chem. Theory Comput. 2011, 7, 3379–3390. [Google Scholar] [CrossRef] [PubMed]
- Braun, E.; Moosavi, S.M.; Smit, B. Anomalous effects of velocity rescaling algorithms: The flying ice cube effect revisited. J. Chem. Theory Comput. 2018, 14, 5262–5272. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M. Dipole moment fluctuation formulas in computer simulations of polar systems. Mol. Phys. 1983, 50, 841–858. [Google Scholar] [CrossRef]
- Riniker, S.; Kunz, A.P.E.; van Gunsteren, W.F. On the calculation of the dielectric permittivity and relaxation of molecular models in the liquid phase. J. Chem. Theory Comput. 2011, 7, 1469–1475. [Google Scholar] [CrossRef] [PubMed]
- Yeh, I.C.; Hummer, G. System-size dependence of diffusion coefficients and viscosities from molecular dynamics simulations with periodic boundary conditions. J. Phys. Chem. B 2004, 108, 15873–15879. [Google Scholar] [CrossRef]
- Glättli, A.; Daura, X.; van Gunsteren, W.F. Derivation of an improved simple point charge model for liquid water: SPC/A and SPC/L. J. Chem. Phys. 2002, 116, 9811–9828. [Google Scholar] [CrossRef]
- Schropp, B.; Tavan, P. The polarizability of point-polarizable water models: Density functional theory/molecular mechanics results. J. Phys. Chem. B 2008, 112, 6233–6240. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. The Liquid State of Matter: Fluids, Simple and Complex; Elsevier: Amsterdam, The Netherlands, 1982; p. 275. [Google Scholar]
- Dyke, T.R.; Muenter, J.S. Electric dipole moments of low J states of H2O and D2O. J. Chem. Phys. 1973, 59, 3125–3127. [Google Scholar] [CrossRef]
- Cole, D.J.; Vilseck, J.Z.; Tirado-Rives, J.; Payne, M.C.; Jorgensen, W.L. Biomolecular force field parameterization via atoms-in-molecule electron density partitioning. J. Chem. Theory Comput. 2016, 12, 2312–2323. [Google Scholar] [CrossRef] [PubMed]
- Bondi, A. Van der Waals volumes and radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Zeiss, G.D.; Meath, W.J. The H2O-H2O dispersion energy constant and the dispersion of the specific refractivity of dilute water vapour. Mol. Phys. 1975, 30, 161–169. [Google Scholar] [CrossRef]
- Gubskaya, A.V.; Kusalik, P.G. The total molecular dipole moment for liquid water. J. Chem. Phys. 2002, 117, 5290–5302. [Google Scholar] [CrossRef]
- Kell, G.S. Density, thermal expansivity, and compressibility of liquid water from 0. deg. to 150. deg. Correlations and tables for atmospheric pressure and saturation reviewed and expressed on 1968 temperature scale. J. Chem. Eng. Data 1975, 20, 97–105. [Google Scholar] [CrossRef]
- Wagner, W.; Pruß, A. The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use. J. Phys. Chem. Ref. Data 2002, 31, 387–535. [Google Scholar] [CrossRef]
- Krynicki, K.; Green, C.D.; Sawyer, D.W. Pressure and temperature dependence of self-diffusion in water. Faraday Discuss. Chem. Soc. 1978, 66, 199–208. [Google Scholar] [CrossRef]
- Lide, D.R. CRC Handbook of Chemistry and Physics; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Harris, K.R.; Woolf, L.A. Temperature and volume dependence of the viscosity of water and heavy water at low temperatures. J. Chem. Eng. Data 2004, 49, 1064–1069. [Google Scholar] [CrossRef]
- Motakabbir, K.A.; Berkowitz, M. Isothermal compressibility of SPC/E water. J. Phys. Chem. 1990, 94, 8359–8362. [Google Scholar] [CrossRef]
- Cerutti, D.S.; Rice, J.E.; Swope, W.C.; Case, D.A. Derivation of fixed partial charges for amino acids accommodating a specific water model and implicit polarization. J. Phys. Chem. B 2013, 117, 2328–2338. [Google Scholar] [CrossRef] [PubMed]
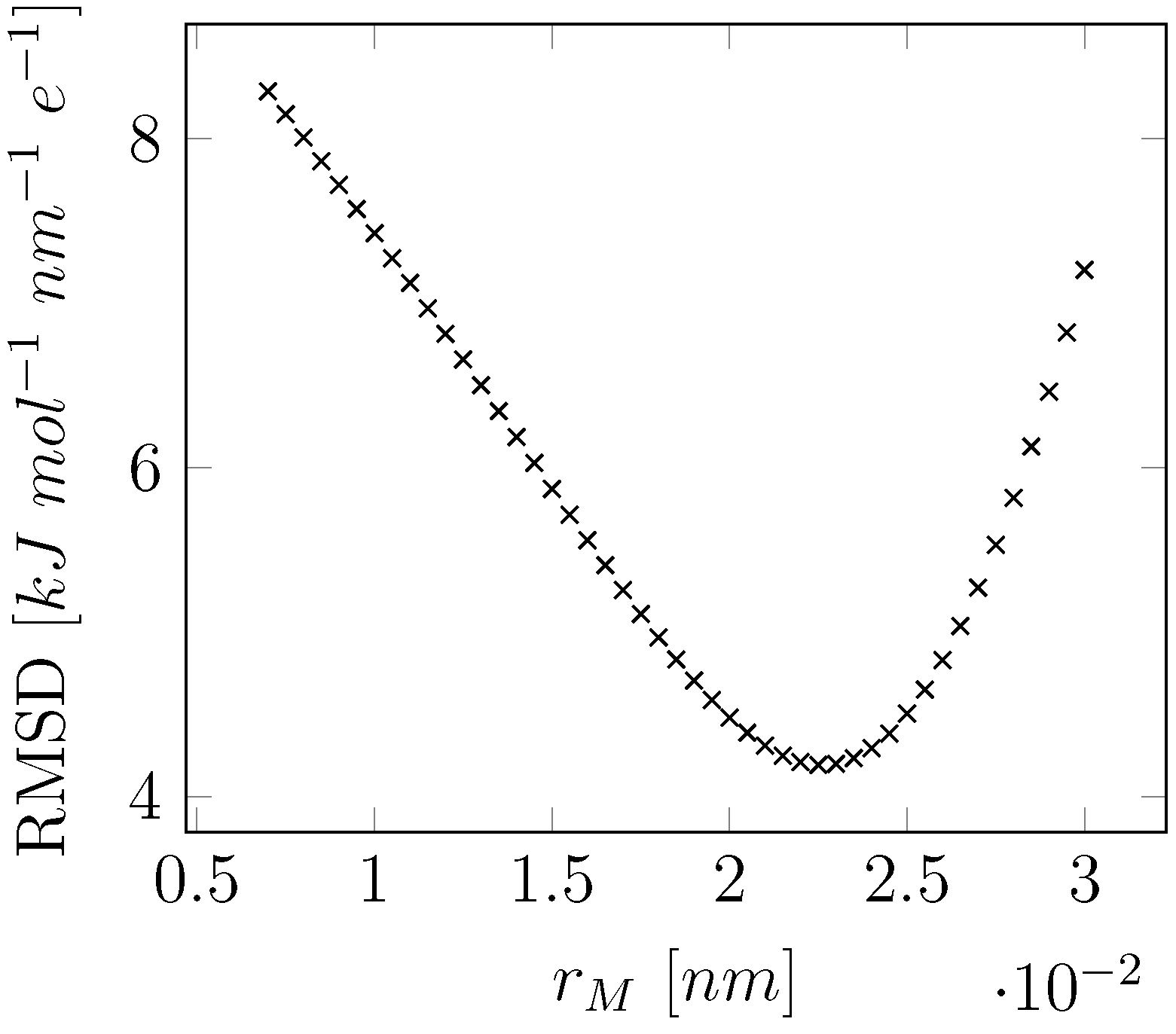
| Expt. | This Work | SPC | COS/G2 | COS/D2 | SWM4-NDP | SWM6 | ||
|---|---|---|---|---|---|---|---|---|
| 45.4 | 43.44 | 45.40 | 56.27 | 56.28 | 63.80 | 50.34 | ||
| 1201.3 | ||||||||
| 0.1605 | 0.1583 | 0.1598 | 0.1582 | 0.1592 | 0.1599 | |||
| e | −0.82 | 1.71636 | 1.91589 | |||||
| e | 0.539 | 0.41 | 0.5265 | 0.57 | 0.55733 | 0.53070 | ||
| e | −1.078 | −1.053 | −1.14 | −1.11466 | −1.13340 | |||
| e | −0.10800 | |||||||
| e | −8.0 | −8.0 | −8.0 | −1.71636 | −1.62789 | |||
| 10−3 nm3 | 1.44 | 1.05 | 1.255 | 1.3 | 0.97825 | 0.88 | ||
| kJ mol−1 nm−1 e−1 | 140 | |||||||
| p | 8 |
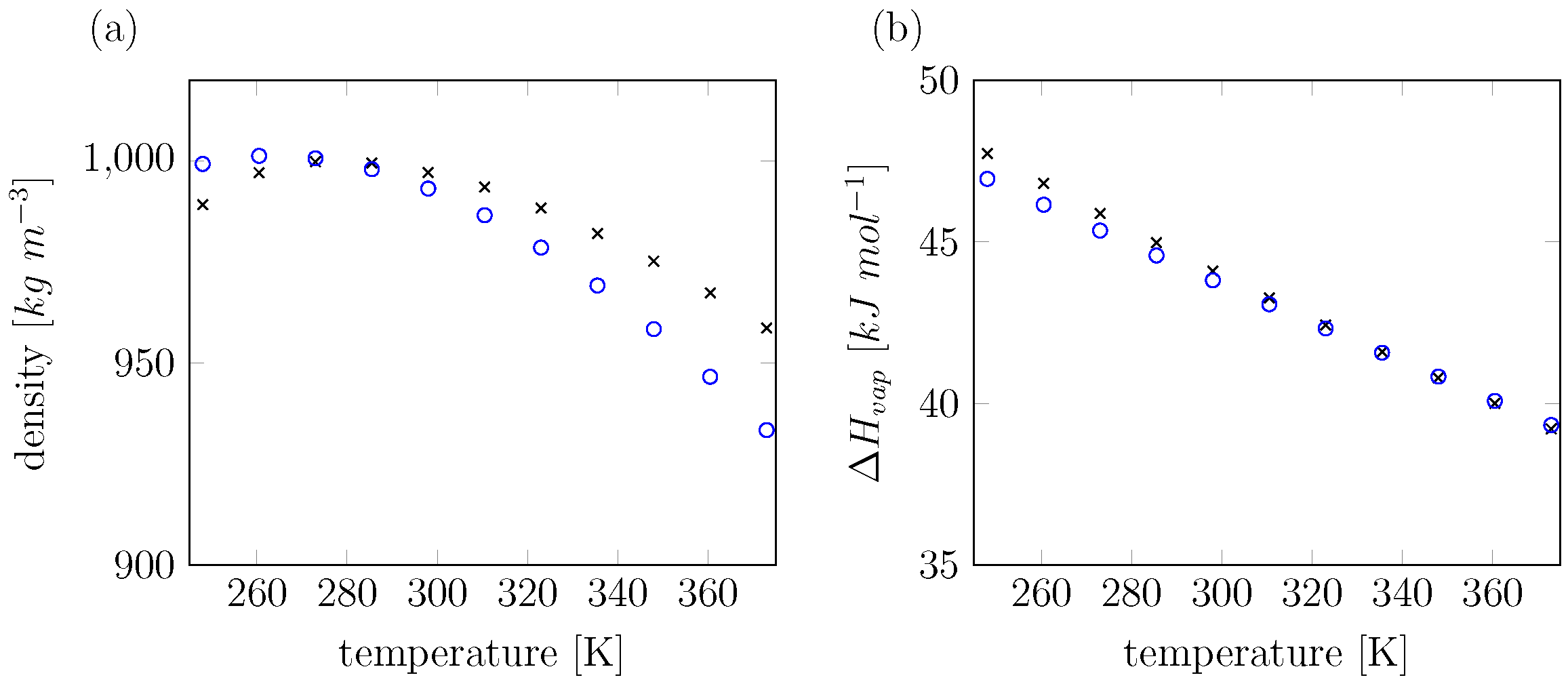
| Expt. | This Work | SPC | COS/G2 | COS/D2 | SWM4-NDP | SWM6 | ||
|---|---|---|---|---|---|---|---|---|
| kg m−3 | 997 | 993 | 973 | 999 | 999 | 994 | 996 | |
| kJ mol−1 | 44.01 | 43.81 | 43.9 | 43.7 | 44.08 | 43.7 | 44.0 | |
| cm2 s−1 | 1.90 | 4.1 | 2.0 | 2.2 | 2.35 | 1.76 | ||
| D | cm2 s−1 | 2.3 | 2.17 | 2.85 | 2.14 | |||
| 78.4 | 77.6 | 64.7 | 96.6 | 78.9 | 78.0 | 78.1 | ||
| D | 1.855 | 1.856 | 2.27 | 1.85 | 1.855 | 1.85 | 1.85 | |
| D | 2.95 | 2.47 | 2.27 | 2.61 | 2.55 | 2.459 | 2.431 | |
| kJ mol−1 | 12.5 | 15.9 | 14.4 | |||||
| J mol−1 K−1 | 75.3 | 91.9 | 93.0 | 107.7 | 88.9 | |||
| K−1 | 2.57 | 3.86 | 9.0 | 7.0 | 4.9 | |||
| cP | 0.89 | 0.72 | 0.66 | 0.87 | ||||
| atm−1 | 45.8 | 41.7 | 47.8 | 47.8 | 44.4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Visscher, K.M.; Swope, W.C.; Geerke, D.P. A QM/MM Derived Polarizable Water Model for Molecular Simulation. Molecules 2018, 23, 3131. https://doi.org/10.3390/molecules23123131
Visscher KM, Swope WC, Geerke DP. A QM/MM Derived Polarizable Water Model for Molecular Simulation. Molecules. 2018; 23(12):3131. https://doi.org/10.3390/molecules23123131
Chicago/Turabian StyleVisscher, Koen M., William C. Swope, and Daan P. Geerke. 2018. "A QM/MM Derived Polarizable Water Model for Molecular Simulation" Molecules 23, no. 12: 3131. https://doi.org/10.3390/molecules23123131
APA StyleVisscher, K. M., Swope, W. C., & Geerke, D. P. (2018). A QM/MM Derived Polarizable Water Model for Molecular Simulation. Molecules, 23(12), 3131. https://doi.org/10.3390/molecules23123131





