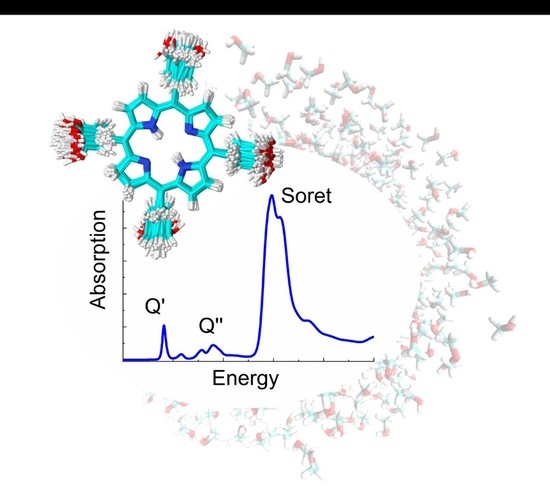
Assessing Configurational Sampling in the Quantum Mechanics/Molecular Mechanics Calculation of Temoporfin Absorption Spectrum and Triplet Density of States
Abstract
1. Introduction
2. Results and Discussion
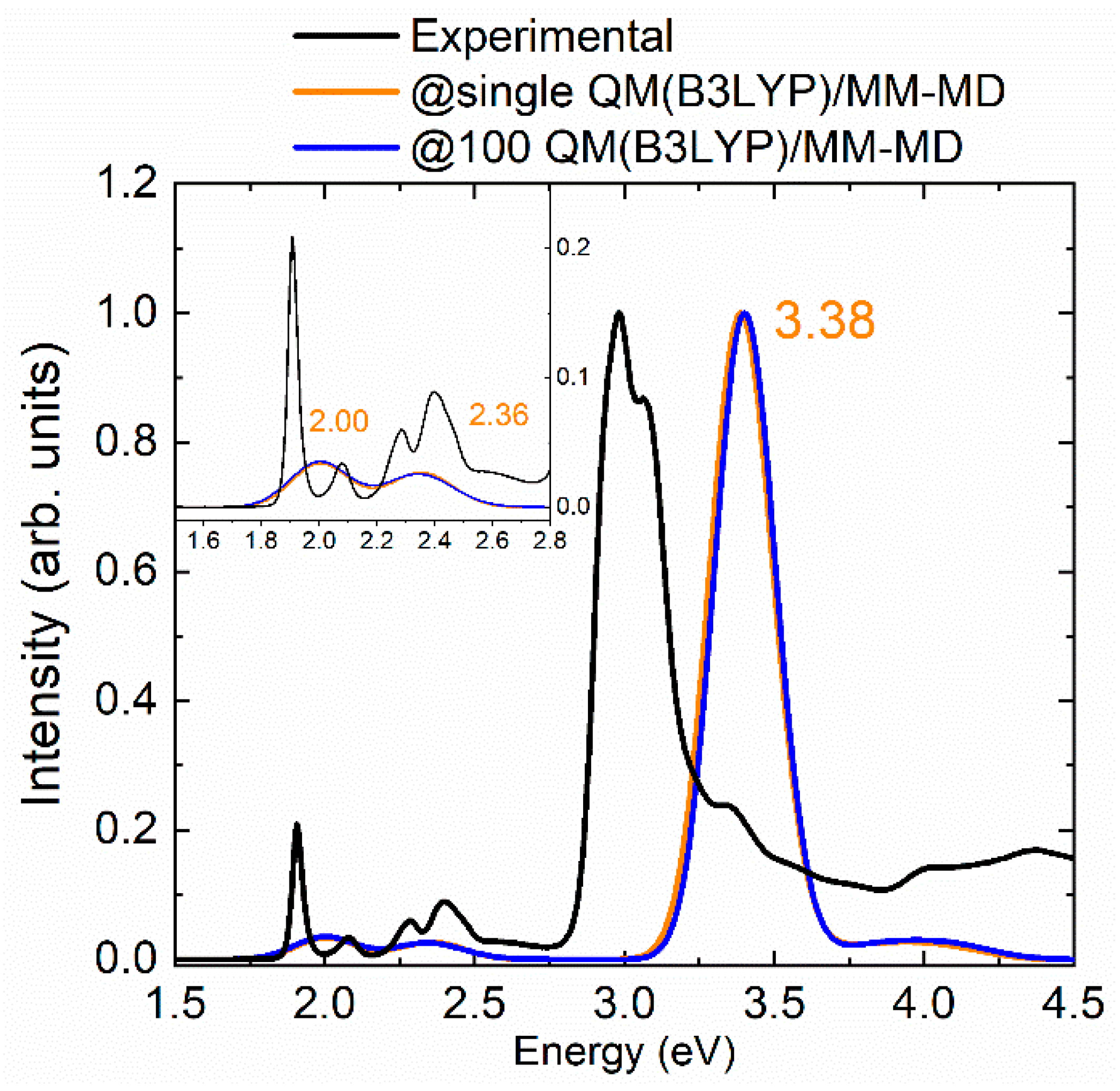
2.1. Absorption Spectrum
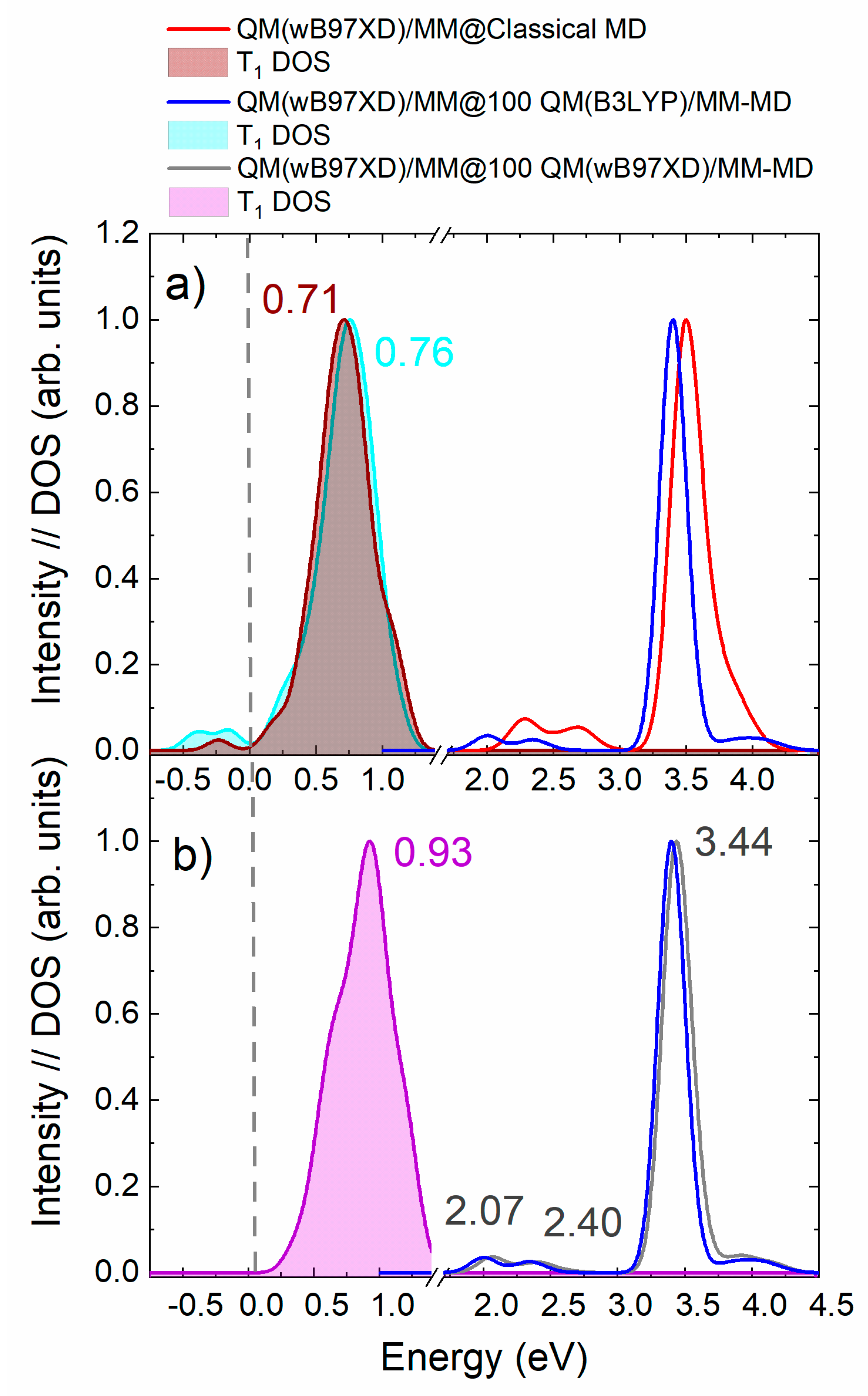
2.2. Density of Triplet States
3. Conclusions
4. Materials and Methods
4.1. Computational Details
4.2. Experimental Methods
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Copper, M.P.; Tan, I.B.; Oppelaar, H.; Ruevekamp, M.C.; Stewart, F.A. Meta-tetra(hydroxyphenyl)chlorin Photodynamic Therapy in Early-Stage Squamous Cell Carcinoma of the Head and Neck. Arch. Otolaryngol.-Head Neck Surg. 2003, 129, 709–711. [Google Scholar] [CrossRef] [PubMed]
- Fan, K.F.; Hopper, C.; Speight, P.M.; Buonaccorsi, G.A.; Bown, S.G. Photodynamic therapy using mTHPC for malignant disease in the oral cavity. Int. J. Cancer 1997, 73, 25–32. [Google Scholar] [CrossRef]
- Agostinis, P.; Berg, K.; Cengel, K.; Foster, T.; Girotti, A.; Gollnick, S.; Hahn, S.; Hamblin, M.; Juzeniene, A.; Kessel, D.; et al. Photodynamic Terapy of cancer: An update. CA Cancer J. Clin. 2011, 61, 250–281. [Google Scholar] [CrossRef] [PubMed]
- Dąbrowski, J.M.; Arnaut, L.G. Photodynamic therapy (PDT) of cancer: From local to systemic treatment. Photochem. Photobiol. Sci. 2015, 14, 1765–1780. [Google Scholar] [CrossRef] [PubMed]
- Hamblin, M.R.; Hasan, T. Photodynamic therapy: A new antimicrobial approach to infectious disease? Photochem. Photobiol. Sci. 2004, 3, 436–450. [Google Scholar] [CrossRef] [PubMed]
- Tardivo, J.P.; Adami, F.; Correa, J.A.; Pinhal, M.A.S.; Baptista, M.S. A clinical trial testing the efficacy of PDT in preventing amputation in diabetic patients. Photodiagn. Photodyn. Ther. 2014, 11, 342–350. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.J. Photodynamic therapy in skin rejuvenation. Clin. Dermatol. 2008, 26, 608–613. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.; Baron, E.D. Photodynamic therapy: Current evidence and applications in dermatology. Semin. Cutan. Med. Surg. 2011, 30, 199–209. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.C.; Finlay, J.C. The role of photodynamic therapy (PDT) physics. Med. Phys. 2008, 35, 3127–3136. [Google Scholar] [CrossRef] [PubMed]
- Bacellar, I.O.L.; Tsubone, T.M.; Pavani, C.; Baptista, M.S. Photodynamic Efficiency: From Molecular Photochemistry to Cell Death. Int. J. Mol. Sci. 2015, 16, 20523–20559. [Google Scholar] [CrossRef] [PubMed]
- Ethirajan, M.; Chen, Y.; Joshi, P.; Pandey, R.K. The role of porphyrin chemistry in tumor imaging and photodynamic therapy. Chem. Soc. Rev. 2011, 40, 340–362. [Google Scholar] [CrossRef] [PubMed]
- Josefsen, L.B.; Boyle, R.W. Unique diagnostic and therapeutic roles of porphyrins and phthalocyanines in photodynamic therapy, imaging and theranostics. Theranostics 2012, 2, 916–966. [Google Scholar] [CrossRef] [PubMed]
- Bown, S.G.; Rogowska, A.Z. New photosensitizers for photodynamic therapy in gastroenterology. Can. J. Gastroenterol. 1999, 13, 389–392. [Google Scholar] [CrossRef] [PubMed]
- Bonnett, R.; White, R.D.; Winfield, U.J.; Berenbaum, M.C. Hydroporphyrins of the meso-tetra(hydroxyphenyl)porphyrin series as tumour photosensitizers. Biochem. J. 1989, 261, 277–280. [Google Scholar] [CrossRef] [PubMed]
- Mehraban, N.; Freeman, H. Developments in PDT Sensitizers for Increased Selectivity and Singlet Oxygen Production. Materials 2015, 8, 4421–4456. [Google Scholar] [CrossRef] [PubMed]
- DeRosa, M.C.; Crutchley, R.J. Photosensitized singlet oxygen and its applications. Coord. Chem. Rev. 2002, 233–234, 351–371. [Google Scholar] [CrossRef]
- Palma, M.; Cardenas-Jiron, G.I.; Rodriguez, M.I.M. Effect of chlorin structure on theoretical electronic absorption spectra and on the energy released by porphyrin-based photosensitizers. J. Phys. Chem. A 2008, 112, 13574–13583. [Google Scholar] [CrossRef] [PubMed]
- Bonnett, R.; Djelal, B.D.; Nguyen, A. Physical and chemical studies related to the development of m-THPC (FOSCAN (R)) for the photodynamic therapy (PDT) of tumours. J. Porphyr. Phthalocyanines 2001, 5, 652–661. [Google Scholar] [CrossRef]
- Senge, M.O.; Brandt, J.C. Temoporfin (Foscan®, 5,10,15,20-Tetra(m-hydroxyphenyl)chlorin)—A second-generation photosensitizer. Photochem. Photobiol. 2011, 87, 1240–1296. [Google Scholar] [CrossRef] [PubMed]
- Betz, C.S.; Rauschning, W.; Stranadko, E.P.; Riabov, M.V.; Volgin, V.N.; Albrecht, V.; Nifantiev, N.E.; Hopper, C. Long-term outcomes following Foscan®-PDT of basal cell carcinomas. Lasers Surg. Med. 2012, 44, 533–540. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z. A review of progress in clinical photodynamic therapy. Technol. Cancer Res. Treat. 2005, 4, 283–293. [Google Scholar] [CrossRef] [PubMed]
- De Vetta, M.; González, L.; Nogueira, J.J. Hydrogen Bonding Regulates the Rigidity of Liposome-Encapsulated Chlorin Photosensitizers. ChemistryOpen 2018, 7, 475–483. [Google Scholar] [CrossRef] [PubMed]
- Senge, M.O. mTHPC—A drug on its way from second to third generation photosensitizer? Photodiagn. Photodyn. Ther. 2012, 9, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Meier, D.; Botter, S.M.; Campanile, C.; Robl, B.; Gräfe, S.; Pellegrini, G.; Born, W.; Fuchs, B. Foscan and foslip based photodynamic therapy in osteosarcoma in vitro and in intratibial mouse models. Int. J. Cancer 2017, 140, 1680–1692. [Google Scholar] [CrossRef] [PubMed]
- Reshetov, V.; Kachatkou, D.; Shmigol, T.; Zorin, V.; D’Hallewin, M.-A.; Guillemin, F.; Bezdetnaya, L. Redistribution of meta-tetra(hydroxyphenyl)chlorin (m-THPC) from conventional and PEGylated liposomes to biological substrates. Photochem. Photobiol. Sci. 2011, 10, 911–919. [Google Scholar] [CrossRef] [PubMed]
- Pegaz, B.; Debefve, E.; Ballini, J.P.; Wagnières, G.; Spaniol, S.; Albrecht, V.; Scheglmann, D.V.; Nifantiev, N.E.; Van Den Bergh, H.; Konan-Kouakou, Y.N. Photothrombic activity of m-THPC-loaded liposomal formulations: Pre-clinical assessment on chick chorioallantoic membrane model. Eur. J. Pharm. Sci. 2006, 28, 134–140. [Google Scholar] [CrossRef] [PubMed]
- Mazzone, G.; Alberto, M.E.; De Simone, B.C.; Marino, T.; Russo, N. Can expanded bacteriochlorins act as photosensitizers in photodynamic therapy? Good news from density functional theory computations. Molecules 2016, 21, 288. [Google Scholar] [CrossRef] [PubMed]
- Eriksson, E.S.E.; Eriksson, L.A. Predictive power of long-range corrected functionals on the spectroscopic properties of tetrapyrrole derivatives for photodynamic therapy. Phys. Chem. Chem. Phys. 2011, 13, 7207–7217. [Google Scholar] [CrossRef] [PubMed]
- Alberto, M.E.; Marino, T.; Quartarolo, A.D.; Russo, N. Photophysical origin of the reduced photodynamic therapy activity of temocene compared to Foscan®: Insights from theory. Phys. Chem. Chem. Phys. 2013, 15, 16167–16171. [Google Scholar] [CrossRef] [PubMed]
- Cossi, M.; Barone, V. Solvent effect on vertical electronic transitions by the polarizable continuum model. J. Chem. Phys. 2000, 112, 2427. [Google Scholar] [CrossRef]
- Mennucci, B. Polarizable continuum model. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 386–404. [Google Scholar] [CrossRef]
- De Vetta, M.; Menger, M.F.S.J.; Nogueira, J.J.; González, L. Solvent Effects on Electronically Excited States: QM/Continuum Versus QM/Explicit Models. J. Phys. Chem. B 2018, 122, 2975–2984. [Google Scholar] [CrossRef] [PubMed]
- Senn, H.M.; Thiel, W. QM/MM methods for biomolecular systems. Angew. Chem. Int. Ed. 2009, 48, 1198–1229. [Google Scholar] [CrossRef] [PubMed]
- Van Der Kamp, M.W.; Mulholland, A.J. Combined quantum mechanics/molecular mechanics (QM/MM) methods in computational enzymology. Biochemistry 2013, 52, 2708–2728. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, J.J.; Roßbach, S.; Ochsenfeld, C.; González, L. Effect of DNA Environment on Electronically Excited States of Methylene Blue Evaluated by a Three-Layered QM/QM/MM ONIOM Scheme. J. Chem. Theory Comput. 2018, 14, 4298–4308. [Google Scholar] [CrossRef] [PubMed]
- Adamo, C.; Jacquemin, D. The calculations of excited-state properties with Time-Dependent Density Functional Theory. Chem. Soc. Rev. 2013, 42, 845–856. [Google Scholar] [CrossRef] [PubMed]
- Zuehlsdorff, T.J.; Isborn, C.M. Combining the ensemble and Franck-Condon approaches for calculating spectral shapes of molecules in solution. J. Chem. Phys. 2018, 148. [Google Scholar] [CrossRef] [PubMed]
- Milanese, J.M.; Provorse, M.R.; Alameda, E.; Isborn, C.M. Convergence of Computed Aqueous Absorption Spectra with Explicit Quantum Mechanical Solvent. J. Chem. Theory Comput. 2017, 13, 2159–2171. [Google Scholar] [CrossRef] [PubMed]
- Nåbo, L.J.; Olsen, J.M.H.; Martínez, T.J.; Kongsted, J. The Quality of the Embedding Potential Is Decisive for Minimal Quantum Region Size in Embedding Calculations: The Case of the Green Fluorescent Protein. J. Chem. Theory Comput. 2017, 13, 6230–6236. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, J.J.; González, L. Computational Photophysics in the Presence of an Environment. Annu. Rev. Phys. Chem. 2018, 69, 473–497. [Google Scholar] [CrossRef] [PubMed]
- Zobel, J.P.; Nogueira, J.J.; González, L. Finite-temperature Wigner phase-space sampling and temperature effects on the excited-state dynamics of 2-nitronaphthalene. Phys. Chem. Chem. Phys. 2018. [Google Scholar] [CrossRef] [PubMed]
- Plasser, F.; Aquino, A.J.A.; Hase, W.L.; Lischka, H. UV absorption spectrum of alternating DNA duplexes. Analysis of excitonic and charge transfer interactions. J. Phys. Chem. A 2012, 116, 11151–11160. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, J.J.; Plasser, F.; González, L. Electronic delocalization, charge transfer and hypochromism in the UV absorption spectrum of polyadenine unravelled by multiscale computations and quantitative wavefunction analysis. Chem. Sci. 2017, 8, 5682–5691. [Google Scholar] [CrossRef] [PubMed]
- Parac, M.; Doerr, M.; Marian, C.M.; Thiel, W. QM/MM Calculation of Solvent Effects on Absorption Spectra of Guanin. J. Comput. Chem. 2009, 30, 1545–1614. [Google Scholar] [CrossRef]
- Etienne, T.; Assfeld, X.; Monari, A. QM/MM calculation of absorption spectra of complex systems: The case of human serum albumin. Comput. Theor. Chem. 2014, 1040–1041, 360–366. [Google Scholar] [CrossRef]
- Kjellgren, E.R.; Haugaard Olsen, J.M.; Kongsted, J. Importance of Accurate Structures for Quantum Chemistry Embedding Methods: Which Strategy Is Better? J. Chem. Theory Comput. 2018, 14, 4309–4319. [Google Scholar] [CrossRef] [PubMed]
- González, L.; Escudero, D.; Serrano-Andrés, L. Progress and challenges in the calculation of electronic excited states. ChemPhysChem 2012, 13, 28–51. [Google Scholar] [CrossRef] [PubMed]
- Serrano-Andrés, L.; Merchán, M. Quantum chemistry of the excited state: 2005 overview. J. Mol. Struct. THEOCHEM 2005, 729, 99–108. [Google Scholar] [CrossRef]
- Cui, G.; Yang, W. Challenges with range-separated exchange-correlation functionals in time-dependent density functional theory calculations. Mol. Phys. 2010, 108, 2745–2750. [Google Scholar] [CrossRef]
- Cai, Z.-L.; Sendt, K.; Reimers, J.R. Failure of density-functional theory and time-dependent density-functional theory for large extended π systems. J. Chem. Phys. 2002, 117, 5543–5549. [Google Scholar] [CrossRef]
- Peach, M.J.G.; Tozer, D.J. Overcoming low orbital overlap and triplet instability problems in TDDFT. J. Phys. Chem. A 2012, 116, 9783–9789. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.M.; Wolf, R.M.; Caldwell, J.W.; Kollman, P.A.; Case, D.A. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. A new mixing of Hartree-Fock and local density-functional theories. J. Chem. Phys. 1993, 98, 1372–1377. [Google Scholar] [CrossRef]
- Ditchfield, R.; Hehre, W.J.; Pople, J.A. An Extended Gaussian-Type Basis for Molecular-Orbital Studies of Organic Molecules. J. Chem. Phys. 1971, 54, 724–728. [Google Scholar] [CrossRef]
- Cieplak, P.; Caldwell, J.; Kollman, P. Molecular mechanical models for organic and biological systems going beyond the atom centered two body additive approximation: Aqueous solution free energies of methanol and N-methyl acetamide, nucleic acid base, and amide hydrogen bonding and chloroform/water partition coefficients of the nucleic acid bases. J. Comput. Chem. 2001, 22, 1048–1057. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P. Settle, A. An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Crowley, M.F.; Darden, T.A.; Cheatham, T., III; Deerfield, D., II. Adventures in improving the scaling and accuracy of a parallel molecular dynamics program. J. Supercomput. 1997, 11, 255–278. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Cerutti, D.S.; Cheatham, T.E., III; Darden, T.A.; Duke, R.E.; Giese, T.J.; Gohlke, A.W.; Goetz, D.G.; Homeyer, S.I.; Kovalenko, A.; et al. AMBER16; University of California: San Francisco, CA, USA, 2017. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 09, Revision A.02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Bonnett, R.; Charlesworth, P.; Djelal, B.D.; Foley, S.; McGarvey, D.J.; Truscott, T.G. Photophysical properties of 5,10,15,20-tetrakis(m-hydroxyphenyl)-porphyrin (m-THPP), 5,10,15,20-tetrakis (m-hydroxyphenyl) chlorin (m-THPC) and 5,10,15,20-tetrakis(m-hydroxyphenyl)bacteriochlorin (m-THPBC): A comparative study. J. Chem. Soc. Perkin Trans. 1999, 2, 325–328. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compound mTHPC are available upon request. |

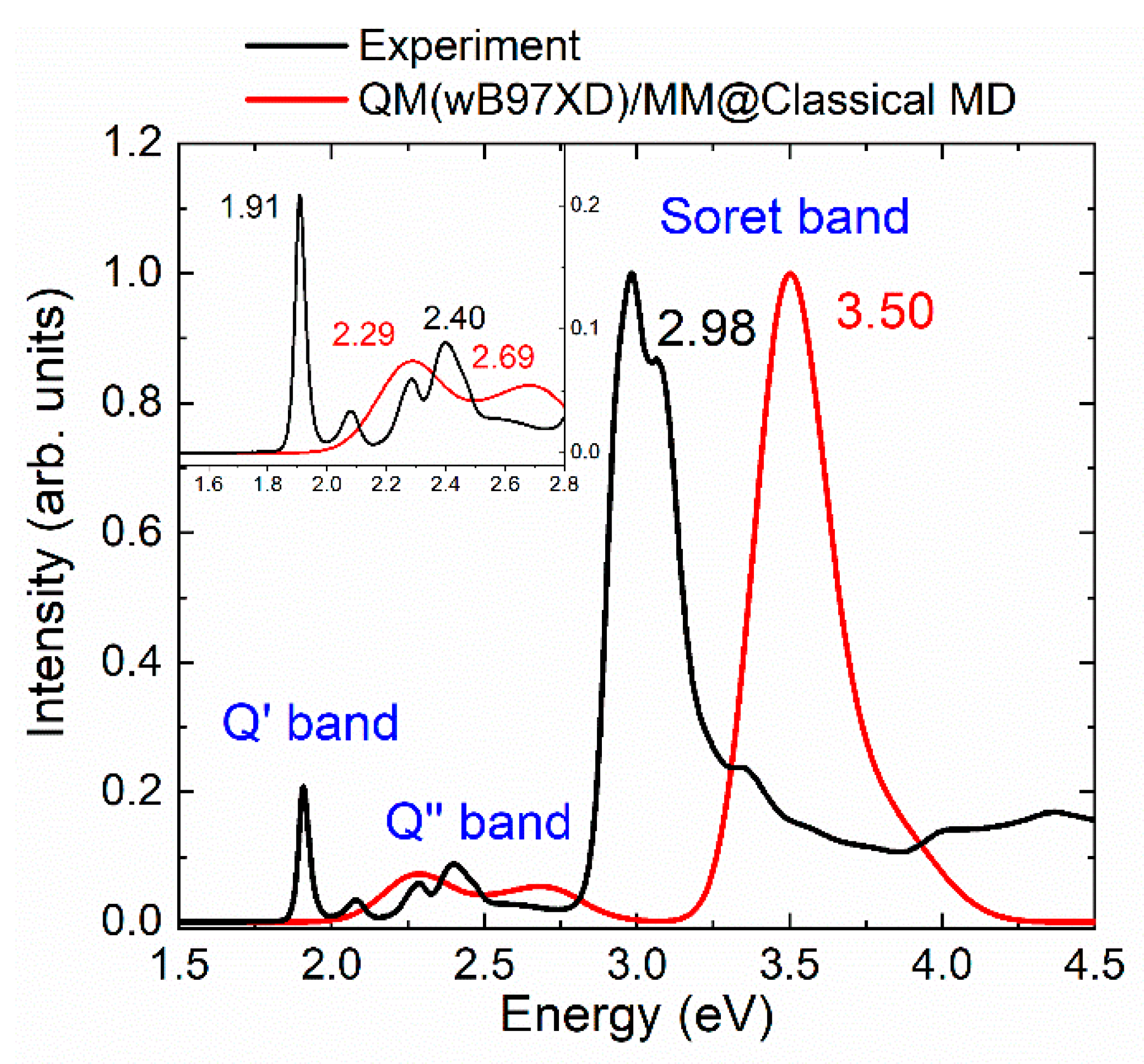
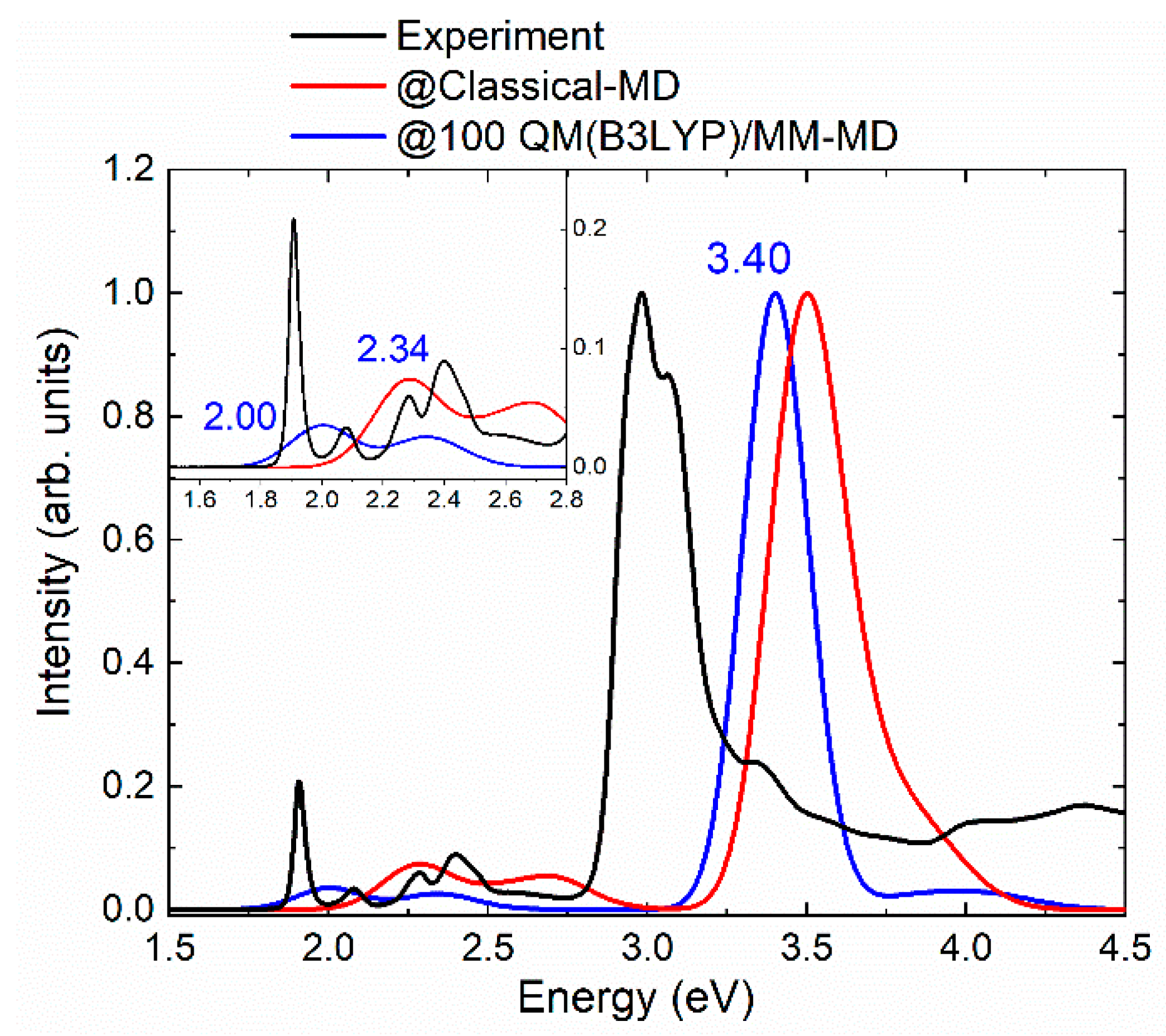
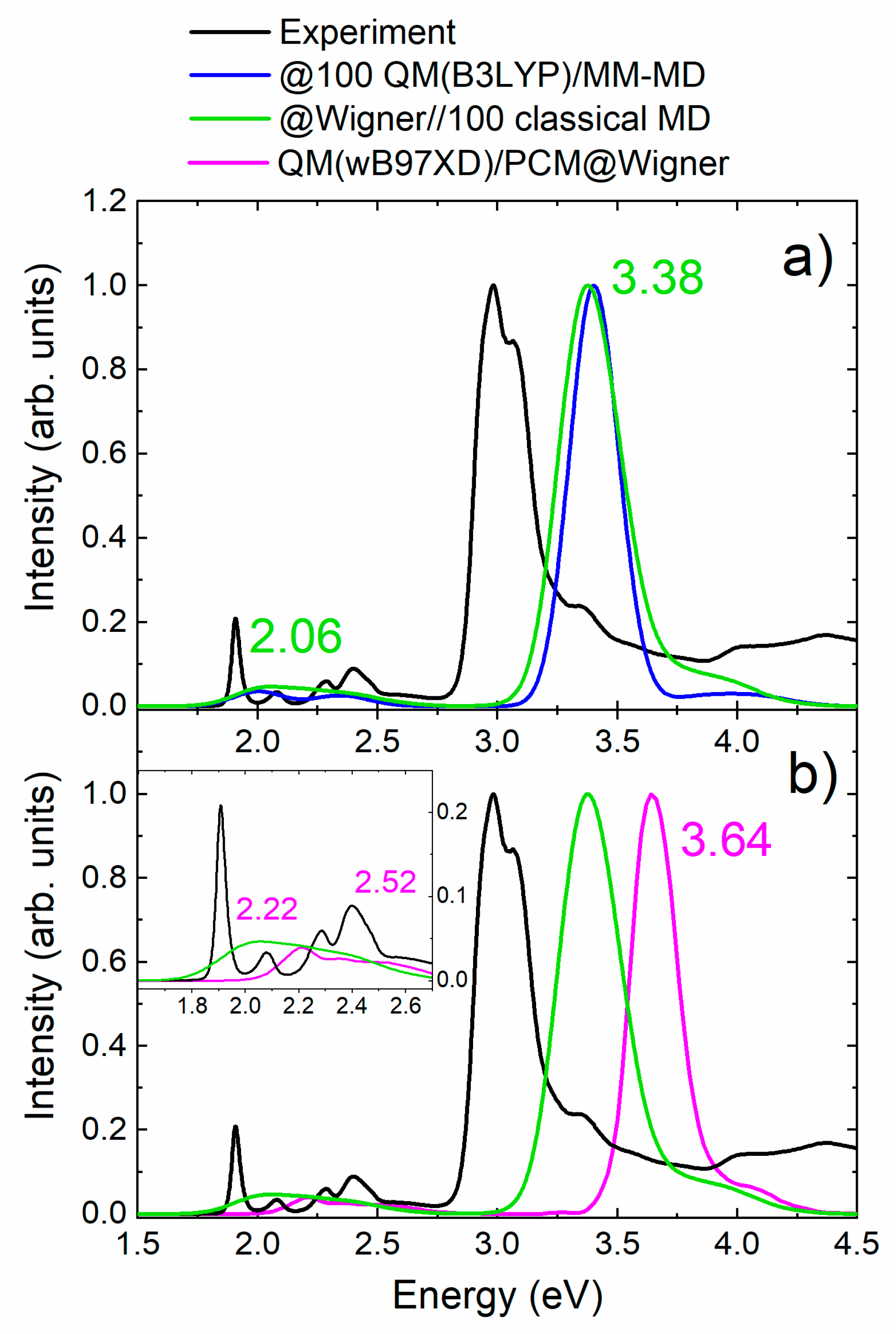
| QM(wB97XD)//QM(wB97XD) | QM(wB97XD)//QM(B3LYP) | ΔE (eV) | |
|---|---|---|---|
| S1 | 2.21 | 2.01 | 0.20 |
| S2 | 2.60 | 2.39 | 0.21 |
| S3 | 3.40 | 3.28 | 0.12 |
| S4 | 3.50 | 3.36 | 0.14 |
| S5 | 4.14 | 4.10 | 0.04 |
| S6 | 4.36 | 4.27 | 0.09 |
| T1 | 1.07 | 0.92 | 0.15 |
| T2 | 1.61 | 1.16 | 0.45 |
| T3 | 2.05 | 1.98 | 0.07 |
| T4 | 2.44 | 2.33 | 0.11 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Vetta, M.; Baig, O.; Steen, D.; Nogueira, J.J.; González, L. Assessing Configurational Sampling in the Quantum Mechanics/Molecular Mechanics Calculation of Temoporfin Absorption Spectrum and Triplet Density of States. Molecules 2018, 23, 2932. https://doi.org/10.3390/molecules23112932
De Vetta M, Baig O, Steen D, Nogueira JJ, González L. Assessing Configurational Sampling in the Quantum Mechanics/Molecular Mechanics Calculation of Temoporfin Absorption Spectrum and Triplet Density of States. Molecules. 2018; 23(11):2932. https://doi.org/10.3390/molecules23112932
Chicago/Turabian StyleDe Vetta, Martina, Omar Baig, Dorika Steen, Juan J. Nogueira, and Leticia González. 2018. "Assessing Configurational Sampling in the Quantum Mechanics/Molecular Mechanics Calculation of Temoporfin Absorption Spectrum and Triplet Density of States" Molecules 23, no. 11: 2932. https://doi.org/10.3390/molecules23112932
APA StyleDe Vetta, M., Baig, O., Steen, D., Nogueira, J. J., & González, L. (2018). Assessing Configurational Sampling in the Quantum Mechanics/Molecular Mechanics Calculation of Temoporfin Absorption Spectrum and Triplet Density of States. Molecules, 23(11), 2932. https://doi.org/10.3390/molecules23112932