Hydration Thermodynamics of Non-Polar Aromatic Hydrocarbons: Comparison of Implicit and Explicit Solvation Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Density Functional Theory in Classical Explicit Solvents (DFT-CES)
2.2. Free-Energy Calculation Using Two-Phase Thermodynamic (2PT) Model
2.3. Simulation Details
3. Results and Discussion
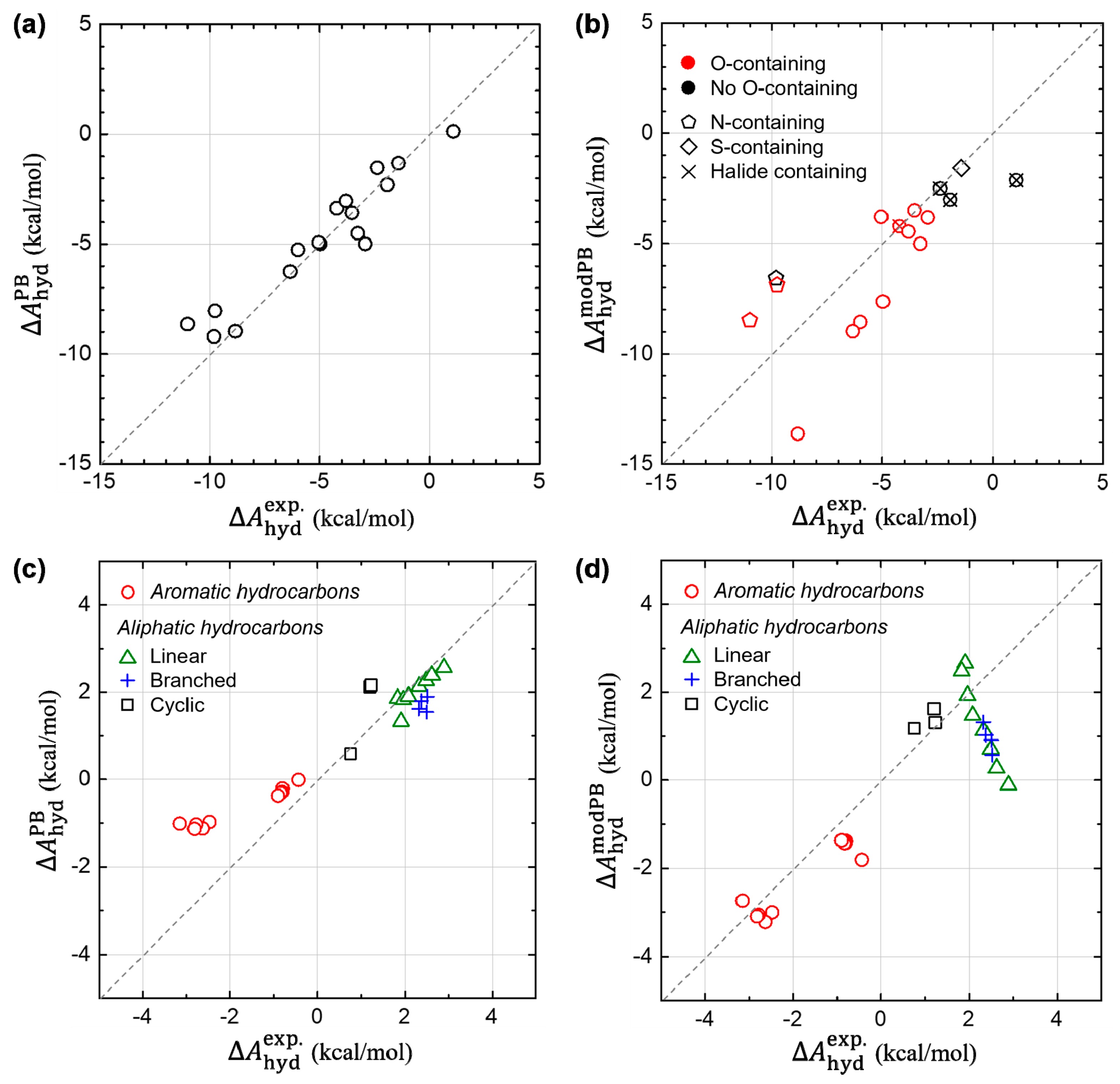
3.1. Hydration Free Energies of Aromatic Hydrocarbons
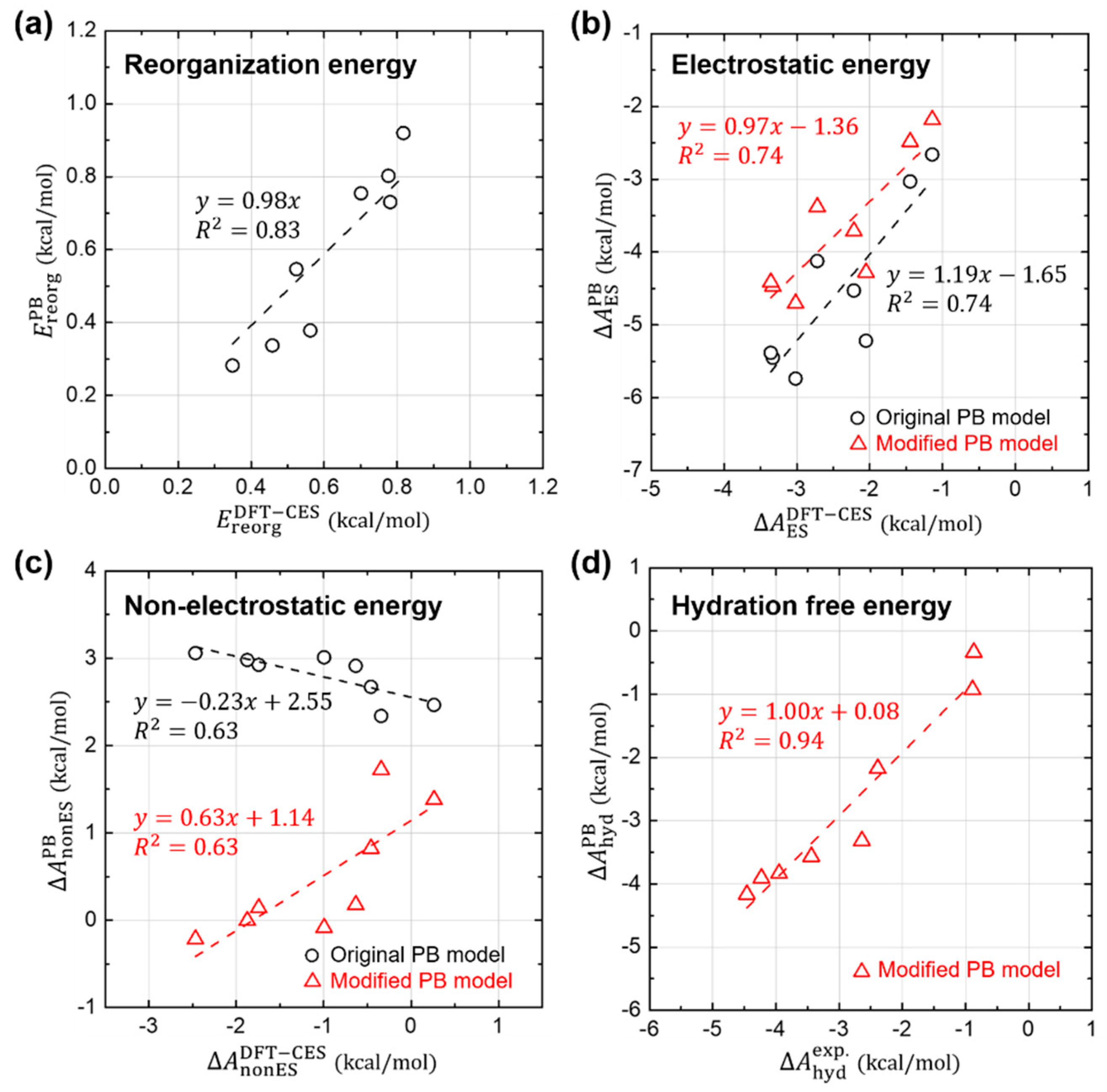
3.2. Validity of Linear-Reponse Theory
3.3. Non-Electrostatic Interaction Components: Surface-Area Dependence
3.4. Component-by-Component Comparisons
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van Gunsteren, W.F.; Luque, F.J.; Timms, D.; Torda, A.E. Molecular mechanics in biology: From structure to function, taking account of solvation. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 847–863. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Schutz, C.N. Analyzing free energy relationships for proton translocations in enzymes: Carbonic anhydrase revisited. J. Phys. Chem. B 2004, 108, 2066–2075. [Google Scholar]
- Williams, P.A.; Cosme, J.; Ward, A.; Angove, H.C.; Vinković, D.M.; Jhoti, H. Crystal structure of human cytochrome P450 2C9 with bound warfarin. Nature 2003, 424, 464–468. [Google Scholar] [CrossRef] [PubMed]
- Burley, S.K.; Petsko, G.A. Aromatic-aromatic interaction: A mechanism of protein structure stabilization. Science 1985, 229, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Timasheff, S.N. The control of protein stability and association by weak interactions with water: How do solvents affect these processes? Annu. Rev. Biophys. Biomol. Struct. 1993, 22, 67–97. [Google Scholar] [CrossRef] [PubMed]
- Makhatadze, G.I.; Privalov, P.L. Contribution of hydration to protein folding thermodynamics: I. The enthalpy of hydration. J. Mol. Biol. 1993, 232, 639–659. [Google Scholar] [CrossRef] [PubMed]
- Makhatadze, G.I.; Privalov, P.L. Contribution of hydration to protein folding thermodynamics: II. The entropy and Gibbs energy of hydration. J. Mol. Biol. 1993, 232, 660–679. [Google Scholar] [CrossRef] [PubMed]
- Makarov, V.; Pettitt, B.M.; Feig, M. Solvation and hydration of proteins and nucleic acids: A Theoretical View of Simulation and Experiment. Acc. Chem. Res. 2002, 35, 376–384. [Google Scholar] [CrossRef] [PubMed]
- Philp, D.; Stoddart, J.F. Self-assembly in natural and unnatural systems. Angew. Chem. Int. Ed. Engl. 1996, 35, 1154–1196. [Google Scholar] [CrossRef]
- Ben-Naim, A. Solvation Thermodynamics, 1st ed.; Plenum Press: New York, NY, USA, 1987; pp. 6–11. [Google Scholar]
- Ben-Naim, A. Standard thermodynamics of transfer. Uses and misuses. J. Phys. Chem. 1978, 82, 792–803. [Google Scholar] [CrossRef]
- Ben-Naim, A. Solvation: From small to macro molecules. Curr. Opin. Struct. Biol. 1994, 4, 264–268. [Google Scholar] [CrossRef]
- Sitkoff, D.; Sharp, K.A.; Honig, B. Accurate Calculation of Hydration Free Energies Using Macroscopic Solvent Models. J. Phys. Chem. 1994, 98, 1978–1988. [Google Scholar] [CrossRef]
- Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E.; Tomasi, J. Electrostatic Interaction of a Solute with a Continuum. A Direct Utilization of Ab Initio Molecular Potentials for the Prevision of Solvent Effects, Chem. Phys. 1981, 55, 117–129. [Google Scholar]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Mennucci, B.E.; Cancès, E.; Tomasi, J. Evaluation of Solvent Effects in Isotropic and Anisotropic Dielectrics and in Ionic Solutions with a Unified Integral Equation Method: Theoretical Bases, Computational Implementation, and Numerical Applications. J. Phys. Chem. B 1997, 101, 10506–10517. [Google Scholar] [CrossRef]
- Klamt, A.; Schüürmann, J. COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient. J. Chem. Soc. Perkin Trans. 2 1993, 0, 799–805. [Google Scholar] [CrossRef]
- Klamt, A. Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena. J. Phys. Chem. 1995, 99, 2224–2235. [Google Scholar] [CrossRef]
- Still, W.C.; Tempczyk, A.; Hawley, R.C.; Hendrickson, T. Semianalytical Treatment of Solvation for Molecular Mechanics and Dynamics. J. Am. Chem. Soc. 1990, 112, 6127–6129. [Google Scholar] [CrossRef]
- Cramer, C.J.; Truhlar, D.G. A Universal Approach to Solvation Modeling. Acc. Chem. Res. 2008, 41, 760–768. [Google Scholar] [CrossRef] [PubMed]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Performance of SM6, SM8, and SMD on the SAMPL1 Test Set for the Prediction of Small-Molecule Solvation Free Energies. J. Phys. Chem. B 2009, 113, 4538–4543. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Briggs, J.M. A priori pKa calculations and the hydration of organic anions. J. Am. Chem. Soc. 1989, 111, 4190–4197. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Briggs, J.M.; Contreras, M.L. Relative partition coefficients for organic solutes from fluid simulations. J. Phys. Chem. 1990, 94, 1683–1686. [Google Scholar] [CrossRef]
- Nicholls, A.; Mobley, D.L.; Guthrie, J.P.; Chodera, J.D.; Bayly, C.I.; Cooper, M.D.; Pande, V.S. Predicting small-molecule solvation free energies: An informal blind test for computational chemistry. J. Med. Chem. 2008, 51, 769–779. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. Interfaces and the driving force of hydrophobic assembly. Nature 2005, 437, 640–647. [Google Scholar] [CrossRef] [PubMed]
- Frank, H.S.; Evans, M.W. Free volume and entropy in condensed systems III. Entropy in binary liquid mixtures; partial molal entropy in dilute solutions; structure and thermodynamics in aqueous electrolytes. J. Chem. Phys. 1945, 13, 507–532. [Google Scholar] [CrossRef]
- Kauzmann, W. Some factors in the interpretation of protein denaturation. Adv. Protein Chem. 1959, 14, 1–63. [Google Scholar] [PubMed]
- Stillinger, F.H. Structure in aqueous solutions of nonpolar solutes from the standpoint of scaled-particle theory. J. Solution Chem. 1973, 2, 141–158. [Google Scholar] [CrossRef]
- Ashbaugh, H.S.; Pratt, L.R. Colloquium: Scaled particle theory and the length scales of hydrophobicity. Rev. Mod. Phys. 2006, 78, 159–178. [Google Scholar] [CrossRef]
- Lum, K.; Chandler, D.; Weeks, J.D. Hydrophobicity at small and large length scales. J. Phys. Chem. B 1999, 103, 4570–4577. [Google Scholar] [CrossRef]
- Gallicchio, E.; Zhang, L.Y.; Levy, R.M. The SGB/NP hydration free energy model based on the surface generalized Born solvent reaction field and novel nonpolar hydration free energy estimators. J. Comput. Chem. 2002, 23, 517–529. [Google Scholar] [CrossRef] [PubMed]
- Nakano, H.; Yamamoto, T. Accurate and efficient treatment of continuous solute charge density in the mean-field QM/MM free energy calculation. J. Chem. Theory Comput. 2012, 9, 188–203. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, M.L.; Aguilar, M.; Olivares del Valle, F. Study of solvent effects by means of averaged solvent electrostatic potentials obtained from molecular dynamics data. J. Comput. Chem. 1997, 18, 313–322. [Google Scholar] [CrossRef]
- Galván, I.F.; Sánchez, M.; Martın, M.; del Valle, F.O.; Aguilar, M. ASEP/MD: A program for the calculation of solvent effects combining QM/MM methods and the mean field approximation. Comput. Phys. Commun. 2003, 155, 244–259. [Google Scholar] [CrossRef]
- Yamamoto, T. Variational and perturbative formulations of quantum mechanical/molecular mechanical free energy with mean-field embedding and its analytical gradients. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.K.; Lee, H.; Kim, H. A seamless grid-based interface for mean-field QM/MM coupled with efficient solvation free energy calculations. J. Chem. Theory Comput. 2016, 12, 5088–5099. [Google Scholar] [CrossRef] [PubMed]
- Bayly, C.I.; Cieplak, P.; Cornell, W.D.; Kollman, P.A. A well-behaved electrostatic potential based method using charge restraints for deriving atomic charges: The RESP model. J. Phys. Chem. 1993, 97, 10269–10280. [Google Scholar] [CrossRef]
- Zwanzig, R.W. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954, 22, 1420–1426. [Google Scholar] [CrossRef]
- Kirkwood, J.G. Statistical mechanics of fluid mixtures. J. Chem. Phys. 1935, 3, 300–313. [Google Scholar] [CrossRef]
- Mruzik, M.R.; Abraham, F.F.; Schreiber, D.E.; Pound, G. A Monte Carlo study of ion–water clusters. J. Chem. Phys. 1976, 64, 481–491. [Google Scholar] [CrossRef]
- Mezei, M.; Swaminathan, S.; Beveridge, D.L. Ab initio calculation of the free energy of liquid water. J. Am. Chem. Soc. 1978, 100, 3255–3256. [Google Scholar] [CrossRef]
- Lin, S.-T.; Blanco, M.; Goddard, W.A., III. The two-phase model for calculating thermodynamic properties of liquids from molecular dynamics: Validation for the phase diagram of Lennard-Jones fluids. J. Chem. Phys. 2003, 119, 11792–11805. [Google Scholar] [CrossRef]
- Lin, S.-T.; Maiti, P.K.; Goddard, W.A., III. Two-phase thermodynamic model for efficient and accurate absolute entropy of water from molecular dynamics simulations. J. Phys. Chem. B 2010, 114, 8191–8198. [Google Scholar] [CrossRef] [PubMed]
- Pascal, T.A.; Lin, S.-T.; Goddard, W.A., III. Thermodynamics of liquids: Standard molar entropies and heat capacities of common solvents from 2PT molecular dynamics. Phys. Chem. Chem. Phys. 2011, 13, 169–181. [Google Scholar] [CrossRef] [PubMed]
- Pascal, T.A.; Goddard, W.A., III. Interfacial thermodynamics of water and six other liquid solvents. J. Phys. Chem. B 2014, 118, 5943–5956. [Google Scholar] [CrossRef] [PubMed]
- Eyring, H.; Marchi, R.P. Significant structure theory of liquids. J. Chem. Educ. 1963, 40, 562–572. [Google Scholar] [CrossRef]
- Marchi, R.P.; Eyring, H. Application of Significant Structure Theory to Water. J. Phys. Chem. 1964, 68, 221–228. [Google Scholar] [CrossRef]
- Gim, S.; Lim, H.-K.; Kim, H. Multiscale simulation method for quantitative prediction of surface wettability at the atomistic level. J. Phys. Chem. Lett. 2018, 9, 1750–1758. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Kaminski, G.A.; Friesner, R.A.; Tirado-Rives, J.; Jorgensen, W.L. Evaluation and reparametrization of the OPLS-AA force field for proteins via comparison with accurate quantum chemical calculations on peptides. J. Phys. Chem. B 2001, 105, 6474–6487. [Google Scholar] [CrossRef]
- Price, D.J.; Brooks, C.L., III. A modified TIP3P water potential for simulation with Ewald summation. J. Comput. Phys. 2004, 121, 10096–10103. [Google Scholar] [CrossRef] [PubMed]
- Andersen, H.C. Rattle: A “velocity” version of the shake algorithm for molecular dynamics calculations. J. Comput. Phys. 1983, 52, 24–34. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅ log (N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Bochevarov, A.D.; Harder, E.; Hughes, T.F.; Greenwood, J.R.; Braden, D.A.; Philipp, D.M.; Rinaldo, D.; Halls, M.D.; Zhang, J.; Friesner, R.A. Jaguar: A high-performance quantum chemistry software program with strengths in life and materials sciences. Int. J. Quantum Chem. 2013, 113, 2110–2142. [Google Scholar] [CrossRef]
- Petersson, G.A.; Bennett, A.; Tensfeldt, T.G.; Al-Laham, M.A.; Shirley, W.A.; Mantzaris, J. A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row atoms. J. Chem. Phys. 1988, 89, 2193–2218. [Google Scholar] [CrossRef]
- Petersson, G.A.; Al-Laham, M.A. A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms. J. Chem. Phys. 1991, 94, 6081–6090. [Google Scholar] [CrossRef]
- Cabani, S.; Gianni, P.; Mollica, V.; Lepori, L. Group contributions to the thermodynamic properties of non-ionic organic solutes in dilute aqueous solution. J. Solution Chem. 1981, 10, 563–595. [Google Scholar] [CrossRef]
- Rankin, K.N.; Sulea, T.; Purisima, E.O. On the transferability of hydration-parametrized continuum electrostatics models to solvated binding calculations. J. Comput. Chem. 2003, 24, 954–962. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5247. [Google Scholar] [CrossRef]
- Ben-Amotz, D.; Underwood, R. Unraveling water’s entropic mysteries: A unified view of nonpolar, polar, and ionic hydration. Acc. Chem. Res. 2008, 41, 957–967. [Google Scholar] [CrossRef] [PubMed]
- Reiss, H.; Frisch, H.L. Statistical mechanics of rigid spheres. J. Chem. Phys. 1959, 31, 369–380. [Google Scholar] [CrossRef]
- Tannor, D.J.; Marten, B.; Murphy, R.; Friesner, R.A.; Sitkoff, D.; Nicholls, A.; Ringnalda, M.; Goddard, W.A., III; Honig, B. Accurate first principles calculation of molecular charge distributions and solvation energies from ab initio quantum mechanics and continuum dielectric theory. J. Am. Chem. Soc. 1994, 116, 11875–11882. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
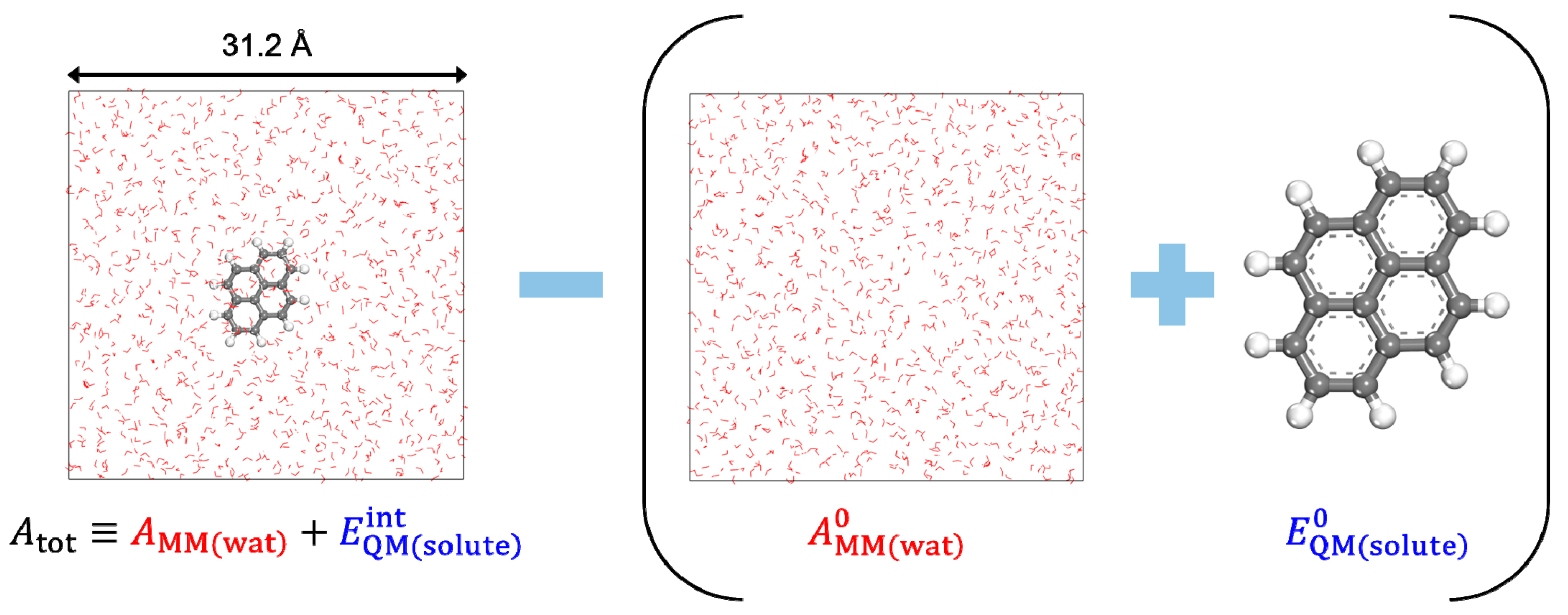




| Solute Molecule | |||||
|---|---|---|---|---|---|
| #1. Benzene | −1.14 | +0.35 | −1.14 | −9.66 | +9.32 |
| #2. Toluene | −0.72 | +0.46 | −1.45 | −9.69 | +9.95 |
| #3. Biphenyl | −2.29 | +0.56 | −2.22 | −15.94 | +15.31 |
| #4. Naphthalene | −2.65 | +0.52 | −2.72 | −13.56 | +13.10 |
| #5. Fluorene | −3.01 | +0.78 | −2.05 | −16.87 | +15.13 |
| #6. Phenanthrene | −4.43 | +0.78 | −3.33 | −17.63 | +15.76 |
| #7. Pyrene | −4.67 | +0.82 | −3.02 | −19.70 | +17.23 |
| #8. Anthracene | −3.65 | +0.70 | −3.36 | −15.80 | +14.81 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, H.; Lim, H.-K.; Kim, H. Hydration Thermodynamics of Non-Polar Aromatic Hydrocarbons: Comparison of Implicit and Explicit Solvation Models. Molecules 2018, 23, 2927. https://doi.org/10.3390/molecules23112927
Lee H, Lim H-K, Kim H. Hydration Thermodynamics of Non-Polar Aromatic Hydrocarbons: Comparison of Implicit and Explicit Solvation Models. Molecules. 2018; 23(11):2927. https://doi.org/10.3390/molecules23112927
Chicago/Turabian StyleLee, Hankyul, Hyung-Kyu Lim, and Hyungjun Kim. 2018. "Hydration Thermodynamics of Non-Polar Aromatic Hydrocarbons: Comparison of Implicit and Explicit Solvation Models" Molecules 23, no. 11: 2927. https://doi.org/10.3390/molecules23112927
APA StyleLee, H., Lim, H.-K., & Kim, H. (2018). Hydration Thermodynamics of Non-Polar Aromatic Hydrocarbons: Comparison of Implicit and Explicit Solvation Models. Molecules, 23(11), 2927. https://doi.org/10.3390/molecules23112927







