3.1.1. Concave extended-Tetrathiafulvalene (exTTF) Derivatives for the Supramolecular Recognition of Fullerenes
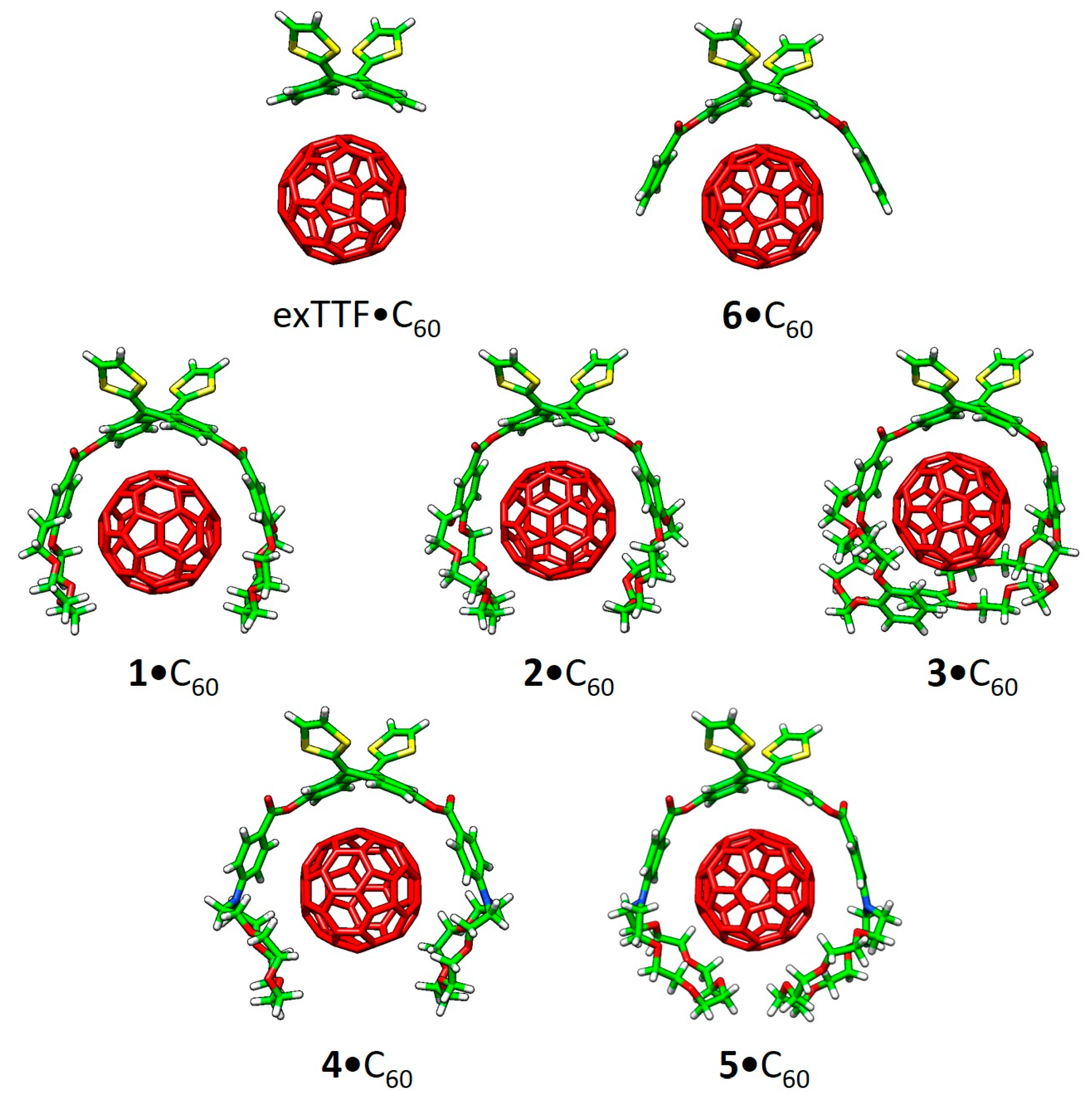
The 2-[9-(1,3-dithiol-2-ylidene)anthracen-10(9H)-ylidene]-1,3-dithiole compound, also known as exTTF (
Figure 2), has aroused great interest in the field of organic electronics due to its resemblance with the popular tetrathiafulvalene (TTF) [
81]. Like TTF, the exTTF compound presents a good electron-donor character, and has been combined in numerous donor–acceptor dyads [
82] to gain insight into the paramount photoinduced electron-transfer process. Another remarkable feature of exTTF in the context of supramolecular chemistry is its π-conjugated curved (concave) structure. In fact, its particular structure and electron-donor character makes the exTTF system very attractive as a potential supramolecular receptor for fullerenes. Initially, DFT calculations predicted binding energies up to 7.00 kcal/mol between a single unit of exTTF and C
60. Unfortunately, no experimental evidence of association in solution was found in either UV–Vis or NMR titrations [
2]. This apparently negative outcome encouraged the quest of novel chemical entities that incorporate the exTTF moiety for an enhanced C
60 recognition. In this line, Pérez et al. synthesized a bivalent tweezer with two exTTF units (MTW in
Figure 2) able to act as a host, and effectively interact with C
60 fullerene as a guest owing to the concave–convex structural complementary that maximizes the number of π–π contacts [
83]. Subsequently, the supramolecular organization and the photophysical properties of the corresponding discrete donor–acceptor MTW
•C
60 and its PTW
•C
60 homologue were studied by theoretical calculations and spectroscopic techniques [
16].
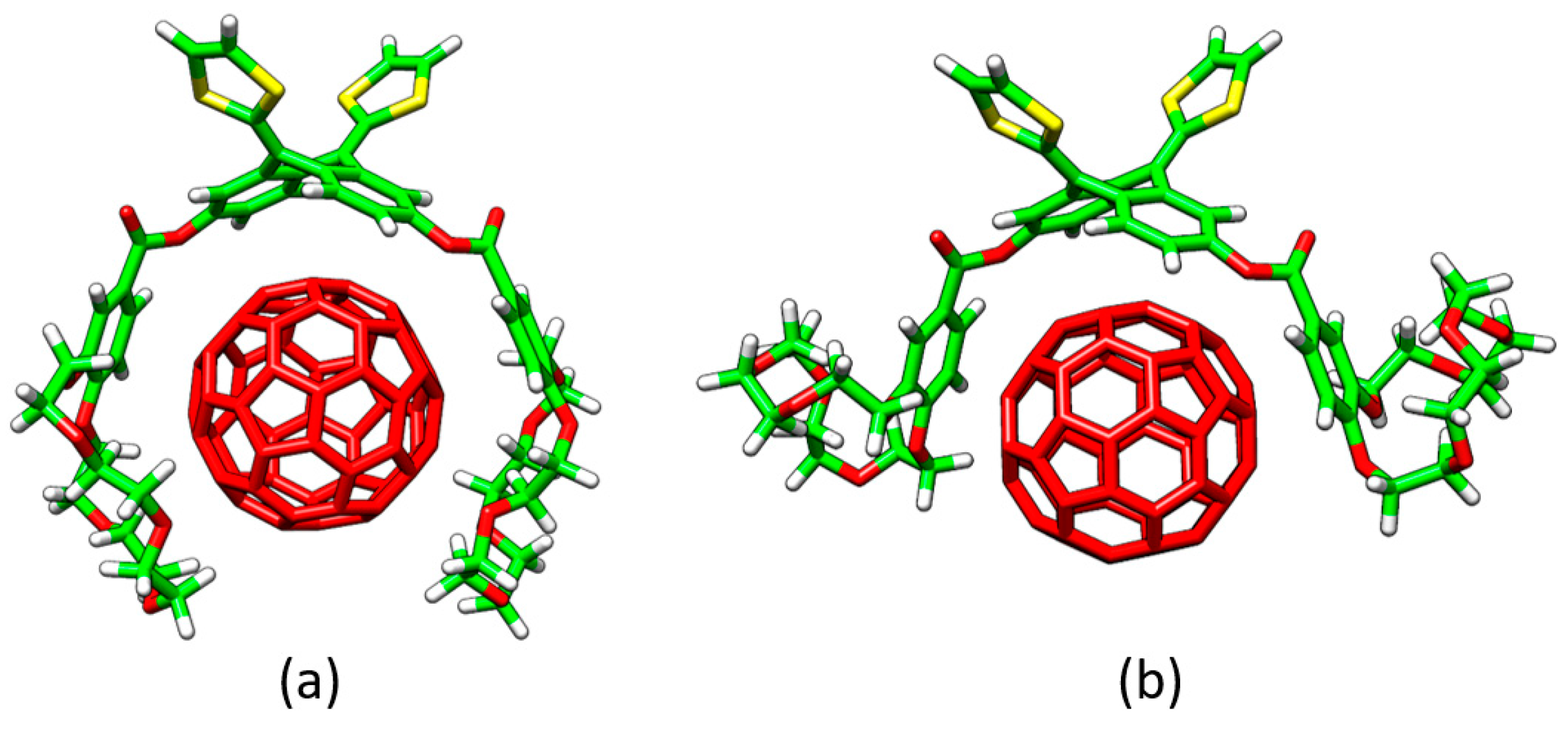
Recently, a series of exTTF derivatives substituted with crown ethers of increasing size specifically designed to host fullerenes were reported (
Figure 3) [
84]. The aim of this joint experimental‒theoretical study was to unveil the nature of the noncovalent interactions that govern the supramolecular organization between the exTTF-crown ether and C
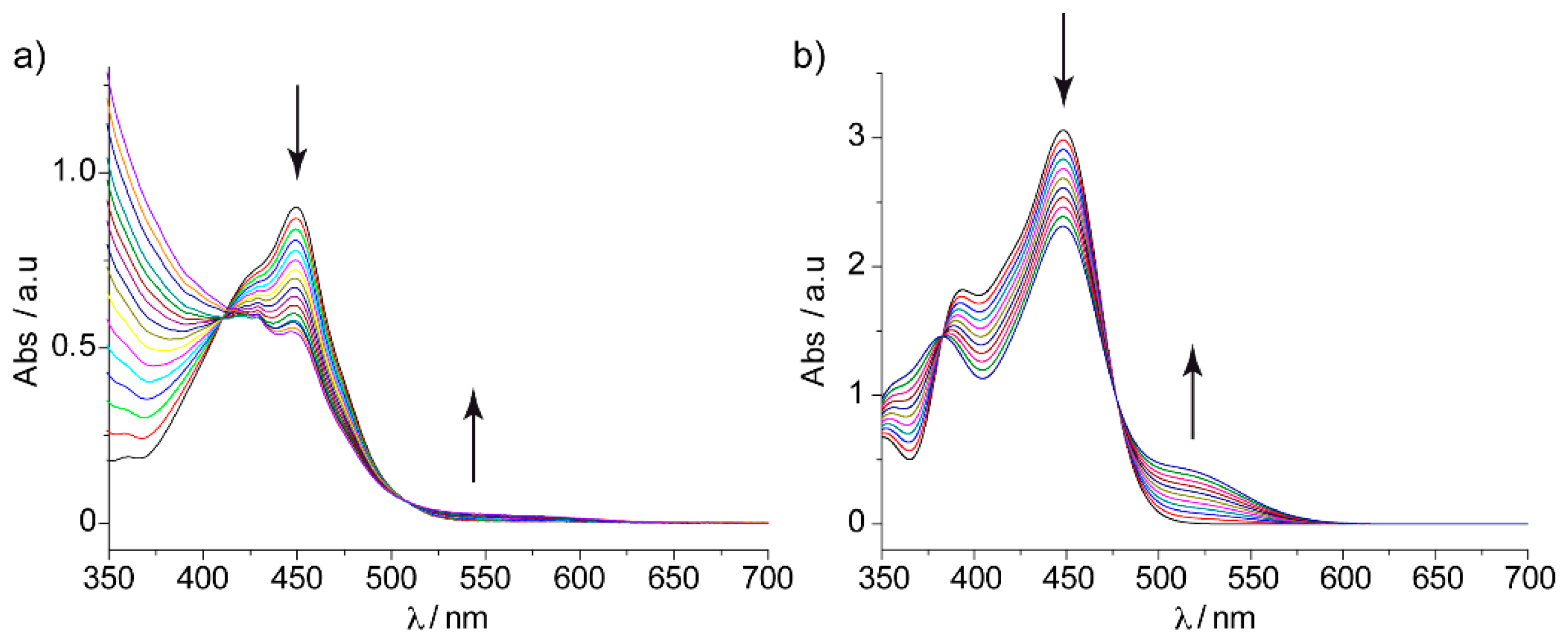
60. Experimentally, absorption titrations were performed to confirm the supramolecular complexation between the exTTF derivatives and C
60. In these experiments, the exTTF absorption bands (350 and 450 nm) gradually decreased upon addition of C
60. The absorption bands associated with C
60 were also detected (namely, a strong absorption band at wavelengths <350 nm, a sharp band at 407 nm, and a broad absorption between 470 and 650 nm). Finally, a charge-transfer feature that peaked at longer wavelengths (475 and 485 nm in PhCl and PhCN, respectively) emerged. The spectroscopic data were employed to estimate the association constants for the exTTF molecular tweezers
1–
6 towards C
60 in PhCl at 298 K (log
Ka = 4.8 ± 0.9, 6.7 ± 0.2, 6.9 ± 0.2, 3.8 ± 0.6, 5.1 ± 0.1 and 3.3 ± 0.4 M
−1 for
1•C
60,
2•C
60,
3•C
60,
4•C
60,
5•C
60 and
6•C
60, respectively).
The different conformations that
1–
6 may adopt to interact with C
60 were initially optimized by using semiempirical PM7 calculations, which are recommended for exploratory purposes owing to its favorable computational cost.
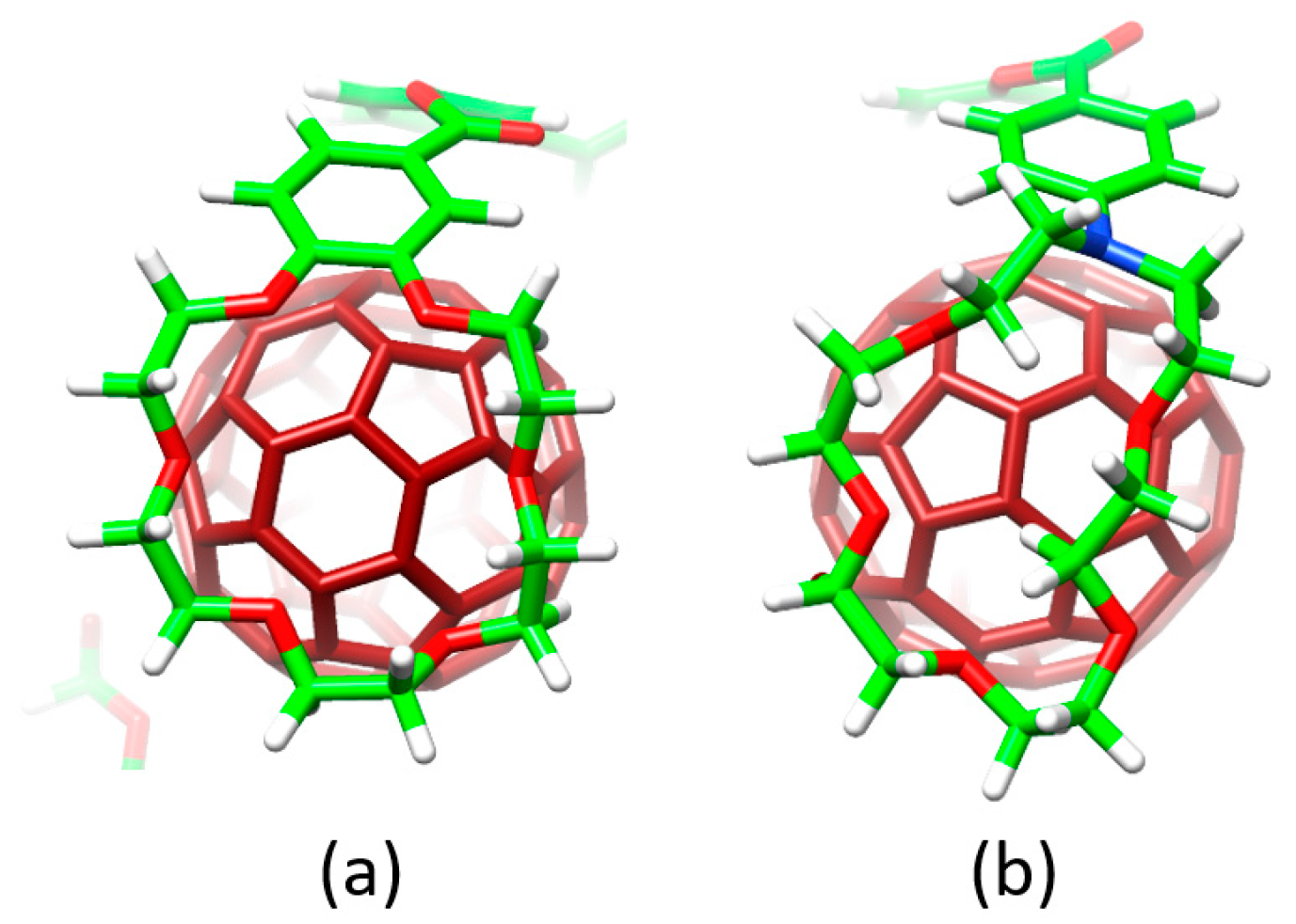
Figure 4a displays the minimum-energy geometries computed for
2•C
60 as a representative example. In all complexes formed by
1–
6 and C
60, the fullerene ball interacts with the anthracene concave region of exTTF and, at the same time, the crown ether-based arms embrace C60 in a pinzer-like shape (
Figure 4a).
Host–guest arrangements, where the crown ethers are not directly interacting with C
60, were also optimized for
1•C
60,
2•C
60 and
3•C
60 to evaluate the stabilization owing to the embracing motion (see
Figure 4b for
2•C
60). For
2•C
60, PM7 predicted binding energies of −72.43 and −51.20 kcal/mol for the embraced and non-embraced conformations, respectively (
Figure 4). Similar results were obtained for the other complexes calculated (
1•C
60 and
3•C
60) [
84]. PM7 calculations were therefore key to estimate quantitatively the energy stabilization of the embracing motion promoted by the exTTF-based hosts for the recognition of fullerene C
60.
The more stable embraced conformations were then optimized using the dispersion-corrected B97-D functional in combination with the cc-pVDZ basis set (
Figure 5). The exTTF
•C
60 complex was also computed as a reference. Note that the B97-D density functional presents an outstanding trade-off between accuracy and computational cost and, thus, is highly recommended for exploratory and optimization purposes [
56]. The optimized structures showed intermolecular contacts of different nature along the host–guest interacting region.
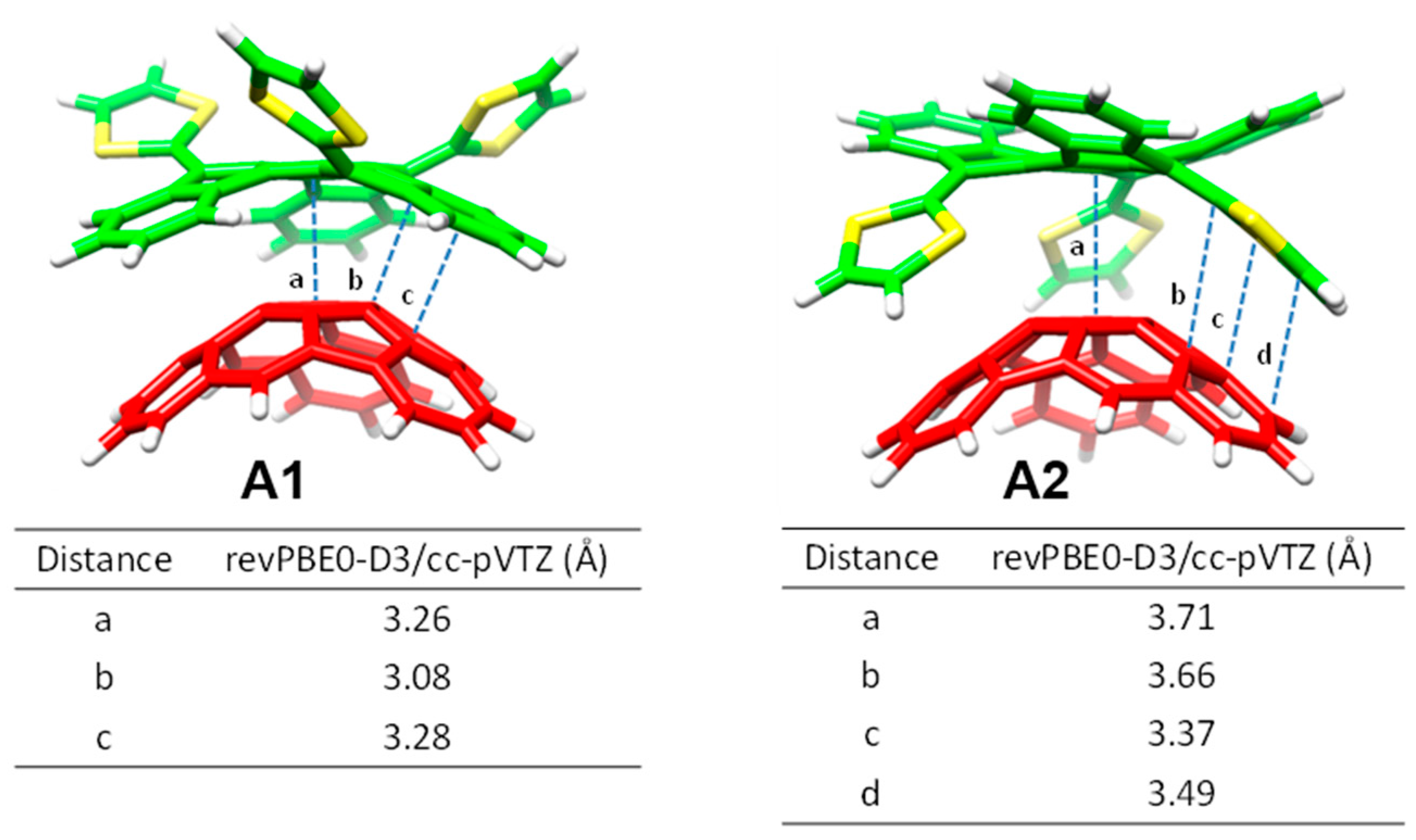
Table 2 collects the shortest intermolecular contacts determining the stabilization of the complexes between the receptors
1–
6 and C
60, as well as the binding energies computed for the resulting supramolecular complexes. To assess the binding energies, single-point energy calculations were carried out on the B97-D/cc-pVDZ-optimized structures using the revPBE0-D3 functional and the more extended triple-ζ cc-pVTZ basis set. Note that triple-ζ basis sets are highly recommended, if the molecular size allows it, to yield reasonable binding energies in weakly-interacting molecular systems with minimal basis set superposition error [
77]. A stable exTTF
•C
60 complex (
Ebind of −10.24 kcal/mol) was obtained due to π–π interactions between the lateral benzene rings of exTTF and the benzene rings of C
60 with centroid–centroid distances of 3.42 Å (
a in
Table 2). As exTTF•C
60 has not been detected experimentally to date, entropic and solvent effects are expected to counterbalance this stabilizing interaction. In the
6•C
60 complex, two additional interactions coming from the presence of the benzoates were found: π–π interactions at 3.25 Å between the benzene rings of the benzoate moiety and C
60 (
b in
Table 2), and
n–π interactions owing to short O(host)···C(guest) intermolecular distances (3.16 Å,
c in
Table 2). The stabilizing effect of these NCIs was demonstrated by the folding angle of the anthracene skeleton in exTTF, which becomes sharper in going from exTTF•C
60 (142.5°) to
6•C
60 (137.0°). The binding energy for
6•C
60 was calculated to be −22.85 kcal/mol, which is more than twice of the binding energy obtained for exTTF•C
60. The significant stabilization predicted in the
6•C
60 formation supported the experimental detection of this complex in solution.
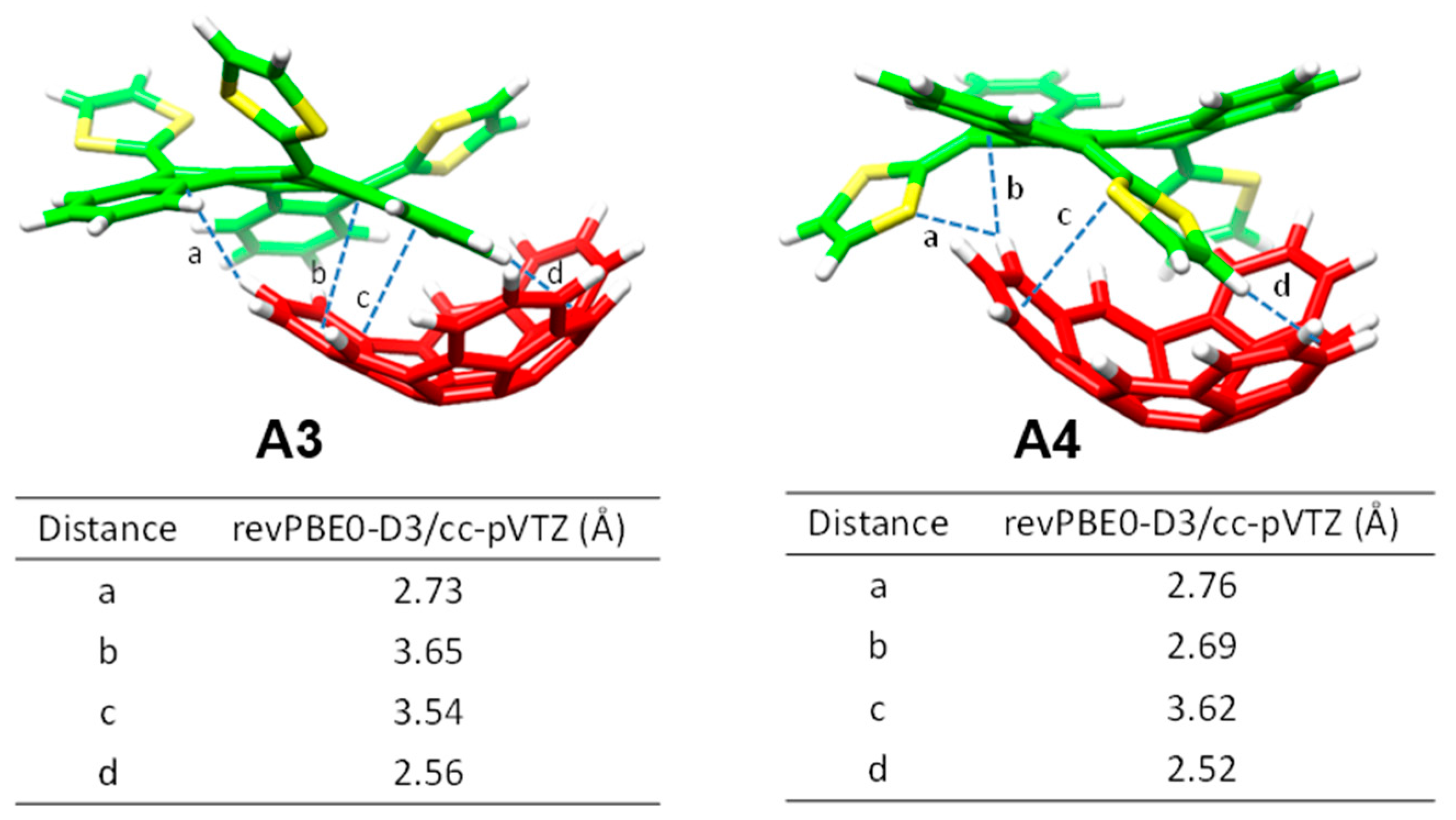
Moving to larger complexes (from
6•C
60 to
1•C
60,
2•C
60, and
3•C
60) where crown ethers are inserted in the electron-donor host system, new
n–π (
d) and CH···π (
e) interactions with intermolecular distances of around 2.9 and 2.6 Å emerge to stabilize the resulting supramolecular assembly (
Table 2). revPBE0-D3 calculations predicted binding energies going from −39.69 kcal/mol for 1•C
60, to −44.76 kcal/mol for
2•C
60, and to −54.36 kcal/mol for
3•C
60. This trend was in line with the increase of the
Ka value obtained experimentally, and was attributed to the increasing size of the crown ethers when going from
1•C
60 to
3•C
60 (i.e., increasing number of stabilizing
n–π and CH···π interactions). The crown ether arms wrap C
60 and lead to more compact complexes, in which the benzene rings of the benzoate moiety are closer (by 0.2 Å) to C
60 as compared, for example, with
6•C
60 (distance
b in
Table 2). This gain in compactness reinforces the stabilizing effect that NCIs between C
60 and the crown ethers exert on the resulting complex stability.
Finally, the effect of the nitrogen atoms on the capability of aza-crown ether derivatives
4 and
5 to host the C
60 species was analyzed. The insertion of the nitrogen bridge between the benzoate units and the crown ethers confers additional flexibility to the aza-crown ethers in
4•C
60 and
5•C
60. This flexibility gives rise to structures more folded than those computed for the oxygenated analogues
1•C
60 and
2•C
60 (
Figure 6). Smaller binding energies for
4•C
60 and
5•C
60 (−36.77 and −43.33 kcal/mol, respectively) were found compared to the oxygenated complexes
1•C
60 and
2•C
60 (−39.69 and −44.76 kcal/mol, respectively). The lower affinity to C
60 obtained for the aza-crown ethers is in line with the experimentally determined binding constants, and was associated to an overall weakening of the host–guest interactions caused by the less favorable aza-crown ether arm orientations.
This example satisfactorily illustrated how quantum-chemical calculations can be used as a very useful tool to rationalize the supramolecular assemblies formed by electron-donor hosts and the C60 guest. In particular, calculations pointed out that the ability of the exTTF-based molecular tweezers to bind C60 comes from an interplay of different π–π, n–π and CH···π interactions, and that the size and nature of the crown ether are key factors for the relative stabilization of the resulting complexes between 1–6 and C60.
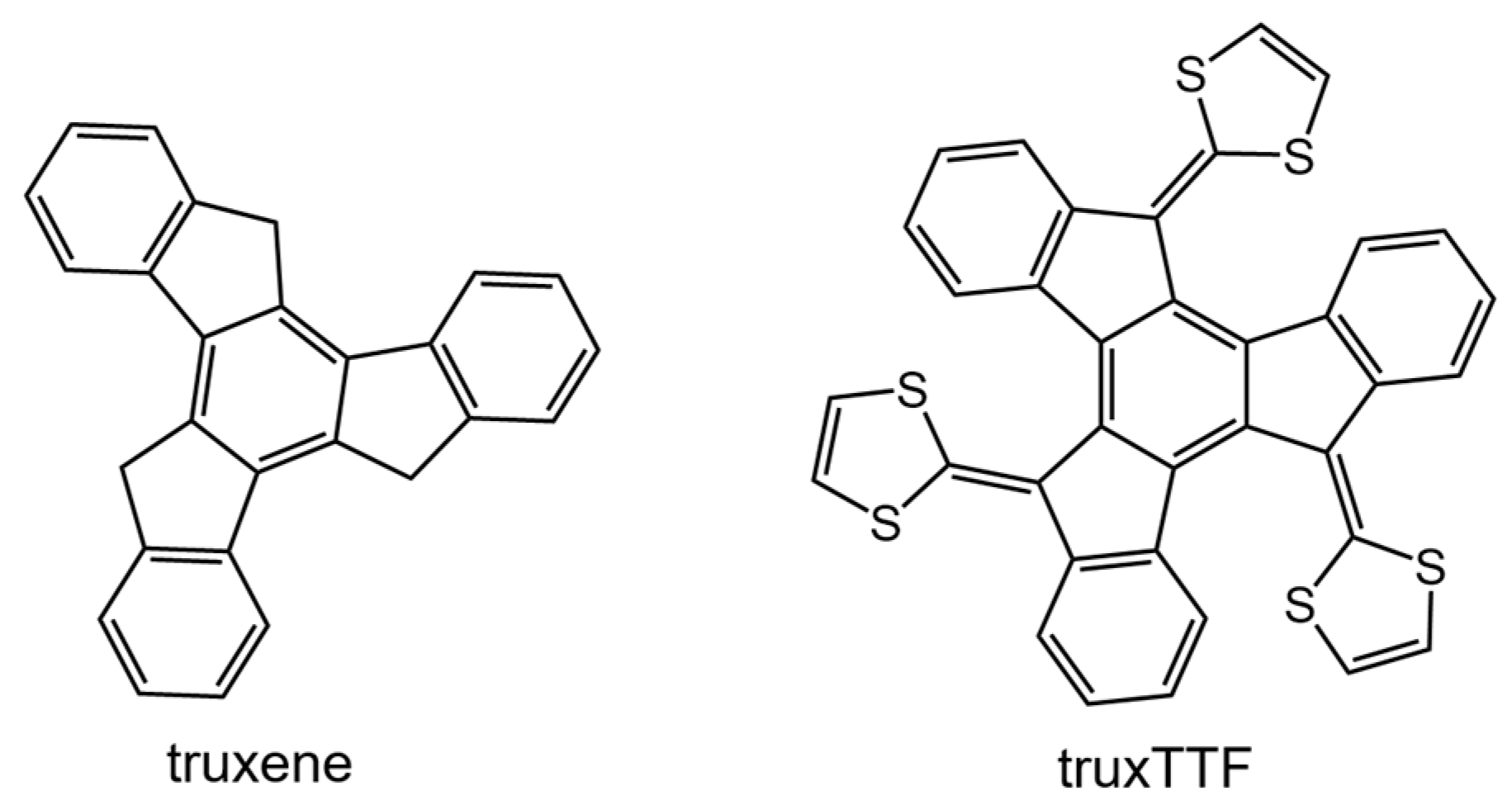
3.1.2. Curved Truxene-Tetrathiafulvalene (truxTTF) Donor as a Supramolecular Partner for Fullerenes
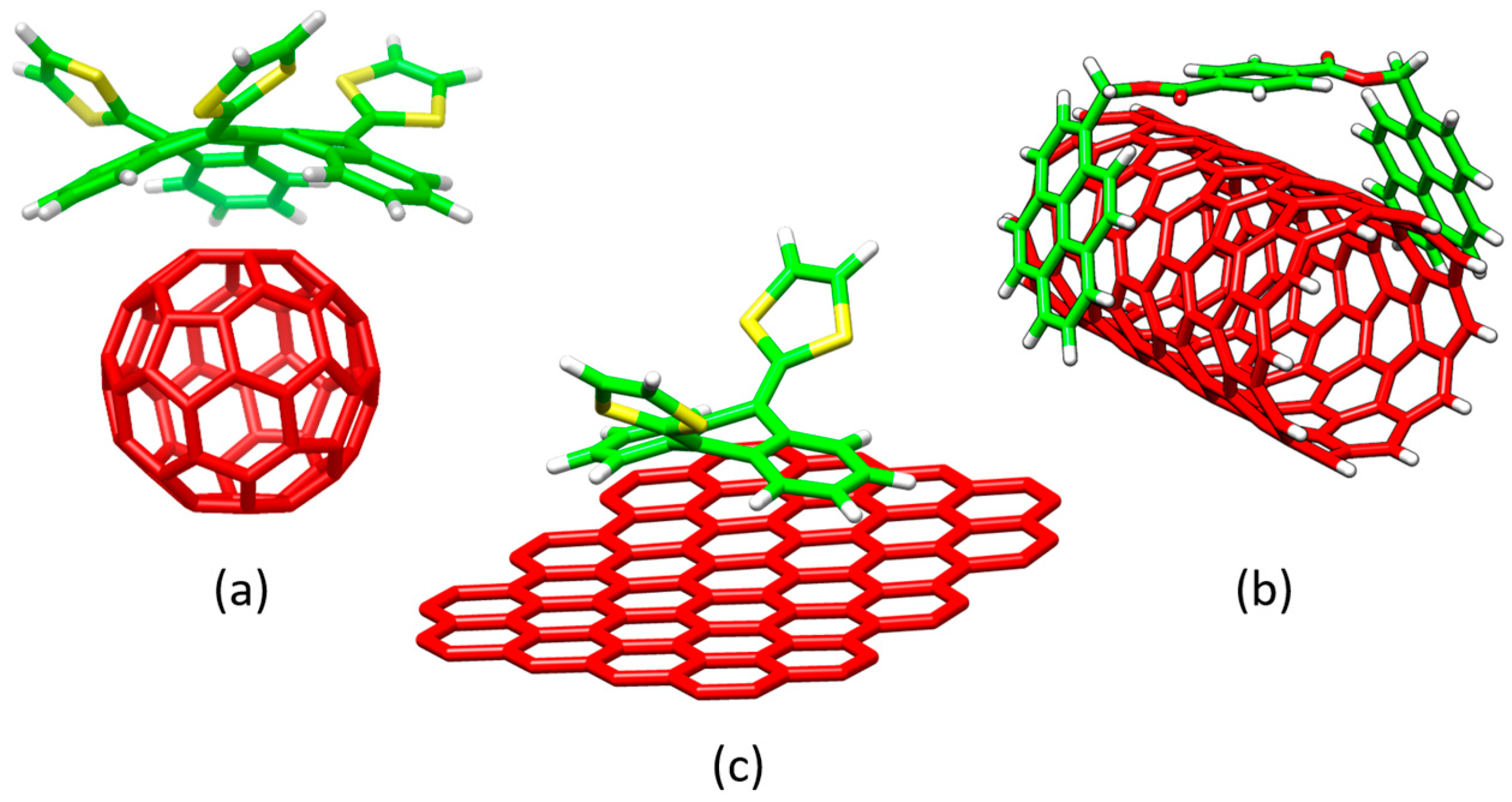
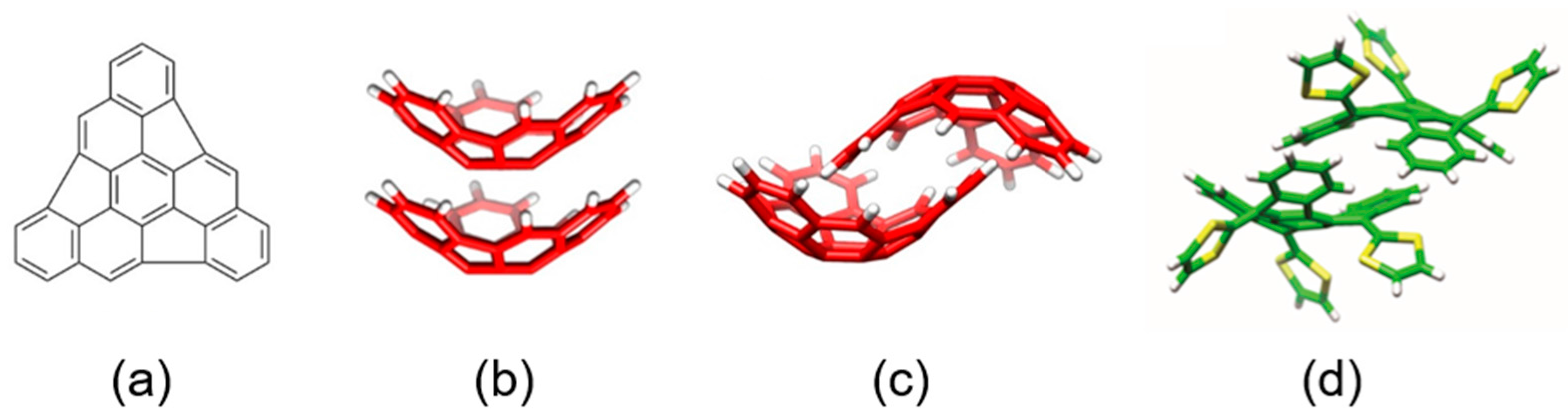
Among the different carbon-based nanofragments, the truxene structure (
Figure 7) has attracted a great deal of interest due to its exceptional solubility, high thermal stability and ease to be chemically modified [
85]. Over the last years, and owing to the advances in the synthesis of truxene derivatives, the scope of applications of this attractive heptacyclic polyarene building block, initially limited to synthesis and photoluminescence, has been extended to organic electronics [
86]. Particularly interesting is the modification of the truxene core through the incorporation of three dithiole rings to give rise to the electron-donor truxene-TTF (truxTTF) compound (
Figure 7) [
87]. In analogy to the exTTF derivatives (
Section 3.1.1), the truxTTF structure is distorted out of planarity due to short dithiole–benzene contacts, generating a double-concave cavity that fulfills the structural requirements as a host for the supramolecular recognition of fullerene derivatives.
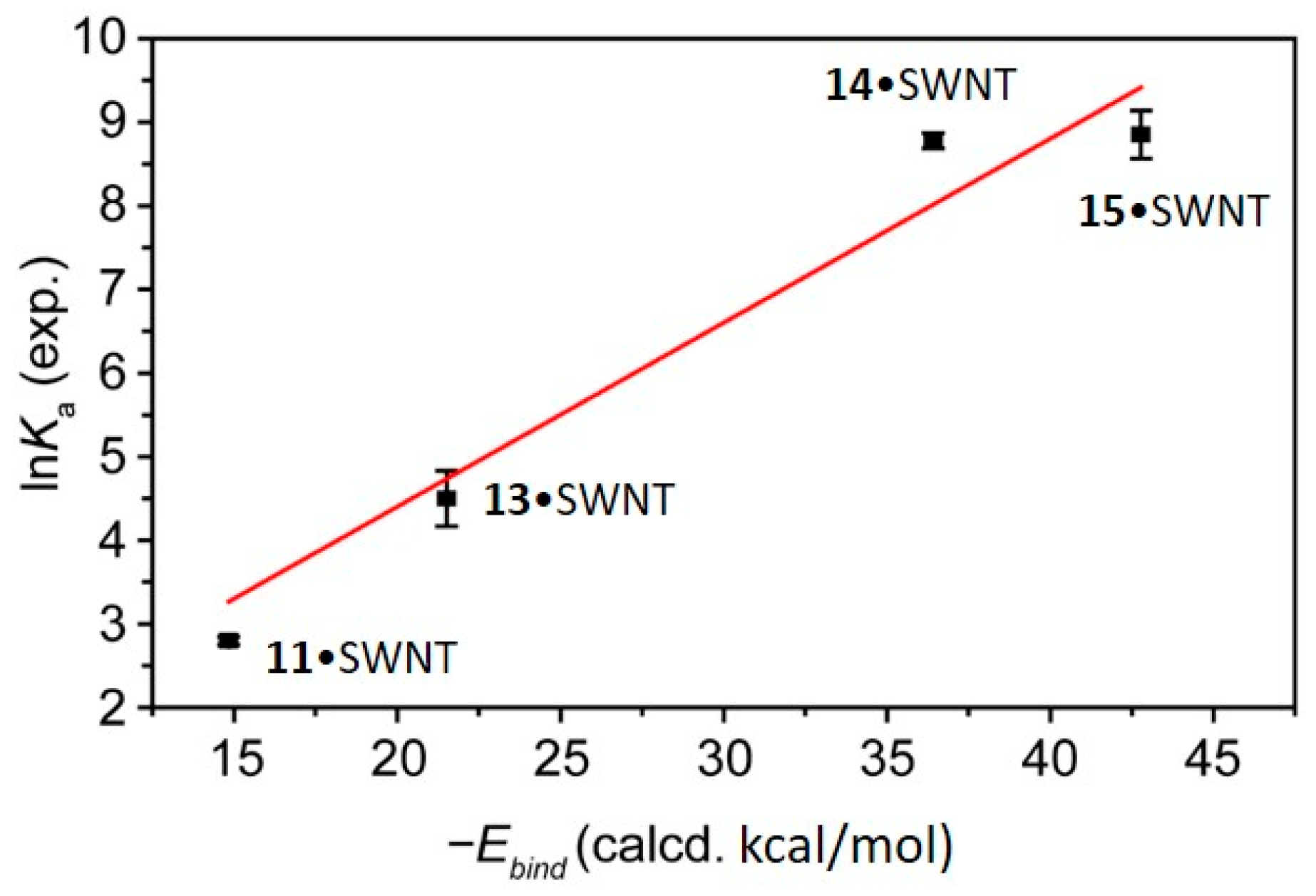
In 2007, Pérez et al. conducted a joint experimental‒theoretical study, and demonstrated that the truxTTF electron-donor was able to effectively host fullerenes due to its concave structure [
87]. Experimentally, the supramolecular association between truxTTF and C
60 was investigated by
1H-NMR titrations. The generation of the bimolecular 1:1 supramolecular complex with a binding constant of 1.2 × 10
−3 M
−1 (see more experimental details in reference [
87]) was confirmed. Additionally,
1H-NMR experiments suggested that the supramolecular interaction occurred preferentially on the aromatic truxene surface of truxTTF.
Notwithstanding the experimental evidences about the formation of the donor‒acceptor truxTTF•C
60 complex, detailed information on the supramolecular organization at atomistic level was not reported so far. To unravel the origin and nature of the interactions between the host and the guest, DFT calculations at the MPWB1K/6-31G** level were performed. The MPWB1K density functional, developed by Truhlar et al., was designed to capture π–π interactions in stacked DNA pairs and amino acid pairs [
88]. Note that in 2007, the Grimme’s dispersion-corrected approximation in its most modern version (DFT-D3) was not still developed and this kind of density functionals were a practical solution for the theoretical treatment of weakly-bound molecular systems. Nowadays, the DFT-D3 or DFT-NL approximations would be more recommended for general supramolecular applications [
26,
69].
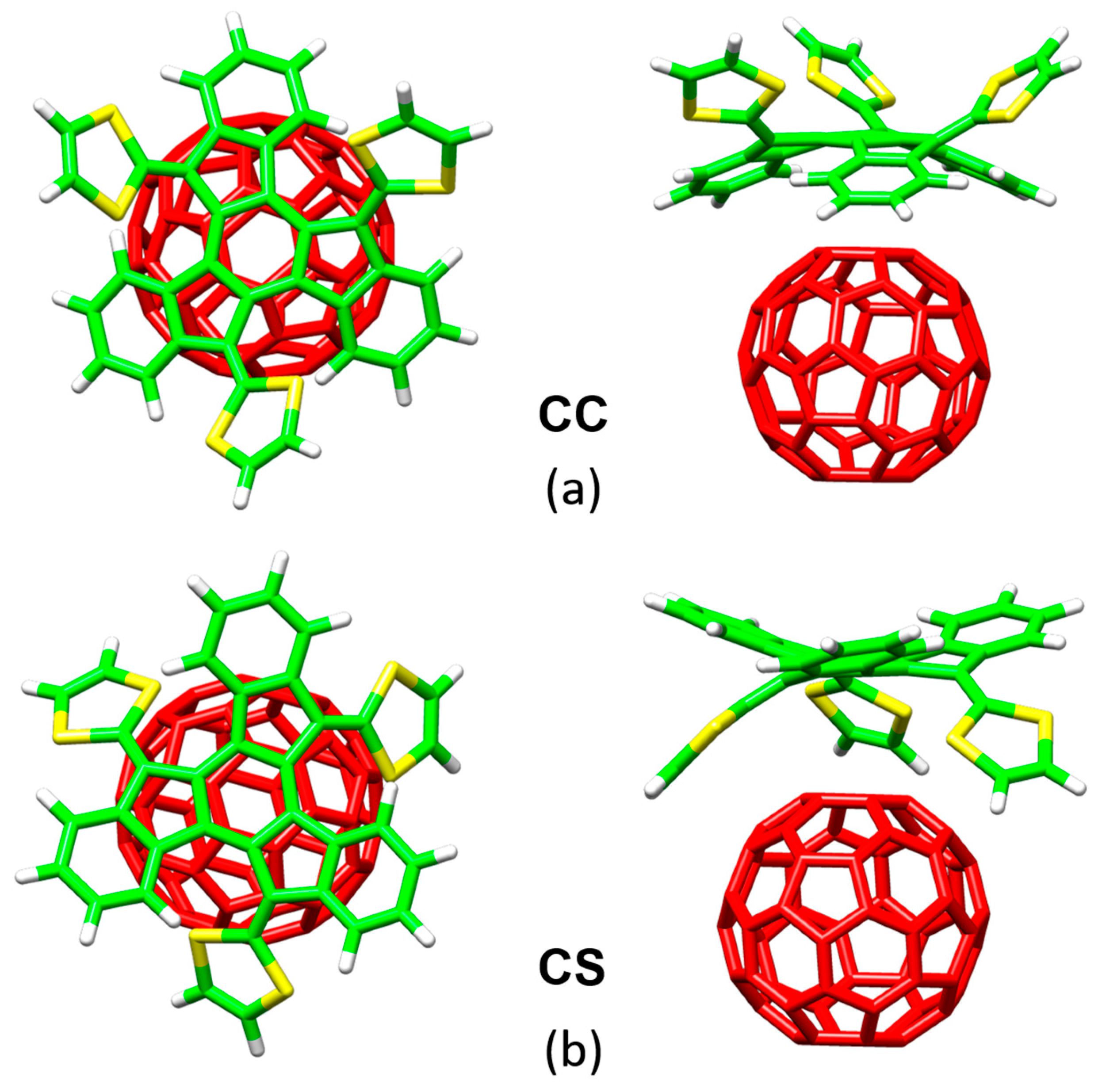
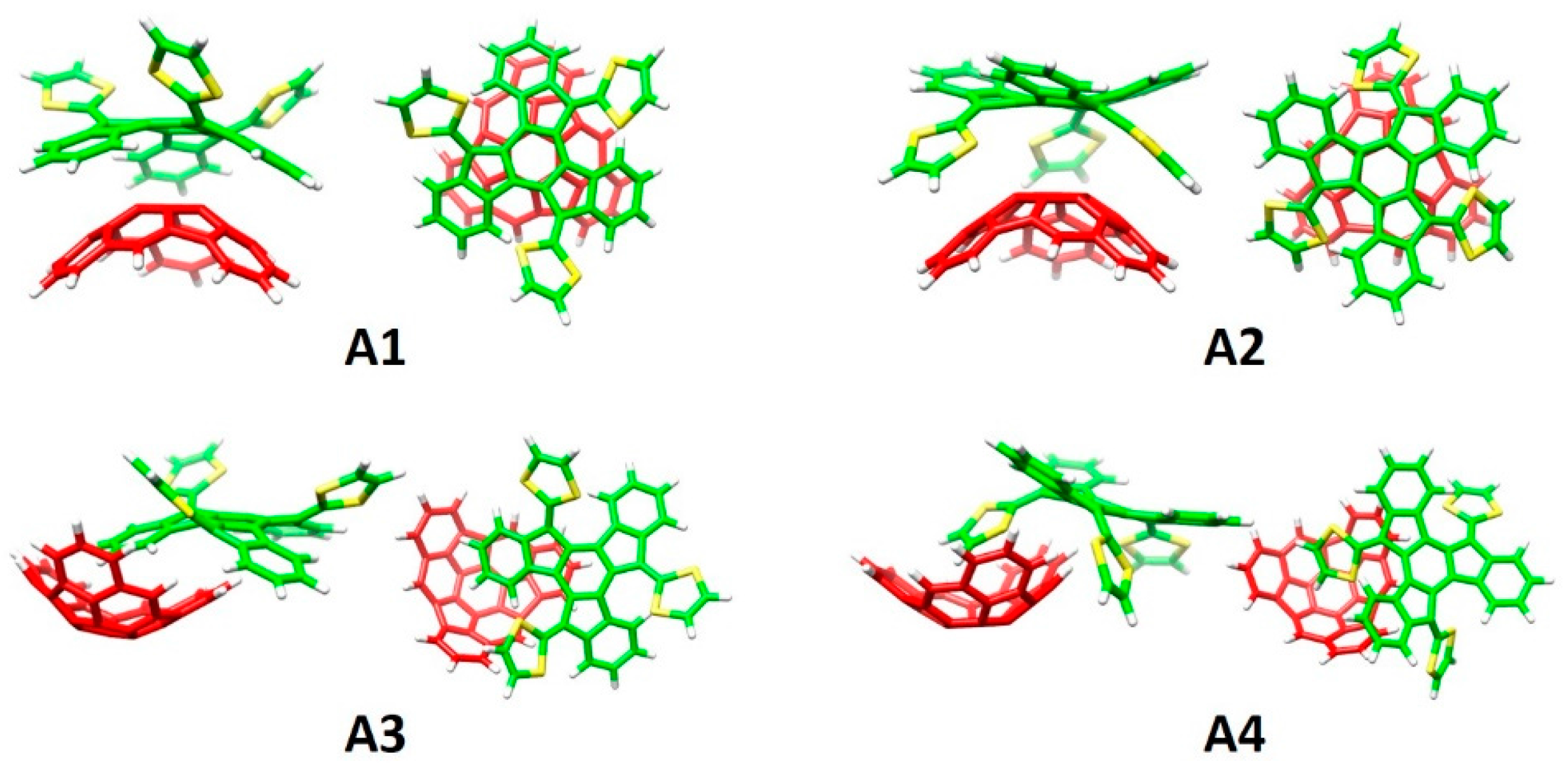
Figure 8 displays the minimum-energy geometries calculated at the MPWB1K/6-31G** level for two different structures of the truxTTF•C
60 complex. In structure
CC, fullerene C
60 was placed inside of the aromatic cavity created by the truxene core, stabilized by multiple π–π contacts. This structure clearly exploited the requirement of structural concave–convex complementary to form the host-guest associate. The central benzene ring of the truxene core stacks on one of the benzene rings of C
60 in a slightly parallel-displaced fashion, in which the benzene rings are twisted by approximately 20° relative to each other and are separated at an average distance of 3.39 Å. This distance turned out to be considerably shorter than the distances reported for the benzene dimer in parallel (3.9 Å) and parallel-displaced (3.6 Å) configurations [
89]. In addition to the interactions of the central benzene rings, the peripheral benzene rings of truxTTF exhibit many intermolecular contacts in the 3.6–3.9 Å range with the C
60 guest that contribute to the stabilization of the complex. Following with the concave–convex complementary concept, the concave cavity formed by the three dithiole rings of the truxTTF electron-donor is also able to bind C
60 as shown in structure
CS (
Figure 8), with short S···C intermolecular contacts (3.5–3.6 Å). In terms of stability, structure
CC was calculated to be the most stable with an interaction energy of −8.98 kcal/mol, whereas structure
CS presented an interaction energy of −2.28 kcal/mol.
In this example, DFT calculations were key to visualize the supramolecular structure of the truxTTF•C
60 complex, and confirm the experimental evidence about the preferable supramolecular orientation between the electron-donor truxTTF host and the electron-acceptor C
60 guest. Additionally, this truxTTF•C
60 supramolecular complex has been of great relevance for the design and understanding of other related supramolecular systems that will be described in
Section 3.2.
3.1.3. Metalloporphyrin-C60 Associates
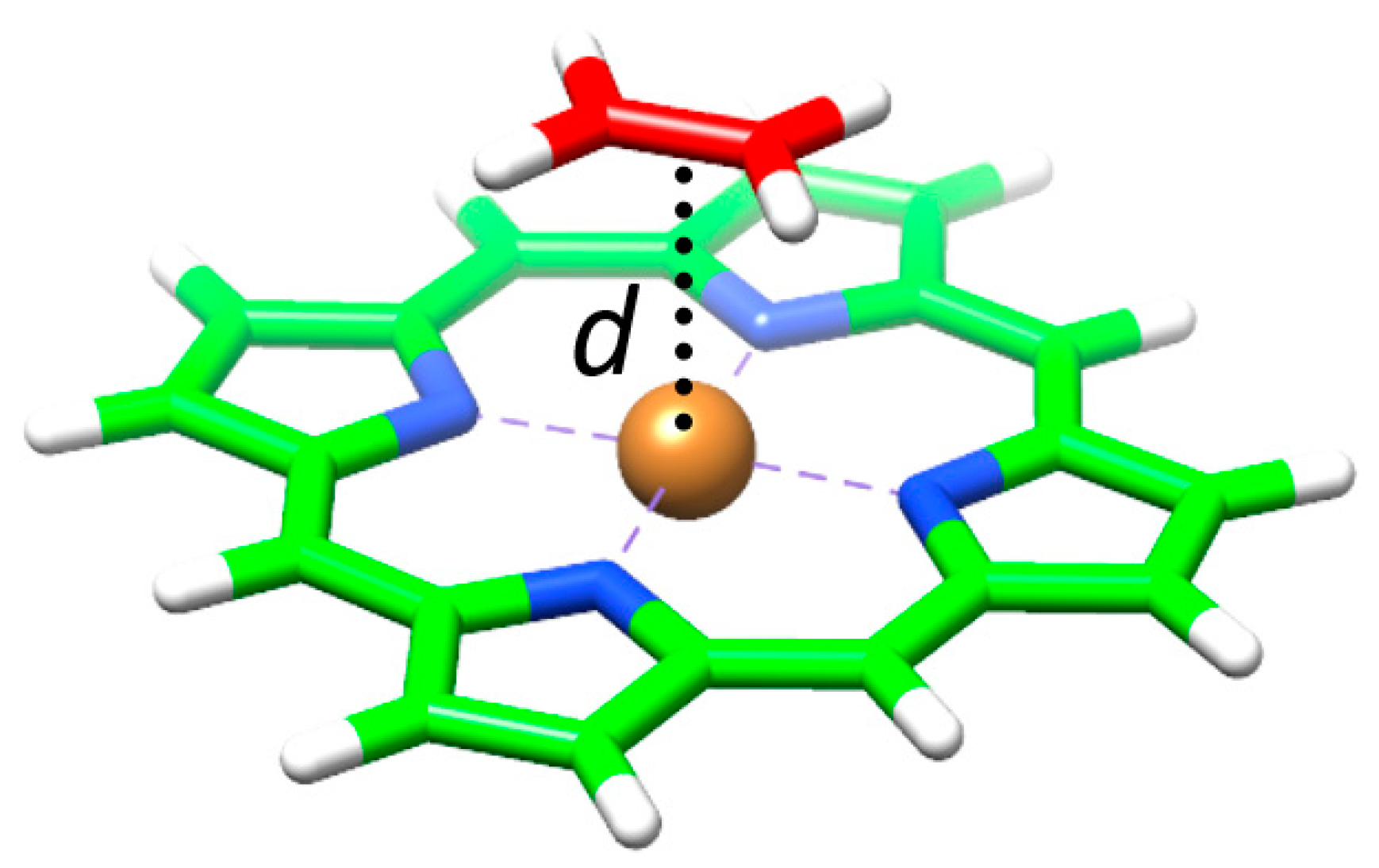
As mentioned above, not only curved electron-donor π-conjugated compounds can act as efficient receptors for fullerene balls. Porphyrins have shown to present an outstanding ability to effectively interact with C
60 by π–π interactions despite the planar‒convex mismatch [
80]. Recently, we thoroughly investigated a series of novel cup-and-ball metalloporphyrin–fullerene conjugates in close collaboration with the experimental groups of Martín and Nierengarten [
90]. Our main goal was to shed light onto the nature and strength of the noncovalent interactions governing the supramolecular assembly of fullerene derivatives with metal-substituted porphyrins.
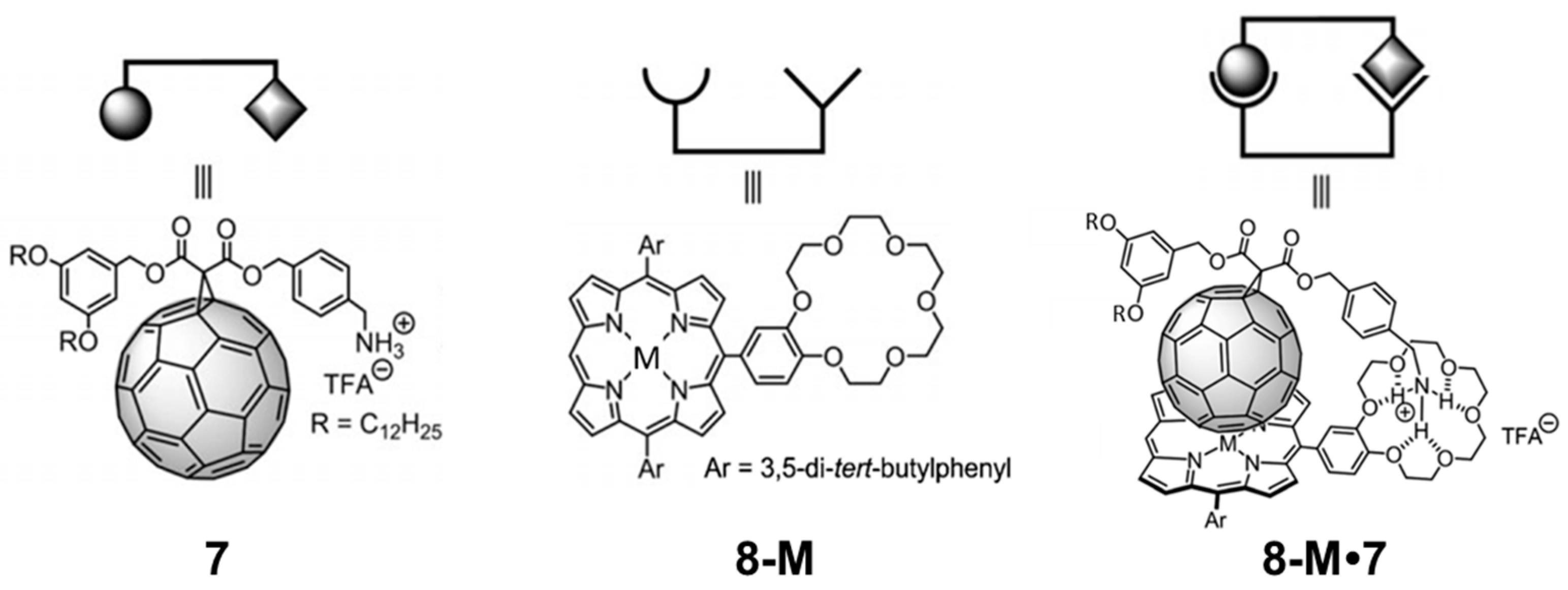
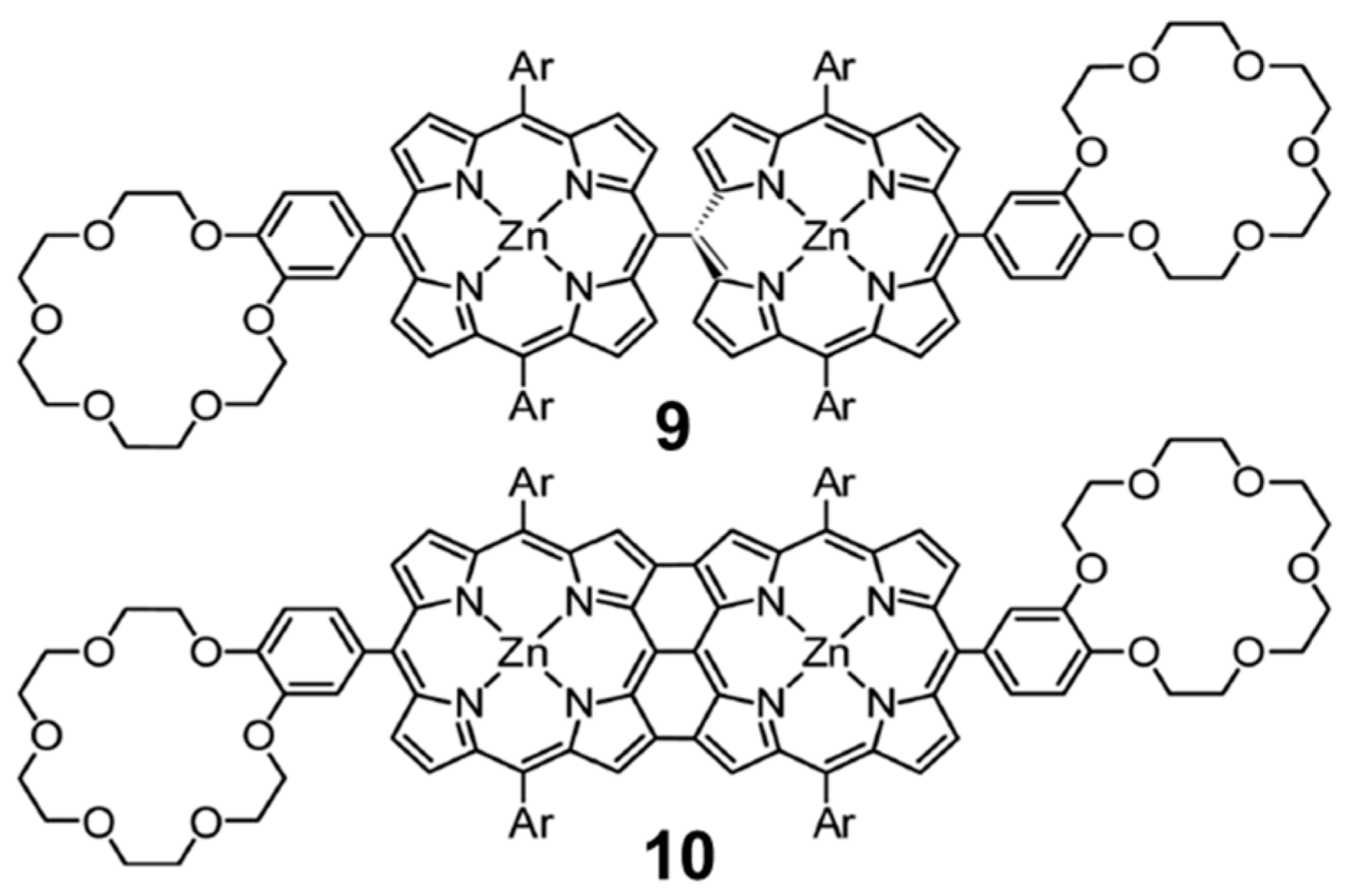
Figure 9 displays the chemical structures of the corresponding porphyrin–crown ether conjugates (
8-M;
M = 2H, Co., Ni, Cu or Zn) and the methano[60] fullerene derivative
7 [
91], as well as the target complexes
8-M•
7. Experimentally, the supramolecular complexation was first evidenced through
1H-NMR spectroscopy, and the measurement of the binding constant of
8-M•
7 was performed by monitoring the changes in the UV–Vis absorption spectra. The logarithmic binding constants (log
Ka) for porphyrins
8-M with the methanofullerene derivative
7 at 25 °C in dichloromethane were 5.5, 6.3, 5.9, 6.3 and 6.9 for
8-2H•
7,
8-Co•
7,
8-Ni•
7,
8-Cu•
7 and
8-Zn•
7, respectively.
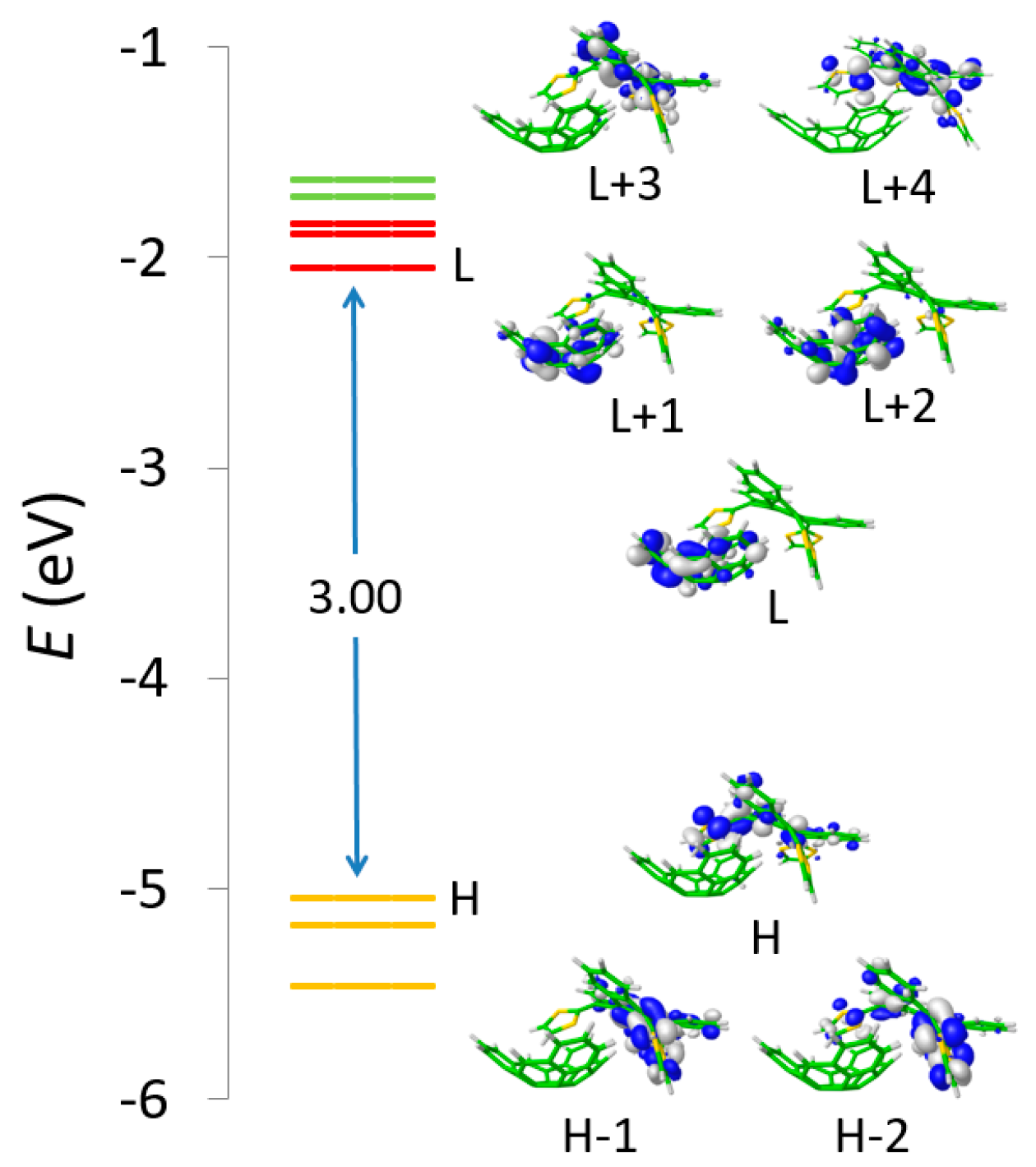
To better understand the nature of the different interactions governing the assemblies and gain insight into the experimental ordering found for the association constants (
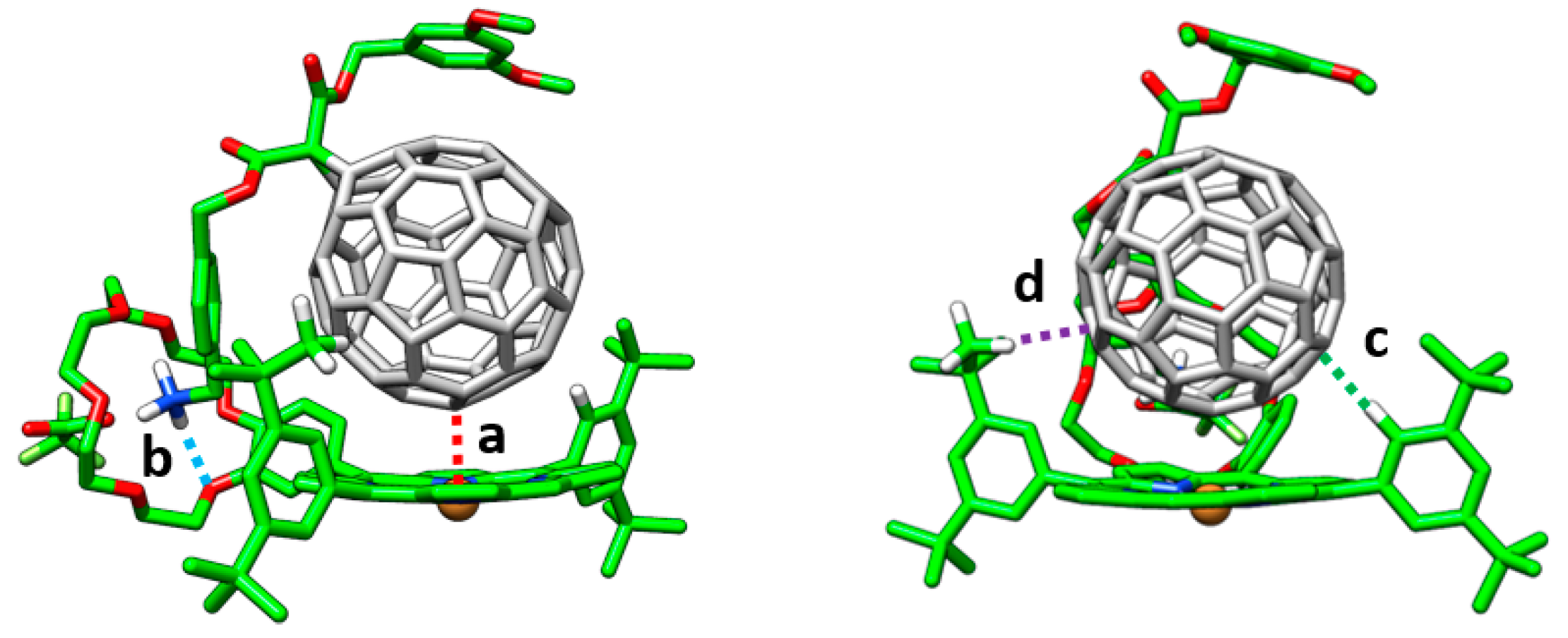
Ka), a comprehensive theoretical investigation of these supramolecular complexes was conducted in a multi-level approach. Geometry optimizations were initially performed at the semiempirical PM7 level and showed that, after full geometry relaxation, the ammonium group of the methanofullerene interacts with the crown ether of the porphyrin by H-bond formation (
Figure 10). Otherwise, the fullerene ball recognizes the center of the porphyrin system interacting by NCIs. Subsequent DFT reoptimizations at the B97-D/6-31G* level of theory led to the supramolecular parameters summarized in
Table 3.
The main interactions determining the supramolecular assembly are represented by the M–C
60 (a) and NH···O (b) distances provided in
Table 3 (
Figure 10 for labelling). In addition, CH···π dispersion interactions (c and d) between the
tert-butyl substituted benzene rings of the porphyrin and the π-cloud of the C
60 buckyball also contribute to the supramolecular stabilization.
The binding energy for the
8-M•
7 complexes was estimated at the PBE0-D3/cc-pVTZ level of theory by using the B97-D/6-31G*-optimized geometries (
Table 3). Ebind increases from −88.7 in
8-Ni•
7 to −92.8 kcal/mol in
8-Zn•
7 due to the more stabilizing M–C
60 interaction that takes place in moving to electron-richer metal atoms. The stabilization for the non-metalated
8-2H•
7 complex amounts to −92.4 kcal/mol, and the largest binding energy was computed for
8-Co•
7 (−93.8 kcal/mol). Theoretical calculations showed that NCIs between the fullerene ball and the phenyl-substituted porphyrin amounts to −22.5 kcal/mol, and the presence of the
tert-butyl groups at the meta position of the phenyl rings (interaction d) causes an additional stabilization of ~4 kcal/mol (−26.3 kcal/mol in total), in good accord with previous theoretical studies [
93]. The ammonium–crown ether NH···O contacts was found to be the main stabilizing driving force, with an interaction energy of −64.9 kcal/mol, which is three times the stabilization of the porphyrin–C
60 interaction.
Taking into account that C
60 interacts with the porphyrin moiety mainly through one electron-rich [6,6] double bond [
94], we computed a simplified model (
MP•C
2H
4), in which the pristine porphyrin (
MP) interacts with a molecule of ethylene (
Figure 11). This reduced model allowed performing more accurate calculations to better understand the relative stabilization of the different assemblies when substituting the metal in the porphyrin. A clear correlation between the calculated binding energy and the metal–ethylene distance (
d) was found: the shorter the distance along the series
NiP•C
2H
4 (3.18 Å) >
CuP•C
2H
4 (3.00 Å) >
ZnP•C
2H
4 (2.75 Å) >
CoP•C
2H
4 (2.62 Å), the larger the stabilization of the complex (
Table 4). The net charge calculated for the metal atom was demonstrated to increase in going from
CoP•C
2H
4 (+0.720e) to
ZnP•C
2H
4 (+1.223e) —
Table 4— and, in a first approach, this was related to the stabilizing electrostatic interaction between the porphyrin and the C
60 guest.
Symmetry-adapted perturbation theory (SAPT) calculations based on the Hartree–Fock wavefunction were performed for
2HP•C
2H
4,
NiP•C
2H
4 and
ZnP•C
2H
4 to decompose the total binding energy into electrostatic, exchange, induction and dispersion energy components (
Table 5). A stabilization in the electrostatic term of more than 10 kcal/mol was predicted in passing from
NiP•C
2H
4 to
ZnP•C
2H
4, whereas the exchange interaction was computed positive, and much larger for
ZnP•C
2H
4 than for
2HP•C
2H
4 and
NiP•C
2H
4. The induction term is meant to decay with the distance between the two interacting moieties as
R−n, where
n = 2–4, and thus it was computed to be non-negligible only in the case of the best interacting
ZnP•C
2H
4 (
Table 5). Finally, the dispersion energy was predicted to be the largest stabilizing contribution in
2HP•C
2H
4 and
NiP•C
2H
4, and it also largely stabilized
ZnP•C
2H
4 in more than 10 kcal/mol. Theoretical calculations therefore suggest that the energy term that mainly contributes to the stabilization of the
2HP•C
2H
4 assembly is the dispersion component, whereas the electrostatic contribution acquires a major role in the metal-based porphyrin complexes, especially in
ZnP•C
2H
4, for which M–ethylene distances are computed shorter and the metal bears a larger positive charge.
This supramolecular example clearly highlights the potential of the theoretical calculations to provide not only precise structural information of the self-assembly but also a detailed analysis of the main forces (electrostatic, exchange-repulsion, induction, dispersion, etc.) contributing to the stabilization of supramolecular complexes.
3.1.4. Ditopic Porphyrin•C60 complexes
Whereas the supramolecular chemistry involving porphyrin and fullerene has been extensively explored through the generation of associates involving porphyrin tweezers and cages [
95,
96] with metal–ligand bonds [
97,
98], hydrogen bonds [
99,
100,
101], electrostatic interactions [
102], mechanical bonds [
103,
104], or a combination of several of these interactions [
105,
106], supramolecular arrays involving conjugated multiporphyrin systems are, however, scarce in the literature. With the experienced gained in the work described above on the monotopic metalloporphyrin–fullerene conjugates, we undertook a collaborative study of the supramolecular complexation of the methano[60]fullerene compound
7 shown in
Figure 9 by the two analogous ditopic porphyrin receptors,
meso–meso 9 and tape
10, displayed in
Figure 12. A 1:2 stoichiometry was foreseen for both
9 and
10 when coupled to
7 based on the design of the host molecules, which was further corroborated by Electro-Spray Ionization (ESI) mass spectroscopy experiments.
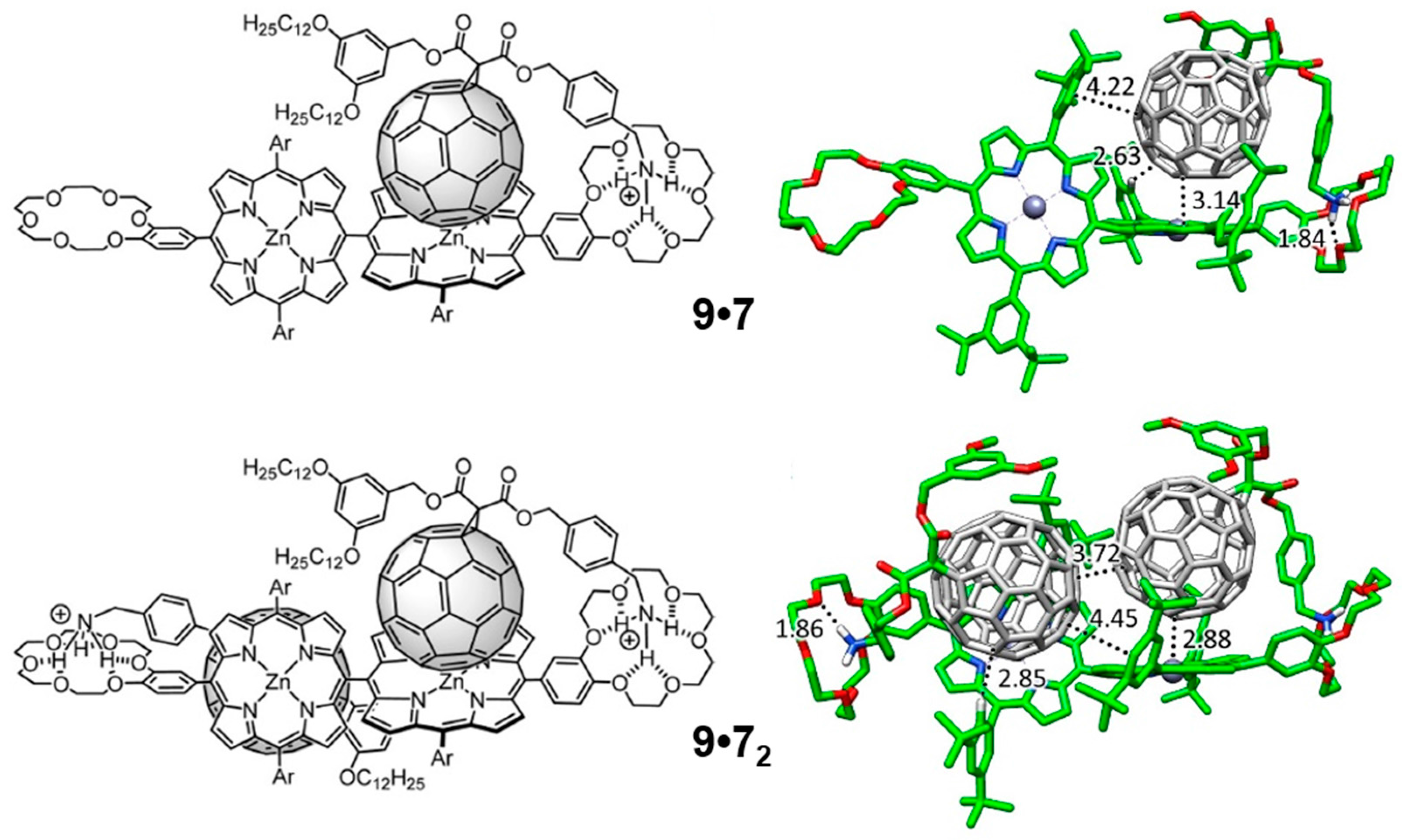
Theoretical calculations were performed to shed light into the nature and strength of the interactions controlling the different supramolecular association processes, with special attention to the negative cooperative effects experimentally evidenced for these systems (see the original Reference [
90] for further details). Minimum-energy geometries were calculated for supramolecular complexes
9•
7 and
9•
72 at the B97-D3/(6-31G**+LANL2DZ) level of theory (
Figure 13). Similarly to the monotopic porphyrin supramolecular arrangements discussed in the previous
Section 3.1.3, compound
7 in
9•
7 interacts with the crown ether through the positively-charged ammonium group, forming three NH···O(ether) hydrogen-bond interactions in the 1.83–2.00 Å range. Additional short H···C contacts between the peripheral
tert-butyl-substituted phenyl rings and C
60 were computed in the range of 2.5–3.2 Å, which add approximately 1 kcal/mol of stabilization per each interaction. Importantly, the vicinal porphyrin, linked to the porphyrin that interacts with
7, approaches the fullerene fragment and gives rise to additional interactions: short H···C contacts in the 2.7–3.2 Å range and a weak π–π interaction between the peripheral benzene ring and the fullerene.
Moving to the 1:2 stoichiometric complex
9•
72, the second molecule of
7 occupies the empty porphyrin surface, and defines similar interactions to those described for
9•
7. The minimum-energy geometry showed that the two fullerenes tend to approximate each other in order to stabilize the resulting complex, with close C···C contacts between the two buckyballs of 3.7 Å (
Figure 13). This was at the expense of distortions out from orthogonality between the two porphyrin units. The peripheral di-
tert-butylphenyl groups placed on the vicinal porphyrin moieties plays an active role in the stabilization of the complex with short H···C(C
60) contacts around 2.8 Å and π–π interactions at 4.4 Å.
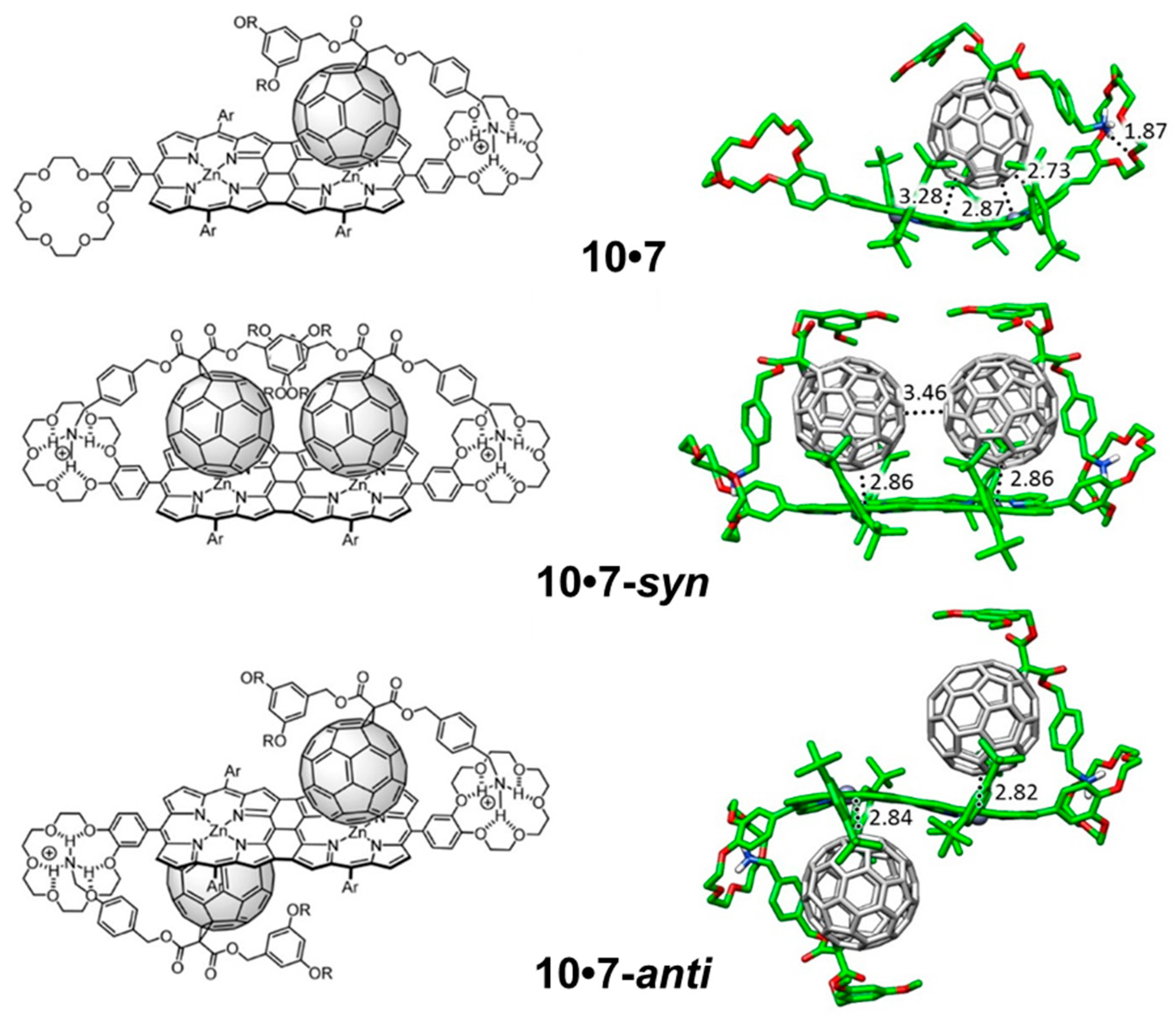
The supramolecular organization between porphyrin tape
10 and
7 (
Figure 14) follows the same pattern as previously described for
9•
7. Here, two different possibilities can be designed for the introduction of the second fullerene-based guest
7 into the
10•
7 complex: the two fullerene balls standing in the same side in a
syn disposition (
10•
72-syn), or the two balls located in opposite sides with respect to the plane generated by the porphyrin tape dimer in an
anti disposition (
10•
72-anti) (
Figure 14). In the former, an important π–π stabilization originates from the fullerene–fullerene proximity. Experiments demonstrated that the association of the first molecule of
7 in porphyrin hosts
9 and
10 led to a complex where the incorporation of a second equivalent of
7 was more difficult (negative cooperativity). The effective π–π interactions between the buckyballs found for
10•
72-syn confers an additional stabilization that would reduce the negative cooperativity with respect to
9•
72-anti, as experimentally evidenced for the tape assembly.
Single-point energy B97-D3 calculations were performed on the optimized geometries by using the more extended cc-pVTZ+LANL2DZ basis set to estimate
Ebind for all the supramolecular complexes (
Table 6). The association of one molecule of
7 by the
meso–meso porphyrin dimer
9 led to a large net stabilization of −108.19 kcal/mol, rising especially from the NH···O(ether) contacts and the porphyrin core–C
60 interaction. Upon insertion of the second molecule of
7,
Ebind is approximately doubled, reaching a value of −211.05 kcal/mol for
9•
72. In the case of
10, the insertion of the second molecule of
7 in a
syn disposition is energetically favored due to the π–π interactions between the buckyballs. The theoretical values calculated for
Ebind therefore indicate that the incorporation of the first guest molecule leads to a more stable complex for
9 than for
10, and suggest that the entrance of the second molecule of
7 is relatively more favored for
10 than for
9 (binding energy differences per unit of
7 between 1:2 and 1:1 complexes of +5.33 and −3.4 kcal/mol for
9 and
10, respectively;
Table 6). These trends were in good agreement with the higher association constant
K1 obtained for
meso–meso porphyrin
9 (log
K1 = 8.7) compared to tape porphyrin
10 (log
K1 = 6.8), and with the smaller decrease that the association constant experiences for
10 in passing from the 1:1 to the 1:2 stoichiometry (log
K2 = 5.4 for both
9•
72 and
10•
72).
To rationalize the experimental trends in the association constant for both the 1:1 and 1:2 supramolecular complexes, net electronic charges were computed at the B97-D3/(6-31G**+ LANL2DZ) level for 9•7 and 10•7 using the Natural Population Analysis (NPA) approach. Upon formation of complexes 9•7 and 10•7, the electron-donor porphyrin dimer transfers 0.19e and 0.26e to the fullerene-based acceptor, respectively. In 9•7, the porphyrin moiety interacting with the C60 ball accumulates a positive charge of +0.16e, whereas the vicinal empty porphyrin bears a residual positive charge of only +0.03e. Moving to 10•7, the C60-interacting porphyrin moiety bears a smaller positive charge of +0.11e compared to the empty porphyrin fragment (+0.15e). The efficient π-conjugation between the two porphyrin moieties in tape 10 allowed to explain the charge transfer from one fragment to the other. Theoretical calculations therefore predicted a notable decrease in the electron density for both meso–meso and tape porphyrin dimers in the ground state upon complexation of the first acceptor molecule of 7. The decrease of electronic density disfavors the entrance of the second guest molecule, and contributes to the remarkable change of the association constant (log Ka), from 8.7 to 5.4 in 9•12 and from 6.8 to 5.4 in 10•72, when the second molecule of 7 is introduced to form the stoichiometric 1:2 complex. For complex 10•72, the stabilizing interaction between the C60 units found for the more stable syn disposition partially compensates the negative effect caused by the reduced electronic density, inducing a reduction of the negative cooperativity as evidenced by experiments.