1. Introduction
We are living in an era where every day sees better innovation than the previous, with the same trend in the enhancement and innovation in the production of different types of medicines, chemical compounds, and drugs for the improved health of humans and other living species on the planet. It requires a great amount of time and money to test these drugs and chemical compounds to determine their pharmacological, chemical, and biological characteristics using expensive equipment, which in turn makes the task more cumbersome. This task of evaluating the biological behavior and existence of side effects of chemical compounds becomes more difficult in countries with economic imbalance. In this regard, computing different types of topological indices has provided the indicators of such medicinal behaviour of several compounds and drugs. The computation method of topological indices has proven its worth by yielding medical information of drugs with less use of chemical-related equipment.
Molecules and molecular compounds are often modeled by molecular graphs. A molecular graph is a representation of the structural formula of a chemical compound in terms of graph theory, whose vertices correspond to the atoms of the compound and edges correspond to chemical bonds. A graph with vertex set V and edge set E is connected if there exists a connection between any pair of vertices in G. For a graph G, the degree of a vertex v is the number of edges incident with v and denoted by .
A graph can be recognized by a numeric number, a polynomial, a drawing, a sequence of numbers, or a matrix. A topological index is a numerical quantity associated with a graph that characterizes the topology of the graph and is invariant under graph automorphism. Among various topological indices, degree-based topological indices are the most important and widely used. These have great application in chemical graph theory. Since the 1970s, two degree-based graph invariants have been extensively studied. These are the first Zagreb index
and the second Zagreb index
, defined as
Details on the two Zagreb topological indices can be found in [
1]. The Zagreb index
was first encountered in a paper published in 1972 [
1], where a series of approximate formulas for total
-electron energy
E were deduced. By means of these formulas, several structural details have been identified, upon which
E depends. Among these was the sum of squares of the vertex degrees of the underlying molecular graph are discussed. In the approximate formulas for
E, there was also a term equal to the sum of cubes of the vertex degrees [
1]. However, the latter term was completely ignored by scholars doing research on degree-based topological indices with various transformations [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13]. Recently, Furtula and Gutman [
14] have restudied this term to establish some basic properties, and have also demonstrated that the predictive ability of this term is similar to that of the first Zagreb index with respect to entropy and acetic factors of the molecules are discussed. Both first Zagreb index and this index yield are used to observe the correlation coefficients with larger value than
. They named this term the “forgotten topological index” or “
F-index”, and it is defined as
For more detail on the “
F-index”, we refer to the articles [
15,
16,
17].
Analogous to other topological polynomials, the
F-polynomial of graph
G is also defined as:
Dendrimers are constructed by hyperbranched macromolecules with a fully-tailored architecture. They can be arranged in a composed manner by either convergent or divergent form. Dendrimers have a huge range of applications in all branches of chemistry, especially in host–guest reactions and self-assembly procedures. Dendrimers are used in the formation of nanotubes, nanolatex, chemical sensors, micro/macro capsules, coloured glass, modified electrodes, and photon funnels such as artificial antennas [
18]. Because dendrimers are widely used in different applied fields, the study of nanostar dendrimers has received a great deal of attention in both chemical and mathematical literature. For other different applications regarding dendrimers, we refer to [
18]. Until now, the study of the
F-index for special chemical and nano-structures has been largely limited. Thus, we have been attracted to studying the mathematical properties of the
F-index and its polynomial version of some dendrimers. In this paper, we determine
F-index and polynomial of poly(propyl) ether imine, porphyrin, and zinc–porphyrin dendrimers.
In order to find the number of edges of the arbitrary graph, the following lemma is used.
Lemma 1. Let G be a graph. Then .
2. -Index and Polynomial of Poly(Propyl) Ether Imine Dendrimer
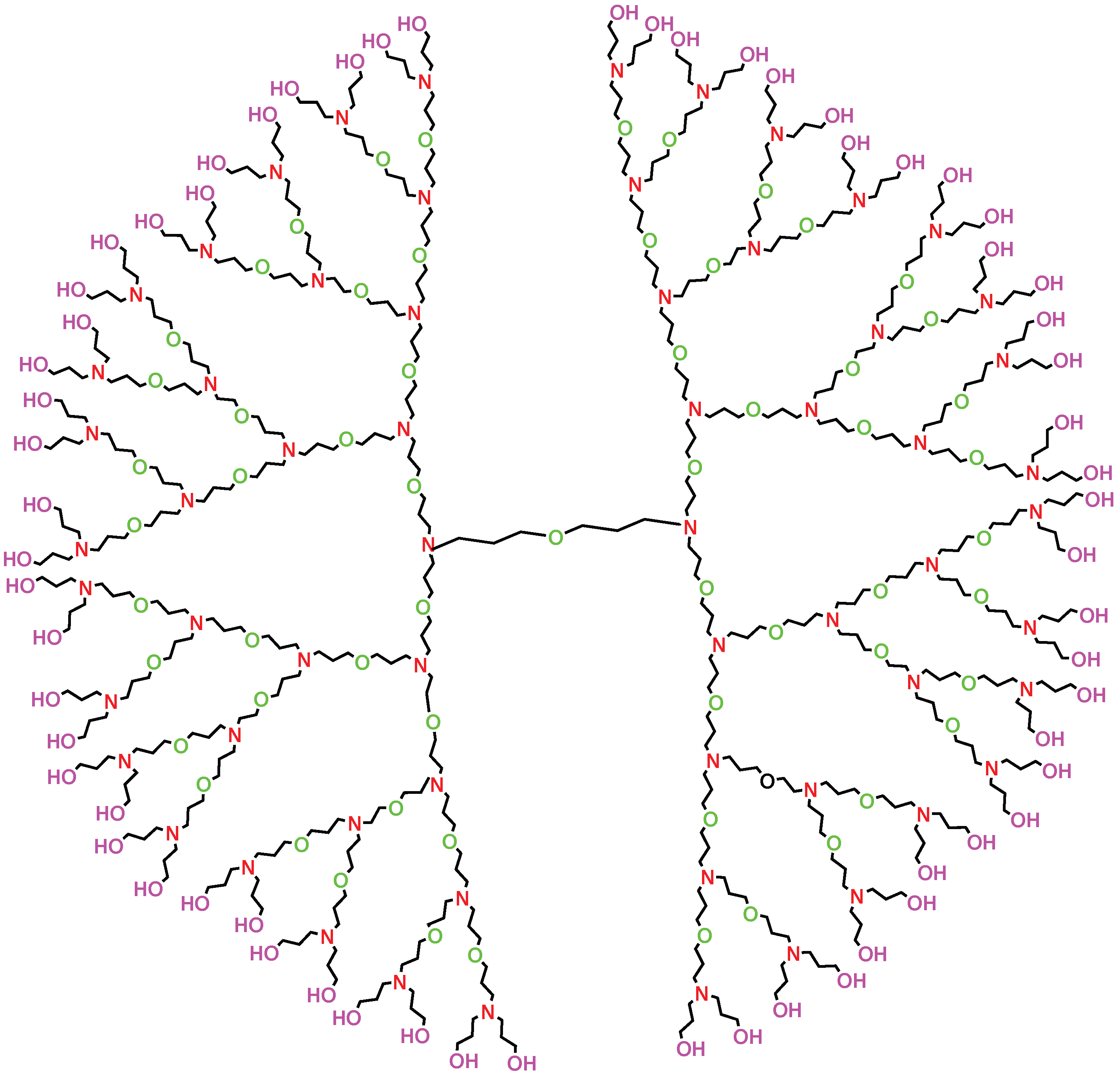
Polynomial of Poly(Propyl) Ether Imine (PETIM) dendrimer starts growing three-dimensionally from the oxygen as the core and branches out at each tertiary nitrogen, which is separated by eight-bond spacer for each generation of the dendrimer. Consider the molecular graph
G of PETIM dendrimer of generation
with
n growth stages, where
(see
Figure 1). The graph of PETIM dendrimer consists of four branches and a central core consisting of eight edges. In each branch, we have
edges. A simple calculation shows that the total number of edges in
G are
. Since
G is a tree, it follows directly that the number of vertices of
G are
.
In G, the total number of vertices of degree 1 are the leaves, which are in number. The vertices of degree 3 are . The remaining vertices are of degree 2. Let denote the number of edges of G connecting vertices of degrees i and j. Clearly, . Let us denote the number of edges connecting vertices of degrees i and j in each branch of the dendrimer by . It is easy to see that the central core consists of six edges with and two edges with and . Then, we have , and . For , we can calculate , , . Therefore, we have , , and . Now, we compute forgotten index and polynomial for the poly(propyl) ether imine (PETIM) dendrimer in the following theorem.
Theorem 1. Let G be the molecular graph of PETIM dendrimer. Then Proof. Let
G be a graph of
dendrimer. The vertex set
is divided into three sets based on the degree of the vertices. The first vertex set
consists of
vertices of degree 1. The second vertex set
consists of
vertices of degree 2. The third vertex set
consists of
vertices of degree 3. From (
1), the
index of
G is given by
Similarly, the edge partitions of
G, based on the degree of end vertices, are defined as
,
and
. Therefore, we have
,
and
. From (
2), the
F-polynomial of
G is calculated as
☐
3. -Index and Polynomial of Porphyrin Dendrimers
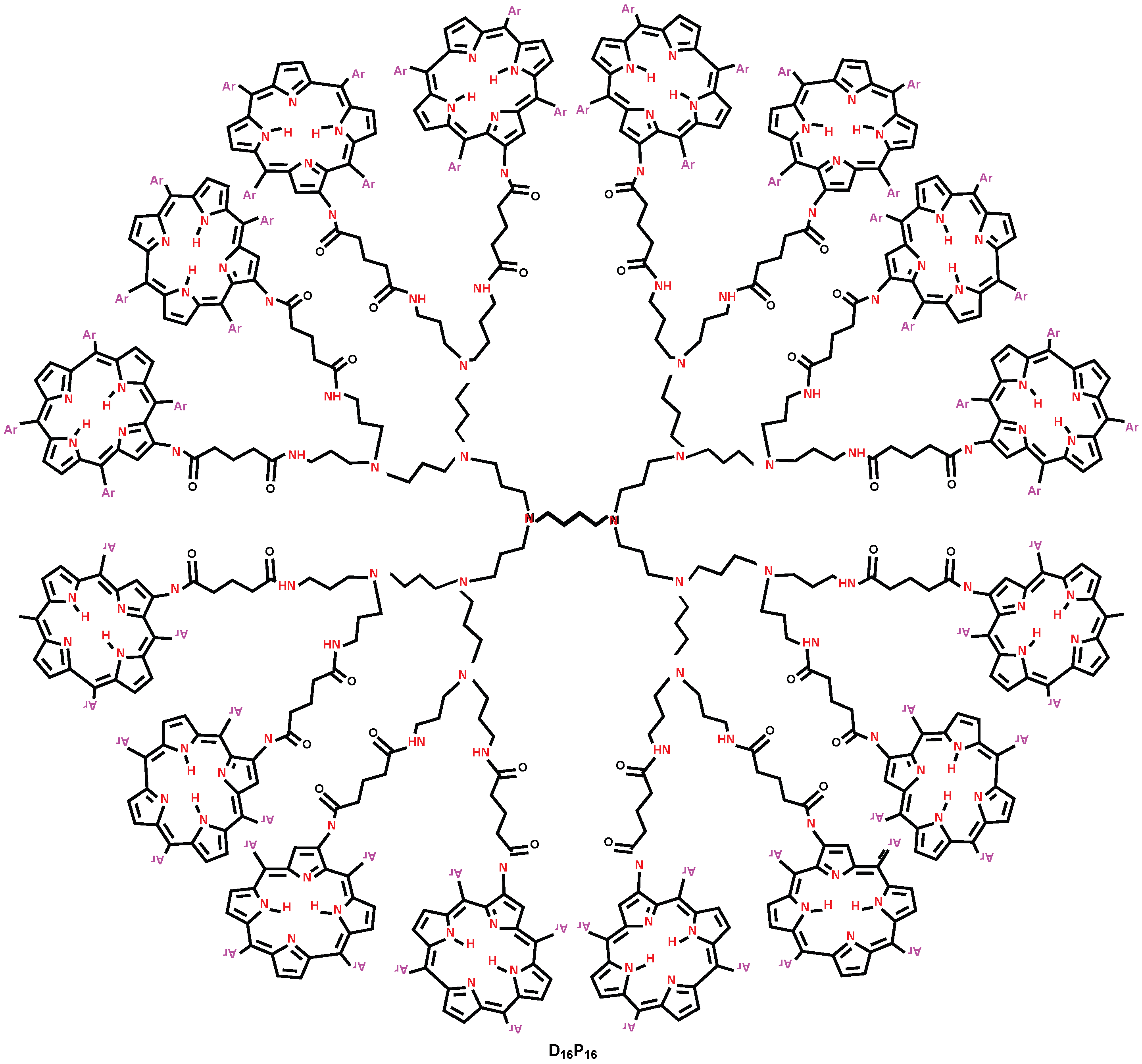
We consider the class of porphyrin dendrimers, denoted by
. Note that
, where
is steps of growth (see
Figure 2). The molecular graph of
has four similar branches and a central core consisting of five extra edges (
Figure 2 and
Figure 3). In each branch of
, we have
vertices, among which
vertices are of degree 1,
vertices are of degree 2,
vertices are of degree 4, and the remaining
vertices are of degree 3. Additionally, the central core contains four vertices of degree 2 and two vertices of degree 3. Therefore, in
, there are a total of
vertices, among which
vertices are of degree 1,
vertices are of degree 2,
vertices are of degree 3, and the remaining
vertices are of degree 4. It is easy to see from Lemma (1) that the total number of edges of
are
.
Since the molecular graph of
has four similar branches and five extra edges (
Figure 2 and
Figure 3), in which we have
,
,
,
,
, and
. By a routine calculation, we have
,
,
,
,
, and
. It is easy to compute
,
,
,
,
, and
.
Now, we compute the F-index and polynomial of this type of dendrimer through the following theorem.
Theorem 2. Let be a Porphyrin dendrimer. Then Proof. Here we can use (
1) and (
2) and compute the
F-inex and polynomial of porphyrin dendrimers in similar fashion as in Theorem 1. ☐
4. -Index and Polynomial of Zinc–Porphyrin Dendrimer
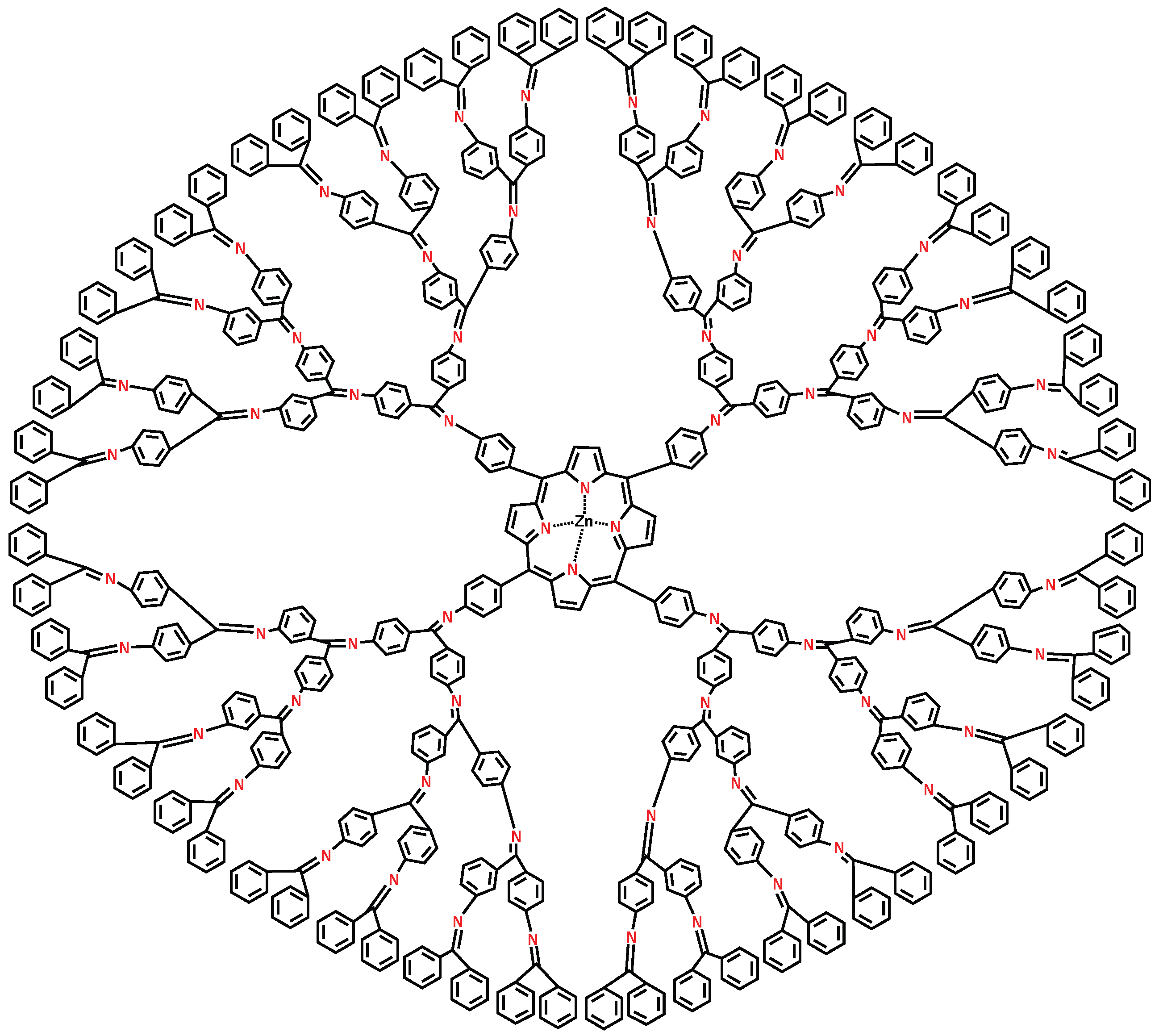
We consider the class of
dendrimer zinc–porphyrin (see
Figure 4), where
n is the steps of growth and
. The molecular graph of
consists of four similar branches and a central core. It is easy to see that the central core of
consists of 49 vertices among which 24 vertices are of degree two and three, respectively, and one vertex of degree four. In each branch of
, we have
vertices, among which
vertices are of degree two and the remaining
vertices are of degree three. Therefore, in
, there are a total of
vertices, among which
vertices are of degree 2,
vertices are of degree 3, and the remaining 1 vertex is of degree 4. It is easy to see from Lemma (1) that the total number of edges of
are
. Additionally, we can calculate
,
,
, and
. Now, we compute the
F-index and polynomial of zinc–porphyrin dendrimer as shown in
Figure 4.
Theorem 3. Let be a zinc–porphyrin dendrimer. Then Proof. The proof is analogous to Theorems 1 and 2. ☐