The Role of Molecular Modeling in TiO2 Photocatalysis
Abstract
:1. Introduction
2. Molecular Modeling Methods
2.1. Molecular Mechanics Methods
2.2. Electronic Structure Methods
2.3. Post-Ab Initio Methods
2.4. Molecular Dynamics Method
2.5. Solvent Effect
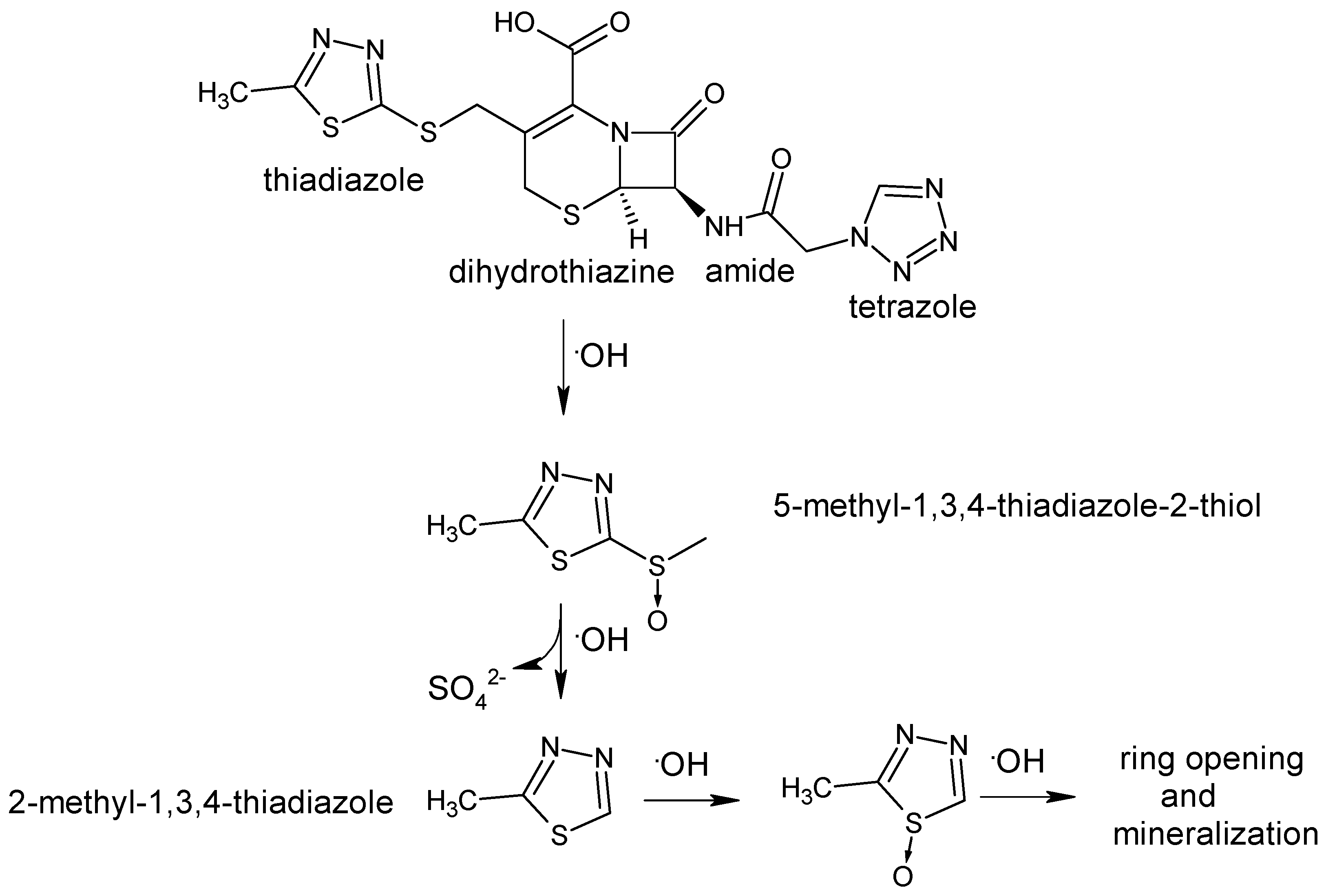
3. Degradation Reaction Model
3.1. Active Species
3.2. Reaction Center
4. Prediction of Degradability
4.1. Electronic Molecular Properties
4.2. DFT Reactivity Descriptors
5. Reaction Mechanisms
5.1. Short-Cut Method
5.2. Transition State Calculations
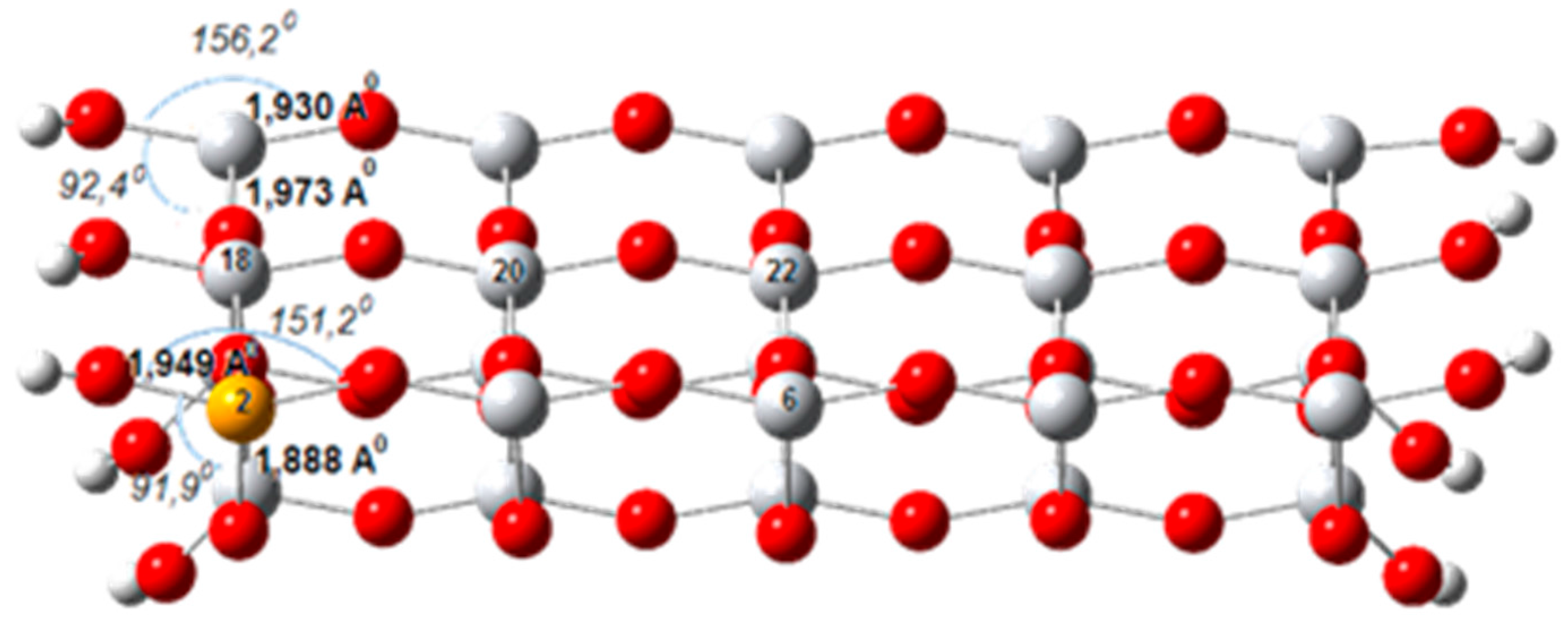
6. TiO2 Surfaces
6.1. Doped TiO2 Surfaces
6.2. Surface Modifiers
7. Summary and Outlook
Conflicts of Interest
References
- Helz, G.R.; Zepp, R.G.; Crosby, D.G. Aquatic and Surface Photochemistry; Lewis Publishers: Baco Raton, FL, USA, 1994; p. 261. [Google Scholar]
- Pelaez, M.; Nolan, N.T.; Pillai, S.C.; Seery, M.K.; Falaras, P.; Kontos, A.G.; Dunlop, P.S.M.; Hamilton, J.W.J.; Byrne, J.A.; O’Shea, K.; et al. A review on the Visible Light Active Titanium Dioxide Photocatalysts for Environmental Applications. Appl. Catal. B 2012, 125, 331–349. [Google Scholar] [CrossRef]
- Pichat, P. (Ed.) Photocatalysis and Water Purification; Wiley-VCH: Weinheim, Germany, 2013. [Google Scholar]
- Schneider, J.; Bahnemann, D.; Ye, J.; Puma, L.G.; Dionysios, D.D. (Eds.) Photocatalysis: Fundamentals and Perspectives; Royal Society of Chemistry: London, UK, 2016. [Google Scholar]
- Bahnemann, D.; Bockelmann, D.; Goslich, R. Mechanistic Studies of Water Detoxification in Illuminated TiO2 Suspensions. Sol. Energy Mater. 1991, 24, 564–583. [Google Scholar] [CrossRef]
- Ollis, D.F.; Pelizzetti, E.; Serpone, N. Photocatalyzed Destruction of Water Contaminants. Environ. Sci. Technol. 1991, 25, 1522–1529. [Google Scholar] [CrossRef]
- Nosaka, Y.; Nosaka, A. Introduction to Photocatalysis: From Basic Science to Applications; Royal Society of Chemistry: London, UK, 2016. [Google Scholar]
- Suib, S.L. (Ed.) New and Future Developments in Catalysis: Solar Photocatalysis; Elsevier: Amsterdam, The Netherlands, 2013; Volume 7. [Google Scholar]
- Pichat, P. Handbook of Heterogeneous Photo-Catalysis; Ertl, G., Knozinger, H., Weitkamp, J., Eds.; Wiley-VCH: Weinheim, Germany, 1997; Volume 4, p. 2111.
- Choi, W.; Termin, A.; Hoffmann, M.R. The Role of Metal Ion Dopants in Quantum-Sized TiO2: Correlation Between Photoreactivity and Charge Carrier Recombination Dynamics. J. Phys. Chem. 1994, 98, 13669–13679. [Google Scholar] [CrossRef]
- Di Paola, A.; Marcì, G.; Palmisano, L.; Schiavello, M.; Uosaki, K.; Ikeda, S.; Ohtani, B. Preparation of Polycrystalline TiO2 Photocatalysts Impregnated with Various Transition Metal Ions: Characterization and Photocatalytic Activity for the Degradation of 4-nitrophenol. Phys. Chem. B 2002, 106, 637–645. [Google Scholar] [CrossRef]
- Karakitsou, K.E.; Verykios, X.E. Effects of Altervalent Cation Doping of Titania on its Performance as a Photocatalyst for Water Cleavage. J. Phys. Chem. 1993, 97, 1184–1189. [Google Scholar] [CrossRef]
- Mu, W.; Herrmann, J.-M.; Pichat, P. Room Temperature Photocatalytic Oxidation of Liquid Cyclohexane into Cyclohexanone over Neat and Modified TiO2. Catal. Lett. 1989, 3, 73–84. [Google Scholar] [CrossRef]
- Nagaveni, K.; Hegde, M.S.; Madras, G. Structure and Photocatalytic Activity of Ti1−xMxO2±δ (M = W, V, Ce, Zr, Fe, and Cu) Synthesized by Solution Combustion Method. Phys. Chem. B 2004, 108, 20204–20212. [Google Scholar] [CrossRef]
- Yalcin, Y.; Kilic, M.; Cinar, Z. Fe+3-doped TiO2: A Combined Experimental and Computational Approach to the Evaluation of Visible Light Activity. Appl. Catal. B 2010, 99, 469–477. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, F.; Zhang, J.; Chen, H.; Anpo, M. Fe3+-TiO2 Photocatalysts Pprepared by Combining Sol–Gel Method with Hydrothermal Treatment and their Characterization. J. Photochem. Photobiol. A 2006, 180, 196–204. [Google Scholar] [CrossRef]
- Asahi, R.; Morikawa, T.; Ohwaki, T.; Aoki, K.; Taga, Y. Visible-Light Photocatalysis in Nitrogen-Doped Titanium Oxides. Science 2001, 293, 269–271. [Google Scholar] [CrossRef] [PubMed]
- Choi, H.; Antoniou, M.G.; Pelaez, M.; de la Cruz, A.A.; Shoemaker, J.A.; Dionysiou, D.D. Mesoporous Nitrogen-Doped TiO2 for the Photocatalytic Destruction of the Cyanobacterial Toxin Microcystin-lr under VisibleLight Irradiation. Environ. Sci. Technol. 2007, 41, 7530–7535. [Google Scholar] [CrossRef] [PubMed]
- Di Valentin, C.; Pacchioni, G.; Selloni, A.; Livraghi, S.; Giamello, E. Characterization of Paramagnetic Species in N-doped TiO2 Powders by EPR Sspectroscopy and DFT Calculations. J. Phys. Chem. B 2005, 109, 11414–11419. [Google Scholar] [CrossRef] [PubMed]
- Emeline, A.V.; Kuzmin, G.N.; Serpone, N. Wavelength-Dependent Potostimulated Adsorption of Molecular O2 and H2 on Second Generation Titania Photocatalysts: The Case of the Visible-Light-Active N-doped TiO2 System. Chem. Phys. Lett. 2008, 454, 279–283. [Google Scholar] [CrossRef]
- Jagadale, T.C.; Takale, S.P.; Sonawane, R.S.; Joshi, H.M.; Patil, S.I.; Kale, B.B.; Ogale, S.B. N-doped TiO2 Nanoparticle Based Visible Light Photocatalyst by Modified Peroxide Sol–Gel Method. J. Phys. Chem. C 2008, 112, 14595–14602. [Google Scholar] [CrossRef]
- Lu, N.; Zhao, H.; Li, J.; Quan, X.; Chen, S. Characterization of Boron-Doped TiO2 Nanotube Arrays Prepared by Electrochemical Method and its Visible Light Activity. Sep. Purif. Technol. 2008, 62, 668–673. [Google Scholar] [CrossRef]
- Ohno, T.; Akiyoshi, M.; Umebayashi, T.; Asai, K.; Mitsui, T.; Matsumura, M. Preparation of S-Doped TiO2 Photocatalysts and their Photocatalytic Activities under Visible Light. Appl. Catal. A 2004, 265, 115–121. [Google Scholar] [CrossRef]
- Sakthivel, S.; Janczarek, M.; Kisch, H. Visible Light Activity and Photoelectrochemical Properties of Nitrogen-Doped TiO2. J. Phys. Chem. B 2004, 108, 19384–19387. [Google Scholar] [CrossRef]
- Sakthivel, S.; Kisch, H. Daylight Photocatalysis by Carbon-Modified Titanium Dioxide. Angew. Chem. Int. Ed. 2003, 42, 4908–4911. [Google Scholar] [CrossRef] [PubMed]
- Sathish, M.; Viswanathan, B.; Viswanath, R.P.; Gopinath, C.S. Synthesis, Characterization, Electronic Structure, and Photocatalytic Activity of Nitrogen-Doped TiO2 Nanocatalyst. Chem. Mater. 2005, 17, 6349–6353. [Google Scholar] [CrossRef]
- Sato, S.; Nakamura, R.; Abe, S. Visible-Light Sensitization of TiO2 Photocatalysts by Wet-Method N Doping. Appl. Catal. A 2005, 284, 131–137. [Google Scholar] [CrossRef]
- Yalcin, Y.; Kilic, M.; Cinar, Z. The Role of Non-Metal Doping in TiO2 Photocatalysis. J. Adv. Oxid. Technol. 2010, 13, 281–296. [Google Scholar]
- Zheng, R.; Lin, L.; Xie, J.; Zhu, Y.; Xie, Y. State of Doped Phosphorus and its Influence on the Physicochemical and Photocatalytic Properties of P-Doped Titania. J. Phys. Chem. C 2008, 112, 15502–15509. [Google Scholar] [CrossRef]
- Jaiswal, R.; Patel, N.; Kothari, D.C.; Miotello, A. Improved Visible Light Photocatalytic Activity of TiO2 Co-Doped with Vanadium and Nitrogen. Appl. Catal. B 2012, 126, 47–54. [Google Scholar] [CrossRef]
- Katsanaki, A.V.; Kontos, A.G.; Maggos, T.; Pelaez, M.; Likodimos, V.; Pavlatou, E.A.; Dionysiou, D.D.; Falaras, P. Photocatalytic Oxidation of Nitrogen Oxides on N-F-Doped Titania Thin Films. Appl. Catal. B 2013, 140–141, 619–625. [Google Scholar] [CrossRef]
- Li, D.; Ohashi, N.; Hishita, S.; Kolodiazhnyi, T.; Haneda, H. Origin of Visible-Light-Driven Photocatalysis: A Comparative Study on N/F-Doped and N-F-Codoped TiO2 Powders by means of Experimental Characterizations and Theoretical Calculations. J. Solid State Chem. 2005, 178, 3293–3302. [Google Scholar] [CrossRef]
- Ling, Q.; Sun, J.; Zhou, Q. Preparation and Characterization of Visible-Light-Driven Titania Photocatalyst Co-Doped with Boron and Nitrogen. Appl. Surf. Sci. 2008, 254, 3236–3241. [Google Scholar] [CrossRef]
- Márquez, A.M.; Plata, J.J.; Ortega, Y.; Sanz, J.F.; Colón, G.; Kubacka, A.; Fernández-García, M. Making Photo-Selective TiO2 Materials by Cation–Anion Codoping: From Structure and Electronic Properties to Photoactivity. J. Phys. Chem. C 2012, 116, 18759–18767. [Google Scholar] [CrossRef]
- Sun, H.; Bai, Y.; Cheng, Y.; Jin, W.; Xu, N. Preparation and Characterization of Visible-Light-Driven Carbon–Sulfur-CoDoped TiO2 Photocatalysts. Ind. Eng. Chem. Res. 2006, 45, 4971–4976. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, G.; Liu, S.; Ang, H.M.; Tadé, M.O.; Wang, S. Visible Light Responsive Titania Photocatalysts Codoped by Nitrogen and Metal (Fe, Ni, Ag, or Pt) for Remediation of Aqueous Pollutants. Chem. Eng. J. 2013, 231, 18–25. [Google Scholar] [CrossRef]
- Wang, X.; Lim, T.-T. Solvothermal Synthesis of C–N Codoped TiO2 and Photocatalytic Evaluation for Bisphenol a Degradation using a Visible-Light Irradiated LED Photoreactor. Appl. Catal. B 2010, 100, 355–364. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, M.; Cheng, B.; Zhao, X. Preparation, Characterization and Photocatalytic Activity of in situ N,S-Codoped TiO2 Powders. J. Mol. Catal. A Chem. 2006, 246, 176–184. [Google Scholar] [CrossRef]
- Foresman, J.B.; Frisch, A. Exploring Chemistry with Electronic Structure Methods; Gaussian Inc.: Pittsburg, PA, USA, 1995. [Google Scholar]
- Holtje, H.-D.; Sippl, W.; Rognan, D.; Folkers, G. Molecular Modeling; Wiley VCH: Weinheim, Germany, 2003. [Google Scholar]
- Jensen, F. Introduction to Computational Chemistry; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Barone, V.; Cossi, M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Andzelm, J.; Kölmel, C.; Klamt, A. Incorporation of Solvent Effects into Density Functional Calculations of Molecular Energies and Geometries. J. Chem. Phys. 1995, 103, 9312–9320. [Google Scholar] [CrossRef]
- Jenks, W.S. Photocatalytic Reactions Pathways: Effect of Molecular Structure, Catalyst and Wavelength. In Photocatalysis and Water Purification; Pichat, P., Ed.; Wiley-VCH: Weinheim, Germany, 2013; pp. 25–51. [Google Scholar]
- Turchi, C.S.; Ollis, D.F. Photocatalytic Degradation of Organic Water Contaminants: Mechanisms Involving Hydroxyl Radical Attack. J. Catal. 1990, 122, 178–192. [Google Scholar] [CrossRef]
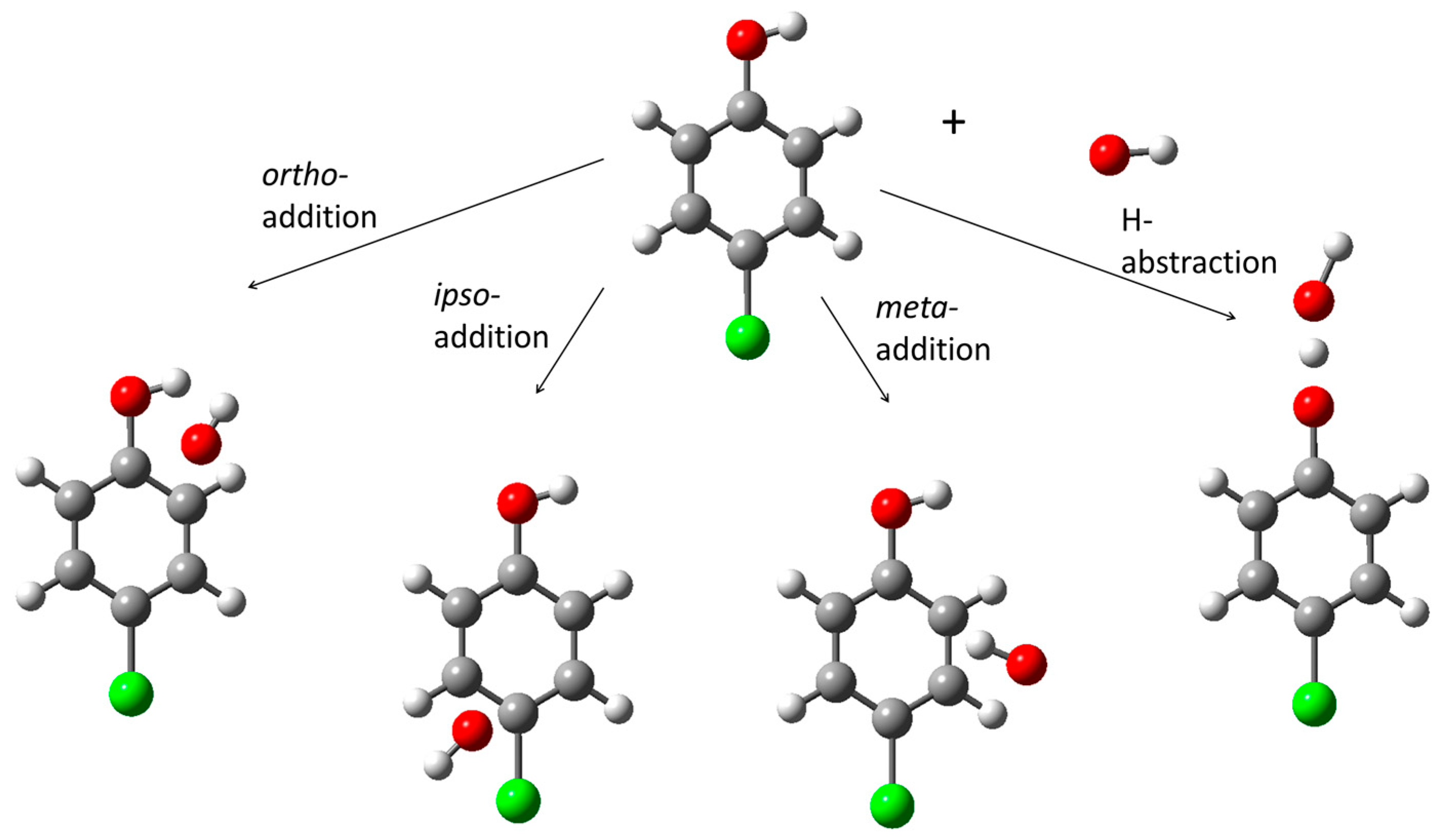
- Kilic, M.; Cinar, Z. Hydroxyl Radical Reactions with 4-chlorophenol as a Model for Heterogeneous Photocatalysis. J. Mol. Struct. THEOCHEM 2008, 851, 263–270. [Google Scholar] [CrossRef]
- Eberhardt, M.K.; Yoshida, M. Radiation-Induced Homolytic Aromatic Substitution. I. Hydroxylation of Nitrobenzene, Chlorobenzene, and Toluene. J. Phys. Chem. 1973, 77, 589–597. [Google Scholar] [CrossRef]
- San, N.; Hatipoglu, A.; Kocturk, G.; Cinar, Z. Photocatalytic Degradation of 4-nitrophenol in Aqueous TiO2 Suspensions: Theoretical Prediction of the Intermediates. J. Photochem. Photobiol. A 2002, 146, 189–197. [Google Scholar] [CrossRef]
- Amalric, L.; Guillard, C.; Blanc-Brude, E.; Pichat, P. Correlation Between the Photocatalytic Degradability over TiO2 in Water of meta and para Substituted Methoxybenzenes and their Electron Density, Hydrophobicity and Polarizability Properties. Water Res. 1996, 30, 1137–1142. [Google Scholar] [CrossRef]
- D’Oliveira, J.-C.; Minero, C.; Pelizzetti, E.; Pichat, P. Photodegradation of dichlorophenols and trichlorophenols in TiO2 Aqueous Suspensions: Kinetic Effects of the Positions of the Cl Atoms and Identification of the intermediates. J. Photochem. Photobiol. A 1993, 72, 261–267. [Google Scholar] [CrossRef]
- Parra, S.; Olivero, J.; Pacheco, L.; Pulgarin, C. Structural Properties and Photoreactivity Relationships of Substituted Phenols in TiO2 Suspensions. Appl. Catal. B 2003, 43, 293–301. [Google Scholar] [CrossRef]
- San, N.; Cinar, Z. Structure-Activity Relations for the Photodegradation Reactions of Monosubstituted anilines in TiO2 Suspensions. J. Adv. Oxid. Technol. 2002, 5, 85–92. [Google Scholar] [CrossRef]
- Vos, A.M.; Nulens, K.H.L.; de Proft, F.; Schoonheydt, R.A.; Geerlings, P. Reactivity Descriptors and Rate Constants for Electrophilic Aromatic Substitution: Acid Zeolite Catalyzed Methylation of Benzene and Toluene. J. Phys. Chem. B 2002, 106, 2026–2034. [Google Scholar] [CrossRef]
- Torrent-Sucarrat, M.; de Proft, F.; Geerlings, P. Stiffness and Raman Intensity: A Conceptual and Computational DFT Study. J. Phys. Chem. A 2005, 109, 6071–6076. [Google Scholar] [CrossRef] [PubMed]
- San, N.; Kilic, M.; Cinar, Z. Reactivity Indices for ortho/para Monosubstituted Phenols. J. Adv. Oxid. Technol. 2007, 10, 51–59. [Google Scholar] [CrossRef]
- Gurkan, Y.Y.; Turkten, N.; Hatipoglu, A.; Cinar, Z. Photocatalytic Degradation of Cefazolin over N-doped TiO2 under UV and Sunlight Irradiation: Prediction of the Reaction Paths via Conceptual DFT. Chem. Eng. J. 2012, 184, 113–124. [Google Scholar] [CrossRef]
- Kilic, M.; Kocturk, G.; San, N.; Cinar, Z. A Model for Prediction of Product Distributions for the Reactions of Phenol Derivatives with Hydroxyl Radicals. Chemosphere 2007, 69, 1396–1408. [Google Scholar] [CrossRef] [PubMed]
- San, N.; Kilic, M.; Tuiebakhova, Z.; Cinar, Z. Enhancement and Modeling of the Photocatalytic Degradation of Benzoic Acid. J. Adv. Oxid. Technol. 2007, 10, 43–50. [Google Scholar] [CrossRef]
- Hatipoglu, A.; San, N.; Cinar, Z. An Experimental and Theoretical Investigation of the Photocatalytic Degradation of meta-cresol in TiO2 Suspensions: A Model for the Product Distribution. J. Photochem. Photobiol. A 2004, 165, 119–129. [Google Scholar] [CrossRef]
- San, N.; Hatipoglu, A.; Kocturk, G.; Cinar, Z. Prediction of Primary Intermediates and the Photodegradation Kinetics of 3-aminophenol in Aqueous TiO2 Suspensions. J. Photochem. Photobiol. A 2001, 139, 225–232. [Google Scholar] [CrossRef]
- Vione, D.; de Laurentiis, E.; Berto, S.; Minero, C.; Hatipoglu, A.; Cinar, Z. Modeling the Photochemical Transformation of Nitrobenzene under Conditions Relevant to Sunlit Surface Waters: Reaction Pathways and Formation of Intermediates. Chemosphere 2016, 145, 277–283. [Google Scholar] [CrossRef] [PubMed]
- Hatipoglu, A.; Vione, D.; Yalcin, Y.; Minero, C.; Cinar, Z. Photo-Oxidative Degradation of Toluene in Aqueous Media by Hydroxyl Radicals. J. Photochem. Photobiol. A 2010, 215, 59–68. [Google Scholar] [CrossRef]
- Gurkan, Y.Y.; Kasapbasi, E.; Cinar, Z. Enhanced Solar Photocatalytic Activity of TiO2 by Selenium(iv) Ion-Doping: Characterization and DFT Modeling of the Surface. Chem. Eng. J. 2013, 214, 34–44. [Google Scholar] [CrossRef]
- Homann, T.; Bredow, T.; Jug, K. Adsorption of Small Molecules on the Anatase(1 0 0) Surface. Surf. Sci. 2004, 555, 135–144. [Google Scholar] [CrossRef]
- Sekiya, T.; Igarashi, M.; Kurita, S.; Takekawa, S.; Fujisawa, M. Structure Dependence of Reflection Spectra of TiO2 Single Crystals. J. Electron. Spectrosc. Relat. Phenom. 1998, 92, 247–250. [Google Scholar] [CrossRef]
- Onal, I.; Soyer, S.; Senkan, S. Adsorption of Water and Ammonia on TiO2-Anatase Cluster Models. Surf. Sci. 2006, 600, 2457–2469. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, A.M., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03; B01; Gaussian Inc.: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Di Valentin, C.; Finazzi, E.; Pacchioni, G.; Selloni, A.; Livraghi, S.; Paganini, M.C.; Giamello, E. N-doped TiO2:Theory and Experiment. Chem. Phys. 2007, 339, 44–56. [Google Scholar] [CrossRef]
- Bredow, T.; Pacchioni, G. A Quantum-Chemical Study of Pd Atoms and Dimers Supported on TiO2 (110) and their Interaction with CO. Surf. Sci. 1999, 426, 106–122. [Google Scholar] [CrossRef]
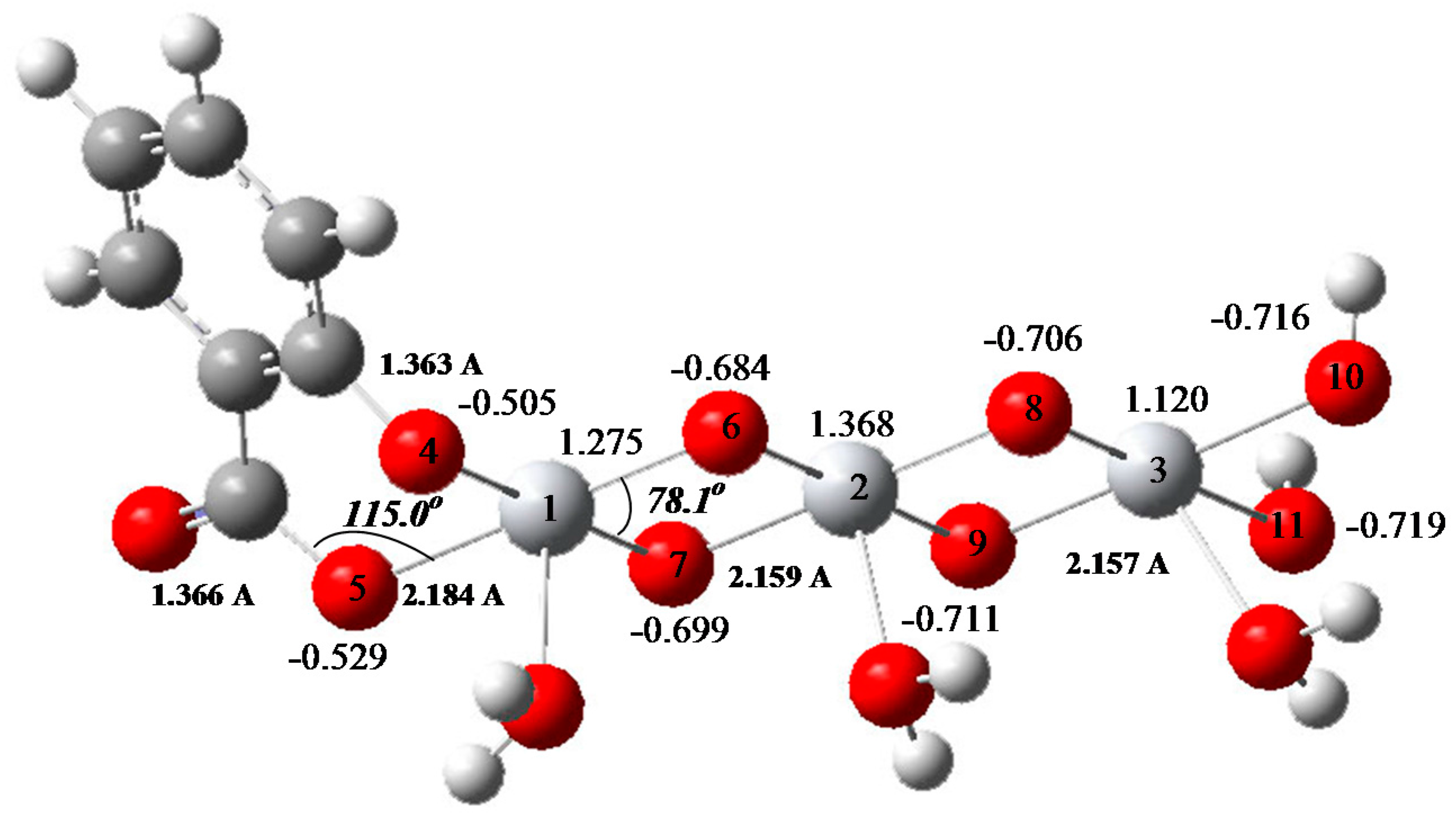
- Li, S.X.; Zheng, F.Y.; Cai, W.L.; Han, A.-Q.; Xie, Y.K. Surface Modification of Nanometer Size TiO2 with Salicylic Acid for Photocatalytic Degradation of 4-nitrophenol. J. Hazard. Mater. 2006, 135, 431–436. [Google Scholar] [PubMed]
- Mert, E.H.; Yalcin, Y.; Kilic, M.; San, N.; Cinar, Z. Surface Modification of TiO2 with Ascorbic Acid for Heterogeneous Photocatalysis: Theory and Experiment. J. Adv. Oxid. Technol. 2008, 11, 199–207. [Google Scholar]
- Rajh, T.; Nedeljkovic, J.M.; Chen, L.X.; Poluektov, O.; Thurnauer, M.C. Improving Optical and Charge Separation Properties of Nanocrystalline TiO2 by Surface Modification with Vitamin C. J. Phys. Chem. B 1999, 103, 3515–3519. [Google Scholar] [CrossRef]
- Kilic, M.; Cinar, Z. A Quantum Mechanical Approach to TiO2 Photocatalysis. J. Adv. Oxid. Technol. 2009, 12, 37–46. [Google Scholar]
- Xagas, A.P.; Bernard, M.C.; Hugot-Le Goff, A.; Spyrellis, N.; Loizos, Z.; Falaras, P. Surface Modification and Photosensitisation of TiO2 Nanocrystalline Films with Ascorbic Acid. J. Photochem. Photobiol. A 2000, 132, 115–120. [Google Scholar] [CrossRef]
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cinar, Z. The Role of Molecular Modeling in TiO2 Photocatalysis. Molecules 2017, 22, 556. https://doi.org/10.3390/molecules22040556
Cinar Z. The Role of Molecular Modeling in TiO2 Photocatalysis. Molecules. 2017; 22(4):556. https://doi.org/10.3390/molecules22040556
Chicago/Turabian StyleCinar, Zekiye. 2017. "The Role of Molecular Modeling in TiO2 Photocatalysis" Molecules 22, no. 4: 556. https://doi.org/10.3390/molecules22040556
APA StyleCinar, Z. (2017). The Role of Molecular Modeling in TiO2 Photocatalysis. Molecules, 22(4), 556. https://doi.org/10.3390/molecules22040556