Detection of Network Motif Based on a Novel Graph Canonization Algorithm from Transcriptional Regulation Networks
Abstract
:1. Introduction
2. Preliminary and Definitions
2.1. Subproblem of Grouping Subgraphs
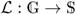 such that H is isomorphic to G if and only if , where
such that H is isomorphic to G if and only if , where  represents a set of graphs and
represents a set of graphs and  indicates a collection of strings. Obviously, the graph canonization problem (GCP) is at least as hard as the graph isomorphic problem.
indicates a collection of strings. Obviously, the graph canonization problem (GCP) is at least as hard as the graph isomorphic problem.2.2. Definitions
3. Methods
3.1. Canonical Labeling Function
3.2. Extended Algorithm on General Cases
3.3. Complexity Analysis
4. Results and Discussion
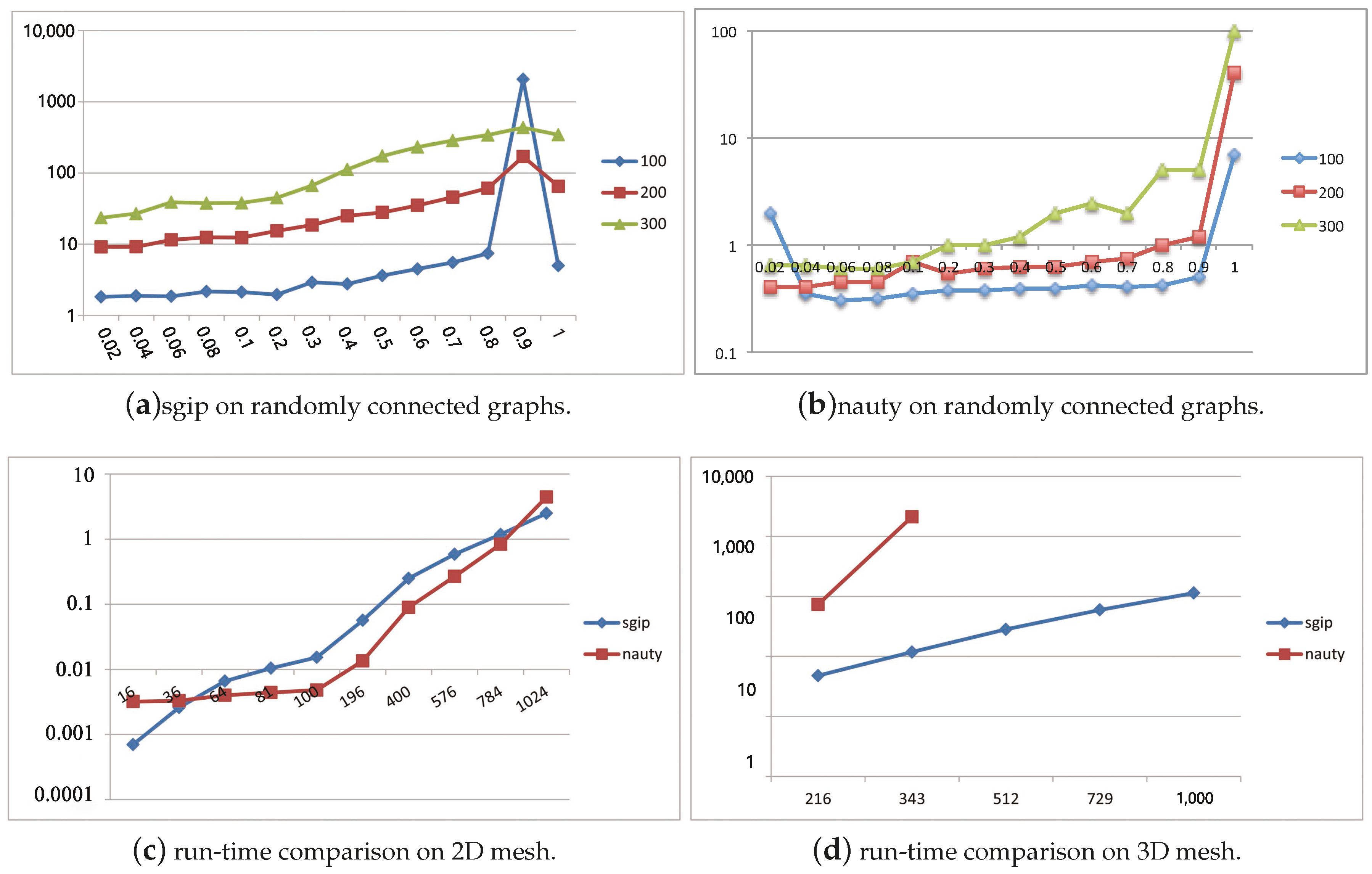
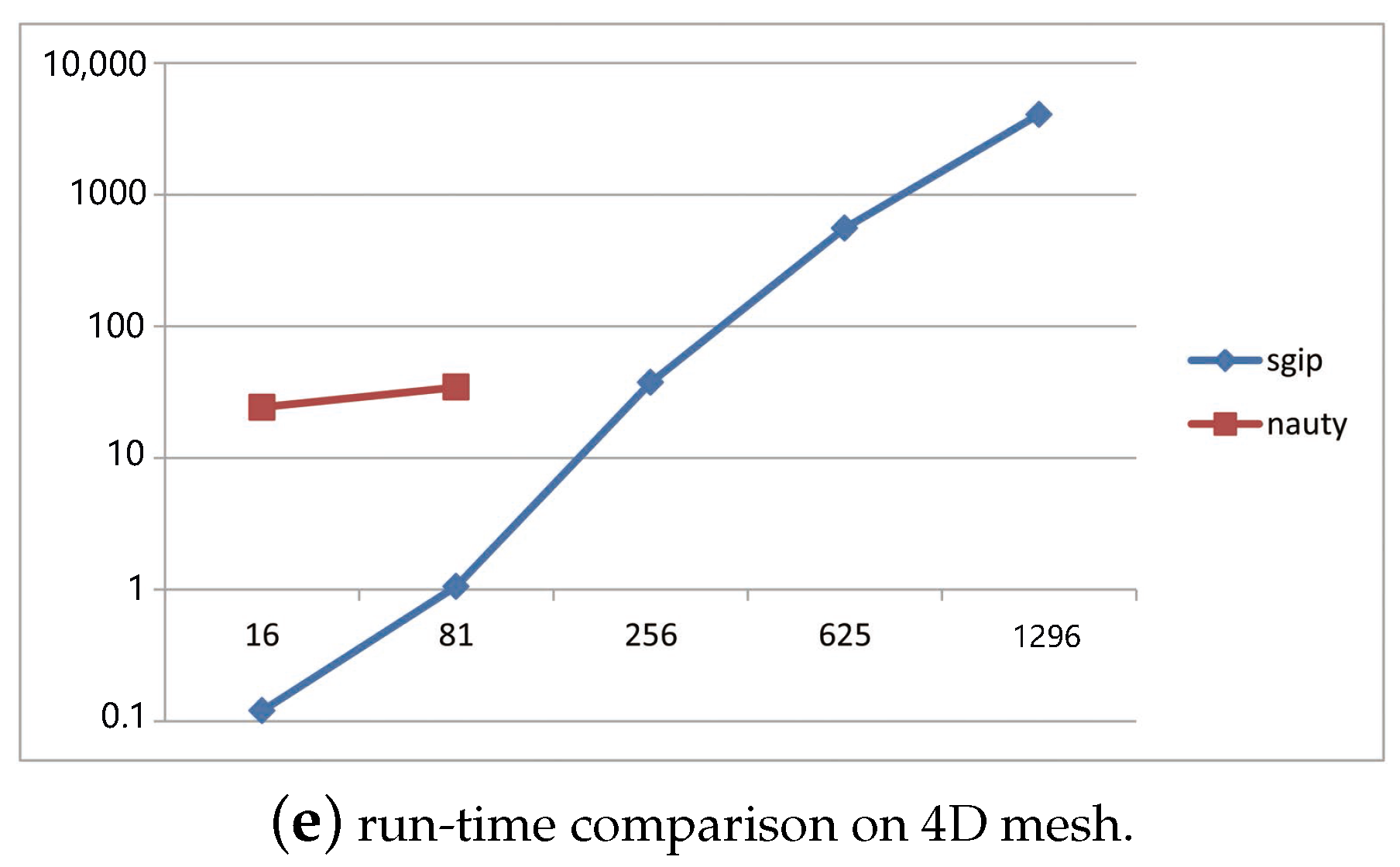
4.1. Tests on Simulated Data
4.2. Tests on Transcriptional Regulation Networks
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Shen-Orr, S.S.; Milo, R.; Mangan, S.; Alon, U. Network motifs in the transcriptional regulation network of Escherichia coli. Nat. Genet. 2002, 31, 64–68. [Google Scholar] [CrossRef] [PubMed]
- Wernicke, S.; Rasche, F. FANMOD: A tool for fast network motif detection. Bioinformatics 2006, 22, 1152–1153. [Google Scholar] [CrossRef] [PubMed]
- Kashtan, N.; Itzkovitz, S.; Milo, R.; Alon, U. Efficient sampling algorithm for estimating subgraph concentrations and detecting network motifs. Bioinformatics 2004, 20, 1746–1758. [Google Scholar] [CrossRef] [PubMed]
- Schreiber, F.; Schwöbbermeyer, H. MAVisto: A tool for the exploration of network motifs. Bioinformatics 2005, 21, 3572–3574. [Google Scholar] [CrossRef] [PubMed]
- Washio, T.; Motoda, H. State of the art of graph-based data mining. ACM SIGKDD Explor. Newsl. 2003, 5, 59–68. [Google Scholar] [CrossRef]
- Rückert, U.; Kramer, S. Frequent free tree discovery in graph data. In Proceedings of the 2004 ACM Symposium on Applied Computing, Nicosia, Cyprus, 14–17 March 2004; Association for Computing Machinery (ACM): New York, NY, USA, 2004; pp. 564–570. [Google Scholar]
- Conte, D.; Foggia, P.; Sansone, C.; Vento, M. Thirty years of graph matching in pattern recognition. Int. J. Pattern Recognit. Artif. Intell. 2004, 18, 265–298. [Google Scholar] [CrossRef]
- Von der Malsburg, C. Pattern recognition by labeled graph matching. Neural Netw. 1988, 1, 141–148. [Google Scholar] [CrossRef]
- Weininger, D. SMILES, a chemical language and information system. 1. Introduction to methodology and encoding rules. J. Chem. Inf. Comput. Sci. 1988, 28, 31–36. [Google Scholar] [CrossRef]
- McNaught, A. The IUPAC International Chemical Identifier: InChl—A New Standard for Molecular Informatics. In Chemistry International; International Union of Pure and Applied Chemistry (IUPAC): Durham, NC, USA, 2006; Volume 28. [Google Scholar]
- Hähnke, V.; Rupp, M.; Krier, M.; Rippmann, F.; Schneider, G. Pharmacophore alignment search tool: Influence of canonical atom labeling on similarity searching. J. Comput. Chem. 2010, 31, 2810–2826. [Google Scholar] [CrossRef] [PubMed]
- Babai, L.; Luks, E. Canonical labeling of graphs. In Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing, Boston, MA, USA, 25–27 April 1983; pp. 171–183. [Google Scholar]
- Luks, E. Isomorphism of graphs of bounded valence can be tested in polynomial time. J. Comput. Syst. Sci. 1982, 25, 42–65. [Google Scholar] [CrossRef]
- Babai, L. On the complexity of canonical labeling of strongly regular graphs. SIAM J. Comput. 1980, 9, 212. [Google Scholar] [CrossRef]
- Kucera, L. Canonical labeling of regular graphs in linear average time. In Proceedings of the 28th Annual Symposium on Foundations of Computer Science, Los Angeles, CA, USA, 12–14 October 1987; IEEE Computer Society: Washington, DC, USA, 1987; pp. 271–279. [Google Scholar]
- Spielman, D.A. Faster isomorphism testing of strongly regular graphs. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory Of Computing, Philadelphia, PA, USA, 22–24 May 1996; Association for Computing Machinery (ACM): New York, NY, USA, 1996; pp. 576–584. [Google Scholar]
- Babai, L.; Codenotti, P. Isomorhism of Hypergraphs of Low Rank in Moderately Exponential Time. In Proceedings of the 2008 49th Annual IEEE Symposium on Foundations of Computer Science, Philadelphia, PA, USA, 25–28 October 2008; IEEE Computer Society: Washington, DC, USA, 2008; pp. 667–676. [Google Scholar]
- McKay, B. Practical Graph Isomorphism. J. Symb. Comput. 1981, 60, 94–112. [Google Scholar] [CrossRef]
- Hartke, S.G.; Radcliffe, A.J. Communicating Mathematics: A Conference in Honor of Joseph A. Gallian’s 65th Birthday, July 16–19, 2007, University of Minnesota, Duluth, Minnesota; Chapter Mckay’s Canonical Graph Labeling Algorithm; American Mathematical Society: Providence, RI, USA, 2009; p. 99. [Google Scholar]
- Miyazaki, T. Groups and computation. In Groups and Computation II Workshop on Groups and Computation June 710 1995; Chapter the Complexity Of McKay’S Canonical Labeling Algorithm; American Mathematical Society: Providence, RI, USA, 1997; p. 239. [Google Scholar]
- Schmidt, D.C.; Druffel, L.E. A Fast Backtracking Algorithm to Test Directed Graphs for Isomorphism Using Distance Matrices. J. ACM 1976, 23, 433–445. [Google Scholar] [CrossRef]
- Cordella, L.; Foggia, P.; Sansone, C.; Vento, M. Performance evaluation of the VF graph matching algorithm. In Proceedings of the International Conference on Image Analysis and Processing, Venice, Italy, 27–29 September 1999; pp. 1172–1177. [Google Scholar]
- Cordella, L.; Foggia, P.; Sansone, C.; Vento, M. An improved algorithm for matching large graphs. In Proceedings of the 3rd IAPR-TC15 Workshop on Graph-Based Representations in Pattern Recognition, Ischia, Italy, 23–25 May 2001; pp. 149–159. [Google Scholar]
- Ullmann, J.R. An Algorithm for Subgraph Isomorphism. J. ACM 1976, 23, 31–42. [Google Scholar] [CrossRef]
- Foggia, P.; Sansone, C.; Vento, M. A Performance Comparison of Five Algorithms for Graph Isomorphism. In Proceedings of the 3rd IAPR-TC15 Workshop on Graph-Based Representations in Pattern Recognition, Ischia, Italy, 23–25 May 2001; pp. 188–199. [Google Scholar]
- Darga, P.T.; Liffiton, M.H.; Sakallah, K.A.; Markov, I.L. Exploiting structure in symmetry detection for CNF. In Proceedings of the 41st Annual Design Automation Conference, San Diego, CA, USA, 7–11 June 2004; Association for Computing Machinery (ACM): New York, NY, USA, 2004; pp. 530–534. [Google Scholar]
- Junttila, T.; Kaski, P. Engineering an efficient canonical labeling tool for large and sparse graphs. In Proceedings of the 9th Workshop on Algorithm Engineering and Experiments and the 4th Workshop on Analytic Algorithms and Combinatorics, New Orleans, LA, USA, 6 January 2007; pp. 135–149. [Google Scholar]
- Döring, A.; Weese, D.; Rausch, T.; Reinert, K. SeqAn An efficient, generic C++ library for sequence analysis. BMC Bioinform. 2008, 9, 11. [Google Scholar] [CrossRef] [PubMed]
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman & Co.: New York, NY, USA, 1979. [Google Scholar]
- Slater, P.J. Leaves of trees. In Proceedings of the Sixth Southeastern Conference on Combinatorics, Graph Theory, and Computing, Boca Raton, FL, USA, 17–20 February 1975; pp. 549–559. [Google Scholar]
- Carmen, H.; Mercé, M.; Pelayo, I.M.; Carlos, S.; Wood, D.R. Extremal Graph Theory for Metric Dimension and Diameter. Electron. J. Comb. 2010, 17, R30. [Google Scholar]
- Foggia, P.; Sansone, C.; Vento, M. A database of graphs for isomorphism and sub-graph isomorphism benchmarking. In Proceedings of the 3rd IAPR-TC15 International Workshop on Graph-based Representations, Ischia, Italy, 23–25 May 2001; pp. 176–187. [Google Scholar]
Sample Availability: Samples of the compounds are available from the authors. |
| Patterns | Appearances in Real Network | Appearances in Randomized Network | p-Value | |||
|---|---|---|---|---|---|---|
| Yeast | E. coli | Yeast | E. coli | Yeast | E. coli | |
| A | 65 | 34 | 10.2 ± 5 | 4.5 ± 2 | 0 | 0 |
| B | 122 | 79 | 33.5 ± 12 | 30 ± 6 | 8.2 × 10−14 | 1.1 × 10−16 |
| C | 396 | 203 | 108 ± 29 | 55 ± 10 | 0 | 0 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Shang, X. Detection of Network Motif Based on a Novel Graph Canonization Algorithm from Transcriptional Regulation Networks. Molecules 2017, 22, 2194. https://doi.org/10.3390/molecules22122194
Hu J, Shang X. Detection of Network Motif Based on a Novel Graph Canonization Algorithm from Transcriptional Regulation Networks. Molecules. 2017; 22(12):2194. https://doi.org/10.3390/molecules22122194
Chicago/Turabian StyleHu, Jialu, and Xuequn Shang. 2017. "Detection of Network Motif Based on a Novel Graph Canonization Algorithm from Transcriptional Regulation Networks" Molecules 22, no. 12: 2194. https://doi.org/10.3390/molecules22122194
APA StyleHu, J., & Shang, X. (2017). Detection of Network Motif Based on a Novel Graph Canonization Algorithm from Transcriptional Regulation Networks. Molecules, 22(12), 2194. https://doi.org/10.3390/molecules22122194




