Multicenter (FX)n/NH3 Halogen Bonds (X = Cl, Br and n = 1–5). QTAIM Descriptors of the Strength of the X∙∙∙N Interaction
Abstract
1. Introduction
- Can an analysis based on local kinetic and potential energies derivatives of QTAIM model contribute to the understanding of these XBs?
- Are delocalization indices and exchange contribution of the IQA scheme a measure of the covalence of these molecular interactions, like in conventional chemical bonds?
2. Computational Details
3. Results and Discussion
3.1. Geometric, Energetic, and Electron Charge Density Analysis
3.2. Local Kinetic and Potential Energies Analysis
3.3. Localization and Delocalization Indices
3.4. IQA Analysis
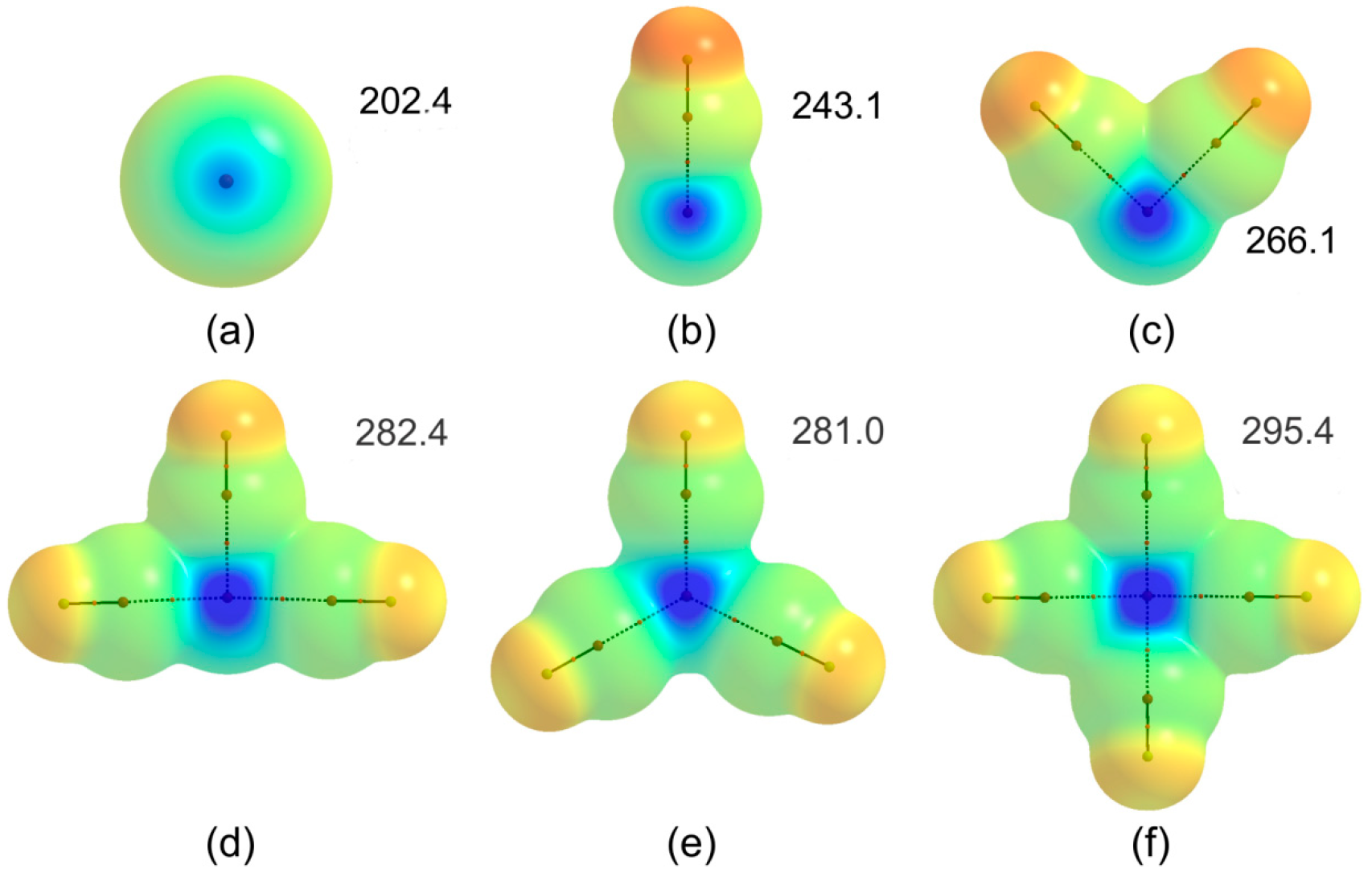
3.5. Molecular Electrostatic Potentials
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef] [PubMed]
- Kolář, M.H.; Hobza, P. Computer Modeling of Halogen Bonds and Other σ-Hole Interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Duarte, D.J.R.; Sosa, G.L.; Peruchena, N.M.; Alkorta, I. Halogen bonding. The role of the polarizability of the electron-pair donor. Phys. Chem. Chem. Phys. 2016, 18, 7300–7309. [Google Scholar] [CrossRef] [PubMed]
- Duarte, D.J.R.; De Las Vallejos, M.M.; Peruchena, N.M. Topological analysis of aromatic halogen/hydrogen bonds by electron charge density and electrostatic potentials. J. Mol. Model. 2010, 16, 737–748. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Resnati, G.; Pilati, T.; Biella, S. Halogen bonding in crystal engineering. Halogen Bond. Fundam. Appl. 2008, 126, 105–136. [Google Scholar] [CrossRef]
- Imai, Y.N.; Inoue, Y.; Nakanishi, I.; Kitaura, K. Cl–π interactions in protein–ligand complexes. Protein Sci. 2008, 17, 1129–1137. [Google Scholar] [CrossRef] [PubMed]
- Lu, Y.; Shi, T.; Wang, Y.; Yang, H.; Yan, X.; Luo, X.; Jiang, H.; Zhu, W. Halogen Bonding—A Novel Interaction for Rational Drug Design? J. Med. Chem. 2009, 52, 2854–2862. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.-H.; Zou, J.; Lu, Y.-X.; Yu, Q.-S.; Xu, H.-Y. Single-Electron Halogen Bond: Ab Initio Study. Int. J. Quantum Chem. 2007, 107, 501–506. [Google Scholar] [CrossRef]
- Smith, D.A.; Brammer, L.; Hunter, C.A.; Perutz, R.N. Metal hydrides form halogen bonds: Measurement of energetics of binding. J. Am. Chem. Soc. 2014, 136, 1288–1291. [Google Scholar] [CrossRef] [PubMed]
- Jabłoński, M.; Palusiak, M. Nature of a Hydride–Halogen Bond. A SAPT-, QTAIM-, and NBO-Based Study. J. Phys. Chem. A 2012, 116, 2322–2332. [Google Scholar] [CrossRef] [PubMed]
- Lv, H.; Zhuo, H.-Y.; Li, Q.-Z.; Yang, X.; Li, W.-Z.; Cheng, J.-B. Halogen bonds with N-heterocyclic carbenes as halogen acceptors: A partially covalent character. Mol. Phys. 2014, 112, 3024–3032. [Google Scholar] [CrossRef]
- Esrafili, M.D.; Mohammdain-Sabet, F.; Esmailpour, P. Theoretical study on cooperative effects between X∙∙∙N and X∙∙∙Carbene halogen bonds (X = F, Cl, Br and I). J. Mol. Model. 2013, 19, 4797–4804. [Google Scholar] [CrossRef] [PubMed]
- Jabłoński, M. Energetic and geometrical evidence of nonbonding character of some intramolecular halogen···oxygen and other Y···Y interactions. J. Phys. Chem. A 2012, 116, 3753–3764. [Google Scholar] [CrossRef] [PubMed]
- Yahia-Ouahmed, M.; Tognetti, V.; Joubert, L. Intramolecular halogen bonding: An interacting quantum atoms study. Theor. Chem. Acc. 2016, 135, 45. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. The intrinsic strength of the halogen bond: Electrostatic and covalent contributions described by coupled cluster theory. Phys. Chem. Chem. Phys. 2016, 18, 33031–33046. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Gao, J.; Bi, F.; Song, B.; Liu, C. Toward the development of the potential with angular distortion for halogen bond: A comparison of potential energy surfaces between halogen bond and hydrogen bond. J. Phys. Chem. A 2014, 118, 9140–9147. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J. Hydrogen and halogen bonds are ruled by the same mechanisms. Phys. Chem. Chem. Phys. 2013, 15, 7249–7259. [Google Scholar] [CrossRef] [PubMed]
- Palusiak, M. On the nature of halogen bond—The Kohn-Sham molecular orbital approach. J. Mol. Struct. THEOCHEM 2010, 945, 89–92. [Google Scholar] [CrossRef]
- Riley, K.E.; Hobza, P. Investigations into the nature of halogen bonding including symmetry adapted perturbation theory analyses. J. Chem. Theory Comput. 2008, 4, 232–242. [Google Scholar] [CrossRef] [PubMed]
- Kirsch, P.; Tong, Q.; Untenecker, H. Crystal design using multipolar electrostatic interactions: A concept study for organic electronics. Beilstein J. Org. Chem. 2013, 9, 2367–2373. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Duan, D.; Zhou, M.; Li, S.; Cui, T.; Liu, B.; Liu, J.; Zou, B.; Zou, G. Structural properties and halogen bonds of cyanuric chloride under high pressure. J. Phys. Chem. B 2011, 115, 4639–4644. [Google Scholar] [CrossRef] [PubMed]
- Phipps, M.J.S.; Fox, T.; Tautermann, C.S.; Skylaris, C.-K. Energy decomposition analysis approaches and their evaluation on prototypical protein-drug interaction patterns. Chem. Soc. Rev. 2015, 44, 3177–3211. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Atoms in Molecules. A Quantum Theory; Clarendon: Oxford, UK, 1990; ISBN 0-19-855865-1. [Google Scholar]
- Popelier, P.L.A. Atoms in Molecules. An Introduction; Prentice-Hall: Manchester, UK, 2000; ISBN 0-582-36798-0. [Google Scholar]
- Rafat, M.; Popelier, P.L.A. Topological Atom-Atom Partitioning of Molecular Exchange Energy and its Multipolar Convergence. In The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design; Matta, C.F., Boyd, R.J., Eds.; Wiley-VCH: Weinheim, Germany, 2007; pp. 121–140. ISBN 978-3-527-30748-7. [Google Scholar]
- Angelina, E.L.; Duarte, D.J.R.; Peruchena, N.M. Is the decrease of the total electron energy density a covalence indicator in hydrogen and halogen bonds? J. Mol. Model. 2013, 19, 2097–2106. [Google Scholar] [CrossRef] [PubMed]
- Duarte, D.J.R.; Sosa, G.L.; Peruchena, N.M. Nature of halogen bonding. A study based on the topological analysis of the Laplacian of the electron charge density and an energy decomposition analysis. J. Mol. Model. 2013, 19, 2035–2041. [Google Scholar] [CrossRef] [PubMed]
- Duarte, D.J.R.; Angelina, E.L.; Peruchena, N.M. On the strength of the halogen bonds: Mutual penetration, atomic quadrupole moment and Laplacian distribution of the charge density analyses. Comput. Theor. Chem. 2012, 998, 164–172. [Google Scholar] [CrossRef]
- Buralli, G.J.; Duarte, D.J.R.; Sosa, G.L.; Peruchena, N.M. Lewis acid-base behavior of hypervalent halogen fluorides in gas phase. Struct. Chem. 2017. [Google Scholar] [CrossRef]
- Eskandari, K.; Zariny, H. Halogen bonding: A lump-hole interaction. Chem. Phys. Lett. 2010, 492, 9–13. [Google Scholar] [CrossRef]
- Blanco, M.A.; Francisco, E. Interacting Quantum Atoms: A Correlated Energy Decomposition Scheme Based on the Quantum Theory of Atoms in Molecules. J. Chem. Theory Comput. 2005, 1, 1096–1109. [Google Scholar] [CrossRef] [PubMed]
- Martin Pendás, A.; Francisco, E.; Blanco, M.A. Binding energies of first row diatomics in the light of the interacting quantum atoms approach. J. Phys. Chem. A 2006, 110, 12864–12869. [Google Scholar] [CrossRef] [PubMed]
- Eskandari, K. Nature of beryllium bonds in view of interacting quantum atoms and natural energy decomposition analysis. Comput. Theor. Chem. 2016, 1090, 74–79. [Google Scholar] [CrossRef]
- Syzgantseva, O.A.; Tognetti, V.; Joubert, L. On the physical nature of halogen bonds: A QTAIM study. J. Phys. Chem. A 2013, 117, 8969–8980. [Google Scholar] [CrossRef] [PubMed]
- Kozuch, S.; Martin, J.M.L. Halogen bonds: Benchmarks and theoretical analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Danovich, D.; Mo, Y.; Shaik, S. On the nature of the halogen bond. J. Chem. Theory Comput. 2014, 10, 3726–3737. [Google Scholar] [CrossRef] [PubMed]
- Clark, T. Halogen bonds and σ-holes. Faraday Discuss. 2017, 203, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03 (Revision D.01); Gaussian Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef]
- Raghavachari, K.; Trucks, G.W.; Pople, J.A.; Head-gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 1989, 157, 479–483. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Bondi, A. van der Waals Volumes and Radii. J. Phys. Chem. 1964, 68, 441–451. [Google Scholar] [CrossRef]
- Bloemink, H.I.; Evans, C.M.; Holloway, J.H.; Legon, A.C. Is the gas-phase complex of ammonia and chlorine monofluoride H3N···ClF or [H3NCl]+···F−? Evidence from rotational spectroscopy. Chem. Phys. Lett. 1996, 248, 260–268. [Google Scholar] [CrossRef]
- Wang, W.; Hobza, P. Origin of the X-Hal (Hal = Cl, Br) bond-length change in the halogen-bonded complexes. J. Phys. Chem. A 2008, 112, 4114–4119. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C. The halogen bond: An interim perspective. Phys. Chem. Chem. Phys. 2010, 12, 7736–7747. [Google Scholar] [CrossRef] [PubMed]
- Lucchesela, R.R.; Schaefer, H.F. Charge-Transfer Complexes. NH3-F2, NH3-Cl2, NH3-ClF, N(CH3)3-F2, N(CH3)3-Cl2 and N(CH3)3-ClF. J. Am. Chem. Soc. 1975, 97, 7205–7210. [Google Scholar] [CrossRef]
- Lu, Y.X.; Zou, J.W.; Wang, Y.H.; Yu, Q.S. Ab initio and atoms in molecules analyses of halogen bonding with a continuum of strength. J. Mol. Struct. THEOCHEM 2006, 776, 83–87. [Google Scholar] [CrossRef]
- McDowell, S.A.C. Halogen and hydrogen bonding to the Br atom in complexes of FBr. J. Chem. Phys. 2010, 132, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Ruedenberg, K. The physical nature of the chemical bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
- Kutzelnigg, W. The Physical Origin of the Chemical Bond. In The Concept of the Chemical Bond; Maksic, Z.B., Ed.; Springer: Berlin, Germany, 1990. [Google Scholar]
- Feynman, R.P. Forces in molecules. Phys. Rev. 1939, 56, 340–343. [Google Scholar] [CrossRef]
- Coulson, C.A. Valence, 2nd ed.; Oxford University Press: London, UK, 1961. [Google Scholar]
- Bacskay, G.B.; Nordholm, S. Covalent bonding: The fundamental role of the kinetic energy. J. Phys. Chem. A 2013, 117, 7946–7958. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; Hernadez-Trujillo, J. Chemical Bonding: From Lewis to Atoms in Molecules. J. Comput. Chem. 2010, 31, 2967–2970. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Duarte, D.J.R.; Peruchena, N.M.; Alkorta, I. Double Hole–Lump Interaction between Halogen Atoms. J. Phys. Chem. A 2015, 119, 3746–3752. [Google Scholar] [CrossRef] [PubMed]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X–H⋯F–Y systems. J. Chem. Phys. 2002, 117, 5529. [Google Scholar] [CrossRef]
- Grabowski, S.J.; Sokalski, W.A.; Leszczynski, J. How short can the H∙∙∙H intermolecular contact be? New findings that reveal the covalent nature of extremely strong interactions. J. Phys. Chem. A 2005, 109, 4331–4341. [Google Scholar] [CrossRef] [PubMed]
- Grabowski, S.J.; Sokalski, W.A.; Leszczynski, J. The possible covalent nature of N-H∙∙∙O hydrogen bonds in formamide dimer and related systems: An ab initio study. J. Phys. Chem. A 2006, 110, 4772–4779. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, S.; Morrison, I. The chemical character of the intermolecular bonds of seven phases of ice as revealed by ab initio calculation of electron densities. Chem. Phys. Lett. 2000, 317, 97–102. [Google Scholar] [CrossRef]
- Angelina, E.L.; Peruchena, N.M. Strength and nature of hydrogen bonding interactions in mono- and di-hydrated formamide complexes. J. Phys. Chem. A 2011, 115, 4701–4710. [Google Scholar] [CrossRef] [PubMed]
- Duarte, D.J.R.; Angelina, E.L.; Peruchena, N.M. Physical meaning of the QTAIM topological parameters in hydrogen bonding. J. Mol. Model. 2014, 20, 2510. [Google Scholar] [CrossRef] [PubMed]
- Fradera, X.; Austen, M.A.; Bader, R.F.W. The Lewis Model and Beyond. J. Phys. Chem. A 1999, 103, 304–314. [Google Scholar] [CrossRef]
- Grabowski, S.J. Hydrogen Bond and Other Lewis Acid Lewis Base Interactions Mechanisms of Formation. In Practical Aspects of Computational Chemistry IV; Leszczynski, J., Shukla, M., Eds.; Springer: New York, NY, USA, 2016; pp. 245–277. ISBN 978-1-4899-7697-0. [Google Scholar]
- Maxwell, P.; Pendás, Á.M.; Popelier, P.L.A. Extension of the interacting quantum atoms (IQA) approach to B3LYP level density functional theory (DFT). Phys. Chem. Chem. Phys. 2016, 18, 20986–21000. [Google Scholar] [CrossRef] [PubMed]
- IUPAC. Compendium of Chemical Terminology, 2nd ed. (the “Gold Book“); Compiled by McNaught, A.D., Wilkinson, A.; Blackwell Scientific Publications: Oxford, UK, 1997. [Google Scholar]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Desiraju, G.R.; Ho, P.S.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
Sample Availability: Not available. |
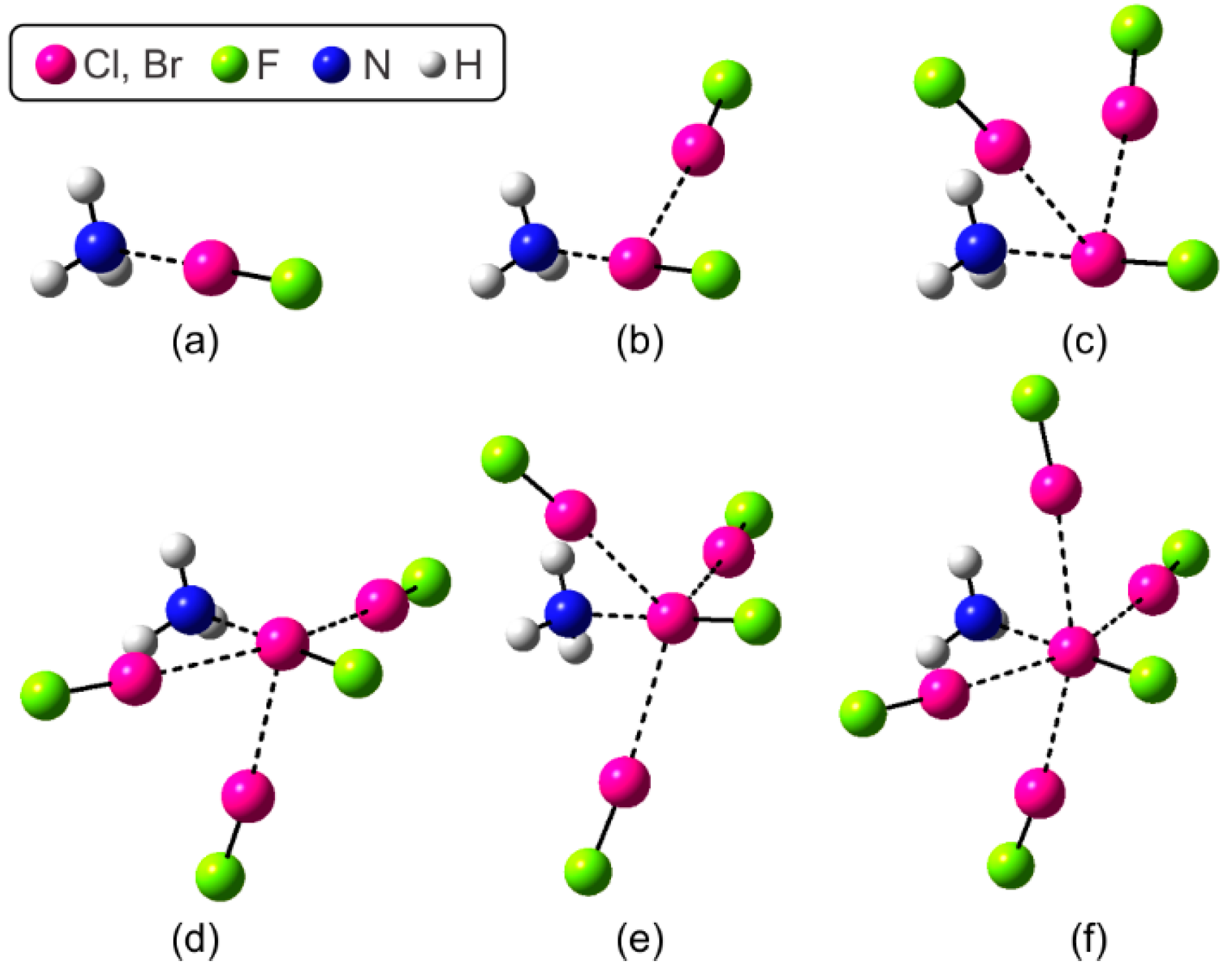
| Complexes a | d(X∙∙∙N) | ΔdvdW(X∙∙∙N) | Δd(X‒F) | EInt(X∙∙∙N) |
|---|---|---|---|---|
| FCl/NH3 (C3v) | 2.272 | 0.441 | 0.074 | −40.9 |
| (FCl)2/NH3 (Cs) | 2.224 | 0.489 | 0.080 | −54.4 |
| (FCl)3/NH3 (Cs) | 2.191 | 0.521 | 0.086 | −66.7 |
| (FCl)4/NH3 (Cs) | 2.165 | 0.548 | 0.093 | −78.1 |
| (FCl)4/NH3 (C3v) | 2.166 | 0.547 | 0.092 | −78.5 |
| (FCl)5/NH3 (Cs) | 2.141 | 0.571 | 0.100 | −89.9 |
| FBr/NH3 (C3v) | 2.325 | 0.542 | 0.067 | −55.8 |
| (FBr)2/NH3 (Cs) | 2.281 | 0.587 | 0.066 | −73.8 |
| (FBr)3/NH3 (Cs) | 2.252 | 0.616 | 0.066 | −88.8 |
| (FBr)4/NH3 (Cs) | 2.230 | 0.638 | 0.067 | −101.8 |
| (FBr)4/NH3 (C3v) | 2.231 | 0.636 | 0.068 | −101.1 |
| (FBr)5/NH3 (Cs) | 2.212 | 0.655 | 0.072 | −112.6 |
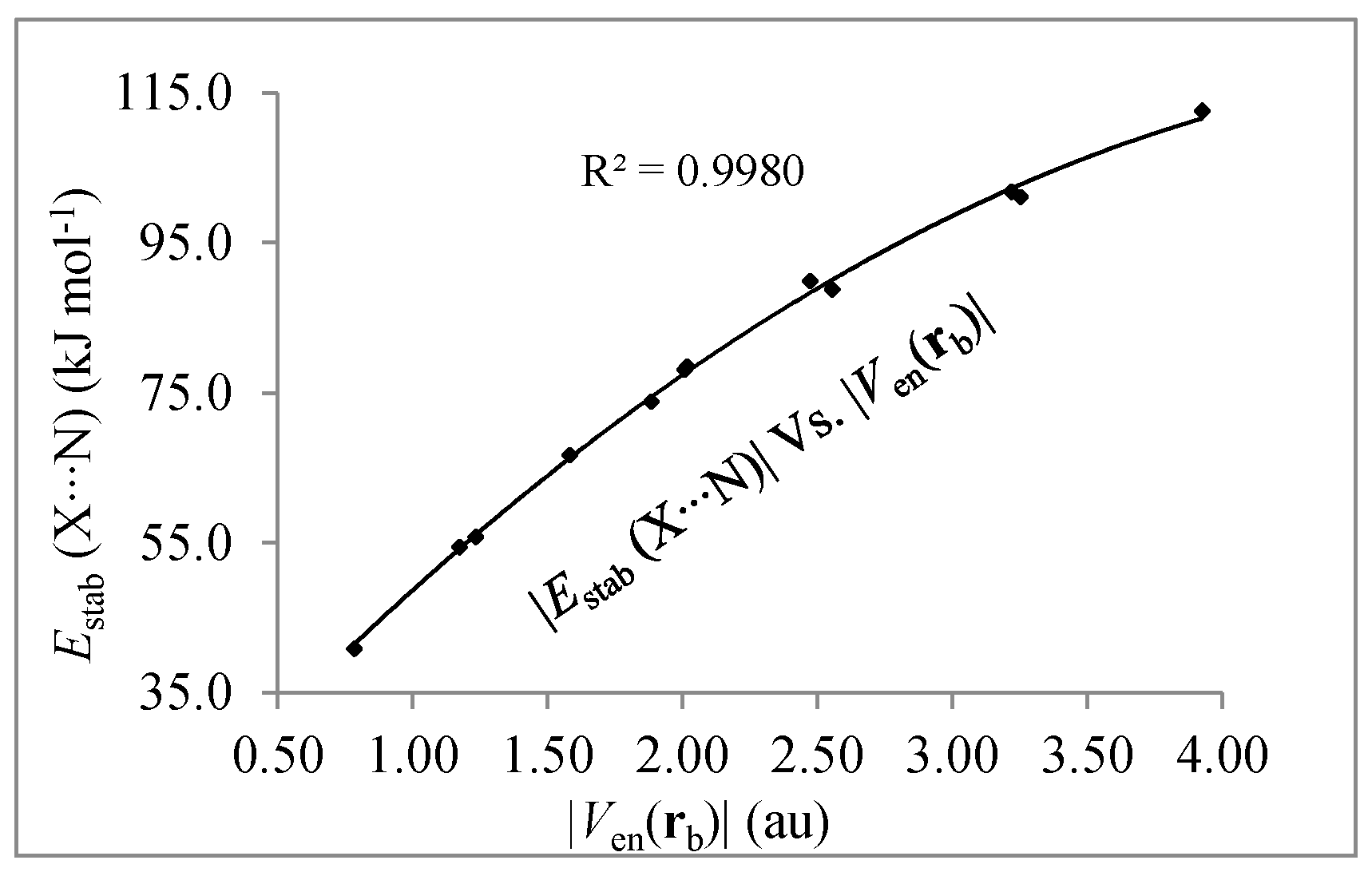
| Complexes b | G(rb) | V(rb) | Ven(rb) | Vrep(rb) |
|---|---|---|---|---|
| FCl/NH3 (C3v) | 0.0425 | −0.0471 | −0.7817 | 0.7346 |
| (FCl)2/NH3 (Cs) | 0.0470 | −0.0550 | −1.1712 | 1.1162 |
| (FCl)3/NH3 (Cs) | 0.0502 | −0.0613 | −1.5793 | 1.5180 |
| (FCl)4/NH3 (Cs) | 0.0529 | −0.0669 | −2.0067 | 1.9398 |
| (FCl)4/NH3 (C3v) | 0.0528 | −0.0669 | −2.0148 | 1.9479 |
| (FCl)5/NH3 (Cs) | 0.0553 | −0.0724 | −2.4701 | 2.3977 |
| FBr/NH3 (C3v) | 0.0415 | −0.0490 | −1.2320 | 1.1830 |
| (FBr)2/NH3 (Cs) | 0.0456 | −0.0567 | −1.8833 | 1.8266 |
| (FBr)3/NH3 (Cs) | 0.0484 | −0.0626 | −2.5532 | 2.4906 |
| (FBr)4/NH3 (Cs) | 0.0504 | −0.0671 | −3.2172 | 3.1501 |
| (FBr)4/NH3 (C3v) | 0.0506 | −0.0676 | −3.2513 | 3.1838 |
| (FBr)5/NH3 (Cs) | 0.0522 | −0.0715 | −3.9234 | 3.8519 |
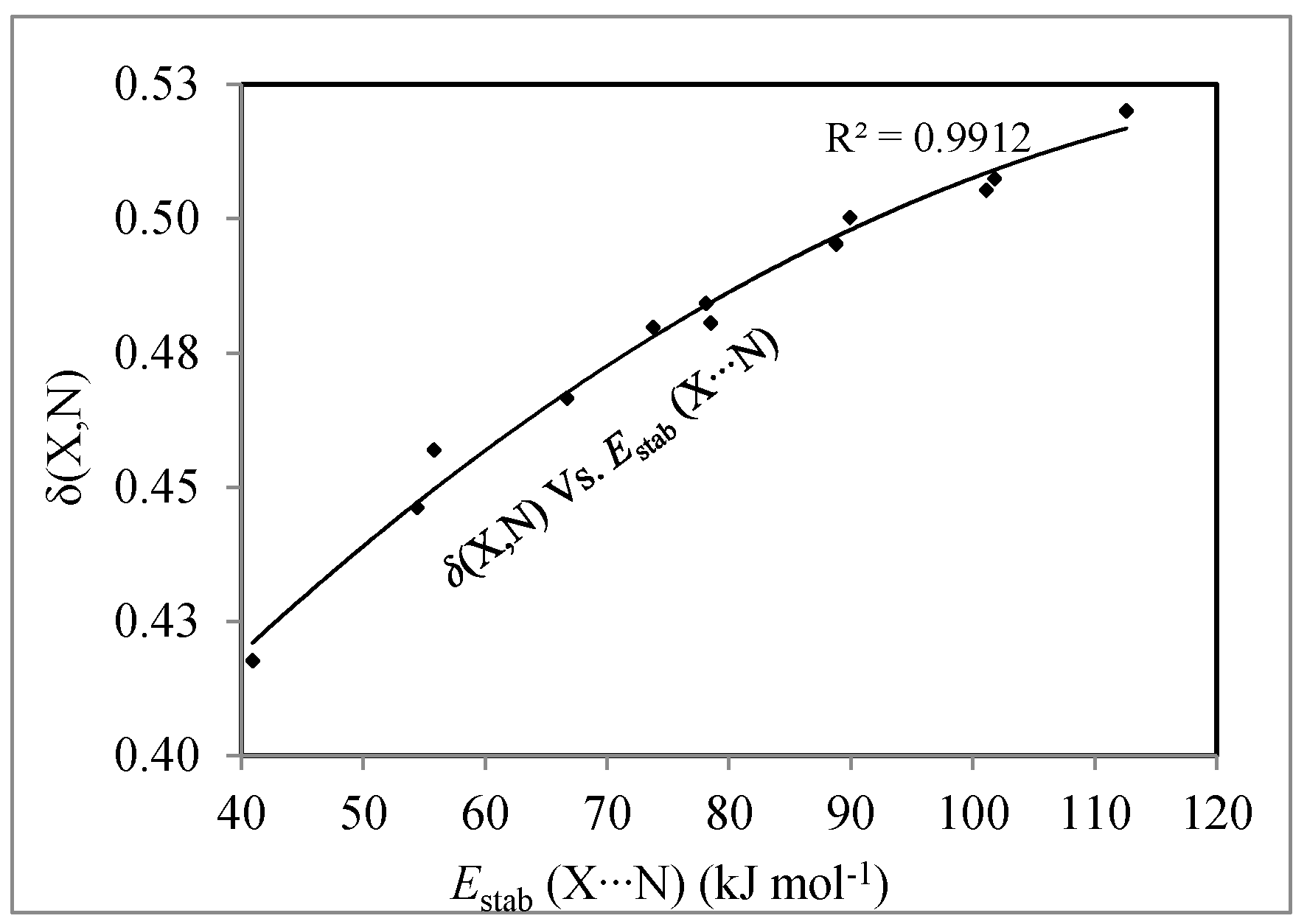
| Complexes | λ(Ω) | δ(X,N) | |
|---|---|---|---|
| X | N | ||
| FCl/NH3 (C3v) | 16.070 | 6.865 | 0.419 |
| (FCl)2/NH3 (Cs) | 15.963 | 6.839 | 0.446 |
| (FCl)3/NH3 (Cs) | 15.885 | 6.821 | 0.467 |
| (FCl)4/NH3 (Cs) | 15.833 | 6.809 | 0.484 |
| (FCl)4/NH3 (C3v) | 15.818 | 6.796 | 0.481 |
| (FCl)5/NH3 (Cs) | 15.782 | 6.793 | 0.500 |
| FBr/NH3 (C3v) | 33.958 | 6.880 | 0.457 |
| (FBr)2/NH3 (Cs) | 33.746 | 6.863 | 0.480 |
| (FBr)3/NH3 (Cs) | 33.609 | 6.851 | 0.495 |
| (FBr)4/NH3 (Cs) | 33.531 | 6.844 | 0.508 |
| (FBr)4/NH3 (C3v) | 33.505 | 6.832 | 0.505 |
| (FBr)5/NH3 (Cs) | 33.475 | 6.830 | 0.520 |
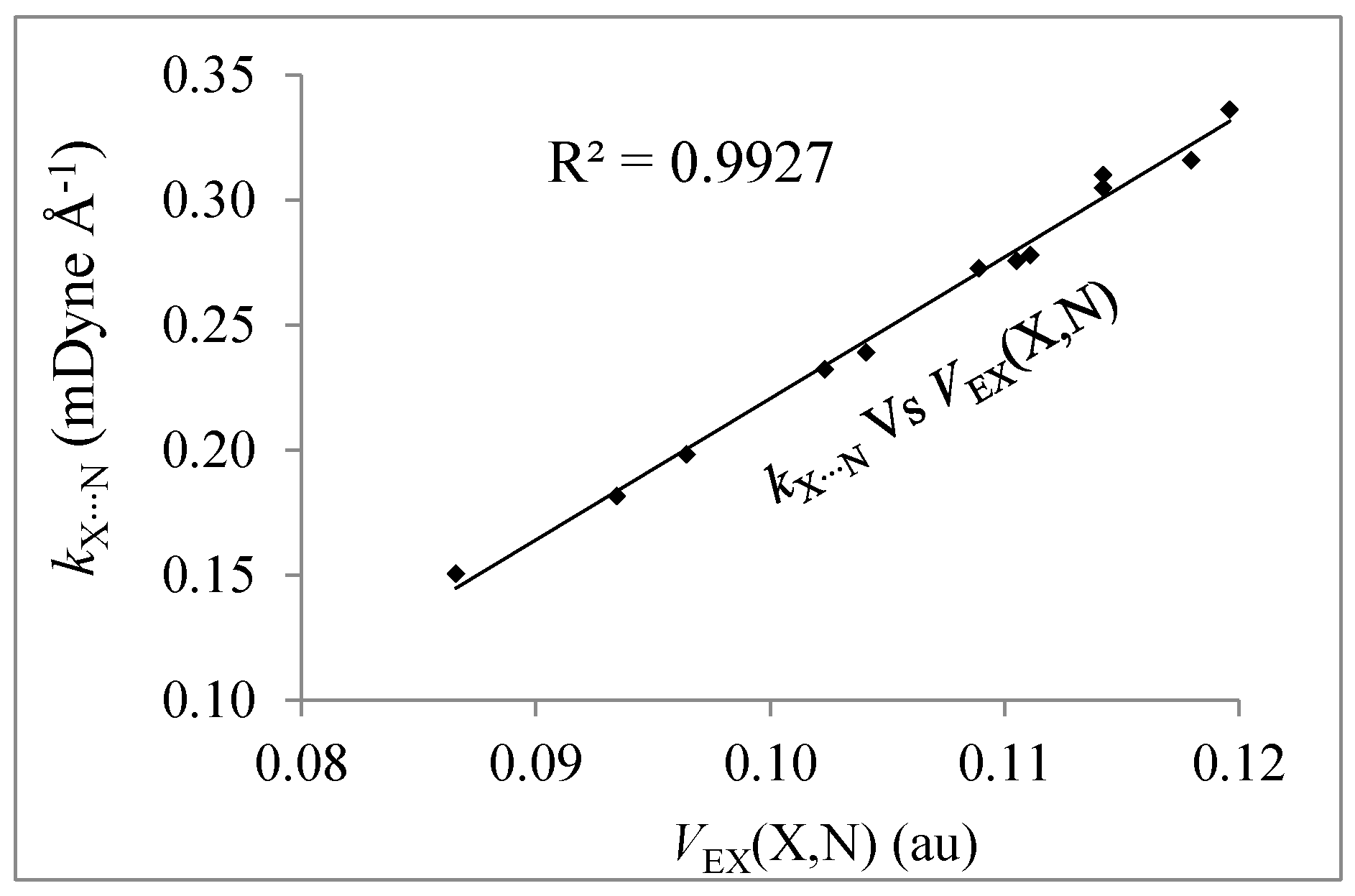
| Complexes | Eint(X,N) | Vnn(X,N) | Ven(X,N) | Ven(N,X) | Vee,C(X,N) | VEX(X,N) | VC(X,N) | %EX | %Cl |
|---|---|---|---|---|---|---|---|---|---|
| FCl/NH3 (C3v) | −0.2231 | 27.7198 | −26.8930 | −32.4325 | 31.4691 | −0.0866 | −0.1365 | 38.8 | 61.2 |
| (FCl)2/NH3 (Cs) | −0.2380 | 28.3166 | −27.4573 | −33.1334 | 32.1326 | −0.0964 | −0.1416 | 40.5 | 59.5 |
| (FCl)3/NH3 (Cs) | −0.2482 | 28.7381 | −27.8627 | −33.6362 | 32.6167 | −0.1041 | −0.1441 | 41.9 | 58.1 |
| (FCl)4/NH3 (Cs) | −0.2565 | 29.0902 | −28.2074 | −34.0642 | 33.0360 | −0.1111 | −0.1454 | 43.3 | 56.7 |
| (FCl)4/NH3 (C3v) | −0.2554 | 29.0769 | −28.1955 | −34.0363 | 33.0101 | −0.1105 | −0.1449 | 43.3 | 56.7 |
| (FCl)5/NH3 (Cs) | −0.2640 | 29.4118 | −28.5250 | −34.4562 | 33.4234 | −0.1179 | −0.1461 | 44.7 | 55.3 |
| FBr/NH3 (C3v) | −0.2722 | 55.7605 | −54.7218 | −65.5421 | 64.3247 | −0.0934 | −0.1787 | 34.3 | 65.7 |
| (FBr)2/NH3 (Cs) | −0.2955 | 56.8462 | −55.7332 | −66.9047 | 65.5985 | −0.1023 | −0.1932 | 34.6 | 65.4 |
| (FBr)3/NH3 (Cs) | −0.3094 | 57.5746 | −56.4298 | −67.8420 | 66.4967 | −0.1089 | −0.2005 | 35.2 | 64.8 |
| (FBr)4/NH3 (Cs) | −0.3181 | 58.1413 | −56.9833 | −68.5692 | 67.2073 | −0.1142 | −0.2039 | 35.9 | 64.1 |
| (FBr)4/NH3 (C3v) | −0.3174 | 58.1007 | −56.9483 | −68.5426 | 67.1870 | −0.1142 | −0.2032 | 36.0 | 64.0 |
| (FBr)5/NH3 (Cs) | −0.3247 | 58.5986 | −57.4442 | −69.2236 | 67.8642 | −0.1196 | −0.205 | 36.8 | 63.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buralli, G.J.; Petelski, A.N.; Peruchena, N.M.; Sosa, G.L.; Duarte, D.J.R. Multicenter (FX)n/NH3 Halogen Bonds (X = Cl, Br and n = 1–5). QTAIM Descriptors of the Strength of the X∙∙∙N Interaction. Molecules 2017, 22, 2034. https://doi.org/10.3390/molecules22112034
Buralli GJ, Petelski AN, Peruchena NM, Sosa GL, Duarte DJR. Multicenter (FX)n/NH3 Halogen Bonds (X = Cl, Br and n = 1–5). QTAIM Descriptors of the Strength of the X∙∙∙N Interaction. Molecules. 2017; 22(11):2034. https://doi.org/10.3390/molecules22112034
Chicago/Turabian StyleBuralli, Gabriel J., Andre N. Petelski, Nélida M. Peruchena, Gladis L. Sosa, and Darío J. R. Duarte. 2017. "Multicenter (FX)n/NH3 Halogen Bonds (X = Cl, Br and n = 1–5). QTAIM Descriptors of the Strength of the X∙∙∙N Interaction" Molecules 22, no. 11: 2034. https://doi.org/10.3390/molecules22112034
APA StyleBuralli, G. J., Petelski, A. N., Peruchena, N. M., Sosa, G. L., & Duarte, D. J. R. (2017). Multicenter (FX)n/NH3 Halogen Bonds (X = Cl, Br and n = 1–5). QTAIM Descriptors of the Strength of the X∙∙∙N Interaction. Molecules, 22(11), 2034. https://doi.org/10.3390/molecules22112034





