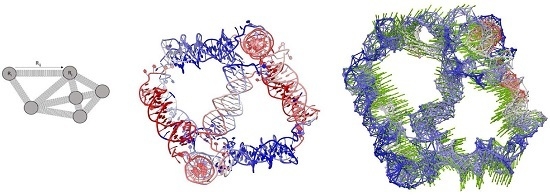
Intrinsic Dynamics Analysis of a DNA Octahedron by Elastic Network Model
Abstract
:1. Introduction
2. Results
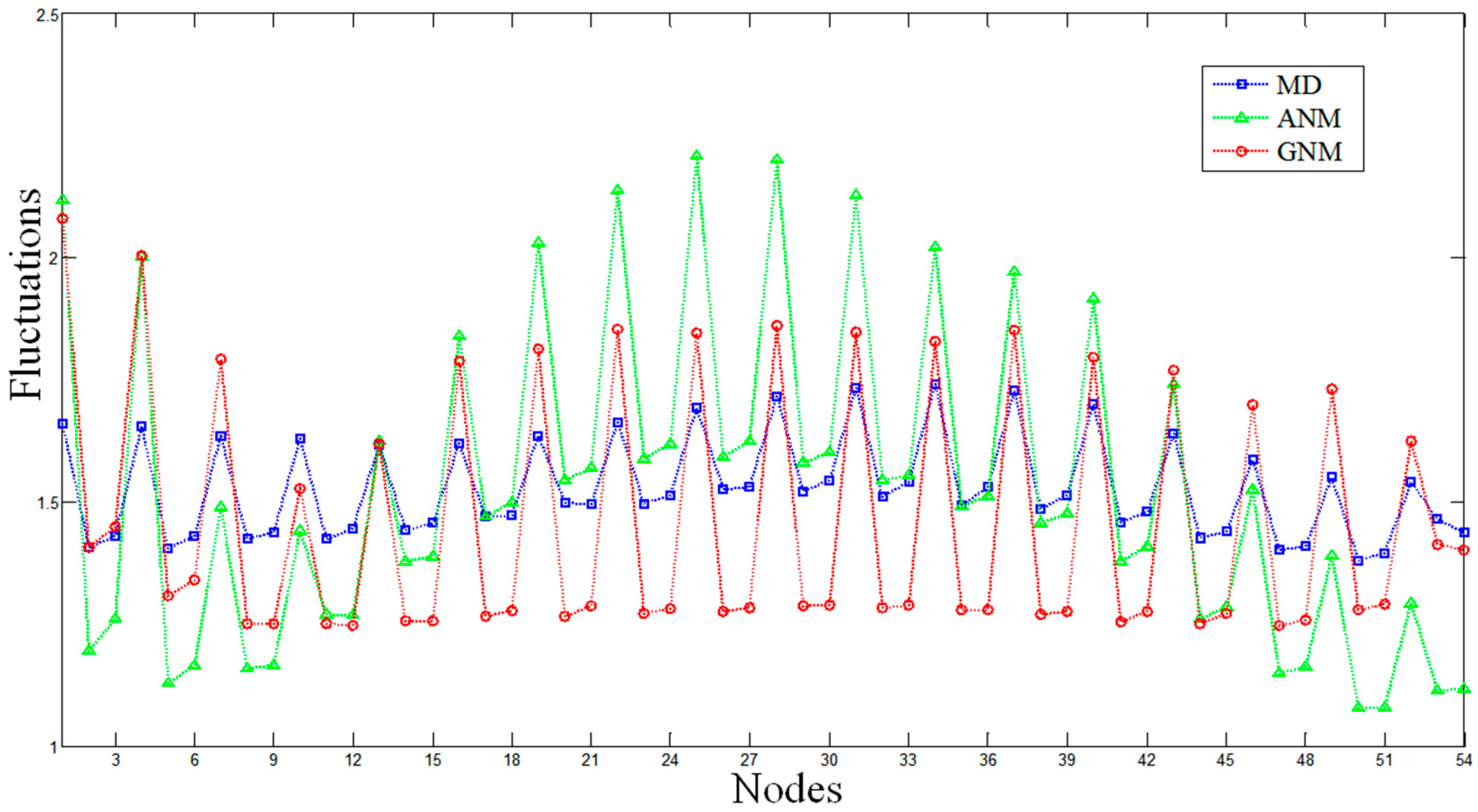
2.1. Comparisons of Fluctuations between the Molecular Dynamics and Elastic Network Models
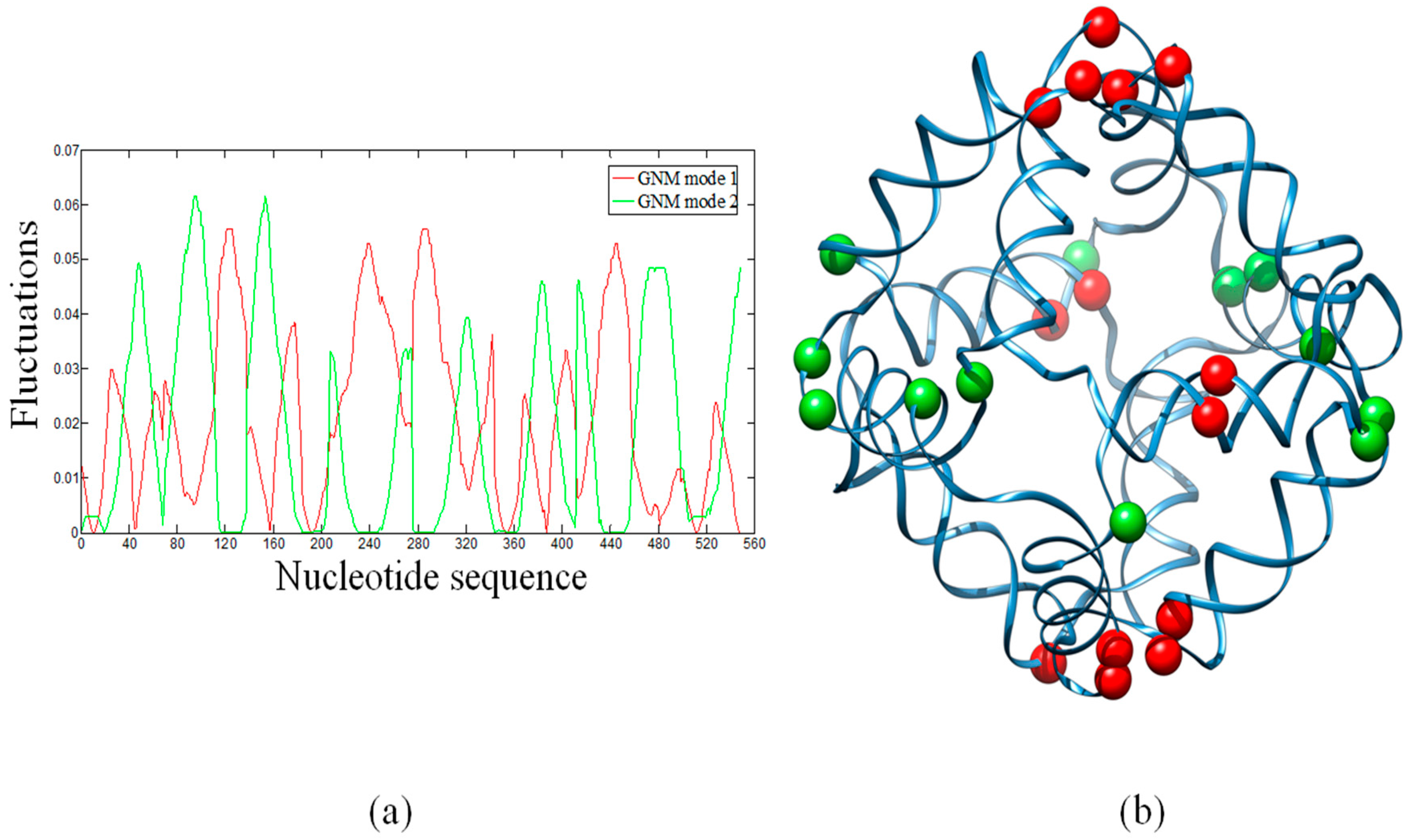
2.2. Hinge Sites Predicted by the Slow Modes
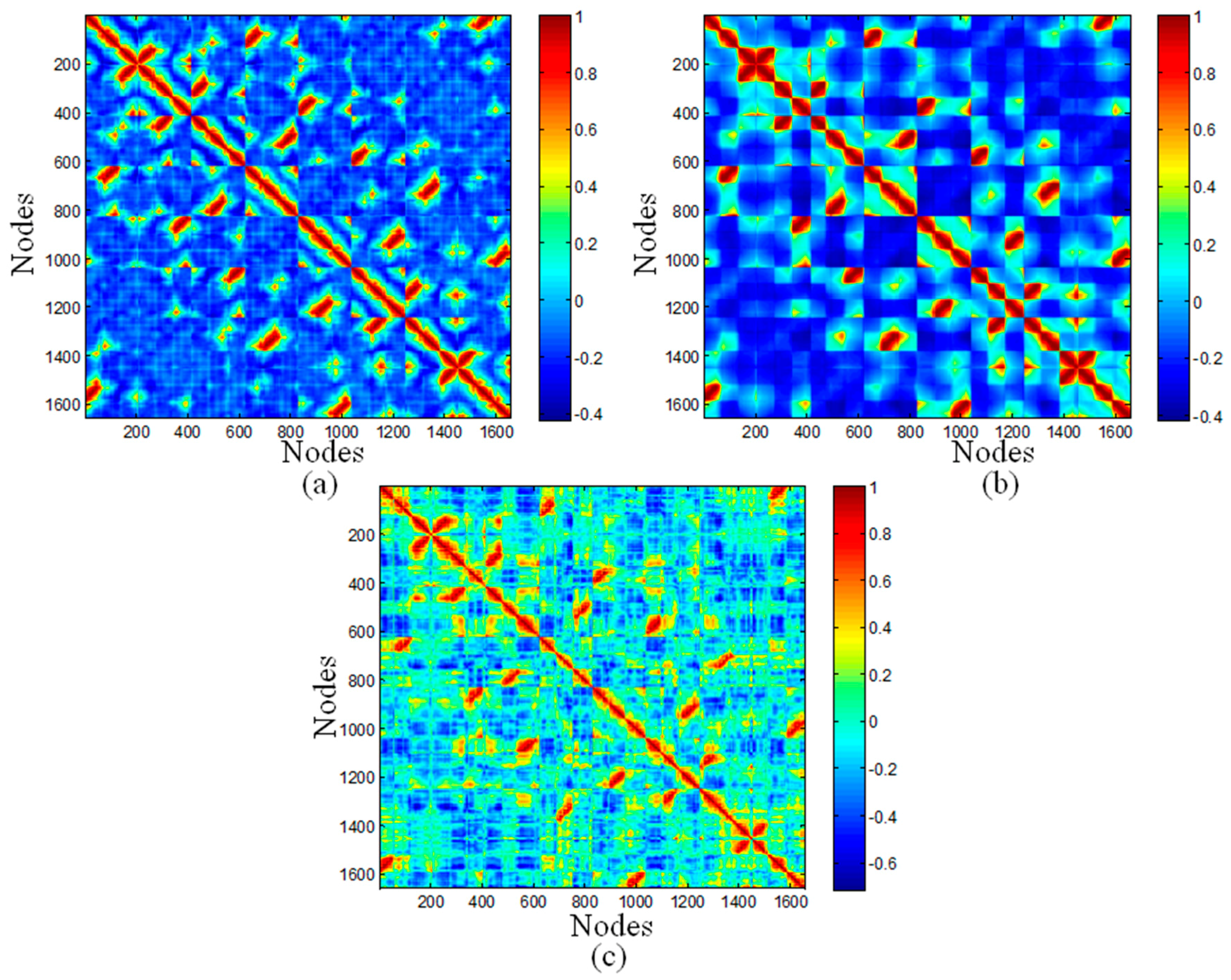
2.3. Cross-Correlation Maps
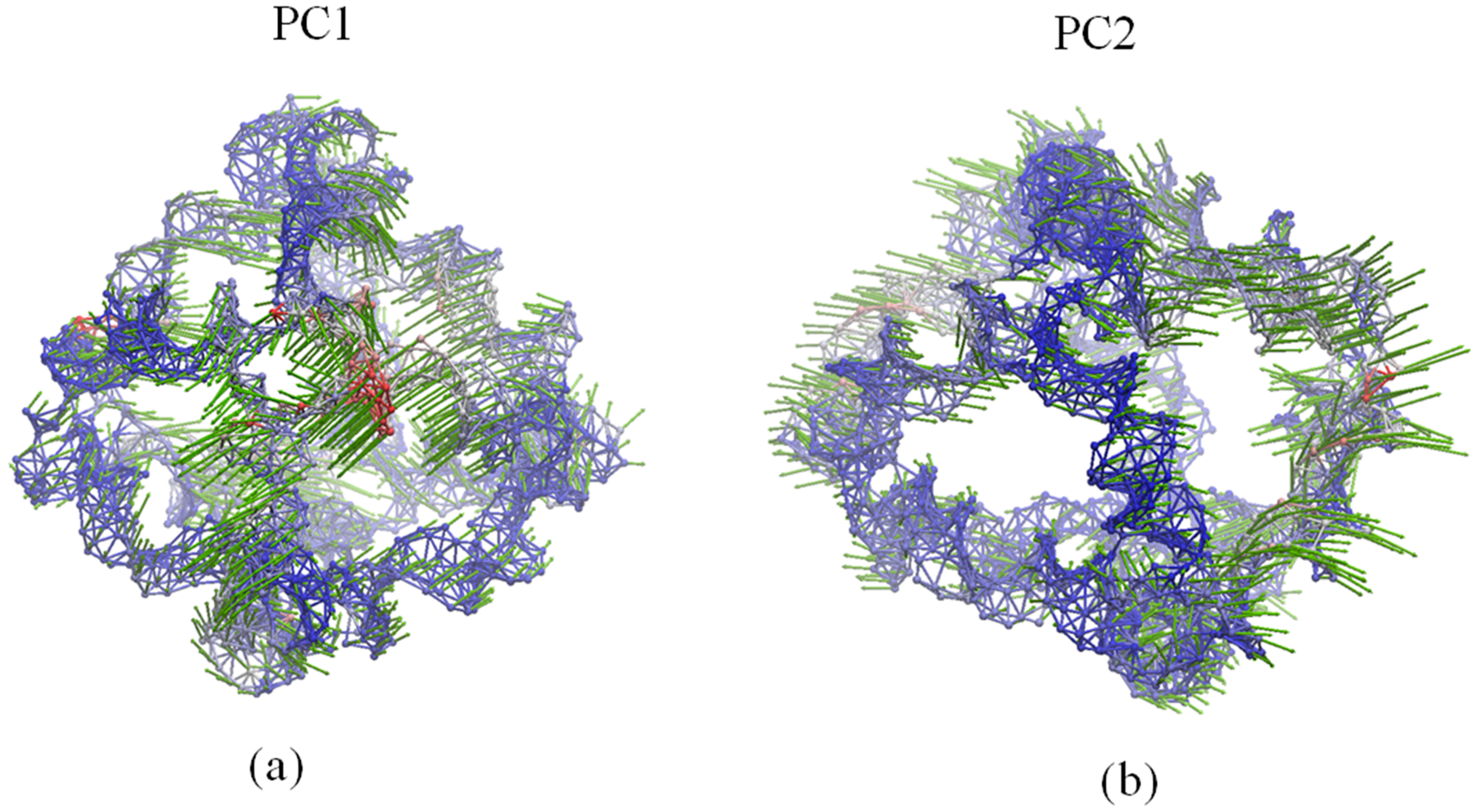
2.4. Global Motions
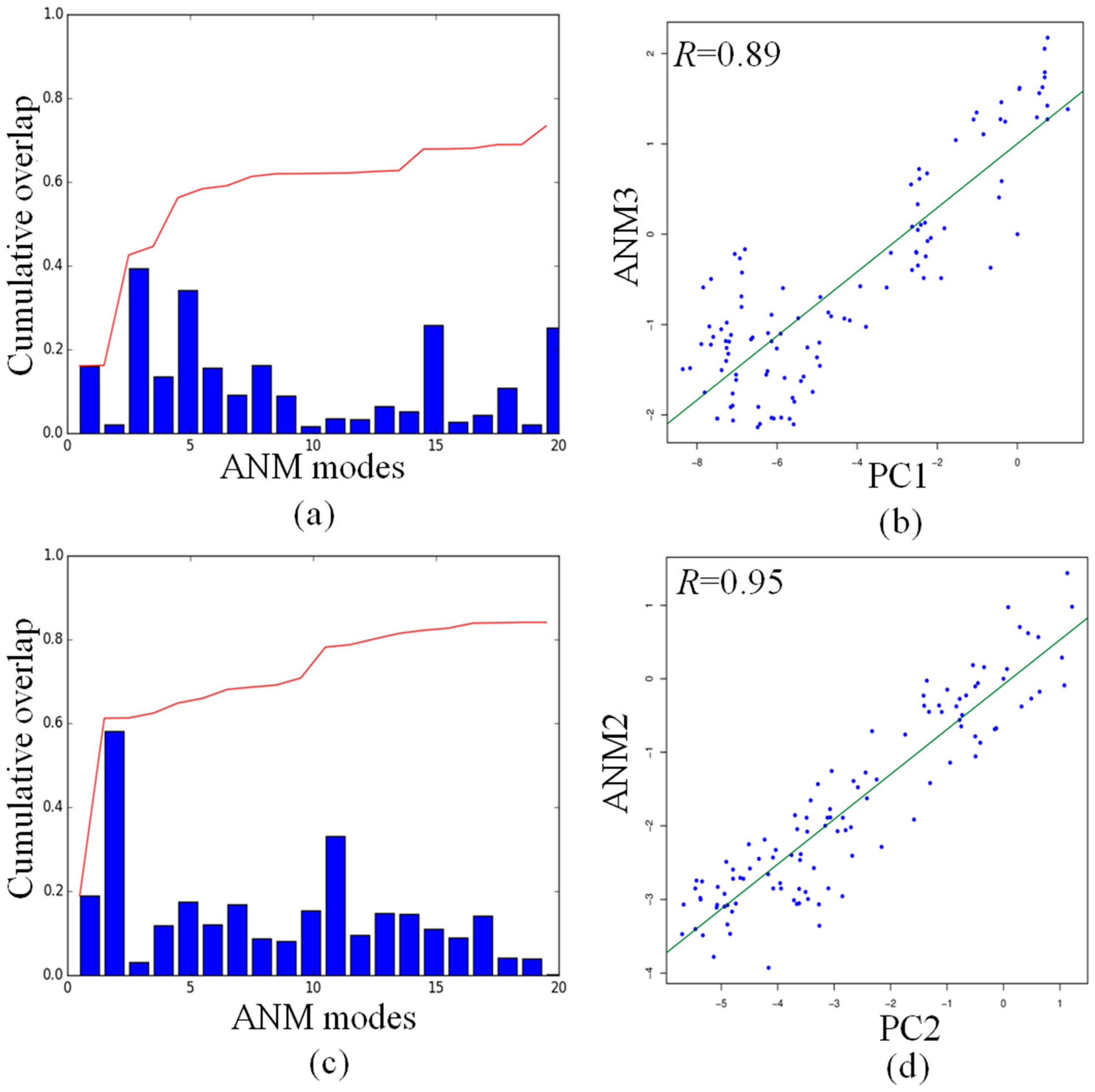
2.5. Comparison of Anysotropic Network Model and Principal Component Analysis Modes
3. Discussion
3.1. Elastic Network Models: From Proteins to DNA
3.2. Elastic Network Models for DNA: Form One Node to Three Nodes
3.3. Limitions of Elastic Network Models and Future Works
4. Materials and Methods
4.1. Computer Modeling and Molecular Dynamics Analysis
4.2. Gaussian Network Model and Anisotropy Network Model
4.3. Overlap of Modes
4.4. Computational Detail
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, F.; Nangreave, F.; Liu, Y.; Yan, H. Structural DNA nanotechnology: State of the art and future perspective. J. Am. Chem. Soc. 2014, 136, 11198–11211. [Google Scholar] [CrossRef] [PubMed]
- Chandrasekaran, A.R.; Levchenko, O. DNA Nanocages. Chem. Mater. 2016, 28, 5569–5581. [Google Scholar] [CrossRef]
- Goodman, R.P.; Schaap, I.A.T.; Tardin, C.F.; Erben, C.M.; Berry, R.M.; Schmidt, C.F.; Turberfield, A.J. Rapid chiral assembly of rigid DNA building blocks for molecular nanofabrication. Science 2005, 310, 1661–1665. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.H.; Seeman, N.C. Synthesis from DNA of a molecule with the connectivity of a cube. Nature 1991, 350, 631–633. [Google Scholar] [CrossRef] [PubMed]
- Andersen, F.F.; Knudsen, B.; Oliveira, C.L.P.; Frøhlich, R.F.; Krüger, D.; Bungert, J.; Agbandje-McKenna, M.; McKenna, R.; Juul, S.; Veigaard, C.; et al. Assembly and structural analysis of a covalently closed nano-scale DNA cage. Nucleic Acids Res. 2008, 36, 1113–1119. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Ye, T.; Su, M.; Zhang, C.; Ribbe, A.E.; Jiang, W.; Mao, C. Hierarchical self-assembly of DNA into symmetric supramolecular polyhedra. Nature 2008, 452, 198–201. [Google Scholar] [CrossRef] [PubMed]
- Mehtab, S.; Bhatia, D.; Krishnan, Y. Icosahedral DNA nanocapsules by modular assembly. Angew. Chem. Int. Ed. 2009, 48, 4134–4137. [Google Scholar] [CrossRef]
- Iinuma, R.; Ke, Y.; Jungmann, R.; Schlichthaerle, T.; Woehrstein, J.B.; Yin, P. Polyhedra self-assembled from DNA tripods and characterized with 3D DNA-PAINT. Science 2014, 344, 65–69. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Z.; Fu, J.; Dhakal, S.; Johnson-Buck, A.; Liu, M.; Zhang, T.; Woodbury, N.W.; Liu, Y.; Walter, N.G.; Yan, H. Nanocaged enzymes with enhanced catalytic activity and increased stability against protease digestion. Nat. Commun. 2016, 7, 10619. [Google Scholar] [CrossRef] [PubMed]
- Juul, S.; Iacovelli, F.; Falconi, M.; Kragh, S.L.; Christensen, B.; Frøhlich, R.; Franch, O.; Kristoffersen, E.L.; Stougaard, M.; Leong, K.W.; et al. Temperature-controlled encapsulation and release of an active enzyme in the cavity of a self-assembled DNA nanocage. ACS Nano 2013, 7, 9724–9734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, X.; Xu, Y.; Yu, T.; Clifford, C.; Liu, Y.; Yan, H.; Chang, Y. A DNA nanostructure platform for directed assembly of synthetic vaccines. Nano Lett. 2012, 12, 4254–4259. [Google Scholar] [CrossRef] [PubMed]
- Iacovelli, F.; Falconi, M. Decoding the conformation-linked functional properties of nucleic acids by the use of computational tools. FEBS J. 2015, 282, 3298–3310. [Google Scholar] [CrossRef] [PubMed]
- Falconi, M.; Oteri, F.; Chillemi, G.; Andersen, F.F.; Tordrup, D.; Oliveira, C.L.P.; Pedersen, J.S.; Knudsen, B.R.; Desideri, A. Deciphering the structural properties that confer stability to a DNA nanocage. ACS Nano 2009, 3, 1813–1822. [Google Scholar] [CrossRef] [PubMed]
- Oliveira, C.L.P.; Juul, S.; Jørgensen, H.L.; Knudsen, B.; Tordrup, D.; Oteri, F.; Falconi, M.; Koch, J.; Desideri, A.; Pedersen, J.S.; et al. Structure of nanoscale truncated octahedral DNA cages: Variation of single-stranded linker regions and influence on assembly yields. ACS Nano 2010, 4, 1367–1376. [Google Scholar] [CrossRef] [PubMed]
- Oteri, F.; Falconi, M.; Chillemi, G.; Andersen, F.F.; Oliveira, C.L.P.; Pedersen, J.S.; Knudsen, B.R.; Desideri, A. Simulative Analysis of a Truncated Octahedral DNA Nanocage Family Indicates the Single-Stranded Thymidine Linkers as the Major Player for the Conformational Variability. J. Phys. Chem. C 2011, 115, 16819–16827. [Google Scholar] [CrossRef]
- Iacovelli, F.; Falconi, M.; Knudsen, B.R.; Desideri, A. Comparative simulative analysis of single and double stranded truncated octahedral DNA nanocages. RSC Adv. 2016, 6, 35160–35166. [Google Scholar] [CrossRef]
- Iacovelli, F.; Alves, C.; Falconi, M.; Oteri, F.; Oliveira, C.L.P.; Desideri, A. Influence of the Single-Strand Linker Composition on the Structural/Dynamical Properties of a Truncated Octahedral DNA Nano-Cage Family. Biopolymers 2014, 101, 992–999. [Google Scholar] [CrossRef] [PubMed]
- Doye, J.P.; Ouldridge, T.E.; Louis, A.A.; Romano, F.; Šulc, P.; Matek, C.; Snodin, B.E.K.; Rovigatti, L.; Schreck, J.S.; Harrison, R.M.; et al. Coarse-graining DNA for simulations of DNA nanotechnology. Phys. Chem. Chem. Phys. 2013, 15, 20395–20414. [Google Scholar] [CrossRef] [PubMed]
- Kocar, V.; Schreck, J.S.; Čeru, S.; Gradišar, H.; Bašić, N.; Pisanski, T.; Doye, J.P.K.; Jerala, R. Design principles for rapid folding of knotted DNA nanostructures. Nat. Commun. 2016, 7, 10803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schreck, J.S.; Romano, F.; Zimmer, M.H.; Louis, A.A.; Doye, J.P.K. Characterizing DNA Star-Tile-Based Nanostructures Using a Coarse-Grained Model. ACS Nano 2016, 10, 4236–4247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Snodin, B.E.; Romano, F.; Rovigatti, L.; Ouldridge, T.E.; Louis, A.A.; Doye, J.P.K. Direct Simulation of the Self-Assembly of a Small DNA Origami. ACS Nano 2016, 10, 1724–1737. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Zhai, X.; Lu, D.; Qiu, W. The architecture of Platonic polyhedral links. J. Math. Chem. 2009, 46, 592–603. [Google Scholar] [CrossRef]
- Hu, G.; Qiu, W.; Ceulemans, A. A New Euler’s Formula for DNA Polyhedra. PLoS ONE 2011, 6, e2630810. [Google Scholar] [CrossRef] [PubMed]
- Hu, G.; Wang, Z.; Qiu, W. A Survey on Mathematical Models for DNA Polyhedra. Match-Commun. Math. Comput. Chem. 2013, 70, 725–742. [Google Scholar]
- Jonoska, N.; Twarock, R. Blueprints for dodecahedral DNA cages. J. Phys. A Math. Theor. 2008, 41, 30404330. [Google Scholar] [CrossRef]
- Cheng, X.S.; Jin, X. The braid index of complicated DNA polyhedral links. PLoS ONE 2012, 7, e48968. [Google Scholar] [CrossRef] [PubMed]
- Alves, C.; Iacovelli, F.; Falconi, M.; Cardamone, F.; Rocca, B.M.; Oliveira, C.L.P.; Desideri, A. A Simple and Fast Semiautomatic Procedure for the Atomistic Modeling of Complex DNA Polyhedra. J. Chem. Inf. Model. 2016, 56, 941–949. [Google Scholar] [CrossRef] [PubMed]
- Bahar, I.; Lezon, T.R.; Yang, L.W.; Eyal, E. Global dynamics of proteins: Bridging between structure and function. Annu. Rev. Biophys. 2010, 39, 23–42. [Google Scholar] [CrossRef] [PubMed]
- Tirion, M.M. Large Amplitude Elastic Motions in Proteins from a Single-Parameter, Atomic Analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar] [CrossRef] [PubMed]
- Bahar, I.; Atilgan, A.R.; Erman, B. Direct evaluation of thermal fluctuations in proteins using a single-parameter harmonic potential. Fold. Des. 1997, 2, 173–181. [Google Scholar] [CrossRef]
- Li, H.; Chang, Y.; Yang, L.W.; Bahar, I. iGNM 2.0: The Gaussian network model database for biomolecular structural dynamics. Nucleic Acids Res. 2016, 44, D415–D422. [Google Scholar] [CrossRef] [PubMed]
- Atilgan, A.R.; Durell, S.R.; Jernigan, R.L.; Demirel, M.C.; Keskin, O.; Bahar, I. Anisotropy of fluctuation dynamics of proteins with an elastic network model. Biophys. J. 2001, 80, 505–515. [Google Scholar] [CrossRef]
- Eyal, E.; Lum, G.; Bahar, I. The anisotropic network model web server at 2015 (ANM 2.0). Bioinformatics 2015, 31, 1487–1489. [Google Scholar] [CrossRef] [PubMed]
- Bakan, A.; Bahar, I. The intrinsic dynamics of enzymes plays a dominant role in determining the structural changes induced upon inhibitor binding. Proc. Natl. Acad. Sci. USA 2009, 106, 14349–14354. [Google Scholar] [CrossRef] [PubMed]
- Skjaerven, L.; Martinez, A.; Reuter, N. Principal component and normal mode analysis of proteins; a quantitative comparison using the GroEL subunit. Proteins 2011, 79, 232–243. [Google Scholar] [CrossRef] [PubMed]
- Raimondi, F.; Felline, A.; Fanelli, F. Catching Functional Modes and Structural Communication in Dbl Family Rho Guanine Nucleotide Exchange Factors. J. Chem. Inf. Model. 2015, 55, 1878–1893. [Google Scholar] [CrossRef] [PubMed]
- Li, X.Y.; Zhang, J.C.; Zhu, Y.Y.; Su, J.G. Domain Motions and Functionally-Key Residues of l-Alanine Dehydrogenase Revealed by an Elastic Network Model. Int. J. Mol. Sci. 2015, 16, 29383–29397. [Google Scholar] [CrossRef] [PubMed]
- Van Wynsberghe, A.W.; Cui, Q. Comparison of mode analyses at different resolutions applied to nucleic acid systems. Biophys. J. 2005, 89, 2939–2949. [Google Scholar] [CrossRef] [PubMed]
- Afonin, K.A.; Kasprzak, W.; Bindewald, E.; Puppala, P.S.; Diehl, A.R.; Hall, K.T.; Kim, T.J.; Zimmermann, M.T.; Jernigan, R.L.; Jaeger, L.; et al. Computational and experimental characterization of RNA cubic nanoscaffolds. Methods 2014, 67, 256–265. [Google Scholar] [CrossRef] [PubMed]
- Emekli, U.; Schneidman-Duhovny, D.; Wolfson, H.J.; Nussinov, R.; Haliloglu, T. HingeProt: Automated prediction of hinges in protein structures. Proteins 2008, 70, 1219–1227. [Google Scholar] [CrossRef] [PubMed]
- Fuglebakk, E.; Tiwari, S.; Reuter, N. Comparing the intrinsic dynamics of multiple protein structures using elastic network models. Biochim. Biophys. Acta 2015, 1850, 911–922. [Google Scholar] [CrossRef] [PubMed]
- Isami, S.; Sakamoto, N.; Nishimori, H.; Awazu, A. Simple Elastic Network Models for Exhaustive Analysis of Long Double-Stranded DNA Dynamics with Sequence Geometry Dependence. PLoS ONE 2015, 10, e0143760. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, A.L.; Teixidó, J.; Borrell, J.I.; Estrada-Tejedor, R. On the Applicability of Elastic Network Models for the Study of RNA CUG Trinucleotide Repeat Overexpansion. PLoS ONE 2016, 11, e0152049. [Google Scholar] [CrossRef] [PubMed]
- Pinamonti, G.; Bottaro, S.; Micheletti, C.; Bussi, G. Elastic network models for RNA: A comparative assessment with molecular dynamics and SHAPE experiments. Nucleic Acids Res. 2015, 43, 7260–7269. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, M.T.; Jernigan, R.L. Elastic network models capture the motions apparent within ensembles of RNA structures. RNA 2014, 20, 792–804. [Google Scholar] [CrossRef] [PubMed]
- Setny, P.; Zacharias, M. Elastic Network Models of Nucleic Acids Flexibility. J. Chem. Theory Comput. 2013, 9, 5460–5470. [Google Scholar] [CrossRef] [PubMed]
- Bahar, I.; Jernigan, R.L. Vibrational dynamics of transfer RNAs: Comparison of the free and synthetase-bound forms. J. Mol. Biol. 1998, 281, 871–884. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Rader, A.J.; Bahar, I.; Jernigan, R.L. Global ribosome motions revealed with elastic network model. J. Struct. Biol. 2004, 147, 302–314. [Google Scholar] [CrossRef] [PubMed]
- Delarue, M.; Sanejouand, Y.H. Simplified normal mode analysis of conformational transitions in DNA-dependent polymerases: The elastic network model. J. Mol. Biol. 2002, 320, 1011–1024. [Google Scholar] [CrossRef]
- Takenaka, T.; Endo, M.; Suzuki, Y.; Yang, Y.; Emura, T.; Hidaka, K.; Kato, T.; Miyata, T.; Namba, K.; Sugiyama, H. Photoresponsive DNA nanocapsule having an open/close system for capture and release of nanomaterials. Chemistry 2014, 20, 14951–14954. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef] [PubMed]
- Bakan, A.; Meireles, L.M.; Bahar, I. ProDy: Protein dynamics inferred from theory and experiments. Bioinformatics 2011, 27, 1575–1577. [Google Scholar] [CrossRef] [PubMed]
- Bahar, I.; Cheng, M.H.; Lee, J.Y.; Kaya, C.; Zhang, S. Structure-Encoded Global Motions and Their Role in Mediating Protein-Substrate Interactions. Biophys. J. 2015, 109, 1101–1109. [Google Scholar] [CrossRef] [PubMed]
- Sample Availability: Not available.

| MD | PC1 | PC2 | PC3 | PC4 | PC5 |
| p | 0.32 | 0.15 | 0.09 | 0.06 | 0.03 |
| k | 0.74 | 0.77 | 0.74 | 0.72 | 0.73 |
| ANM | ANM1 | ANM2 | ANM3 | ANM4 | ANM5 |
| p | 0.06 | 0.05 | 0.05 | 0.04 | 0.04 |
| k | 0.81 | 0.79 | 0.82 | 0.73 | 0.81 |
| GNM | GNM1 | GNM2 | GNM3 | GNM4 | GNM5 |
| p | 0.10 | 0.09 | 0.07 | 0.04 | 0.04 |
| k | 0.66 | 0.54 | 0.56 | 0.65 | 0.49 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; He, L.; Iacovelli, F.; Falconi, M. Intrinsic Dynamics Analysis of a DNA Octahedron by Elastic Network Model. Molecules 2017, 22, 145. https://doi.org/10.3390/molecules22010145
Hu G, He L, Iacovelli F, Falconi M. Intrinsic Dynamics Analysis of a DNA Octahedron by Elastic Network Model. Molecules. 2017; 22(1):145. https://doi.org/10.3390/molecules22010145
Chicago/Turabian StyleHu, Guang, Lei He, Federico Iacovelli, and Mattia Falconi. 2017. "Intrinsic Dynamics Analysis of a DNA Octahedron by Elastic Network Model" Molecules 22, no. 1: 145. https://doi.org/10.3390/molecules22010145
APA StyleHu, G., He, L., Iacovelli, F., & Falconi, M. (2017). Intrinsic Dynamics Analysis of a DNA Octahedron by Elastic Network Model. Molecules, 22(1), 145. https://doi.org/10.3390/molecules22010145