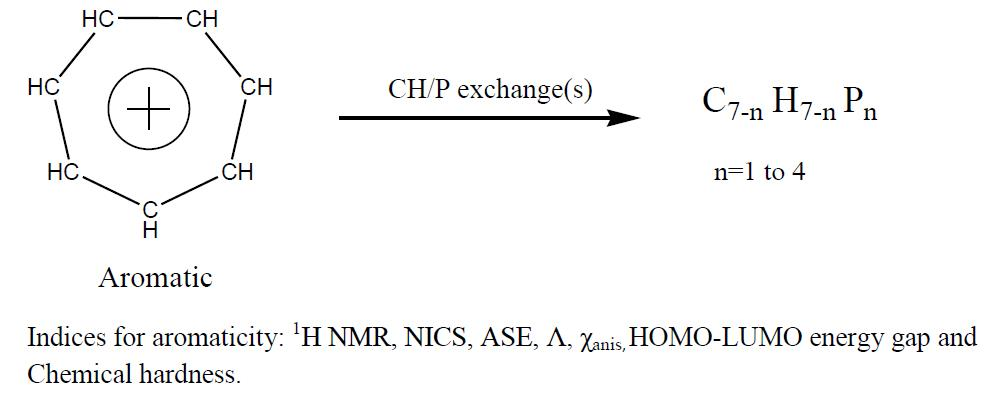
Effect of Mono- and Poly-CH/P Exchange(s) on the Aromaticity of the Tropylium Ion
Abstract
:1. Introduction
- Structure—tendency towards bond length equalization and planarity (if applicable).
- Energy—enhanced stability.
- Reactivity—lowered reactivity, electrophilic aromatic substitution (if applicable).
- Magnetic properties—proton nucleus magnetic resonance (1H-NMR) chemical shift, magnetic susceptibility exaltation and anisotropies, nucleus-independent chemical shift (NICS), ring current plots.
2. Results and Discussion
2.1. Optimized Geometries
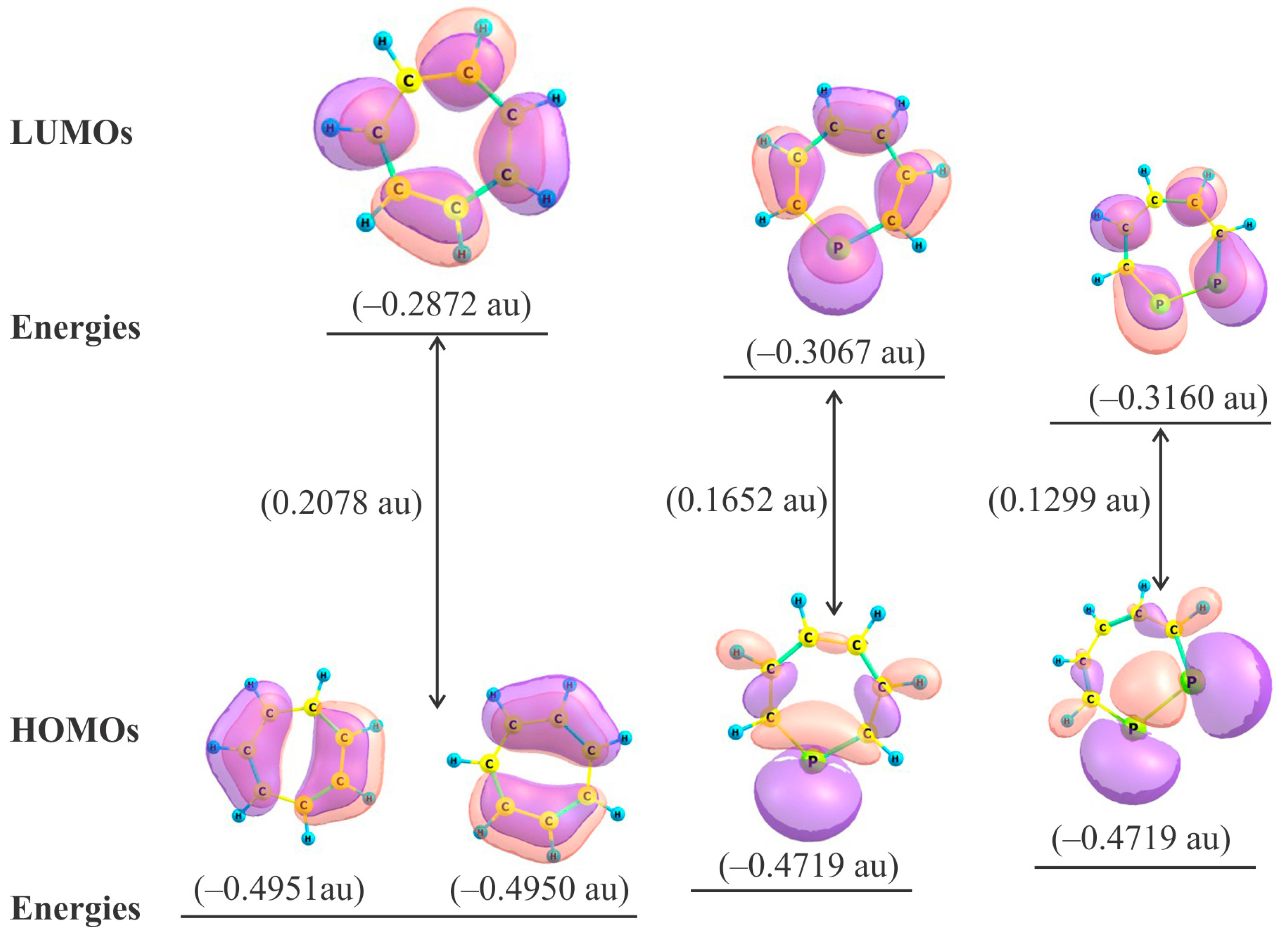
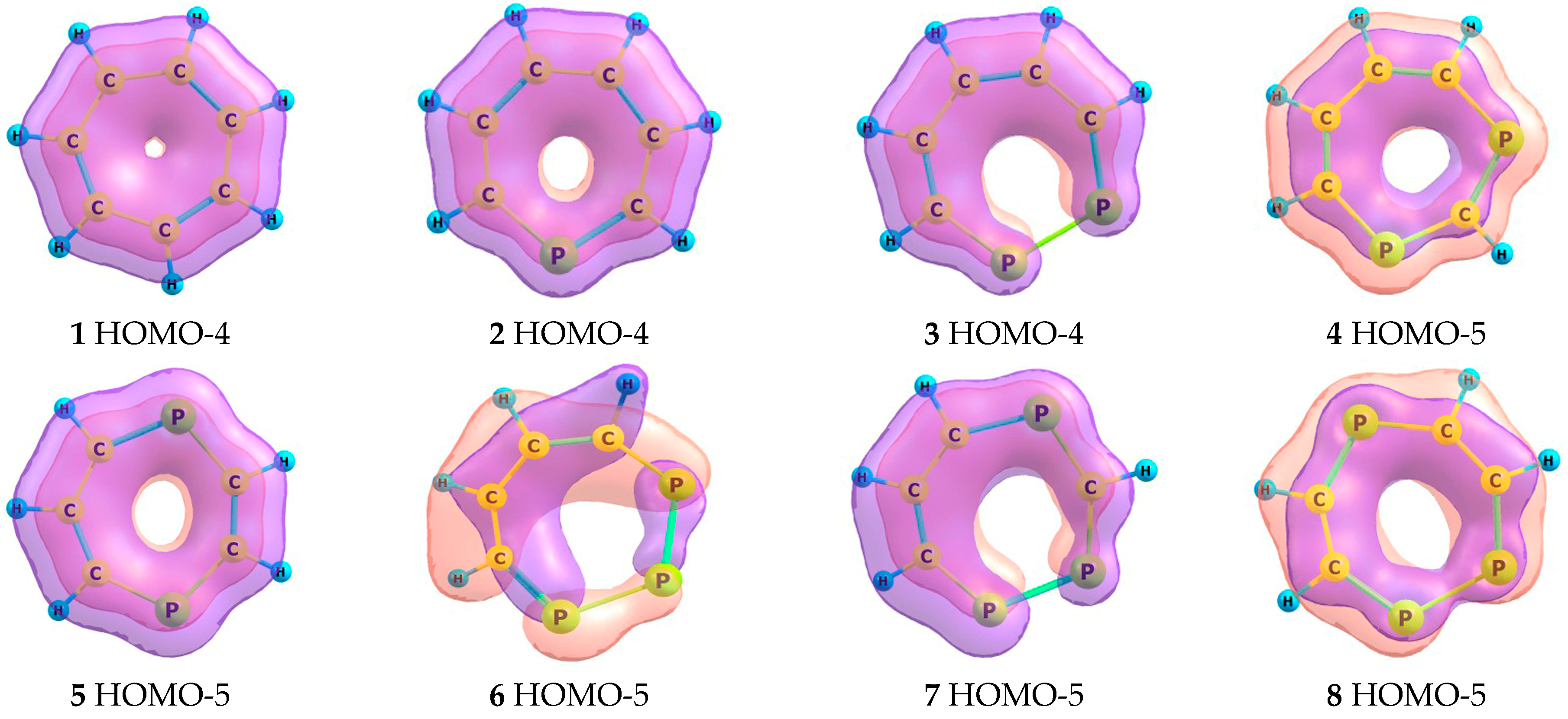
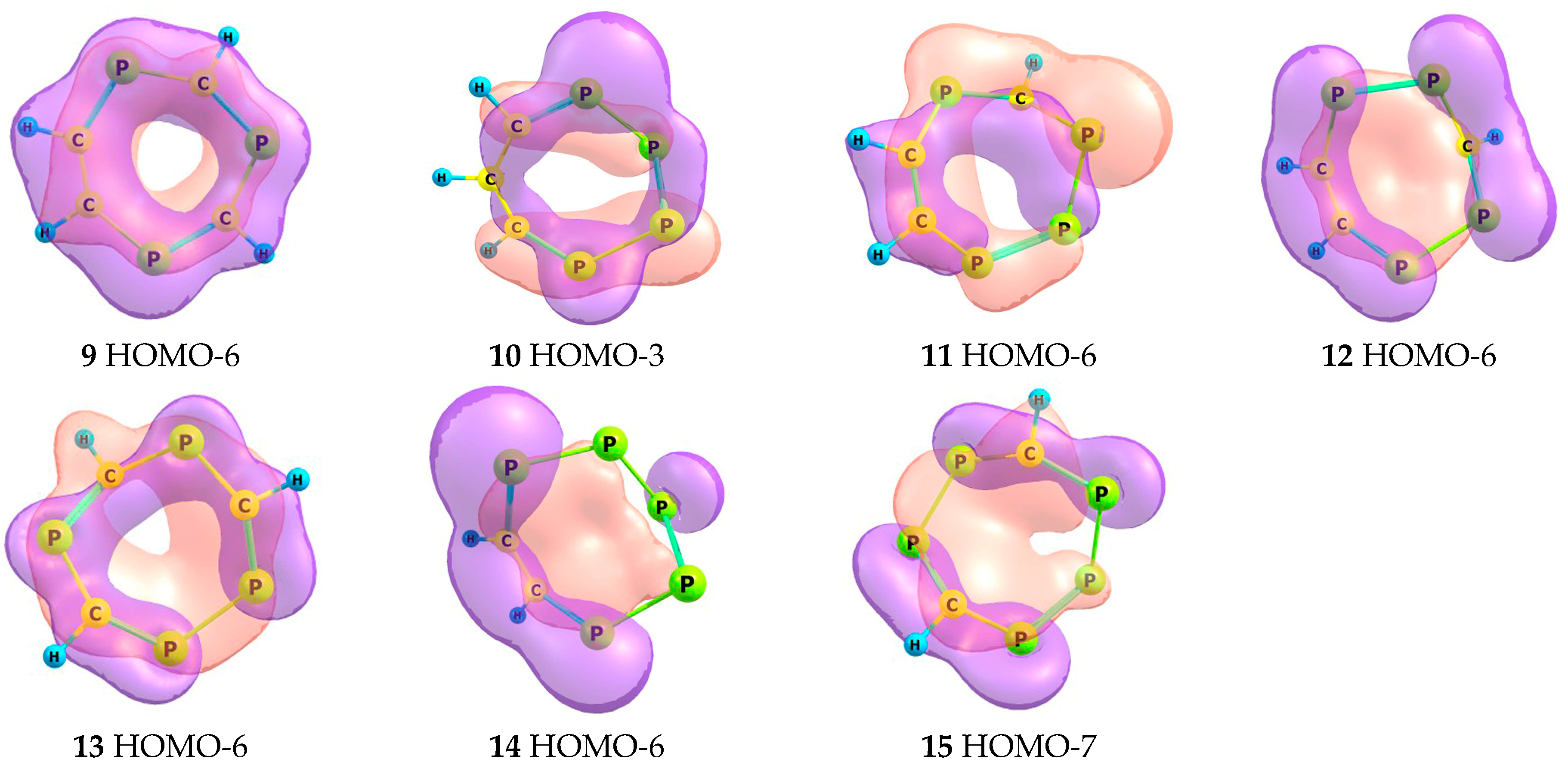
2.2. Frontier Molecular Orbitals
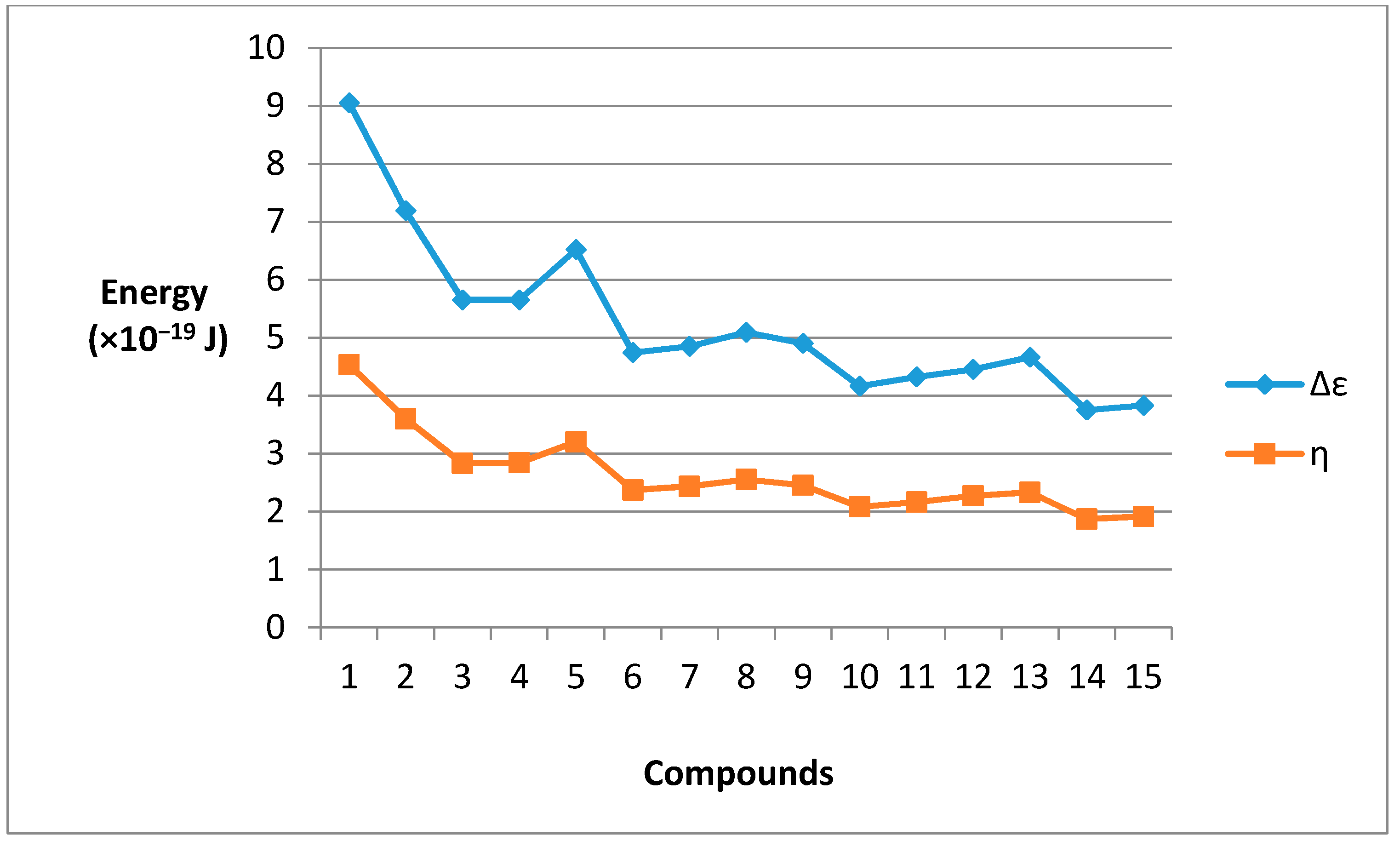
2.3. HOMO − LUMO Energy Gap
2.4. ASE
2.5. Magnetic Criteria
2.5.1. 1H-NMR Chemical Shifts
2.5.2. NICS Values
2.5.3. Magnetic Susceptibility Exaltation
2.5.4. Magnetic Anisotropy
3. Computational Method and Models
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Garratt, P.J. Aromaticity; Wiley-Inc.: Hoboken, NJ, USA, 1986. [Google Scholar]
- Minkin, V.J.; Glukhovtsev, M.N.; Simkin, B.Y. Aromaticity and Antiaromaticity; Electronic and Structural Aspects; John Wiley & Sons, Inc.: New York, NY, USA, 1994. [Google Scholar]
- Bergmann, E.D.; Pullman, B. Aromaticity, Pseudo-Aromaticity, Anti-Aromaticity, Proceedings of Jerusalem Symposium on Quantum Chemistry and Biochemistry, Jerusalem, Israel, 31 March–3 April 1970; Academic Press Inc.: Jerusalem, Israel, 1971.
- Cyranski, M.K.; Krygowski, T.M.; Katritzky, A.R.; Schleyer, P.v.R. To what extent can aromaticity be defined uniquely. J. Org. Chem. 2002, 67, 1333–1338. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Jiao, H. What is aromaticity? Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Freeman, P.K.; Jiao, H.; Goldfuss, B. Aromaticity and Antiaromaticity in Five-Membered C4H4X Ring Systems: Classical and Magnetic Concepts May Not Be Orthogonal. Angew. Chem. Int. Ed. Engl. 1995, 34, 337–340. [Google Scholar] [CrossRef]
- Mills, N.S.; Benish, M. The Aromaticity/Antiaromaticity Continuum. I. Comparison of the aromaticity of the dianion and the antiaromaticity of the dication of tetrabenzo[5.5]fulvalene via magnetic measures. J. Org. Chem. 2006, 71, 2207–2213. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Karelson, M.; Wells, A.P. Aromaticity as a Quantitative Concept. 6. Aromaticity Variation with Molecular Environment. J. Org. Chem. 1996, 61, 1619–1623. [Google Scholar] [CrossRef] [PubMed]
- Katritzky, A.R.; Karelson, M.; Sild, S.; Krygowski, T.M.; Jug, K. Aromaticity as a Quantitative Concept. 7. Aromaticity Reaffirmed as a Multidimensional Characteristic. J. Org. Chem. 1998, 63, 5228–5231. [Google Scholar] [CrossRef]
- Thematic issue on Aromaticity. Chem. Rev. 2001, 101, 1115–1566.
- Thematic issue on Delocalization of pi- and sigma. Chem. Rev. 2005, 105, 3433–3947.
- Thematic issue on Challenges in Aromaticity: 150 years after Kekule’s benzene. Chem. Soc. Rev. 2015, 44, 6397–6643.
- Hückel, E. Grundzüge der Theorie Ungesättiger und Aromatischer Verbindungen. Z. Elektrochem. Angew. Phys. Chem. 1937, 43, 752–788. [Google Scholar]
- Platt, J.R. The box model and electron densities in conjugated systems. J. Chem. Phys. 1954, 22, 1448–1455. [Google Scholar]
- Breslow, R. Aromatic character. Chem. Eng. News 1965, 43, 90–100. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, R. Nucleus-independent chemical shifts (NICS) as an aromaticity criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar]
- Krygowski, T.M.; Szatylowicz, H.; Stasyuk, O.A.; Dominikowska, J.; Palusiak, M. Aromaticity from the viewpoint of molecular geometry: Application to planar systems. Chem. Rev. 2014, 114, 6383–6422. [Google Scholar] [CrossRef] [PubMed]
- Julg, A.; Francois, P. Researches sur la géométrie de quelques hydrocarbures non-alternants: Son influence sur les énergies de transition, une nouvelle définition de l’aromaticité. Theor. Chim. Acta 1967, 8, 249–259. [Google Scholar] [CrossRef]
- Bird, C.W. A new aromaticity index and its application to five-membered ring heterocycles. Tetrahedron 1985, 41, 1409–1414. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Pülhofer, F. Recommendations for the evaluation of aromatic stabilization energies. Org. Lett. 2002, 4, 2873–2876. [Google Scholar] [CrossRef] [PubMed]
- Pascal, P. Magnetochemical Researches. Ann. Chim. Phys. 1910, 19, 5–70. [Google Scholar]
- Mitchell, R.H. Measuring aromaticity by NMR. Chem. Rev. 2001, 101, 1301–1315. [Google Scholar] [CrossRef] [PubMed]
- Schleyer, P.v.R.; Maerker, C.; Dransfeld, A.; Jiao, H.; Hommes, N.J.R.v.E. Nucleus-independent chemical shifts: A simple and efficient aromaticity probe. J. Am. Chem. Soc. 1996, 118, 6317–6318. [Google Scholar] [CrossRef]
- Appel, R. pπ-Double bonds between phosphorus and carbon—A challenge. Pure Appl. Chem. 1987, 59, 977–982. [Google Scholar] [CrossRef]
- Nyulászi, L.; Veszprémi, T.; Réffy, J. A new look at the similarities of the conjugative ability and reactivity of P=C and C=C double bonding. J. Phys. Chem. 1993, 97, 4011–4015. [Google Scholar] [CrossRef]
- Nyulászi, L.; Várnai, P.; Krill, S.; Regitz, M. Aromaticity of thia- and selena-phospholes: A photoelectron spectroscopic and quantum chemical study. J. Chem. Soc. Perkin Trans. 1995, 2, 315–318. [Google Scholar] [CrossRef]
- Nyulászi, L.; Várnai, P.; Veszprémi, T. About the aromaticity of five-membered heterocycles. J. Mol. Struct. THEOCHEM 1995, 358, 55–61. [Google Scholar] [CrossRef]
- Cloke, F.G.N.; Hitchcock, P.B.; Nixon, J.F.; Wilson, D.J.; Tabellion, F.; Fischbeck, U.; Preuss, F.; Regitz, M. Synthetic, structural and theoretical studies on new aromatic 1,2,4-diazaphosphole ring systems: Crystal and molecular structure of P2C2But2NPh. Chem. Commun. 1999. [Google Scholar] [CrossRef]
- Mathey, F. Expanding the analogy between phosphorus-carbon and carbon-carbon double bonds. Acc. Chem. Res. 1992, 25, 90–96. [Google Scholar] [CrossRef]
- Schmidpeter, A. Molecules that we made: An essay on phosphorus chemistry. Heteroat. Chem. 1999, 10, 529–537. [Google Scholar] [CrossRef]
- Bansal, R.K.; Heinicke, J. Anellated heterophospholes and phospholides and analogies with related non-phosphorus systems. Chem. Rev. 2001, 101, 3549–3578. [Google Scholar] [CrossRef] [PubMed]
- Simpson, M.C.; Protasiewicz, J.D. Phosphorus as a carbon copy and as a photocopy: New conjugated materials featuring multiply bonded phosphorus. Pure Appl. Chem. 2013, 85, 801–815. [Google Scholar] [CrossRef]
- Bansal, R.K.; Gupta, R.; Maheshwari, P.; Kour, M. Analogy of phosphaalkenes and azaphospholes with their respective non-phosphorus analogues. Curr. Org. Chem. 2016, 20, 2099–2108. [Google Scholar] [CrossRef]
- Dillon, K.B.; Mathey, F.; Nixon, J.F. Phosphorus: The Carbon Copy; Wiley: New York, NY, USA, 1988; pp. 203–226. [Google Scholar]
- Nyulászi, L. Aromaticity of phosphorus heterocycles. Chem. Rev. 2001, 101, 1229–1246. [Google Scholar] [CrossRef] [PubMed]
- Nyulászi, L.; Benkὅ, Z. Aromatic phosphorus heterocycles. In Aromaticity in Heterocyclic Compounds; Krygowski, T.M., Cyranski, M.K., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2009; Volume 19, pp. 27–81. [Google Scholar]
- Gupta, R.; Bansal, R.K. Aromaticity/antiaromaticity of phospha-analogues of carbocyclic ions: A DFT investigation. Comp. Theor. Chem. 2016, 1076, 1–10. [Google Scholar] [CrossRef]
- Gupta, R.; Maheshwari, P.; Kour, M. Reinvestigation of the aromaticity of mono- and polyphosphacyclopentadienide ions at the DFT level. Comp. Theor. Chem. 2015, 1060, 10–16. [Google Scholar] [CrossRef]
- Ghiasi, R. Theoretical study of classical isomers tropylium, azatropylium, phosphatropylium, and arsatropylium cations: Structure, properties and aromaticity. Main Group Chem. 2008, 7, 147–154. [Google Scholar] [CrossRef]
- Lin, L.; Lievens, P.; Nguyen, M.T. In search of aromatic seven-membered rings. J. Mol. Struct. 2010, 943, 23–31. [Google Scholar] [CrossRef]
- Firouzi, R.; Ardani, S.S. Description of heteroaromaticity on the basis of π-electron density anisotropy. Phys. Chem. Chem. Phys. 2014, 16, 11538–11548. [Google Scholar] [CrossRef] [PubMed]
- Nyulászi, L. Toward a planar σ3–phosphorus. J. Phys. Chem. 1996, 100, 6194–6198. [Google Scholar] [CrossRef]
- Nyulászi, L. Pentaphosphole: An aromatic ring with a planar σ3–phosphorus. Inorg. Chem. 1996, 35, 4690–4693. [Google Scholar] [CrossRef]
- Glukhovtsev, M.; Dransfeld, A.; Schleyer, P.v.R. Why pentaphosphole, P5H, is planar in contrast to phosphole, (CH)4PH. J. Phys. Chem. 1996, 100, 13447–13454. [Google Scholar] [CrossRef]
- Cloke, F.G.N.; Hitchcock, P.B.; Hunnable, P.; Nixon, J.F.; Nyulászi, L.; Niecke, E.; Thelen, V. The First Delocalized Phosphole Containing a Planar Tricoordinate Phosphorus Atom: 1-[Bis (trimethylsilyl) methyl]-3, 5-bis (trimethylsilyl)-1,2,4-triphosphole. Angew. Chem. Int. Ed. 1998, 37, 1083–1086. [Google Scholar] [CrossRef]
- Manolopoulos, D.E.; May, J.C.; Down, S.E. Theoretical studies of the fullerenes: C34 to C70. Chem. Phys. Lett. 1991, 181, 105–111. [Google Scholar] [CrossRef]
- Haddon, R.C.; Fukunaga, T. Unified theory of the thermodynamic and kinetic criteria of aromatic character in the [4n + 2] annulenes. Tetrahedron Lett. 1980, 21, 1191–1192. [Google Scholar] [CrossRef]
- Schmalz, T.G.; Seitz, W.A.; Klein, D.J.; Hite, G.E. Elemental carbon cages. J. Am. Chem. Soc. 1988, 110, 1113–1127. [Google Scholar] [CrossRef]
- Zhou, Z.; Parr, R.G.; Garst, J.F. Absolute hardness as a measure of aromaticity. Tetrahedron Lett. 1988, 29, 4843–4846. [Google Scholar] [CrossRef]
- Zhou, Z.; Parr, R.G. New measures of aromaticity: Absolute hardness and relative hardness. J. Am. Chem. Soc. 1989, 111, 7371–7379. [Google Scholar] [CrossRef]
- Zhou, Z.; Parr, R.G. Activation hardness: New index for describing the orientation of electrophilic aromatic substitution. J. Am. Chem. Soc. 1990, 112, 5720–5724. [Google Scholar] [CrossRef]
- Liu, X.; Schmalz, T.G.; Klein, D.J. Favorable structures for higher fullerenes. Chem. Phys. Lett. 1992, 188, 550–554. [Google Scholar] [CrossRef]
- Parr, R.G.; Zhou, Z. Absolute hardness: Unifying concept for identifying shells and subshells in nuclei, atoms, molecules, and metallic clusters. Acc. Chem. Res. 1993, 26, 256–258. [Google Scholar] [CrossRef]
- Aihara, J.; Oe, S.; Yoshida, M.; Osawa, E.J. Further test of the isolated pentagon rule: Thermodynamic and kinetic stabilities of C84 fullerene isomers. Comput. Chem. 1996, 17, 1387–1394. [Google Scholar] [CrossRef]
- Aihara, J. Circuit resonance energy: A key quantity that links energetic and magnetic criteria of aromaticity. J. Am. Chem. Soc. 2006, 128, 2873–2879. [Google Scholar] [CrossRef] [PubMed]
- Pearson, R.G. Absolute electronegativity and hardness correlated with molecular orbital theory. Proc. Natl. Acad. Sci. USA 1986, 83, 8440–8441. [Google Scholar] [CrossRef] [PubMed]
- Pearson, R.G. Recent Advances in the Concept of Hard and Soft Acids and Bases. J. Chem. Educ. 1987, 64, 561–567. [Google Scholar] [CrossRef]
- Minsky, A.; Meyer, A.Y.; Rabinovitz, M. Paratropicity and antiaromaticity: Role of the homo-lumo energy gap. Tetrahedron 1985, 41, 785–791. [Google Scholar] [CrossRef]
- Dauben, H.J.; Wilson, J.D.; Laity, J.L. Diamagnetic susceptibility exaltation as a criterion of aromaticity. J. Am. Chem. Soc. 1968, 90, 811–813. [Google Scholar] [CrossRef]
- Dauben, H.J.; Wilson, J.D.; Laity, J.L. Diamagnetic susceptibility in hydrocarbons. J. Am. Chem. Soc. 1969, 91, 1991–1998. [Google Scholar] [CrossRef]
- Schleyer, P.v.R.; Jiao, H.J.; Hommes, N.J.R.v.E.; Malkin, V.G.; Malkina, O.L. An evaluation of the aromaticity of inorganic rings: Refined evidence from magnetic properties. J. Am. Chem. Soc. 1997, 119, 12669–12670. [Google Scholar] [CrossRef]
- Benson, R.C.; Flygare, W.H. Molecular Zeeman effect of cyclopentadiene and isoprene and comparison of the magnetic susceptibility anisotropies. J. Am. Chem. Soc. 1970, 92, 7523–7529. [Google Scholar]
- Schmalz, T.G.; Norris, C.L.; Flygare, W.H. Localized magnetic susceptibility anisotropies. J. Am. Chem. Soc. 1973, 95, 7961–7967. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian 03, Revision B.05; Gaussian, Inc.: Wallingford, CT, USA, 2003.
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990. [Google Scholar]
- Sample Availability: Not Available.
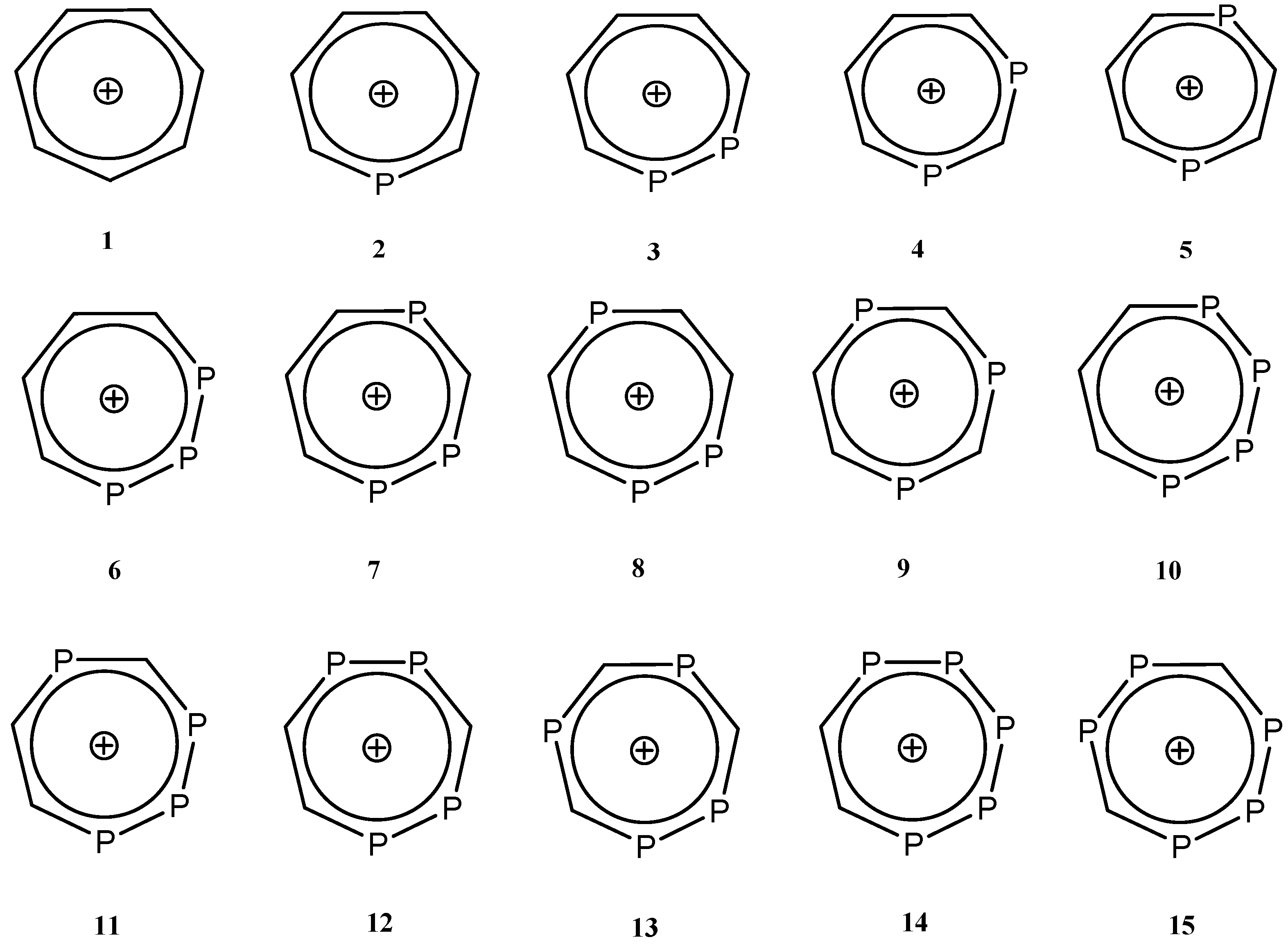
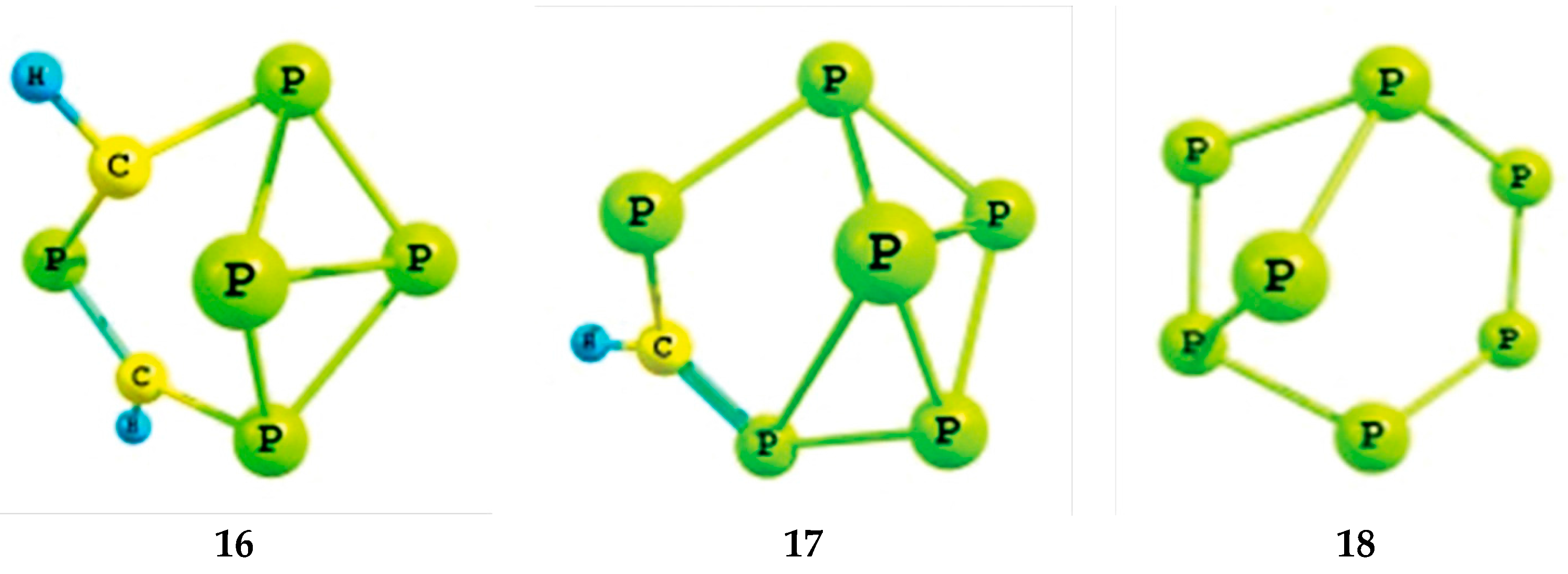
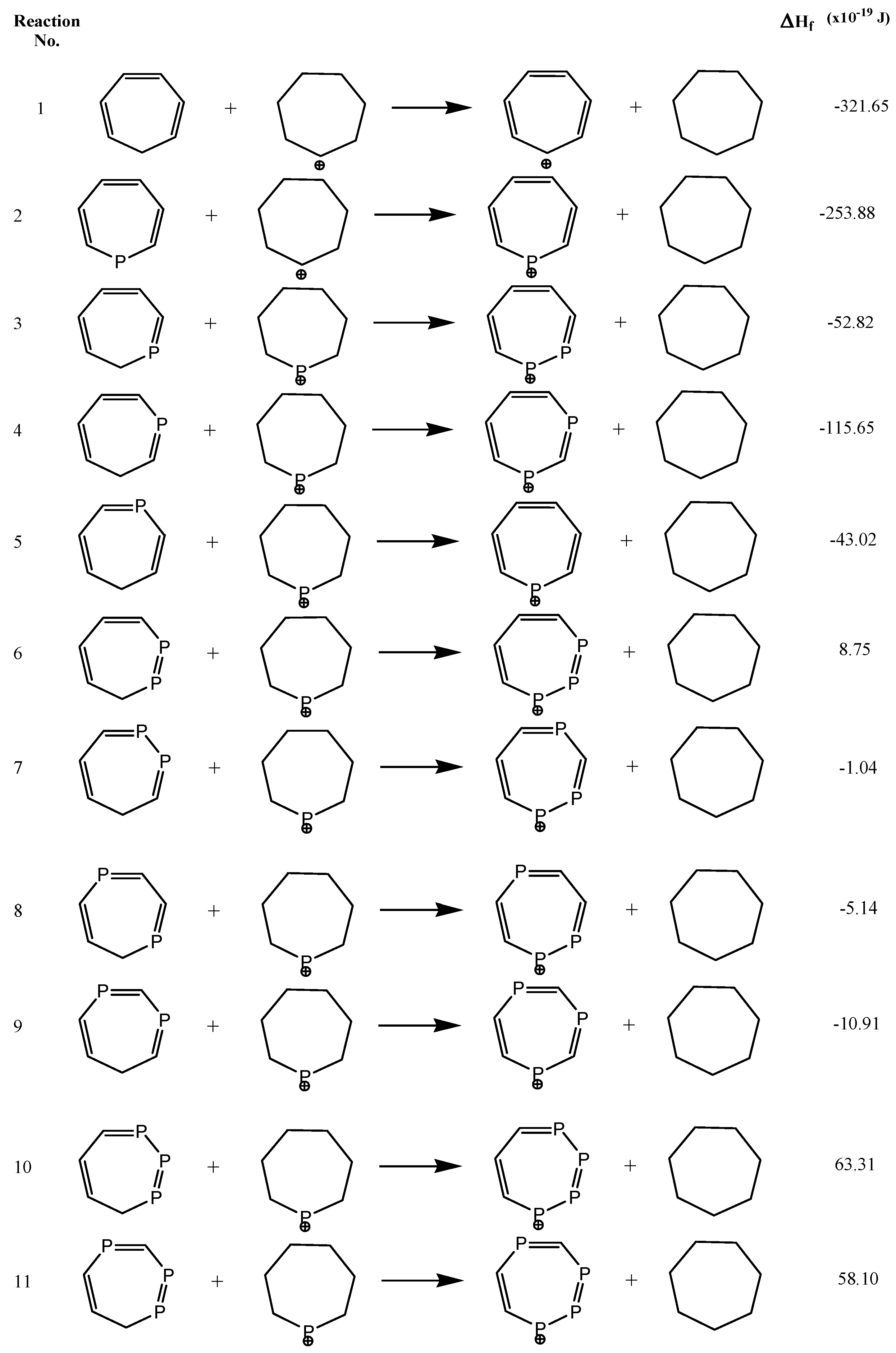
| Species | C-C (1.53 Å) | C=C (1.33 Å) | P-C (1.87 Å) | P=C (1.67 Å) | P-P (2.72 Å) | P=P (2.04 Å) |
|---|---|---|---|---|---|---|
| 1 | 1.40 | 1.40 | - | - | - | - |
| 2 | 1.41 | 1.39 | 1.75 | - | - | - |
| 3 | 1.40 | 1.40 | 1.75 | 1.75 | 2.15 | - |
| 4 | 1.41 | 1.35 | 1.75 | 1.75 | - | - |
| 5 | 1.40 | 1.40 | 1.75 | 1.75 | - | - |
| 6 | 1.40 | 1.41 | - | 1.76 | 2.13 | - |
| 7 | 1.40 | 1.40 | 1.75 | 1.75 | 2.17 | - |
| 8 | - | 1.38 | 1.76 | 1.74 | - | - |
| 9 | - | 1.40 | 1.76 | - | 2.13 | 2.14 |
| 10 | 1.40 | 1.39 | 1.75 | 1.75 | - | 2.14 |
| 11 | - | 1.38 | 1.76 | 1.74 | 2.14 | 2.11 |
| 12 | - | 1.40 | 1.75 | 1.75 | 2.14 | 2.15 |
| 13 | - | - | 1.75 | 1.74 | 2.17 | - |
| 14 | - | 1.38 | 1.76 | - | 2.14 | 2.11 |
| 15 | - | - | 1.75 | 1.75 | 2.15 | 2.13 |
| Species | HOMO (a.u.) | LUMO (a.u.) | LUMO − HOMO (a.u.) | Δε (×10−19 J) | η (×10−19 J) |
|---|---|---|---|---|---|
| 1 | −0.4951 | −0.2872 | 0.2078 | 9.05 | 4.53 |
| 2 | −0.4719 | −0.3067 | 0.1652 | 7.19 | 3.60 |
| 3 | −0.4459 | −0.3160 | 0.1299 | 5.65 | 2.83 |
| 4 | −0.4485 | −0.3179 | 0.1306 | 5.65 | 2.84 |
| 5 | −0.4650 | −0.3176 | 0.1474 | 6.52 | 3.20 |
| 6 | −0.4376 | −0.3287 | 0.1089 | 4.74 | 2.37 |
| 7 | −0.4372 | −0.3259 | 0.1113 | 4.85 | 2.43 |
| 8 | −0.4431 | −0.3264 | 0.1167 | 5.09 | 2.55 |
| 9 | −0.4384 | −0.3258 | 0.1126 | 4.90 | 2.45 |
| 10 | −0.4284 | −0.3328 | 0.0956 | 4.16 | 2.08 |
| 11 | −0.4332 | −0.3341 | 0.0991 | 4.32 | 2.16 |
| 12 | −0.4357 | −0.3335 | 0.1022 | 4.45 | 2.27 |
| 13 | −0.4331 | −0.3261 | 0.1070 | 4.66 | 2.33 |
| 14 | −0.4271 | −0.3412 | 0.0859 | 3.75 | 1.87 |
| 15 | −0.4272 | −0.3394 | 0.0878 | 3.83 | 1.91 |
| Species | 1H-NMR Chem. Shift (δ) | NICS(0) | NICS(1) | NICS(1)zz | Ʌ | χanis | ASE (×10−19J) | |
|---|---|---|---|---|---|---|---|---|
| 1 | H1 | 9.39 | −6.30 | −9.52 | −26.42 | −20.72 | −79.89 | −321.65 |
| H2 | 9.34 | |||||||
| H3 | 9.38 | |||||||
| H4 | 9.38 | |||||||
| H5 | 9.35 | |||||||
| H6 | 9.34 | |||||||
| H7 | 9.36 | |||||||
| 2 | H2 | 11.14 | −5.28 | −8.72 | −23.78 | −34.05 | −102.65 | −253.88 |
| H3 | 9.39 | |||||||
| H4 | 9.24 | |||||||
| H5 | 9.24 | |||||||
| H7 | 11.14 | |||||||
| H6 | 9.39 | |||||||
| 3 | H3 | 11.53 | −4.32 | −7.78 | −21.73 | −32.72 | −116.79 | −52.82 |
| H4 | 9.31 | |||||||
| H5 | 9.37 | |||||||
| H6 | 9.31 | |||||||
| H7 | 11.53 | |||||||
| 4 | H2 | 13.16 | −4.19 | −7.78 | −20.70 | −35.95 | −105.56 | −115.65 |
| H4 | 10.86 | |||||||
| H5 | 9.18 | |||||||
| H7 | 10.86 | |||||||
| H6 | 9.15 | |||||||
| 5 | H2 | 11.11 | −4.34 | −7.92 | −21.31 | −36.66 | −109.68 | −43.02 |
| H3 | 11.11 | |||||||
| H5 | 11.18 | |||||||
| H6 | 9.24 | |||||||
| H7 | 11.18 | |||||||
| 6 | H4 | 10.98 | −4.69 | −8.00 | −21.26 | −39.93 | −121.50 | 8.75 |
| H5 | 9.36 | |||||||
| H6 | 9.36 | |||||||
| H7 | 10.98 | |||||||
| 7 | H3 | 13.59 | −3.26 | −6.97 | −18.62 | −33.49 | −119.21 | −1.04 |
| H5 | 11.19 | |||||||
| H6 | 9.09 | |||||||
| H7 | 11.56 | |||||||
| 8 | H3 | 11.27 | −3.59 | −7.31 | −19.91 | −35.64 | −121.98 | −5.14 |
| H4 | 11.18 | |||||||
| H6 | 11.18 | |||||||
| H7 | 11.27 | |||||||
| 9 | H2 | 13.02 | −2.99 | −6.75 | −17.54 | −37.45 | −107.94 | −10.91 |
| H4 | 13.02 | |||||||
| H6 | 10.78 | |||||||
| H7 | 10.78 | |||||||
| 10 | H5 | 10.84 | −5.06 | −8.06 | −20.06 | −44.93 | −115.3 | 63.31 |
| H6 | 9.12 | |||||||
| H7 | 10.84 | |||||||
| 11 | H4 | 12.73 | −4.68 | −8.13 | −20.46 | −45.94 | −109.43 | 58.10 |
| H6 | 10.61 | |||||||
| H7 | 10.45 | |||||||
| 12 | H3 | 12.31 | −5.18 | −8.96 | -23.86 | −47.65 | −114.03 | 89.09 |
| H6 | 11.03 | |||||||
| H7 | 11.03 | |||||||
| 13 | H3 | 13.06 | −2.70 | −6.99 | −17.83 | −38.43 | −105.24 | 45.17 |
| H5 | 12.74 | |||||||
| H7 | 13.06 | |||||||
| 14 | H7 | 11.06 | −7.83 | −9.79 | −22.83 | −54.31 | −107.81 | 93.69 |
| H6 | 10.12 | |||||||
| 15 | H3 | 12.63 | −3.25 | −7.54 | −19.96 | −42.88 | −105.24 | 173.95 |
| H7 | 11.54 | |||||||
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puri, A.; Gupta, R. Effect of Mono- and Poly-CH/P Exchange(s) on the Aromaticity of the Tropylium Ion. Molecules 2016, 21, 1099. https://doi.org/10.3390/molecules21081099
Puri A, Gupta R. Effect of Mono- and Poly-CH/P Exchange(s) on the Aromaticity of the Tropylium Ion. Molecules. 2016; 21(8):1099. https://doi.org/10.3390/molecules21081099
Chicago/Turabian StylePuri, Ankita, and Raakhi Gupta. 2016. "Effect of Mono- and Poly-CH/P Exchange(s) on the Aromaticity of the Tropylium Ion" Molecules 21, no. 8: 1099. https://doi.org/10.3390/molecules21081099
APA StylePuri, A., & Gupta, R. (2016). Effect of Mono- and Poly-CH/P Exchange(s) on the Aromaticity of the Tropylium Ion. Molecules, 21(8), 1099. https://doi.org/10.3390/molecules21081099