Theoretical Study on the Second Hyperpolarizailities of Oligomeric Systems Composed of Carbon and Silicon π-Structures
Abstract
:1. Introduction
2. Results and Discussion
3. Theories and Calculation Methods
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nagase, S. Theory and Calculations of Molecules Containing Heavier Main Group Elements and Fullerenes Encaging Transition Metals: Interplay with Experiment. Bull. Chem. Soc. Jpn. 2014, 87, 167–195. [Google Scholar] [CrossRef]
- Asay, M.; Sekiguchi, A. Recent Developments in the Reactivity of Stable Disilynes. Bull Chem. Soc. Jpn. 2012, 85, 1245–1261. [Google Scholar] [CrossRef]
- Teramae, H. Ab Initio Studies on the Silicon Compound: On the Electronic Structure of Disilene Reconsidered. J. Am. Chem. Soc. 1987, 109, 4140–4142. [Google Scholar] [CrossRef]
- West, R.; Fink, M.J.; Michl, J. Tetramesityldisilene, a Stable Compound Containing a Silicon–Silicon Double Bond. Science 1981, 214, 1343–1344. [Google Scholar] [CrossRef] [PubMed]
- Wiberg, N.; Vasisht, S.K.; Fischer, G.; Mayer, P. Disilynes. III [1] A Relatively Stable Disilyne RSi≡SiR (R = SiMe(SitBu3)2). Z. Anorg. Allg. Chem. 2004, 630, 1823–1828. [Google Scholar] [CrossRef]
- Sekiguchi, A.; Kinjo, R.; Ichinohe, M. A Stable Compound Containing a Silicon–Silicon Triple Bond. Science 2004, 305, 1755–1757. [Google Scholar] [CrossRef] [PubMed]
- Weidenbruch, M.; Willms, S.; Saak, W.; Henkel, G. Hexaaryltetrasilabuta-1,3-diene: A Molecule with Conjugated Si–Si Double Bonds. Angew. Chem. Int. Ed. 1997, 36, 2503–2504. [Google Scholar] [CrossRef]
- Kobayashi, M.; Matsuo, T.; Fukunaga, T.; Hashizume, D.; Fueno, H.; Tanaka, K.; Tamao, K. Air-Stable, Room-Temperature Emissive Disilenes with π-Extended Aromatic Groups. J. Am. Chem. Soc. 2010, 132, 15162–15163. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Matsuo, T.; Hashizume, D.; Fueno, H.; Tanaka, K.; Tamao, K. Coplanar Oligo(p‑phenylenedisilenylene)s as Si=Si Analogs of Oligo(p‑phenylenevinylene)s: Evidence for Extended π‑Conjugation through the Carbon and Silicon π‑Frameworks. J. Am. Chem. Soc. 2015, 137, 15026–15035. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Sun, H.-B.; Tanaka, T.; Takada, K. Finer Features for Functional Microdevices. Nature 2001, 412, 697–698. [Google Scholar] [CrossRef] [PubMed]
- Kawata, S.; Kawata, Y. Three-Dimensional Optical Data Storage Using Photochromic Materials. Chem. Rev. 2000, 100, 1777–1788. [Google Scholar] [CrossRef] [PubMed]
- Day, D.; Gu, M.; Smallridge, A. RewriTable 3D Bit Optical Data Storage in a PMMA-Based Photorefractive Polymer. Adv. Mater. 2001, 13, 1005–1007. [Google Scholar] [CrossRef]
- Soljačić, M.; Joannopoulos, J.D. Enhancement of Nonlinear Effects Using Photonic Crystals. Nat. Mater. 2004, 3, 211–219. [Google Scholar] [CrossRef] [PubMed]
- Dirk, C.W.; Cheng, L.-T.; Kuzyk, M.G. A Simplified Three-Level Model Describing the Molecular Third-Order Nonlinear Optical Susceptibility. Int. J. Quantum Chem. 1992, 43, 27–36. [Google Scholar] [CrossRef]
- Tykwinski, R.R.; Gubler, U.; Martin, R.E.; Diederich, F.; Bosshard, C.; Günter, P. Structure-Property Relationships in Third-Order Nonlinear Optical Chromophores. J. Phys. Chem. B 1998, 102, 4451–4465. [Google Scholar] [CrossRef]
- Brédas, J.L.; Adant, C.; Tackx, P.; Persoons, A.; Pierce, B.M. Third-Order Nonlinear Optical Response in Organic Materials: Theoretical and Experimental Aspects. Chem. Rev. 1994, 94, 243–278. [Google Scholar] [CrossRef]
- Terenziani, F.; Katan, C.; Badaeva, E.; Tretiak, S.; Blanchard-Desce, M. Enhanced Two-Photon Absorption of Organic Chromophores: Theoretical and Experimental Assessments. Adv. Mater. 2008, 20, 4641–4678. [Google Scholar] [CrossRef] [Green Version]
- Spassova, M.; Champagne, B.; Kirtman, B. Large Effect of Dopant Level on Second Hyperpolarizability of Alkali-Doped Polyacetylene Chains. Chem. Phys. Lett. 2005, 412, 217–222. [Google Scholar] [CrossRef]
- Nakano, M.; Kishi, R.; Ohta, S.; Takahashi, H.; Kubo, T.; Kamada, K.; Ohta, K.; Botek, E.; Champagne, B. Relationship between Third-Order Nonlinear Optical Properties and Magnetic Interactions in Open-Shell Systems: A New Paradigm for Nonlinear Optics. Phys. Rev. Lett. 2007, 99. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Champagne, B. Theoretical Design of Open-Shell Singlet Molecular Systems for Nonlinear Optics. J. Phys. Chem. Lett. 2015, 6, 3236–3256. [Google Scholar] [CrossRef]
- Nakano, M.; Champagne, B. Nonlinear Optical Properties in Open-Shell Molecular Systems. WIREs Comput. Mol. Sci. 2016, 6, 198–210. [Google Scholar] [CrossRef]
- Nakano, M. Open-Shell-Character-Based Molecular Design Principles: Applications to Nonlinear Optics and Singlet Fission. Chem. Rec. 2016. [Google Scholar] [CrossRef] [PubMed]
- Quah, H.S.; Chen, W.; Schreyer, M.K.; Yang, H.; Wong, M.W.; Ji, W.; Vittal, J.J. Multiphoton Harvesting Metal-Organic Frameworks. Nat. Commun. 2015, 6, 7954. [Google Scholar] [CrossRef] [PubMed]
- Matsui, H.; Fukuda, K.; Ito, S.; Nagami, T.; Nakano, M. Open-Shell Singlet Nature and σ‑/π-Conjugation Effects on the Third-Order Nonlinear Optical Properties of Si Chains: Polysilane and Poly(disilene-1,2-diyl). J. Chem. Phys. A 2016, 120, 948–955. [Google Scholar] [CrossRef] [PubMed]
- Bejan, I.; Scheschkewitz, D. Two Si–Si Double Bonds Connected by a Phenylene Bridge. Angew. Chem. Int. Ed. 2007, 46, 5783–5786. [Google Scholar] [CrossRef] [PubMed]
- Nakano, M.; Champagne, B. Diradical Character Dependences of the First and Second Hyperpolarizabilities of Asymmetric Open-Shell Singlet Systems. J. Chem. Phys. 2013, 138, 244306. [Google Scholar] [CrossRef] [PubMed]
- Hayes, E.F.; Siu, A.K.Q. Electronic Structure of the Open Forms of Three-Membered Rings. J. Am. Chem. Soc. 1971, 93, 2090–2091. [Google Scholar] [CrossRef]
- Yamaguchi, K.; Fueno, T.; Fukutome, H. A Molecular-Orbital Theoretical Classification of Reactions of Singlet Ground-State Molecules. Chem. Phys. Lett. 1973, 22, 461–465. [Google Scholar] [CrossRef]
- Yamaguchi, K. Theory and Applications. In Self-Consistent Field; Carbo, R., Klobukowski, M., Eds.; Elsevier: Amsterdam, The Netherlands, 1990; p. 727. [Google Scholar]
- Cohen, H.D.; Roothaan, C.C.J. Electric Dipole Polarizability of Atoms by the Hartree-Fock Method. I. Theory for Closed-Shell Systems. J. Chem. Phys. 1965, 43, S34–S39. [Google Scholar] [CrossRef]
- Kishi, R.; Bonness, S.; Yoneda, K.; Takahashi, H.; Nakano, M.; Botek, E.; Champagne, B.; Kubo, T.; Kamada, K.; Ohta, K.; et al. Long-Range Corrected Density Functional Theory Study on Static Second Hyperpolarizabilities of Singlet Diradical Systems. J. Chem. Phys. 2010, 132, 094107. [Google Scholar] [CrossRef] [PubMed]
- De Wergifosse, M.; Wautelet, F.; Champagne, B.; Kishi, R.; Fukuda, K.; Matsui, H.; Nakano, M. Challenging Compounds for Calculating Hyperpolarizabilities: P-Quinodimethane Derivatives. J. Phys. Chem. A 2013, 117, 4709–4715. [Google Scholar] [CrossRef] [PubMed]
- Head-Gordon, M. Characterizing Unpaired Electrons from the One-Particle Density Matrix. Chem. Phys. Lett. 2003, 372, 508–511. [Google Scholar] [CrossRef]
- Nakano, M.; Fukui, H.; Minami, T.; Yoneda, K.; Shigeta, Y.; Kishi, R.; Champagne, B.; Botek, E.; Kubo, T.; Ohta, K.; et al. (Hyper)polarizability Density Analysis for Open-Shell Molecular Systems Based on Natural Orbitals and Occupation Numbers. Theor. Chem. Acc. 2011, 130, 711–724, Erratum. Theor. Chem. Acc. 2011, 130, 725–726. [Google Scholar] [CrossRef]
- Nakano, M.; Shigemoto, I.; Yamada, S.; Yamaguchi, K. Sizeconsistent Approach and Density Analysis of Hyperpolarizability: Second Hyperpolarizabilities of Polymeric Systems with and without Defects. J. Chem. Phys. 1995, 103, 4175–4191. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision B.01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
- Sample Availability: Samples of the compounds are not available from the authors.
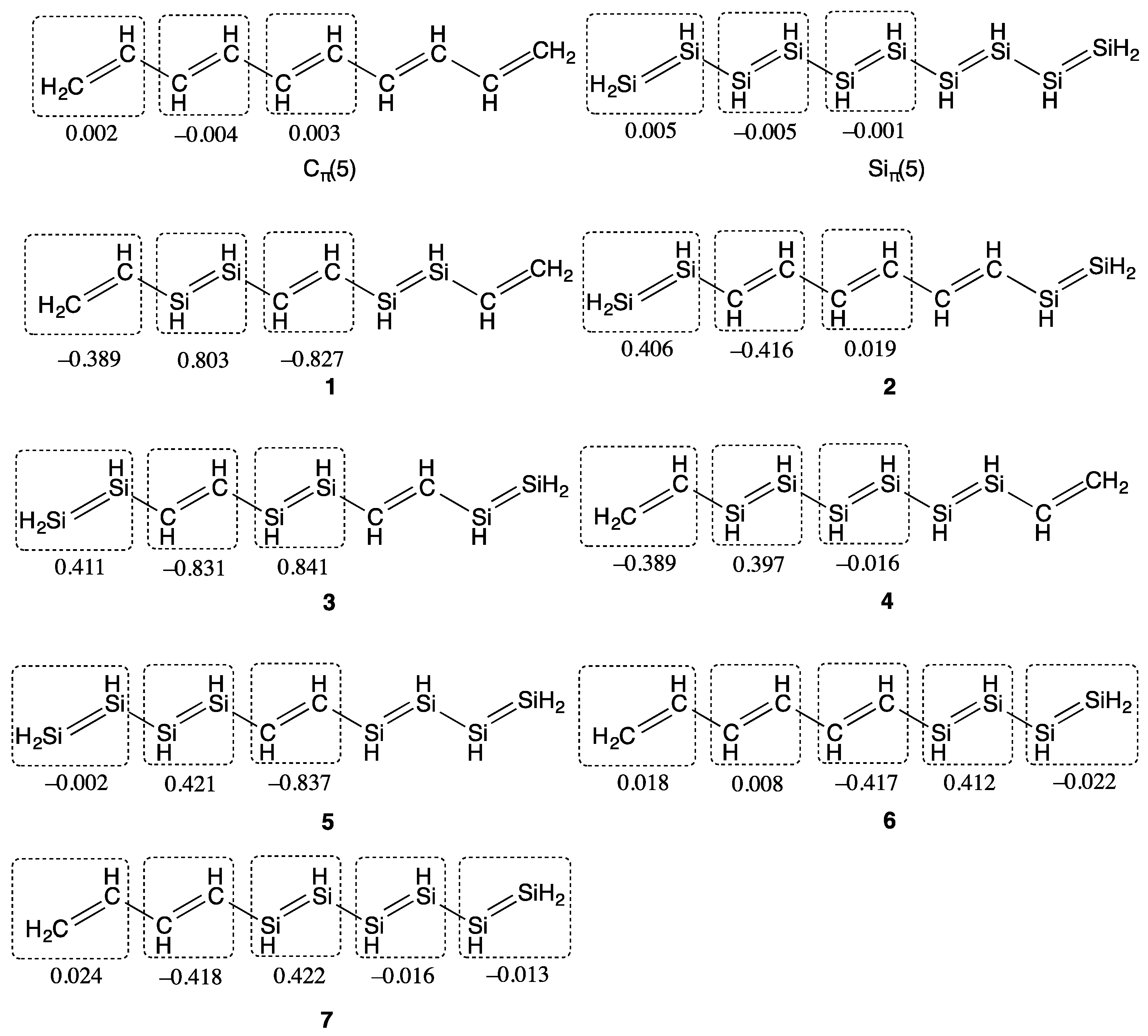
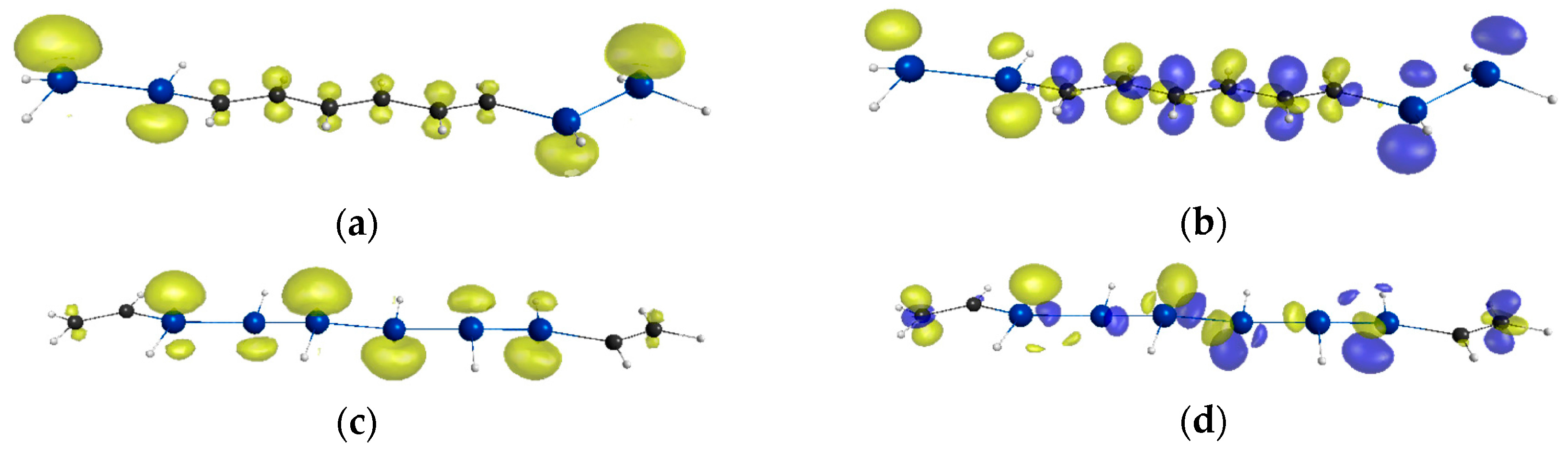
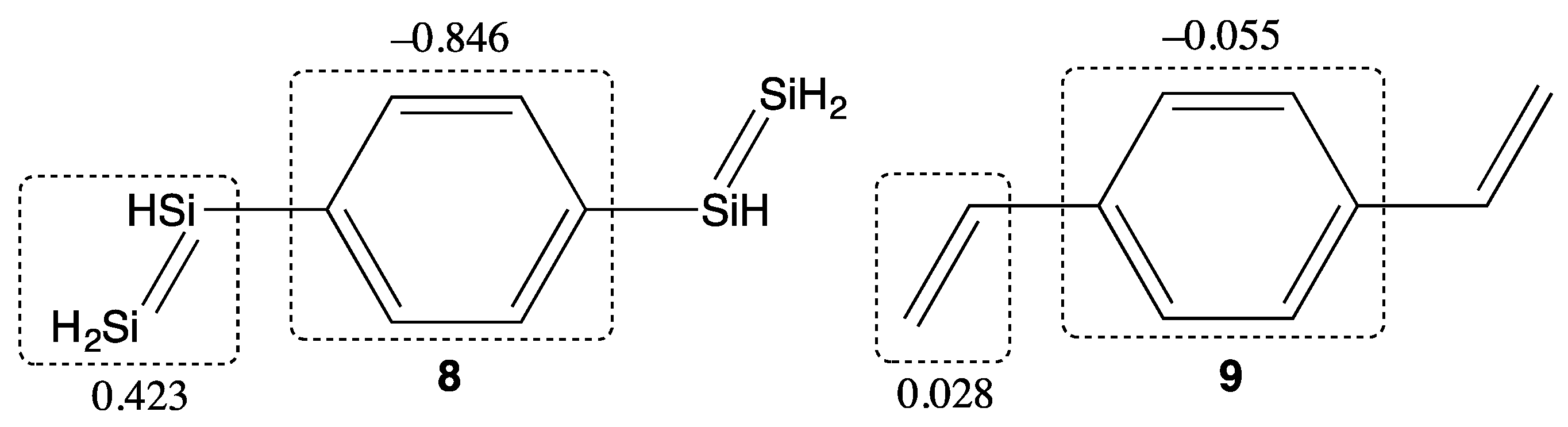
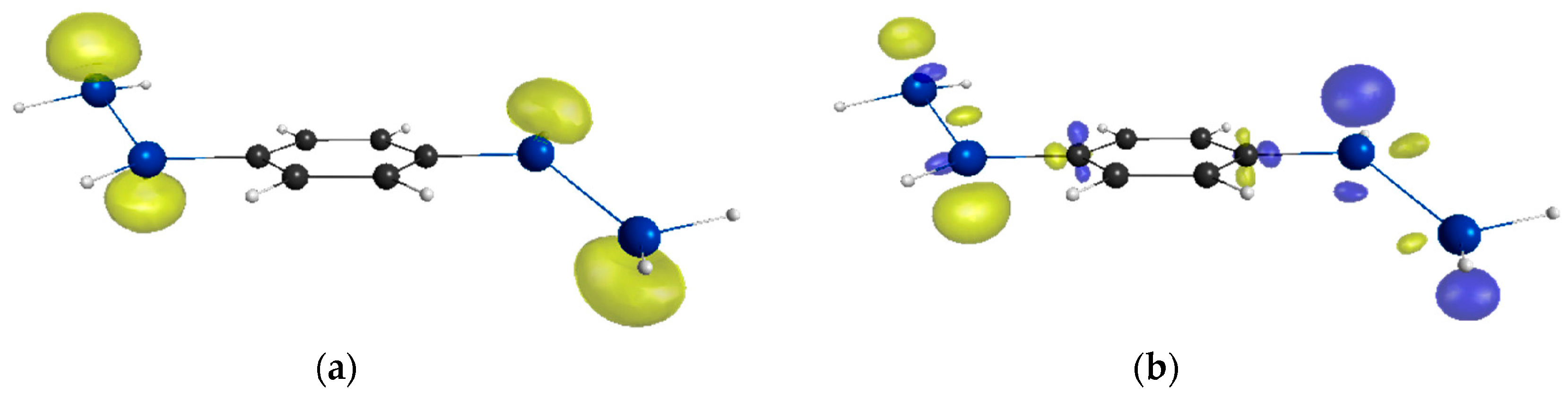
| Compounds | y 2 | γ/105 a.u. 3 |
|---|---|---|
| Cπ(5) | 0.000 1 | 2.27 1 |
| Siπ(5) | 0.495 1 | 48.5 1 |
| 1 | 0.182 | 5.90 |
| 2 | 0.254 | 12.8 |
| 3 | 0.235 | 15.0 |
| 4 | 0.340 | 12.1 |
| 5 | 0.344 | 31.3 |
| 6 | 0.287 | 9.58 |
| 7 | 0.360 | 15.6 |
| Compound | y 1 | γ/105 a.u. 2 |
|---|---|---|
| 8 | 0.160 | 1.81 |
| 9 | 0.000 | 0.366 |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsui, H.; Nagami, T.; Takamuku, S.; Ito, S.; Kitagawa, Y.; Nakano, M. Theoretical Study on the Second Hyperpolarizailities of Oligomeric Systems Composed of Carbon and Silicon π-Structures. Molecules 2016, 21, 1540. https://doi.org/10.3390/molecules21111540
Matsui H, Nagami T, Takamuku S, Ito S, Kitagawa Y, Nakano M. Theoretical Study on the Second Hyperpolarizailities of Oligomeric Systems Composed of Carbon and Silicon π-Structures. Molecules. 2016; 21(11):1540. https://doi.org/10.3390/molecules21111540
Chicago/Turabian StyleMatsui, Hiroshi, Takanori Nagami, Shota Takamuku, Soichi Ito, Yasutaka Kitagawa, and Masayoshi Nakano. 2016. "Theoretical Study on the Second Hyperpolarizailities of Oligomeric Systems Composed of Carbon and Silicon π-Structures" Molecules 21, no. 11: 1540. https://doi.org/10.3390/molecules21111540
APA StyleMatsui, H., Nagami, T., Takamuku, S., Ito, S., Kitagawa, Y., & Nakano, M. (2016). Theoretical Study on the Second Hyperpolarizailities of Oligomeric Systems Composed of Carbon and Silicon π-Structures. Molecules, 21(11), 1540. https://doi.org/10.3390/molecules21111540









