iPPBS-Opt: A Sequence-Based Ensemble Classifier for Identifying Protein-Protein Binding Sites by Optimizing Imbalanced Training Datasets
Abstract
:1. Introduction
2. Materials and Methods
2.1. Benchmark Dataset
| AA | A | B | C | D | E | F | G | H | I | K | L | M |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MaxASA | 106 | 160 | 135 | 163 | 194 | 197 | 84 | 184 | 169 | 205 | 164 | 188 |
| AA | N | P | Q | R | S | T | V | W | X | Y | Z | |
| MaxASA | 157 | 136 | 198 | 248 | 130 | 142 | 142 | 227 | 180 | 222 | 196 |
2.2. Flexible Sliding Window Approach
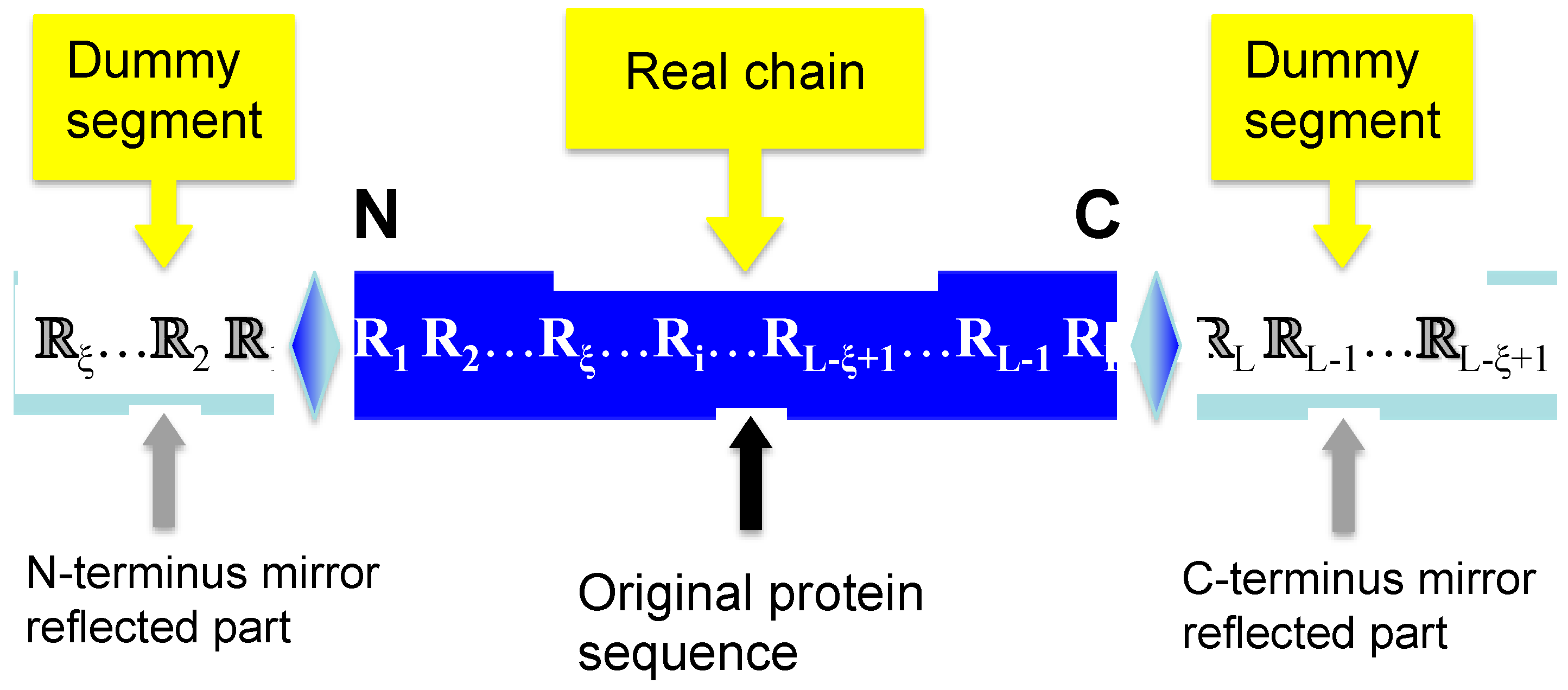
2.3. Using Pseudo Amino Acid Composition to Represent Peptide Chains
2.3.1. Physicochemical Properties
| Amino Acid Code | Physicochemical Property (cf. Equation (11)) a | ||||||
|---|---|---|---|---|---|---|---|
| H1 | H2 | V | P1 | P2 | SASA | NCI | |
| A | 0.62 | −0.5 | 27.5 | 8.1 | 0.046 | 1.181 | 0.007187 |
| C | 0.29 | −1 | 44.6 | 5.5 | 0.128 | 1.461 | −0.03661 |
| D | −0.9 | 3 | 40 | 13 | 0.105 | 1.587 | −0.02382 |
| E | −0.74 | 3 | 62 | 12.3 | 0.151 | 1.862 | 0.006802 |
| F | 1.19 | −2.5 | 115.5 | 5.2 | 0.29 | 2.228 | 0.037552 |
| G | 0.48 | 0 | 0 | 9 | 0 | 0.881 | 0.179052 |
| H | −0.4 | −0.5 | 79 | 10.4 | 0.23 | 2.025 | −0.01069 |
| I | 1.38 | −1.8 | 93.5 | 5.2 | 0.186 | 1.81 | 0.021631 |
| K | −1.5 | 3 | 100 | 11.3 | 0.219 | 2.258 | 0.017708 |
| L | 1.06 | −1.8 | 93.5 | 4.9 | 0.186 | 1.931 | 0.051672 |
| M | 0.64 | −1.3 | 94.1 | 5.7 | 0.221 | 2.034 | 0.002683 |
| N | −0.78 | 2 | 58.7 | 11.6 | 0.134 | 1.655 | 0.005392 |
| P | 0.12 | 0 | 41.9 | 8 | 0.131 | 1.468 | 0.239531 |
| Q | −0.85 | 0.2 | 80.7 | 10.5 | 0.18 | 1.932 | 0.049211 |
| R | −2.53 | 3 | 105 | 10.5 | 0.291 | 2.56 | 0.043587 |
| S | −0.18 | 0.3 | 29.3 | 9.2 | 0.062 | 1.298 | 0.004627 |
| T | −0.05 | −0.4 | 51.3 | 8.6 | 0.108 | 1.525 | 0.003352 |
| V | 1.08 | −1.5 | 71.5 | 5.9 | 0.14 | 1.645 | 0.057004 |
| W | 0.81 | −3.4 | 145.5 | 5.4 | 0.409 | 2.663 | 0.037977 |
| Y | 0.26 | −2.3 | 117.3 | 6.2 | 0.298 | 2.368 | 0.023599 |
2.3.2. Stationary Wavelet Transform Approach
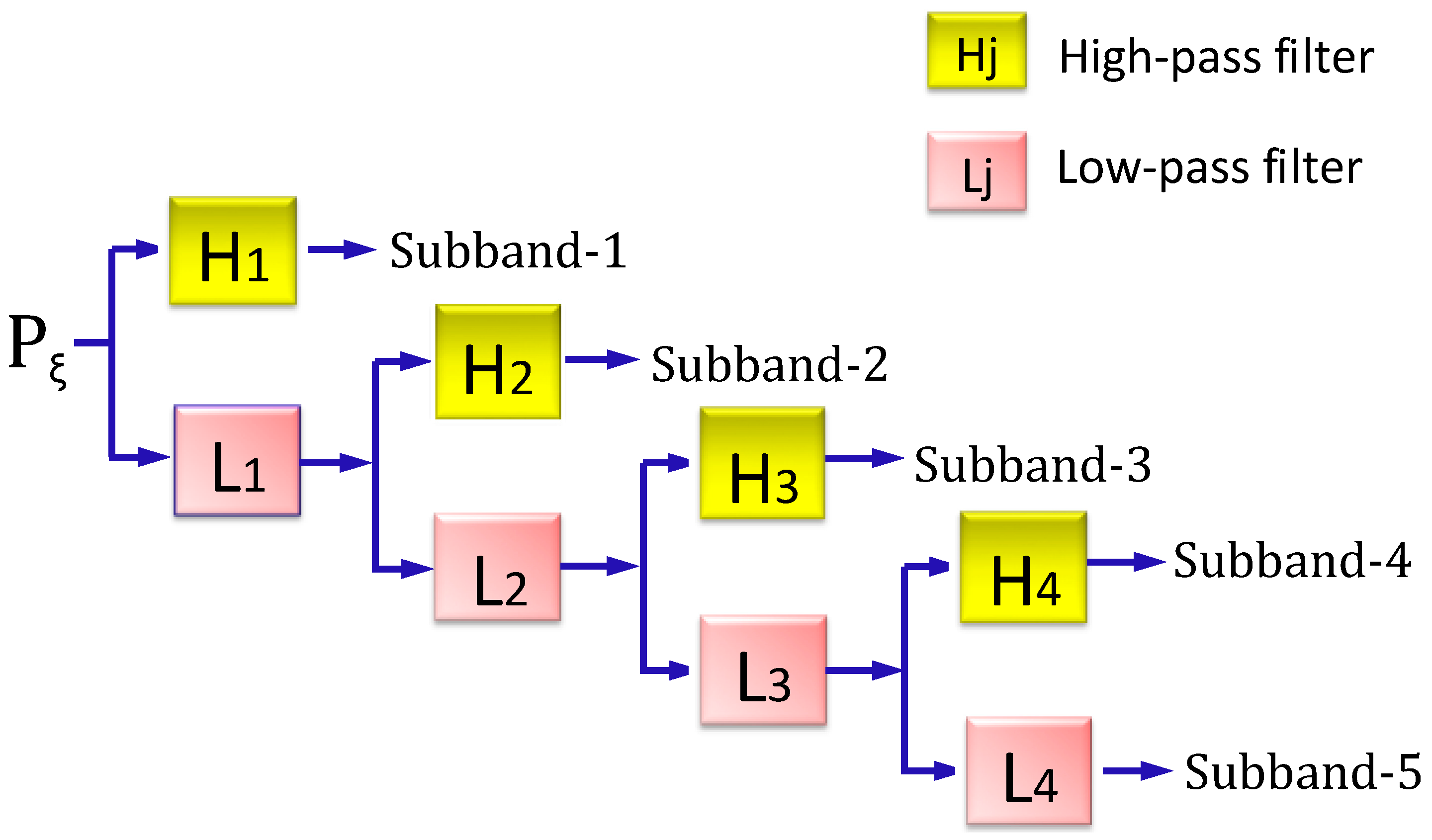
2.4. Optimizing Imbalanced Training Datasets
2.5. Fusing Multiple Physicochemical Properties
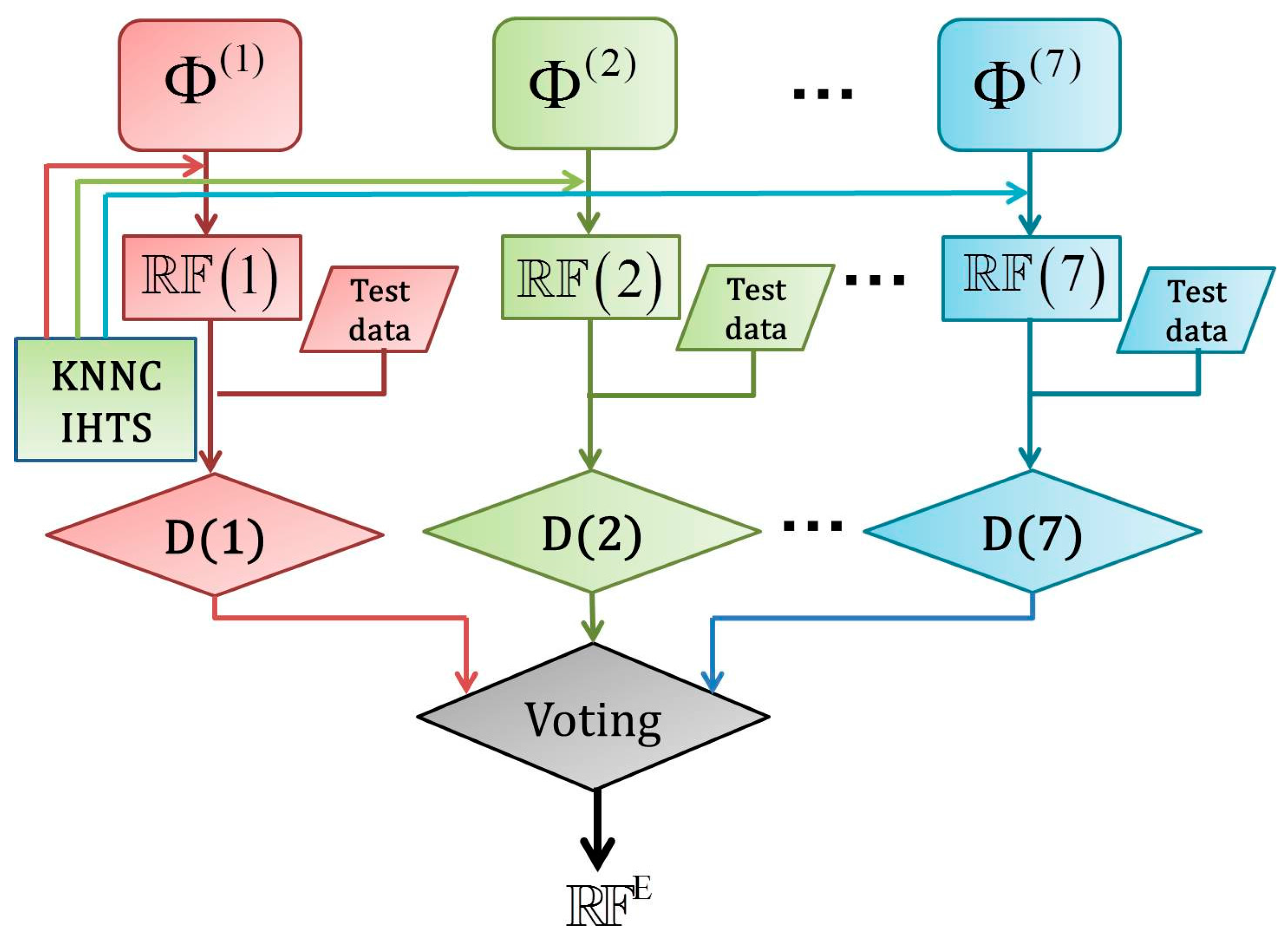
3. Result and Discussion
3.1. Metrics for Measuring Success Rates
3.2. Cross-Validation and Target Cross-Validation
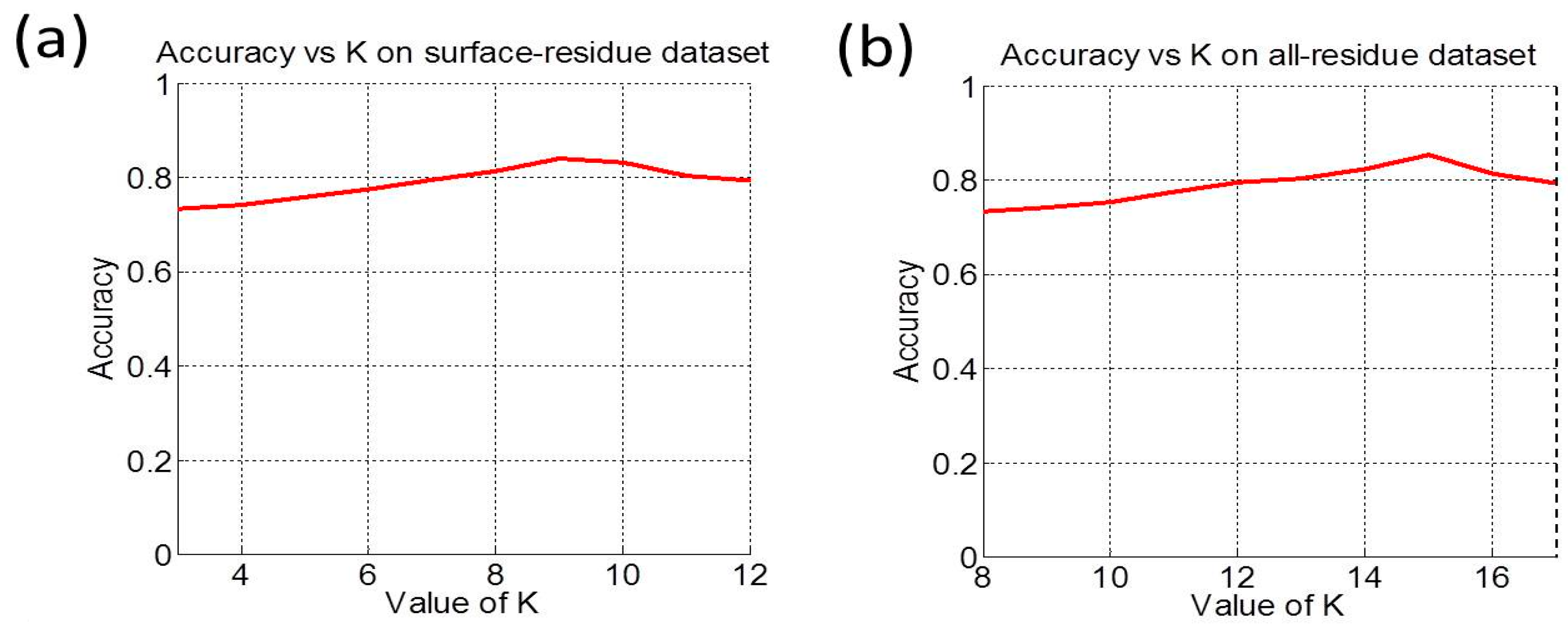
| Benchmark Dataset | Method | Acc (%) | MCC | Sn (%) | Sp (%) | AUC |
|---|---|---|---|---|---|---|
| Surface-residue | Deng a | N/A | 0.3456 | 76.77 | 63.16 | 0.7976 |
| Chen b | 75.09 | 0.4248 | 43.81 | 92.12 | 0.8004 | |
| iPPBS-PseAAC c | 84.04 | 0.5821 | 58.26 | 94.14 | 0.8934 | |
| All-residue | Deng a | N/A | 0.3763 | 76.33 | 78.61 | 0.8465 |
| Chen b | 73.77 | 0.3286 | 24.95 | 96.52 | 0.8001 | |
| iPPBS-PseAAC c | 85.45 | 0.4662 | 39.14 | 96.66 | 0.8820 |
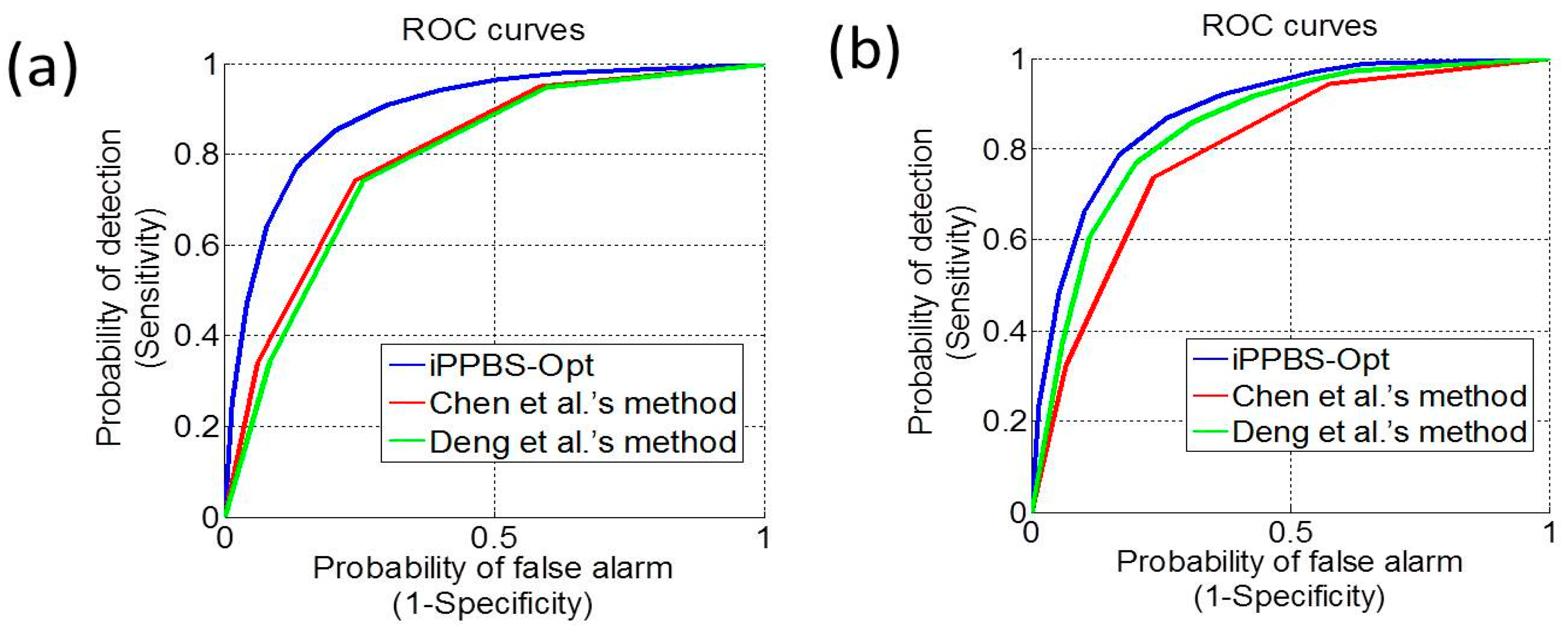
3.3. Comparison with the Existing Methods
3.4. Web Server and User Guide

4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chou, K.C.; Cai, Y.D. Predicting protein-protein interactions from sequences in a hybridization space. J. Proteome Res. 2006, 5, 316–322. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.L.; Chan, D.S.; Leung, C.H. Group 9 organometallic compounds for therapeutic and bioanalytical applications. Acc. Chem. Res. 2014, 47, 3614–3631. [Google Scholar] [CrossRef] [PubMed]
- Ma, D.L.; He, H.Z.; Leung, K.H.; Chan, D.S.; Leung, C.H. Bioactive luminescent transition-metal complexes for biomedical applications. Angew. Chem. 2013, 52, 7666–7682. [Google Scholar] [CrossRef] [PubMed]
- Tomasselli, A.G.; Heinrikson, R.L. Prediction of the Tertiary Structure of a Caspase-9/Inhibitor Complex. FEBS Lett. 2000, 470, 249–256. [Google Scholar]
- Leung, C.H.; Chan, D.S.; He, H.Z.; Cheng, Z.; Yang, H.; Ma, D.L. Luminescent detection of DNA-binding proteins. Nucleic Acids Res. 2012, 40, 941–955. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.H.; Chan, D.S.; Ma, V.P.; Ma, D.L. DNA-binding small molecules as inhibitors of transcription factors. Med. Res. Rev. 2013, 33, 823–846. [Google Scholar] [CrossRef] [PubMed]
- Jones, D.; Heinrikson, R.L. Prediction of the tertiary structure and substrate binding site of caspase-8. FEBS Lett. 1997, 419, 49–54. [Google Scholar]
- Wei, D.Q.; Zhong, W.Z. Binding mechanism of coronavirus main proteinase with ligands and its implication to drug design against SARS. (Erratum: ibid., 2003, Vol. 310, 675). Biochem. Biophys. Res. Commun. 2003, 308, 148–151. [Google Scholar]
- Chou, K.C. Review: Structural bioinformatics and its impact to biomedical science. Curr. Med. Chem. 2004, 11, 2105–2134. [Google Scholar] [CrossRef] [PubMed]
- Deng, L.; Guan, J.; Dong, Q.; Zhou, S. Prediction of protein-protein interaction sites using an ensemble method. BMC Bioinform. 2009, 10. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.W.; Jeong, J.C. Sequence-based prediction of protein interaction sites with an integrative method. Bioinformatics 2009, 25, 585–591. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Some remarks on protein attribute prediction and pseudo amino acid composition (50th Anniversary Year Review). J. Theor. Biol. 2011, 273, 236–247. [Google Scholar] [CrossRef] [PubMed]
- Ding, H.; Deng, E.Z.; Yuan, L.F.; Liu, L. iCTX-Type: A sequence-based predictor for identifying the types of conotoxins in targeting ion channels. BioMed Res. Int. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Lin, H.; Deng, E.Z.; Ding, H.; Chen, W. iPro54-PseKNC: A sequence-based predictor for identifying sigma-54 promoters in prokaryote with pseudo k-tuple nucleotide composition. Nucleic Acids Res. 2014, 42, 12961–12972. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Xu, J.; Lan, X.; Xu, R.; Zhou, J. iDNA-Prot|dis: Identifying DNA-binding proteins by incorporating amino acid distance-pairs and reduced alphabet profile into the general pseudo amino acid composition. PLoS ONE 2014, 9, e106691. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wen, X.; Wen, L.S.; Wu, L.Y. iNitro-Tyr: Prediction of nitrotyrosine sites in proteins with general pseudo amino acid composition. PLoS ONE 2014, 9, e105018. [Google Scholar] [CrossRef] [PubMed]
- Xu, R.; Zhou, J.; Liu, B.; He, Y.A.; Zou, Q. Identification of DNA-binding proteins by incorporating evolutionary information into pseudo amino acid composition via the top-n-gram approach. J. Biomol. Struct. Dyn. 2015, 33, 1720–1730. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Fang, L.; Wang, S.; Wang, X.; Li, H. Identification of microRNA precursor with the degenerate K-tuple or Kmer strategy. J. Theor. Biol. 2015, 385, 153–159. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Feng, P.; Ding, H. iRNA-Methyl: Identifying N6-methyladenosine sites using pseudo nucleotide composition. Anal. Biochem. 2015, 490, 26–33. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Fang, L.; Long, R.; Lan, X. iEnhancer-2L: A two-layer predictor for identifying enhancers and their strength by pseudo k-tuple nucleotide composition. Bioinformatics 2015. [Google Scholar] [CrossRef] [PubMed]
- Yan, C.; Dobbs, D.; Honavar, V. A two-stage classifier for identification of protein-protein interface residues. Bioinformatics 2004, 20, i371–i378. [Google Scholar] [CrossRef] [PubMed]
- Ofran, Y.; Rost, B. Predicted protein-protein interaction sites from local sequence information. FEBS Lett. 2003, 544, 236–239. [Google Scholar] [CrossRef]
- Jones, S.; Thornton, J.M. Principles of protein-protein interactions. Proc. Natl. Acad. Sci. USA 1996, 93, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
- Mihel, J.; Šikić, M.; Tomić, S.; Jeren, B.; Vlahovicek, K. PSAIA-rotein structure and interaction analyzer. BMC Struct. Biol. 2008, 8. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Huang, D.S.; Jiang, C. A new strategy for protein interface identification using manifold learning method. IEEE Trans. Nanobiosci. 2014, 13, 118–123. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Shen, H.B. Review: Recent progresses in protein subcellular location prediction. Anal. Biochem. 2007, 370. [Google Scholar] [CrossRef]
- Chou, K.C. Prediction of signal peptides using scaled window. Peptides 2001, 22, 1973–1979. [Google Scholar] [CrossRef]
- Shen, H.B. Signal-CF: A subsite-coupled and window-fusing approach for predicting signal peptides. Biochem. Biophys. Res. Commun. 2007, 357, 633–640. [Google Scholar]
- Xu, Y.; Ding, J.; Wu, L.Y. iSNO-PseAAC: Predict cysteine S-nitrosylation sites in proteins by incorporating position specific amino acid propensity into pseudo amino acid composition. PLoS ONE 2013, 8, e55844. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Shao, X.J.; Wu, L.Y.; Deng, N.Y. iSNO-AAPair: Incorporating amino acid pairwise coupling into PseAAC for predicting cysteine S-nitrosylation sites in proteins. PeerJ 2013, 1, e171. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.R.; Xiao, X.; Lin, W.Z. iMethyl-PseAAC: Identification of Protein Methylation Sites via a Pseudo Amino Acid Composition Approach. Biomed. Res. Int. 2014, 2014. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.R.; Xiao, X. iUbiq-Lys: Prediction of lysine ubiquitination sites in proteins by extracting sequence evolution information via a grey system model. J. Biomol. Struct. Dyn. 2015, 33, 1731–1742. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Wen, X.; Shao, X.J.; Deng, N.Y. iHyd-PseAAC: Predicting hydroxyproline and hydroxylysine in proteins by incorporating dipeptide position-specific propensity into pseudo amino acid composition. Int. J. Mol. Sci. 2014, 15, 7594–7610. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Review: Prediction of human immunodeficiency virus protease cleavage sites in proteins. Anal. Biochem. 1996, 233. [Google Scholar] [CrossRef]
- Chou, K.C. Prediction of protein cellular attributes using pseudo amino acid composition. Proteins 2001, 43, 246–255. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.T. An optimization approach to predicting protein structural class from amino acid composition. Protein Sci. 1992, 1, 401–408. [Google Scholar] [CrossRef] [PubMed]
- Chou, J.J. Predicting cleavability of peptide sequences by HIV protease via correlation-angle approach. J. Protein Chem. 1993, 12, 291–302. [Google Scholar] [CrossRef] [PubMed]
- Elrod, D.W. Bioinformatical analysis of G-protein-coupled receptors. J. Proteome Res. 2002, 1, 429–433. [Google Scholar]
- Feng, K.Y.; Cai, Y.D. Boosting classifier for predicting protein domain structural class. Biochem. Biophys. Res. Commun. 2005, 334, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.B.; Yang, J. Fuzzy KNN for predicting membrane protein types from pseudo amino acid composition. J. Theor. Biol. 2006, 240, 9–13. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.B. A top-down approach to enhance the power of predicting human protein subcellular localization: Hum-mPLoc 2.0. Anal. Biochem. 2009, 394, 269–274. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Yang, J.; Xu, Z.J. SLLE for predicting membrane protein types. J. Theor. Biol. 2005, 232, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.Z.; Fang, J.A. iDNA-Prot: Identification of DNA Binding Proteins Using Random Forest with Grey Model. PLoS ONE 2011, 6, e24756. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Min, J.L.; Wang, P. iGPCR-Drug: A web server for predicting interaction between GPCRs and drugs in cellular networking. PLoS ONE 2013, 8, e72234. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Wu, Z.C. iLoc-Virus: A multi-label learning classifier for identifying the subcellular localization of virus proteins with both single and multiple sites. J. Theor. Biol. 2011, 284, 42–51. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Pseudo amino acid composition and its applications in bioinformatics, proteomics and system biology. Curr. Proteom. 2009, 6, 262–274. [Google Scholar] [CrossRef]
- Liu, B.; Liu, F.; Wang, X.; Chen, J.; Fang, L. Pse-in-One: A web server for generating various modes of pseudo components of DNA, RNA, and protein sequences. Nucleic Acids Res. 2015, 43, W65–W71. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Using amphiphilic pseudo amino acid composition to predict enzyme subfamily classes. Bioinformatics 2005, 21, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Cao, D.S.; Xu, Q.S.; Liang, Y.Z. propy: A tool to generate various modes of Chou’s PseAAC. Bioinformatics 2013, 29, 960–962. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.X.; Lapointe, J. Theoretical and experimental biology in one—A symposium in honour of Professor Kuo-Chen Chou’s 50th anniversary and Professor Richard Giegé’s 40th anniversary of their scientific careers. J. Biomed. Sci. Eng. 2013, 6, 435–442. [Google Scholar] [CrossRef]
- Mohabatkar, H.; Mohammad Beigi, M.; Esmaeili, A. Prediction of GABA(A) receptor proteins using the concept of Chou’s pseudo-amino acid composition and support vector machine. J. Theor. Biol. 2011, 281, 18–23. [Google Scholar] [CrossRef] [PubMed]
- Mondal, S.; Pai, P.P. Chou’s pseudo amino acid composition improves sequence-based antifreeze protein prediction. J. Theor. Biol. 2014, 356, 30–35. [Google Scholar] [CrossRef] [PubMed]
- Hajisharifi, Z.; Piryaiee, M.; Mohammad Beigi, M.; Behbahani, M.; Mohabatkar, H. Predicting anticancer peptides with Chou’s pseudo amino acid composition and investigating their mutagenicity via Ames test. J. Theor. Biol. 2014, 341, 34–40. [Google Scholar] [CrossRef] [PubMed]
- Nanni, L.; Lumini, A.; Gupta, D.; Garg, A. Identifying bacterial virulent proteins by fusing a set of classifiers based on variants of Chou's pseudo amino acid composition and on evolutionary information. IEEE-ACM Trans. Comput. Biol. Bioinform. 2012, 9, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Hayat, M.; Khan, A. Discriminating Outer Membrane Proteins with Fuzzy K-Nearest Neighbor Algorithms Based on the General Form of Chou’s PseAAC. Protein Pept. Lett. 2012, 19, 411–421. [Google Scholar] [CrossRef] [PubMed]
- Du, P.; Gu, S.; Jiao, Y. PseAAC-General: Fast building various modes of general form of Chou’s pseudo-amino acid composition for large-scale protein datasets. Int. J. Mol. Sci. 2014, 15, 3495–3506. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Impacts of bioinformatics to medicinal chemistry. Med. Chem. 2015, 11, 218–234. [Google Scholar] [CrossRef] [PubMed]
- Zhong, W.Z.; Zhou, S.F. Molecular science for drug development and biomedicine. Int. J. Mol. Sci. 2014, 15, 20072–20078. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.R.; Xiao, X. iRSpot-TNCPseAAC: Identify recombination spots with trinucleotide composition and pseudo amino acid components. Int. J. Mol. Sci. 2014, 15, 1746–1766. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Feng, P.M.; Lin, H. iRSpot-PseDNC: Identify recombination spots with pseudo dinucleotide composition. Nucleic Acids Res. 2013, 41, e68. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.H.; Deng, E.Z.; Xu, L.Q.; Ding, H. iNuc-PseKNC: A sequence-based predictor for predicting nucleosome positioning in genomes with pseudo k-tuple nucleotide composition. Bioinformatics 2014, 30, 1522–1529. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Lei, T.Y.; Jin, D.C. PseKNC: A flexible web-server for generating pseudo K-tuple nucleotide composition. Anal. Biochem. 2014, 456, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Liu, F.; Fang, L.; Wang, X. repDNA: A Python package to generate various modes of feature vectors for DNA sequences by incorporating user-defined physicochemical properties and sequence-order effects. Bioinformatics 2015, 31, 1307–1309. [Google Scholar] [CrossRef] [PubMed]
- Du, P.; Wang, X.; Xu, C.; Gao, Y. PseAAC-Builder: A cross-platform stand-alone program for generating various special Chou’s pseudo-amino acid compositions. Anal. Biochem. 2012, 425, 117–119. [Google Scholar] [CrossRef] [PubMed]
- Tanford, C. Contribution of hydrophobic interactions to the stability of the globular conformation of proteins. J. Am. Chem. Soc. 1962, 84, 4240–4274. [Google Scholar] [CrossRef]
- Hopp, T.P.; Woods, K.R. Prediction of protein antigenic determinants from amino acid sequences. Proc. Natl. Acad. Sci. USA 1981, 78, 3824–3828. [Google Scholar] [CrossRef] [PubMed]
- Krigbaum, W.R.; Knutton, S.P. Prediction of the amount of secondary structure in a globular protein from its amino acid composition. Proc. Natl. Acad. Sci. USA 1973, 70, 2809–2813. [Google Scholar] [CrossRef] [PubMed]
- Grantham, R. Amino acid difference formula to help explain protein evolution. Science 1974, 185, 862–864. [Google Scholar] [CrossRef] [PubMed]
- Charton, M.; Charton, B.I. The structural dependence of amino acid hydrophobicity parameters. J. Theor. Biol. 1982, 99, 629–644. [Google Scholar] [CrossRef]
- Rose, G.D.; Geselowitz, A.R.; Lesser, G.J.; Lee, R.H.; Zehfus, M.H. Hydrophobicity of amino acid residues in globular proteins. Science 1985, 229, 834–838. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Tian, F.; Li, B.; Wu, S.; Li, Z. Genetic algorithm-based virtual screening of combinative mode for peptide/protein. Acta Chim. Sin. Chin. Ed. 2006, 64, 691–697. [Google Scholar]
- Martel, P. Biophysical aspects of neutron scattering from vibrational modes of proteins. Prog. Biophys. Mol. Biol. 1992, 57, 129–179. [Google Scholar] [CrossRef]
- Gordon, G. Extrinsic electromagnetic fields, low frequency (phonon) vibrations, and control of cell function: A non-linear resonance system. J. Biomed. Sci. Eng. 2008, 1, 152–156. [Google Scholar] [CrossRef]
- Madkan, A.; Blank, M.; Elson, E.; Goodman, R. Steps to the clinic with ELF EMF. Nat. Sci. 2009, 1, 157–165. [Google Scholar] [CrossRef]
- Wang, J.F. Insight into the molecular switch mechanism of human Rab5a from molecular dynamics simulations. Biochem. Biophys. Res. Commun. 2009, 390, 608–612. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.F.; Gong, K.; Wei, D.Q. Molecular dynamics studies on the interactions of PTP1B with inhibitors: From the first phosphate-binding site to the second one. Protein Eng. Des. Sel. 2009, 22, 349–355. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Low-frequency resonance and cooperativity of hemoglobin. Trends Biochem. Sci. 1989, 14, 212–213. [Google Scholar] [CrossRef]
- Wang, J.F. Insights from studying the mutation-induced allostery in the M2 proton channel by molecular dynamics. Protein Eng. Des. Sel. 2010, 23, 663–666. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. The biological functions of low-frequency phonons: 6. A possible dynamic mechanism of allosteric transition in antibody molecules. Biopolymers 1987, 26, 285–295. [Google Scholar] [CrossRef] [PubMed]
- Schnell, J.R.; Chou, J.J. Structure and mechanism of the M2 proton channel of influenza A virus. Nature 2008, 451, 591–595. [Google Scholar] [CrossRef] [PubMed]
- Mao, B. Collective motion in DNA and its role in drug intercalation. Biopolymers 1988, 27, 1795–1815. [Google Scholar]
- Zhang, C.T.; Maggiora, G.M. Solitary wave dynamics as a mechanism for explaining the internal motion during microtubule growth. Biopolymers 1994, 34, 143–153. [Google Scholar]
- Chou, K.C. Review: Low-frequency collective motion in biomacromolecules and its biological functions. Biophys. Chem. 1988, 30, 3–48. [Google Scholar] [CrossRef]
- Liu, H.; Wang, M. Low-frequency Fourier spectrum for predicting membrane protein types. Biochem. Biophys. Res. Commun. 2005, 336, 737–739. [Google Scholar] [CrossRef] [PubMed]
- Shensa, M. The discrete wavelet transform: Wedding the a trous and Mallat algorithms. IEEE Trans. Signal Process. 1992, 40, 2464–2482. [Google Scholar] [CrossRef]
- Mallat, S.G. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 674–693. [Google Scholar] [CrossRef]
- Sun, Y.; Wong, A.K.; Kamel, M.S. Classification of imbalanced data: A review. Int. J. Pattern Recognit. Artif. Intell. 2009, 23, 687–719. [Google Scholar] [CrossRef]
- Laurikkala, J. Improving Identification of Difficult Small Classes by Balancing Class Distribution, 63–66; Springer: Berlin, Heidelberg, German, 2001. [Google Scholar]
- Xiao, X.; Min, J.L.; Lin, W.Z.; Liu, Z. iDrug-Target: Predicting the interactions between drug compounds and target proteins in cellular networking via the benchmark dataset optimization approach. J. Biomol. Struct. Dyn. 2015, 33, 2221–2233. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Xiao, X.; Qiu, W.R. iDNA-Methyl: Identifying DNA methylation sites via pseudo trinucleotide composition. Anal. Biochem. 2015, 474, 69–77. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.T. Monte Carlo simulation studies on the prediction of protein folding types from amino acid composition. Biophys. J. 1992, 63, 1523–1529. [Google Scholar] [CrossRef]
- Chou, K.C. A vectorized sequence-coupling model for predicting HIV protease cleavage sites in proteins. J. Biol. Chem. 1993, 268, 16938–16948. [Google Scholar] [PubMed]
- Zhang, C.T. An analysis of protein folding type prediction by seed-propagated sampling and jackknife test. J. Protein Chem. 1995, 14, 583–593. [Google Scholar] [CrossRef] [PubMed]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2011, 16, 321–357. [Google Scholar]
- Kandaswamy, K.K.; Moller, S.; Suganthan, P.N.; Sridharan, S.; Pugalenthi, G. AFP-Pred: A random forest approach for predicting antifreeze proteins from sequence-derived properties. J. Theor. Biol. 2011, 270, 56–62. [Google Scholar] [CrossRef] [PubMed]
- Pugalenthi, G.; Kandaswamy, K.K.; Kolatkar, P. RSARF: Prediction of Residue Solvent Accessibility from Protein Sequence Using Random Forest Method. Protein Pept. Lett. 2012, 19, 50–56. [Google Scholar] [CrossRef] [PubMed]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Shen, H.B. Euk-mPLoc: A fusion classifier for large-scale eukaryotic protein subcellular location prediction by incorporating multiple sites. J. Proteome Res. 2007, 6, 1728–1734. [Google Scholar]
- Shen, H.B. Predicting eukaryotic protein subcellular location by fusing optimized evidence-theoretic K-nearest neighbor classifiers. J. Proteome Res. 2006, 5, 1888–1897. [Google Scholar]
- Shen, H.B. QuatIdent: A web server for identifying protein quaternary structural attribute by fusing functional domain and sequential evolution information. J. Proteome Res. 2009, 8, 1577–1584. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Liu, H.; Yang, J. Prediction of linear B-cell epitopes using amino acid pair antigenicity scale. Amino Acids 2007, 33, 423–428. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Using subsite coupling to predict signal peptides. Protein Eng. 2001, 14, 75–79. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Lin, H.; Feng, P.M.; Ding, C. iNuc-PhysChem: A Sequence-Based Predictor for Identifying Nucleosomes via Physicochemical Properties. PLoS ONE 2012, 7, e47843. [Google Scholar] [CrossRef] [PubMed]
- Wu, Z.C.; Xiao, X. iLoc-Hum: Using accumulation-label scale to predict subcellular locations of human proteins with both single and multiple sites. Mol. BioSyst. 2012, 8, 629–641. [Google Scholar]
- Lin, W.Z.; Fang, J.A.; Xiao, X. iLoc-Animal: A multi-label learning classifier for predicting subcellular localization of animal proteins. Mol. BioSyst. 2013, 9, 634–644. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Wang, P.; Lin, W.Z. iAMP-2L: A two-level multi-label classifier for identifying antimicrobial peptides and their functional types. Anal. Biochem. 2013, 436, 168–177. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Some Remarks on Predicting Multi-Label Attributes in Molecular Biosystems. Mol. BioSyst. 2013, 9, 1092–1100. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.T. Review: Prediction of protein structural classes. Crit. Rev. Biochem. Mol. Biol. 1995, 30, 275–349. [Google Scholar] [CrossRef]
- Zhou, G.P.; Assa-Munt, N. Some insights into protein structural class prediction. Proteins: Struct. Funct. Genet. 2001, 44, 57–59. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Cai, Y.D. Prediction and classification of protein subcellular location:-sequence-order effect and pseudo amino acid composition. J. Cell. Biochem. 2003, 90, 1250–1260. [Google Scholar] [CrossRef] [PubMed]
- Dehzangi, A.; Heffernan, R.; Sharma, A.; Lyons, J.; Paliwal, K.; Sattar, A. Gram-positive and Gram-negative protein subcellular localization by incorporating evolutionary-based descriptors into Chou’s general PseAAC. J. Theor. Biol. 2015, 364, 284–294. [Google Scholar] [CrossRef] [PubMed]
- Khan, Z.U.; Hayat, M.; Khan, M.A. Discrimination of acidic and alkaline enzyme using Chou’s pseudo amino acid composition in conjunction with probabilistic neural network model. J. Theor. Biol. 2015, 365, 197–203. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Srivastava, A.; Kumari, B.; Kumar, M. Prediction of beta-lactamase and its class by Chou’s pseudo-amino acid composition and support vector machine. J. Theor. Biol. 2015, 365, 96–103. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.B.; Yang, J. Euk-PLoc: An ensemble classifier for large-scale eukaryotic protein subcellular location prediction. Amino Acids 2007, 33, 57–67. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C.; Shen, H.B. Hum-PLoc: A novel ensemble classifier for predicting human protein subcellular localization. Biochem. Biophys. Res. Commun. 2006, 347, 150–157. [Google Scholar] [CrossRef] [PubMed]
- Forsen, S. Graphical rules for enzyme-catalyzed rate laws. Biochem. J. 1980, 187, 829–835. [Google Scholar]
- Chou, K.C. Graphic rules in steady and non-steady enzyme kinetics. J. Biol. Chem. 1989, 264, 12074–12079. [Google Scholar] [PubMed]
- Wu, Z.C.; Xiao, X. 2D-MH: A web-server for generating graphic representation of protein sequences based on the physicochemical properties of their constituent amino acids. J. Theor. Biol. 2010, 267, 29–34. [Google Scholar] [CrossRef] [PubMed]
- Althaus, I.W.; Chou, J.J.; Gonzales, A.J.; Kezdy, F.J.; Romero, D.L.; Aristoff, P.A.; Tarpley, W.G.; Reusser, F. Kinetic studies with the nonnucleoside HIV-1 reverse transcriptase inhibitor U-88204E. Biochemistry 1993, 32, 6548–6554. [Google Scholar] [CrossRef] [PubMed]
- Chou, K.C. Graphic rule for drug metabolism systems. Curr. Drug Metab. 2010, 11, 369–378. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.P. The disposition of the LZCC protein residues in wenxiang diagram provides new insights into the protein-protein interaction mechanism. J. Theor. Biol. 2011, 284, 142–148. [Google Scholar] [CrossRef] [PubMed]
- Fawcett, J.A. An Introduction to ROC Analysis. Pattern Recognit. Lett. 2005, 27, 861–874. [Google Scholar] [CrossRef]
- Chen, W.; Lin, H. Pseudo nucleotide composition or PseKNC: An effective formulation for analyzing genomic sequences. Mol. BioSyst. 2015, 11, 2620–2634. [Google Scholar] [CrossRef] [PubMed]
- Sample Availability: All the samples used in this study for training and testing the predictor are available by downloading them from the web-server at http://www.jci-bioinfo.cn/iPPBS-Opt.
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Liu, Z.; Xiao, X.; Liu, B.; Chou, K.-C. iPPBS-Opt: A Sequence-Based Ensemble Classifier for Identifying Protein-Protein Binding Sites by Optimizing Imbalanced Training Datasets. Molecules 2016, 21, 95. https://doi.org/10.3390/molecules21010095
Jia J, Liu Z, Xiao X, Liu B, Chou K-C. iPPBS-Opt: A Sequence-Based Ensemble Classifier for Identifying Protein-Protein Binding Sites by Optimizing Imbalanced Training Datasets. Molecules. 2016; 21(1):95. https://doi.org/10.3390/molecules21010095
Chicago/Turabian StyleJia, Jianhua, Zi Liu, Xuan Xiao, Bingxiang Liu, and Kuo-Chen Chou. 2016. "iPPBS-Opt: A Sequence-Based Ensemble Classifier for Identifying Protein-Protein Binding Sites by Optimizing Imbalanced Training Datasets" Molecules 21, no. 1: 95. https://doi.org/10.3390/molecules21010095
APA StyleJia, J., Liu, Z., Xiao, X., Liu, B., & Chou, K.-C. (2016). iPPBS-Opt: A Sequence-Based Ensemble Classifier for Identifying Protein-Protein Binding Sites by Optimizing Imbalanced Training Datasets. Molecules, 21(1), 95. https://doi.org/10.3390/molecules21010095





