Abstract
Crystals of 1,6-hexanedioic acid (I) undergo a temperature-dependent reversible phase transition from monoclinic P21/c at a temperature higher than the critical temperature (Tc) 130 K to another monoclinic P21/c at temperature lower than Tc. The phase transition is of first order, involving a discontinuity and a tripling of the b-axis at Tc whereas the other unit cell parameters vary continuously. The transition is described by the phenomenological Landau theory. The crystal structure analyses for data collected at 297(2) K and 120.0(1) K show that there is half of a molecule of (I) in the asymmetric unit at 297(2) K whereas there are one and a half molecules of (I) in the asymmetric unit at 120.0(1) K. At both temperatures, 297(2) and 120.0(1) K, intermolecular O-H···O hydrogen bonds link the molecules of I into infinite 1D chains along [101] direction. However there are significantly more O-H···O hydrogen bonds presented in the 120.0(1) K polymorph, thereby indicating this phase transition is negotiated via hydrogen bonds. The relationship of the conformational changes and hydrogen bonding for these two polymorphs are explained in detail.
1. Introduction
Reports on several types of phase transitions due to hydrogen bonding [1,2] and their conformation changes [3] have been published. In our previous investigations, we have reported the studies of hydrogen bonding phase transitions in phenol/benzoic acid and amine adducts [4,5,6,7,8]. In those crystals the structural phase transitions have been from monoclinic-to-triclinic [4] and from orthorhombic-to-monoclinic [7]. The phenomenological Landau theory of ferroelastic phase transitions was developed to identify the primary order parameters of these structural phase transitions leading eventually to the clarification of these structural phase transitions [5,6,8]. Owing to our interest in phase transitions of organic compounds both in structural and theoretical studies, we have prepared crystalline forms of 1,6-hexanedioic acid or adipic acid (I, Figure 1) which is an interesting aliphatic dicarboxylic acid due to its undulatory behavior in the solid state. A monoclinic polymorph of adipic acid has been reported by Ranganathan, Kulkarni and Rao [9] which did not exhibit polymorphism, but underwent a phase transition. Recently, Ohki, Nakamura and Chihara reported that the adipic acid undergoes a phase transition at about 136 K [10]. However, our study shows that I actually exhibits polymorphism in forms of triclinic polymorph [11] and monoclinic polymorph (in this study). Moreover we found that the triclinic polymorph [11] does not undergo phase transition whereas the monoclinic polymorph shows a reversible first-order temperature dependent phase-transition.
In this paper, we report the preparation, temperature-dependent phase transition and the X-ray structural analyses of I at 297(2) and 120.0(1) K which will be referred to as room-temperature phase (RTP) and low-temperature phase (LTP), respectively. The phase transition of I is described macroscopically by the Landau phenomenological theory approach.

Figure 1.
Schematic diagram of adipic acid (I).
2. Results and Discussion
Adipic acid reported in this study crystallizes in a centrosymmetric monoclinic P21/c space group. Using the same crystal to collect data at high temperature and low temperature, it was found that the crystal of I undergoes a reversible temperature-dependent phase transition from monoclinic P21/c at the temperature higher than the critical temperature (Tc) 130 K to another monoclinic P21/c at temperature lower than Tc. The crystal data of I at 297(2) K (RTP) and 120.0(1) K (LTP) are summarized in Table 1. Selected bond lengths, bond angles and torsion angles of the RTP and LTP structures are listed in Table 2. The interplanar angles between the functional units in I are listed in Table 3 and the hydrogen bonds are listed in Table 4.

Table 1.
Crystal data and parameters for structure refinement of I at 297(2) and 120.0(1) K.
| Crystal Properties | 297(2) K (RTP) | 120.0(1) K (LTP) |
|---|---|---|
| CCDC deposition numbers | 989931 | 989973 |
| Formula | C6H10O4 | C6H10O4 |
| Formula Weight | 146.14 | 146.14 |
| Color; Shape | Colorless; Block | Colorless; Block |
| Crystal System | Monoclinic | Monoclinic |
| Space Group | P21/c | P21/c |
| Z | 2 | 6 |
| Lattice Constants | a =7.3647(3)Å | a = 7.3865(6)Å |
| b = 5.1503(3)Å | b = 14.9130(13)Å | |
| c = 10.1332(5)Å | c = 10.0475(9)Å | |
| β = 112.274(3)° | β = 111.656(6)° | |
| Volume [Å3] | 355.42(3) | 1028.66(15) |
| Dx [Mg·m−3] | 1.366 | 1.415 |
| μ [mm−1] | 0.115 | 0.120 |
| F(000) | 156 | 468 |
| θ range [°] | 2.99–32.50 | 2.57–27.50 |
| h, k, l | −10/11, −7/7, −14/15 | −9/9, −19/7, −13/13 |
| Reflections Collected | 5118 | 10307 |
| Reflections Unique | 1279 | 2346 |
| Tmin/Tmax | 0.9661/0.9394 | 0.9373/0.9649 |
| R(int) | 0.0270 | 0.0523 |
| Number of Parameters | 67 | 136 |
| GoF | 1.052 | 1.180 |
| Final R index[I > 2σ(I)] | 0.0453 | 0.0949 |

Table 2.
Selected bond lengths (Å), angles (°) and torsion angles (°) for I.
| Monoclinic at 297(2) K | Monoclinic at 120.0(1) K | ||
|---|---|---|---|
| Bonds | |||
| O1-C1 | 1.2242(11) | O1A-C1A | 1.219(5) |
| O2-C1 | 1.2989(11) | O2A-C1A | 1.308(5) |
| O2-H1O | 0.98(2) | O2A-H1OA | 0.82 |
| C1-C2 | 1.4931(11) | C1A-C2A | 1.523(6) |
| C2-C3 | 1.5091(13) | C2A-C3A | 1.499(6) |
| C3-C3 i | 1.5135(15) | C3A-C3 ii | 1.546(8) |
| O1B-C1B | 1.220(5) | ||
| O2B-C1B | 1.316(5) | ||
| O2B-H1OB | 0.82 | ||
| C1B-C2B | 1.505(5) | ||
| C2B-C3B | 1.514(5) | ||
| C3B-C4B | 1.514(5) | ||
| Angles | |||
| O1-C1-O2 | 122.79(8) | O1A-C1A-O2A | 123.9(4) |
| O1-C1-C2 | 122.93(8) | O1A-C1A-C2A | 123.5(4) |
| O2-C1-C2 | 114.28(8) | O2A-C1A-C2A | 112.6(3) |
| C1-C2-C3 | 114.80(8) | C1A-C2A-C3A | 113.4(3) |
| O1B-C1B-O2B | 123.1(3) | ||
| O1B-C1B-C2B | 123.7(3) | ||
| O2B-C1B-C2B | 113.3(3) | ||
| C1B-C2B-C3B | 114.7(3) | ||
| Torsion angles | |||
| O1-C1-C2-C3 | −7.40(15) | O1A-C1A-C2A-C3A | −2.6(6) |
| O2-C1-C2-C3 | 172.92(9) | O2A-C1A-C2A-C3A | 177.2(3) |
| C1-C2-C3-C3 i | −174.46(9) | C1A-C2A-C3A-C3A ii | 177.6(4) |
| O1B-C1B-C2B-C3B | 9.6(6) | ||
| O2B-C1B-C2B-C3B | −170.1(3) | ||
| C1B-C2B-C3B-C4B | 172.8(3) | ||
symmetry codes: i = −x, −y, −z; ii = −x + 1, −y + 2, −z + 2.

Table 3.
Interplanar angles between the functional units in I.
| Phase | Plane | Plane | Interplanar angle (°) |
|---|---|---|---|
| RTP | O1/O2/C1/C2 | C2/C3/C2A/C3A | 6.95(9) |
| at 297(2) K | |||
| LTP | O1A/O2A/C1A/C2A | C2A/C3A/C2AA/C3AA | 4.2(4) |
| at 120.0(1) K | O1B/O2B/C1B/C2B | C2B/C3B/C4B/C5B | 8.1(4) |
| O3B/O4B/C5B/C6B | C2B/C3B/C4B/C5B | 9.3(4) |

Table 4.
Geometries of intermolecular hydrogen bonds in I.
| Crystals | D-H···A | D-H (Å) | H···A (Å) | D···A (Å) | D-H···A (°) |
|---|---|---|---|---|---|
| RTP | O2-H1O···O1 iii | 0.985(19) | 1.673(19) | 2.6508(11) | 171.3(18) |
| at 297(2) K | |||||
| LTP | O2A-H1OA···O1A iv | 0.82 | 1.85 | 2.668(4) | 176 |
| at 120.0(1) K | O2B-H1OB···O3B v | 0.82 | 1.83 | 2.648(4) | 175 |
| O4B-H2BA···O1B vi | 0.82 | 1.84 | 2.658(4) | 175 |
Symmetry codes: iii = 1 − x, −y, 1 − z; iv = −x, 2 − y, 1 − z; v = −1 + x, y, −1 + z; vi = 1 + x, y, 1 + z.
2.1. Crystal Structure
Plots of an asymmetric unit of I at the temperature 297(2) K (RTP) and 120.0(1) K (LTP) are shown in Figure 2a, b and Figure 3a, b respectively. The asymmetric unit of the RTP structure consists of half a molecule (Figure 2a), whereas there are one and a half crystallographic independent molecules in the asymmetric unit of the LTP structure (Figure 3a). In the RTP molecular structure which is shown in Figure 2b, there is an inversion center on the central C-C bond and the molecular backbone adopts the expected planar zig-zag structure. For the LTP molecular structure which is shown in Figure 3a, the half-molecule fragment resembles the asymmetric unit of the RTP. However the LTP molecule is relatively more planar (compared to the RTP molecule) with the torsion angle C1A-C2A-C3A-C3Aii being 177.6(4)° and the angle made by the carboxylic acid O1A-C1A-C2A-C3A = −2.6(6)° (Figure 3b), the corresponding angles being −174.46(9) and −7.40(15)° in the RTP (Table 2). The molecular back bone of the full molecule fragment of the LTP is buckled with the torsion angles C1B-C2B-C3B-C4B = 172.8(3)°, C2B-C3B-C4B-C5B = 176.1(3)° and C3B-C4B-C5B-C6B = −174.0(3)°.
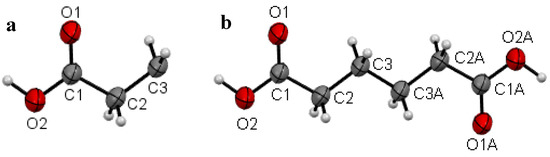
Figure 2.
(a) Asymmetric unit of I with the atomic numbering schemes at 297(2) K (RTP) and (b) molecular view of I with the atomic numbering schemes at 297(2) K (RTP). The atoms with suffix “A” were generated by symmetry code −x, −y, −z.
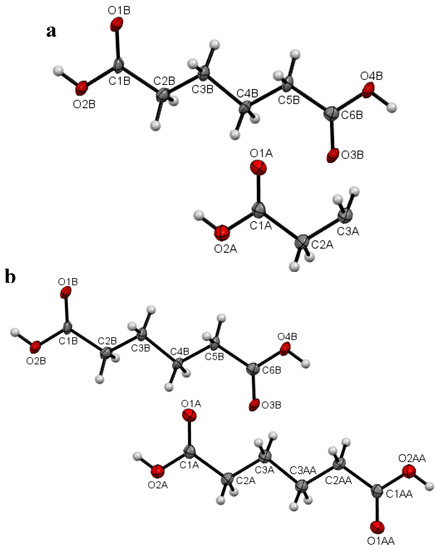
Figure 3.
(a) Asymmetric unit of I with the atomic numbering schemes at 120.0(1) K (LTP) and (b) molecular view of I with the atomic numbering schemes at 120.0(1) K (LTP). The atoms with suffix “AA” were generated by symmetry code –x + 1, −y + 2, −z + 2.
The bond lengths and angles in RTP and LTP structures are in normal ranges and agree with the corresponding values in the triclinic polymorph [11]. The interplanar angles of the functional groups in the temperature polymorphs are listed in Table 3. With temperature changes, the bond lengths and angles of I are almost unchanged in the molecule with half symmetry (half-molecule fragment) which can be seen in (Table 2). However even though these parameters are slightly different in the full-molecule fragment (molecule B in Figure 3b) which lost its symmetry but the torsion angles are significantly different, resulting in significant conformational changes. As can be seen in Table 4, the RTP structure has one O-H···O hydrogen bond whereas the LTP structure has three O-H···O hydrogen bonds. Their geometries and symmetry operations are listed in Table 4. The extra hydrogen bonds, i.e., O2B-H1OB···O3Bv and O4B-H2OB···O1Bvi (Table 4) interconnecting the molecule of LTP structure are not observed in the RTP structure.
In the crystal packing of both RTP and LTP structures, the molecules are linked via centrosymmetric pairs of intermolecular O-H···O hydrogen bonds, forming infinite one-dimensional chains along the [101] direction (Figure 4a,b). These chains are further stacked along the b-axis.
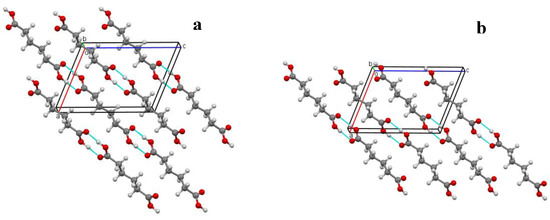
Figure 4.
Packing diagram of I at (a) 297 (2) K (RTP) and (b) 120.0 (1) K (LTP) viewed down the b-axis. Hydrogen bonds are drawn as dash lines.
Summarizing, these extra O-H···O hydrogen bonds presented in the LTP structure initiates the reversible temperature-dependent phase transformation leading to the conformational changes of the full-molecule fragment structure in the LTP.
The cell parameters of I were measured in the temperature range from 297(2) to 90.0(1) K (Table 5) and the plot is depicted in Figure 5. It is clearly seen that there is a discontinuous jump of the b parameter at 130 K. As the temperature is decreased from the room temperature to close to transition temperature Tc = 130 K, the a parameter increases by ~0.05 Å while the b and c parameters show only small variations (Figure 5). Below the transition temperature, the cell parameters is still monoclinic with the same space group and the a and c parameters remains nearly the same. Surprisingly that the b parameter changes to 14.942(11) Å which is almost triple of its value at room temperature (Table 5 and Figure 5). The β angle shows only slight variation on cooling to the low temperature (Figure 6). These data show that the phase transition is of first order, involving a discontinuity and a tripling of the b-axis at Tc whereas the a-axis and c-axis are continuous and essentially unchanged. In addition, the β angle (Figure 6) also varies insignificantly during transition. The temperature dependence of the unit cell volume, which was shown in Figure 7, almost triple on cooling in accordance to the changes of the cell parameters.

Table 5.
Temperature dependent cell parameters for I.
| Temp (K) | a (Å) | b (Å) | c (Å) | β (°) | Volume (Å3) |
|---|---|---|---|---|---|
| 297 | 7.3660(4) | 5.1539(3) | 10.1383(5) | 112.333(4) | 356.0(2) |
| 290 | 7.38(3) | 5.182(18) | 10.04(4) | 110.56(7) | 359.5(1) |
| 280 | 7.37(3) | 5.19(2) | 10.06(5) | 110.62(9) | 360.2(1) |
| 270 | 7.38(2) | 5.193(16) | 10.16(3) | 112.02(9) | 360.6(1) |
| 260 | 7.37(2) | 5.191(13) | 10.14(3) | 111.97(8) | 359.6(9) |
| 250 | 7.355(17) | 5.191(11) | 10.15(2) | 111.76(7) | 359.8(9) |
| 240 | 7.342(15) | 5.188(10) | 10.09(2) | 110.96(5) | 358.7(9) |
| 230 | 7.342(13) | 5.198(9) | 10.10(2) | 110.98(4) | 360.0(8) |
| 220 | 7.315(14) | 5.188(9) | 10.08(2) | 111.04(5) | 357.2(8) |
| 210 | 7.299(13) | 5.185(9) | 10.08(2) | 111.09(4) | 355.9(8) |
| 200 | 7.302(16) | 5.194(11) | 10.11(2) | 111.19(7) | 357.3(8) |
| 190 | 7.30(2) | 5.202(14) | 10.12(3) | 111.05(11) | 358.9(7) |
| 180 | 7.30(2) | 5.206(15) | 10.12(3) | 110.96(10) | 359.0(8) |
| 170 | 7.33(3) | 5.24(2) | 10.21(5) | 111.36(11) | 365.3(7) |
| 160 | 7.239(8) | 5.187(5) | 10.088(14) | 111.26(3) | 353.0(6) |
| 150 | 7.215(7) | 5.179(5) | 10.074(14) | 111.23(3) | 350.8(6) |
| 140 | 7.243(16) | 5.206(11) | 10.09(2) | 110.67(10) | 355.8(6) |
| 130 | 7.414(5) | 14.942(11) | 10.087(9) | 111.77(3) | 1037.8(3) |
| 120 | 7.44(2) | 14.97(4) | 10.12(3) | 111.51(5) | 1048.7(7) |
| 110 | 7.37(4) | 15.01(9) | 10.09(6) | 111.63(15) | 1039.0(8) |
| 100 | 7.3791(3) | 14.8734(7) | 10.0347(5) | 111.525(2) | 1024.52(7) |
| 90 | 7.41(3) | 14.99(7) | 10.10(5) | 111.23(9) | 1046.0(7) |

Figure 5.
Temperature dependence of cell lengths (a, b and c-axis) of I. Cell Parameters (Å) vs. Temperature (K).
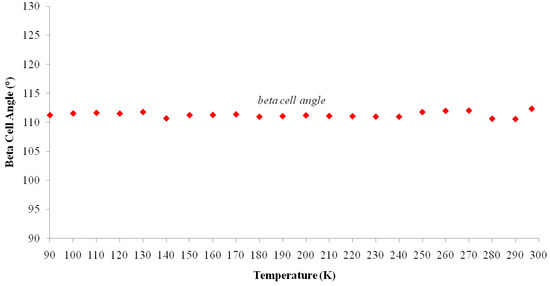
Figure 6.
Temperature dependence of angle β of I. Beta Cell Angle (°) vs. Temperature (K).
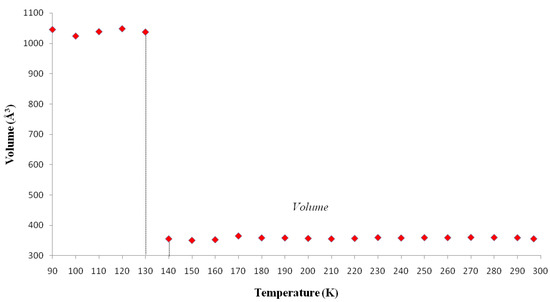
Figure 7.
Temperature dependence of volume of I. Volume (Å3) vs. Temperature (K).
2.2. Landau Phenomenological Theory of First Order Structural Phase Transitions in I
The crystallographic data show that the crystal I undergoes an isosymmetric phase transition based on the geometric anomaly from monoclinic P21/c at high temperatures (above 140 K) to another monoclinic P21/c at low temperatures (below 130 K) without any significant structural change. In order to discuss this anomaly, Q is assumed as the order parameter in the Landau phenomenological theory of the structural phase transition in the crystal I [12]. At the microscopic level this order parameter may represent a set of displacements, such as conformational changes (which is very obvious from the contents of the asymmetric units in Figure 2b, leading to a tripling of the b-axis and a discontinuity in unit cell volume (see Table 2). Thus this isosymmetric phase transition is not brought about by qualitative change in crystal symmetry, but by quantitative change of formation of hydrogen bonds leading to conformational changes. Similar type of phase transition can be induced by quantitative changes such as atomic size, amount of ionic displacement or statistical weight of atomic distribution [13]; and a representative example of isosymmetric phase transition is the γ-α transition in cerium and its alloys [14].
In the present paper on crystal I, in order to relate the geometrical quantity of elastic strain with the thermodynamic order parameter Q in Landau phenomenological theory, the Landau potential for the crystal I is formulated with the bilinear coupling between order parameter Q and the elastic strain components. This is assumed that the crystal is in thermodynamic equilibrium with respect to spontaneous strain [12]. In the geometrical representation of monoclinic crystal, the Cartesian coordinate system of axes X, Y, and Z are such that X and Y are parallel to a-axis and b-axis respectively and Z is perpendicular to both these axes and thus it is parallel to c* axis (of the reciprocal lattice). For the notation of elastic strain components, we follow the standard Voigt notation adopted in the theory of elastic deformations of a continuous homogeneous medium [15] to describe the dimensionless strain tensors ek, with the abbreviated subscript k taking integral values from 1 to 6.
The Landau potential F is expressed in the power series of order parameter Q and the bilinear coupling with elastic strain components as follow:
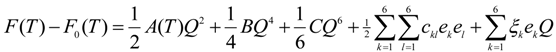
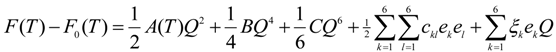
The term F0(T) is the free energy of the high temperature phase and we adopt the temperature dependence of A(T) as:
where a0 is a constant and T0 is the critical temperature. The parameters B and C are assumed to be weakly temperature dependent over the range of temperatures considered and are therefore taken as constants. The first three terms in (1) represent the Landau potential of the order parameter Q. The fourth term represents the quadratic elastic energy per unit volume of a monoclinic crystal, where ckl is the elastic constants in Voigt notation. The last term is the coupling energy between the order parameter and the elastic strain, with the coupling constants ξk. Minimizing Equation (1) with respect to ek, the simplification leads to 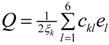 . We can then rewrite ek in term of Q as:
where λk are the coefficients depending on the elastic constants ξk of monoclinic crystal and coupling constants . Eliminating the terms in strain components in Equation (1) using ek in Equation (3), we obtain the normalized free energy as:
. We can then rewrite ek in term of Q as:
where λk are the coefficients depending on the elastic constants ξk of monoclinic crystal and coupling constants . Eliminating the terms in strain components in Equation (1) using ek in Equation (3), we obtain the normalized free energy as:
 where
where  .
.
A(T) = a0 (T − T0)
 . We can then rewrite ek in term of Q as:
. We can then rewrite ek in term of Q as:
ek = λk (ckl, ξk)Q
 .
.Equation (4) is the functional for the usual Landau form of free energy in the first order phase transition if B < 0 and C > 0 and in this case it is proposed for the phase transition of crystal I. The analytical expression for Q in terms of the Landau parameters can be obtained by minimizing Equation (4) with respect to Q as shown:


We have shown in our previous work [8] that the values of Q, which correspond to the minima of free energy (given by Equation (5) for T <  ), are the values of the spontaneous order parameter (denoted as Q'). Q' varies non-linearly with temperature T with a discontinuity at
), are the values of the spontaneous order parameter (denoted as Q'). Q' varies non-linearly with temperature T with a discontinuity at 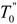 is an indication of first order phase transition.
is an indication of first order phase transition.
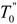 ), are the values of the spontaneous order parameter (denoted as Q'). Q' varies non-linearly with temperature T with a discontinuity at
), are the values of the spontaneous order parameter (denoted as Q'). Q' varies non-linearly with temperature T with a discontinuity at 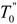 is an indication of first order phase transition.
is an indication of first order phase transition.Table 2 shows the measured lattice parameters for crystal I equilibrated at the temperatures from 90 K to 297 K. The temperature variation for the lattice parameters a, b, c and β are plotted in Figure 5 to Figure 7. From Figure 5, the abrupt jump in the b-unit cell length at the transition temperature may be over-exaggerated owing to the tripling of the unit cell length, however, based on the crystallographic data for temperatures below 130 K, we can estimate the magnitude of this linear strain along the b-axis, e2 as:
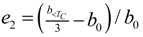 where b<TC is the LTP b-unit cell length. The expressions for the other elastic strain components for monoclinic P21/c to P21/c phase transition in terms of lattice parameters such as
where b<TC is the LTP b-unit cell length. The expressions for the other elastic strain components for monoclinic P21/c to P21/c phase transition in terms of lattice parameters such as 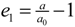 ,
,  , e4 = 0,
, e4 = 0,  and e6 = 0 , are formulated according to Schlenker et al. [16]. The values for a0, b0, c0 are the average values of the HTP a-unit cell, b-unit cell and c-unit cell length respectively. β0 is the average value of HTP, and as variation of β from LTP to HTP is very small, thus it is considered in the calculation that β ≈ β0. The scalar spontaneous strain es, according to that proposed by Aizu [17] is:
and e6 = 0 , are formulated according to Schlenker et al. [16]. The values for a0, b0, c0 are the average values of the HTP a-unit cell, b-unit cell and c-unit cell length respectively. β0 is the average value of HTP, and as variation of β from LTP to HTP is very small, thus it is considered in the calculation that β ≈ β0. The scalar spontaneous strain es, according to that proposed by Aizu [17] is:
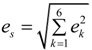
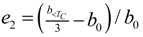
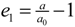 ,
,  , e4 = 0,
, e4 = 0,  and e6 = 0 , are formulated according to Schlenker et al. [16]. The values for a0, b0, c0 are the average values of the HTP a-unit cell, b-unit cell and c-unit cell length respectively. β0 is the average value of HTP, and as variation of β from LTP to HTP is very small, thus it is considered in the calculation that β ≈ β0. The scalar spontaneous strain es, according to that proposed by Aizu [17] is:
and e6 = 0 , are formulated according to Schlenker et al. [16]. The values for a0, b0, c0 are the average values of the HTP a-unit cell, b-unit cell and c-unit cell length respectively. β0 is the average value of HTP, and as variation of β from LTP to HTP is very small, thus it is considered in the calculation that β ≈ β0. The scalar spontaneous strain es, according to that proposed by Aizu [17] is:
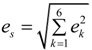
With respect to the structural properties of monoclinic symmetry in crystal I, the spontaneous strain from Equation (6) will be reduced to 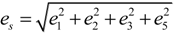 . Since from the data β ≈ β0, e3 and e5 ≈ 0, thus
. Since from the data β ≈ β0, e3 and e5 ≈ 0, thus 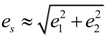 .
.
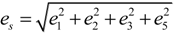 . Since from the data β ≈ β0, e3 and e5 ≈ 0, thus
. Since from the data β ≈ β0, e3 and e5 ≈ 0, thus 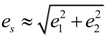 .
.In order to establish the linear relationship between the strain components and Q, which gives strong indication that crystal I undergoes first order isosymmetric phase transition, a plot of the square of spontaneous strain e2 versus temperature is shown in Figure 8. The graph shows a clear discontinuity at the transition temperature (130 K) that corresponds to the discontinuity in the b-unit cell length (Figure 5) and unit cell volume shown (Figure 7). Since the elastic strain components are linearly proportional to Q as shown in Equation (3), thus the discontinuity of the geometric quantities in crystal I implies the first order isosymmetric phase transition of crystal I. Although the geometric anomalies of tripling of b-unit cell length and unit cell volume may be an exaggerated picture of a first order phase transition in crystal I, however, the above analysis is an indirect prediction based on the discontinuities of  and order parameter Q2 [12].
and order parameter Q2 [12].
 and order parameter Q2 [12].
and order parameter Q2 [12].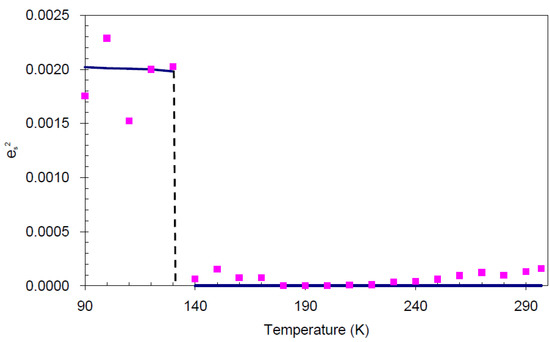
Figure 8.
Temperature variation of  (square of spontaneous strain). The line indicates the trend of the data, and the values are calculated from raw data.
(square of spontaneous strain). The line indicates the trend of the data, and the values are calculated from raw data.
 (square of spontaneous strain). The line indicates the trend of the data, and the values are calculated from raw data.
(square of spontaneous strain). The line indicates the trend of the data, and the values are calculated from raw data.
3. Experimental Section
General Information
Adipic acid or 1,6-hexanedioic acid (I) was obtained commercially (Fluka, Buchs, Switzerland). Crystals of 1,6-hexanedioic acid were grown by the slow evaporation from ethyl acetate solution to afford the colorless block-shaped single crystals of I. The crystal obtained was subjected on X-ray structural analyses. The single crystal of 0.30 × 0.52 × 0.55 mm3 in size was mounted on a glass fiber with epoxy cement for X-ray crystallographic study. Using the same crystal, the cell parameters were measured in the temperature range from 297(2) to 90.0(1) K. Two crystallographic data of I were collected at 297(2) and 120.0(1) K, respectively, and these crystallographic data and experimental details are presented in Table 1. The data were collected using a Bruker APEX2 CCD diffractometer with a graphite monochromated MoKα radiation at a detector distance of 5 cm and with APEX2 software [18]. Crystallographic data at 120.0(1) K were collected with the Oxford Cyrosystem Cobra low-temperature attachment. The collected data were reduced using SAINT program [18] and the empirical absorption corrections were performed using the SADABS program [18]. The structures were solved by direct methods and refined by least-squares using the SHELXTL software package [19]. For the RTP polymorph, all non-hydrogen atoms were refined anisotropically and all H atoms were located from difference Fourier maps and isotropically refined. For the LTP polymorph, all H atoms were placed in calculated positions with distances of O–H = 0.82 Å and C–H = 0.97 Å after checking their positions in the difference map. The Uiso values were constrained to be 1.2Ueq of the carrier atoms. The final refinement converged well. The selected bond lengths are presented in Table 2. Materials for publication were prepared using SHELXTL [19], PLATON [20] and Mercury [21]. The crystallographic-information files for I at temperature 297(2) and 120.0(1) K have been deposited in the Cambridge Crystallographic Data Base Center with deposition numbers CCDC989931 and CCDC989973, respectively.
4. Conclusions
The cell parameters of crystal I were measured in the temperature range from 297 to 90 K. The transition occurs at TC = 130 K. These data show that the isosymmetric phase transition is of first order, involving discontinuities and a tripling of the b-axis and cell volume at TC (Figure 4a). The analysis of bilinear coupling between order parameter Q and elastic strain components formulated in the Landau potential shows that the Landau phenomenological theory of first order structural phase transition in crystal I is adequate in illustrating the feature of phase transition through the spontaneous strain. These spontaneous strain is caused by the conformational changes of the molecular structure resulting from extra hydrogen bonding at the low temperature structure which has initiated the first order reversible temperature-dependent phase transition in crystal I.
Acknowledgments
SC thanks the Prince of Songkla University for generous support. The authors thank the Malaysian Government and Universiti Sains Malaysia for the Research University Golden Goose Grant No. 1001/PFIZIK/811012. The authors extend their appreciation to the Deanship of Scientific Research at King Saud University for funding the work through research group project No. RGP-VPP-207.
Author Contributions
Suchada Chantrapromma and Hoong-Kun Fun contributed to the experimental and X-ray structure determination parts and Hoong-Kun Fun and Lye-Hock Ong contributed to the theoretical part. All authors contributed to the manuscript preparation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hashimoto, M.; Harada, M.; Mizuno, M.; Hamada, M.; Ida, T.; Suhara, M. Phase transitions, hydrogen bond and crystal dynamics of p-methylbenzyl alcohol as studied by single crystal X-ray diffraction and H-NMR. Z. Naturforsch. 2002, 57a, 381–387. [Google Scholar]
- Choudhury, R.R.; Chitra, R.; Sastry, P.U.; Das, A.; Ramanadham, M. Phase transition in triglycine family of hydrogen bonded ferroelectrics: An interpretation based on structural studies. Pramana 2004, 63, 107–115. [Google Scholar] [CrossRef]
- Katrusiak, A. Conformational transformation coupled with the order-disorder phase transition in 2-methyl-1,3-cyclohexanedione crystals. Acta Crystallogr. B 2000, 56, 872–881. [Google Scholar] [CrossRef]
- Usman, A.; Chantrapromma, S.; Fun, H.K. The 143 and 300 K polymorphs of hexamethylenetetraminium 2,4-dinitrophenolate monohydrate. Acta Crystallogr. C 2001, 57, 1443–1446. [Google Scholar] [CrossRef]
- Fun, H.K.; Usman, A.; Chantrapromma, S.; Osman, J.; Ong, L.H.; Tilley, D.R.; Ishibashi, Y. Phase transitions in hydrogen-bonded phenol-amine adducts: Analysis by ferroelastic theory. Solid State Commun. 2003, 127, 677–682. [Google Scholar] [CrossRef]
- How, P.T.; Lee, B.S.; Fun, H.K.; Razak, I.A.; Chantrapromma, S. Microscopic theory of phase transitions in hydrogen-bonded phenol-amine adducts. Phys. Rev. B 2005, 71, 174109. [Google Scholar]
- Chantrapromma, S.; Fun, H.K.; Usman, A. Orthorhombic-to-monoclinic temperature-dependent phase transition of hexamethylenetetraminium-3,5-dinitrobenzoate-3,5-dinitrobenzoic acid monohydrate crystal. J. Mol. Struct. 2006, 789, 30–36. [Google Scholar] [CrossRef]
- Fun, H.K.; Rosli, M.M.; Lee, B.S.; Ong, L.H.; Chantrapromma, S. First order temperature-dependent phase transition of hexamethylenetetraminium 3,5-dinitrobenzoate hemihydrate crystal: Landau phenomenological theory approach. J. Mol. Struct. 2007, 837, 132–141. [Google Scholar] [CrossRef]
- Ranganathan, A.; Kulkarni, G.U.; Rao, C.N.R. Understanding the hydrogen bond in terms of the location of the bond critical point and the geometry of the lone pairs. J. Phys. Chem. A 2003, 107, 6073–6081. [Google Scholar] [CrossRef]
- Ohki, H.; Nakamura, N.; Chihara, H. Phase transition in solid adipic acid. J. Phys. Soc. Jpn. 1988, 57, 382–383. [Google Scholar] [CrossRef]
- Fun, H.K.; Chantrapromma, S. A triclinic polymorph of hexanedioic acid. Acta Crystallogr. E 2009, 65, o624. [Google Scholar] [CrossRef]
- Salje, E.K.H. Phase Transition in Ferroelastic and Co-elastic Crystals; Cambridge University Press: University of Cambridge, Cambridge, UK, 1990; pp. 28–32. [Google Scholar]
- Gesi, K. Phenomenological theory of an isomorphous transition in polar crystals-application to the II-III transition in ferroelectric Ca2Pb(C2H5COO)6. J. Phys. Soc. Jpn. 1976, 40, 483–489. [Google Scholar] [CrossRef]
- Jayaraman, A. Fusion curve of cerium to 70 kilobar and phenomena associated with supercritical behavior of fcc cerium. Phys. Rev. 1965, 137, A179. [Google Scholar] [CrossRef]
- Nye, J.F. Physical Properties of Crystals: Their Representation by Tensor and Matrices; Oxford University Press: Oxford, UK, 1972; pp. 93–109. [Google Scholar]
- Schlenker, J.L.; Gibbs, G.V.; Boisen, M.B. Strain-tensor components expressed in terms of lattice parameters. Acta Crystallogr. A 1978, 34, 52–54. [Google Scholar] [CrossRef]
- Aizu, K. Determination of the state parameters and formulation of spontaneous strain for ferroelastics. J. Phys. Soc. Jpn. 1970, 28, 706–716. [Google Scholar] [CrossRef]
- APEX2 (Version 1.27), SAINT (Version 7.12a) and SADABS (Version 2004/1). Bruker AXS Inc.: Madison, WI, USA, 2005.
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. D 2009, 65, 148–155. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. Mercury CSD 2.0-new features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Sample Availability: Samples of the compounds are available from the authors.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/4.0/).