Edge-Termination and Core-Modification Effects of Hexagonal Nanosheet Graphene
Abstract
:1. Introduction
2. Results and Discussion
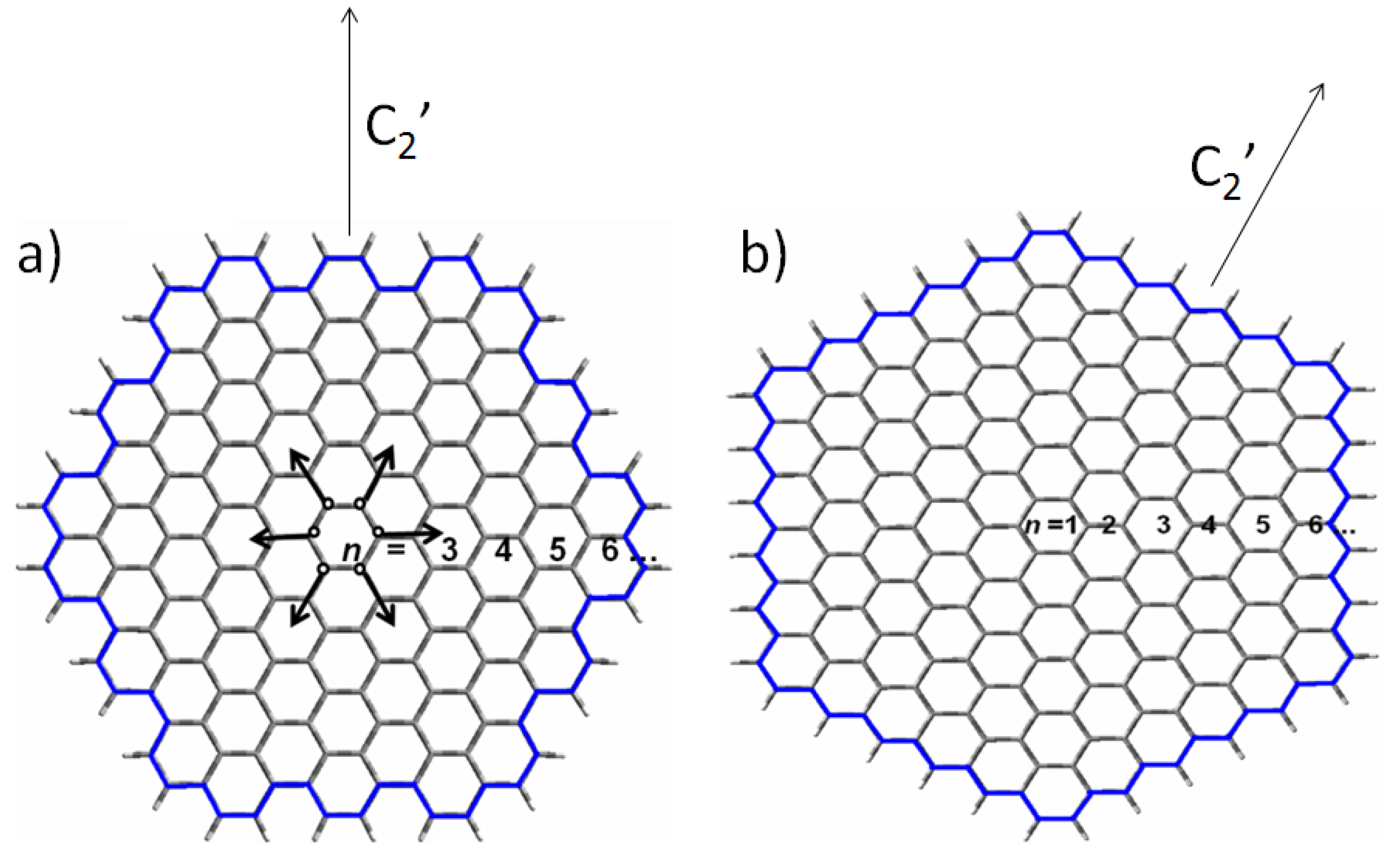
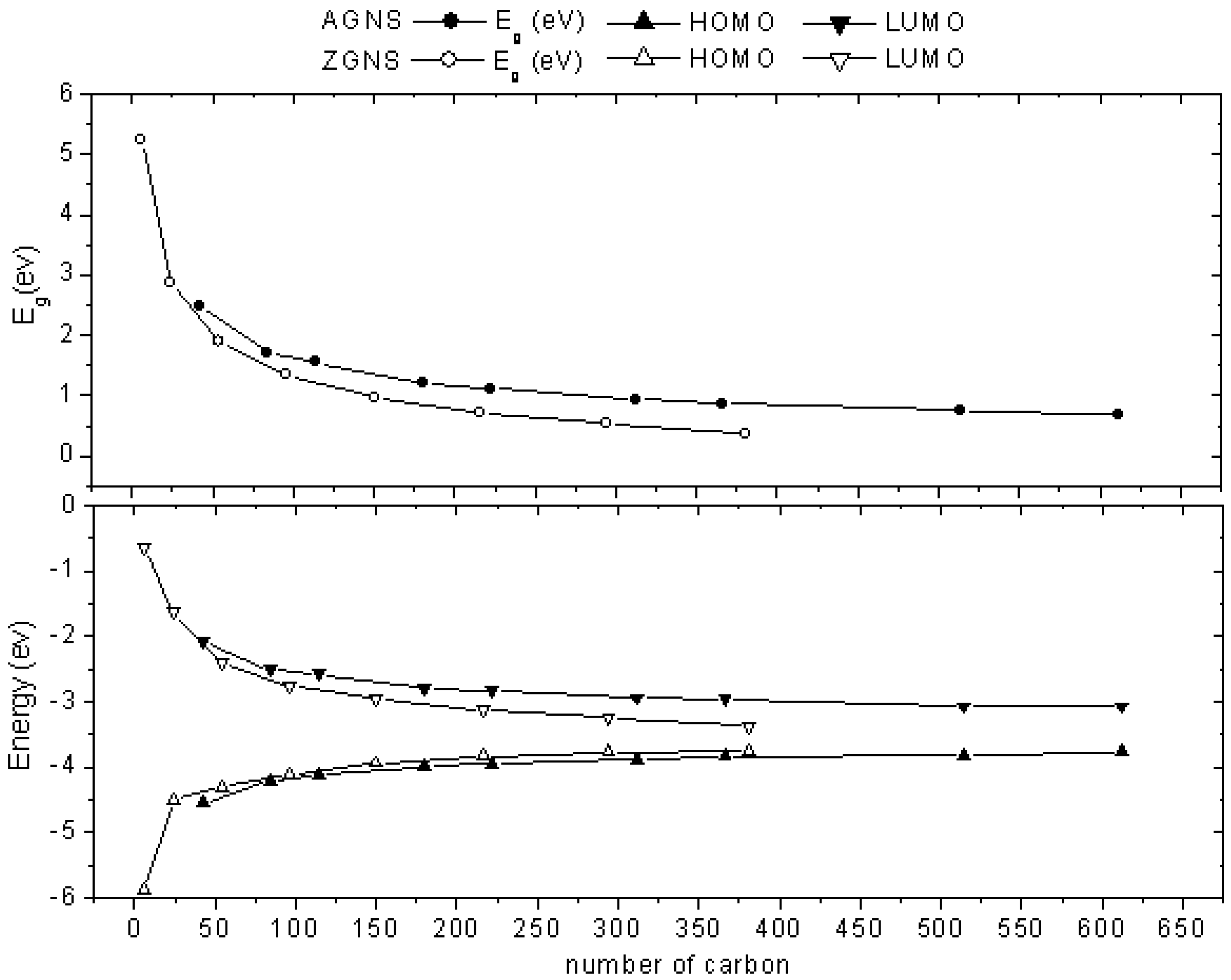
2.1. Size-Dependent Effect
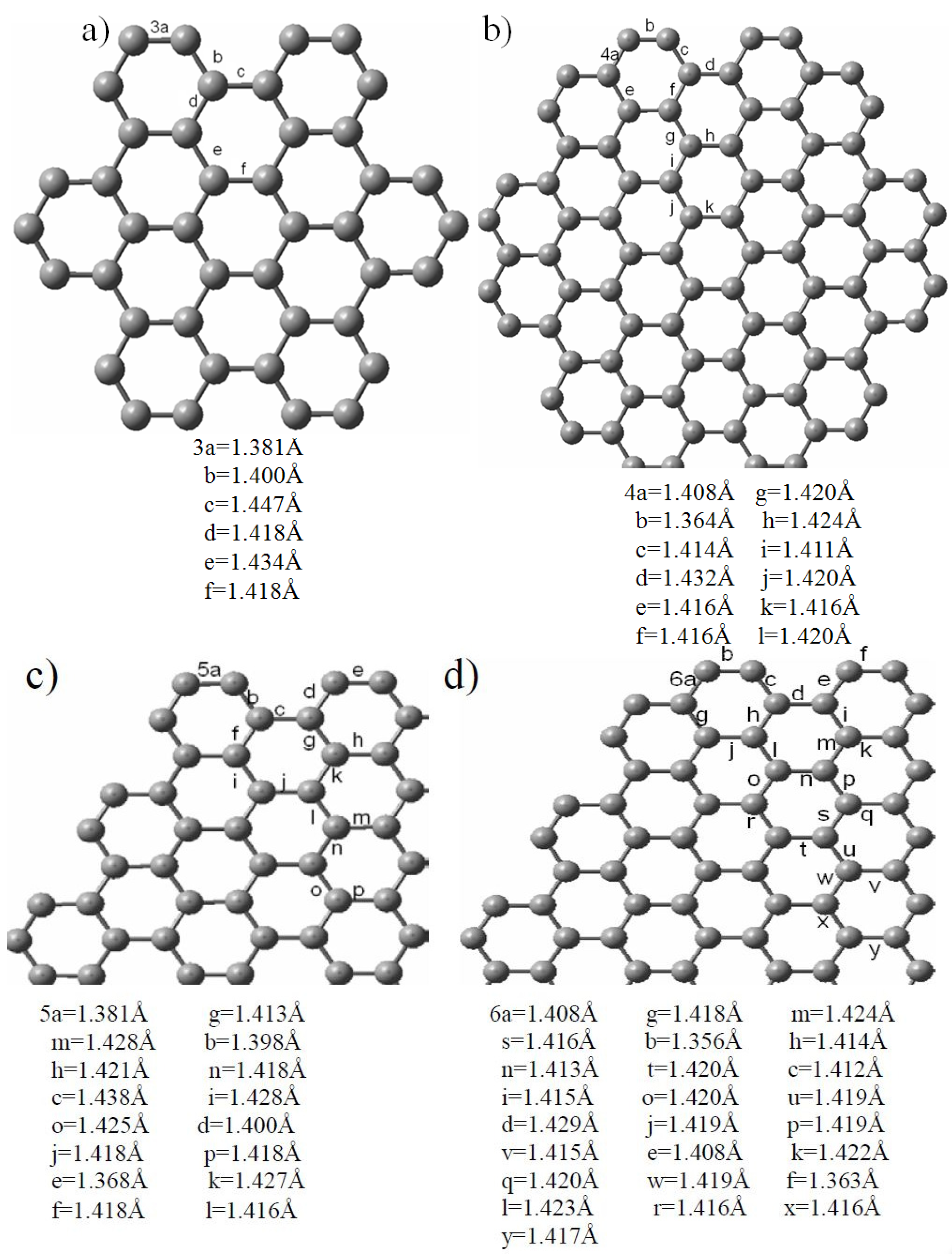
2.2. Edge-Termination Effect
| Terminator | EHOMO (eV) | ELUMO (eV) | Eg (eV) |
|---|---|---|---|
| H | −4.000 | −2.790 | 1.210 |
| F | −4.216 | −3.102 | 1.114 |
| Cl | −4.010 | −3.025 | 0.985 |
| CN | −5.966 | −4.994 | 0.972 |
| OH | −3.176 | −2.303 | 0.873 |
| SH | −3.705 | −2.880 | 0.825 |
| Terminator | EHOMO (eV) | ELUMO (eV) | Eg (eV) |
|---|---|---|---|
| H | −3.840 | −3.130 | 0.710 |
| F | −3.890 | −3.235 | 0.655 |
| Cl | −3.861 | −3.322 | 0.539 |
| CN | −5.933 | −5.422 | 0.511 |
| OH | −3.021 | −2.478 | 0.543 |
| SH | −3.635 | −3.224 | 0.411 |

2.3. Core Modification Effect (Nanosheet Defect)

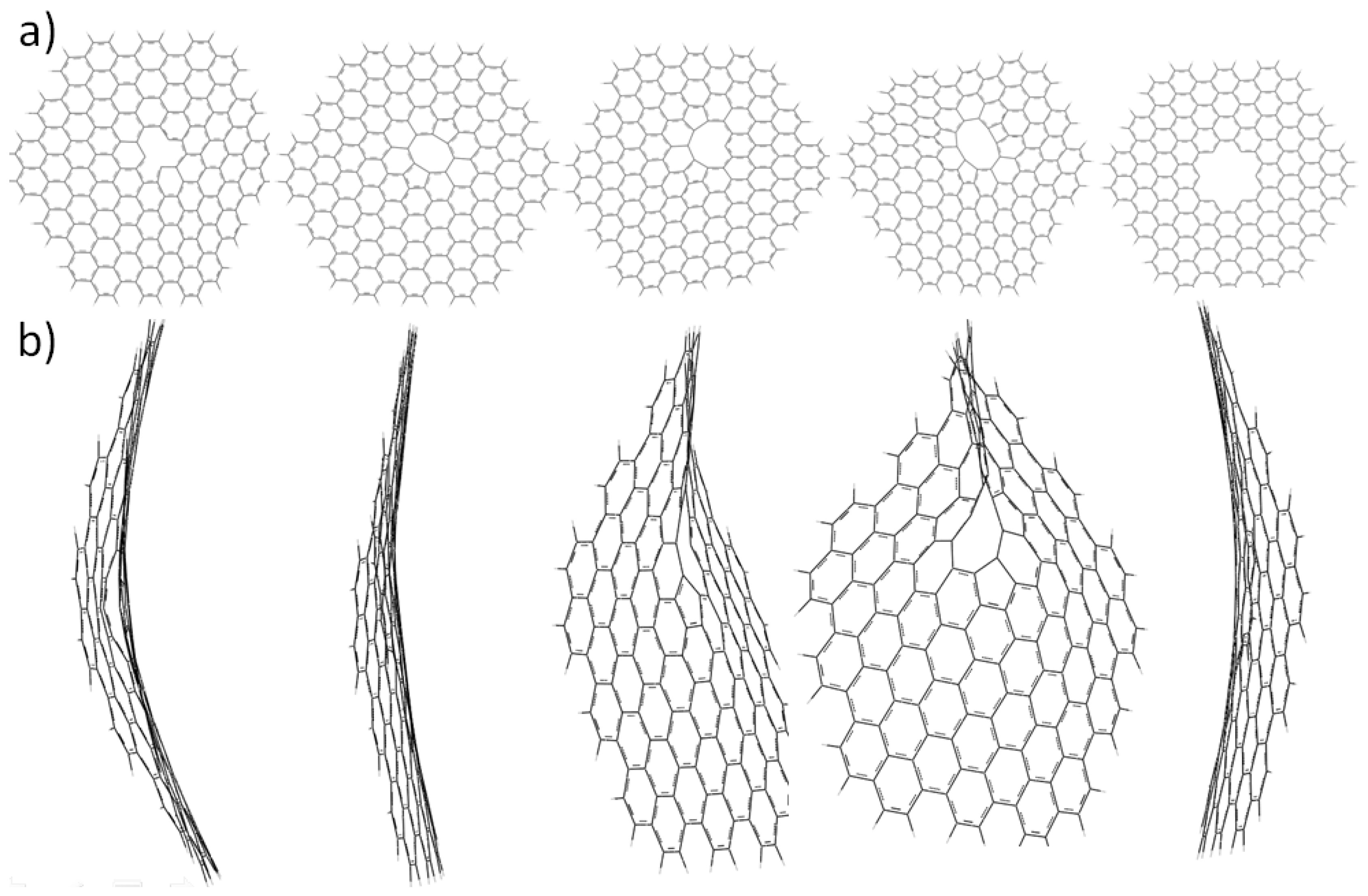
3. Experimental
4. Conclusions
Supplementary Materials
Acknowledgements
Conflicts of Interest
References
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V.; Dubonos, S.V.; Firsov, A.A. Two-dimensional gas of massless dirac fermions in graphene. Nature 2005, 438, 197–200. [Google Scholar] [CrossRef]
- Zhou, S.Y.; Gweon, G.H.; Graf, J.; Fedorov, A.V.; Spataru, C.D.; Diehl, R.D.; Kopelevich, Y.; Lee, D.H.; Louie, S.G.; Lanzara, A. First direct observation of Dirac fermions in graphite. Nat. Phys. 2006, 2, 595–599. [Google Scholar] [CrossRef]
- Wang, X.; Ouyang, Y.; Jiao, L.; Wang, H.; Xie, L.; Wu, J.; Guo, J.; Dai, H. Graphene nanoribbons with smooth edges behave as quantum wires. Nat. Nanotech. 2011, 6, 563–567. [Google Scholar] [CrossRef]
- Pan, M.; Girão, E.C.; Jia, X.; Bhaviripudi, S.; Li, Q.; Kong, J.; Meunier, V.; Dresselhaus, M.S. Topographic and spectroscopic characterization of electronic edge states in CVD grown graphene Nanoribbons. Nano Lett. 2012, 12, 1928–1933. [Google Scholar] [CrossRef]
- Nakada, K.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Edge state in graphene ribbons: Nanometer size effect and edge shape dependence. Phys. Rev. B 1996, 54, 17954–17961. [Google Scholar] [CrossRef]
- Son, Y.-W.; Cohen, M.L.; Louie, S.G. Energy gaps in graphene nanoribbons. Phys. Rev. Lett. 2006, 97, 216803–216807. [Google Scholar] [CrossRef]
- Son, Y.-W.; Cohen, M.L.; Louie, S.G. Half-metallic graphene nanoribbons. Nature 2006, 444, 347–349. [Google Scholar] [CrossRef]
- Trauzettel, B.; Bulaev, D.V.; Loss, D.; Burkard, G. Spin qubits in graphene quantum dots. Nat. Phys. 2007, 3, 192–196. [Google Scholar] [CrossRef]
- Wang, W.L.; Meng, S.; Kaxiras, E. Graphene nanoflakes with large spin. Nano Lett. 2008, 8, 241–245. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Wang, W.L.; Meng, S.; Kaxiras, E. Comment on graphene nanoflakes with large spin: Broken-symmetry states. Nano Lett. 2008, 8, 766–766. [Google Scholar] [CrossRef]
- Ezawa, M. Graphene nanoribbon and grapehene nanodisk. Physica E 2008, 40, 1421–1423. [Google Scholar] [CrossRef]
- Ezawa, M. Metallic graphene nanodisks: Electronic and magnetic properties. Phys. Rev. B 2007, 76, 245415–245420. [Google Scholar] [CrossRef]
- Rossier, J.F.; Palacios, J.J. Magnetism in graphene nano-islands. Phys. Rev. Lett. 2007, 99, 177204–177207. [Google Scholar] [CrossRef]
- Dias, J.R. Resonance-theoretic calculation of the ground state spin density of the pπ-system of edge atoms on graphene nanodots and nanoribbons. Chem. Phys. Lett. 2008, 467, 200–203. [Google Scholar] [CrossRef]
- Neto, A.H.C.; Guinea, F.; Peres, N.M.R.; Novoselov, K.S.; Geim, A.K. The electronic properties of graphene. Rev. Mod. Phys. 2009, 81, 109–162. [Google Scholar] [CrossRef]
- Brey, L.; Fertig, H.A. Electronic states of graphene nanoribbons studied with the dirac equation. Phys. Rev. B 2006, 73, 235411–235416. [Google Scholar] [CrossRef]
- Tan, Y.-Z.; Yang, B.; Parvez, K.; Narita, A.; Osella, S.; Beljonne, D.; Feng, X.; Müllen, K. Atomically precise edge chlorination of nanographenes and its application in graphene nanoribbons. Nat. Comm. 2013, 4, 2646. [Google Scholar]
- Fujii, S.; Enoki, T. Nanographene and graphene edges: Electronic structure and nanofabrication. Acc. Chem. Res. 2013, 46, 2201–2210. [Google Scholar]
- Fujii, S.; Enoki, T. Cutting of oxidized graphene into nanosized poeces. J. Am. Chem. Soc. 2010, 132, 10034–10041. [Google Scholar] [CrossRef]
- Nagai, H.; Nakano, M.; Yoneda, K.; Fukui, H.; Minami, T.; Bonness, S.; Kishi, R.; Takahashi, H.; Kubo, T.; Kamada, K.; et al. Theoretical study on third-order nonlinear optical properties in hexagonal graphene nanoflakes: Edge shape effect. Chem. Phys. Lett. 2009, 477, 355–359. [Google Scholar] [CrossRef]
- Tachikawa, H.; Kawabata, H. Electronic states of defect sites of graphene model compounds: ADFT and direct molecular orbital-molecular dynamics study. J. Phys. Chem. C 2009, 113, 7603–7609. [Google Scholar] [CrossRef]
- Hajgato, B.; Deleuze, M.S. Quenching of magnetism in hexagonal graphene nanoflakes by non-local electron correlation. Chem. Phys. Lett. 2012, 553, 6–10. [Google Scholar] [CrossRef]
- Karlicky, F.; Zbořil, R.; Otyepka, M. Band gaps and structural properties of graphene halides and their derivatives: A hybrid functional study with localized orbital basis sets. J. Chem. Phys. 2012, 137, 034709. [Google Scholar] [CrossRef]
- Bhowmick, S.; Singh, A.K.; Yakobson, B.I. Quantum dots and nanoroads of graphene embedded in hexagonal boron nitride. J. Phys. Chem. C 2011, 115, 9889–9893. [Google Scholar] [CrossRef]
- Luo, Z.; Kim, S.; Kawamoto, N.; Rappe, A.M.; Johnson, A.T.C. Growth mechanism of hexagonal-shape graphene flakes with zigzag edges. Nano. Lett. 2011, 5, 9154–9160. [Google Scholar]
- Geng, D.; Wu, B.; Guo, Y.; Huang, L.; Xue, Y.; Chen, J.; Yu, G.; Jiang, L.; Hu, W.; Liu, Y. Uniform hexagonal graphene flakes and films grown on liquid copper surface. Proc. Natl. Acad. Sci. USA 2012, 109, 7992–7996. [Google Scholar] [CrossRef]
- Acik, M.; Chabal, Y.J. Selected topics in applied physics technology, physics, and modeling of graphene devices. Jpn. J. Appl. Phys. 2011, 50, 070101–070116. [Google Scholar]
- Qi, X.; Guo, X.; Zheng, C. Density functional study the interaction of oxygen molecule with defect sites of graphene. Appl. Surf. Sci. 2012, 259, 195–200. [Google Scholar] [CrossRef]
- Banhart, F.; Kotakoski, J.; Krasheninnikov, A.V. Structural defects in graphene. ACS Nano 2010, 5, 26–41. [Google Scholar]
- Wang, M.C.; Yan, C.; Ma, L.; Hu, N.; Chen, M.W. Molecular dynamics investigation on edge stress and shape transition in graphene nanoribbons. Comput. Mater. Sci. 2012, 54, 236–239. [Google Scholar] [CrossRef]
- Tachikawa, H.; Kawabata, H. Virtual issue: Graphene and functionalized graphene. J. Phys. Chem. C 2009, 113, 7603–7069. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; Garcia, A.; Junquera, J.; Ordejon, P.; Sanchez-Portal, D. The Siesta method for ab initio order-N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Ordejon, P.; Artacho, E.; Soler, J.M. Self-consistent order-N density-functional calculations for very large systems. Phys. Rev. B 1996, 53, R10441–R10443. [Google Scholar] [CrossRef]
- Sanchez-Portal, D.; Ordejón, P.; Artacho, E.; Soler, J.M. Density-functional method for very large systems with LCAO basis sets. Int. J. Quantum Chem. 1997, 65, 453–461. [Google Scholar] [CrossRef]
- Burke, K.; Perdew, J.P.; Ernzerhof, M. Why the generalized gradient approximation works and how to go beyond it. Int. J. Quantum Chem. 1997, 61, 287–293. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Ab initio calculations of structural, elastic, and electronic properties of silver nitrides—Springer. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef]
- Sample Availability: Not available.
© 2014 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Deng, J.-P.; Chen, W.-H.; Chiu, S.-P.; Lin, C.-H.; Wang, B.-C. Edge-Termination and Core-Modification Effects of Hexagonal Nanosheet Graphene. Molecules 2014, 19, 2361-2373. https://doi.org/10.3390/molecules19022361
Deng J-P, Chen W-H, Chiu S-P, Lin C-H, Wang B-C. Edge-Termination and Core-Modification Effects of Hexagonal Nanosheet Graphene. Molecules. 2014; 19(2):2361-2373. https://doi.org/10.3390/molecules19022361
Chicago/Turabian StyleDeng, Jin-Pei, Wen-Hao Chen, Shou-Po Chiu, Chih-Hsun Lin, and Bo-Cheng Wang. 2014. "Edge-Termination and Core-Modification Effects of Hexagonal Nanosheet Graphene" Molecules 19, no. 2: 2361-2373. https://doi.org/10.3390/molecules19022361
APA StyleDeng, J.-P., Chen, W.-H., Chiu, S.-P., Lin, C.-H., & Wang, B.-C. (2014). Edge-Termination and Core-Modification Effects of Hexagonal Nanosheet Graphene. Molecules, 19(2), 2361-2373. https://doi.org/10.3390/molecules19022361




