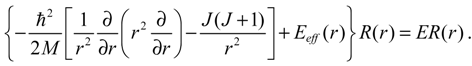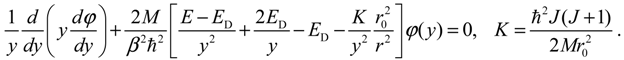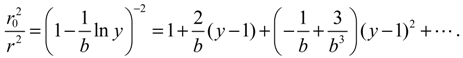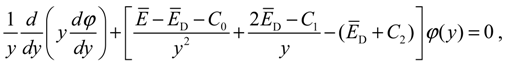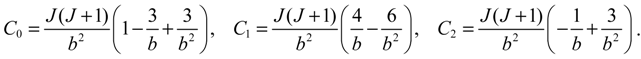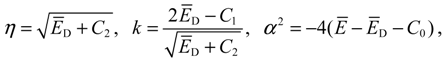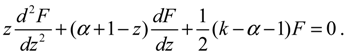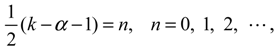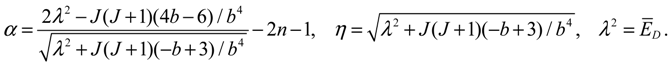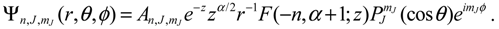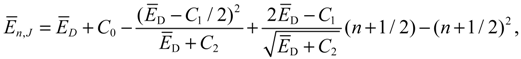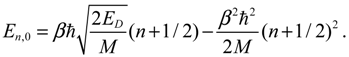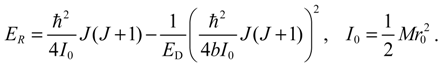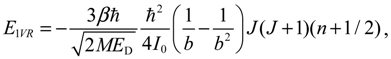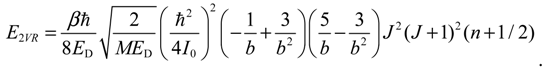1. Introduction
One of the greatest challenges in molecular dynamics (MD) is to model processes involving many degrees of freedom, some of which have to be treated quantum mechanically. The combined quantum mechanics (QM) and molecular mechanics (MM) approach to MD [
1,
2] provides tremendous computational advantages over full quantum mechanical models by treating a limited region of a molecular system quantum mechanically, while treating the rest of the system by using conventional MM methods. The QM part corresponds to what is to be studied in detail, such as the regions involving charge transfer, electron excitations or chemical reactions. The atoms in the QM part are explicitly expressed as electrons and nuclei such that their motions are described quantum mechanically. Quantum effects in MD simulation have been taken into account by various techniques, such as pseudo-spectral methods [
3], path integral methods [
4], Car–Parrinello-type simulations [
5], molecular wave packet dynamics [
6] and density matrix evolution method [
7]. The performance of a hybrid QM/MM method has been extensively investigated by Billing and coworkers [
8]. Brickmann and Schmitt [
9] employed a sequence of approximations to transfer the mixed QM/MM dynamics into a Hamilton–Jacobi-type scheme, which is able to formulate the equations of motion by using a single Hamiltonian.
The QM/MM approach to MD simulation of molecular systems mainly relies on the Born–Oppenheimer approximation that a molecular motion can be separated into two independent motions: one is the classical atomic motion on a single adiabatic potential energy surface and the other is the quantum electronic motion in the presence of a time-dependent potential generated by the moving classical atoms. However, there are a huge number of problems for which the interaction between classical and quantum motion is so significant that the Born–Oppenheimer approximation may become invalid. For such problems, the QM/MM approach to MD simulation inevitably faces the crucial issue of self-consistency. The quantum degrees of freedom must evolve correctly under the influence of the surrounding classical motion, and meanwhile, the classical degrees of freedom must respond correctly to the quantum transitions. Therefore, a self-consistent QM/MM approach has to consider not only the effect of the classical degrees of freedom on the quantum ones but also the backreaction of the quantum effect on the classical degrees of freedom.
Two mixed quantum-classical methods that have been developed in the literature to treat the interactions between classical and quantum systems in a self-consistent way are the mean-field method [
10] and the surface-hopping method [
11]. The mean-field method calculates the force for the classical motion by averaging over the quantum wave function. This method is invariant to the choice of quantum representations and applicable to both bound and continuum states, but it suffers from the neglect of correlations between classical and quantum degree of freedom. On the other hand, the surface-hopping method was developed to manifest quantum-classical correlation, but it is not invariant to the choice of quantum representations and is intrinsically limited to discrete quantum states. Although both methods have their respective limitations, they have been proven to be successful in many applications.
In the latest decade, a novel solution to the quantum backreaction problem in a mixed QM/MM simulation has been proposed using the Bohmian formulation of quantum mechanics [
12,
13]. The mixed quantum-classical Bohmian (MQCB) approach combines the merits of the above two methods and gives a consistent treatment of mixing quantum and classical degrees of freedom without reference to any basis set. The MQCB method has been applied to the process of vibrational decoherence of I
2 in a dense helium environment [
14], to the case of rotational diffractive surface scattering of a diatomic molecule [
15] and to a model of O
2 interacting with a Pt surface [
16], all with good agreement with the full quantum-mechanical treatments.
The current formulation of Bohmian mechanic is mainly based on Cartesian coordinates, which is inconvenient to the description of molecular angular motions. This paper aims to incorporate quantum Hamilton mechanics (QHM) [
17,
18,
19] into the framework of the MQCB method to enhance its capability of handling orbital and spin angular motions. It is well known that the Bohmian velocity vanishes in all of the stationary states with zero angular quantum number, and therefore, the corresponding Bohmian particles will remain standing at their initial positions at any time [
20]. QHM, on the one hand, conquers the problem of Bohmian stationarity by formulating Bohmian mechanics in complex space, and on the other, describes MD in terms of Hamilton equations of motion, which are coordinate-independent and suitable to any curvilinear coordinates.
With the proposed modifications by QHM, the computational procedures of MQCB developed in the literature can be used to simulate molecular dynamics, including vibration, rotation and spin motions. The correctness of the derived state-dependent molecular dynamics will be verified by comparing with the quantum mechanical description of a diatomic molecule for which the Schrödinger equation has an analytical solution. Of significance is that the spin dynamics, which cannot be described by spatial wave functions, emerges naturally from the established state-dependent molecular dynamics.
In
Section 2, we introduce the working equations of the MQCB method to describe the motion of a diatomic molecule in Cartesian coordinates. QHM is then introduced in
Section 3 to reformulate Bohmian mechanics under spherical coordinates. We show that QHM is a single mechanics simultaneously playing the roles of QM and MM by pointing out that QHM comprises two sets of Hamilton equations with the first set describing the vibration-rotation motion of the molecule and the second set describing the time evolution of the wave function. State-dependent vibrational dynamics fully consistent with QM is derived from QHM in
Section 4.
Section 5 demonstrates how to incorporate molecular spin dynamics into MD simulation under the same motion space governed by QHM. The resulting state-dependent molecular dynamics is found to agree with the prediction of QM and well match the experimental vibration-rotation spectrum.
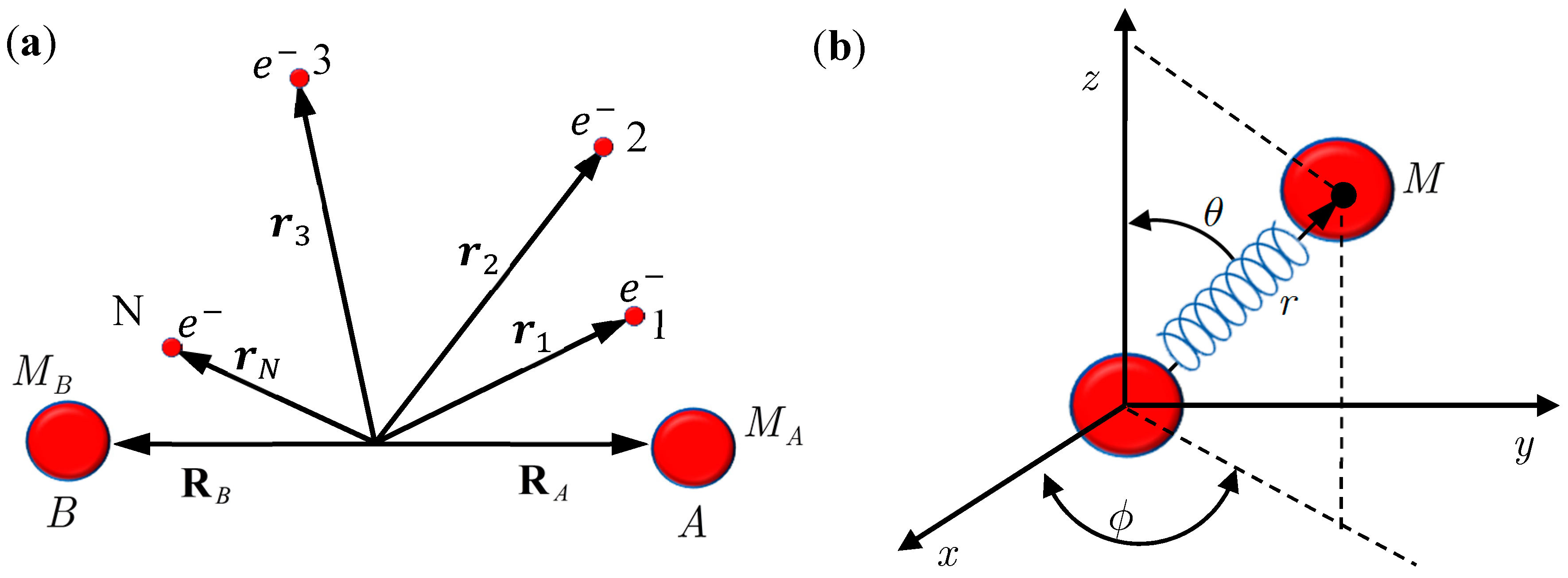
Figure 1.
(a) A diatomic molecule composed of Nuclei A and B, together with a number of N electrons; (b) An equivalent single-particle model of the diatomic molecule with rotation and vibration motion described by the spherical coordinates.
Figure 1.
(a) A diatomic molecule composed of Nuclei A and B, together with a number of N electrons; (b) An equivalent single-particle model of the diatomic molecule with rotation and vibration motion described by the spherical coordinates.
2. Mixed Quantum-Classical Mechanics
In this section, we review the basics of the MQCB method by applying it to simulate the motion of a diatomic molecule, which is composed of Nuclei A and B, of mass
MA and
MB together with a number
N of electrons (see
Figure 1). The internuclear position vector will be denoted by
X and the position vectors of the electrons with respect to
O, the center of mass of A and B, by
r1,
r2,⋯,
rN. The position vectors of A and B are denoted by
RA and
RB, so that =
RA −
RB. The Schrödinger equation describing the motion of the molecule takes the following form [
12,
13]:
where
x = [
r1 r2 ⋯
r3] is the collective vector representing the quantum motion of the electrons and
X is the vector representing the classical motion of the nuclei.
Writing the wave function as
Ψ(
t,
x,
X) =
RB(
t,
x,
X) exp (
iSB(
t,
x,
X)) with
RB and
SB being real, Equation (2.1) can be separated into three coupled equations in terms of
RB,
SB and their derivatives. For a computed
SB, the Bohmian velocity is given by:
where
m is the mass of electron and
M =
MAMB/(
MA +
MB) is the reduced mass of the molecule. With the introduction of the quantum potential:
Equation (2.2) can be recast into classical-like equations of motion:
A workable scheme of MQCB has been implemented successfully by replacing the full-dimensional wave function
Ψ(
t,
x,
X) by a wave function
![Molecules 19 16122 i001]()
in the
x quantum subspace that depends parametrically on the classical position
X(
t). The approximate wave function
![Molecules 19 16122 i001]()
obeys the Schrödinger equation:
where
d /
dt denotes the material derivative ∂ / ∂
t +
Ẋ ∙ 𝛻 along the classical trajectory
X(
t). The MQCB method and the mean-field method share the same quantum degree of freedom described by Equation (2.4), but differ from each other in the way that the classical degree of freedom is governed by the quantum wave function. Instead of Equation (2.5), the classical trajectory
X(
t) for the mean-field method is computed by the mean potential:
Upon applying Equation (2.5) or Equation (2.7) to a diatomic molecule, we find that it is convenient to express the vector
X in the spherical coordinates (
r,θ,ϕ) in order to describe the vibration and rotation of the two atoms with respect to their center of mass. However, the expressions of quantum motion described by Equation (2.2) to Equation (2.7) are valid only for Cartesian coordinates. To give an explicit manifestation of the orbital and spin angular motion of the molecules, the reformulation of Bohmian mechanics under spherical coordinates is necessary.
It will be shown in the next section that QHM provides MQCB with state-dependent molecular dynamics, which preserve the quantization property of orbital and spin angular momentum. By contrast, in the mean-field method, the classical trajectories X(t) over different quantum states are averaged out to give a state-independent result, as can be seen from Equation (2.7). To compare with the QHM formulation discussed later, here let us have a quick look on the description of the vibration-rotation motion of a diatomic molecule by the classical Equation (2.7). With the effective potential Veff(t,X) = Veff(t,r,θ,ϕ) given by Equation (2.7), the classical Hamiltonian governing the 3D relative motion of the two nuclei with respect to their center of mass can be expressed by:
The molecular dynamics (
r(
t),
θ(
τ),
ϕ(
t)) can be solved from the Hamilton equations:
It is clear that the vibrational and rotational motions of the molecule are determined uniquely by the effective potential
Veff(
t,
r,θ,ϕ) with initial conditions (
r(0),
θ(0),
ϕ(0)) and (
pr(0),
pθ(0),
pϕ(0)). In the case of a central-force potential
Veff(
r), the total energy
Hc, the squared angular momentum
L2 and the z-component angular momentum
Lz are conserved quantities along any dynamic trajectory (
r(
t),
θ(
τ),
ϕ(
t)):
where the three conservation constants depend continuously on the initial conditions. In the next section, a quantum version of the classical Hamilton Equations (2.9) and (2.10) will be derived by QHM. The resulting quantum Hamilton equations can describe molecular dynamics in a general non-stationary quantum state Ψ(
t,r,θ,ϕ), and a quantum version of the conservation law (2.11) comes out naturally, if Ψ(
t,r,θ,ϕ) is an eigenfunction.
3. Quantum Hamilton Mechanics
Consider the diatomic molecule as shown in
Figure 1b. Let
q be the internuclear position vector expressed in a curvilinear coordinate system,
Veff(
t,
q) be the instantaneous internuclear potential, and
M be the reduced mass. The Schrödinger equation describing the molecular motion can be recast into the quantum Hamilton-Jacobi equation [
17,
20]:
where the action function
S is the logarithmic wave function defined as:
The canonical momentum
p in Equation (3.1) is related to the action function
S via the law of canonical transformation:
The appearance of the imaginary number
![Molecules 19 16122 i009]()
indicates that the momentum
p has to be defined in a complex domain. In Cartesian coordinates, we have
![Molecules 19 16122 i010]()
and the particle’s velocity
![Molecules 19 16122 i011]()
can be determined by the wave function Ψ as
which is the governing equation in the complex-valued Bohmian mechanics [
21]. It is the complex momentum
p from Equation (3.3) rather than the real momentum from Equation (2.2) that matches the momentum distribution provided by standard quantum mechanics [
20]. The relationship between the real and complex momentum can be found as:
It can be seen that the real Bohmian trajectory solved from
![Molecules 19 16122 i013]()
only carry information about the dynamics of the momentum flow, while the complex trajectory solved from
![Molecules 19 16122 i014]()
also includes information about the probability
RB = |Ψ|. The dynamics in the complex phase space (
q,
p) thus explains in a natural way how to get the correct momentum distribution and explains why algorithms based on complex trajectories are stable and accurate [
22,
23,
24,
25,
26,
27,
28]. The advantages of implementing numerical codes in a complex phase space are similar to those of considering complex fields instead of real ones in electromagnetism [
20].
When compared with the classical Hamiltonian
Hc in Equation (2.8), the quantum Hamiltonian
HΨ defined in Equation (3.1) has an additional term called complex quantum potential, which in the state Ψ can be expressed by:
The state-dependent molecular dynamics to be developed here all originate from the state-dependent nature of
Q. With the quantum Hamiltonian
HΨ defined in Equation (3.1), the accompanying Hamilton equations appear as the usual form:
The Hamilton equations are coordinate-independent and valid for arbitrary coordinate systems. Especially, in the Cartesian coordinates, we have ∂
HΨ/∂
q =
p/
M and the first set of the Hamilton equations (3.7) turns out to be the Bohmian velocity, like the one defined in Equation (2.2).
We now specialize
q to the spherical coordinates
q = (
r,θ,ϕ) with
r denoting the internuclear distance, and (
θ,ϕ) denoting the orientation of the molecule. By expanding the inner product
p ∙ p and the divergence ∇∙
p in spherical coordinates, quantum Hamiltonian
HΨ in Equation (3.1) can be expressed by [
17]:
This is the quantum counterpart of the classical Hamiltonian defined in Equation (2.8). Substituting
HΨ into Equation (3.7), we obtain the first set of the Hamilton equations as:
where the canonical momentum (
pr, pθ, pϕ) has been given according to Equation (3.3):
Equation (3.9) is the quantum counterpart of the classical equation (2.9) and provides the vibrational and rotational dynamics (
r(
t),
θ(
τ),
ϕ(
t)) of the molecule in the state Ψ(
t,r,θ,ϕ), which may be stationary or non-stationary. On the other hand, it can be shown that the second set of Hamilton equation (3.7) with
p given by Equation (3.3) is just the Schrödinger equation. In other words, the two sets of Hamilton equations (3.7) provide a new approach to MM/QM formulation, where the first set plays the role of MM to derive the molecular dynamics (3.9), while the second set plays the role of QM to give the time evolution of the wave function Ψ.
The quantum Hamiltonian (3.8) can be expressed in a more comprehensive way with the help of Equation (3.9):
where the first three terms constitute the classical kinetic energy
T, and the last two terms form the total potential:
The dynamic equations of motion for the molecule can be described either by the Hamilton equations (3.9) or by the Lagrange equations based on the quantum Lagrangian:
from which the quantum Lagrange equations of motion can be obtained as
It can be seen that apart from the internuclear force produced by
Veff, there are additional quantum forces acting on the molecule yielded by the quantum potential
Q. In the next two sections, we proceed to show that the action of the quantum potential leads to the state-dependent molecular dynamics compatible with the description of the wave function Ψ.
4. State-Dependent Molecular Vibration
By replacing Equations (2.2) and (2.5) with Equations (3.9) and (3.14), respectively, the computational procedures of MQCB developed in the literature can be used to simulate molecular dynamics including vibration, rotation and spin motions. Before this new QM/MM approach becomes workable, we have to verify that the governing equations derived in
Section 3 yield correct molecular dynamics. The verification is based on the comparison with the quantum mechanical description of a diatomic molecule for which the Schrödinger equation relating to the nuclear motion has an analytical solution. The test model is illustrated in
Figure 1a, which is an equivalent single-particle model of a diatomic molecule with rotational and vibrational motion described by the spherical coordinates. The effective internuclear potential is modeled by the Morse function and the corresponding Schrödinger equation is solved analytical in the
appendix with eigenfunction Ψ
n,J,mJ (
r,θ,ϕ) =
Rn,J (
r)Θ
J,mJ (
θ)Φ
mJ (
ϕ) given by Equation (A15) and eigenvalue
En,J given by Equation (A17). All of the parameters and constants appearing below refer to the
Appendix.
Substituting Ψ
n,J,mJ (
r,θ,ϕ) into Equation (3.9), we obtain the state-dependent molecular dynamics as:
where
r = βr is the dimensionless radial distance and
τ = t(ℏ
β2/ M is the dimensionless time. In a quantum state specified by the three quantum numbers
n,
J and
mJ, the internuclear distance
r(
t) and the molecular orientations
θ(
τ) and
ϕ(
t) can be expressed as functions of time by solving Equation (4.1).
As a comparison, if the standard Bohmian mechanics based on Equation (2.2) is used to simulate the molecular dynamics in the eigenstate Ψn,J,mJ (r,θ,ϕ), we will find the molecule to be motionless in all the states with J = 0. The constitution of the complex momentum in Equation (3.5) explains why it is possible to observe non-vanishing momentum in cases where the Bohmian momentum ∇SB vanishes.
The first test on the accuracy of the state-dependent molecular dynamics is to examine the quantization laws existing in the eigenstate Ψ
n,J,mJ (
r,θ,ϕ). In the previous section, we have seen that in the conventional MM description, the three conservation constants depend continuously on the initial conditions, being unable to manifest the quantization laws. Now replacing Equations (2.8) and (2.9) by Equations (3.8) and (3.9), we can derive the expected quantization laws. With the eigenfunction Ψ
n,J,mJ (
r,θ,ϕ) given by Equation (A15) and (
pr,pθ,pϕ) given by Equation (3.10), the Hamiltonian
H, the squared angular momentum
L2 and the z-component angular momentum
Lz defined in Equation (3.8) can be computed as:
We find that the resulting values of
![Molecules 19 16122 i033]()
,
L2 and
H are independent of time and are quantized according to the three quantum numbers
n,
J and
mJ. Unlike the probabilistic interpretation in standard quantum mechanics, here, we have given a dynamic interpretation of the quantization laws by showing that the three physical quantities have constant discrete values along any quantum trajectory (
r(
t),
θ(
τ),
ϕ(
t)) solved from Equation (4.1) in the quantum state specified by the three quantum numbers (
n,J,mJ).
The second test is on the consistence between the predictions of the equilibrium bond length made between quantum mechanics and state-dependent molecular dynamics. We will show that the equilibrium bond length
req that maximizes the radial probability
Pr satisfies the dynamical equilibrium condition
dr /
dt = 0. We first prove this property for the ground vibrational state. Referring to the
Appendix, the corresponding radial wave function with
n = 0 is given by
The dependence of
R0,J (
r) on the angular quantum number
J is reflected in the relation of
α and
η to
J, as shown in Equation (A14). Substituting
R0,J (
r) into Equation (4.1a) yields the equation of motion for the rotation-dependent vibration in the ground state:
The above radial dynamics has a stable equilibrium point at
zeq =
α,
i.e.,
The other equilibrium point is at
zeq = 0,
i.e.,
req = ∞, corresponding to the condition of molecular dissociation. Equation (4.5) expresses the equilibrium bond length
req as an explicit function of the angular momentum quantum number
J. This closed-form expression describes analytically how the equilibrium bond length
req increases monotonically with the angular quantum number
J. Of significance is that the equilibrium bond length
req obtained from the molecular dynamics (4.1a) always coincides with that obtained by QM method. This coincidence has its theoretic origin. We recall the definition of the radial probability:
by noting that
Rn,J (
r) given by Equation (A13) is a real function of
r. On the other hand, according to the dynamic Equation (4.1a), the equilibrium position
req satisfies the condition:
It appears that the equilibrium condition (4.7) is just the condition requiring the radial probability
Pn,J in Equation (4.6) to have an extreme value.
All of the properties obtained from the dynamics equation (4.1a) can be re-derived from the action of the radial total force
![Molecules 19 16122 i037]()
. As an illustration, we consider the case with
J = 0 for which Θ
J,mJ (
θ) = 1 and the total potential defined in Equation (3.12) has a simple expression,
where we note
α = 2
λ − 1 and
η =
λ from Equation (A14) for the case of
J = 0. The radial total force
![Molecules 19 16122 i037]()
now can be determined from
![Molecules 19 16122 i039]()
as
The internuclear distance free from radial force can be found from the condition
fr (
r) = 0, which leads to
This value is exactly the equilibrium bond length
req already obtained in Equation (4.5) by using the equilibrium condition
dr / dt = 0.
The evaluation of
![Molecules 19 16122 i037]()
in the vicinity of
req gives
![Molecules 19 16122 i042]()
, if
r >
req, and
![Molecules 19 16122 i043]()
, if
r <
req. The sign of
![Molecules 19 16122 i037]()
in the neighborhood of
req indicates that the two nuclei attract each other when their distance is longer than
req and repel each other when their distance is shorter than
req. Consequently, there is always a restoring force to make
r return to its equilibrium position
req.
Figure 2 gives a numerical verification of the coincidence of four positions for the state with
n = 1 and
J = 0: (a) the local minimum of the total potential; (b) the position with
fTotal (
r) = 0; (c) the equilibrium position with zero velocity
dr /
dt = 0; and (d) the local maximum of the radial probability
P1,0, where the first three positions come from the state-dependent molecular dynamics, while the last position from the QM description.
Figure 2.
Illustration of the coincidence of four positions for the state with n = 1 and J = 0: (a) The local minimum of the total potential VTotal and the local maximum of the radial probability P1,0; (b) The position free from the radial force fTotal (r) = 0; (c) The equilibrium position with zero velocity dr / dτ = 0.
Figure 2.
Illustration of the coincidence of four positions for the state with n = 1 and J = 0: (a) The local minimum of the total potential VTotal and the local maximum of the radial probability P1,0; (b) The position free from the radial force fTotal (r) = 0; (c) The equilibrium position with zero velocity dr / dτ = 0.
The complex trajectories of
r(
τ) solved from Equation (4.4) for the four types of diatomic molecules are shown in
Figure 3a. It can be seen that the complex trajectories are closed contours circulating about their respective equilibrium positions
req computed from Equation (4.5) by using the molecular parameters listed in
Table 1. We find that the period of vibration is independent of the actual trajectories and is quantized with respective to the angular quantum number
J. This trajectory-independent property can be proven by applying the residue theorem to Equation (4.4):
where the contour
c is an arbitrary closed trajectory solved from Equation (4.4). The contour integral depends only on the poles enclosed by the contours. Because all of the trajectories enclose only one pole at
z =
α, the contour integral has only one possible value equal to the residue evaluated at this pole. Due to the dependence of
α on the angular quantum number
J as shown in Equation (A14), the resulting period of vibration is allowed only for some discrete values determined by
J.
Figure 3.
(
a) The ground-state quantum trajectories solved from Equation (4.4) for the four types of diatomic molecules on the complex plane of
r. The complex trajectories are closed contours circulating around their respective equilibrium positions
req; (
b) The time responses of Re(
r(
t)) give the periods of vibration as
TH2 = 0.3840,
THCl = 1.2496,
TO2 = 0.1203, and
TN2 = 0.0941, from which the vibrational frequencies
f = 1/
T = ℏ
β2 / (
MT) are computed and compared with the experimental data listed in
Table 1.
Figure 3.
(
a) The ground-state quantum trajectories solved from Equation (4.4) for the four types of diatomic molecules on the complex plane of
r. The complex trajectories are closed contours circulating around their respective equilibrium positions
req; (
b) The time responses of Re(
r(
t)) give the periods of vibration as
TH2 = 0.3840,
THCl = 1.2496,
TO2 = 0.1203, and
TN2 = 0.0941, from which the vibrational frequencies
f = 1/
T = ℏ
β2 / (
MT) are computed and compared with the experimental data listed in
Table 1.
Figure 3b illustrates the time responses Re(
r(
τ)) for the four diatomic molecules in the ground state
n =
J = 0, wherein the periods of vibration have a simple expression
The
λ values of the four molecules and their periods of vibration computed by Equation (4.12) are listed in
Table 1. Also shown in
Table 1 are the experimental values
fexp of the ground-state vibration frequencies. The comparison between the computational and experimental results gives a relative error about 1%, which is caused by the inexistence of an exact solution to the Schrödinger Equation (A1). The radial wave function
Rn,J given by Equation (A13) is only a second-order approximation as described by Equation (A6). The approximation gets better as
r is closer to the equilibrium bond length
r0 of the Morse potential.
Table 1.
Parameters of four diatomic molecules and the comparison of the computed ground-state vibration frequencies fQHM with the measured frequency fexp.
Table 1.
Parameters of four diatomic molecules and the comparison of the computed ground-state vibration frequencies fQHM with the measured frequency fexp.
| Diatomic Molecules | H-H | H-Cl | O-O | N-N |
|---|
| Bond length r0 (m) | 74 × 10−12 | 127.5 × 10−12 | 148 × 10−12 | 145 × 10−12 |
| Reduced mass (kg/atom) | 0.837 × 10−27 | 1.628 × 10−27 | 13.28 × 10−27 | 11.63 × 10−27 |
| Potential width β (m−1) | 1.94 × 1010 | 1.81 × 1010 | 2.67 × 1010 | 2.70 × 1010 |
| ED (kg · m2· sec−2) | 7.11 × 10−19 | 7.39 × 10−19 | 8.28 × 10−19 | 15.77 × 10−19 |
![Molecules 19 16122 i046]() | 16.8403 | 25.6722 | 52.7203 | 67.2966 |
| T = 4π / (2λ − 1) | 0.3845 | 0.2496 | 0.1203 | 0.09406 |
| T = TM / (ħβ2) | 8.091 × 10−15 | 11.74 × 10−15 | 21.31 × 10−15 | 14.24 × 10−15 |
| fQHM = 1 / T | 12,360 × 1010 | 8522 × 1010 | 4693 × 1010 | 7021 × 1010 |
| Experiment fexp | 12,470 × 1010 | 8652 × 1010 | 4666 × 1010 | 6987 × 1010 |
| |fexp − fQHM| / fexp | 0.8821% | 1.503% | 0.5786% | 0.4866% |
The vibration period
T given by Equation (4.12) can also be derived by using a state-dependent force constant. A quantum force constant is defined as the second-order derivative of the total potential
VTotal (
r) evaluated at the equilibrium position
req:
The resulting force constant is state-dependent by noting that
VTotal depends on the three quantum numbers (
n,J,mJ) as given by Equation (3.12). A specific
VTotal has been expressed explicitly in Equation (4.8) for the case of
n =
J =0, and the substitution of
VTotal into Equation (4.13) yields the force constant as:
Then the classical relation between the vibration period
T and the force constant
K gives:
which reproduces the result of Equation (4.12) derived by state-dependent molecular dynamics.
The above discussions of ground vibrational state reveal a remarkable observation that by replacing the internuclear potential with the total potential
VTotal, the conventional MM turns out to be state-dependent MM, which then yields consistent results with QM. This observation applies to every quantum state of the molecule. In every quantum state Ψ
n,J,mJ, there is a total potential
VTotal, which completely determines the molecular quantum dynamics within this state.
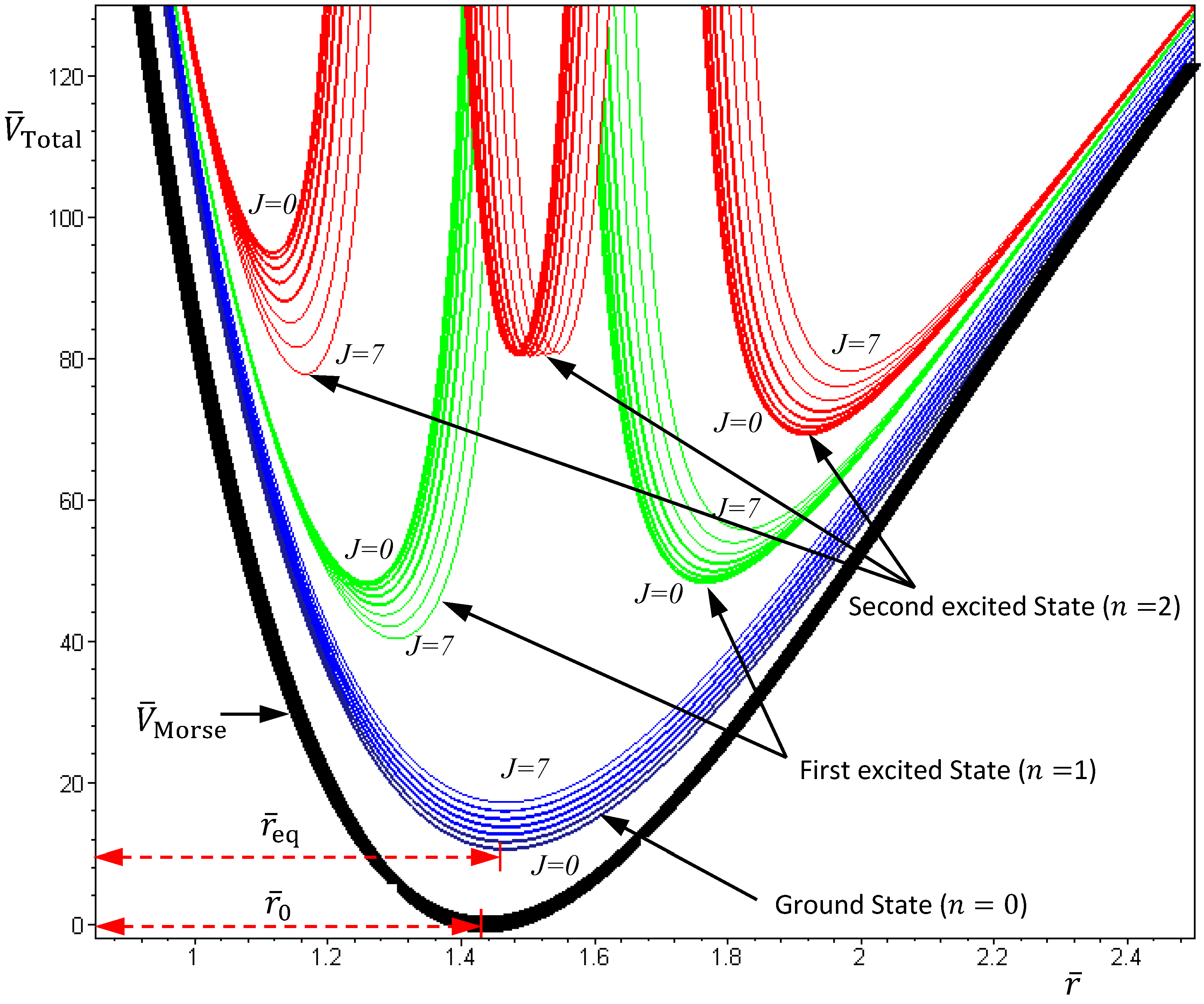
Figure 4 plots the total potentials for the first three vibrational states and their accompanying rotational states. It can be seen that for a vibrational state with quantum number
n, there are
n + 1 sub-shells, within which rotational states with different quantum number
J reside.
Figure 4.
The variation of the total potential VTotal with respect to the two quantum numbers n and J. The lowermost points req of VTotal correspond to the equilibrium bond lengths, and the curvatures of VTotal at req correspond to the force constants of the molecule. This figure schematically illustrates how the bond length and the force constant change due to the change of quantum states.
Figure 4.
The variation of the total potential VTotal with respect to the two quantum numbers n and J. The lowermost points req of VTotal correspond to the equilibrium bond lengths, and the curvatures of VTotal at req correspond to the force constants of the molecule. This figure schematically illustrates how the bond length and the force constant change due to the change of quantum states.
In excited vibrational states
n ≥ 1, the quantum dynamics (4.1a) has multiple equilibrium points, and the total potential possesses multiple-shell structure. To illustrate this property, we consider the first excited state as an example. The corresponding radial wavefunction is given by:
and the radial dynamics is obtained from Equation (4.1a) as:
There are two stable equilibrium points in this state, which can be solved from the condition
dz /
dt = 0 as:
On the other hand, the total potential in the first excited state is given by Equation (3.12):
By evaluating the constant
α at
n = 1 with
λ = 2 and
b = 3, we have:
Substituting this
α into Equation (4.19), the variation of
VTotal (
r,
θeq) with respect to the angular quantum number
J is plotted in
Figure 4. It appears that there is a node at
z =
α + 1, where the total potential approaches to infinity. This infinite potential barrier separates
VTotal (
r,
θ) into two shells. The lowermost point of the inner shell corresponds to the inner equilibrium point
![Molecules 19 16122 i055]()
, while the lowermost point of the outer shell corresponds to the outer equilibrium point
![Molecules 19 16122 i056]()
, as given by Equation (4.18). Also shown in
Figure 4 is the total potential of the second excited state, which has three shells separated by the two nodes.
5. State-Dependent Orbital and Spin Dynamics
So far our discussions on molecular quantum dynamics are restricted to the radial vibration motion governed by Equation (4.1a). To take angular dynamics into account, all the three equations in Equation (4.1) have to be considered. In the previous sections we have seen that the QM descriptions of the quantum state Ψn,J,mJ can be reproduced in terms of the state-dependent molecular dynamics. Here, we go one-step further to show that the spin dynamics, which cannot be described by the spatial wave function Ψn,J,mJ, emerges naturally from the molecular dynamics (4.1) in the ground state where orbital angular momentum is zero.
Setting
n =
J =
mJ = 0 and substituting
R0,0 (
z) =
e−z/2zα/2/
r, Θ
0,0 (
θ) = Φ
0 (
ϕ) = 1 into Equation (4.1) yields the 3D quantum dynamics in the ground state:
where
α and
η are given by Equation (A14) with
J = 0. We can see that even though the orbital angular quantum number
J is set to zero, the angular velocity
![Molecules 19 16122 i058]()
is actually not zero. The main reason why spin motion cannot be attributed to orbital motion in standard quantum mechanics is due to the definition of the orbital angular momentum
L2. To make this point more apparent, we inspect the expression of
L2 defined in Equation (4.2b) with the help of Equation (3.9b):
In case of
J =
mJ = 0, we have
![Molecules 19 16122 i059]()
, ∂
2 lnΨ
n,J,mJ (
r,θ,ϕ) / ∂
θ2 = ∂
2 ln
Rn,J (
r) / ∂
θ2 = 0 and the above equation is reduced to:
In the real domain, the only solution is
![Molecules 19 16122 i060]()
and
θ =
π / 2, which is the well-known spinless motion. However, in the complex domain, Equation (5.3) has a nontrivial solution:
which is just the
θ dynamics in Equation (5.1) in dimensionless form. In other words, the condition of
L2 = 0 does not completely nullify the complex-valued angular motion, and we can regard the spin dynamics as the remnant angular dynamics as the orbital angular momentum is zero.
The integration of the
θ dynamics with
θ =
θR +
iθI gives the three regions of trajectories as shown in
Figure 5a. Within the Ω
0 region, the sign of
dθR /
dτ changes alternatively and produces zero mean velocity. Within the Ω
− region,
θR(
τ) is monotonically decreasing with a mean value of
dθR /
dt equal to −1. Within Ω
+ region,
θR (
τ) is monotonically increasing with a mean value of
dθR /
dτ equal to one.
Figure 5.
The complex θ(τ) trajectories for the states (a) J = 0, and (b) J = 1 with mJ = 0 solved from Equation (4.1) with r at its equilibrium position. The upper region Ω− contains spin-down dynamics with dθR / dτ < 0, the central region Ω0 contains spinless dynamics exhibiting periodic motion around the equilibrium points and the lower region Ω+ contains spin-up dynamics with dθR / dτ > 0.
Figure 5.
The complex θ(τ) trajectories for the states (a) J = 0, and (b) J = 1 with mJ = 0 solved from Equation (4.1) with r at its equilibrium position. The upper region Ω− contains spin-down dynamics with dθR / dτ < 0, the central region Ω0 contains spinless dynamics exhibiting periodic motion around the equilibrium points and the lower region Ω+ contains spin-up dynamics with dθR / dτ > 0.
Although orbital angular momentum is completely depressed by the condition
J =
mJ = 0, non-zero angular motion does exist in the regions of Ω
− and Ω
+. To relate this remnant angular motion to spin, the next step is to identify the magnitude of this remnant angular momentum. In the regions of Ω
− and Ω
+, we note the following relations for the complex variable
θ =
θR +
iθI:
Therefore, angular momentum in the
θ direction becomes:
In the region Ω
0, the
θ(
τ) dynamics exhibits periodic motion around the equilibrium points and yields zero mean angular velocity. According to the behavior of the
θ dynamics, three spin regions can be defined,
The spin dynamics we discuss so far originates from the wavefunction Ψ =
Rn,J (
ρ)Θ
J,mJ (
θ)Φ
mJ (
ϕ) with Θ
J,mJ (
θ) given by
![Molecules 19 16122 i063]()
, the first-type Legendre function. Indeed,
![Molecules 19 16122 i063]()
is only a special solution for Θ
J,mJ (
θ) whose general solution can be represented by:
where
![Molecules 19 16122 i064]()
is the second-type Legendre function. It can be shown by integration Equation (4.1) with
![Molecules 19 16122 i065]()
that the direction of the angular motion produced by
![Molecules 19 16122 i066]()
is always anti-parallel to that produced by
![Molecules 19 16122 i063]()
. Therefore, in the same quantum state specified by the spatial quantum numbers (
n,J,mJ), the molecule can behave either according to the spin dynamics with
![Molecules 19 16122 i067]()
or to the anti-spin dynamics with
![Molecules 19 16122 i065]()
. For the former case, we say that the molecule is in a sub-state of (
n,J,mJ) denoted by (
n,J,mJ,1/2), and for the latter case, the molecule is in the sub-state (
n,J,mJ,−1/2). Furthermore, an entangled spin dynamics can be simulated according to the state-dependent molecular dynamics by expressing Θ
J,mJ(
θ) as a linear combination of
![Molecules 19 16122 i063]()
and
![Molecules 19 16122 i066]()
as described by Equation (5.8).
In the ground state, we have seen that the orbital angular motion vanishes and the remnant angular motion in the
θ direction emerges as the spin dynamics. We proceed to demonstrate that in excited states, orbital and spin motions coexist and both contribute to angular momentum. To examine the interaction between orbital and spin dynamics, we next consider quantum states with
J = 1 and
mJ = 0. Since the
z-component angular momentum
Lz is zero in these quantum states, we are interested in where the orbital angular momentum emerges and how it interacts with the spin angular momentum. The
θ and
ϕ dynamics for these quantum states are governed by Equations (4.1b) and (4.1c) as:
The trajectories of
θ (
t) on the complex
θR −
θI plane are illustrated in
Figure 5b, where it can be seen that as in the ground state, three regions representing three angular motions come about. In the region Ω
− (
θI ≫ 0),
θR is monotonically decreasing, while in the region Ω
+ (
θI ≪ 0),
θR is monotonically increasing. In the central region Ω
0,
θR is a periodic function of time. In conjunction with the relation (5.5), the mean angular momentum of Equation (5.9) becomes:
Comparing with Equation (5.7), we find that in the regions of Ω
− and Ω
+, the angular momentum contains an additional component ħ contributed from the orbital motion
J = 1 apart from the spin angular momentum ħ/2, indicating that the orbital angular motion, in the states with
J = 1, and
mJ = 0, is produced solely by the
θ dynamics because of
![Molecules 19 16122 i070]()
.
For a quantum state with quantum number
J ≠ 0 and
mJ ≠ 0, the
θ and
ϕ dynamics can be expressed by:
Making use of Equation (5.5) once again, we obtain a general expression for the angular momentum in the
θ and
ϕ directions as:
In summary, in the Ω
0 region, one has zero-mean
θ dynamics and a quantized
z-component angular momentum
mJħ, which is a well-known result in QM; while in the Ω
− and Ω
+ regions, one has an angular momentum ±(
J + 1/2)ħ in the
θ direction and a zero-mean orbital angular momentum in the
ϕ direction, which is otherwise unknown to QM.
The angular momentum given by Equation (5.12), which is derived from the state-dependent molecular dynamics, provides us with a trajectory-based method to determine the rotational energy of a diatomic molecule and its rotational spectrum. The most used formula of rotational energy takes the following form:
which treats the molecule as a rigid rotor with moment of inertia
I0 =
Mr02 / 2. A typical rotational spectrum consists of a series of peaks corresponding to transitions between adjacent levels satisfying ∆
J = ±1:
The rigid-rotor model assumes a constant internuclear distance
r0 and neglects the stretch of the bond as the molecule rotates. To account for bond stretching due to rotation, we consider a refined rotation-energy component
ER in the eigenvalue expansion given by Equation (A20), from which the wavenumber of the transition from
J + 1 to
J can be derived as:
where
D is a correction factor known as the centrifugal distortion constant.
Table 2 lists the measured far infrared absorption spectrum (
νexp) [
29] for the diatomic molecule H-Cl and the predicted spectrum by the rigid model (
νrigid) and the non-rigid model (
νnonrigid) with
B = 10.58 cm
−1 and
D = 5.6 × 10
−4 cm
−1 determined from the molecular parameters listed in
Table 1.
Table 2.
Comparisons of the four predictions νrigid, νnonrigid, νQHM and νfitting with the measured rotational spectrum νexp.
Table 2.
Comparisons of the four predictions νrigid, νnonrigid, νQHM and νfitting with the measured rotational spectrum νexp.
| Transitions | νrigid
(cm-1) | νnon-rigid
(cm-1) | νQHM
(cm-1) | νfitting
(cm-1) | νexp
(cm-1) | ![Molecules 19 16122 i074]() |
|---|
| J = 0 → 1 | 21.16 | 21.16 | 20.80 | 20.88 | 20.88 | 0.383% |
| J = 1 → 2 | 42.32 | 42.30 | 41.57 | 41.74 | 41.74 | 0.407% |
| J = 2 → 3 | 63.48 | 63.42 | 62.29 | 62.58 | 62.58 | 0.463% |
| J = 3 → 4 | 84.64 | 84.49 | 82.93 | 83.38 | 83.32 | 0.468% |
| J = 4 → 5 | 105.8 | 105.52 | 103.47 | 104.14 | 104.13 | 0.634% |
| J = 5 → 6 | 126.96 | 126.48 | 123.87 | 124.83 | 124.73 | 0.689% |
| J = 6 → 7 | 148.12 | 147.35 | 144.11 | 145.45 | 145.37 | 0.867% |
| J = 7 → 8 | 169.28 | 168.13 | 164.16 | 165.97 | 165.89 | 1.024% |
| J = 8 → 9 | 186.65 | 188.81 | 184.01 | 186.40 | 186.23 | 1.192% |
Instead of using the quantum rotational energy obtained from the eigenvalues of Schrödinger equation, we will give an estimate of the wavenumber of transition based on the classical expression of the rotational energy
![Molecules 19 16122 i075]()
with
r and
![Molecules 19 16122 i058]()
computed by the state-dependent molecular dynamics:
where
![Molecules 19 16122 i058]()
is given by Equation (5.12) and the bond length
r is denoted by
rJ to emphasize its dependence on the angular quantum number
J as given by Equation (4.5) and Equation (A14). An alternative estimate of the wavenumber caused by rotation absorption transition turns out to be:
With the molecular parameters of HCl given by
Table 1, the bond length
rJ is calculated by using Equation (4.5) and then substituted into Equation (5.17) to yield the estimated spectrum
νQHM.
Table 2 compares the four predictions
νrigid,
νnonrigid,
νQHM and
νfitting with the measured rotational spectrum
νexp. It can be seen that the wavenumber
νfitting is closest to
νexp, because
νfitting is obtained by tuning the parameters
B and
D, so that Equation (5.15) best fits the experimental data. The curve fitting gives the best values as
B* = 10.44 cm
−1 and
D* = 5.2 × 10
−4 cm
−1. The two wavenumbers
νnonrigid and
νQHM can be compared on the same footing, since both adopt the same molecular parameters listed in
Table 1 in the computation. Their difference lies in the model of rotational energy used to compute wavenumbers. The wavenumber
νnonrigid is based on the eigen-energy model (A20), while
νQHM is based on the QHM model (5.16).
Table 2 reveals that the wavenumber
νQHM is much closer to the experimental results than
νnonrigid.
Theoretically, the description of state-dependent molecular dynamics by QHM is equivalent to QM; however, the actual accuracy depends on the degree of approximation involved in the solution to the wave function. The equilibrium bond length rJ computed from Equation (4.5) is based on the radial wave function Rn,J given by Equation (A13), which is an approximate solution to the radial Schrödinger Equation (A5) by employing the second-order expansion (A6). When the quantum number J increases, the bond length deviates further from the equilibrium position r0 of the Morse potential, and the accuracy of the expansion (A6) gets worse. This tendency explains the degradation of the prediction accuracy of νQHM with respect to the measured rotational spectrum νexp.
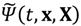 in the x quantum subspace that depends parametrically on the classical position X(t). The approximate wave function
in the x quantum subspace that depends parametrically on the classical position X(t). The approximate wave function 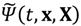 obeys the Schrödinger equation:
obeys the Schrödinger equation:
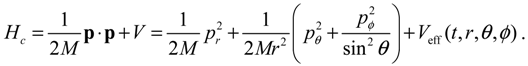
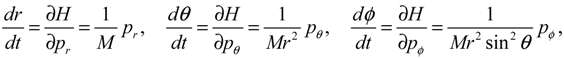
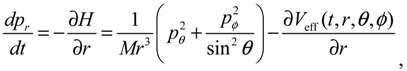
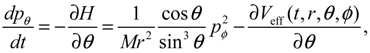
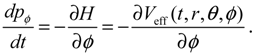
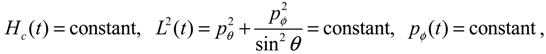
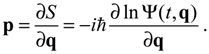
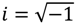 indicates that the momentum p has to be defined in a complex domain. In Cartesian coordinates, we have
indicates that the momentum p has to be defined in a complex domain. In Cartesian coordinates, we have 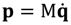 and the particle’s velocity
and the particle’s velocity 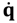 can be determined by the wave function Ψ as
can be determined by the wave function Ψ as
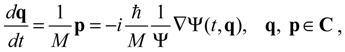
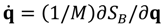 only carry information about the dynamics of the momentum flow, while the complex trajectory solved from
only carry information about the dynamics of the momentum flow, while the complex trajectory solved from 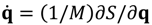 also includes information about the probability RB = |Ψ|. The dynamics in the complex phase space (q,p) thus explains in a natural way how to get the correct momentum distribution and explains why algorithms based on complex trajectories are stable and accurate [22,23,24,25,26,27,28]. The advantages of implementing numerical codes in a complex phase space are similar to those of considering complex fields instead of real ones in electromagnetism [20].
also includes information about the probability RB = |Ψ|. The dynamics in the complex phase space (q,p) thus explains in a natural way how to get the correct momentum distribution and explains why algorithms based on complex trajectories are stable and accurate [22,23,24,25,26,27,28]. The advantages of implementing numerical codes in a complex phase space are similar to those of considering complex fields instead of real ones in electromagnetism [20].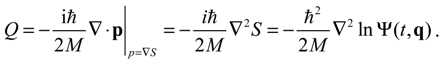
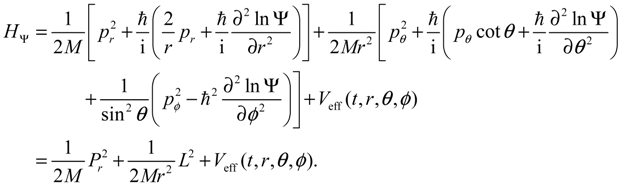
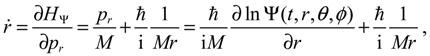
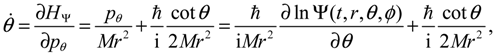
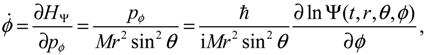
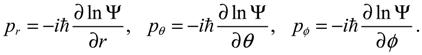
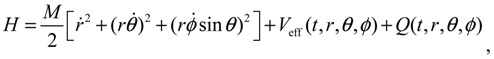
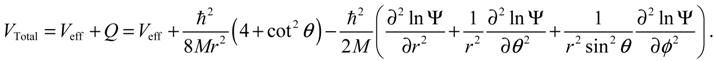
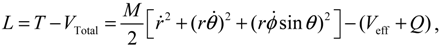
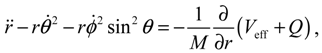
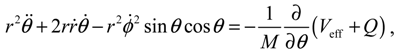
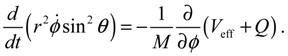
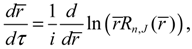
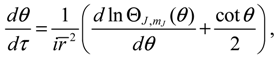
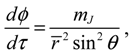
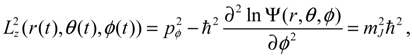
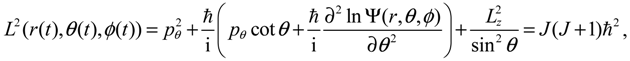
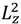 , L2 and H are independent of time and are quantized according to the three quantum numbers n, J and mJ. Unlike the probabilistic interpretation in standard quantum mechanics, here, we have given a dynamic interpretation of the quantization laws by showing that the three physical quantities have constant discrete values along any quantum trajectory (r(t),θ(τ),ϕ(t)) solved from Equation (4.1) in the quantum state specified by the three quantum numbers (n,J,mJ).
, L2 and H are independent of time and are quantized according to the three quantum numbers n, J and mJ. Unlike the probabilistic interpretation in standard quantum mechanics, here, we have given a dynamic interpretation of the quantization laws by showing that the three physical quantities have constant discrete values along any quantum trajectory (r(t),θ(τ),ϕ(t)) solved from Equation (4.1) in the quantum state specified by the three quantum numbers (n,J,mJ).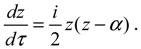
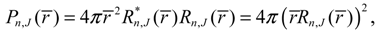
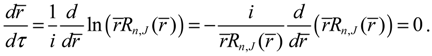
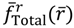 . As an illustration, we consider the case with J = 0 for which ΘJ,mJ (θ) = 1 and the total potential defined in Equation (3.12) has a simple expression,
. As an illustration, we consider the case with J = 0 for which ΘJ,mJ (θ) = 1 and the total potential defined in Equation (3.12) has a simple expression,
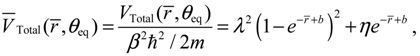
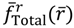 now can be determined from
now can be determined from 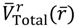 as
as
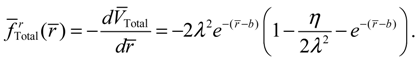
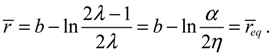
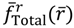 in the vicinity of req gives
in the vicinity of req gives 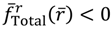 , if r > req, and
, if r > req, and 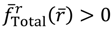 , if r < req. The sign of
, if r < req. The sign of 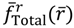 in the neighborhood of req indicates that the two nuclei attract each other when their distance is longer than req and repel each other when their distance is shorter than req. Consequently, there is always a restoring force to make r return to its equilibrium position req.
in the neighborhood of req indicates that the two nuclei attract each other when their distance is longer than req and repel each other when their distance is shorter than req. Consequently, there is always a restoring force to make r return to its equilibrium position req.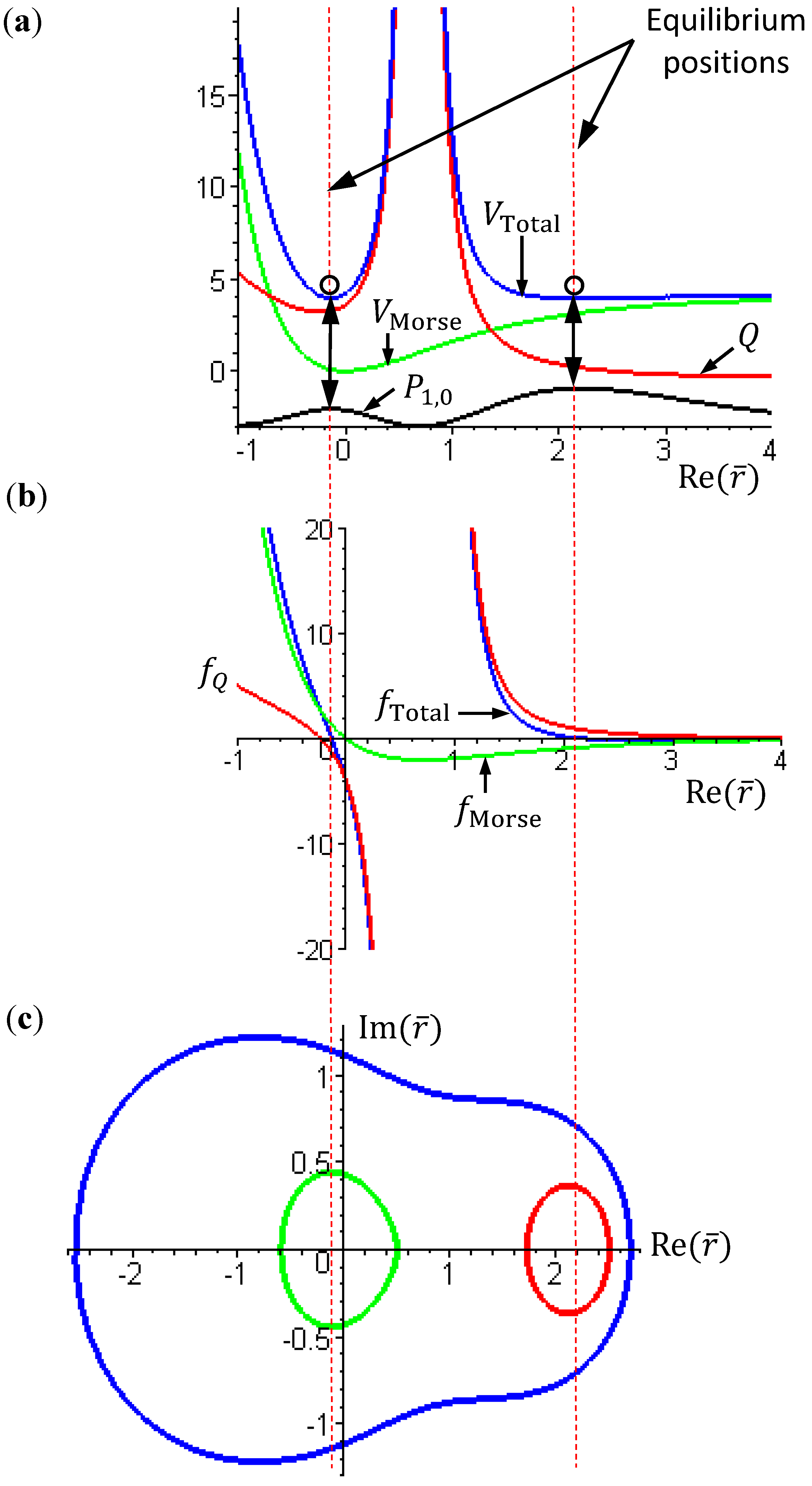
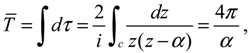
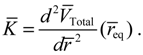
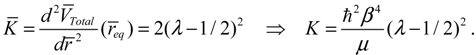
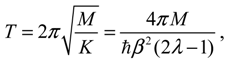
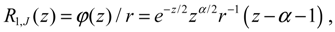
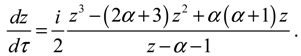
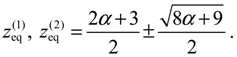
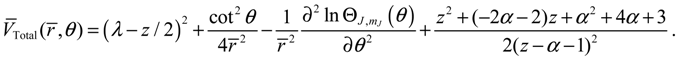
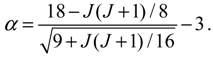
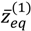 , while the lowermost point of the outer shell corresponds to the outer equilibrium point
, while the lowermost point of the outer shell corresponds to the outer equilibrium point 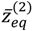 , as given by Equation (4.18). Also shown in Figure 4 is the total potential of the second excited state, which has three shells separated by the two nodes.
, as given by Equation (4.18). Also shown in Figure 4 is the total potential of the second excited state, which has three shells separated by the two nodes.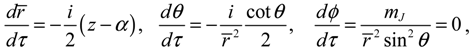
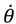 is actually not zero. The main reason why spin motion cannot be attributed to orbital motion in standard quantum mechanics is due to the definition of the orbital angular momentum L2. To make this point more apparent, we inspect the expression of L2 defined in Equation (4.2b) with the help of Equation (3.9b):
is actually not zero. The main reason why spin motion cannot be attributed to orbital motion in standard quantum mechanics is due to the definition of the orbital angular momentum L2. To make this point more apparent, we inspect the expression of L2 defined in Equation (4.2b) with the help of Equation (3.9b):
 , ∂2 lnΨn,J,mJ (r,θ,ϕ) / ∂θ2 = ∂2 lnRn,J (r) / ∂θ2 = 0 and the above equation is reduced to:
, ∂2 lnΨn,J,mJ (r,θ,ϕ) / ∂θ2 = ∂2 lnRn,J (r) / ∂θ2 = 0 and the above equation is reduced to:
 and θ = π / 2, which is the well-known spinless motion. However, in the complex domain, Equation (5.3) has a nontrivial solution:
and θ = π / 2, which is the well-known spinless motion. However, in the complex domain, Equation (5.3) has a nontrivial solution:
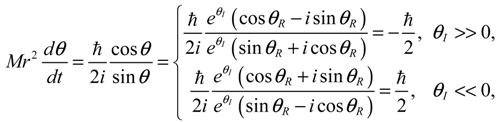
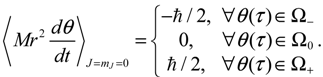
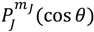 , the first-type Legendre function. Indeed,
, the first-type Legendre function. Indeed, 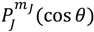 is only a special solution for ΘJ,mJ (θ) whose general solution can be represented by:
is only a special solution for ΘJ,mJ (θ) whose general solution can be represented by:
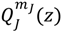 is the second-type Legendre function. It can be shown by integration Equation (4.1) with
is the second-type Legendre function. It can be shown by integration Equation (4.1) with 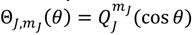 that the direction of the angular motion produced by
that the direction of the angular motion produced by 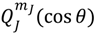 is always anti-parallel to that produced by
is always anti-parallel to that produced by 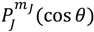 . Therefore, in the same quantum state specified by the spatial quantum numbers (n,J,mJ), the molecule can behave either according to the spin dynamics with
. Therefore, in the same quantum state specified by the spatial quantum numbers (n,J,mJ), the molecule can behave either according to the spin dynamics with 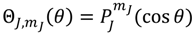 or to the anti-spin dynamics with
or to the anti-spin dynamics with 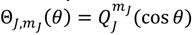 . For the former case, we say that the molecule is in a sub-state of (n,J,mJ) denoted by (n,J,mJ,1/2), and for the latter case, the molecule is in the sub-state (n,J,mJ,−1/2). Furthermore, an entangled spin dynamics can be simulated according to the state-dependent molecular dynamics by expressing ΘJ,mJ(θ) as a linear combination of
. For the former case, we say that the molecule is in a sub-state of (n,J,mJ) denoted by (n,J,mJ,1/2), and for the latter case, the molecule is in the sub-state (n,J,mJ,−1/2). Furthermore, an entangled spin dynamics can be simulated according to the state-dependent molecular dynamics by expressing ΘJ,mJ(θ) as a linear combination of 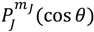 and
and 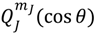 as described by Equation (5.8).
as described by Equation (5.8).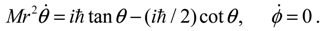
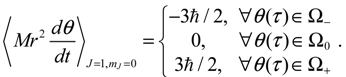
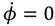 .
.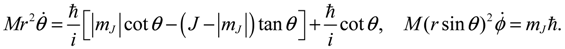
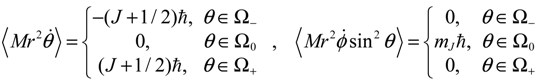
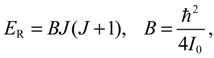
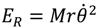 with r and
with r and 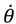 computed by the state-dependent molecular dynamics:
computed by the state-dependent molecular dynamics:
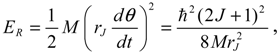
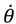 is given by Equation (5.12) and the bond length r is denoted by rJ to emphasize its dependence on the angular quantum number J as given by Equation (4.5) and Equation (A14). An alternative estimate of the wavenumber caused by rotation absorption transition turns out to be:
is given by Equation (5.12) and the bond length r is denoted by rJ to emphasize its dependence on the angular quantum number J as given by Equation (4.5) and Equation (A14). An alternative estimate of the wavenumber caused by rotation absorption transition turns out to be:
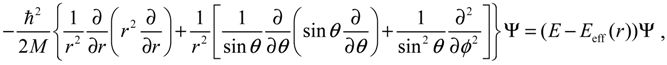
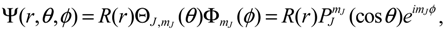
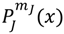 denoting the associated Legendre polynomial. The radial function R(r) satisfies the equation:
denoting the associated Legendre polynomial. The radial function R(r) satisfies the equation: