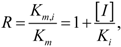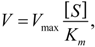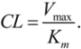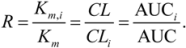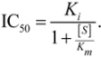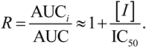2.1. Comparison of in-Vitro-Bioassay and Clinical Data
With the advances in laboratory robotic technologies, increasing attention has been drawn to CYP HTS data and its use in DDCI model development [
52,
57,
58,
59,
60,
61,
62,
63,
64,
65]. FDA recommends using these data at the drug-development stage but the final drug labeling is based on clinical trial data [
18]. Therefore, it is of interest to compare the HTS bioassay and clinical inhibition data (since the latter were used for supervised machine learning in the present work).
The data from two HTS bioassays for CYP3A4 inhibition were available in the PubChem
™ database [
66], assay identification numbers (AIDs) 884 [
67,
68] and 1851 [
67,
68]. AID 1851 was a combined bioassay with inhibition data for five CYP isoforms, including 3A4; both bioassays covered large chemical libraries. AID 884 tested 14,155 substances for 13,072 compounds [
67,
68], and AID 1851 tested 17,143 substances for 16,555 compounds [
67,
68]. However, many tested compounds were not on the list of FDA-approved drugs. Presumably, these non-drugs were compounds rejected at the research and development stages of the drug discovery process. Fewer than 7% of the compounds in AID 1851 have been identified in PubChem
™ as drugs, and no compounds have been tagged as drugs in AID 884. A query of the bioassays with a 121-compound dataset of the present work revealed that only 46 and 34 of them were present in the libraries of AIDs 884 and 1851, respectively. Extrapolation from these numbers (7/100 × 16555 × 46/34/13072) suggests that about 12% of drugs may be present in AID 884, assuming equal ratios of the overlap between our database and the subsets of drugs in each of the bioassays. Consequently, FDA-approved drugs were poorly represented in each of the bioassays.
A tested outcome of the AID 1851 bioassay was “whether a compound inhibited pro-luciferin conversion with any of the five isozymes” [
67]. Our reanalysis of the raw kinetic data recorded in PubChem
™ for the aforementioned 34 chemicals did not provide additional information (as compared with AID 884). Therefore, only the outcomes of AID 884 were used for the comparative analysis presented in
Table 1. In AID 884, the dose-response curve has been constructed using a luciferin-labeled CYP3A4 substrate (6'-phenylpiperazinylyl) [
68]. For most chemicals, the dose-response curve has been measured only once. Multiple curves were only present for chemicals obtained from more than one vendor. For these chemicals, a mean IC
50 and its 95% confidence interval (CI) were calculated. For single-curve chemicals, a single-point IC
50 value (as given by the dose-response curve) and a mean CI, averaged over all multiple-curve CIs, were applied.
Table 1.
Extrapolation from in vitro bioassay to in vivo pharmacokinetic CYP3A4 inhibition data, and data categorization.
Table 1.
Extrapolation from in vitro bioassay to in vivo pharmacokinetic CYP3A4 inhibition data, and data categorization.
| Name | Clinical *Category | IC50 (95% CI),AID #884 (µM) | MRDD | BA (%) | R-1 (95% CI) | C-1 | BA-ADME | R-2 (95%CI) | C-2 | R-3 (95% CI) | C-3 | Cmax (µM) | R-4 (95%CI) | C-4 |
|---|
| clotrimazole | P | 0.07 (0.00,0.17) | 6.67 ‡ [69] | 100 | 280.33 (115.25,∞) | P | 30–70 | 196.53 (80.98,∞) | P | 280.33 (115.25,∞) | P | 0.087 [70] | 2.26 (1.51,∞) | ND |
| isoniazid | P | 9.92 (0.00,26.37) | 15 [71] | 80 [72,73] | 12.03 (5.15,∞) | P | >70 | 12.03 (5.15,∞) | P | 12.03 (5.15,∞) | P | 76.61 [70] | 8.73 (3.91,∞) | P |
| diltiazem | P | 3.98 (0.00,10.88) † | 8 [74] | 38 [72,73] | 2.84 (1.67,∞) | ND | <30 | 2.45 (1.53,∞) | ND | 5.85 (2.77,∞) | P | 0.356 [70] | 1.09 (1.03,∞) | ND |
| ketoconazole | P | 0.13 (0.00,7.03) † | 8 [75] | 50 [76] | 60.79 (2.07,∞) | P | 30–70 | 84.70 (2.50,∞) | P | 120.58 (3.14,∞) | P | 7 [77] | 56.60 (2.00,∞) | P |
| glibenclamide | W | 5.99 (0.00,12.80) | 0.29 [78] | 80 [72,73] | 1.08 (1.04,∞) | ND | 30–70 | 1.07 (1.03,∞) | ND | 1.10 (1.05,∞) | ND | 0.2 [77] | 1.03 (1.02,∞) | ND |
| methoxsalen | W | 10.50 (3.39,17.61) | 0.6 [74] | 26 [79] | 1.07 (1.04,1.21) | W | >70 | 1.26 (1.16,1.82) | ND | 1.26 (1.16,1.82) | ND | 0.184 [80] | 1.02 (1.01,1.05) | ND |
| omeprazole | W | 10.00 (3.10,16.9) † | 2 [74] | 47 [72,73] | 1.27 (1.16,1.88) | W | 30–70 | 1.41 (1.25,2.31) | W | 1.58 (1.34,2.87) | W | | | |
| clemastine | W | 5.01 (0.00,13.48) | 0.134 [81] | 37 [72,73] | 1.03 (1.01,∞) | ND | 30–70 | 1.05 (1.02,∞) | ND | 1.08 (1.03,∞) | ND | 0.00233 [82] | 1.00 (1.00,∞) | ND |
| dexmedetomidine | W | 0.16 (0.00,7.06) † | 0.2 ‡ [83] | 100 | 7.30 (1.14,∞) | ND | 30–70 | 5.71 (1.10,∞) | ND | 7.30 (1.14,∞) | ND | | | |
| lansoprazole | W | 20.48 (7.63,33.33) | 0.5 [74] | 81 [72,73] | 1.05 (1.03,1.14) | ND | 30–70 | 1.05 (1.03,1.12) | ND | 1.07 (1.04,1.18) | ND | 1.92 [84] | 1.09 (1.06,1.25) | ND |
| nifedipine | W | 11.29 (7.70,14.88) | 1.71 [85] | 50 [72,73] | 1.22 (1.17,1.32) | ND | 30–70 | 1.31 (1.23,1.45) | ND | 1.44 (1.33,1.64) | W | 0.027 [86] | 1.00 (1.00,1.00) | ND |
| pilocarpine | W | 15.85 (8.95,22.75) † | 0.5 [74] | | | | <30 | 1.05 (1.03,1.08) | ND | 1.15 (1.11,1.27) | ND | 0.099 [70] | 1.01 (1.00,1.01) | ND |
| mitoxantrone | W | 25.12 (18.22,32.02) † | 2 ‡ [87] | 100 | 1.18 (1.14,1.25) | ND | <30 | 1.05 (1.04,1.07) | ND | 1.18 (1.14,1.25) | ND | 0.36 [70] | 1.01 (1.01,1.02) | ND |
| irbesartan | W | 15.85 (8.95,22.75) † | 5 [74] | 70 [72,73] | 1.52 (1.36,1.91) | W | 30–70 | 1.52 (1.36,1.91) | W | 1.74 (1.51,2.30) | W | 7.98 [88] | 1.50 (1.35,1.89) | W |
| losartan | W | 19.95 (13.05,26.85) † | 1.67 [74] | 36 [72,73] | 1.07 (1.05,1.11) | ND | 30–70 | 1.14 (1.10,1.21) | ND | 1.20 (1.15,1.30) | ND | 0.596 [89] | 1.03 (1.02,1.05) | ND |
| sildenafil | W | 10.00 (3.10,16.9) † | 1.67 [74] | 38 [72,73] | 1.13 (1.08,1.43) | ND | 30–70 | 1.25 (1.15,1.79) | ND | 1.35 (1.21,2.14) | ND | 0.447 [90] | 1.04 (1.03,1.14) | ND |
| pergolide | W | 12.59 (5.69,19.49) † | 0.05 [74] | 38 [72,73] | 1.00 (1.00,1.01) | ND | <30 | 1.00 (1.00,1.01) | ND | 1.01 (1.01,1.03) | ND | | | |
As shown in
Table 1, CIs on the IC
50 values were large. A 95% CI exceeded the mean for 71% of the 17 analyzed drugs. For inhibitors with low IC
50 values, which included the potent inhibitors, the statistics was even poorer: A CI exceeded the mean for 100% of inhibitors with IC
50 < 10 µM. Obviously, the power of analyzed HTS data was hardly sufficient for making inferences, which highlights the importance of study design in HTS experiments and suggests that a single-point cut-off on IC
50 [
58,
91] is inappropriate for categorizing HTS data.
Two kinds of changes in activity were observed in the HTS bioassay: Compounds with positive activity readings, which increased the rate of catalysis of the test substrate, have been categorized as activators; compounds with negative activity readings have been categorized as inhibitors. The dose-response curve has been interpreted in PubChem™ for 19 of the 46 drugs of the training set covered by AID 884, while the kinetics results for 27 drugs have been inconclusive. Of the 19 drugs, 17 were inhibitors and two were activators. These numbers suggest an approximate 10% mismatch between the clinical and HTS inhibition data (because all drugs recruited in the present study were categorized as inhibitors based on clinical reports).
In vitro IC
50 values have been reported for many compounds in the AID 884 bioassay, but their relation to
in vivo inhibition has not been determined. To map the
in vitro data to clinically observable
in vivo bioactivity, the IC
50 values were extrapolated to pharmacokinetically relevant quantities. Following the FDA guidance [
18], a ratio,
R, of the inhibited area-under-the-curve (AUC) to uninhibited AUC was used to quantify the
in vivo inhibition activity. The extrapolation was carried out using Equation 6 provided in the
Experimental Section. Two approaches were conducted to estimate the physiological concentration of the inhibitor: One by the maximum recommended daily dose (MRDD) and bioavailability, and another by the greatest reported clinical plasma peak concentration,
Cmax, which was taken as the maximum hepatic inlet concentration. The results of calculations and subsequent categorization are presented in
Table 1. A threshold of 2 on
R was applied for inhibition strength categorization. Drugs with
R > 2 were categorized as potent inhibitors (P = “strong” ∪ “moderate”), while those with 1.25 ≤
R ≤ 2 as weak inhibitors (W). Compounds with
R lower than a threshold of 1.25 were considered to be irrelevant to clinical manifestations of CYP3A4 inhibition.
An agreement between the in vivo and in vitro categorization was poor. More than half of the in vitro inhibitors could not be categorized. The categorization was not feasible either because the CI was crossing a threshold on R or because the calculated R was outside the range of in vivo inhibition. When reported bioavailability values were used for calculating R-1, three of four potent inhibitors and three of 12 weak inhibitors were identified correctly by in vitro data, giving a 37.5% rate of success.
Calculations of
R with bioavailability derived using ACD/ADME
™ and with the default bio-availability of 100% were carried out to test a hypothesis about their utility in the calculations of
R. Bioavailability is a challenging topic for both
ab initio modeling and cross-chemical extrapolation [
72,
92]. Hypothetically, a bioavailability surrogate could be applied to non-drugs in HTS libraries and other compounds, for which bioavailability has not yet been determined. When using the ACD-calculated bioavailability or a default bioavailability of 100%, the results of
R calculations were similar to aforementioned
R-1. With the ACD-calculated bioavailability, three of four potent inhibitors and two of 13 weak inhibitors were correctly attributed, giving a 29% success rate; with the default bioavailability, four of four potent inhibitors and three of 13 weak inhibitors were correctly attributed, giving a 41% success rate. Thus, based upon the results of the present study, no evidence suggested that the default bioavailability of 100% in calculations of
R was not appropriate.
Given a well-recognized uncertainty associated with experimentally determined MRDD and bioavailability values, directly measured plasma Cmax values may be thought of as an appealing alternative. When Cmax values compiled from the literature and clinical trials (Dr. Minjun Chen personal communication) were attempted in R-4 calculations, only two of four potent and one of 10 weak inhibitors were assigned correctly. This translates into a 21% success rate, which is almost twice as poor as the success rate of R-3 calculations with reported MRDD and default bioavailability values.
Within the groups of inhibitors, which were successfully categorized using the
in vitro data (non-NDs in
Table 1), no gross miscategorization upon
in vitro to
in vivo extrapolation was observed, although an overlap between the clinical dataset and PubChem
™ data was small. However, little of the PubChem
™ data were useful for potency categorization because of the low power of underlying IC
50 values. Similarly, the IC
50 values alone, without extrapolation to
in vivo, were of little utility for inhibitor categorization. Perhaps, deficiencies in the
in vitro data can be eliminated in the future with improved study design, after which the HTS information may become appropriate for modeling DDCIs. Still, about a 10% mismatch between the HTS measurements and results of clinical trials may be anticipated. This number is relatively small provided the complexity of the
in vivo responses; the latter is especially important for CYP3A4. CYP3A4 regulation is perhaps the most complex of all CYP isoforms, because of both peculiarities in the structure/kinetics and system-biological effects. For instance, both hepatic and enteric forms of CYP3A4 are expressed in large relative amounts, and it has been shown that these forms are kinetically distinct [
93] and may contribute differently to the pharmacokinetic profile of a xenobiotic. Also, the activity of CYP3A4 is regulated at multiple levels by inducers, transporters, and other factors [
53]. Altogether, a 10% mismatch does not seem unreasonable but suggests that, even in theory, the performance of HTS data in dissecting DDCIs is capped below 100% because of causal oversimplification by an
in vitro system. To the contrary,
in vivo clinical data are exempt of such a limitation, while their utility depends on a technical implementation of supervised machine learning; hypothetically, an advanced machine classifier based on clinical data can be fully successful. However,
in vitro systems enable the study of more combinations of agents than the clinical approaches do. Perhaps, future computational approaches bearing on both strategies will become most effective.
The PubChem AID 884 bioassay was also used to examine an association between the molecular weight (MW) and inhibition properties of chemical compounds. A histogram of MWs of compounds tested for CYP3A4 activity in the AID 884 bioassay was unimodal. It followed a skewed bell-shape distribution with the mode at 330 ± 30, median at 331 Da, mean at 344 Da, and geometric mean at 316 Da. There were 3,680 compounds active in the test for CYP3A4 inhibition, and 7,418 were inactive. The histograms of active and inactive compounds were also unimodal and similarly shaped, but the descriptive statistics were different. The mode, median, mean, and geometric mean of inactive compounds were 285 ± 20, 294, 311, and 280 Da. Those of active compounds were 350 ± 10, 373, 397, and 378 Da. The 95% parametric CIs on the means were less than 5 Da. These data suggested that inactive and active compounds dominated different bands on the MW range: The low- and high-MW bands were populated with inactive and active compounds, respectively.
The MW histograms of active and inactive compounds were much overlapped and skewed. Because of that, the optimal point for MW banding was not immediately clear. Ostensibly, the point could be determined if the underlying theoretical distributions of the active and inactive compounds would have been known. However, the histograms were imperfectly shaped. An expectation was that MW of a randomly drawn organic compound follows the lognormal distribution. Descriptive statistics of the lognormal distribution satisfy the following inequality: {mode = e(μ − σ^2)} < {median = eμ} < {mean = e[μ + (σ^2)/2]}, where μ and σ2 are the mean = median = mode and variance of the reciprocal normal distribution on the logarithmic scale. Only the descriptive statistics of active compounds satisfied the inequality. The MW of active compounds was approximately lognormally distributed with an estimated mean of 2.578 and standard deviation (SD) of 0.1313 on the log10 scale. For inactive compounds and dominated by them the full library, the inequality did not hold. It means that although the general tendency in these histograms was lognormal (as indicated by the median < mean), the lognormal distribution was inappropriate because the theoretical and observed bell shapes did not match. Moreover, the histograms of inactive compounds and of the full library could not be meaningfully fit with neither of normal, lognormal, or Weibull distributions. In these histograms, the low-MW side of the bell shape seemingly followed the normal distribution, while the high-MW side resembled a lognormal density. Therefore, unlikely the library of AID 884 compounds was a balanced random draw. The structure of the distribution suggested an unidentified bias in the HTS dataset that was caused, perhaps, either by different vendors of the tested substances, or different subsets of the substances, or maybe several biased draws from the chemical space. Conceivably, the poor-fit histograms could be described by a superposition of several random processes, but such level of details was outside the scope of the present study. Therefore, an alternative approach was adopted, in which a threshold for MW banding was empirically extracted directly from the histograms.
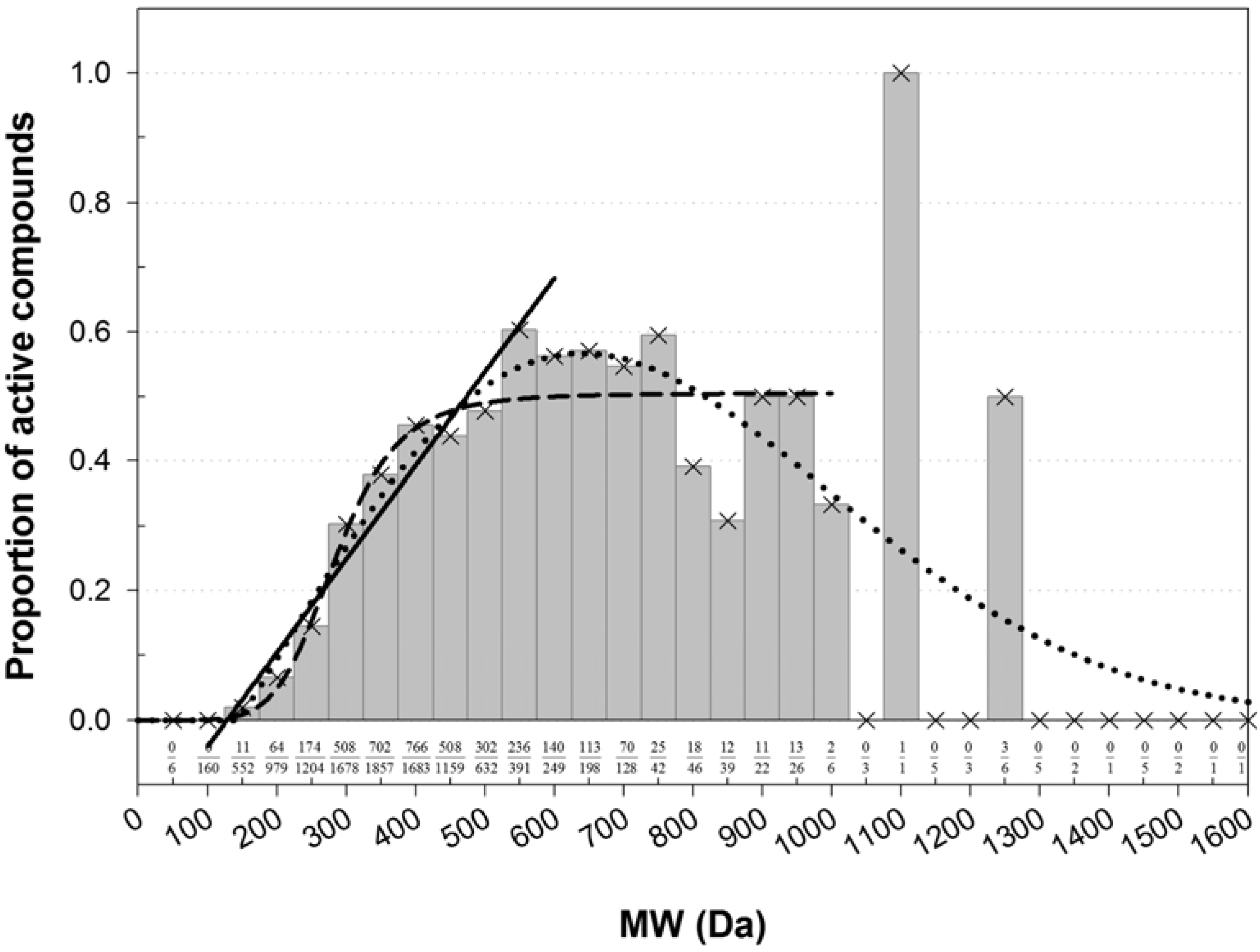
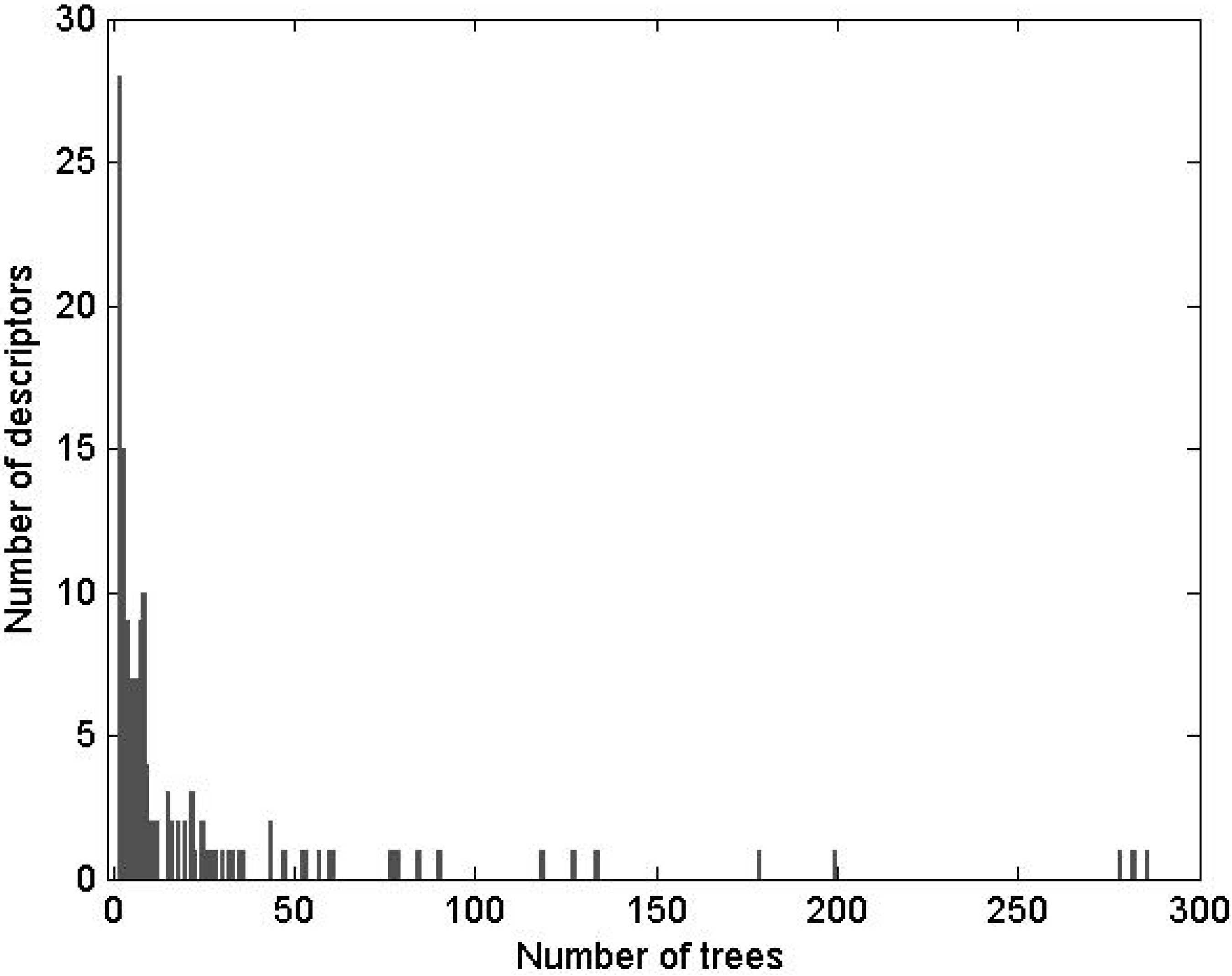
Instead of a ratio of two theoretical distributions, the enrichment with active compounds was studied using a normalized histogram (
Figure 1). Clearly, there was an association between MW and the frequency of active compounds. The bins were most populous in the low-MW range. There, a fraction of active compounds increased in a quasi-linear fashion from zero at about 60–172 Da to a quasi-plateau that began at 450–550 Da (
Figure 1). Poor statistics above 1,000 Da prevented confident characterization of the fraction of active compounds at high MWs. However, there was no evidence that the fraction was increasing with increasing MW. In the high-MW band the fraction was either constant at about 0.5, or maybe decreasing at very high MWs. However, in the area of high counts, the normalized histogram could be almost equally-well fitted with a linear, sigmoid, or bell-shaped dependence (
Figure 1). The shapes of different kind intersected at about 450 Da, which was taken as a threshold for MW banding.
Among the active compounds, 2,733 had MW lesser and 947 greater than the threshold. The respective proportions of active/(active + inactive) were
ν1 = 2733/9278 = 0.2946 (95% CI: 0.2853–0.3039) and
ν2 = 947/1820 = 0.5203 (95% CI: 0.4974–0.5433). One-tailed Z-test for two proportions suggested that these proportions were statistically significantly distinct; there was an almost 100% chance (
p < 2.235 × 10
−78) that the proportion of active compounds in the low-MW band was less than the proportion of active compounds in the high-MW band. This was in agreement with Lipinski's rule of five, which MW condition postulates that MW of drugs with favorable ADMET properties shall not exceed 500 Da [
94]. The ratio of proportions was
ν2/
ν1 = 1.766 (95% CI: 1.670–1.862),
i.e., it was about twice more likely to encounter an inhibitor of CYP3A4 among compounds in the high-MW band compared to the low-MW band.
Figure 1.
Normalized histogram of MW of compounds active in AID 884. The number of active compounds in each bin was normalized by the total number of active and inactive compounds in that bin. The proportions of active compounds are labeled at the bottom. The histogram shape was fitted with functions from the bell-shaped and sigmoid families and with a linear function. In the each family, only the best fit was retained. A fit with a four-parameter Weibull function (as implemented in the SigmaPlot® software; a = 0.5670, b = 686.7269, c = 2.0494, x0 = 639.5385) was carried out on the entire domain of MW, r2 = 0.5837. A fit with the logistic function (y = 0.5047/[1 + (285.1/x)6.266]) was carried out for MW ≤ 950 Da, r2 = 0.8970. A line (y = 0.001437x − 0.1825) was fitted to the bins in the range 150–550 Da, r2 = 0.9479. The fitted shapes intersected at about the same point of 450 Da, which was taken as a threshold separating the MW range in a low-MW band that was depleted with active compounds and a high-MW band that was enriched with active compounds.
Figure 1.
Normalized histogram of MW of compounds active in AID 884. The number of active compounds in each bin was normalized by the total number of active and inactive compounds in that bin. The proportions of active compounds are labeled at the bottom. The histogram shape was fitted with functions from the bell-shaped and sigmoid families and with a linear function. In the each family, only the best fit was retained. A fit with a four-parameter Weibull function (as implemented in the SigmaPlot® software; a = 0.5670, b = 686.7269, c = 2.0494, x0 = 639.5385) was carried out on the entire domain of MW, r2 = 0.5837. A fit with the logistic function (y = 0.5047/[1 + (285.1/x)6.266]) was carried out for MW ≤ 950 Da, r2 = 0.8970. A line (y = 0.001437x − 0.1825) was fitted to the bins in the range 150–550 Da, r2 = 0.9479. The fitted shapes intersected at about the same point of 450 Da, which was taken as a threshold separating the MW range in a low-MW band that was depleted with active compounds and a high-MW band that was enriched with active compounds.
![Molecules 17 03407 g001]()
2.2. Docking Classifier of Potent and Weak Inhibitors of CYP3A4
Crystal structures of human CYP3A4 with and without inhibitor correlated with the well-known structural flexibility of the protein. The flexibility and consequent substrate adaptability of CYP3A4 observed in the structures were consistent with atypical kinetic behavior that has been described for CYP3A4 [
95,
96,
97]. MW of CYP3A4 inhibitors studied crystallographically ranged from 226 to 734 Da, while the volume of active site [
98], conjugated to the size of substrate, increased up to 80%. Multiple substrate binding modes (productive and non-productive) as well as multiple binding sites (at the site entrance, the catalytic site, and even the secondary binding site) were observed in the crystallographic complexes. Based on the structural analysis, four protein data bank (PDB) structures with seven possible binding pockets were selected for docking studies (refer to the
Experimental Section for details). Four molecular docking programs were applied and, thus, 28 sets of docking scores were generated.
The docking scores were combined using a logistic regression (LR) procedure. LR variables were selected either by using the forward-stepwise, backward-stepwise, or a manual selection procedure. Although the stepwise variable selection procedures are widely used, they are not perfect, and their drawbacks are well understood [
99]. Therefore, an emphasis in the present work was made on manual selection (a so-called “full” model [
99]).
The LR models were trained using 33 potent and 88 weak CYP3A4 inhibitors (see the
Experimental Section for details). Receiver operating characteristic (ROC) curves of the refined interim models are shown in
Figure 2. ROC curves were calculated by varying the cutoff probability point from one on the left side to zero on the right side of the ROC plot; which cutoff is theoretically most appropriate is a matter of debate. In practice, the choice of cutoff is often driven by the utility or by cost-effectiveness considerations. Common choices are 0.5 (SAS
® default), or a cutoff point based on prior or posterior probabilities. The prior or posterior cutoff points are appealing when categories are highly unbalanced, that is when events in one of the categories are very rare. In this case, a rare-events correction to the model intercept can be used [
100]. In the present work, the categories of the training set were split approximately 1:3, which suggests that the minority type was unbalanced but not rare. In this case, increasing the size of the training set and using the default cutoff of 0.5 is a preferred way of handling the data; appropriately increased size of the training set allows for the adequate representation of patterns that comprise the minority distribution.
Figure 2.
ROC plot of the interim DLR models for potent and weak inhibitors of CYP3A4. A, B, C, and D denote maximum specificity, maximum correct classification, equal sensitivity and specificity, and maximum sensitivity points on the ROC curves, respectively.
Figure 2.
ROC plot of the interim DLR models for potent and weak inhibitors of CYP3A4. A, B, C, and D denote maximum specificity, maximum correct classification, equal sensitivity and specificity, and maximum sensitivity points on the ROC curves, respectively.
As shown in
Figure 2, maximum correct classification and equal sensitivity/specificity could not be achieved with the same cutoff point. A balanced model with equal sensitivity and specificity could be obtained using a cutoff based on the prior probability of categorization of potent inhibitors (33/121), which comprised the minority population (
Table 2). However, because the training set was unbalanced, the maximum correct classification could not be achieved with the prior cutoff. The maximum correct classification was achieved with the default cutoff of 0.5. To maximize the correct classification, a cutoff of 0.5 was adopted in the present study.
Table 2.
Effect of LR probability cutoff on model performance.
Table 2.
Effect of LR probability cutoff on model performance.
| Model | Cutoff point | Probability cutoff | Sensitivity | Specificity | Correct classification |
|---|
| Forward model | maximum specificity | 0.60 | 0.15 | 1.00 | 0.77 |
| maximum correct classification | 0.50 | 0.36 | 0.94 | 0.79 |
| specificity = sensitivity | 0.24 | 0.55 | 0.57 | 0.56 |
| maximum sensitivity | 0.04 | 1.00 | 0.00 | 0.27 |
| Backward model | maximum specificity | 0.80 | 0.36 | 1.00 | 0.83 |
| maximum correct classification | 0.50 | 0.64 | 0.94 | 0.86 |
| specificity = sensitivity | 0.28 | 0.79 | 0.78 | 0.79 |
| maximum sensitivity | 0.08 | 1.00 | 0.73 | 0.47 |
| Manual model | maximum specificity | 0.50 | 0.42 | 1.00 | 0.84 |
| maximum correct classification |
| specificity = sensitivity | 0.26 | 0.68 | 0.69 | 0.69 |
| maximum sensitivity | 0.10 | 1.00 | 0.27 | 0.47 |
| Manual model, MW > 450 | maximum specificity | 0.50 | 0.72 | 1.00 | 0.87 |
| maximum correct classification |
| specificity = sensitivity | 0.43 | 0.78 | 0.76 | 0.77 |
| maximum sensitivity | 0.07 | 1.00 | 0.38 | 0.64 |
ROC AUC is often used as an empirical statistic for model comparison (and its close relationship to rank tests in non-parametric statistics can be shown). The ROC AUC is interpreted as a measure of model quality. Clearly, if ROC AUC is 1, the model is perfect, and if it is 0.5 (the diagonal), the model is worthless. The calculated ROC AUCs were 0.66, 0.89, and 0.80 for the forward-stepwise, backward-stepwise, and manual selection LR models, respectively. The results suggest that the backward-stepwise and manual selection models were not excellent (ROC AUC > 0.9), however, but they were good (ROC AUC > 0.8).
The AUCs were roughly proportional to the number of docking scores recruited in the model: There were 3, 13, and 7 scores in the forward-stepwise, backward-stepwise, and manual selection LR models, respectively. As can be seen in
Figure 2, the backward-stepwise and manual selection models were opposite in terms of specificity and sensitivity,
i.e., the backward-stepwise model was better at sensitivity and the manual selection model was better at specificity. Namely, adding more parameters to the model improved representation of the major category of weak inhibitors but it did not help the machine classifier to better learn about the minor category of potent inhibitors, perhaps, because of under population of the latter. There were 121 compounds in the training set. Applying a 1:20 rule for candidate predictor variables in a LR model [
101], it was perceived that the backward-stepwise model may be over-trained, while the forward-stepwise may be under-trained. A conservative choice was made in favor of the manually selected “full” model with a balanced number of parameters. The manual selection model showed 100% specificity at the cutoff point of maximum correct classification of the model on the ROC curve (
Figure 2), which was achieved using the default categorizing probability cutoff. Thus, the manual selection model with a categorizing probability cutoff of 0.5 was adopted as the final model at the LR parameter-optimization stage.
Docking scores included in the final model are presented in
Table 3. The table also shows the contribution and significance of each score. A docking score that was calculated using Surflex
™ at the 1W0F-catalytic site gave the highest contribution, while the score that was calculated using FRED
™ at the 2V0M-catalytic site was the next highest contribution. All docking scores were significant for the final model with
p-values of less than 0.05, except for the 1W0F-entrance site score from FRED
™, with a
p-value less than 0.1. Six of seven selected scores were pertinent to the catalytic site. This circumstance suggests that competitive inhibition at the active site is perhaps the major determinant of the high potency of CYP3A4 inhibition, as given by the chemicals of the training set. Thus, allosteric sites, which often result in atypical Michaelis-Menten kinetics, must be those that contribute mostly to weak inhibition of CYP3A4.
Table 3.
Summary of the final DLR model.
Table 3.
Summary of the final DLR model.
| Analysis of Maximum Likelihood Estimates |
|---|
| Parameter | DF | Estimated Coefficient | Standard Error | Wald χ2 | Pr > χ2 |
|---|
| 1W0F-catalytic site-by Surflex™ | 1 | 5.5653 | 1.5783 | 12.4342 | 0.0004 |
| 2V0M-catalytic site-by FRED™ * | 1 | −2.2601 | 0.8146 | 7.6972 | 0.0055 |
| 2J0D-catalytic site-by Surflex™ | 1 | −1.7176 | 0.6328 | 7.3684 | 0.0066 |
| 2V0M-catalytic site-by Glide™ | 1 | 1.5078 | 0.5545 | 7.3927 | 0.0065 |
| 2V0M-full active site-by FRED™ † | 1 | 1.4618 | 0.5385 | 7.3740 | 0.0066 |
| 1W0F-catalytic site-by Glide™ | 1 | −1.2597 | 0.5007 | 6.3288 | 0.0119 |
| 1W0F-entrance site-by FRED™ | 1 | −1.0350 | 0.6189 | 2.7967 | 0.0845 |
| Intercept | 1 | −1.8088 | 0.3556 | 25.8789 | <0.0001 |
The final DLR model constructed using the full training set (the joint model) had a 100% specificity, 42.4% sensitivity, and a rate-of-correct-classification of 84.3%. A tenfold cross-validation (CV) was carried out by splitting the training set in a proportion of 1:9 and leaving out the 10% of the sample. The average model rates-of-correct-classification for ten random splits of the training subsets (i.e., each subset contained 90% of the total sample) and the CV subsets (10% of the total sample in each subset) were 83.8% and 79.3%, respectively.
As shown in the previous section, MW was an important factor affecting inhibition properties of chemical compounds. Similarly to compounds active in the HTS assay, a histogram of MWs of the training-set inhibitors also followed the lognormal distribution (p = 0.217, the Shapiro-Wilk test for normality). The mean was estimated at log10(381), which was indistinguishable from the HTS geometric mean, and the estimated SD was 0.1885.
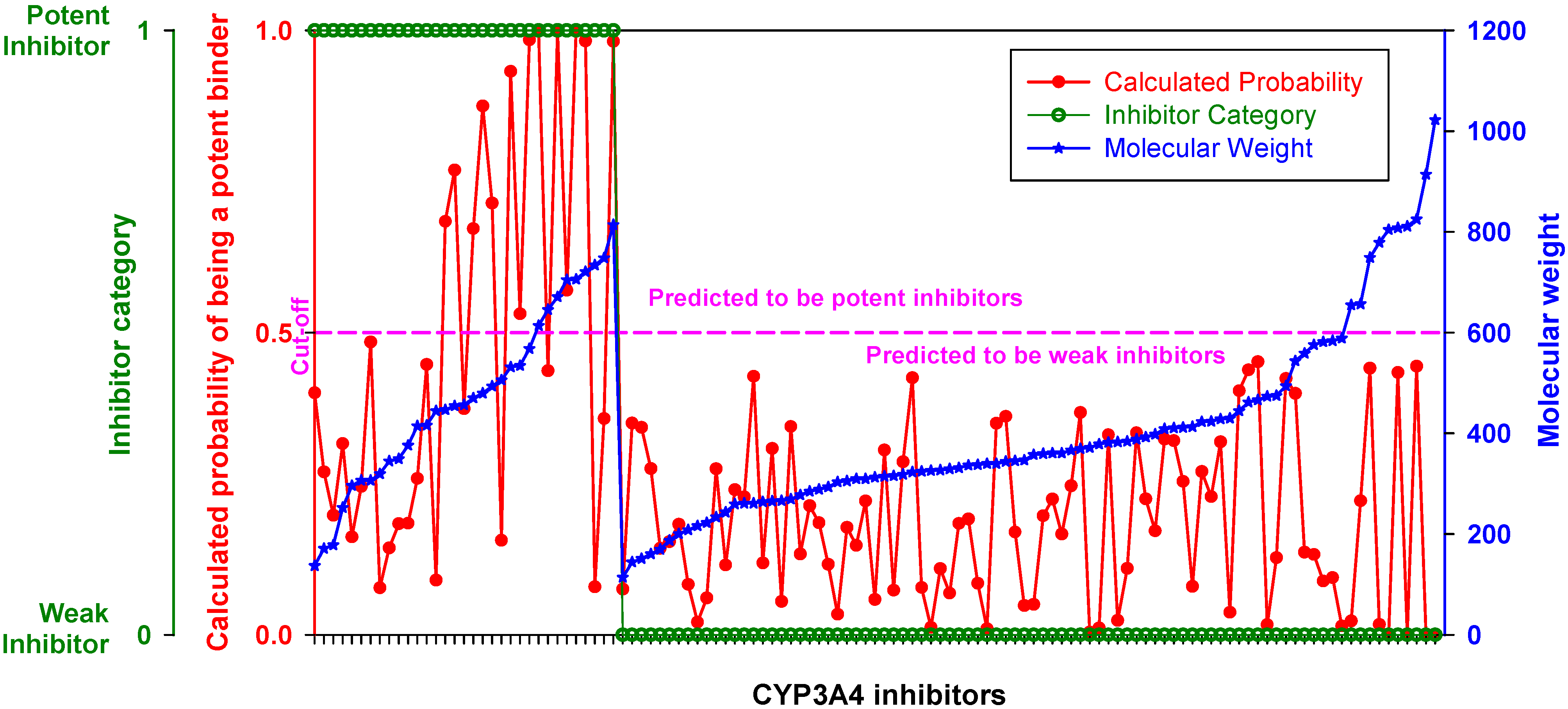
When inhibitors of the training set were ranked by MW, the DLR model showed a stepwise increase in sensitivity at the threshold of 450 Da described in the previous section (
Figure 3,
Table 2). Below the threshold, the DLR model recognized only one potent inhibitor (tetracycline), whereas above the threshold the model recognized almost 75% of potent inhibitors. Nonetheless, it correctly classified all weak inhibitors, regardless of MW,
i.e., there was no false positive error.
Figure 3.
Performance of the DLR model. Potent and weak CYP3A4 inhibitors were sorted by molecular weight, which is shown in blue; their clinical categorization is shown in green; calculated probability scores are depicted in red. The dashed line denotes a chosen probability cut-off for the LR model.
Figure 3.
Performance of the DLR model. Potent and weak CYP3A4 inhibitors were sorted by molecular weight, which is shown in blue; their clinical categorization is shown in green; calculated probability scores are depicted in red. The dashed line denotes a chosen probability cut-off for the LR model.
Adding MW to the pool of docking scores of LR as the 29th independent variable was not helpful: The coefficient at MW was not statistically significant in the 29- and 7-parameter models (p-value of 0.1375 and 0.2217, respectively). The forward- and backward-stepwise procedures also did not select MW as a LR variable. MW was not helpful, perhaps, because it was 35–75% correlated with the docking scores, i.e., it carried redundant information.
To determine if the training set was enriched with potent inhibitors in the high-MW band, a statistical test was carried out. Among 82 inhibitors in the low-MW band, only 15 were categorized as potent; among 39 inhibitors in the high-MW band, the number of potent inhibitors was 18. The respective proportions were
ν1 = 15/82 = 0.1829 (95% CI: 0.1141–0.2801) and
ν2 = 18/39 = 0.4615 (95% CI: 0.3157–0.6143). According to the one-tailed
Z-test for two proportions, there was a greater than 99.9% chance that the proportion of potent inhibitors in the low-MW band was less than the proportion of potent inhibitors in the high-MW band,
i.e., that H
0:
ν1 −
ν2 = 0 could be rejected in favor of H
1:
ν1 −
ν2 < 0 (
p < 6.50 × 10
−4). The power of the test was 93% (β = 0.0676 at α = 0.05). It meant that the examined inhibitor data were such that the chance of committing a type II error, when accepting the null hypothesis, was almost as low as the targeted chance of type I error (
i.e., 5%). Commonly, a study design with the power of 80% is considered acceptable (which implies a four times lesser penalty for a type II error as compared to a type I error) [
102]. Thus, chances of committing both type I and type II errors were small, which suggests that the size of the training set was sufficient to confidently conclude that the compounds in the high-MW band were enriched with potent inhibitors of the CYP3A4 isozyme.
The enrichment of the high-MW band with potent inhibitors was about 50%,
i.e., it was similar to the enrichment with general CYP3A4 inhibitors described in the previous section. In the low-MW band, however, the fraction of potent inhibitors did not exceed 20%, which was approximately by 30% less than that described for general CYP3A4 inhibitors in the previous section. Combined, these data suggested that in the high-MW band CYP3A4 inhibitors were 2–3 times more likely to be potent compared to inhibitors in the low-MW band. Thus, the effect of MW on potency of CYP3A4 inhibition was more profound than on the category of inhibition itself described in the previous section. Profusion of inhibitors and potent inhibitors in the high-MW band may be related to a greater probability of finding a chiral center in large organic compounds. Because CYP3A4 is stereo- and regio-specific, involvement of enantiomeric decoys unlikely improves but hinders the rate of metabolic reactions. Preliminary examination of inhibitors of other CYP isozymes (data not shown) suggested that (1) a similar dependence between MW and inhibition potency can be observed for inhibitors of other isozymes with adaptive active site, such as 2C9, but unlikely of rigid isozymes, such as 2D6; and that (2) the MW threshold may be unique for each adaptable isozyme. It is not clear at this point, if the MW effect is determined by the volume of the active site, or the active-site adaptability, or the number of binding pockets at the active site (see also
Section 2.5). More crystallographic complexes of CYP isozymes and ligands resolved in the future may help to clarify the topic. Also, if the observed phenomenon is indeed related to the probability of a chiral center in the ligand, perhaps, the MW effect will best manifest in isozymes, which spectrum of specificity includes large compounds,
i.e., such CYP isozymes as 3A4 and 2C9.
Now, since the actual proportions of potent inhibitors and their respective CIs were known, they could be applied to examine the results of machine classification. Suppose that the number of potent inhibitors in the training set has been forgotten; how many of them will be expected after application of a machine classifier? The prior suggested an expected range for the number of potent inhibitors. If the number of machine-classified potent inhibitors would be within 9–23 in the low-MW band and 12–24 in the high-MW band, that would not contradict a statistical expectation at the 95% confidence level. Similarly, for the whole training set the proportion of potent inhibitors was 0.2727 (95% CI: 0.2013–0.3582). Thus, from 24 to 43 machine-classified potent inhibitors would be expected.
The DLR model correctly classified only 14 potent inhibitors among the 121 compounds of the training set. That was less than categorized 33 potent inhibitors at 99.9% probability (
p < 1.01 × 10
−3). The underestimation stemmed from the low-MW band, in which the correct classification (1/82) was less than expected (15/82) at more than 99.99% probability (
p < 1.15 × 10
−4). In the high-MW band, however, the null hypothesis (that the proportion of correctly classified potent inhibitors, 13/39, is the same as the proportion of categorized ones, 18/39) could not be rejected (
p > 0.123, 87.6%). Thus, the natural bias in the number of potent inhibitors categorized across the MW range was exaggerated in the classification results of the DLR model. Perhaps, it was caused either by a bias in model training towards weak inhibitors, which constituted the dominant major category in the low-MW band in a proportion greater than 4:5, or a statistical fluctuation in the data. Taking into account the results of DLR model application to the testing set (see
Section 2.6), the latter appeared as a quite likely possibility.
As evident from
Figure 3, lowering the probability cutoff point was not helpful, because the domain of probability scores of weak inhibitors almost exactly overlapped with the domain of potent inhibitors in the low-MW band. At 450 Da, the probability scores of potent inhibitors displayed a stepwise increase, which was appropriate for correct classification. The phenomenon could be related either to an almost 1:1 balance between potent and weak inhibitors in the high-MW band, or to an increase in the probability of a chiral center discussed above, or, likely, to the number of contacts that ligand makes at the docking site,
i.e., ultimately with the large size and adaptability of the active site pocket on CYP3A4 (see
Section 2.5 and
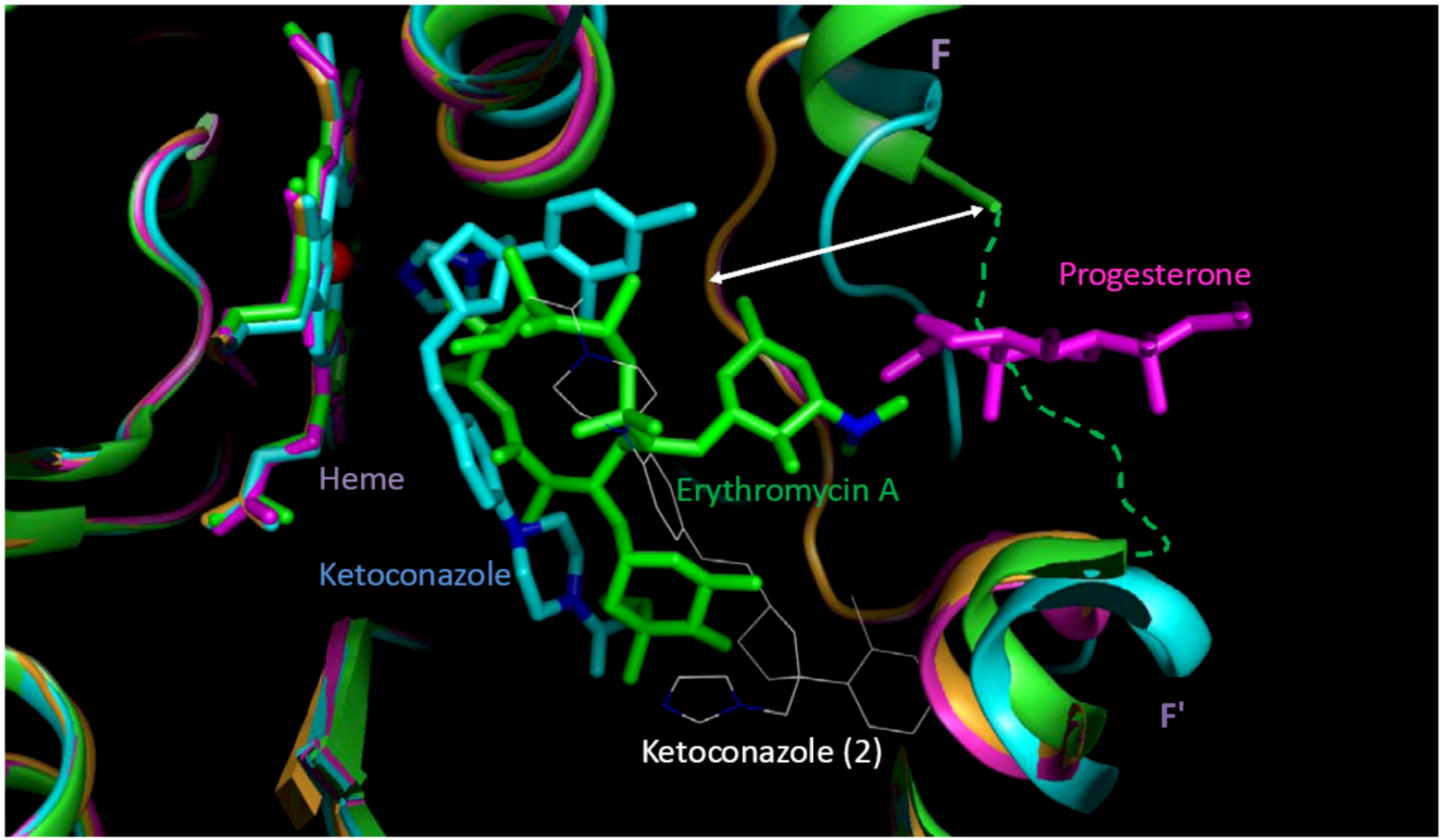
Section 3). Another reason could be that the docking study did not cover all binding sites, especially those with a preference for small molecules such as extra-allosteric sites. It is also possible that an effector molecule(s) binding may take place when the substrate/inhibitor is small. For instance, two ketoconazole molecules are bound in one of the crystal structures of CY3A4 used for docking in the present study [
98]. However, at least four molecules of 7-benzyloxyquinoline, which has MW less than half that of ketoconazole, bind simultaneously to CYP3A4 [
14]. Moreover, unlike other CYP isozymes, the active site pocket of CYP3A4 is enriched with water molecules; the mean coordination number of water molecules in proximity of the heme is at least two to three times greater than in other CYP isozymes [
103]. However, the docking procedures employed in the present study did not imply the use of explicit water molecules in docking simulations (although, the mean-field solvent effects were implicitly accounted for in several of the scoring functions). Water molecules in the active site may play an important role in protein-ligand binding. On the one hand, shielding the transition state from water (and thus reducing the activation energy barrier of the transition state) is the main purpose of enzymatic catalysis (which can be achieved either by elasticity of the active site, or by presence in the active site of hetero- or homo-effector molecule(s), similar to the 2V0M structure); but on the other hand, water molecules at high-occupancy hydration sites can mediate the hydrogen-bond network of the active site and stabilize the protein-ligand complex (along with the conformation of the protein and the transition state). Also, they contribute to the free energy of binding. Indeed, the process of ligand binding is also a process of dislodging water from the active site. As water molecules are released from the active site, the entropy of the protein-ligand complex usually goes down, while the entropy of the full system (which also includes the solvent) usually goes up (more free water). However, the arrangement of water molecules in the active site is often different for different ligands. Docking software used in the present study did not offer modeling of explicit water molecules. Ligand interactions with water molecules were either neglected or taken into account using a mean-field approach as implemented in the scoring functions. Recent studies have shown a modest success in incorporating explicit water molecules in docking simulations [
104,
105,
106]. Similar methodology applied to CYP3A4 may improve the accuracy of the DLR model in the future. Also, additional crystallographic studies on CYP3A4 ligands from the low-MW band may help in understanding the modalities of small ligand binding and expand the database of docking scores of the model.
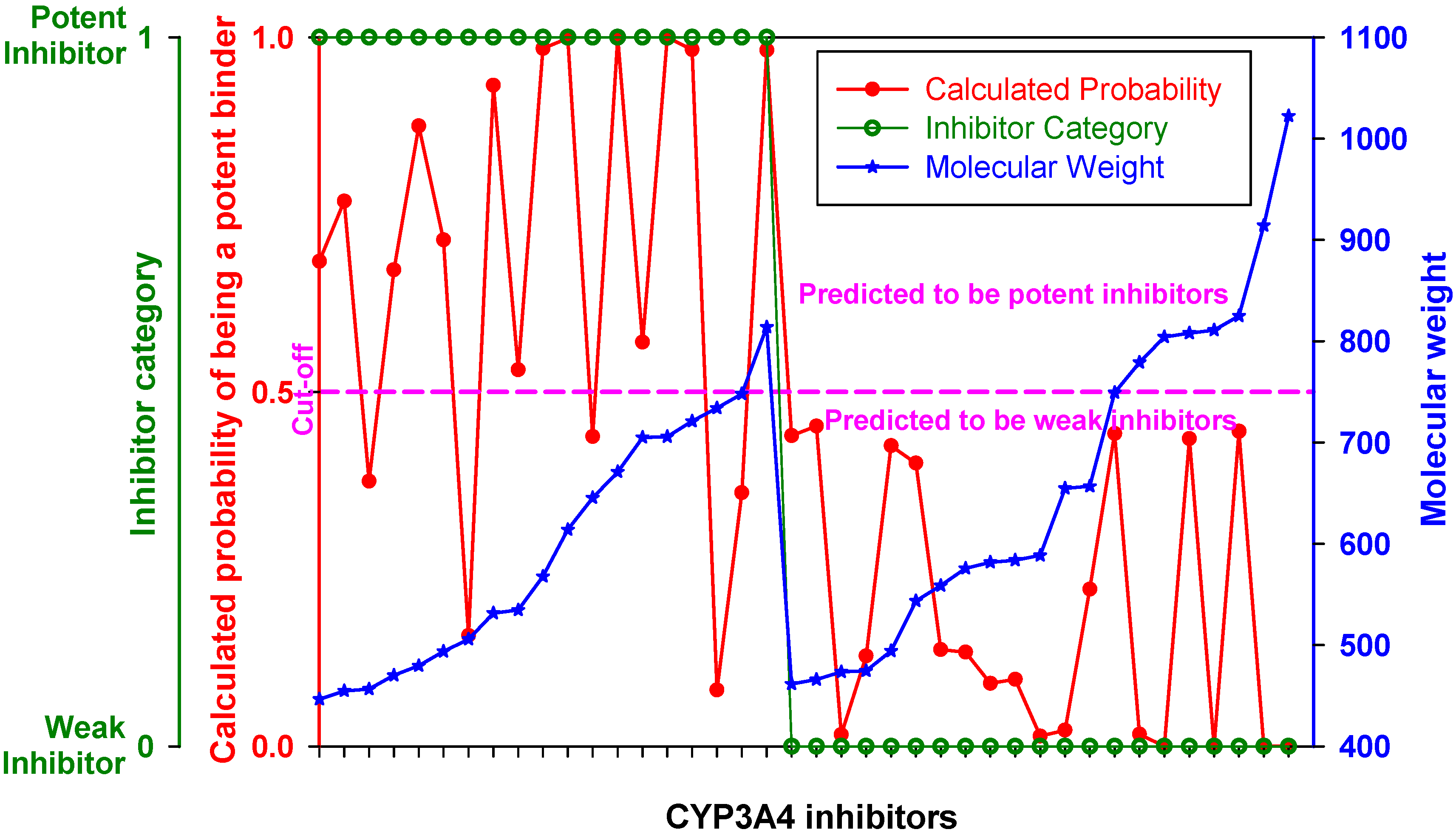
Figure 4 represents the ROC curve and shows performance of the DLR model in the high-MW band of CYP3A4 inhibitors. The ROC AUC of the model using thus truncated applicability domain (TD-DLR) was 0.85,
i.e., the area outside the ROC curve shrunk by one quarter compared to the full-domain DLR model (FD-DLR). Similar to FD-DLR, the TD-DLR joint model had 100% specificity, while sensitivity and the rate-of-correct-classification improved to 72.2% (from 42.4%) and 87.1% (from 84.3%), respectively (
Table 4). The average model rates-of-correct-classification for the split subsets (90% of the sample) and CV subsets (10% of the sample) of TD-DLR were 84.1% and 70.8%, respectively. That is, the cross-validated model rate-of-correct-classification for TD-DLR was almost 10% less than for FD-DLR. The latter, perhaps, was related to a smaller volume of training data in TD-DLR, which training set comprised less than one third of that of FD-DLR.
Figure 4.
(a) ROC curve of the DLR model for the high-MW band (18 potent and 21 weak inhibitors). A, B, C, and D represent maximum specificity, maximum correct classification, equal sensitivity and specificity, and maximum sensitivity points, respectively. (b) Performance of the DLR model in the high-MW band.
Figure 4.
(a) ROC curve of the DLR model for the high-MW band (18 potent and 21 weak inhibitors). A, B, C, and D represent maximum specificity, maximum correct classification, equal sensitivity and specificity, and maximum sensitivity points, respectively. (b) Performance of the DLR model in the high-MW band.
Table 4.
Comparison of SDAR-, SAR- and DLR-modeling * methods.
Table 4.
Comparison of SDAR-, SAR- and DLR-modeling * methods.
| Modelingmethod | Correctclassification | Sensitivity | Specificity | Type II error | Type I error | Numberof descriptors |
|---|
| Joint | Split | CV | Joint | Split | CV | Joint | Split | CV | Joint | Split | CV | Joint | Split | CV | Joint | Split/CV |
|---|
| SDAR | 99.2 | 95.7 | 64.9 | 97.0 | 90.5 | 53.3 | 100 | 97.7 | 68.8 | 3.0 | 9.5 | 46.7 | 0 | 2.3 | 31.2 | 27 | 12 to 40 |
| SAR | 95.0 | 92.5 | 66.9 | 81.8 | 76.1 | 27.3 | 100 | 97.5 | 81.8 | 18.2 | 23.9 | 72.7 | 0 | 2.5 | 18.2 | 5 | 6.6 |
| FD-DLR | 84.3 | 83.8 | 79.3 | 42.4 | 44.1 | 35.5 | 100 | 98.7 | 95.7 | 57.6 | 55.9 | 64.5 | 0 | 1.3 | 4.3 | 7 | 7 |
| TD-DLR | 87.1 | 84.1 | 70.8 | 72.2 | 71.5 | 63.3 | 100 | 94.6 | 83.3 | 27.8 | 29.5 | 36.7 | 0 | 5.4 | 16.7 | 7 | 7 |
| Consensus | 95.0 | | | 81.8 | | | 100 | | | 18.2 | | | 0 | | | | |
Only five drugs in the high-MW band were misclassified by TD-DLR. However, all of the drugs belonged to the category of potent inhibitors (as specificity of the model was 100%). The misclassified drugs were amiodarone, amprenavir, delavirdine, clarithomycin, and erythromycin.
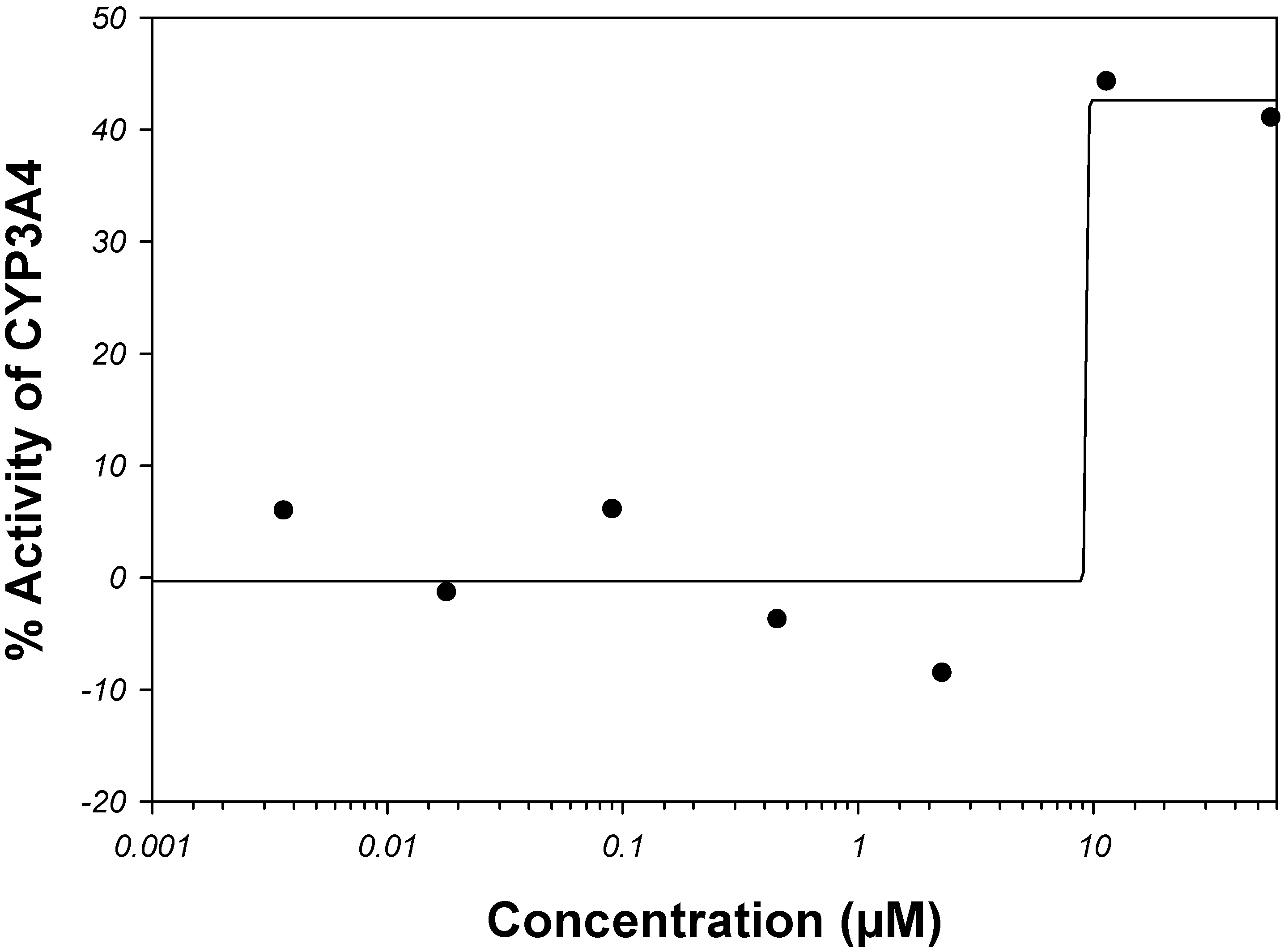
Amiodarone is a vasodilator. It is metabolized in the liver primarily by CYP3A4 and, at low concentrations, by CYP2C8 (see the
Supplemental Material). The rate of catalysis of substrate luciferin-6'-phenylpiperazinylyl in the
in vitro CYP3A4 system has increased in the presence of amiodarone, as given by PubChem
™ bioassay AID 884 (
Figure 5); therefore, amiodarone has been classified in PubChem
™ as an activator and not inhibitor of CYP3A4 [
68,
107]. Although, potency of CYP3A4 inhibition may vary widely depending on a test substrate [
57], we are unaware of examples in which the sign of reaction rate changes from the inhibition to activation. Of course, hypothetically, amiodarone can bind to an allosteric site outside the analyzed binding sites within the CYP3A4 active site pocket in such a way that it acts as an activator for the luciferin-6’-phenylpiperazinylyl substrate and an inhibitor for some other substrate(s).
Figure 5.
Dose-activity data of amiodarone as reported in PubChem
™ bioassay AID 884 [
68,
107]. A four-parameter Hill equation was fitted to the data.
Figure 5.
Dose-activity data of amiodarone as reported in PubChem
™ bioassay AID 884 [
68,
107]. A four-parameter Hill equation was fitted to the data.
Amprenavir and delavirdine are the first-generation antiretroviral drugs for treatment of human immunodeficiency virus (HIV) infection. Amprenavir is a HIV protease inhibitor, while delavirdine is a non-nucleoside inhibitor of the HIV reverse transcriptase. Both amprenavir and delavirdine are mechanism-based inhibitors of CYP3A4. Presumably, delavirdine, binds covalently to the apoprotein and inactivates it; amprenavir is a substrate but its unknown reactive metabolites also inactivate the CYP3A4 isozyme [
108,
109,
110]. Clarithromycin and erythromycin are macrolide ring antibiotics and also mechanism-based inactivators of CYP3A4. They are first metabolized by CYP3A4 to form reactive nitrosoalkanes via
N-demethylation, which then impair the enzyme [
108,
109,
110].
DLR is a mechanistic model. As such, it depends on and takes into account the potency of affine ligand binding of the parent compound. However, to exhibit potent clinical CYP3A4 inhibition effects, a mechanism-based inhibitor does not have to be a potent affine binder to CYP3A4, especially if the isozyme is inhibited by reaction metabolites but not the parent compound. If the parent compound does not have superior affine-binding properties, a high-fidelity DLR method shall not recognize it as a potent inhibitor.
In brief, one of the inhibitors (amiodarone) misclassified by the DLR model was, probably, also miscategorized in the literature, while all other misclassified compounds (amprenavir, clarithromycin, delavirdine, and erythromycin) were mechanism-based irreversible inactivators, to which the computational molecular docking approach does not necessarily apply. Taking into account that machine learning was conducted using clinical, not
in vitro, data, it is surprising how reasonably well the DLR method performed on inhibitors from the high-MW band. It supports a conclusion of the previous section that only a small part of clinically-characterized CYP3A4 inhibitors disagrees with
in vitro binding-assay data, while most of the clinically observed CYP3A4 inhibition effects originate from the potent affine binding of interfering agents directly at the active center of CYP3A4. Together with two other classifiers described in the following sections, the DLR model was incorporated in the consensus classifier, which was then applied to the EV set (see
Section 2.6).
2.5. Comparison of the DLR, SDAR, and SAR Classifiers
Three very different machine learning classifiers were developed in the present study, and each of them showed a fairly high rate-of-correct-classification.
Table 4 shows a comparison of the DLR, SDAR, and SAR model performances during 9:1 split training and CV. The rate-of-correct-classification of the models during tenfold CV was 79.3% and 70.8% for FD- and TD-DLR, respectively, 64.9% for SDAR, and 66.9% for SAR. Although the methodologies of DLR, SDAR, and SAR model development were vastly different, the produced models shared a deep fundamental connection in terms of classification features that were employed by the models to describe the CYP3A4 inhibitors. The similarities embraced: (1) two major descriptors of the SAR model were based on electronegativity, while (2) the
13C and
15N-NMR spectra used in SDAR models were dependent on the electronegativity of the substituent groups connected to the atom; similarly, (3) most significant independent variables of the DLR model represented scores of the Hammerhead, FRED
™, and Glide
™ scoring functions. These scoring functions incorporate electronegativity either in the form of electrostatic potential, which determines the electronegativity, or its derivatives such as repulsive, polar, and salvation terms of the Hammerhead scoring function [
113]. Because the DLR model essentially was a mechanistic binding model, the observed descriptor commonality suggested its association with the potency of CYP3A4 binding. In other words, all methods indicated that the category of potent inhibitors consisted mostly of potent CYP3A4 binders, while the category of weak inhibitors consisted either of predominantly weak binders or compounds that set off clinical manifestations of CYP3A4 inhibition by other mechanisms.
The question arises as to whether a potent clinically observed inhibitor of CYP3A4 must be its potent binder. An answer may reside with the sensitivity and specificity of the models. During CV the specificity was consistently higher than the sensitivity as given by all methods, and the final models came out as 100% specific (
Table 4). This suggests that the probability of recognizing a weak inhibitor as potent was smaller than the probability of recognizing a potent inhibitor as weak. Since a pattern of potent inhibitors learned by the classifiers seemingly was associated with affine binding to CYP3A4, other mechanisms related to clinically devised potent inhibition probably were underrepresented in the training set and,
i.e. potent inhibitors of CYP3A4 present in the training set that were not potent affine binders to CYP3A4 comprised a minor class. They were not appropriately learned by the classifiers because the size of training set was insufficient for that, and, therefore, they were misclassified by the models. This could be a likely reason for persistent inferior sensitivity observed for all models.
Similarly, all classification methods summarized in
Table 4 showed a relatively high, 37–73% rate of false-negative estimates during CV. SAR and FD-DLR models had the highest rate of false-negative estimates. The false-negative rate was high for FD-DLR because the model identified in the training set only one of 15 potent inhibitors in the low-MW band. For the SDAR model, the true positive rate was low and the false-negative rate was high, perhaps, because the 1D NMR spectra did not contain enough chemical structure-specific information to adequately represent diversity of the training set in the chemical space. Inhibition of CYP3A4 is unlikely to originate from a single carbon or nitrogen atom as expressed by 1D NMR spectra, but rather from the entire chemical structural entity. The accuracy of SDAR models may improve as more structural information is added to the spectra, as has been shown for 3D-QSDAR models [
114,
115]. Supplementing the carbon and nitrogen chemical shifts with information about distances between the atoms provides an additional opportunity to more comprehensively describe the chemical properties of a compound and, thus, improve SDAR modeling.
Extrapolation from the classification results of the final joint models suggests that from 3% to 30% of non-affine inhibitors of CYP3A4 may be detected as potent in clinical studies. As discussed in the docking section, these non-affine inhibitors may be inducers, mechanism-based inhibitors, or perhaps agents intervening with the active transport and others. The suggested range of numbers is wider but similar to the 10% mismatch between the HTS measurements and results of clinical trials reported and discussed in
Section 2.1.
Also, there could be compounds that were incorrectly assigned to a wrong category based on information that was available when the training set was compiled; propofol may be one of them. Initially, it was attributed to the category of potent CYP3A4 inhibitors based on information external to the Merck Manual (refer to the
Supplemental Material). FD-DLR, SDAR, and SAR classified propofol as a weak inhibitor of CYP3A4 (while for TD-DLR it was outside the MW domain of the model). However, later after the work had been completed, propofol was categorized as a weak inhibitor of CYP3A4 in a new release of the Merck Manual [
32].
SAR and TD-DLR both classified amiodarone (MW of 645 Da) as a weak CYP3A4 inhibitor. As summarized in the docking section, the mechanism of amiodarone interference with catabolism mediated by the CYP3A4 isozyme is at least more complex than trivial inhibition by affine binding. However, the final joint SDAR model classified amiodarone as a potent inhibitor. Taking into account that SDAR showed the lowest of all methods rate-of-correct-classification at CV, SDAR model overtraining may be a reasonable explanation for the discrepancy.
As the SDAR model showed signs of overtraining, and applicability of the DLR model to the training set was restricted by MW, four additional compounds within the low-MW band shared false-negative classification from the final joint SAR model. These four compounds were clotrimazole, diltiazem, haloperidol, and sertraline. It remains to be seen whether these compounds were indeed misclassified by the SAR and FD-DLR models, or were they miscategorized during compilation of the training set (perhaps, due to erroneous or incomplete literature information). However, the following information was subsequently found in the literature:
(1) Clotrimazole is one of the most potent specific reversible inhibitors of CYP3A4
in vitro; it is even more potent than ketoconazole [
116]. However, unlike ketoconazole, its clinical potency is uncertain [
117], and its kinetics is unique
in vitro [
118], which suggests a uniqueness in the mechanism of its affinity to CYP3A4, perhaps, involving a distinctive binding modality different from the “mainstream” affine inhibitors;
(2) Diltiazem is an irreversible (mechanism-based) inactivator of CYP 3A4 [
119];
(3) Haloperidol inhibition potency is substrate-specific, ranging from potent (with nifedipine as substrate) to weak (with testosterone) and less than weak (with felodipine or simvastatin) [
120];
(4) Sertraline has been recently asserted as a weak inhibitor of CYP3A4 [
121].
It appears that all low-MW drugs misclassified by both DLR and SAR show variability in terms of CYP3A4 inhibition, which singles out their unique machine learning patterns from the “major” pattern of potent inhibitors. Perhaps, these minor patterns were on the one hand, distinct enough from the “mainstream” to deserve separate clusters in the SAR analysis, but on the other hand, statistically underrepresented in the training set to form well-resolved-mode-of-action based clusters. Therefore, they were segregated by the SAR model in the group of false-negative estimates.
For compounds in the low-MW band, multiple ligand binding could be thought as a putative molecular-biologic reason for distinctions between the minor- and major-type learning patterns. At multiple ligand binding, some of the molecules may be actual inhibitor(s) of the enzymatic catalysis, while others may carry a role of homo- or hetero-effectors that change the molecular basis of the affinity patterns of the actual inhibitors. Apart from several examples of such “molecular symbiosis” (e.g., ketoconazole molecules in the active site of 2V0M [
98]) little is known about the effectors. It is quite possible that the affinity patterns would be unique for each combination of multiple ligands. In this case, unlikely even a large database of CYP3A4 inhibitors would be representative of multiple discretized minority types that may be typical of CYP3A4 inhibitors in the low-MW band, which would mean the greatest challenge for both experimental (
in vitro or clinical) and computational methods; the smaller is the molecular size (and the larger is the active site), the more likely misclassification and miscategorization will take place.
2.6. Development of a Consensus Classifier and Its Application to an External Set of Compounds
The developed classifiers were applied to an external testing set of 120 known inhibitors of CYP3A4 [
122], which potency of inhibition has not been documented in the Merck Manual [
32]. The DLR, SDAR, and SAR methods identified 25, 34, and 29 compounds, respectively, as potent inhibitors of CYP3A4. Presuming, both the training and testing sets were drawn from the same general population, and using proportion priors of the training set, the obtained numbers were within the expected CI range of 24–43. DLR, SDAR, and SAR identified of the testing set 9, 23, and 13 potent inhibitors among the 89 low-MW-band compounds, and 16, 11, and 16 potent inhibitors in the high-MW band (31 compounds), respectively (
Table 5). Except for the low-MW-band-FD-DLR result, all other numbers were within the anticipated ranges of 10–25 and 9–20 for the low- and high-MW band, respectively.
For the FD-DLR model, the number of potent inhibitors in the low-MW band was slightly outside the calculated 95% confidence bounds on the mean. However, the direct one-tailed Z-test for two proportions, in which the calculated potent inhibitors in the low-MW band of the testing set (9/89) were gauged against the potent inhibitors observed in the low-MW band of the training set (15/82), suggested that the difference between the two proportion was insignificant at the 95% level (p > 0.0619), i.e., FD-DLR performed as it is supposed to on the low-MW band of the testing set. Comparison of proportions of true positive outcomes of the FD-DLR model (i.e., the calculated potent inhibitors) in the low-MW band using the testing and training sets produced a different result. The null hypothesis (9/89 = 1/82) was rejected at the 95% level (p < 6.65 × 10−3), and the alternative (9/89 > 1/82) was accepted. In the high-MW band, the test for proportions did not identify abnormalities in model performance using both the testing and training set data; the null hypothesis (16/31 = 13/39) was accepted at the 95% level (p > 0.0615). From these analyses it was concluded that FD-DLR did train appropriately on the training set, so that it could perform as expected in both the high- and low-MW bands, as suggested by the results of its application to the testing set. However, in the low-MW band of the training set it failed to identify a statistically significant number of potent inhibitors for an unknown reason, perhaps, because of a statistical fluctuation in the data.
Table 5.
External-test compounds classified as potent inhibitors (P) of CYP3A4 by DLR, SDAR, and SAR in the low- (a) and high-MW (b) bands.
Table 5.
External-test compounds classified as potent inhibitors (P) of CYP3A4 by DLR, SDAR, and SAR in the low- (a) and high-MW (b) bands.
| (a) | Compound * | FD-DLR | SDAR | SAR | (b) | Compound * | TD-DLR | SDAR | SAR |
|---|
| | tioconazole | P | P | P | | dalfopristin | P | P | P |
| | corticosterone | P | P | | | delapril | P | P | P |
| | ditiocarb sodium | P | P | | | gallopamil | P | P | P |
| | econazole | | P | P | | glipizide | P | P | P |
| | oltipraz | | P | P | | astemizole | P | | P |
| | piroxicam | P | P | | | calcium folinate | P | P | |
| | quercetin | | P | P | | dirithromycin | P | P | |
| | salbutamol | P | P | | | irinotecan | P | | P |
| | trimethoprim | | P | P | | lopinavir | P | | P |
| | troglitazone | | P | P | | midecamycin | P | | P |
| | almotriptan | | P | | | paclitaxel | P | P | |
| | bifonazole | | P | | | raloxifene | | P | P |
| | carvedilol | | P | | | reserpine | P | | P |
| | dihydralazine | | P | | | avasimibe | | | P |
| | dimethyl sulfoxide | P | | | | barnidipine | | P | |
| | disulfamide | | | P | | benidipine | P | | |
| | flutamide | | P | | | buprenorphine | | P | |
| | ipriflavone | | P | | | cerivastatin | | P | |
| | malathion | | P | | | efonidipine | | | P |
| | mequitazine | | P | | | flurithromycin | | | P |
| | mizolastine | P | | | | josamycin | | | P |
| | nilvadipine | P | | | | lercanidipine | | | P |
| | nimodipine | P | | | | mibefradil | P | | |
| | oxiconazole | | | P | | roxithromycin | P | | |
| | pantoprazole | | | P | | terfenadine | | | P |
| | papaverine | | | P | | vindesine | P | | |
| | pioglitazone | | | P | | * Confidence in compound classification as potent inhibitor of CYP3A4 is denoted by bold, regular and
italics font for probable, plausible, and uncertain consensus estimates, respectively. Probable and plausible estimates were taken as positive majority rules consensus outcomes for potent inhibition. |
| | prednisone | | P | | |
| | quinelorane | | P | | |
| | ranitidine | | | P | |
| | sertindole | | P | | |
| | sulpiride | | P | | |
| | theophylline | | | P | |
| | valdecoxib | | P | | |
A literature search suggested that of 14 low-MW inhibitors of the training set misclassified by DLR, four were mechanism-based inhibitors of CYP3A4 (cimetidine [
123,
124], diltiazem [
119], isoniazid [
121], and diclofenac [
125]); six were, in fact, either relatively weak inhibitors or inhibitors of questionable potency (fluconazole [
126,
127,
128,
129], metronidazole [
126,
130,
131], miconazole [
129], propofol [
32], sertraline [
132], and voriconazole [
133]); and for two of the inhibitors the experimental data were controversial (clotrimazole [
117,
118] and haloperidol [
120]). The literature on norfloxacin and doxycycline was scant, which prevented interpretation of classification/categorization of these compounds. Nevertheless, even changing categorization of the six “relatively weak inhibitors or inhibitors of questionable potency” from potent to weak (
i.e., using 9/82 and 27/121 in hypothesis testing for the fraction of potent inhibitors in the low-MW band and on the whole domain, respectively) did not change any of the reported above results. Thus, no systematic reason in DLR misclassification of the low-MW compounds of the training set was identified, although the docking method, in general, is expected to perform better on larger compounds [
134]. In this connection, the validity of classification of dimethyl sulfoxide (DMSO) as a potent inhibitor (
Table 5a) was intriguing. DMSO (MW = 78 Da) was among the smallest compounds in both the training and testing sets. Surprisingly, DMSO has been reported as a strong inhibitor, which inhibits testosterone 6b-hydroxylation by CYP3A4 in a concentration-dependent manner [
135]. On the other hand, the 1'-hydroxylation activity of midazolam, which is another standard laboratory substrate for CYP3A4, is only weakly inhibited by large amounts of DMSO [
135]. DMSO was classified as a potent inhibitor only by DLR. Therefore, it seems that different classifiers partially learned from different aspects of the minority type populations of the training set.
To increase confidence in classification, the classification methods developed in the present study were combined using a consensus approach. Several consensus strategies may apply to Boolean outcomes. They could be either of conjunction, disjunction, majority rules, percent agreement [
136], or even artificial intelligence [
60]. Conjunction and disjunction resulted, respectively, in five and 60 inhibitors of the testing set classified as potent. Both numbers were outside the expected CI range. The null hypotheses about proportions equality to the training set prior were rejected by the one-tailed Z-test test for two sample proportions at a more than 99.99% probability level.
Synthesis of results was carried out following the strategy of majority rules consensus. Using it, 23 inhibitors of the testing set were classified as potent (
Table 5). Similar numbers for the low- and high-MW bands were 10 and 13, respectively. All the numbers were within the expectancy range. A hypothesis about identity of the fractions of estimated potent inhibitors in the low- and high-MW bands was rejected with a 99.99% probability in favor of the alternative that the high-MW range was enriched with potent inhibitors. This result, obtained by using the estimated potent inhibitors of the testing set, was similar to one reported above for the actual potent inhibitors of the training set. This circumstance suggests that the synthetic consensus model accurately learned information that was available in the training set, so that even a subtle statistical attribute was carefully reproduced.
A percent agreement consensus strategy was applied to assign confidence levels to the classification results. If potency of inhibitor classification was in full agreement among the DLR, SDAR, and SAR methods, classification of the inhibitor as potent was regarded as a ‘probable’ outcome. If the agreement was less than that but more than 50%, the outcome was deemed ‘plausible’. Estimates with below than 50% agreement between the methods were considered ‘uncertain’.
Dalfopristin, delapril, gallopamil, glipizide, and tioconazole were classified by the consensus model as probable potent inhibitors, and 18 other inhibitors were classified as plausible potent inhibitors of CYP3A4. Among the latter, seven chemicals were classified as potent inhibitors by both DLR and SDAR, five chemicals by DLR and SAR, and six chemicals by SAR and SDAR; i.e., the frequencies of dual-model conjunction on the testing set of 120 compounds were similar.
A search revealed that about a third of the compounds attributed to the class of potent inhibitors have been described in the literature as potent inhibitors of CYP3A4. Two of the five probable potent inhibitors—dalfopristin, a Gram-positive antibiotic, and tioconazole, an antifungal imidazole—have been characterized in the literature as strong inhibitors of CYP3A4 [
137,
138]. Among the 18 plausible potent inhibitors of CYP3A4, potency information was found for lopinavir, oltipraz, quercetin, raloxifene, and troglitazone.
Lopinavir is a HIV reverse transcriptase inhibitor,
i.e., a drug from a class with many potent inhibitors of CYP3A4. It has also been reported as a strong inhibitor of CYP3A4 [
32,
139]. Quercetin is a plant flavanoid with anti-inflammatory properties. It has been described as a moderate-to-strong inhibitor of CYP3A4 [
140]. Troglitazone belongs to the glitazone family of drugs, which are used to treat diabetes. Oltipraz and raloxifene are multiple action drugs, although both are often used as chemo-preventive anti-cancer agents. Troglitazone, oltipraz, and raloxifene form reactive metabolites (during CYP3A4 metabolism) that have been shown to covalently bind to CYP3A4 [
141,
142,
143]. As mechanism-based inactivators, they may be considered potent inhibitors of CYP3A4. Interestingly, neither troglitazone nor oltipraz or raloxifene were classified as a potent inhibitor by DLR. These drugs corroborate a hypothesis that was formulated in the context of potent inhibitors of the training set misclassified by DLR (amprenavir, clarithromycin, delavirdine, and erythromycin). This hypothesis suggests that mechanism-based inactivators together with inhibitors, which affinity-based inhibition activity is confounded either by effector molecules or at a higher level of biochemical machinery (such as transcriptional induction), may be outside the domain of potent inhibitors recognized by DLR. So far, it appears that the docking method associates such inhibitors predominantly with weak potency of CYP3A4 inhibition.
Mechanism-based inhibitors, perhaps, can be modeled more accurately using inhibitor-structure-based methods, such as SDAR and SAR. Also, the LR part of the DLR model can be supplemented with inhibitor-structure-based QSAR descriptors, but that would be equivalent to using docking scores alongside structure-based descriptors in SDAR, SAR or other structure-activity methods. In any case, improvements in the machine classification of mechanism-based and other minority-type inhibitors would be possible only if they are sufficiently represented in the training set.
For the other 13 plausible potent inhibitors of CYP3A4 relevant information was not found. Thus, where experimental data were available, there was a fair correlation between the consensus estimates and experimental data. The proposed models may be useful in setting priorities for the experimental testing of drugs and chemicals for interactions with CYP3A4, for screening virtual libraries of compounds, and for interpreting HTS in vitro data and results of machine learning classifiers that rely on these data.