For the AD approaches discussed earlier, general rules to define thresholds are discussed in the literature except for distance-based approaches. Thresholds can be defined in several ways for the distance-based approaches, thus resulting in an ambiguity over selection of appropriate thresholds for this study. As a result, before an overall comparison of results with different AD approaches could be performed, thresholds for distance-based approaches had to be finalized.
To decide upon appropriate thresholds for distance-based approaches, several threshold defining strategies were implemented for the different distance measures considered in this study. All these strategies discussed below required calculating distances of training compounds from their centroid. To evaluate further possibilities, the study was extended implementing these strategies however considering average distance of each training compound from their first 5 nearest neighbors. Model statistics were recorded each time and the most appropriate distance based thresholds were then selected from above mentioned results for all distance measures considered in this study. Until this point, all the four categories of AD approaches were associated with appropriate thresholds and finally subjected to overall comparison of results.
The results were tabulated informing the model’s statistics for each AD approach on the compounds considered inside the applicability domain using the following parameters:
Where
![]()
is the predicted value for the
i-th compound and
![]()
its experimental value;
nTR is the number of compounds in the training set and
nEXT the number in the test set;
![]()
is the mean response of the training set. Moreover, in order to somehow quantify the role of the compounds considered inside and outside AD,
![]()
was defined by the following equation:
where
RMSEPOUT is the root mean square error in prediction for the test compounds outside AD, while
RMSEPIN is the root mean square error in prediction for the test compounds inside AD. Negative values indicate that the compounds detected outside AD are predicted better than the compounds inside AD, thus highlighting some possible drawbacks in the definition of interpolation space. On the contrary, positive values of
![]()
indicate a reliable partition for the compounds detected as inside and outside AD.
Multi Dimensional Scaling (MDS) was used to visualize the relative position of test compounds with respect to the training space. MDS enables the representation of p-dimensional data by means of a 2D plot. The implementation allowed a better understanding of how the interpolation space was characterized and if the compounds outside the AD were more concentrated around the training set extremities or not.
3.1. Defining Thresholds for Distance-Based AD Approaches
Initially, the distances of training compounds from their centroid were calculated and from this resulting vector, the maximum and average distance value (
maxdist and
d) were derived. The first threshold strategy defined the AD considering
maxdist as threshold [
2]. The second and third strategies considered twice and thrice the values of
d as their thresholds, respectively. The fourth strategy performed percentile approach on the above derived vector of distances sorted in ascending order and the distance value corresponding to 95 percentile (
p95) was chosen as the threshold. Finally, the fifth strategy (
dsz) considered average distance
d as well as the standard deviation from the distance vector (
std) and the threshold was then defined as
![]()
, where
z is the arbitrary parameter and is set to 0.5 as default value [
26].
For all the cases, distance of a test compound from the training set centroid is compared with the defined threshold. If the distance of this test compound from the training set centroid is less than or equal to the threshold value, it is considered inside the AD. Thus, these approaches differ the way in which thresholds are derived, however the principle behind considering a given test compound to be inside or outside AD remains the same. Results derived with all the four threshold strategies are shown in
Table 2 for CAESAR Model 2 considering different distance measures.
Table 2.
Statistics for CAESAR Model 2 implementing distance-based approaches with different thresholds. For the acronyms maxdist, d, p95, dsz, and ΔRMSEP, refer to text.
Table 2.
Statistics for CAESAR Model 2 implementing distance-based approaches with different thresholds. For the acronyms maxdist, d, p95, dsz, and ΔRMSEP, refer to text.
| Approach | Thresholds | Compounds outside the AD | Q2 | ΔRMSEP |
|---|
| CAESAR | EPI Suite | CAESAR | EPI Suite | CAESAR | EPI Suite |
|---|
| out of 95 (%) | out of 108 (%) |
|---|
| Euclidean (maxdist) | 0.942 | 0 (0.0) | 4 (3.7) | 0.797 | 0.703 | - | 1.436 |
| Euclidean (3*d) | 1.018 | 0 (0.0) | 1 (0.9) | 0.797 | 0.676 | - | 0 |
| Euclidean (2*d) | 0.679 | 7 (7.4) | 12 (11.1) | 0.802 | 0.718 | 0.146 | 0.753 |
| Euclidean (p95) | 0.663 | 7 (7.4) | 12 (11.1) | 0.802 | 0.718 | 0.146 | 0.753 |
| Euclidean (dsz) | 0.423 | 15 (15.8) | 36 (33.3) | 0.791 | 0.741 | −0.064 | 0.381 |
| CityBlock (maxdist) | 1.472 | 0 (0.0) | 1 (0.9) | 0.797 | 0.676 | - | 2.713 |
| CityBlock (3*d) | 1.863 | 0 (0.0) | 0 (0.0) | 0.797 | 0.616 | - | - |
| CityBlock (2*d) | 1.242 | 3 (3.1) | 6 (5.5) | 0.804 | 0.699 | 0.267 | −1.049 |
| CityBlock (p95) | 1.084 | 8 (8.4) | 11 (10.1) | 0.801 | 0.705 | 0.068 | 0.717 |
| CityBlock (dsz) | 0.748 | 18 (18.9) | 38 (35.1) | 0.786 | 0.739 | −0.093 | 0.361 |
| Mahalanobis (maxdist) | 6.614 | 0 (0.0) | 0 (0.0) | 0.797 | 0.616 | - | - |
| Mahalanobis (3*d) | 6.027 | 0 (0.0) | 0 (0.0) | 0.797 | 0.616 | - | - |
| Mahalanobis (2*d) | 4.018 | 6 (6.3) | 5 (4.6) | 0.791 | 0.624 | −0.174 | 0.162 |
| Mahalanobis (p95) | 4.034 | 6 (6.3) | 5 (4.6) | 0.791 | 0.624 | −0.174 | 0.162 |
| Mahalanobis (dsz) | 2.497 | 21 (22.1) | 27 (25.0) | 0.778 | 0.706 | −0.138 | 0.354 |
No test compounds emerged outside the AD with first two strategies considering CAESAR test set, due to the higher threshold values; however, comparing the model statistics with the other approaches, this probably implies some possible drawbacks of these strategies in defining the interpolation space. Comparable results were derived considering the third and fourth strategies which imply the thresholds corresponding to twice the value of
d and that corresponding to 95 percentile converged significantly for both the test sets. Model statistics improved in most of the cases, thus reflecting a reasonable choice of compounds outside AD. The final strategy taking into account also the standard deviation provided the maximum number of test compounds outside the AD, however with no (or significant) improvement to the model statistics for both the test sets. A similar pattern was observed for compounds considered outside the AD with both the test sets, however, with respect to the number of compounds considered outside the AD with different threshold strategies, the values were comparatively higher with EPI Suite test set. This reflected how diverse both the test sets were in terms of their compounds and indicating that the CAESAR test set comprised of compounds more similar to the training data as compared to the other test set. None of the strategies performed well with Mahalanobis distance measure for CAESAR test set resulting in a negative
ΔRMSEP. Similar pattern for compounds outside AD was observed for CAESAR model 5 and the corresponding results can be found in
Table 3.
Table 3.
Statistics for CAESAR Model 5 implementing distance-based approaches with different thresholds. Maxdist: Maximum distance between training compounds and centroid of the training set; d: Average distance of training compounds from their mean; ΔRMSEP: Difference between RMSEP for compounds outside and inside the AD.
Table 3.
Statistics for CAESAR Model 5 implementing distance-based approaches with different thresholds. Maxdist: Maximum distance between training compounds and centroid of the training set; d: Average distance of training compounds from their mean; ΔRMSEP: Difference between RMSEP for compounds outside and inside the AD.
| Approach | Thresholds | Compounds outside the AD | Q2 | ΔRMSEP |
|---|
| CAESAR | EPI Suite | CAESAR | EPI Suite | CAESAR | EPI Suite |
|---|
| out of 95 (%) | out of 108 (%) |
|---|
| Euclidean (maxdist) | 0.942 | 0 (0.0) | 2 (1.8) | 0.774 | 0.647 | - | 0.598 |
| Euclidean (3*d) | 0.958 | 0 (0.0) | 2 (1.8) | 0.774 | 0.647 | - | 0.598 |
| Euclidean (2* d) | 0.639 | 3 (3.1) | 9 (8.3) | 0.783 | 0.665 | 0.329 | 0.354 |
| Euclidean (p95) | 0.614 | 4 (4.2) | 11 (10.1) | 0.783 | 0.673 | 0.266 | 0.367 |
| Euclidean (dsz) | 0.393 | 23 (24.2) | 32 (29.6) | 0.753 | 0.646 | −0.128 | 0.044 |
| CityBlock (maxdist) | 1.472 | 0 (0.0) | 2 (1.8) | 0.774 | 0.647 | - | 0.598 |
| CityBlock (3*d) | 1.791 | 0 (0.0) | 1 (0.9) | 0.774 | 0.634 | - | 0.037 |
| CityBlock (2*d) | 1.194 | 1 (1.0) | 5 (4.6) | 0.772 | 0.657 | −0.417 | 0.457 |
| CityBlock (p95) | 1.085 | 4 (4.2) | 11 (10.1) | 0.767 | 0.665 | 0.309 | 0.308 |
| CityBlock (dsz) | 0.723 | 21 (22.1) | 32 (29.6) | 0.751 | 0.639 | −0.156 | 0.022 |
| Mahalanobis (maxdist) | 6.957 | 0 (0.0) | 0 (0.0) | 0.774 | 0.633 | - | - |
| Mahalanobis (3*d) | 6.121 | 0 (0.0) | 0 (0.0) | 0.774 | 0.633 | - | - |
| Mahalanobis (2*d) | 4.081 | 3 (3.1) | 6 (5.5) | 0.767 | 0.621 | −0.445 | −0.275 |
| Mahalanobis (p95) | 3.859 | 5 (5.2) | 6 (5.5) | 0.764 | 0.621 | −0.327 | −0.275 |
| Mahalanobis (dsz) | 2.495 | 23 (24.2) | 18 (16.6) | 0.760 | 0.637 | −0.081 | 0.035 |
The study was further extended by implementing the above mentioned threshold strategies for each distance measure, but considering average distance of each training compound from its first 5 nearest neighbors. Given a
n by
n distance matrix where
n is total number of training compounds, in all the cases, average distance of each training sample from its first five nearest training neighbors is found. Later, the gross average is derived from these average distance values which will be denoted henceforth as
D. In the first and second case, twice and thrice the value of
D is considered as threshold, respectively. For the third case, percentile approach discussed earlier in potential density distribution methods, is applied on the sorted average distances of all training compounds (used to calculate
D) and the value corresponding to 95 percentile (
p95) is considered as threshold [
27]. For the last strategy (
DSZ), besides calculating the gross average distance
D from the first five nearest neighbors, also the standard deviation (
Std) is calculated on the average distances. Finally, the threshold is defined as
![]()
, where
z is the arbitrary parameter and is set to 0.5 as default value [
26]. For all the cases, average distance of a test compound from its first five nearest neighbors in the training set is compared with the defined threshold. If the average distance for this test compound is less than or equal to the threshold value, it is considered inside the AD.
Results derived with all the four threshold strategies are shown in
Table 4 and
Table 5 for CAESAR Model 2 and Model 5, respectively, considering different distance measures.
Table 4.
Statistics for CAESAR Model 2 implementing different 5NN based threshold strategies. For the acronyms D, p95, DSZ, and ΔRMSEP, refer to text.
Table 4.
Statistics for CAESAR Model 2 implementing different 5NN based threshold strategies. For the acronyms D, p95, DSZ, and ΔRMSEP, refer to text.
| Approach | Thresholds | Compounds outside the AD | Q2 | ΔRMSEP |
|---|
| CAESAR | EPI Suite | CAESAR | EPI Suite | CAESAR | EPI Suite |
|---|
| out of 95(%) | out of 108(%) |
|---|
| Euclidean (3*D) | 1.522 | 2 (2.1) | 1 (0.9) | 0.804 | 0.676 | 0.394 | 2.713 |
| Euclidean (2* D) | 1.015 | 9 (9.5) | 16 (14.8) | 0.795 | 0.750 | −0.037 | 0.765 |
| Euclidean (p95) | 1.164 | 8 (8.4) | 13 (12.0) | 0.797 | 0.745 | 0.859 | 1.342 |
| Euclidean (DSZ) | 0.693 | 14 (14.7) | 31 (28.7) | 0.787 | 0.767 | −0.113 | 0.517 |
| CityBlock (3*D) | 2.371 | 4 (4.2) | 5 (4.6) | 0.803 | 0.679 | 0.187 | 0.968 |
| CityBlock (2*D) | 1.581 | 10 (10.5) | 18 (16.7) | 0.794 | 0.742 | −0.042 | 0.664 |
| CityBlock (p95) | 1.918 | 7 (7.4) | 11 (10.2) | 0.799 | 0.741 | 0.034 | 0.944 |
| CityBlock (DSZ) | 1.083 | 16 (16.8) | 27 (25.0) | 0.801 | 0.731 | 0.037 | 0.446 |
| Mahalanobis (3*D) | 1.718 | 3 (3.2) | 4 (3.7) | 0.803 | 0.628 | 0.221 | 0.295 |
| Mahalanobis (2*D) | 1.145 | 9 (9.5) | 18 (16.7) | 0.794 | 0.748 | −0.045 | 0.691 |
| Mahalanobis (p95) | 1.388 | 6 (6.3) | 11 (10.2) | 0.801 | 0.735 | 0.908 | 1.183 |
| Mahalanobis (DSZ) | 0.786 | 19 (20.0) | 29 (26.9) | 0.795 | 0.745 | −0.019 | 0.470 |
Table 5.
Statistics for CAESAR Model 5 implementing different 5NN based threshold strategies. D: The gross average distance of training set compounds from their 5NN; ΔRMSEP: Difference between RMSEP for compounds outside and inside the AD.
Table 5.
Statistics for CAESAR Model 5 implementing different 5NN based threshold strategies. D: The gross average distance of training set compounds from their 5NN; ΔRMSEP: Difference between RMSEP for compounds outside and inside the AD.
| Approach | Thresholds | Compounds outside the AD | Q2 | ΔRMSEP |
|---|
| CAESAR | EPI Suite | CAESAR | EPI Suite | CAESAR | EPI Suite |
|---|
| out of 95 (%) | out of 108 (%) |
|---|
| Euclidean (3*D) | 1.681 | 0 (0.0) | 2 (2.8) | 0.774 | 0.644 | - | 0.364 |
| Euclidean (2* D) | 1.121 | 7 (7.4) | 13 (12.0) | 0.781 | 0.690 | 0.130 | 0.437 |
| Euclidean (p95) | 1.331 | 1 (1.0) | 7 (6.5) | 0.772 | 0.656 | −0.331 | 0.126 |
| Euclidean (DSZ) | 0.782 | 18 (18.9) | 22 (20.4) | 0.784 | 0.743 | 0.072 | 0.512 |
| CityBlock (3*D) | 2.684 | 1 (1.1) | 5 (4.6) | 0.772 | 0.648 | −0.456 | 0.307 |
| CityBlock (2*D) | 1.789 | 9 (9.5) | 12 (11.1) | 0.788 | 0.690 | 0.190 | 0.462 |
| CityBlock (p95) | 2.302 | 2 (2.1) | 8 (7.4) | 0.785 | 0.657 | 0.529 | 0.310 |
| CityBlock (DSZ) | 1.232 | 19 (20.0) | 30 (27.8) | 0.782 | 0.753 | 0.055 | 0.433 |
| Mahalanobis (3*D) | 2.006 | 0 (0.0) | 4 (3.7) | 0.774 | 0.624 | −0.326 | −0.149 |
| Mahalanobis (2*D) | 1.337 | 6 (6.3) | 10 (9.3) | 0.779 | 0.683 | 0.115 | 0.482 |
| Mahalanobis (p95) | 1.668 | 2 (2.1) | 6 (5.6) | 0.771 | 0.631 | −0.193 | −0.043 |
| Mahalanobis (DSZ) | 0.933 | 21 (22.1) | 24 (22.2) | 0.792 | 0.713 | 0.110 | 0.356 |
As obvious from
Table 4, lowest number of test compounds were considered outside AD with the strategy considering 3*
D as threshold. When the thresholds were lowered to 2*
D, several other test compounds were considered outside the AD, however, the model performed worse with CAESAR test set. Same pattern was observed considering EPI Suite test set however, without lowering the model statistics and the number of test compounds outside the AD were comparatively higher in this case. Strategy taking into account also the standard deviation, was associated with the lowest threshold value thus, restricting the AD. Large number of compounds were considered outside the AD without improving the model statistics. The percentile approach considered reasonable number of test compounds outside AD without any major impact on the model statistics and the results were comparatively better with EPI Suite test set. Similar results and considerations were derived with CAESAR model 5.
The next and the final step was to finalize upon one threshold strategy for distance-based approaches. All the four above mentioned strategies behaved differently depending on the distance measure considered. A strategy that improved the model statistics for one distance measure couldn’t have similar impact for another distance measure. This observation couldn’t allow an easy interpretation towards finalizing upon one strategy. However, considering improved model statistics with reasonable number of test compounds considered outside the AD, the percentile approach was a preferred choice. Moreover, when the methodologies for different AD methods were described earlier, Probability Density Distribution method reflected the statistical significance of defining percentiles. These considerations concluded finalizing upon the percentile approach for overall comparison of the results. This approach was implemented initially considering the distance of training compounds from their centroid (p95) and in the later case, based on average distance of training compounds from their 5 nearest neighbors (p95). Both the considerations were different in defining the interpolation space and thus, resulted in different number of compounds outside the AD with the same distance measure. Information derived in both the cases was significant and thus was retained for the overall comparison of the results.
3.2. Overall Comparisons
The distance-based approaches were then compared with other previously discussed AD approaches, considering the both CAESAR (95 compounds) and EPI suite (108 compounds) test sets. The results are summarized in
Table 6 and
Table 7 for CAESAR Model 2 and Model 5, respectively.
As shown in
Table 6, by performing PCA analysis along with Bounding Box approach on Model 2, two test compounds were considered outside the AD. Convex Hull and Probability Density approach led to maximum number of test compounds outside the AD, thus decreasing the generalization ability of the models.
p95 approach lowered the model statistics for Mahalanobis distance measure.
Q2 slightly lowered for Convex Hull that considered several test compounds outside the AD. On the other hand, model statistics improved for Probability Density Distribution approach which was associated with the maximum number of test compounds outside the AD (42.6%). As a general remark, the model statistics improved for several approaches with increase in number of test compounds considered outside the AD. Since the CAESAR test set comprised compounds more similar to the training set, not many test compounds emerged outside the AD; however, the EPI suite test set is comparatively different from the training data and thus considerably more compounds were outside the AD by different approaches.
ΔRMSEP remained positive considering most of the AD approaches. Similar pattern for compounds outside the AD was derived for CAESAR model 5 and the corresponding results are reported in
Table 7.
Table 6.
Statistics for CAESAR Model 2 applied to CAESAR and EPI Suite test sets for different AD approaches.
Table 6.
Statistics for CAESAR Model 2 applied to CAESAR and EPI Suite test sets for different AD approaches.
| Approach | Compounds outside the AD | Q2 | ΔRMSEP |
|---|
| CAESAR | EPI Suite | CAESAR | EPI Suite | CAESAR | EPI Suite |
|---|
| out of 95 (%) | out of 108 (%) |
|---|
| Euclidean Dist. (p95) | 7 (7.4) | 12 (11.1) | 0.802 | 0.718 | 0.146 | 0.753 |
| City Block Dist. (p95) | 8 (8.4) | 11 (10.1) | 0.801 | 0.705 | 0.068 | 0.717 |
| Mahalanobis Dist. (p95) | 6 (6.3) | 5 (4.6) | 0.791 | 0.624 | −0.174 | 0.162 |
| 5NN-Euclidean Dist. (p95) | 8 (8.4) | 13 (12.0) | 0.797 | 0.745 | 0.859 | 1.342 |
| 5NN-CityBlock Dist. (p95) | 7 (7.4) | 11 (10.2) | 0.799 | 0.741 | 0.034 | 0.944 |
| 5NN-Mahalanobis Dist. (p95) | 6 (6.3) | 11 (10.2) | 0.801 | 0.735 | 0.908 | 1.183 |
| Bounding Box | 0 (0.0) | 2 (1.8) | 0.797 | 0.678 | - | 1.798 |
| PCA Bounding Box | 2 (2.1) | 3 (2.8) | 0.804 | 0.688 | 0.371 | 1.533 |
| Convex Hull | 22 (23.2) | 31 (28.7) | 0.789 | 0.721 | −0.052 | 0.368 |
| Potential Function | 29 (30.5) | 46 (42.6) | 0.831 | 0.766 | 0.156 | 0.374 |
Table 7.
Statistics for CAESAR Model 5 applied to CAESAR and EPI Suite test sets for different AD approaches.
Table 7.
Statistics for CAESAR Model 5 applied to CAESAR and EPI Suite test sets for different AD approaches.
| Approach | Compounds outside the AD | Q2 | ΔRMSEP |
|---|
| CAESAR | EPI Suite | CAESAR | EPI Suite | CAESAR | EPI Suite |
|---|
| out of 95 (%) | out of 108 (%) |
|---|
| Euclidean Dist. (p95) | 4 (4.2) | 11 (10.1) | 0.783 | 0.673 | 0.266 | 0.367 |
| City Block Dist. (p95) | 4 (4.2) | 11 (10.1) | 0.767 | 0.665 | 0.309 | 0.308 |
| Mahalanobis Dist. (p95) | 5 (5.2) | 6 (5.5) | 0.764 | 0.621 | −0.327 | −0.275 |
| 5NN-Euclidean Dist. (p95) | 1 (1.0) | 7 (6.5) | 0.772 | 0.656 | −0.331 | 0.126 |
| 5NN-CityBlock Dist. (p95) | 2 (2.1) | 8 (7.4) | 0.785 | 0.657 | 0.529 | 0.310 |
| 5NN-Mahalanobis Dist. (p95) | 2 (2.1) | 6 (5.6) | 0.771 | 0.631 | −0.193 | −0.043 |
| Bounding Box | 0 (0.0) | 1 (0.9) | 0.774 | 0.634 | - | 0.037 |
| PCA Bounding Box | 0 (0.0) | 2 (1.8) | 0.774 | 0.634 | - | 0.021 |
| Convex Hull | 16 (16.8) | 21 (19.4) | 0.780 | 0.643 | 0.049 | 0.051 |
| Potential Function | 28 (29.5) | 47 (43.5) | 0.787 | 0.813 | 0.062 | 0.455 |
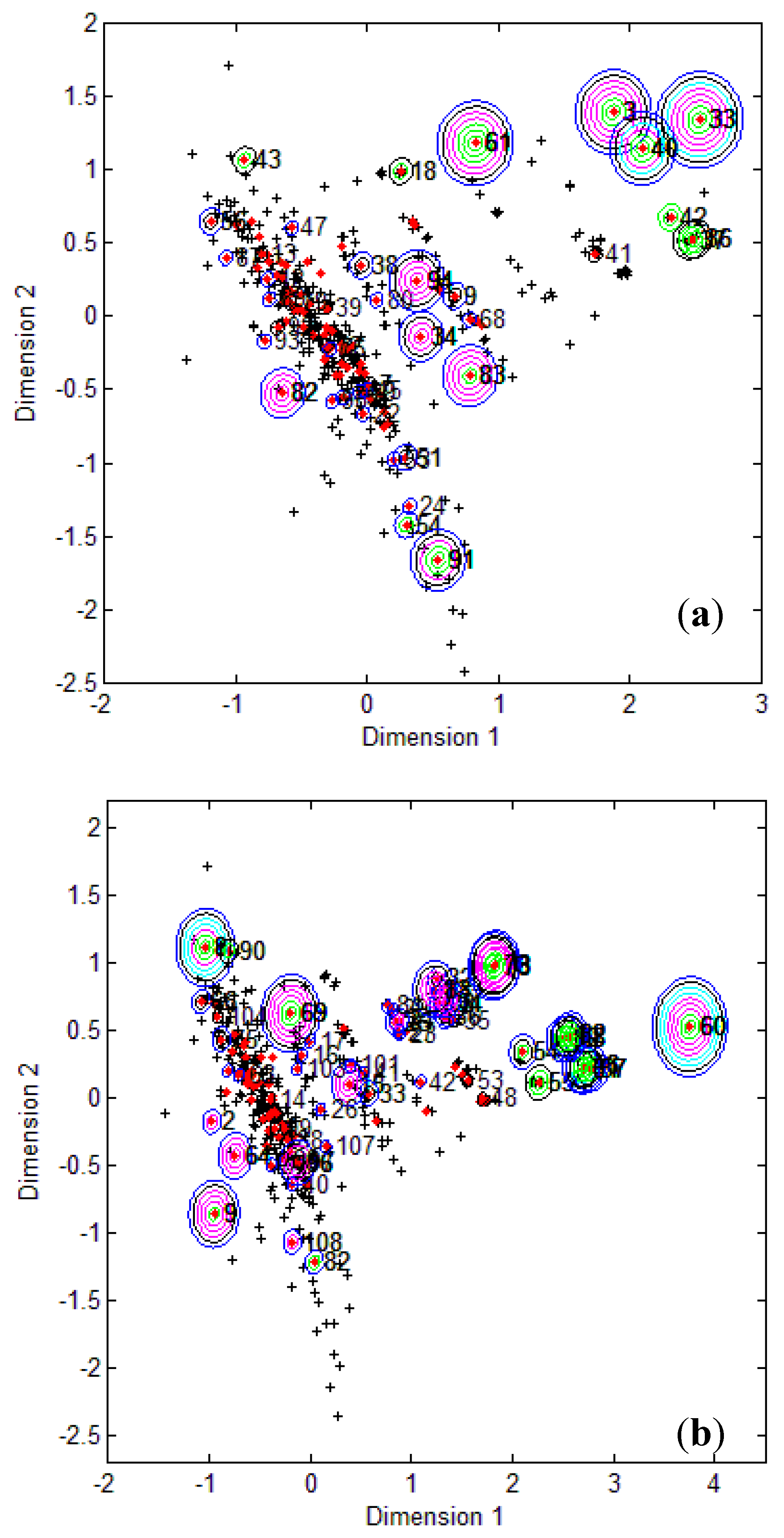
To visualize where test set compounds were located with respect to the training compounds, multidimensional scaling (MDS) was performed. This enabled the representation of 5 dimensional data (the molecular descriptors defining the CAESAR models) by means of a two dimensional plot.
From the MDS plots in
Figure 1, it is clear that several test compounds that were localized towards the extremities of training set were considered outside the AD with most of the approaches. For example, CAESAR test compound 33 and EPI Suite test compound 60 were considered outside on the basis of 7 and 9 AD approaches, respectively. However, there were several compounds that were quite close to the training space but still falling outside the AD, especially with Convex Hull and Probability Density approaches (for example, CAESAR test compound 38 and EPI Suite test compound 33). Since the internal empty regions within chemical space cannot be easily detected and correlation between descriptors cannot be explained with Bounding Box, this approach failed to consider any test compound outside the AD. When the same approach was implemented on this dataset after PCA analysis, the correlation between descriptors was taken into account and as a result, two compounds from the test set were considered outside the AD. With respect to the EPI Suite test set, the MDS plots showed how most of test compounds outside the AD were lying in the training set extremities and were almost the same for different AD approaches. Those compounds were further more distant from training set than in the CAESAR test set. Similar results were derived for CAESAR model 5 and the corresponding plots are shown in
Figure 2.
Figure 1.
CAESAR test set (
a) and Epi Suite test set (
b) projected in the training space of Model 2. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
Figure 1.
CAESAR test set (
a) and Epi Suite test set (
b) projected in the training space of Model 2. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
Figure 2.
CAESAR test set (
a) and Epi Suite test set (
b) projected in the training space of Model 5. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
Figure 2.
CAESAR test set (
a) and Epi Suite test set (
b) projected in the training space of Model 5. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
It was observed for both the CAESAR models that some compounds very close to the training compounds were considered outside the AD while others lying further were considered inside it. This could be explained by the fact that most of the implemented approaches considered only interpolation by simply excluding all test compounds in the extremities and including all those surrounded by training set compounds even if they are situated within empty regions of the chemical space.
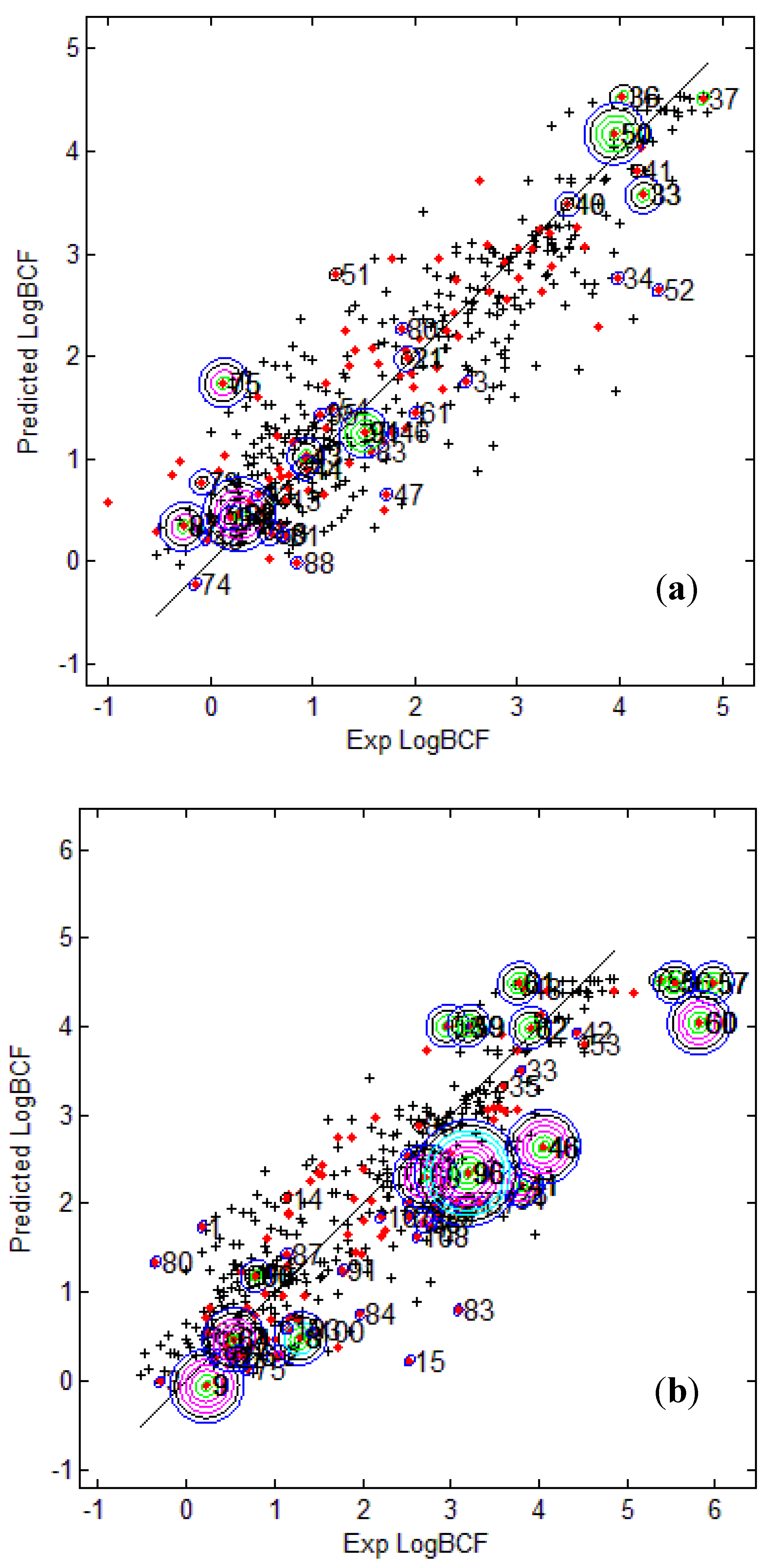
Figure 3 provides the calculated logBCF values from the CAESAR Model 2 plotted against the experimental log BCF values (Exp logBCF). It can be noted that several test compounds not so reliably predicted were considered outside the AD. On the other hand, well predicted test compounds like 34 in CAESAR test set and 59 in EPI Suite test set were considered outside by 2 and 5 AD approaches respectively. This indicates that the strategy used by different AD approaches might have considered some well predicted compounds outside the AD, thus affecting the model statistics. As seen earlier in
Table 6 and
Table 7, Convex Hull and Probability Density Distribution approaches had considerable number of test compounds outside the AD; however, both the approaches differed significantly with respect to the model statistics. The results corresponding to CAESAR model 5 are plotted in
Figure 4.
Figure 3.
Predicted Vs observed log BCF values for CAESAR test set (
a) and Epi Suite test set (
b) with Model 2. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
Figure 3.
Predicted Vs observed log BCF values for CAESAR test set (
a) and Epi Suite test set (
b) with Model 2. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
Figure 4.
Predicted Vs observed log BCF values for CAESAR test set (
a) and Epi Suite test set (
b) with Model 5. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
Figure 4.
Predicted Vs observed log BCF values for CAESAR test set (
a) and Epi Suite test set (
b) with Model 5. Training set (+); test set (
![]()
); compounds outside the AD with different approaches; distance based
p95 (
![]()
), distance based 5NN (
![]()
), Bound. Box and PCA Bound. Box (
![]()
), Conv. Hull (○), Pot. Funct. (
![]()
).
The plots indicate that several test compounds unreliably predicted were localized on the extremities of the training space and considered outside the AD while several well predicted test compounds were also considered outside with different approaches. This observation holds true for both the test sets however, the number of test compounds considered outside the AD were considerably higher for EPI Suite test set.
Figure 3b shows that the three compounds 56, 57 and 60 considered outside the AD by several approaches were underestimated, and thus the model statistics highly improved with AD approaches not considering them within the domain of applicability.
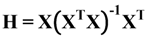

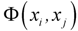 is the potential induced on xj by xi and width of the curve is defined by smoothing parameter s. The cut off value associated with Gaussian potential functions, namely fp, can be calculated by methods based on sample percentile [18]:
is the potential induced on xj by xi and width of the curve is defined by smoothing parameter s. The cut off value associated with Gaussian potential functions, namely fp, can be calculated by methods based on sample percentile [18]:
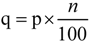 , where p is the percentile value of probability density, n is the number of compounds in the training set and j is the nearest integer value of q. Test compounds with potential function values lower than this threshold are considered outside the AD.
, where p is the percentile value of probability density, n is the number of compounds in the training set and j is the nearest integer value of q. Test compounds with potential function values lower than this threshold are considered outside the AD.
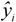 is the predicted value for the i-th compound and
is the predicted value for the i-th compound and 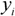 its experimental value; nTR is the number of compounds in the training set and nEXT the number in the test set;
its experimental value; nTR is the number of compounds in the training set and nEXT the number in the test set; 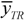 is the mean response of the training set. Moreover, in order to somehow quantify the role of the compounds considered inside and outside AD,
is the mean response of the training set. Moreover, in order to somehow quantify the role of the compounds considered inside and outside AD, 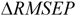 was defined by the following equation:
was defined by the following equation: 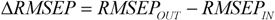
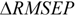 indicate a reliable partition for the compounds detected as inside and outside AD.
indicate a reliable partition for the compounds detected as inside and outside AD. , where z is the arbitrary parameter and is set to 0.5 as default value [26].
, where z is the arbitrary parameter and is set to 0.5 as default value [26]. 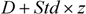 , where z is the arbitrary parameter and is set to 0.5 as default value [26]. For all the cases, average distance of a test compound from its first five nearest neighbors in the training set is compared with the defined threshold. If the average distance for this test compound is less than or equal to the threshold value, it is considered inside the AD.
, where z is the arbitrary parameter and is set to 0.5 as default value [26]. For all the cases, average distance of a test compound from its first five nearest neighbors in the training set is compared with the defined threshold. If the average distance for this test compound is less than or equal to the threshold value, it is considered inside the AD. ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).
 ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).
 ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).
 ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).
 ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).
 ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).
 ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).
 ); compounds outside the AD with different approaches; distance based p95 (
); compounds outside the AD with different approaches; distance based p95 (  ), distance based 5NN (
), distance based 5NN (  ), Bound. Box and PCA Bound. Box (
), Bound. Box and PCA Bound. Box (  ), Conv. Hull (○), Pot. Funct. (
), Conv. Hull (○), Pot. Funct. (  ).
).