Technique to Solve Linear Fractional Differential Equations Using B-Polynomials Bases
Abstract
:1. Introduction
2. Caputo’s Fractional Differential-Order Operator
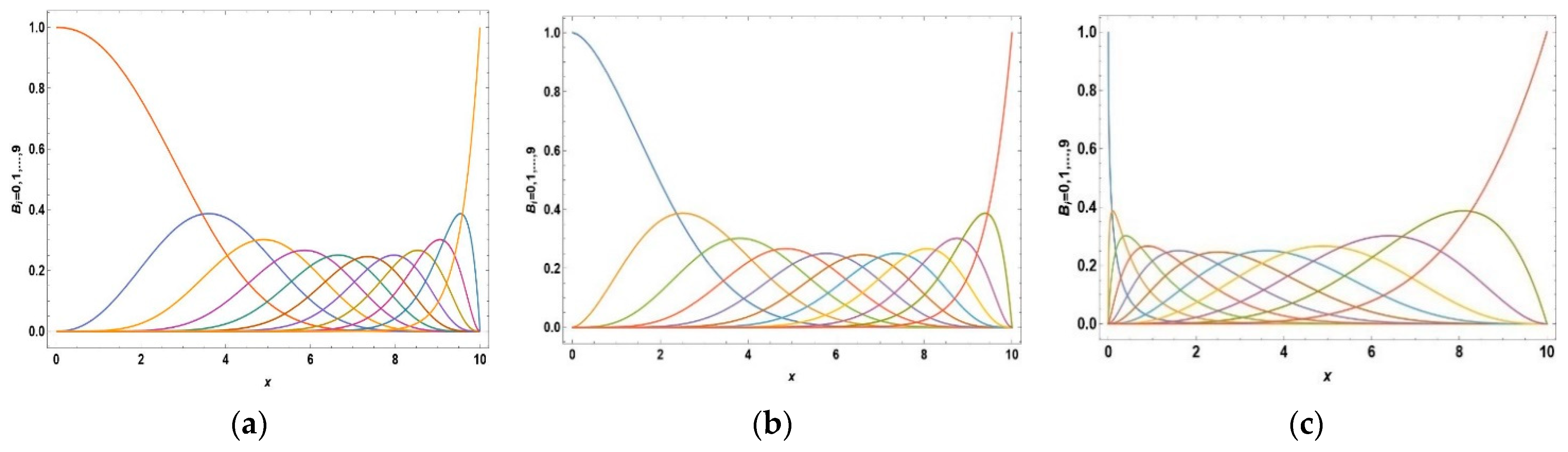
3. Fractional-Order B-Poly Basis
4. Technique for Approximating Solutions
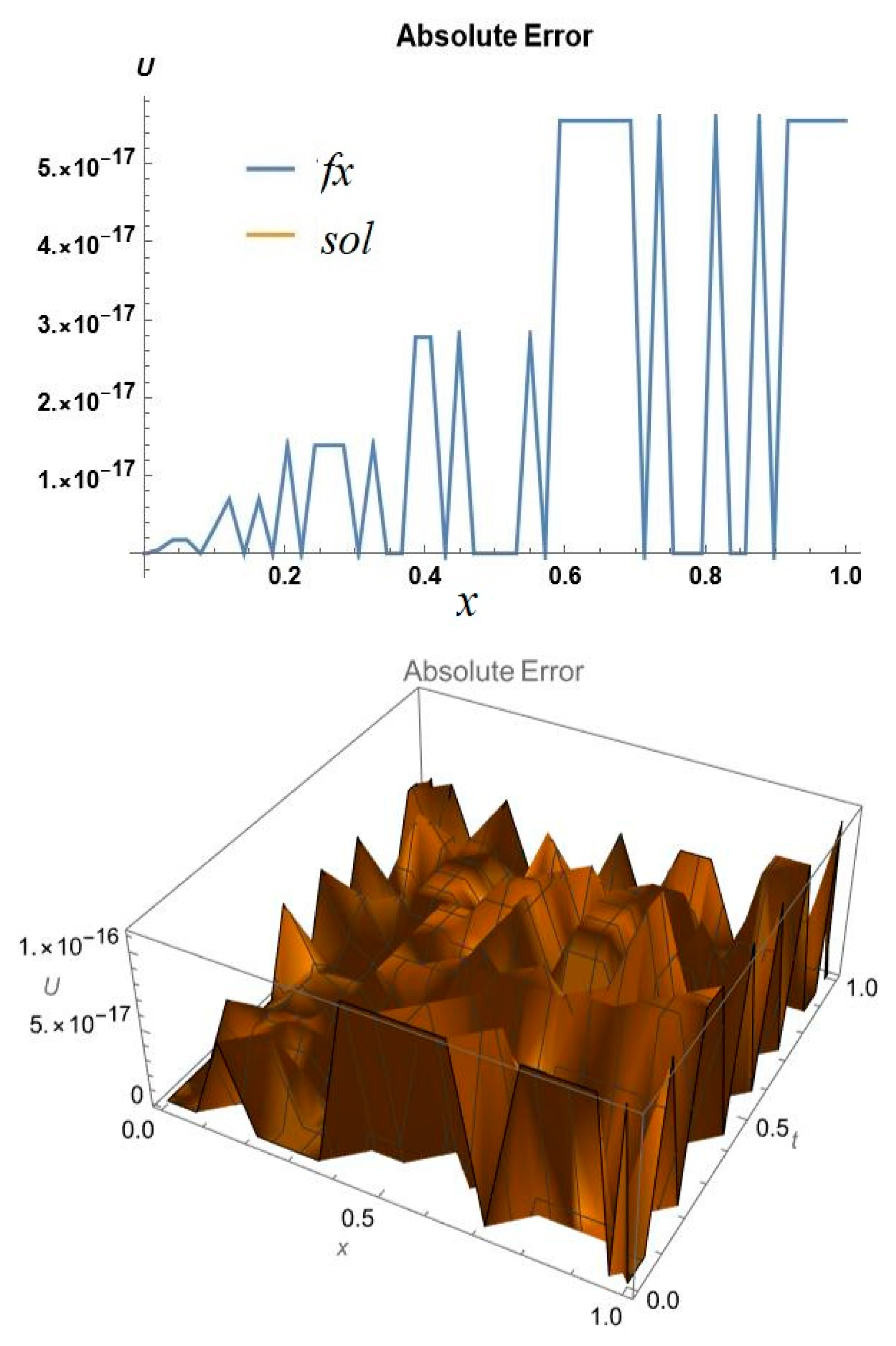
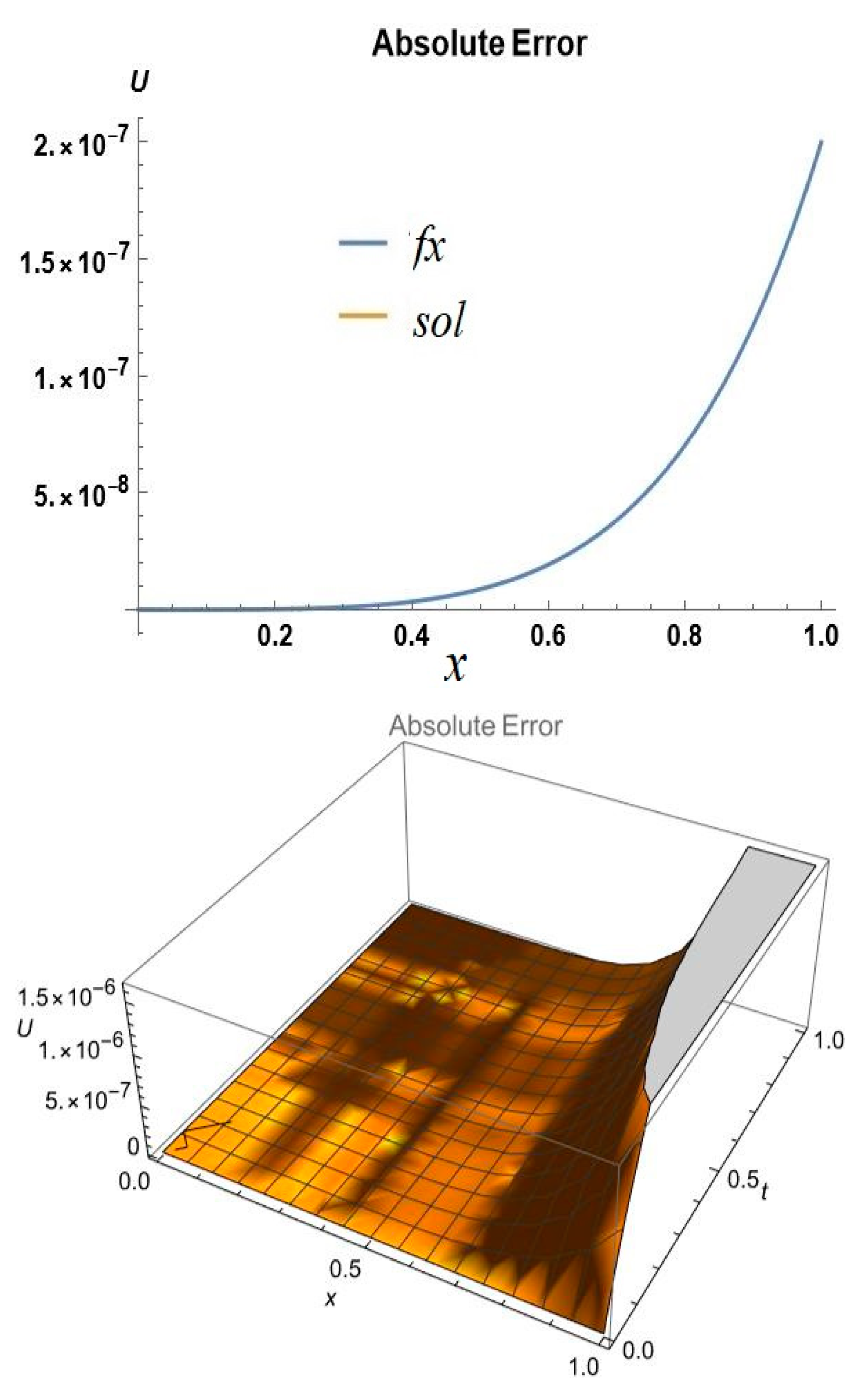
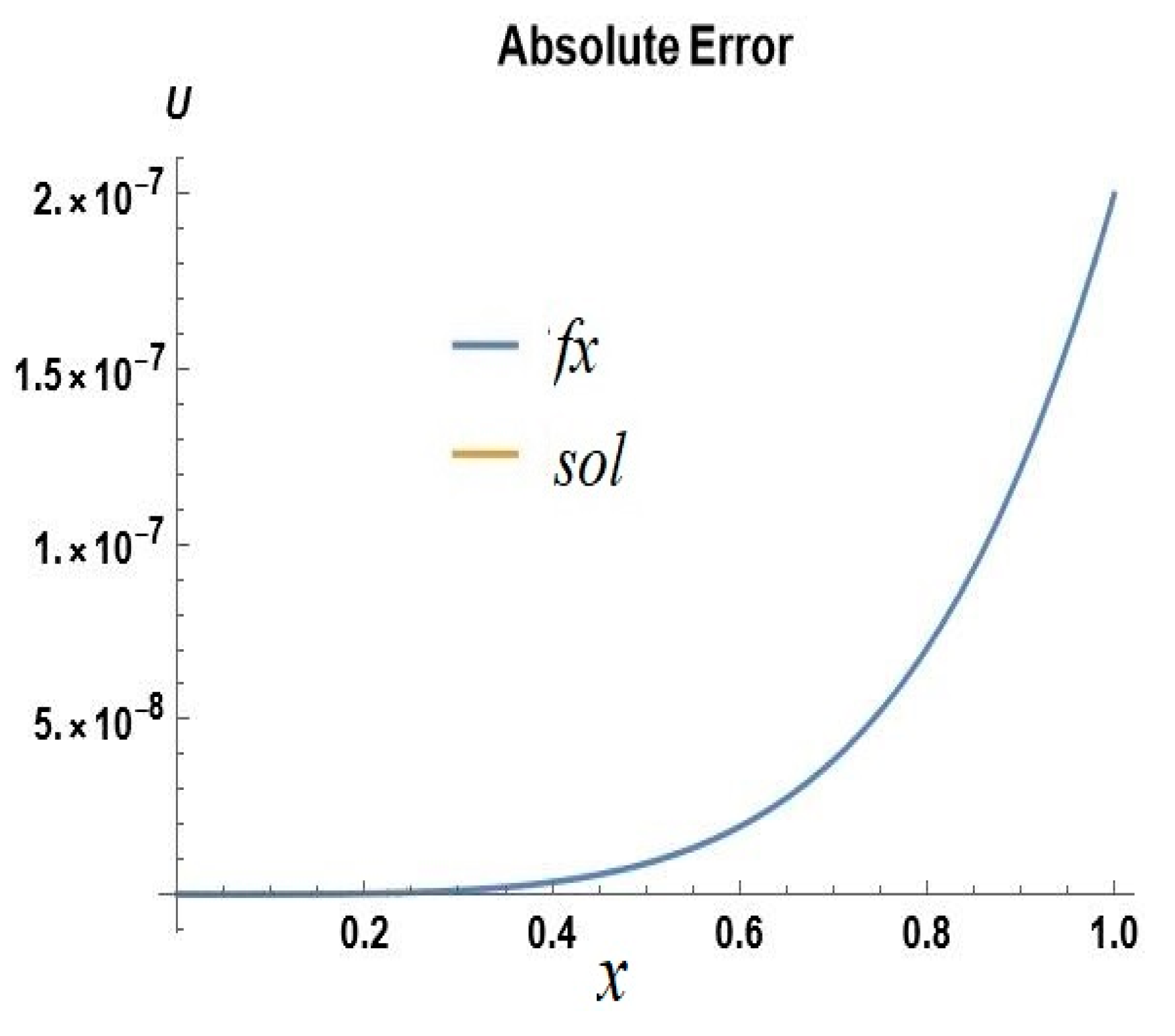
5. Error Analysis
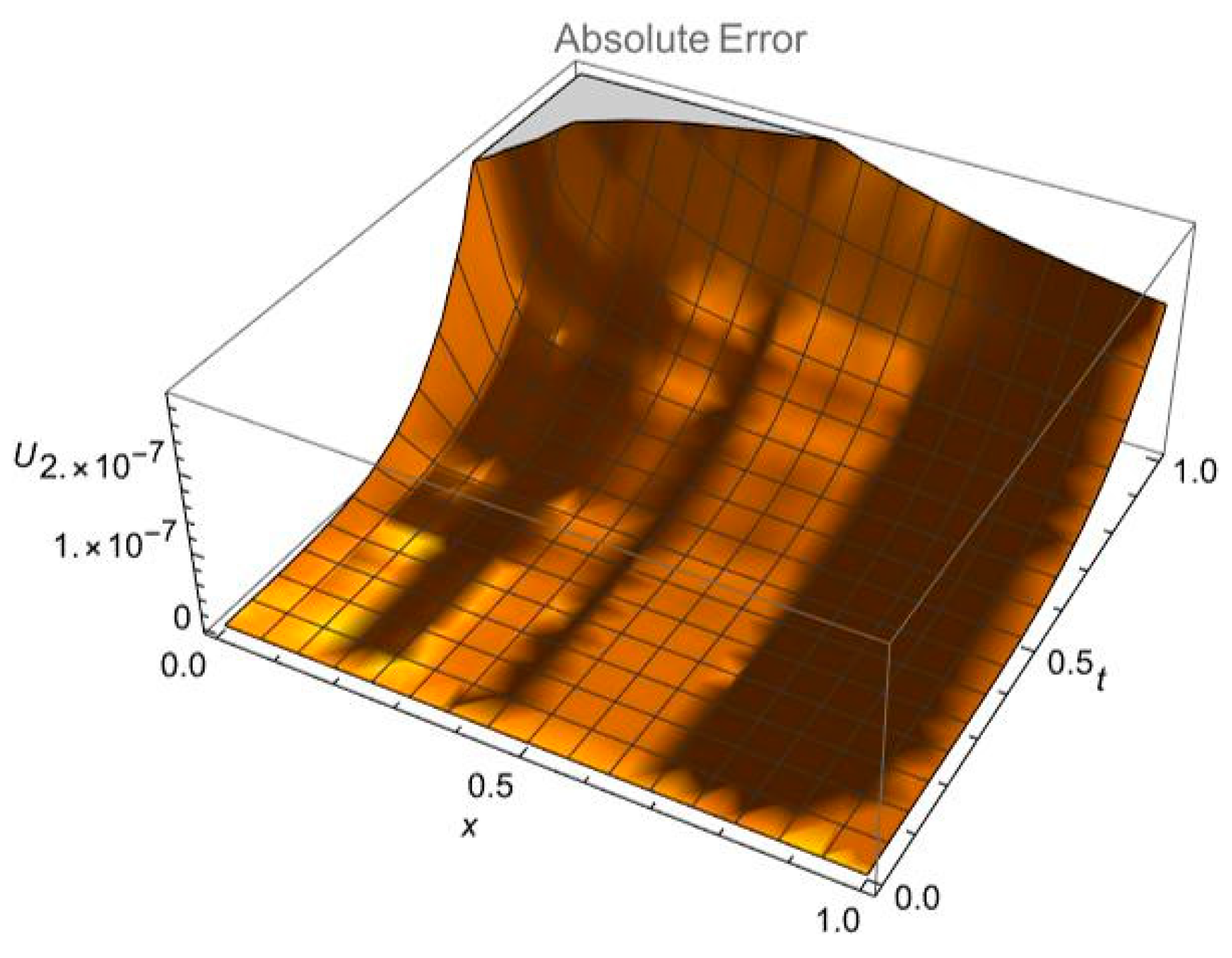
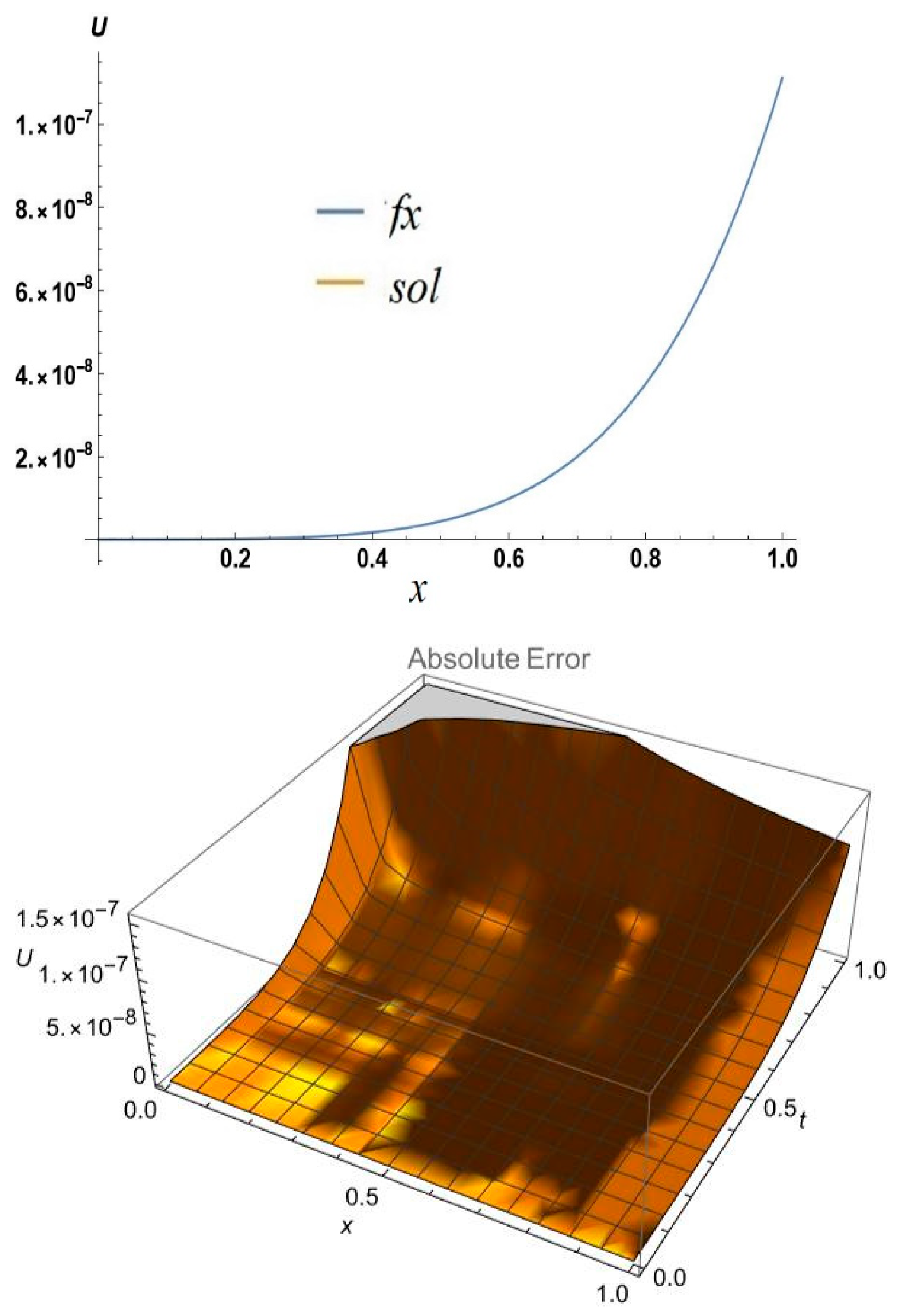
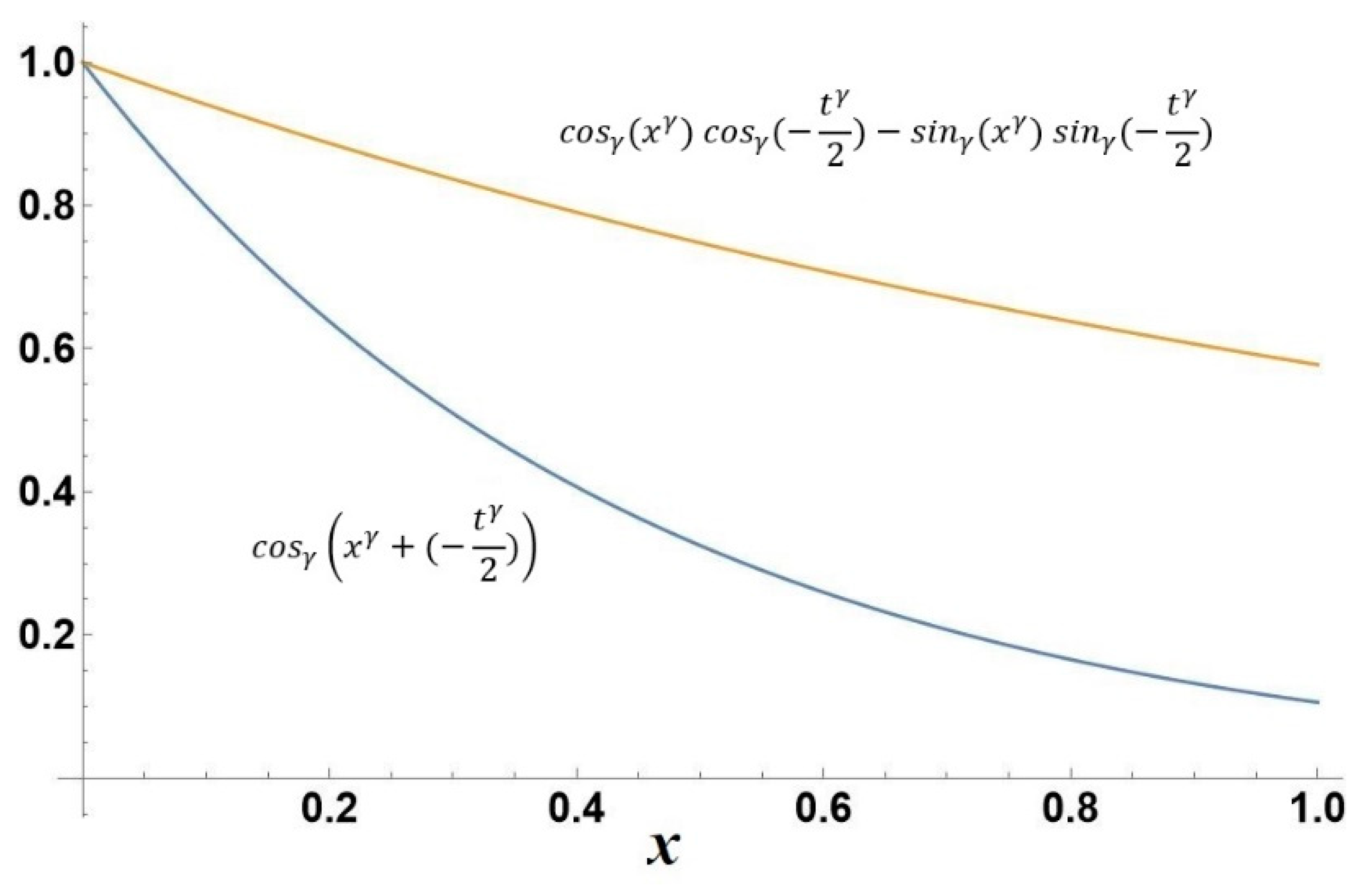
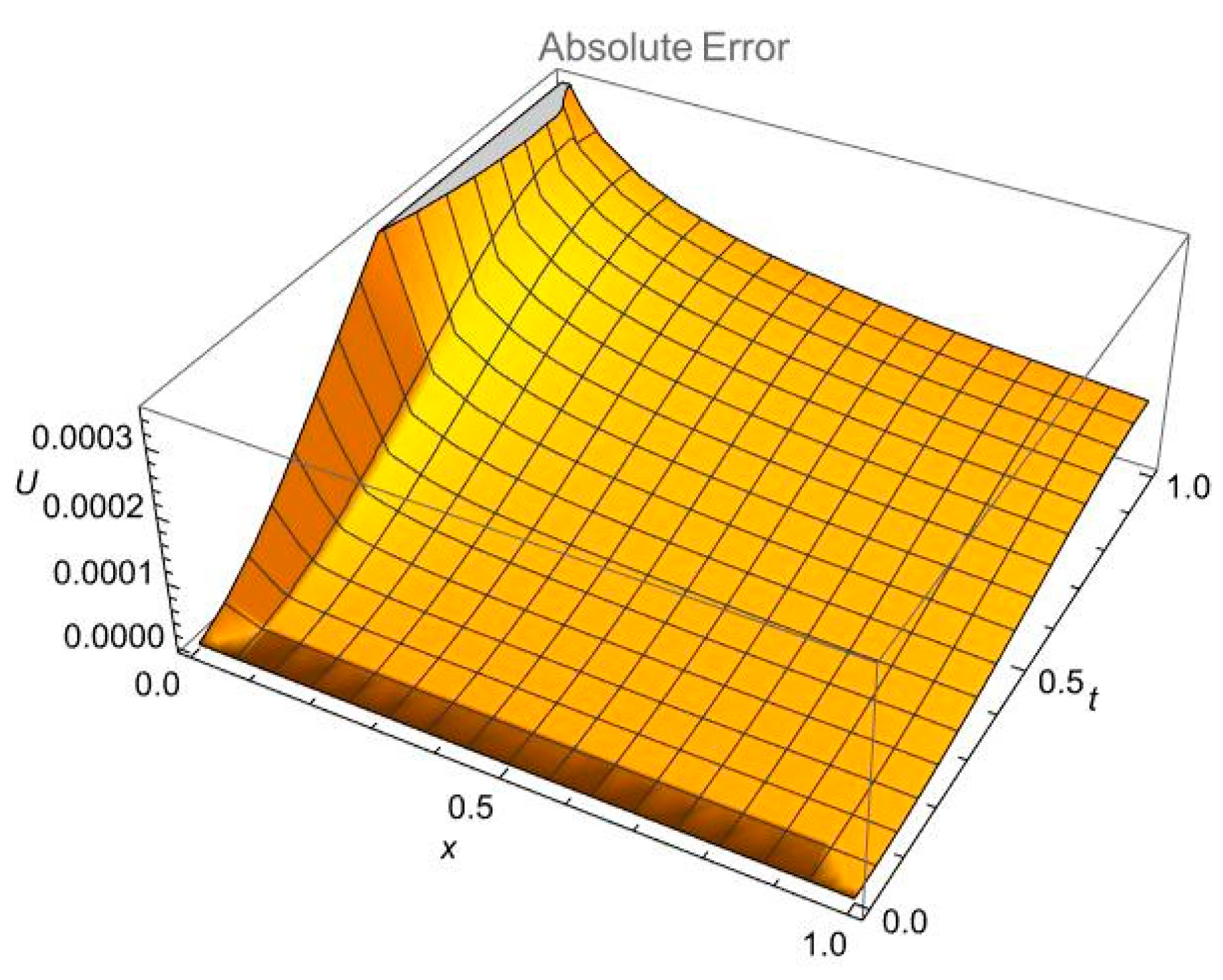
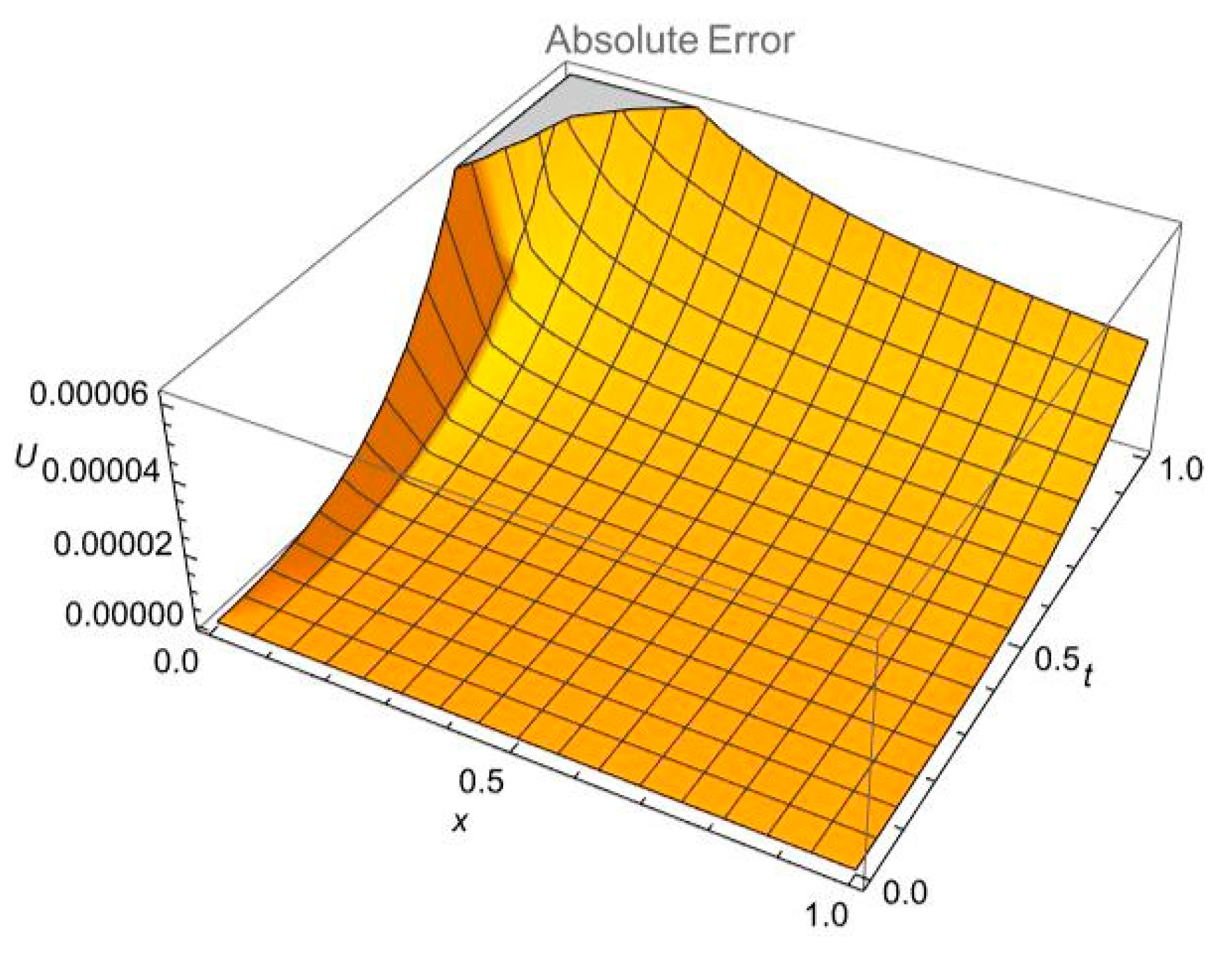
6. Results and Discussions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Kilbas, A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematics Studies, 204, Fractional Calculus and Applied Analysis; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Igor, P. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution. In Fractional Differential Equations; Mathematics in Science and Engineering Series; Academic Press: Cambridge, MA, USA, 1998; Volume 198. [Google Scholar]
- Bagley, R.L.; Calico, R.A. Fractional order state equations for the control of viscoelasticallydamped structures. J. Guid. Control Dyn. 1991, 14, 304–311. [Google Scholar] [CrossRef]
- Sun, H.; Abdelwahab, A.; Onaral, B. Linear approximation of transfer function with a pole of fractional power. IEEE Trans. Autom. Control 1984, 29, 441–444. [Google Scholar] [CrossRef]
- Ichise, M.; Nagayanagi, Y.; Kojima, T. An analog simulation of non-integer order transfer functions for analysis of electrode processes. J. Electroanal. Chem. 1971, 33, 253–265. [Google Scholar] [CrossRef]
- Laskin, N. Fractional market dynamics. Phys. A Stat. Mech. Appl. 2000, 287, 482–492. [Google Scholar] [CrossRef]
- Kusnezov, D.; Bulgac, A.; Dang, G.D. Quantum Lévy Processes and Fractional Kinetics. Phys. Rev. Lett. 1999, 82, 1136–1139. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Zhang, F. A survey on the stability of fractional differential equations. Eur. Phys. J. Spec. Top. 2011, 193, 27–47. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A note on the stability of fractional order systems. Math. Comput. Simul. 2009, 79, 1566–1576. [Google Scholar] [CrossRef]
- Torvik, P.J.; Bagley, R.L. On the Appearance of the Fractional Derivative in the Behavior of Real Materials. J. Appl. Mech. Trans. ASME 1984, 51, 294–298. [Google Scholar] [CrossRef]
- Jawad, A.J.M.; Petković, M.D.; Biswas, A. Modified simple equation method for nonlinear evolution equations. Appl. Math. Comput. 2010, 217, 869–877. [Google Scholar]
- Zayed, E.M.E. A note on the modified simple equation method applied to Sharma–Tasso–Olver equation. Appl. Math. Comput. 2011, 218, 3962–3964. [Google Scholar] [CrossRef]
- Wei, Y.; Guo, Y.; Li, Y. A new numerical method for solving semilinear fractional differential equation. J. Appl. Math. Comput. 2021, 1–23. [Google Scholar] [CrossRef]
- Mahor, T.C.; Mishra, R.; Jain, R. Analytical solutions of linear fractional partial differential equations using fractional Fourier transform. J. Comput. Appl. Math. 2021, 385, 113202. [Google Scholar] [CrossRef]
- Inc, M. The approximate and exact solutions of the space- and time-fractional Burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 2008, 345, 476–484. [Google Scholar] [CrossRef] [Green Version]
- Roman, P. Application of the Adams-Bashfort-Mowlton Method to the Numerical Study of Linear Fractional Oscillators Models. In AIP Conference Proceedings; AIP Publishing LLC.: Melville, NY, USA, 2021. [Google Scholar]
- Srivastava, H.M.; Alomari, A.-K.N.; Saad, K.M.; Hamanah, W.M. Some Dynamical Models Involving Fractional-Order Derivatives with the Mittag-Leffler Type Kernels and Their Applications Based upon the Legendre Spectral Collocation Method. Fractal Fract. 2021, 5, 131. [Google Scholar] [CrossRef]
- Guy, J. Lagrange characteristic method for solving a class of nonlinear partial differential equations of fractional order. Appl. Math. Lett. 2006, 19, 873–880. [Google Scholar] [CrossRef] [Green Version]
- Safari, M.; Ganji, D.D.; Moslemi, M. Application of He’s Variational Iteration Method and Adomian’s Decomposition Method to the Fractional KdV-Burgers-Kuramoto Equation. Comput. Math. Appl. 2009, 58, 2091–2097. [Google Scholar] [CrossRef] [Green Version]
- Cui, M. Compact finite difference method for the fractional diffusion equation. J. Comput. Phys. 2009, 228, 7792–7804. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z.M. Fractional Green Function for Linear Time-Fractional Inhomogeneous Partial Differential Equations in Fluid Mechanics. J. Appl. Math. Comput. 2007, 24, 167. [Google Scholar] [CrossRef]
- Huang, Q.; Huang, G.; Zhan, H. A Finite Element Solution for the Fractional Advection-Dispersion Equation. Adv. Water Resour. 2008, 31, 1578–1589. [Google Scholar] [CrossRef]
- Guo, S.; Mei, L.; Li, Y.; Sun, Y. The Improved Fractional Sub-Equation Method and Its Applications to the Space-Time Fractional Differential Equations in Fluid Mechanics. Phys. Lett. Sect. A Gen. At. Solid State Phys. 2012, 376, 407–411. [Google Scholar] [CrossRef]
- Zheng, B. (G′/G)-Expansion Method for Solving Fractional Partial Differential Equations in the Theory of Mathematical Physics. Commun. Theor. Phys. 2012, 58, 623–630. [Google Scholar] [CrossRef]
- Lu, B. The first integral method for some time fractional differential equations. J. Math. Anal. Appl. 2012, 395, 684–693. [Google Scholar] [CrossRef] [Green Version]
- Peykrayegan, N.; Ghovatmand, M.; Skandari, M.H.N. On the convergence of Jacobi-Gauss collocation method for linear fractional delay differential equations. Math. Methods Appl. Sci. 2021, 44, 2237–2253. [Google Scholar] [CrossRef]
- Toh, Y.T.; Phang, C. Collocation Method for Fractional Differential Equation via Laguerre Polynomials with Eigenvalue Degree. In AIP Conference Proceedings; AIP Publishing LLC.: Melville, NY, USA, 2021. [Google Scholar]
- Khader, M.M.; Saad, K.M.; Baleanu, D.; Kumar, S. A spectral collocation method for fractional chemical clock reactions. Comput. Appl. Math. 2020, 39, 394. [Google Scholar] [CrossRef]
- Su, W.-H.; Yang, X.-J.; Jafari, H.; Baleanu, D. Fractional complex transform method for wave equations on Cantor sets within local fractional differential operator. Adv. Differ. Equ. 2013, 2013, 97. [Google Scholar] [CrossRef] [Green Version]
- Bhatti, M.I. Solution of Fractional Harmonic Oscillator in a Fractional B-poly Basis. Phys. Tech. Sci. 2014, 2, 8. [Google Scholar] [CrossRef]
- Bhatti, M.; Bracken, P.; Dimakis, N.; Herrera, A. Solution of mathematical model for gas solubility using fractional-order Bhatti polynomials. J. Phys. Commun. 2018, 2, 085013. [Google Scholar] [CrossRef]
- Bhatti, M.I. Analytic Matrix Elements of the Schrödinger Equation. Adv. Stud. Theor. Phys. 2013, 7, 11. [Google Scholar] [CrossRef]
- I Bhatti, M.; Hinojosa, E. 26 Results of hyperbolic partial differential equations in B-poly basis. J. Phys. Commun. 2020, 4, 095010. [Google Scholar] [CrossRef]
- Bhatti, M.I.; Rahman, H.; Dimakis, N. Approximate Solutions of Nonlinear Partial Differential Equations Using B-Polynomial Bases. Fractal Fract. 2021, 5, 106. [Google Scholar] [CrossRef]
- Bhatti, M.I.; Bracken, P. Solutions of differential equations in a Bernstein polynomial basis. J. Comput. Appl. Math. 2007, 205, 272–280. [Google Scholar] [CrossRef] [Green Version]
- Jong, S.-G.; Choe, H.-C.; Ri, Y.-D. A New Approach for an Analytical Solution for a System of Multi-term Linear Fractional Differential Equations. Iran. J. Sci. Technol. Trans. A Sci. 2021, 45, 955–996. [Google Scholar] [CrossRef]
- Bhatti, M.I. Solutions of the Harmonic Oscillator Equation in a B-Polynomial Basis. Adv. Stud. Theor. Phys. 2009, 3, 451–460. [Google Scholar]
- Massopust, P.R.; Zayed, A.I. On the Invalidity of Fourier Series Expansions of Fractional Order. Fract. Calc. Appl. Anal. 2015, 18, 1507–1517. [Google Scholar] [CrossRef] [Green Version]
- Fletcher, C.A.J. Computational Galerkin Methods; Springer: Berlin/Heidelberg, Germany, 1984. [Google Scholar]
- Alinhac, S. Hyperbolic Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Wolfram Research, Inc. Mathematica 12.0; Wolfram Research, Inc.: Champaign, IL, USA, 2019. [Google Scholar]
- Singh, A.K.; Singh, V.K.; Singh, O.P. The Bernstein Operational Matrix of Integration. Appl. Math. Sci. 2009, 3, 2427–2436. [Google Scholar]
- Farouki, R.T. Legendre–Bernstein basis transformations. J. Comput. Appl. Math. 2000, 119, 145–160. [Google Scholar] [CrossRef] [Green Version]

| n | Basis Set | Caputo’s Derivative of Basis Set (Equation (2)) | ||
|---|---|---|---|---|
| 1/2 | 1/2 | 1 | ||
| 3/4 | 3/4 | 1 | ||
| 5/3 | 5/3 | 1 | ||
| 5/4 | 5/4 | 1 | ||
| 9/4 | 9/4 | 1 | ||
| 9/5 | 9/5 | 1 |
| x | t | Absolute Difference | ||
| 0.1 | 0.1 | 0.941097 | 0.941097 | 1.036 × 10−11 |
| 0.2 | 0.2 | 0.886784 | 0.886784 | 1.091 × 10−10 |
| 0.3 | 0.3 | 0.836674 | 0.836674 | 5.120 × 10−10 |
| 0.4 | 0.4 | 0.790420 | 0.790420 | 1.660 × 10−9 |
| 0.5 | 0.5 | 0.747668 | 0.747668 | 4.333 × 10−9 |
| 0.6 | 0.6 | 0.708152 | 0.708152 | 9.785 × 10−9 |
| 0.7 | 0.7 | 0.671593 | 0.671593 | 1.991 × 10−8 |
| 0.8 | 0.8 | 0.637742 | 0.637742 | 3.744 × 10−8 |
| 0.9 | 0.9 | 0.606376 | 0.606376 | 6.617 × 10−8 |
| 1.0 | 1.0 | 0.577288 | 0.577288 | 1.112 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatti, M.I.; Rahman, M.H. Technique to Solve Linear Fractional Differential Equations Using B-Polynomials Bases. Fractal Fract. 2021, 5, 208. https://doi.org/10.3390/fractalfract5040208
Bhatti MI, Rahman MH. Technique to Solve Linear Fractional Differential Equations Using B-Polynomials Bases. Fractal and Fractional. 2021; 5(4):208. https://doi.org/10.3390/fractalfract5040208
Chicago/Turabian StyleBhatti, Muhammad I., and Md. Habibur Rahman. 2021. "Technique to Solve Linear Fractional Differential Equations Using B-Polynomials Bases" Fractal and Fractional 5, no. 4: 208. https://doi.org/10.3390/fractalfract5040208
APA StyleBhatti, M. I., & Rahman, M. H. (2021). Technique to Solve Linear Fractional Differential Equations Using B-Polynomials Bases. Fractal and Fractional, 5(4), 208. https://doi.org/10.3390/fractalfract5040208







