Abstract
In this paper, we study the improved perturbed nonlinear Schrödinger equation with cubic quadratic nonlinearity (IPNLSE-CQN) to describe the propagation properties of nonlinear periodic waves (PW) in fiber optics. We obtain the chirped periodic waves (CPW) with some Jacobi elliptic functions (JEF) and also obtain some solitary waves (SW) such as dark, bright, hyperbolic, singular and periodic solitons. The nonlinear chirp associated with each of these optical solitons was observed to be dependent on the pulse intensity. The graphical behavior of these waves will also be displayed.
1. Introduction
A chirp is a signal whose frequency changes over time. The chirping sound generated by birds is the source of the term chirp. For example, ultrashort pulses in optical transmission systems may show chirp, which interacts with the dispersion characteristics of the materials through which they propagate to increase or reduce total pulse dispersion. The propagation of chirped soliton pulses in fiber optics is getting popular due to a wide range of applications in amplification and pulse compression. As a result, these objects are especially useful in the design of optical pulse compressors, fiber-optic amplifiers, and soliton-based communications links [1,2]. The NLSE is used to describe these pulses, and it only includes the effects of group velocity dispersion (GVD) and self-phase modulation that are valid in the picosecond region. Higher-order effects such as self-steeping (SS), self-frequency (SF) shift, and quintic nonlinearity can occur when optical pulses are short (in the femtosecond region). Models with higher-order terms governing most practical cases, unlike the NLSE, are not entirely integrable and cannot be solved correctly by the well-known inverse scattering transform [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17].
Recently, many researchers have studied the chirped soliton-like solutions for various NLSE, such as Alka et al. who studied chirped solitons for NLSE with SS and SF shift effect along with quintic nonlinearity [18]. Vysa et al. studied the NLSE with SS and SF shift effect in order to obtain the chirped chiral solitons [19]. For a higher-order NLSE with competing cubic-quintic-septic nonlinearities, non-Kerr quintic nonlinearity, SS, and SF shift, Bouzida et al. obtained families of chirped soliton-like solutions. Hmurcik and Kaup used numerical methods to investigate a pulse with a linear chirp and a hyperbolic-secant-amplitude profile [20]. It was also demonstrated that there are exact chirped soliton solutions for the generalised NLSE with polynomial nonlinearity and non-Kerr terms of arbitrary order [21]. In addition, the chirped solitary pulses for a nonic NLSE were studied on a continuous-wave background [5,22,23,24,25,26,27,28,29,30,31]. In this paper, we studied the IPNLSE-CQN in order to obtain some chirped periodic and soliton waves. We also show that the resultant chirp associated with each of these optical solitons, which includes both linear and nonlinear terms, where nonlinear terms is directly and inversely proportional to the wave’s intensity.
2. Mathematical Analysis
The IPNLSE-CQN dimensionless form is given by [32,33,34,35]:
Here a, b, , and stand for spatio-temporal dispersion (STD), GVD, inter-modal dispersion, SS perturbation term and nonlinear dispersion respectively. Where and are constant. The parameter p is the full nonlinearity parameter. By putting the , so that Equation (1) reduce to:
In order to obtain the PW solution of Equation (2), we consider the following transformation:
where and and are real functions of , while w is the wave number constant . The chirping that corresponds to this waveform can be expressed as:
Now insert Equation (3) into Equation (2). Then, we get the real and imaginary parts that can be written as:
and
Now multiply Equation (6) with and integration yield,
where is the integration constant. Hence, the resultant chirping can be expressed as:
by substitution of Equation (7) into Equation (5), as the required differential equation can be shown as:
divide by on both side of the Equations (9) and (10), as:
multiply the Equations (11) and (12) by and integration;
where is an another integration constant. Now after substituting into Equations (13) and (14) we get the equation:
where is expressed as:
with the coefficients:
Equation (15) shows the dynamics of partial with energy and potentials. The general wave solution of Equation (2) is:
where satisfies the Equation (15) and can be obtained with the help of Equation (7). Now using these relations into Equation (8) we can obtained chirping function as:
Hence, it is clear that the structure of the Equation (21) is nontrivial, which contains the first and second term with intensity dependent terms while the last term is linear. In Equation (21), it is clear that the first and second term represent the nonlinear chirp that is inversely and directly proportional to the intensity and the last term is linear chirp. Now, we have to obtain the chirped solutions for Equation (21) with the condition that along with and under some constrained conditions.
3. CPW Solution
To investigate the different forms of elliptic ordinary differential equations in Equation (15), we have to obtain the exact CPW solutions of Equation (2) by using the transformation Equation (20). We also express our result in terms of JEF. The more results shows in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20.
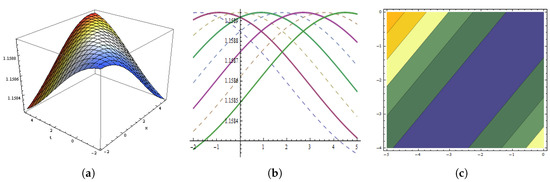
Figure 1.
The graphical behavior of the in Equation (25) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
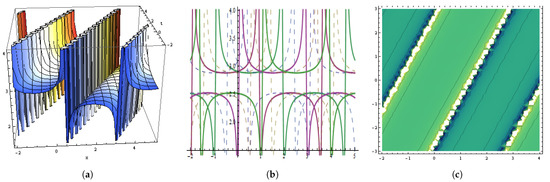
Figure 2.
The graphical behavior of the in Equation (32) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
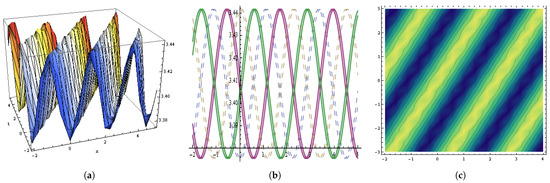
Figure 3.
The graphical behavior of the in Equation (39) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
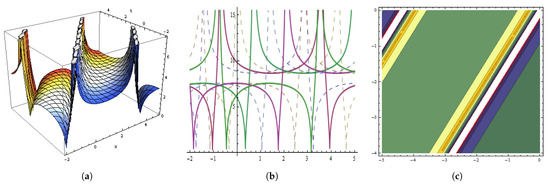
Figure 4.
The graphical behavior of the in Equation (46) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
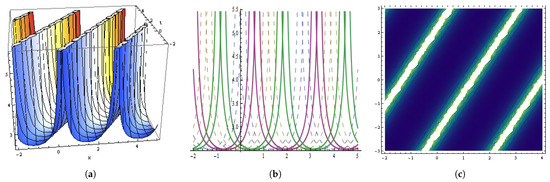
Figure 5.
The graphical behavior of the in Equation (53) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
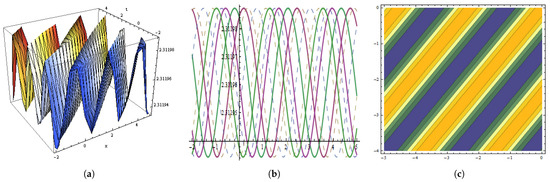
Figure 6.
The graphical behavior of the in Equation (60) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
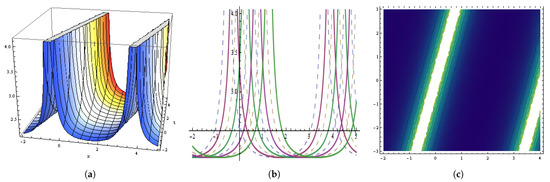
Figure 7.
The graphical behavior of the in Equation (67) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
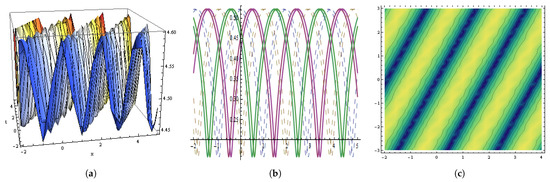
Figure 8.
The graphical behavior of the in Equation (74) at , , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
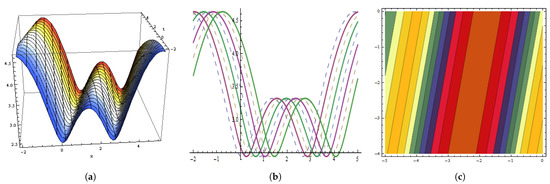
Figure 9.
The graphical behavior of the in Equation (81) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
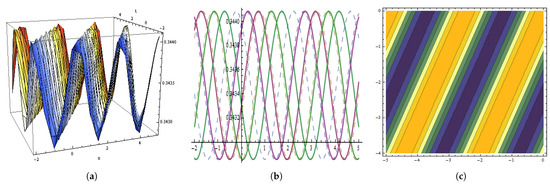
Figure 10.
The graphical behavior of the in Equation (88) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
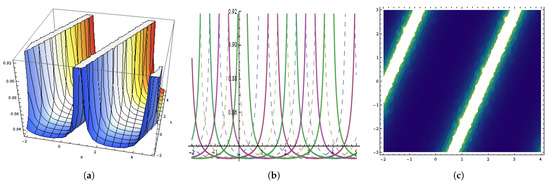
Figure 11.
The graphical behavior of the in Equation (95) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
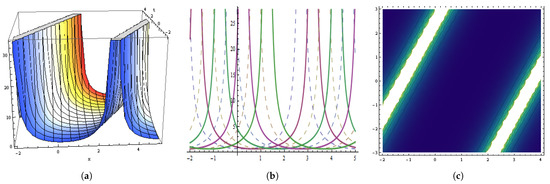
Figure 12.
The graphical behavior of the in Equation (102) at , , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
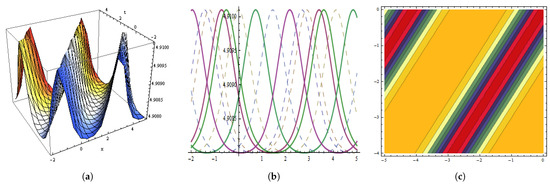
Figure 13.
The graphical behavior of the in Equation (109) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
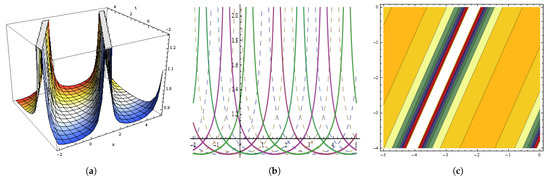
Figure 14.
The graphical behavior of the in Equation (116) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
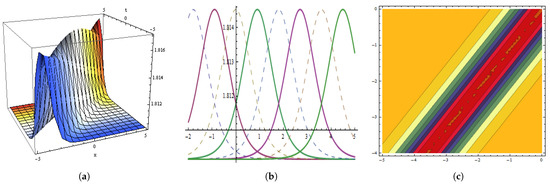
Figure 15.
The graphical behavior of the in Equation (120) at , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
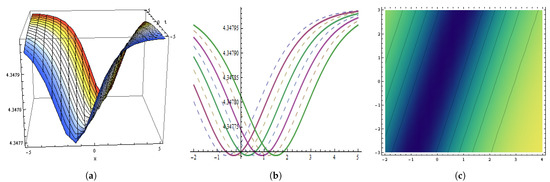
Figure 16.
The graphical behavior of the in Equation (123) at , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
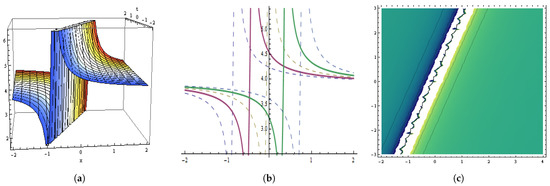
Figure 17.
The graphical behavior of the in Equation (126) at , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
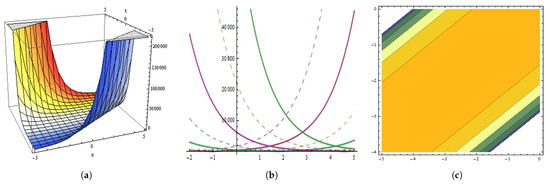
Figure 18.
The graphical behavior of the in Equation (129) at , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
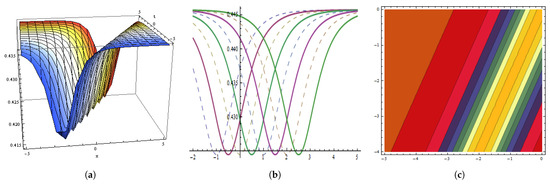
Figure 19.
The graphical behavior of the in Equation (147) at , , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
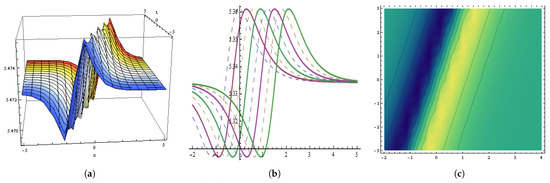
Figure 20.
The graphical behavior of the in Equation (150) at , , , , , , , , , . (a) Represent three dimensions. (b) Show two dimensions. (c) Represents contour figures.
3.1. cn-Form
We can obtain the chirped periodic solution of Equation (15) for -form that are represented as [36]:
where is the constant and is JEF with modulus w containing values . The variables D and L are shown below:
We can also find the following values:
Periodic solutions of -form for Equation (2) obtained by substituting the equations Equations (20) and (22):
where . By equating the Equations (19) and (24), we can get integration constant and :
The resultant chirping can be written as:
3.2. dc-Form
Another periodic solution of Equation (15) can be obtained in this way [36]:
where is the constant and is JEF with modulus w taking values . The values of V and Y are expressed as:
3.3. dn-Type
We obtain the periodic solution of -form [36]:
where is the constant and is JEF with modulus w having values . The parameters R and F are defined as:
we can also find and H:
3.4. ds-Type
The PW solution of -form are shown below [36]:
where is the constant and is JEF with modulus w having values . The parameters E and M are represented as:
we can also get the and H:
We can get the periodic solutions of -form for Equation (2) by putting the Equation (43) in Equation (20):
where . The integration constant and are represented as:
The chirping that associated with this exact PW can be written as:
3.5. sc-Type
Equation (15) can be solved for the periodic solution of -form that can be present as [36]:
where is the constant and is JEF with modulus w having values . The parameters G and B are present as:
we can also find the following parameters:
We can find the periodic solutions of -form for Equation (2) by combining the solution of the Equation (50) in Equation (20):
where . The constant and are as follow:
By combining the solution of Equations (21) and (50), since the corresponding chirping are shown below:
3.6. sn-Type
Obtain another periodic solution of Equation (15) that are as follow [36]:
where is the constant and is JEF with modulus w containing values . Obtain the P and U to solve the above solution that are present as:
we can also get the following parameters by solving above equations:
Periodic solutions of -form for Equation (2) are represented as:
where . The constant and are written as:
3.7. -Type
Periodic solution for Equation (15) are obtained as follow [36]:
where is the constant and is JEF with modulus w having values . By solving above solution, we can obtain following parameters:
The value of the following parameters are represented as:
3.8. -Type
The PW solution for Equation (15) are written as [36]:
where is the constant and is JEF with modulus w having values . By solving above solution, we can find following parameters:
The value of following parameters that are expressed as:
Obtain the periodic solutions for Equation (2) by insert the solution of the Equation (71) in Equation (20):
where . The constant of integration can be expressed as:
The corresponding chirping are as follow:
3.9. -Type
We can find the periodic solution for Equation (15) that are written as [36]:
where is the constant and is JEF with modulus w having values . By solving above solution, we can get following parameters:
The value of following parameters that are shown below:
Obtain the periodic solutions for Equation (2) by equating the solution of the Equation (78) in Equation (20):
where . The constant of integration are represented as:
The corresponding chirping are represented as:
3.10. -Type
Equation (15) provides another periodic solution that are shown below [36]:
where is the constant and is JEF with modulus w having values . By solving above solution, we can get following parameters:
The following parameters are obtained as:
Obtain the periodic solutions for Equation (2) that are represented as:
where . The integration constants are shown below:
The following chirping are shown below:
3.11. -Type
Equation (15) gives another periodic solution that are expressed as [36]:
where is the constant and is JEF with modulus w having values . In order to solve above solution, we find following parameters:
we can find the values of and H that are present as:
Obtain the periodic bounded solutions for Equation (2) that are as follow:
where . The integration constants are written as:
The accompanying chirping are shown below:
3.12. -Type
Equation (15) shows another periodic solution that are takes form [36]:
where is the constant and is JEF with modulus w having values . The value of and g are given by:
The following parameters are as follow:
Periodic bounded solutions for Equation (2) takes form:
where . The integration constants takes form:
3.13. -Type
Another PW solution of Equation (15) are obtain as [36]:
where is the constant and is JEF with modulus w having values . The parameters and y are defined as:
The following parameters are also defined as:
The chirped periodic solution of Equation (2) may be written as:
where . The value of integration constants can be given as:
By equating the Equations (21) and (106), so that the following chirping takes form:
3.14. -Type
The bounded periodic solution of Equation (15) is as follows [36]:
where is the constant and is JEF with modulus w having values . The values of and e are defined as:
we can get the parameters and H by solving above relations:
Obtain the bounded periodic solutions for Equation (2) that are given as:
where . The value of following constants are defined as:
The chirping that accompanies with this PW is defined by:
4. The SW Limit
Here, we can find the chirped SW solutions of Equation (2). The JEF convert into trigonometric functions at the long-wave limit, which correspond to and . The nonlinear chirp of each of these optical pulses is also calculated.
4.1. Bright SW
In the limiting case , the function and Equation (25) gives the SW solution of Equation (2) as follows:
The values of D and L are defined as:
The chirping associated with the nonlinearly chirped SW is easy to accomplish:
4.2. Dark Wave
In the limiting case , the function and Equation (60) present the SW solution of Equation (2) as follows:
where the variables are defined as:
The nonlinearly chirped SW’s chirping may be represented as:
4.3. Singular-I Wave
In the limiting case , the function , the CPW solution of Equation (46) converts to the SW solution of Equation (2):
where the parameters are defined as:
The corresponding chirping associated with the SW solution are represented as:
4.4. Hyperbolic-I Wave
In the limiting case , the function and Equation (53) shows the SW solution of Equation (2) as follows:
where the variables are present as:
The chirping that belongs to SW solution can be written as:
4.5. Periodic-I Wave
In the limiting case , the function and Equation (25) express the SW solution of Equation (2) as follows:
The values of D and L are defined as:
The chirping associated with the nonlinearly chirped SW is expressed as:
4.6. Periodic-II Wave
In the limiting case , the function , the CPW solution of Equation (46) converts to the SW solution of Equation (2):
where the parameter are express as:
The corresponding chirping associated with the SW solution are shown below:
4.7. Periodic-III Wave
In the limiting case , the function and Equation (60) shows the SW solution of Equation (2) that are shown below:
where the variable takes form:
The nonlinearly chirped SW’s chirping can be expressed as:
4.8. Kink Type
In the limiting case , the function and Equation (53) express the SW solution of Equation (2) that can be written as:
where the variables are present as:
The chirping that belongs to CSW solution can be present as:
4.9. Periodic Type
In the limiting case , the function and Equation (32) shows the SW solution of Equation (2) as follows:
where the variable can be expressed as:
The chirping that belongs to SW solution takes form:
4.10. Dipole Soliton
In the limiting case , the function and Equation (74) gives the SW solution of Equation (2) as follows:
where the parameters takes form:
The chirping that belongs to SW can be written as:
4.11. SW
In the limiting case , the function and the chirped solution of Equation (88) gives the SW solution of Equation (2) takes form:
where the parameters are given as:
The following chirping as follow:
4.12. SW
In the limiting case , the function and the chirped solution of Equation (109) express the SW solution of Equation (2) shown below:
where the value of and y are shown below:
The following chirping are expressed as:
4.13. SW
In the limiting case , the function and Equation (74) gives the SW solution of Equation (2) as follows:
where the parameter takes form:
The chirping that belongs to SW can be written as:
4.14. SW
In the limiting case , the function and Equation (102) gives the SW solution of Equation (2) can be written as:
where the parameter can be express as:
The resultant chirping shown below:
4.15. SW
In the limiting case , the function and Equation (116) gives the SW solution of Equation (2) can be represent as:
where the parameter can be present as:
The resultant chirping present as:
5. Results and Discussion
In this section, we will discuss and compare our results with other authors results. Biswas et al. used the extended trial function technique to find solitons for the perturbed NLSE with 10 types of fibre nonlinearity. In the presence of a few Hamiltonian perturbation terms, Bouzida et al. [32] provide a large range of chirped soliton solutions for the improved NLSE with dual-power law nonlinearity. Savescu et al. [33] investigated the perturbed NLSE with full nonlinearity in order to discuss the dynamic of solitons in nano fibre optics. Biswas et al. [34] also studied the perturbed NLSE in order to obtain the optical solitons solutions by trial equation method.
In this manuscript, we display the different forms of CPW and SW solutions. Equation (25) gives the -form periodic solution while in Equation (120) it changed into a bright SW when and in Equation (132) it changed into periodic-I SW when . Equation (32) present the periodic -form solution while in Equation (144) it changed into Bell SW when . Equation (46) represent the periodic -form solution while in Equation (126) it changed into singular-I SW when and in Equation (135) it changed into periodic-II SW when . Equation (53) present the -form periodic solution while in Equation (129) it changed into hyperbolic-I SW when and in Equation (141) it convert into kink SW when . Equation (60) shows the periodic -form solution while in Equation (123) it changed into dark SW when and in Equation (138) it changed into periodic-III SW when . Equation (67) shows the -form periodic solution. Equation (74) present the periodic -form solution while in Equation (147) it changed into Sw when and in Equation (156) it changed into SW when . Equation (81) express the -form periodic solution. Equation (88) gives -form periodic solution while in Equation (150) it changed into SW when . Equation (95) shows the -form periodic solution. Equation (102) present the -form periodic solution while in Equation (159) it changed into SW when . Equation (109) express the periodic -form solution while in Equation (153) it changed into SW when . Equation (116) gives the periodic -form solution while in Equation (163) it changed into SW when .
6. Conclusions
In this paper, we have investigated IPNLSE-CQN in order to obtain some chirped periodic solution based on JEF and also obtain SW solution. There are a number of exact solutions with nontrivial phase chirping that varies as a function of intensity. Localized solutions of bright, dark, singular and other type of solutions are among them. For each of these optical solitons, the corresponding chirp has been produced. The graphical description of obtained chirped solitons have also been shown.
Author Contributions
Validation, S.A.; writing—review and editing, S.A., S.T.R.R.; supervision, A.R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
MDPI Research Data Policies.
Acknowledgments
Taif University Researchers Supporting Project number (TURSP-2020/305), Taif University, Taif, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Desaix, M.; Helczynski, L.; Anderson, D.; Lisak, M. Propagation properties of chirped soliton pulses in optical nonlinear Kerr media. Phys. Rev. E 2002, 65, 056602. [Google Scholar] [CrossRef]
- Kruglov, V.I.; Peacock, A.C.; Harvey, J.D. Exact Self-Similar Solutions of the Generalized Nonlinear Schrödinger Equation with Distributed Coefficients. Phys. Rev. Lett. 2003, 90, 113902. [Google Scholar] [CrossRef]
- Akram, U.; Seadawy, A.R.; Rizvi, S.T.R.; Younis, M.; Althobaiti, S.; Sayed, S. Traveling waves solutions for the fractional Wazwaz Benjamin Bona Mahony model in arising shallow water waves. Results Phys. 2021, 20, 103725. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Bilal, M.; Younis, M.; Rizvi, S.T.R. Resonant optical solitons with conformable time fractional nonlinear Schrödinger equation. Int. J. Mod. Phys. B 2021, 35, 2150044. [Google Scholar] [CrossRef]
- Younas, U.; Seadawy, A.R.; Younis, M.; Rizvi, S.T.R. Optical solitons and closed form solutions to the (3+1)-dimensional resonant Schrödinger dynamical wave equation. Int. J. Mod. Phys. B 2020, 34, 2050291. [Google Scholar] [CrossRef]
- Younas, U.; Younis, M.; Seadawy, A.R.; Rizvi, S.T.R.; Althobaiti, S.; Sayed, S. Diverse exact solutions for modified nonlinear Schrödinger equation with conformable fractional derivative. Results Phys. 2021, 20, 103766. [Google Scholar] [CrossRef]
- Younas, U.; Seadawy, A.R.; Younis, M.; Rizvi, S.T.R. Dispersive of propagation wave structures to the Dullin-Gottwald-Holm dynamical equation in a shallow water waves. Chin. J. Phys. 2020, 68, 348–364. [Google Scholar] [CrossRef]
- Hou, H.; You, T.; Zhou, Q.; Liu, M.; Ouyang, Y.; Liu, X.; Liu, W. Q-switched all-fiber laser based on titanium trisulfide. Optik 2020, 205, 164234. [Google Scholar] [CrossRef]
- Özkan, Y.S.; Seadawy, A.R.; Yaşar, E. Multi-wave, breather and interaction solutions to (3+1) dimensional Vakhnenko–Parkes equation arising at propagation of high-frequency waves in a relaxing medium. J. Taibah Univ. Sci. 2021, 15, 666–678. [Google Scholar] [CrossRef]
- Donne, G.D.; Hubert, M.B.; Seadawy, A.; Etienne, T.; Betchewe, G.; Doka, S.Y. Chirped soliton solutions of Fokas-Lenells equation with perturbation terms and the effect of spatio-temporal dispersion in the modulational instability analysis. Eur. Phys. J. Plus 2020, 135, 212. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Bilal, M.; Younis, M.; Rizvi, S.T.R.; Althobaiti, S.; Makhlouf, M.M. Analytical mathematical approaches for the double chain model of DNA by a novel computational technique. Chaos Solitons Fractals 2021, 144, 110669. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Rehman, S.U.; Younis, M.; Rizvi, S.T.R.; Althobaiti, S.; Makhlouf, M.M. Modulation Instability analysis and longitudinal wave propagation in an elastic cylindrical rod modeled with Pochhammer-Chree equation and its modulation instability analysis. Phys. Scr. 2021, 96, 045202. [Google Scholar] [CrossRef]
- Seadawy, A.R.; El-Rashidy, K. Dispersive solitary wave solutions of Kadomtsev-Petviashvili and modified Kadomtsev-Petviashvili dynamical equations in unmagnetized dust plasma. Results Phys. 2018, 8, 1216–1222. [Google Scholar] [CrossRef]
- Bilal, M.; Seadawy, A.R.; Younis, M.; Rizvi, S.T.R.; Rashidy, A.E.; Mahmoud, S.F.M. Analytical wave structures in plasma Physics modeled by Gilson Pickering equation by two integration norms. Results Phys. 2021, 23, 103959. [Google Scholar] [CrossRef]
- Rehman, S.U.; Younis, M.; Seadawy, A.R.; Rizvi, S.T.R.; Sulaiman, T.A.; Yousuf, A. Modulation instability analysis and optical solitons of the generalized model for description of propagation pulses in optical fiber with four nonlinear terms. Mod. Phys. Lett. B 2020, 35, 2150112. [Google Scholar] [CrossRef]
- Cheemaa, N.; Seadawy, A.R.; Chen, S. More general families of exact solitary wave solutions of the nonlinear Schrodinger equation with their applications in nonlinear optics. Eur. Phys. J. Plus 2018, 133, 547. [Google Scholar] [CrossRef]
- Cheemaa, N.; Seadawy, A.R.; Chen, S. Some new families of solitary wave solutions of generalized Schamel equation and their applications in plasma physics. Eur. Phys. J. Plus 2019, 134, 117. [Google Scholar] [CrossRef]
- Goyal, A.; Gupta, R.; Kumar, C.N.; Raju, T.S. Chirped femtosecond solitons and double-kink solitons in the cubic-quintic nonlinear Schrödinger equation with self-steepening and self-frequency shift. Phys. Rev. A 2011, 84, 063830. [Google Scholar]
- Vyas, V.M.; Patel, P.; Panigrahi, P.K.; Kumar, C.N.; Greiner, W. Chirped chiral solitons in the nonlinear Schrödinger equation with self-steepening and self-frequency shift. Phys. Rev. A 2008, 78, 021803. [Google Scholar] [CrossRef] [Green Version]
- Hmurcik, L.V.; Kaup, D.J. Solitons created by chirped initial profiles in coherent pulse propagation. J. Opt. Soc. Am. 1979, 69, 597–604. [Google Scholar] [CrossRef]
- Triki, H.; Porsezian, K.; Grelu, P. Chirped soliton solutions for the generalized nonlinear Schrödinger equation with polynomial nonlinearity and non-Kerr terms of arbitrary order. J. Opt. 2016, 18, 075504. [Google Scholar] [CrossRef]
- Triki, H.; Porsezian, K.; Choudhuri, A.; Dinda, P.T. Chirped solitary pulses for a nonic nonlinear Schrödinger equation on a continuous-wave background. Phys. Rev. A 2016, 93, 063810. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D.; Wang, J. Travelling wave solutions of generalized coupled Zakharov Kuznetsov and dispersive long wave equations. Res. Phys. 2016, 6, 1136–1145. [Google Scholar] [CrossRef] [Green Version]
- Helal, M.A.; Seadawy, A.R. Exact soliton solutions of a D-dimensional nonlinear Schrödinger equation with damping and difusive terms. Z. Angew. Math. Phys. 2011, 62, 839–847. [Google Scholar] [CrossRef]
- Helal, M.A.; Seadawy, A.R. Variational method for the derivative nonlinear Schrödinger equation with computational applications. Phys. Scr. 2009, 80, 350–360. [Google Scholar] [CrossRef]
- Ali, I.; Seadawy, A.R.; Rizvi, S.T.R.; Younis, M.; Ali, K. Conserved quantities along with Painleve analysis and Optical solitons for the nonlinear dynamics of Heisenberg ferromagnetic spin chains model. Int. J. Mod. Phys. B 2020, 34, 2050283. [Google Scholar] [CrossRef]
- Saha, M.; Sarma, A.K. Solitary wave solutions and modulations instability analysis of the nonlinear schrödinger equation with higher order dispersion and nonlinear terms. Commun. Nonlin. Sci. Numer. Simulat. 2013, 18, 2420–2425. [Google Scholar] [CrossRef]
- Palacios, S.L. Optical solitons in highly dispersive media with a dual-power nonlinearity law. J. Opt. A Pure Appl. Opt. 2003, 5, 180–182. [Google Scholar] [CrossRef]
- Rizvi, S.T.R.; Seadawy, A.R.; Ali, I.; Bibi, I.; Younis, M. Chirp-free optical dromions for the presence of higher order spatio-temporal dispersions and absence of self-phase modulation in birefringent fibers. Mod. Phys. Lett. B 2020, 34, 2050399. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Cheemaa, N. Propagation of nonlinear complex waves for the coupled nonlinear Schrödinger Equations in two core optical fibers. Phys. A Stat. Mech. Its Appl. 2019, 529, 121330. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Cheemaa, N. Applications of extended modified auxiliary equation mapping method for high order dispersive extended nonlinear schrodinger equation in nonlinear optics. Mod. Phys. Lett. B 2019, 33, 1950203. [Google Scholar] [CrossRef]
- Bouzida, A.; Triki, H.; Ullah, M.Z.; Zhou, Q.; Biswas, A.; Belic, M. Chirped optical solitons in nano optical fibers with dual-power law nonlinearity. Optik 2017, 142, 77–81. [Google Scholar] [CrossRef]
- Savescu, M.; Khan, K.R.; Kohl, R.W.; Moraru, L.; Yildirim, A.; Biswas, A. Optical Soliton Perturbation with Improved Nonlinear Schrödinger’s Equation in Nano Fibers. J. Nanoelectron. Optoelectron. 2013, 8, 208–220. [Google Scholar] [CrossRef]
- Biswas, A.; Yildirim, Y.; Yasar, M.; Triki, H.; Zhou, Q.; Moshokoa, S.P.; Ullah, M.Z.; Belic, M. Optical soliton perturbation with full nonlinearity in polarization preserving fibers using trial equation method. J. Optoelectron. Adv. Mater. 2018, 20, 385–402. [Google Scholar]
- Ekici, M.; Zhou, Q.; Sonmezoglu, A.; Moshokoa, S.P.; Ullah, M.Z.; Biswas, A.; Belic, M. Solitons in magneto-optic waveguides by extended trial function scheme. Superlattices Microstruct. 2017, 6036, 30745. [Google Scholar] [CrossRef] [Green Version]
- Filiz, A.; Ekici, M.; Sonmezoglu, A. F-Expansion Method and New Exact Solutions of the Schrödinger-KdV Equation. Sci. World J. 2014, 2014, 3928877. [Google Scholar] [CrossRef] [PubMed] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).