Distributed Event-Triggered Approach for Multi-Agent Formation Based on Cooperative Localization with Mixed Measurements

Abstract

This paper concentrates on multi-agent formation control problems under mixed measurements of distance and bearing. Towards this objective, a distributed event-triggered estimation-based control framework is developed such that only at necessary time instants, the event for estimation (namely, cooperative localization among a subgroup of agents) is triggered to recover relative position information by utilizing a mixed distance and bearing measurements from different agents. Firstly, it is shown by using the stiffness theory that a subgroup of agents are capable of recovering relative position information if a sufficient number of independent distance and range measurements are available. Secondly, a distributed event-triggered mechanism is presented for achieving an affine formation control, which can be implemented in an asynchronous manner and also ensures Zeno-free behavior. Simulation studies are provided to demonstrate the effective performance of the proposed approach.

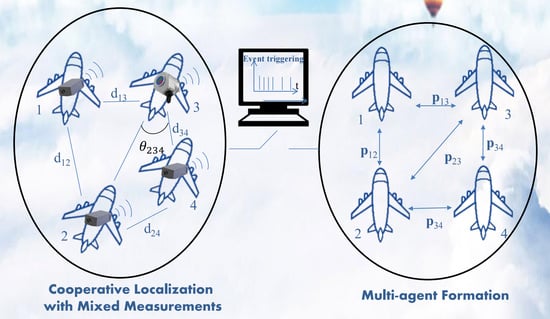
1. Introduction

Formation control [1,2] is one of the most fundamental issues in the realm of multi-agent cooperative control, which is inspired by the formation tactics of biological organisms, such as birds flying in a V-formation to reduce the energy expenditure [3] and ants efficiently feeding with separation distances [4]. A distributed formation control of multi-agent systems has received a lot of attention from enormous researches and applications, such as ocean data retrieval, satellite formation flying and source seeking and exploration [5,6]. The objective of the multi-agent formation is to design interaction control strategies for individual agents such that a collective behavior with desired geometric shapes emerges [7].

According to the difference of sensed and controlled variables, several control schemes have been considered in the existing literature, such as a displacement-based, distance-based and bearing-based formation control for groups of mobile agents. There are enormous and efficient researches on displacement-based distributed formation control methods with local and global convergence results [8,9,10,11]. However, in some applications, it is limited by the sensor capability such that we need to use the distances [5,12,13,14] or bearings [2,15,16,17] or both measurements [18,19,20,21,22] to achieve desired formation shapes. The challenging problem for distance-based methods is to achieve global stability of the desired formation due to the absence of an available common orientation sense. The instinct issue of the bearing-based methods is that the scaling freedom of the formation is released. To overcome the shortcomings of distance-based and bearing-based methods, an approach to formation control with both distance and bearing measurements is studied. However, for an n-agent system, there exist some challenges such as the absence of a unified framework to deal with distance and bearing measurements simultaneously, and the existence of an undesired equilibrium in many of the existing systems [19,21].

The most existing work on formation control utilizes relative position information as feedback. However, the agents in a multi-agent system may only have the capability of measuring one type of information such as distances or bearing angles. Therefore, the main idea of this paper is to develop a distributed estimation scheme, called relative localization, to recover the relative position information based on range and bearing measurements from different agents and, then, present a distributed control law to achieve an affine formation. Nevertheless, since relative localization can only be executed in discrete time asynchronously due to measurement sampling, communication and computation, a distributed event-triggered control framework is considered, in place of a continuous time feedback control framework, such that, only at a necessary time, the event for estimation (namely, cooperative localization among a subgroup of agents) is triggered to recover relative position information. Firstly, we show by using the stiffness theory that an agent together with its neighbors are capable of recovering relative position information from mixed range and bearing measurements if a sufficient number of independent measurements is available in the subgraph. Based on this fundamental result, relative coordinates of neighboring agents in a subgraph can be solved locally in a local coordinate frame, which are then used as feedback information to a formation control law. Secondly, a distributed event-triggered mechanism is presented for an affine formation control. It shows that the distributed event-triggered formation control strategy can be implemented in an asynchronous manner without requiring all agents simultaneously to recover relative position information. Moreover, it is shown that Zeno behavior is avoided under the proposed mechanism. As is well known, the developed event-triggered protocol also has its advantage on relieving the burden of sensing, communication and computing in the process of generating control signals [23,24,25], which is a great benefit to solve the problem in this paper as the estimation process can not be performed in continuous time. In fact, our schemes can be applied to various kinds of formation control strategies rather than the one for affine formation control discussed in the paper. A distributed event-triggered formation control framework based on cooperative localization with mixed measurements is constructed in Figure 1.

The contributions of this paper are as follows. Firstly, relative localization results based on the stiffness theory are integrated into a distributed affine formation control with mixed distance and bearing measurements, which extends the application range of formation control. Secondly, a distributed event-triggered mechanism with asynchronous sampling and estimation computing is developed for an affine formation control, which avoids running the relative localization algorithm in continuous time and reduces information exchange among agents. Finally, the proposed approach can ensure the convergence of n agents to a desired affine formation exponentially in the 2-dimensional space while avoiding Zeno-triggering phenomena.

The organization of this paper is as follows. In Section 2, some preliminaries are given and the problem setup is formulated. In Section 3, a fundamental result on cooperative localization based on the stiff theory is presented. Then, a distributed event-triggered formation control strategy is developed, the analysis of exponential convergence is given, and the Zeno-free behavior is concluded in Section 4. Section 5 shows simulation results to illustrate the efficiency of our proposed approach. Concluding remarks are discussed in Section 6.

2. Preliminaries and Problem Formulation

2.1. Graph Theory

An undirected graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ consists of a node set $\mathcal{V}$ and an edge set $\mathcal{E}$, where an edge is a pair of distinct nodes of $\mathcal{G}$. Instead, a directed graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$ consists of a node set $\mathcal{V}$ and an edge set $\mathcal{E}$, where an edge is an ordered pair of distinct nodes of $\mathcal{G}$. Denote $\left|\mathcal{V}\right|=n$ and $\left|\mathcal{E}\right|=l$. For each agent $i\in \mathcal{V}$, the set of its neighbors is denoted as ${\mathcal{N}}_i=j\in \mathcal{V}:(j,i)\in \mathcal{E}$.

A configuration of n points in ${\mathbb{R}}^2$ is defined by their coordinates in the Euclidean space ${\mathbb{R}}^2$, denoted as $p={[p_1^{\mathrm{T}},\dots ,p_n^{\mathrm{T}}]}^{\mathrm{T}}$, where each $p_i\in {\mathbb{R}}^2$ denotes agent i’s position for $i\in 1,2,\dots n$. A configuration is generic if all the coordinates $p_1,\dots ,p_n$ are algebraically independent over the integer coefficients [26].

A framework in ${\mathbb{R}}^2$ is a graph $\mathcal{G}$ equipped with a configuration p with each agent living in the 2-dimensional space, denoted as ${\mathcal{F}}_p=(\mathcal{G},p)$. In this paper, we consider frameworks modelled by undirected graphs. Two frameworks $(\mathcal{G},p)$ in ${\mathbb{R}}^{d_1}$ and $(\mathcal{G},q)$ in ${\mathbb{R}}^{d_2}$ are stated to be equivalent, and we write $(\mathcal{G},p)\cong (\mathcal{G},q)$, if $\parallel p_i-p_j\parallel =\parallel q_i-q_j\parallel ,\forall (i,j)\in \mathcal{E}$. Moreover, two frameworks $(\mathcal{G},p)$ and $(\mathcal{G},q)$ are stated to be congruent, and we write $(\mathcal{G},p)\equiv (\mathcal{G},q)$, if $\parallel p_i-p_j\parallel =\parallel q_i-q_j\parallel ,\forall i,j\in \mathcal{V}.$

2.2. Affine Formation

Consider a configuration $p={[p_1^{\mathrm{T}},\dots ,p_n^{\mathrm{T}}]}^{\mathrm{T}}$. We denoted the affine image of p as:

$$\mathcal{A}\left(p\right):=\left\{\begin{array}{c}q={[q_1^{\mathrm{T}},\dots ,q_n^{\mathrm{T}}]}^{\mathrm{T}}:q_i=A{p}_i+a,\\ A\in {\mathbb{R}}^{2\times 2},a\in {\mathbb{R}}^2,i=1,\dots ,n\end{array}\right\}$$

(1)

or, equivalently:

$$\mathcal{A}\left(p\right):=\left\{q=(I_n\otimes A)p+{\mathbf{1}}_n\otimes a:A\in {\mathbb{R}}^{2\times 2},a\in {\mathbb{R}}^2\right\}.$$

(2)

where ⊗ denotes the Kronecker product.

Let us denote the affine span of p as [27]

$$\mathcal{S}:=\left\{\begin{array}{c}\sum _{i=1}^n{\theta }_i{p}_i:{\theta }_i\in \mathbb{R}\mathrm{for} \mathrm{all}i\mathrm{and}\sum _{i=1}^n{\theta }_i=1\end{array}\right\}.$$

(3)

The affine span of three non-collinear points (in a space of dimension at least two) is the two-dimensional plane passing through the three points. Given any $\mathcal{S}$, it can always be translated to a linear space containing the origin.

Consider an undirected communication graph and a configuration p in ${\mathbb{R}}^2$ of n points. A symmetric matrix L in the following form:

$$L(i,j)=\left\{\begin{array}{cc}-w_{ij}& ifi\ne j \mathrm{and} j\in {\mathcal{N}}_i,\hfill \\ 0& ifi\ne j \mathrm{and} j\notin {\mathcal{N}}_i,\hfill \\ {\displaystyle \sum _{k\in {\mathcal{N}}_i}{w}_{ik}}& ifi=j,\hfill \end{array}\right.$$

(which, as will be noted, satisfies $L{\mathbf{1}}_n=0$) is called a stress matrix if it also satisfies $(L\otimes I_2)p=0$. The parameter $w_{ij}$ is a scalar weight of edge $(i,j)$ and is a real number. The stress matrix L is often interpreted in a tensegrity framework, with positive stress corresponding to a cable and negative stress to a strut. In physics, $w_{ij}$ is interpreted as the axial force per unit length along the member $(i,j)$ [28,29]. The weights $w_{ij}$ can be designed by solving a semi-definite programming as shown in [10].

We now recall the definitions of universal rigidity and formation stabilizability, and introduce two results to characterize the universal rigidity in terms of the stress matrix and the stabilizability of an affine formation.

Definition 1

([10]). A framework $(\mathcal{G},p)$ in ${\mathbb{R}}^d$ is called universally rigid if, for any configuration, q in ${\mathbb{R}}^s$ with s being any positive integer, $(\mathcal{G},p)\cong (\mathcal{G},q)$ implies $(\mathcal{G},p)\equiv (\mathcal{G},q)$.

Lemma 1

([28]). Suppose that an undirected graph $\mathcal{G}$ has n nodes with $n\ge d+2$ and that $p={[p_1^{\mathrm{T}},\dots ,p_n^{\mathrm{T}}]}^{\mathrm{T}}$ is a generic configuration in ${\mathbb{R}}^d$. The framework $(\mathcal{G},p)$ is universally rigid if—and only if—there exists a stress matrix L that is of rank $n-d-1$ and is positive semi-definite.

Definition 2

([10]). For a target configuration p, an affine formation of p is stated to be stabilizable over the undirected graph $\mathcal{G}$ if there exists a symmetric matrix L associated with $\mathcal{G}$, such that the state of the closed-loop system $\dot{p}=-(L\otimes I_2)p$ converges to a point in $\mathcal{A}\left(p\right)$.

Lemma 2

([10]). Suppose that an undirected graph $\mathcal{G}$ has n nodes with $n\ge d+2$ and that $p={[p_1^{\mathrm{T}},\dots ,p_n^{\mathrm{T}}]}^{\mathrm{T}}$ is a generic configuration in ${\mathbb{R}}^d$. Then, an affine formation of p is stabilizable over $\mathcal{G}$ if—and only if—$\mathcal{G}$ is universally rigid.

2.3. Stiffness Theory

Consider two frameworks ${\mathcal{F}}_p$ and ${\mathcal{F}}_q$ on the same underlying graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$. Suppose that the edge set $\mathcal{E}$ consists of two types of measurements, namely, $\mathcal{E}={\mathcal{E}}_D\cup {\mathcal{E}}_B$, where an edge $(i,j)\in {\mathcal{E}}_D$ means that node j has the capability of distance measurement and can measure the distance between i and j and, similarly, an edge $(i,j)\in {\mathcal{E}}_B$ means that node j has the capability of bearing measurement and can measure the bearing angle information about agent j in its local frame.

For $i\in 1,\cdots ,n$, we introduced the range-based infinitesimal motion constraint:

$${(p_i-p_j)}^{\mathrm{T}}({\dot{p}}_i-{\dot{p}}_j)=0,(i,j)\in {\mathcal{E}}_D,$$

(4)

and the bearing-based infinitesimal motion constraint:

$${({(p_i-p_j)}^{\perp })}^{\mathrm{T}}({\dot{p}}_i-{\dot{p}}_j)=0,(i,j)\in {\mathcal{E}}_B.$$

(5)

where the operator ${(·)}^{\perp }$ rotates a plane vector by $\pi /2$ counterclockwise. According to (4) and (5), the matrix form of these constraints is given by:

$$R\left(p\right)\dot{p}=0$$

(6)

where $R\left(p\right)\in {\mathbb{R}}^{l\times 2n}$. We, then, presented several definitions and preliminary results regarding stiff frameworks.

Definition 3

([30]). Suppose ${\mathcal{F}}_p$ and ${\mathcal{F}}_q$ are both defined on the same graph $\mathcal{G}(\mathcal{V},{\mathcal{E}}_D\cup {\mathcal{E}}_B)$. Then, ${\mathcal{F}}_q$ is stated to be a shake with respect to ${\mathcal{F}}_p$ if—and only if—(4) is satisfied for all $(i,j)\in {\mathcal{E}}_D$ and (5) is satisfied for all $(i,j)\in {\mathcal{E}}_B$.

Definition 4

([30]). A framework ${\mathcal{F}}_p$ is stated to be a stiff framework if all shakes of ${\mathcal{F}}_p$ can be obtained via only translations.

Lemma 3

([30]). A framework ${\mathcal{F}}_p$ of n agents is stiff if $rank \left(R\right(p\left)\right)=2n-2$.

2.4. Problem Formulation

Most existing work on formation control utilizes relative position information as feedback. However, in a multi-agent system, some agents may only have the capability of range measurements while some others may only have the capability of bearing measurements. Therefore, the main idea of this paper was to develop a distributed estimation scheme, called relative localization, to recover the relative position information based on range and bearing measurements and, then, present a distributed control law to achieve an affine formation. Nevertheless, since relative localization can only be conducted in a discrete time asynchronously due to measurement sampling, communication and computation, a distributed event-triggered control framework was considered, in place of a continuous time feedback control framework.

Consider a network of n agents with an undirected communication graph $\mathcal{G}=(\mathcal{V},\mathcal{E})$, and an edge $(i,j)\in \mathcal{E}$ means that agent i and j can mutually talk to each other. Denote ${\mathcal{E}}^{*}$ as the directed edge set that is expanded from $\mathcal{E}$ such that $(i,j)$ and $(j,i)$ are both in ${\mathcal{E}}^{*}$ when an undirected edge $(i,j)$ belongs to $\mathcal{E}$. Next, the n agents construct a directed sensor graph ${\mathcal{G}}^s=(\mathcal{V},{\mathcal{E}}_D\cup {\mathcal{E}}_B)$ with mixed distance and bearing measurements, where it is assumed that ${\mathcal{E}}_D\subset {\mathcal{E}}^{*}$ and ${\mathcal{E}}_B\subset {\mathcal{E}}^{*}$. Denote the state of n agents as $p={[p_1^{\mathrm{T}},\dots ,p_n^{\mathrm{T}}]}^{\mathrm{T}}$. Then, the measurements are summarized in the following:

(1)

The set of distance measurements $\mathcal{D}$:

$$\mathcal{D}\left(p\right)=\{d_{ij}\in {\mathcal{R}}^{+}:(i,j)\in {\mathcal{E}}_D\}$$

(7)

where $d_{ij}:=\left|\right|p_j-p_i\left|\right|=d_{ji}$.

(2)

The set of bearing measurements $\mathcal{B}$:

$$\mathcal{B}\left(p\right)=\{{\varphi }_{ij}\in [-\pi ,\pi ):(i,j)\in {\mathcal{E}}_B\}.$$

(8)

It was assumed that each agent i had its own local coordination frame ${\sum }_i$ for $i=1,\dots ,n$, but they had a common sense of direction. In other words, without the loss of generality, we could state that all the local coordinate systems have a relative orientation offset, say, ${\alpha }_g$, with respect to the global coordinate system. An illustration for the distance and bearing measurements is given in Figure 2. By introducing an auxiliary angle ${\delta }_{jik}=|{\varphi }_{ij}-{\varphi }_{ik}|\in [0,2\pi )$ with $k\in {\mathcal{N}}_i$, the interior angle ${\theta }_{jik}$ between the edge $(j,i)$ and the edge $(k,i)$ was calculated by:

$${\theta }_{jik}:=\left\{\begin{array}{cc}{\delta }_{jik}& \mathrm{if} {\delta }_{jik}\le \pi ,\hfill \\ 2\pi -{\delta }_{jik}& \mathrm{otherwise},\hfill \end{array}\right.$$

(9)

with ${\theta }_{jik}\in [0,\pi )$.

In addition, each agent was equipped with an internal odometer to measure the relative motion within a very short time.

Suppose each agent is governed by single integrator dynamics:

$${\dot{p}}_i=u_i,i=1,\dots ,n,$$

(10)

where $u_i\in {\mathbb{R}}^2$. Considering the relative orientation offset ${\alpha }_g$, the actual dynamics system of each agent i became:

$${\dot{p}}_i=T\left({\alpha }_g\right)u_i^a$$

(11)

where $u_i^a$ is the actual control input of agent i and $T(·)$ is the rotation matrix.

In this paper, we determined the following assumption.

Assumption 1.

Configuration p is generic.

3. Sufficient Conditions on Relative Localization

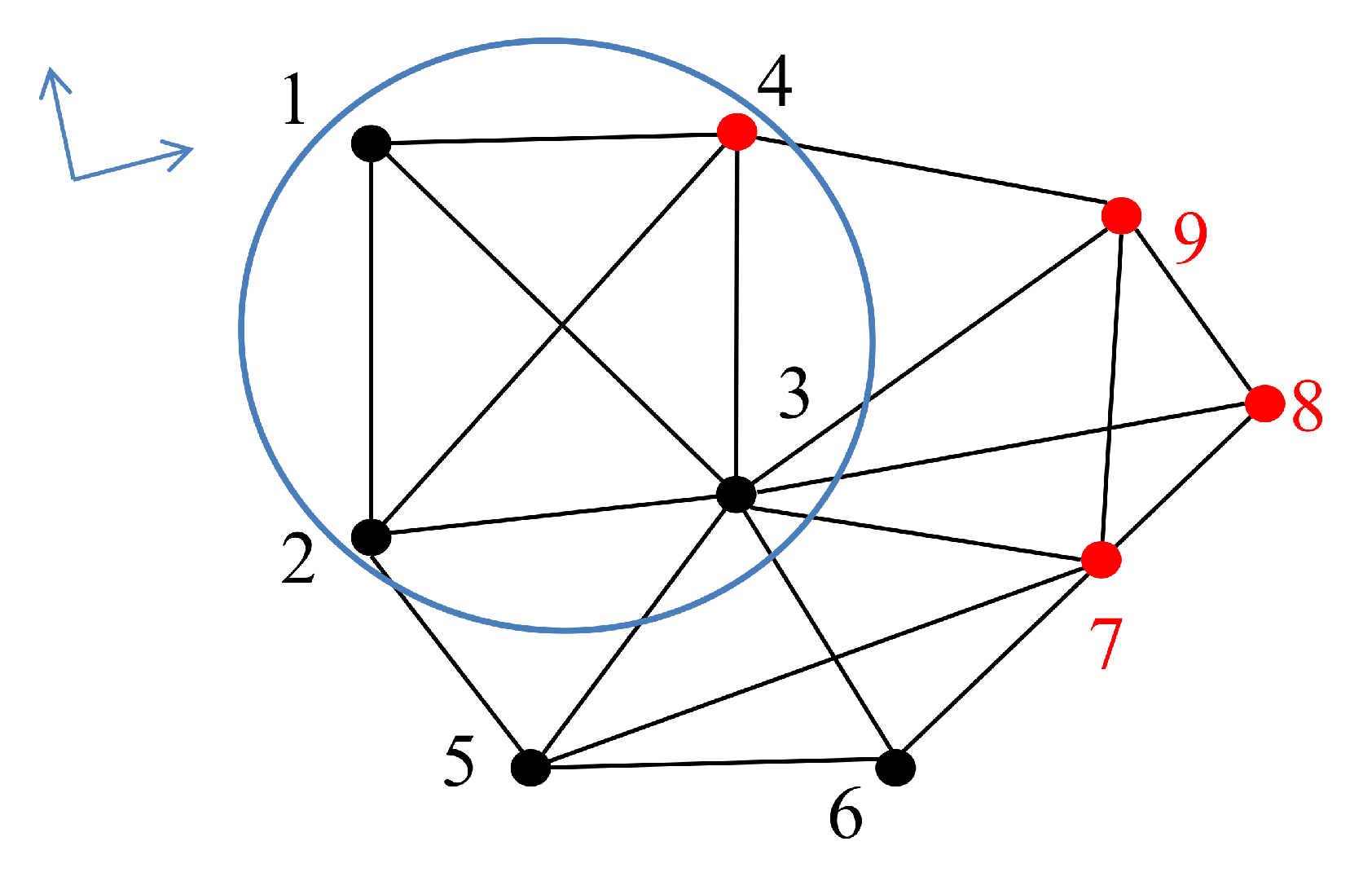
In this section, we show how to cooperatively recover relative position information in each agent’s local coordinate frame based on distance and bearing measurements. Towards this objective, the sensing graph ${\mathcal{G}}^s$ was partitioned into several subgraphs according to their neighboring relationship, stating ${\mathcal{G}}_1^s,\cdots ,{\mathcal{G}}_M^s$. An illustration of the sensing graph with mixed measurements is given in Figure 3.

Denote the mth subgraph as ${\mathcal{G}}_m^s=({\mathcal{V}}_m,{\mathcal{E}}_m^D\cup {\mathcal{E}}_m^B)$ for $m=1,\dots ,M$ where M is the number of subgraphs. The number of ${\mathcal{V}}_m$ is $|{\mathcal{V}}_m|=r_m$. Denote ${\mathcal{F}}_{p^m}$ the framework associated with the mth subgraph ${\mathcal{G}}_m^s$, where $p^m={[{p_1^m}^{\mathrm{T}},\dots ,{p_{r_m}^m}^{\mathrm{T}}]}^{\mathrm{T}}$ is the position vector of the agents in ${\mathcal{G}}_m^s$. After this partition, it was desired that the agents in the same subgraph ${\mathcal{G}}_m^s$ could cooperatively solve the relative positions in their local coordinate frame at a time when relative localization was needed. In other words, it was not necessary to have all the agents in ${\mathcal{G}}_m^s$ to compute the relative position information at the same time, which, thus, could lead to asynchronous and distributed event triggering.

Configuration $p^m$ was stated to be relatively localizable over the subgraph ${\mathcal{G}}_m^s$ if the relative positions of agents in ${\mathcal{G}}_m^s$ could be uniquely determined in a local coordinate frame. The following result provides a sufficient condition for relative localization over subgraph ${\mathcal{G}}_m$.

Theorem 1.

A configuration $p^m$ is relatively localizable over the subgraph ${\mathcal{G}}_m^s$ if $rank \left(R\left(p^m\right)\right)=2r_m-2$.

Proof. 

The constraint matrix corresponding to all measurements between agents in ${\mathcal{G}}_m^s$ was given by

$$R\left(p^m\right){\dot{p}}^m=0$$

(12)

where $R\left(p^m\right)\in {\mathbb{R}}^{l_m\times 2r_m}$.

Suppose $\mathrm{rank}\left(R\left(p^m\right)\right)=2r_m-2$. Then, by Lemma 3, it was observed that the framework ${\mathcal{F}}_{p^m}=({\mathcal{G}}_m^s,p^m)$ was stiff. In other words, since it had $\mathrm{rank}\left(R\left(p^m\right)\right)=2r_m-2$, it was known that the kernel of the constrain matrix $R\left(p^m\right)$ was of dimension 2 and there were two linearly independent solutions ${\dot{p}}^m$ to (12). Let ${\mathcal{F}}_{q^m}$ be any framework over the same subgraph ${\mathcal{G}}_m^s$ satisfying (12). Then, it would be known that it only has the freedom of translation relative to ${\mathcal{F}}_{p^m}$. Therefore, if we had set the coordinate of agent i as the origin of its coordinate frame, the position vectors of all agents in ${\mathcal{G}}_m^s$ could be solved uniquely in the local coordinate frame of agent i. This implies that $p^m$ was relatively localizable. □

Remark 1.

When Theorem 1 is satisfied, the relative position information can be solved by using the gradient method in subgraph ${\mathcal{G}}_m^s$. We used the vector $q={[{q_1^m}^{\mathrm{T}},\dots ,{q_{r_m}^m}^{\mathrm{T}}]}^{\mathrm{T}}$ to denote the location information recovered in a local coordinate system where the coordinate of agent i with bearing measurement capabilities was 0. That is, $q_1^m,\dots ,q_{r_m}^m$ were the relative coordinates with respect to agent i, which were exactly the information required for the formation control. In a mathematical way, $q_1^m,\dots ,q_{r_m}^m$ could be written as $q_j^m=T(-{\alpha }_g)(p_j^m-p_i^m)$, for $j=1,\dots ,r_m$, where $T(·)$ is the rotation matrix.

At each time, an agent only needed to collaborate with its neighbors via communication to satisfy the condition in Theorem 1 and, then, it would be able to compute relative coordinates of its neighbors based on mixed range and bearing measurements in the subgraph. Different agents could compute these relative coordinates locally in different time when needed. In the next section, we provided a distributed event-triggered control strategy, for which an event was triggered to update the control law and only at the time when the event occurred, relative localization needed to be conducted.

4. Distributed Event-Triggered Formation Control

For an affine formation control, when the relative position can be available in a continuous time, a novel distributed control law was proposed in [10] as follows:

$$u_i\left(t\right)=-\sum _{j\in {\mathcal{N}}_i}{w}_{ij}\left(p_i\left(t\right)-p_j\left(t\right)\right)$$

(13)

where $w_{ij}$ is a signed real weight. Then, the closed-loop system was:

$${\dot{p}}_i\left(t\right)=-\sum _{j\in {\mathcal{N}}_i}{w}_{ij}\left(p_i\left(t\right)-p_j\left(t\right)\right),$$

(14)

and the matrix form of (14) was:

$$\dot{p}\left(t\right)=-(L\otimes I_2)p\left(t\right),$$

(15)

where L is the stress matrix. According to Lemma 1 and Lemma 2, if graph $\mathcal{G}$ was universally rigid, then a stress matrix L could be found being positive semidefinite and of rank $n-3$. Moreover, by using this choice of the stress matrix, the desired affine formation was stabilizable.

However, as discussed in this paper, no relative position could be obtained in a continuous time. Instead, mixed range and bearing information were measured in a discrete time and, moreover, recovering relative positions from range and bearing measurements takes time and computation resources. Therefore, we modified the continuous-time formation control law by proposing a distributed event-triggered mechanism such that each agent ran relative localization algorithms only at a necessary time and, furthermore, computation could be performed in an asynchronous setup. That is,

$$u_i^a\left(t\right)=\sum _{j\in {\mathcal{N}}_i}{w}_{ij}{q}_j\left({\tau }_s^i\right)=-\sum _{j\in {\mathcal{N}}_i}{w}_{ij}T(-{\alpha }_g)\left(p_i\left({\tau }_s^i\right)-p_j\left({\tau }_s^i\right)\right),\forall t\in \left[{\tau }_s^i,{\tau }_{s+1}^i\right)$$

(16)

where ${\tau }_s^i$ represents the event-triggering time instants. Later, in this section, we showed when the events should have been triggered.

Substituting the control law (16) into the original system (11), we obtained:

$${\dot{p}}_i\left(t\right)=-\sum _{j\in {\mathcal{N}}_i}{w}_{ij}\left(p_i\left({\tau }_s^i\right)-p_j\left({\tau }_s^i\right)\right),\forall t\in \left[{\tau }_s^i,{\tau }_{s+1}^i\right)$$

(17)

For convenience, we used the notation ${\widehat{p}}_i\left(t\right)$ and ${\widehat{p}}_j\left(t\right)$ to describe $p_i\left({\tau }_s^i\right)$ and $p_j\left({\tau }_s^i\right)$, respectively. Now, let us introduce the state error $e_i\left(t\right)$ for agent i and denote $e={[e_1\left(t\right),\dots ,e_n\left(t\right)]}^{\mathrm{T}}$. The state error $e_i\left(t\right)$ was defined as

$$e_i\left(t\right)=p_i\left({\tau }_s^i\right)-p_i\left(t\right)={\widehat{p}}_i\left(t\right)-p_i\left(t\right),t\in \left[{\tau }_s^i,{\tau }_{s+1}^i\right)$$

(18)

where ${\tau }_s^i$ is the event-triggering time instant of agent i and $s=\{0,1,\cdots \}$.

Remark 2.

Notice that at time instant $t={\tau }_s^i$, $e_i\left(t\right)=0$, and for $t\in \left[{\tau }_s^i,{\tau }_{s+1}^i\right)$, $e_i\left(t\right)$ was indeed the relative movement of agent i from ${\tau }_s^i$ to t. In a short time interval, $e_i\left(t\right)$ could be measured by the internal odometer of agent i.

Thus, the closed-loop dynamic system (17) could be written as:

$${\dot{p}}_i\left(t\right)=-\sum _{j\in {\mathcal{N}}_i}{w}_{ij}\left({\widehat{p}}_i\left(t\right)-{\widehat{p}}_j\left(t\right)\right).$$

(19)

The matrix form of the closed-loop system was given by:

$$\dot{p}\left(t\right)=-(L\otimes I_2)\widehat{p}\left(t\right),$$

(20)

where $\widehat{p}={[{\widehat{p}}_1^{\mathrm{T}},\dots ,{\widehat{p}}_n^{\mathrm{T}}]}^{\mathrm{T}}$.

Now, we are ready to present the main results that our distributed event-triggered control law ensured a convergence towards the desired affine formation.

Theorem 2.

Consider the following event-triggering function:

$$f\left(e_i\right)=\parallel e_i{\parallel }^2-\frac{{\delta }_i(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}{\parallel z_i\parallel }^2$$

(21)

with $z_i={\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}\left({\widehat{p}}_i-{\widehat{p}}_j\right)$, ${\delta }_i\in (0,1)$ and $\eta >|{\mathcal{N}}_i|$. The system (20) with ${\tau }_s^i$, $s=0,1,2,\dots$, being the event-triggering time instants of agent i, asymptotically converged to an affine formation if the event was triggered in the conditions of:

$$f\left(e_i\right)\ge 0.$$

(22)

Proof. 

We considered a candidate Lyapunov function for the closed-loop system (20) as $V=\frac{1}{2}{p}^{\mathrm{T}}(L\otimes I_2)p$. Taking the time derivative of V along the solution of (20) yielded:

$$\begin{array}{cc}\hfill \dot{V}& =p^{\mathrm{T}}(L\otimes I_2)\dot{}p\hfill \\ & =-{(\widehat{p}-e)}^{\mathrm{T}}(L\otimes I_2)(L\otimes I_2)\widehat{p}.\hfill \end{array}$$

Let us introduce an auxiliary vector $z:=(L\otimes I_2)\widehat{p}$ and $z={[z_1^{\mathrm{T}},z_2^{\mathrm{T}},\dots ,z_n^{\mathrm{T}}]}^{\mathrm{T}}$ which were used to simplify the form of $\dot{V}$. Equivalently,

$$z_i\left(t\right)=\sum _{j\in {\mathcal{N}}_i}{w}_{ij}\left({\widehat{p}}_i\left(t\right)-{\widehat{p}}_j\left(t\right)\right),i=1,\dots ,N.$$

(23)

According to the properties of the stress matrix L and Young’s inequality $\left|a^{\mathrm{T}}b\right|\le {(\eta /2)\parallel a\parallel }^2+(1/2\eta ){\parallel b\parallel }^2$ with $\eta >0$ [31], it had:

$$\begin{array}{cc}\hfill \dot{V}=& -z^{\mathrm{T}}z+e^{\mathrm{T}}(L\otimes I_2)z\hfill \\ \hfill =& -\sum _{i=1}^n{z}_i^{\mathrm{T}}{z}_i+\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}{w}_{ij}{\left(e_i-e_j\right)}^{\mathrm{T}}{z}_i\hfill \\ \hfill =& -\sum _{i=1}^n{z}_i^{\mathrm{T}}{z}_i+\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}\left(w_{ij}{e}_i^{\mathrm{T}}{z}_i-w_{ij}{e}_j^{\mathrm{T}}{z}_i\right)\hfill \\ \hfill \le & -\sum _{i=1}^n{z}_i^{\mathrm{T}}{z}_i+\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}\left(\frac{\eta }{2}(w_{ij}^2{e}_i^{\mathrm{T}}{e}_i)+\frac{1}{\eta }{z}_i^{\mathrm{T}}{z}_i+\frac{\eta }{2}(w_{ij}^2{e}_j^{\mathrm{T}}{e}_j)\right)\hfill \\ \hfill =& -(1-\frac{|{\mathcal{N}}_i|}{\eta })\sum _{i-1}^n{z}_i^{\mathrm{T}}{z}_i+\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}\frac{\eta }{2}(w_{ij}^2{e}_i^{\mathrm{T}}{e}_i)+\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}\frac{\eta }{2}(w_{ij}^2{e}_j^{\mathrm{T}}{e}_j),\hfill \end{array}$$

(24)

where $|{\mathcal{N}}_i|$ means the number of neighbors of agent i. As L was symmetric, it had the following equality:

$$\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}(w_{ij}^2{e}_j^{\mathrm{T}}{e}_j)=\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}(w_{ij}^2{e}_i^{\mathrm{T}}{e}_i).$$

Then, (24) was simplified as:

$$\begin{array}{cc}\hfill \dot{V}& \le -\sum _{i=1}^n(1-\frac{|{\mathcal{N}}_i|}{\eta })z_i^{\mathrm{T}}{z}_i+\sum _{i=1}^n\sum _{j\in {\mathcal{N}}_i}\eta (w_{ij}^2{e}_i^{\mathrm{T}}{e}_i)\hfill \\ \hfill & =-\sum _{i=1}^n\left((1-\frac{|{\mathcal{N}}_i|}{\eta })\parallel z_i{\parallel }^2-\eta \sum _{j\in {\mathcal{N}}_i}{w}_{ij}^2{\parallel e_i\parallel }^2\right)\hfill \end{array}$$

(25)

Let the positive parameter $\eta$ be $\eta >|{\mathcal{N}}_i|$ for all $i\in \mathcal{V}$. It had:

$$\dot{V}\le -\sum _{i=1}^n\left(1-{\delta }_i\right)(1-\frac{|{\mathcal{N}}_i|}{\eta }){\parallel z_i\parallel }^2,$$

(26)

if one enforced:

$$\parallel e_i{\parallel }^2\le \frac{{\delta }_i(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}{\parallel z_i\parallel }^2$$

(27)

where ${\delta }_i\in (0,1)$ and z were given in (23).

To reduce the update frequency of the control input, the event-triggered mechanism was introduced. For each agent i, the event was triggered when the function

$$f\left(e_i\right)=\parallel e_i{\parallel }^2-\frac{{\delta }_i(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}{\parallel z_i\parallel }^2$$

(28)

with ${\delta }_i\in (0,1)$ became non-negative, i.e., $f\left(e_i\right)\ge 0$.

If $f\left(e_i\right)<0$, the control input of agent i would remain constant and the error $e_i$ may increase gradually. At the instant ${\tau }_s^i$ for $s=0,1,\dots$, $e_i$ would be reset to zero as Function (22) was triggered and the relative localization task was executed. As a result, (27) always held and $\dot{V}$ stayed negative. Let us denote ${\delta }_{\max }=\max {\delta }_i$ for $i\in \{1,\cdots ,n\}$ in order to bound $\dot{V}$ by:

$$\begin{array}{cc}\hfill \dot{V}& \le -\sum _{i=1}^n\left(1-{\delta }_i\right)\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2}{z}_i^{\mathrm{T}}{z}_i\hfill \\ \hfill & =-\left(1-{\delta }_{\max }\right)\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2}{\widehat{p}}^T{(L\otimes I_2)}^2\widehat{p}\hfill \\ \hfill & \le -\left(1-{\delta }_{\max }\right){\lambda }_{\max }\left(L\right)\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2}{\widehat{p}}^T(L\otimes I_2)\widehat{p}\hfill \\ \hfill & =-\mathcal{B}{\widehat{p}}^T(L\otimes I_2)\widehat{p},\hfill \end{array}$$

(29)

with:

$$\mathcal{B}=\left(1-{\delta }_{\max }\right){\lambda }_{\max }\left(L\right)\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2}>0.$$

As for the Lyapunov candidate function V, it had:

$$\begin{array}{cc}\hfill V=& \frac{1}{2}({\widehat{p}}^T-e)(L\otimes I_2)(\widehat{p}-e)\hfill \\ \hfill =& \frac{1}{2}\left({\widehat{p}}^T(L\otimes I_2)\widehat{p}-2{\widehat{p}}^T(L\otimes I_2)e+e^T(L\otimes I_2)e\right).\hfill \end{array}$$

(30)

Note that:

$$\begin{array}{cc}\hfill e^T(L\otimes I_2)e& \le {\lambda }_{\max }{\left(L\right)\left|\right|e\left|\right|}^2\hfill \\ \hfill & \le {\lambda }_{\max }\left(L\right)\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}{\parallel z_i\parallel }^2\hfill \\ \hfill & \le {\lambda }_{\max }^2\left(L\right)\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}{\widehat{p}}^T(L\otimes I_2)\widehat{p},\hfill \end{array}$$

(31)

and:

$$\begin{array}{cc}\hfill |e^T(L\otimes I_2)\widehat{p}|\le & \left|\right|(L\otimes I_2)\widehat{p}\left|\right|\left|\right|e\left|\right|\hfill \\ \hfill \le & \sqrt{{\lambda }_{\max }\left(L\right){\widehat{p}}^T(L\otimes I_2)\widehat{p}}·\hfill \\ \hfill & \sqrt{{\lambda }_{\max }\left(L\right)\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}{\widehat{p}}^T(L\otimes I_2)\widehat{p}}\hfill \\ \hfill =& \sqrt{\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}}{\lambda }_{\max }\left(L\right){\widehat{p}}^T(L\otimes I_2)\widehat{p}\hfill \\ \hfill =& \mathcal{A}{\widehat{p}}^T(L\otimes I_2)\widehat{p},\hfill \end{array}$$

(32)

with the shorthand notation:

$$\mathcal{A}=\sqrt{\frac{(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}}{\lambda }_{\max }\left(L\right).$$

Then, we substituted (31) and (32) into (30) and obtained:

$$\begin{array}{cc}\hfill V\le & \frac{1}{2}(1-2\mathcal{A}+{\mathcal{A}}^2){\widehat{p}}^T(L\otimes I_2)\widehat{p}\hfill \\ \hfill =& \frac{1}{2}{\left(1-\mathcal{A}\right)}^2{\widehat{p}}^T(L\otimes I_2)\widehat{p}.\hfill \end{array}$$

(33)

It was then obtained that:

$$\begin{array}{cc}\hfill \dot{V}& \le -\mathcal{B}{\widehat{p}}^T(L\otimes I_2)\widehat{p}\hfill \\ \hfill & \le -\frac{2\mathcal{B}}{{\left(1-\mathcal{A}\right)}^2}V.\hfill \end{array}$$

(34)

We set $\mathcal{C}=\frac{2\mathcal{B}}{{\left(1-\mathcal{A}\right)}^2}$. According to the Comparison Lemma [32], it had:

$$V\left(p\left(t\right)\right)\le V\left(p\left(0\right)\right)e^{-\mathcal{C}t}$$

(35)

with $t\ge 0$ such that all agents converged to the desired affine formation exponentially. □

In practice, we also required to check the inter-event times $\{{\tau }_{s+1}^i-{\tau }_s^i\}$ to avoid Zeno behaviors. It was necessary to illustrate the lower bound of the inter-event times $\{{\tau }_{s+1}^i-{\tau }_s^i\}$ away from zero. The following theorem is given for this conclusion.

Theorem 3.

Consider the n-agent system with the same distributed event-triggered control law as in Theorem 2. The system did not exhibit Zeno behavior, that is, agents would not execute measurement sampling, communication and relative localization computation for an infinite number of times in any finite time period.

Proof. 

It was equivalent to showing that the lower bound of the time interval ${\tau }^i={\tau }_{s+1}^i-{\tau }_s^i$ was a positive constant. Notice that during the time period $[{\tau }_s^i,{\tau }_{s+1}^i)$, ${\widehat{p}}_i$ and ${\widehat{p}}_j$ used to update ${\dot{p}}_i$ remain constants. Moreover, given ${\dot{e}}_i=-{\dot{p}}_i$, it had the error evolution:

$$e_i\left(t\right)=-(t-{\tau }_s^i)z_i,\forall t\in \left[{\tau }_s^i,{\tau }_{s+1}^i\right).$$

(36)

Let ${\tau }^i$ be the lower bound such that $f\left(e_i\right)=0$ occurs. According to (36) and the event-triggering condition (22), one, thus, had:

$${\left({\tau }^i\right)}^2{z}_i^{\mathrm{T}}{z}_i-\frac{{\delta }_i(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}{z}_i^{\mathrm{T}}{z}_i=0.$$

(37)

Then, the lower bound of the time interval was given by:

$${\tau }^i=\sqrt{\frac{{\delta }_i(\eta -|{\mathcal{N}}_i\left|\right)}{{\eta }^2{\sum }_{j\in {\mathcal{N}}_i}{w}_{ij}^2}}>0.$$

(38)

The proof is complete. □

Remark 3.

Note that the design parameter ${\delta }_i$ affected the triggering frequency as well as the convergence rate of the closed-loop system. If ${\delta }_i$ was closer to 1, then event-triggering would be less frequent and agent i would contribute less to the convergence rate of the whole formation. The parameter η also affected the triggering behavior: a larger η indicates a smaller threshold value in the triggering condition (22), which would result in more frequent triggering and a shorter triggering time interval as shown in (38).

5. Simulation Results

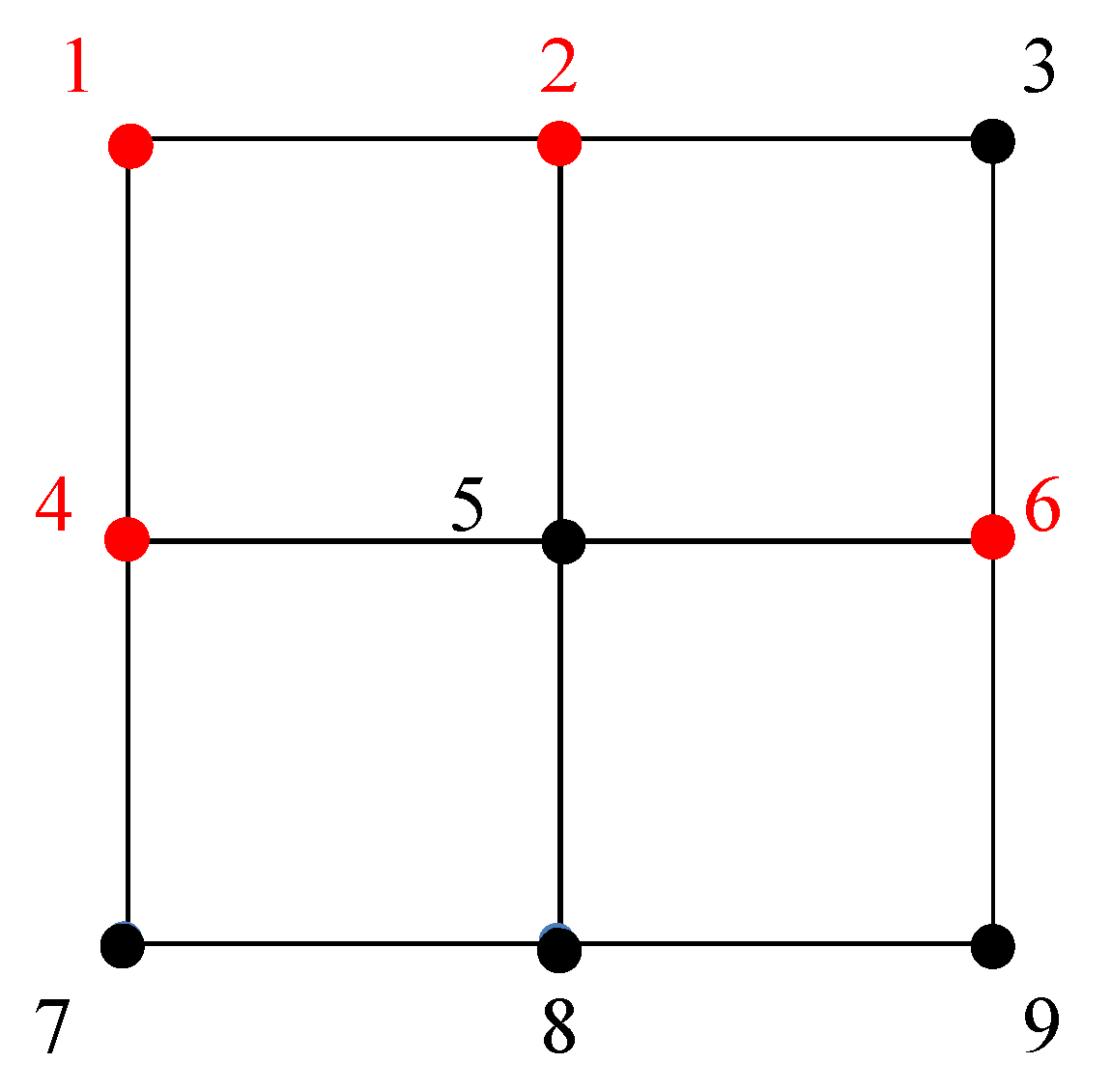
In this section, we present some simulations to illustrate our theoretical algorithms for the distributed affine formation control with both distance and bearing measurements. We considered a nine-agent system with 24 edges and the target configuration is shown in Figure 4. For agents one, two, four and six, they could measure the bearing information while the others could measure the distances of their neighbors. The graph in Figure 4 was divided into 4 subgraphs which were $\{1,2,4,5\}$, $\{2,3,5,6\}$, $\{4,5,7,8\}$ and $\{5,6,8,9\}$.

We gave simulations to verify the proposed distributed event-triggered affine formation control. Consider the same system as above with the distributed event-triggered formation control law (19) and (21). The stress matrix was given by

$$L=\left[\begin{array}{ccccccccc}4& -4& 1& -2& -1& 1& 0& 1& 0\\ -4& 9& -5& 1& -3& 2& 0& 0& 0\\ 1& -5& 4& 1& 1& -2& 0& 0& 0\\ -2& 1& 1& 4& -4& 0& -1& 1& 0\\ -1& -3& 1& -4& 19& -9& 1& -8& 4\\ 1& 2& -2& 0& -9& 7& 0& 5& -4\\ 0& 0& 0& -1& 1& 0& 1& -1& 0\\ 1& 0& 0& 1& -8& 5& -1& 6& -4\\ 0& 0& 0& 0& 4& -4& 0& -4& 4\end{array}\right],$$

(39)

where L was constructed by solving a semi-definite programming as shown in [10] such that $\mathrm{rank}\left(L\right)=6$.

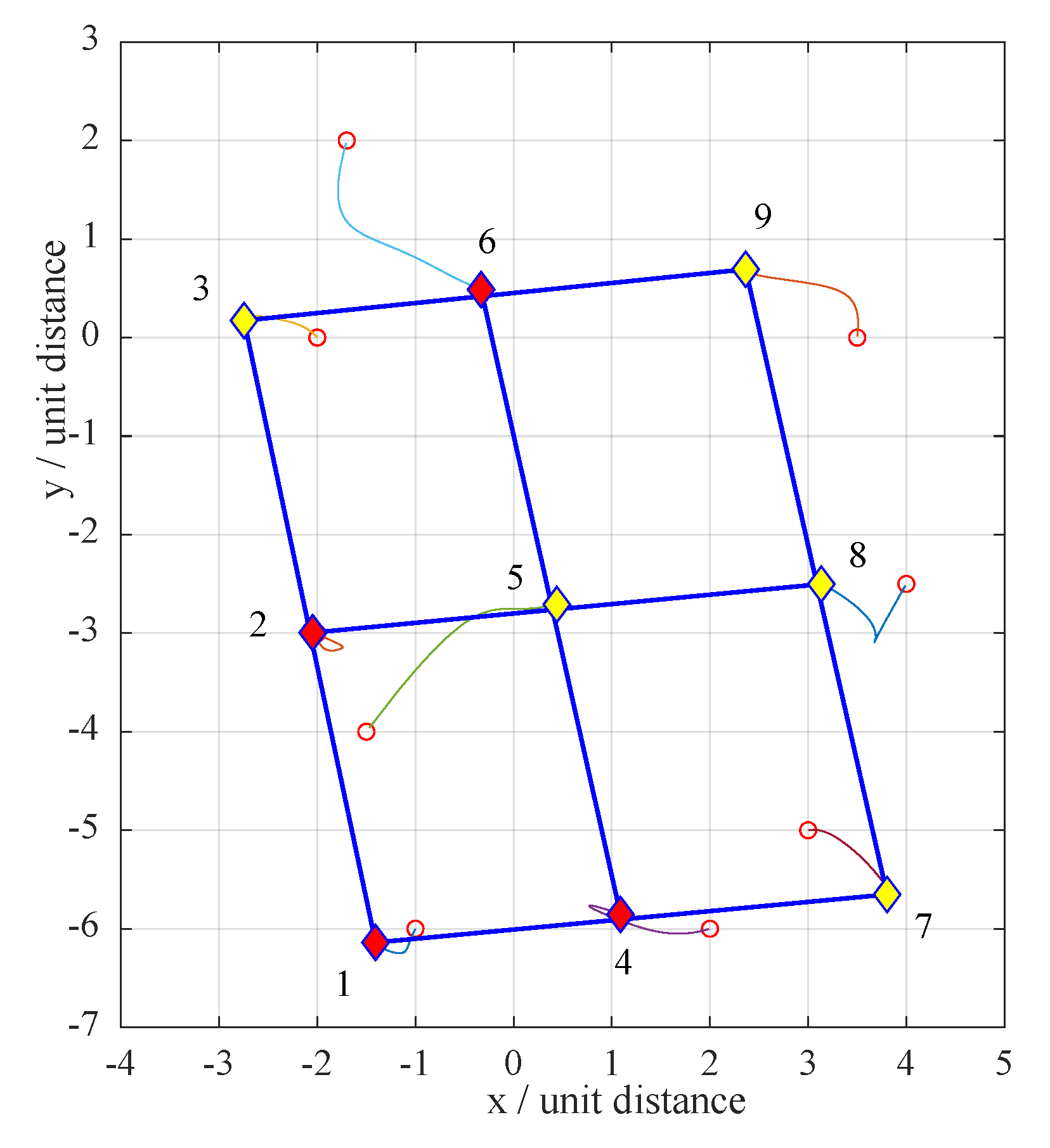
The parameters were set as $\delta =0.6$ and $\eta =12$. Figure 5 shows the evolutionary trajectories of nine agents to achieve the desired affine formation shape in ${\mathbb{R}}^2$. It was given with arbitrary initial states (based on distance and bearing measurements).

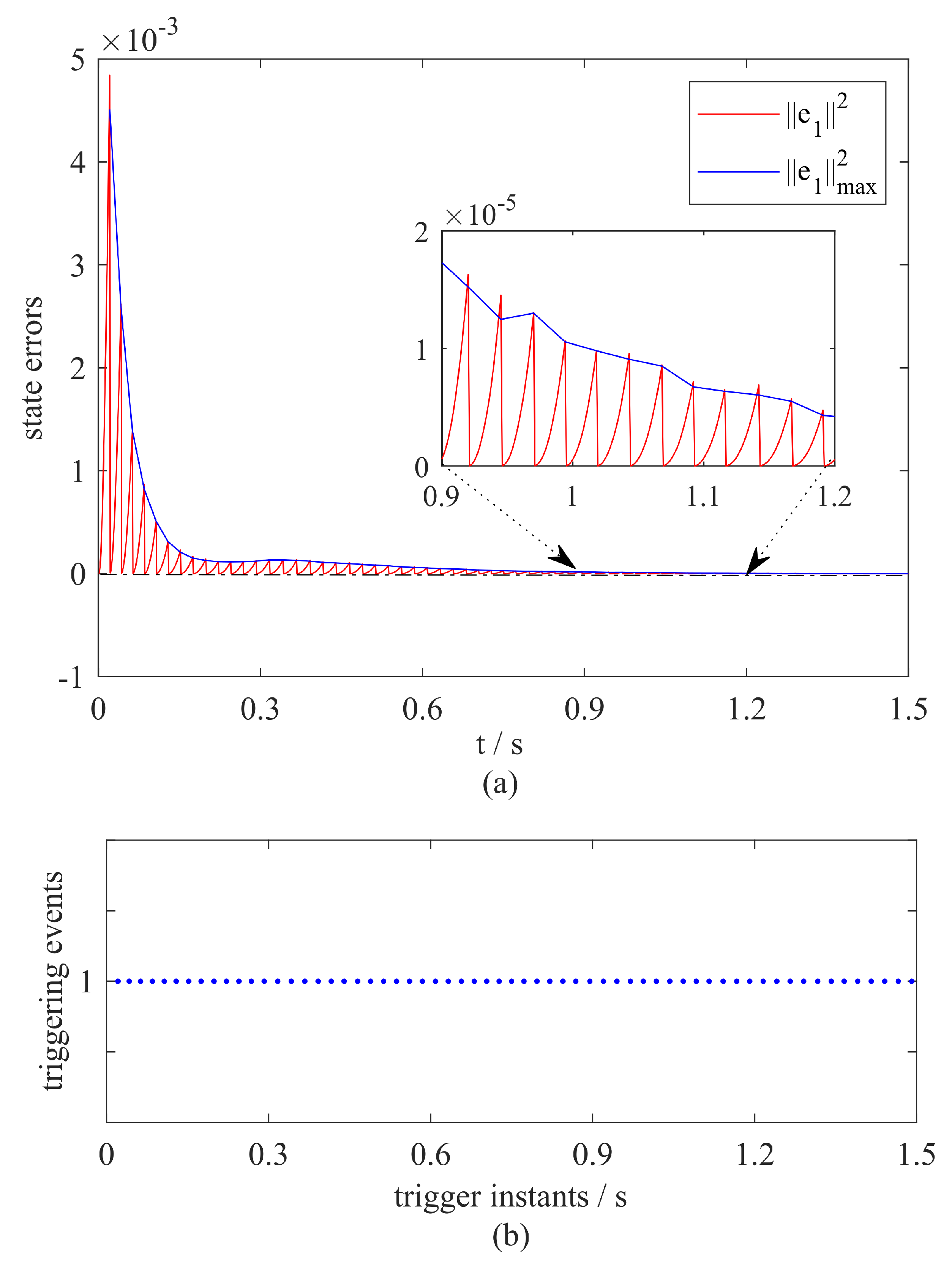
As shown in Figure 6a, the evolution of $\left|\right|e_1{\left|\right|}^2$ under the proposed distributed event-triggered control law together with relative localization schemes were plotted in red, while the specified state-dependent threshold $\left|\right|e_1{\left|\right|}_{\max }^2$ satisfying (21) was drawn with the blue line. Figure 6a shows that $\left|\right|e_1{\left|\right|}^2$ was reset as 0 with the control inputs being updated when an event was triggered, namely, $\left|\right|e_1{\left|\right|}^2$ was equal or larger than the threshold $\left|\right|e_1{\left|\right|}_{\max }^2$. As t went on, $\left|\right|e_1{\left|\right|}_{\max }^2$ converging to zero which meant that agent 1 was approaching to form a desired formation together with others. The event-triggered time instants for agent 1 are plotted clearly in Figure 6b, which is evident of avoiding Zeno behaviors.

6. Conclusions

In this paper, we investigated formation control problems with mixed range and bearing measurements. Towards this goal, a distributed event-triggered formation control framework was developed such that, only at necessary time instants, the event for the relative localization was triggered to estimate the relative position information by utilizing mixed range and bearing measurements. Firstly, it was shown by using the stiffness theory that an agent together with its neighbors were capable of recovering relative position information from mixed range and bearing measurements as long as a sufficient number of independent measurements was available in the subgraph. Secondly, a distributed event-triggered mechanism was presented for an affine formation control. It showed that the distributed event-triggered formation control strategy could be implemented in an asynchronous manner without requiring all agents simultaneously to recover relative position information. Moreover, it was shown that Zeno behavior was avoided under the proposed mechanism. This paper focused on an event-triggered affine formation control in the two-dimensional space. Future work will include the extension of the proposed solution to an affine formation control in three-dimensional or even higher-dimensional spaces based on mixed range and bearing measurements. Moreover, inspired by an adaptive cooperative control [33] and active disturbance rejection control [34], further work can be considered to develop a distributed event-triggered approach for an adaptive and robust affine formation control with mixed measurements.