A Novel Analytical View of Time-Fractional Korteweg-De Vries Equations via a New Integral Transform
Abstract
:1. Introduction
2. Preliminaries
3. Configuration of the SDM
4. Basic Formulation of the SITM
5. Existence and Uniqueness Results for Shehu Decomposition Method
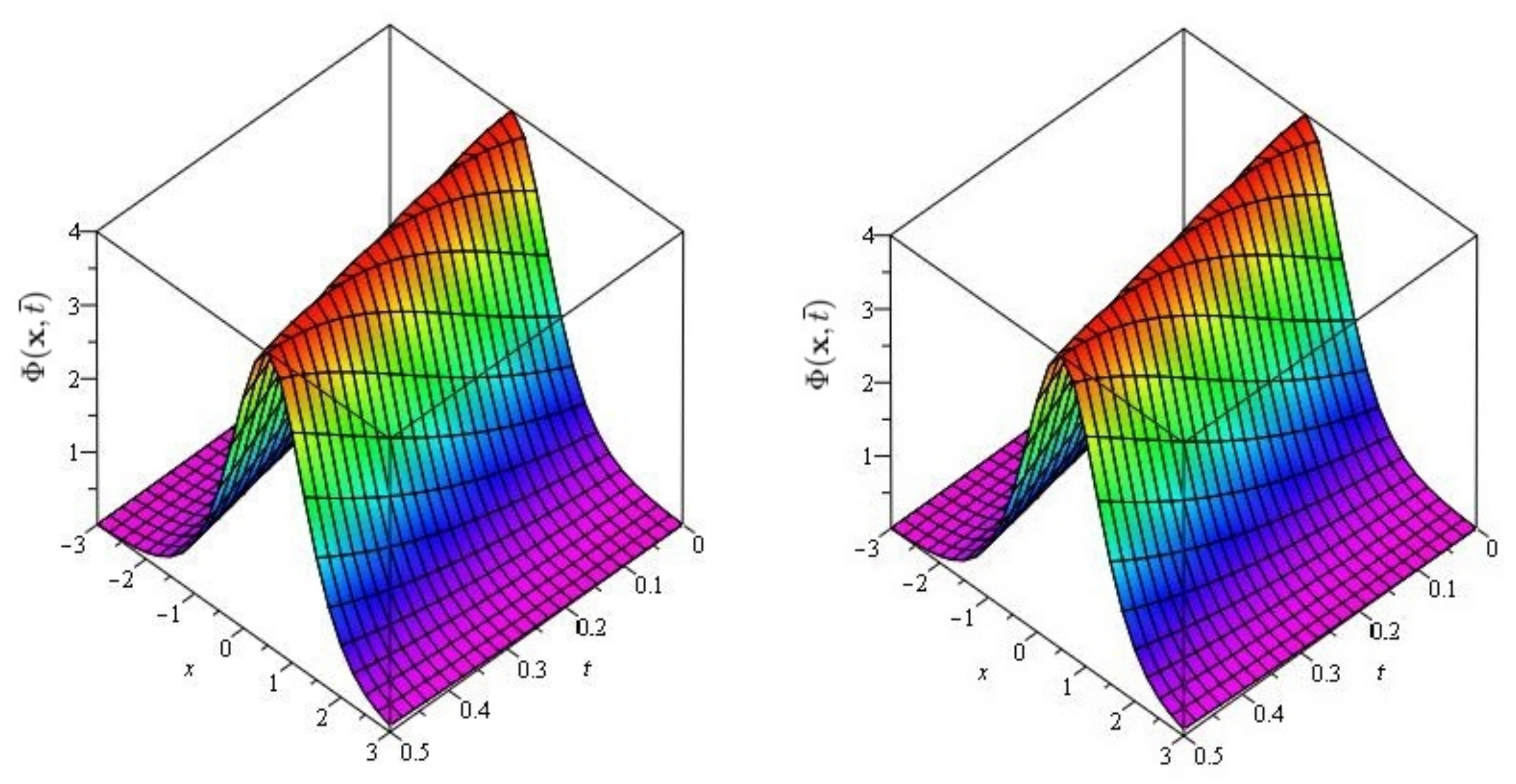
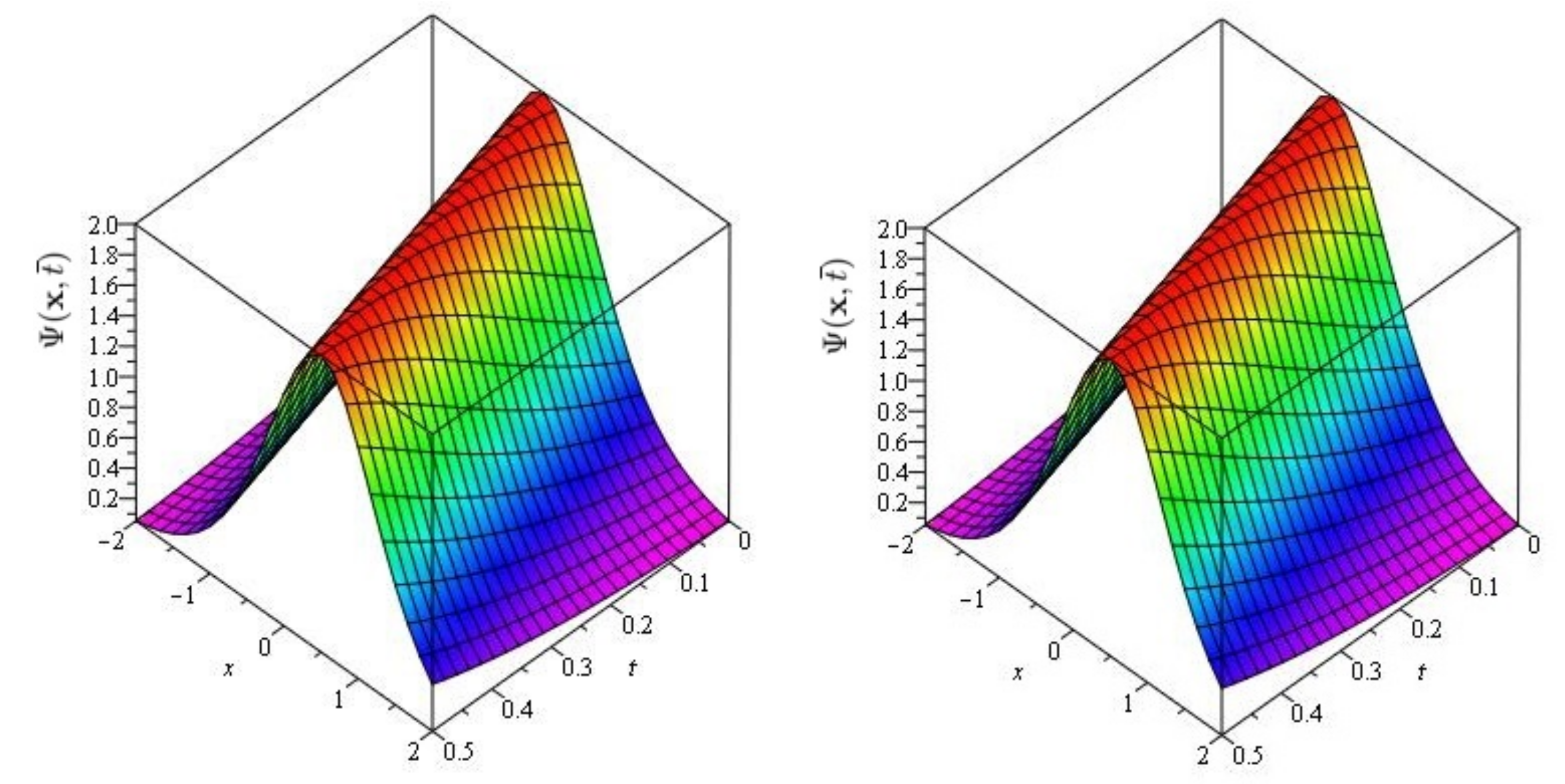
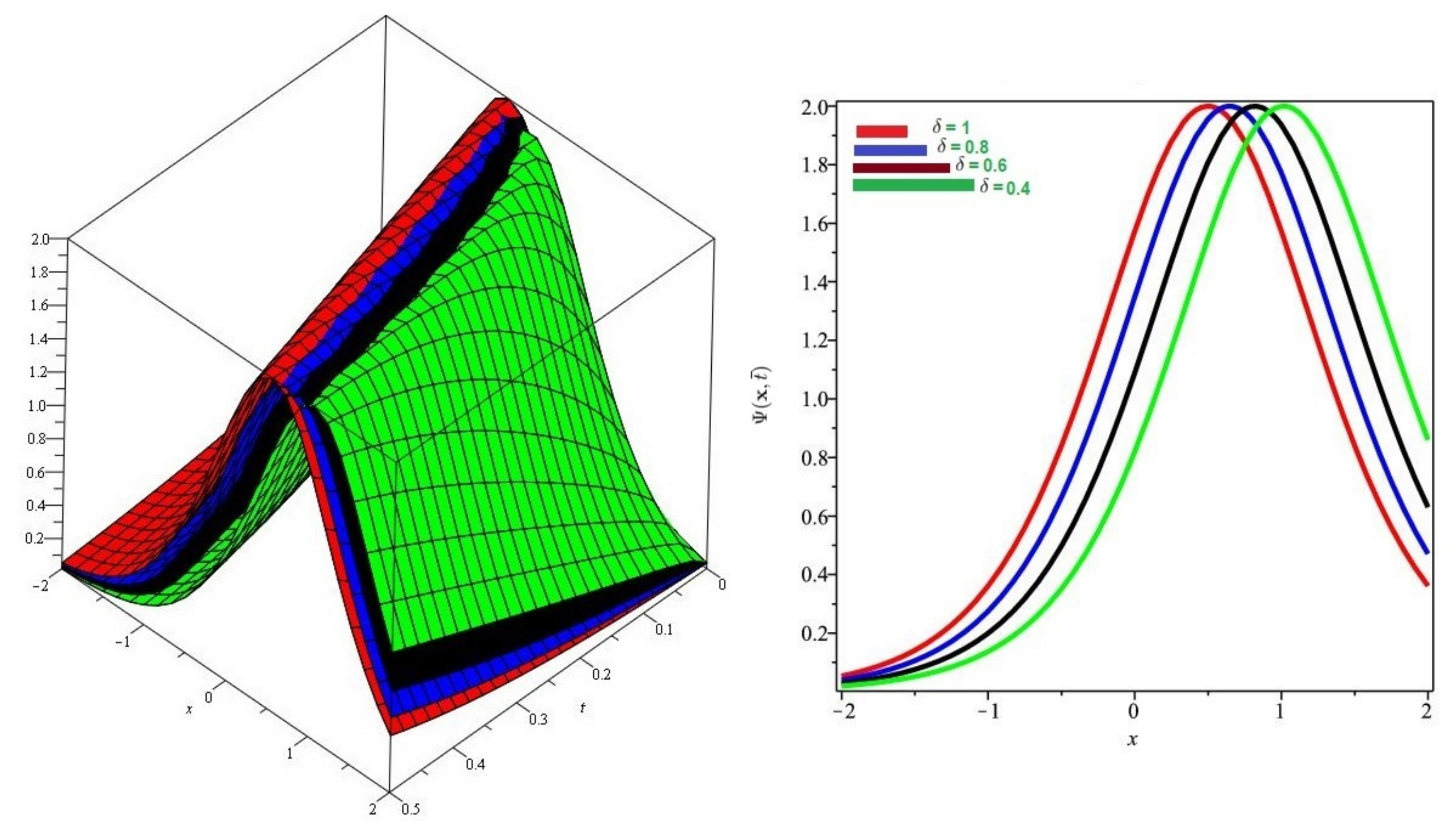
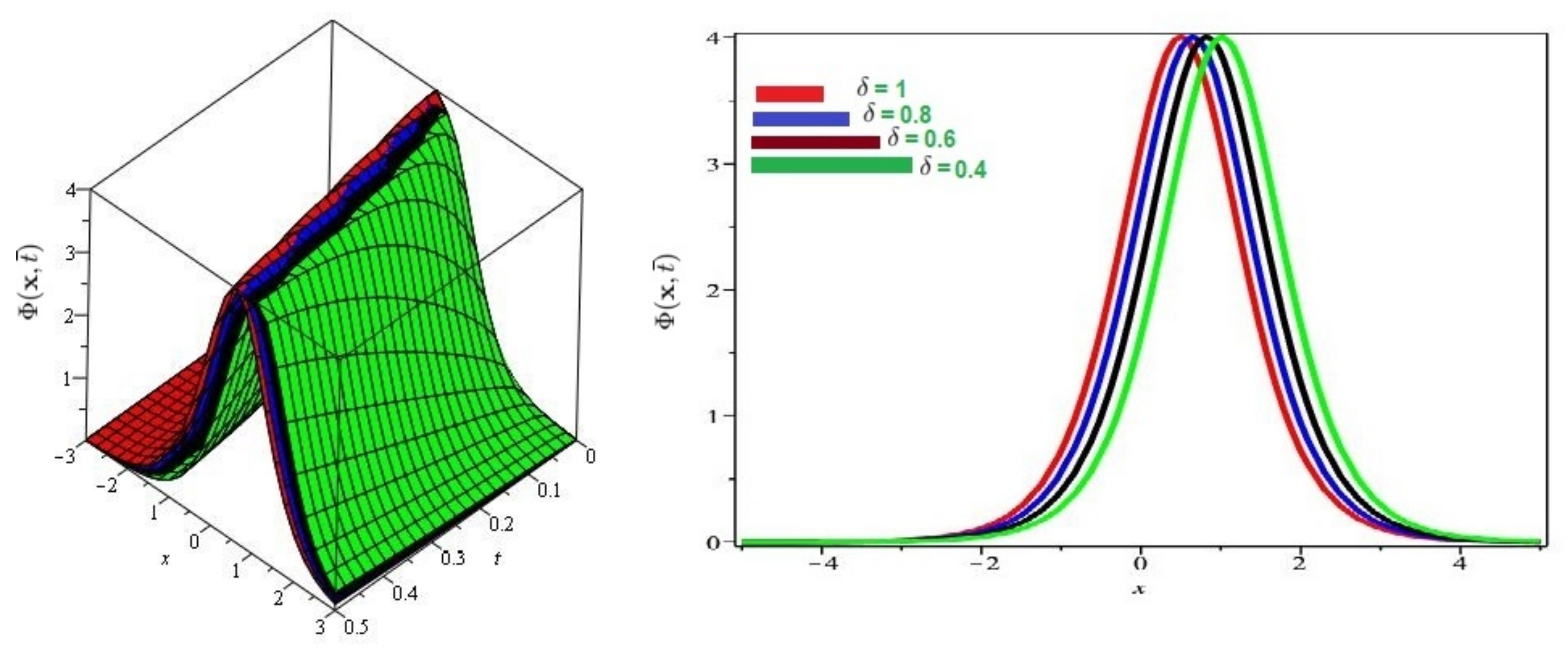
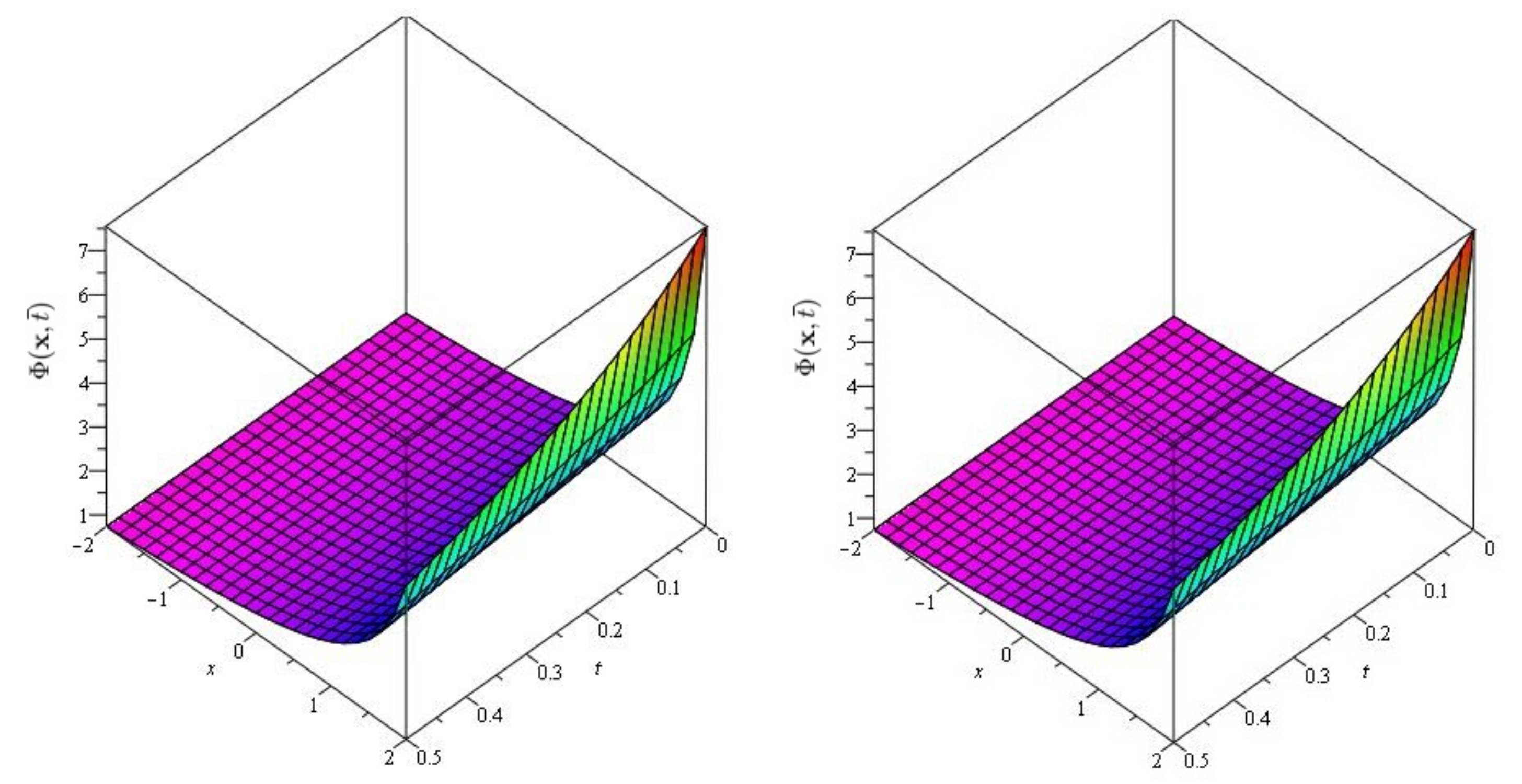
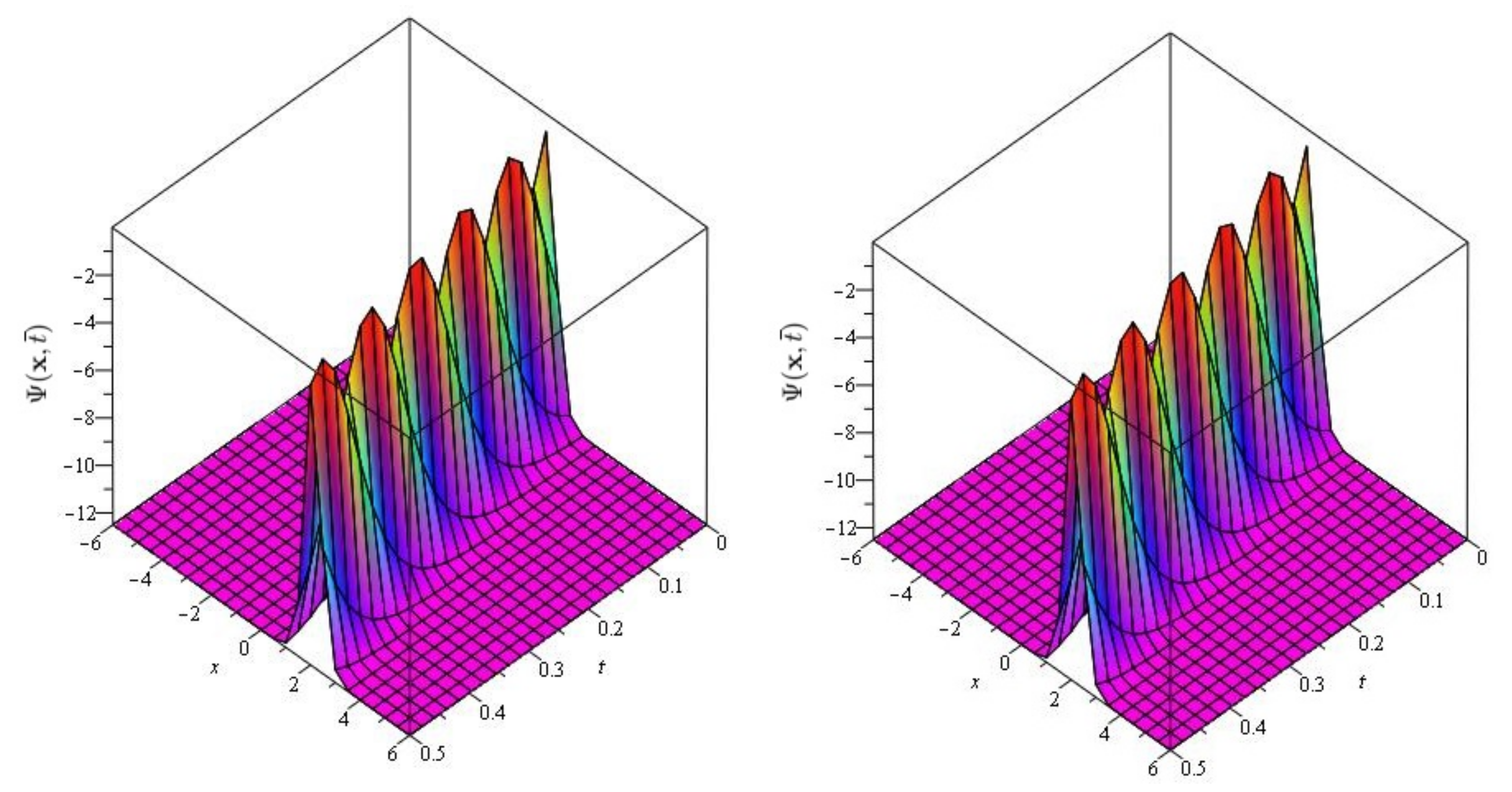
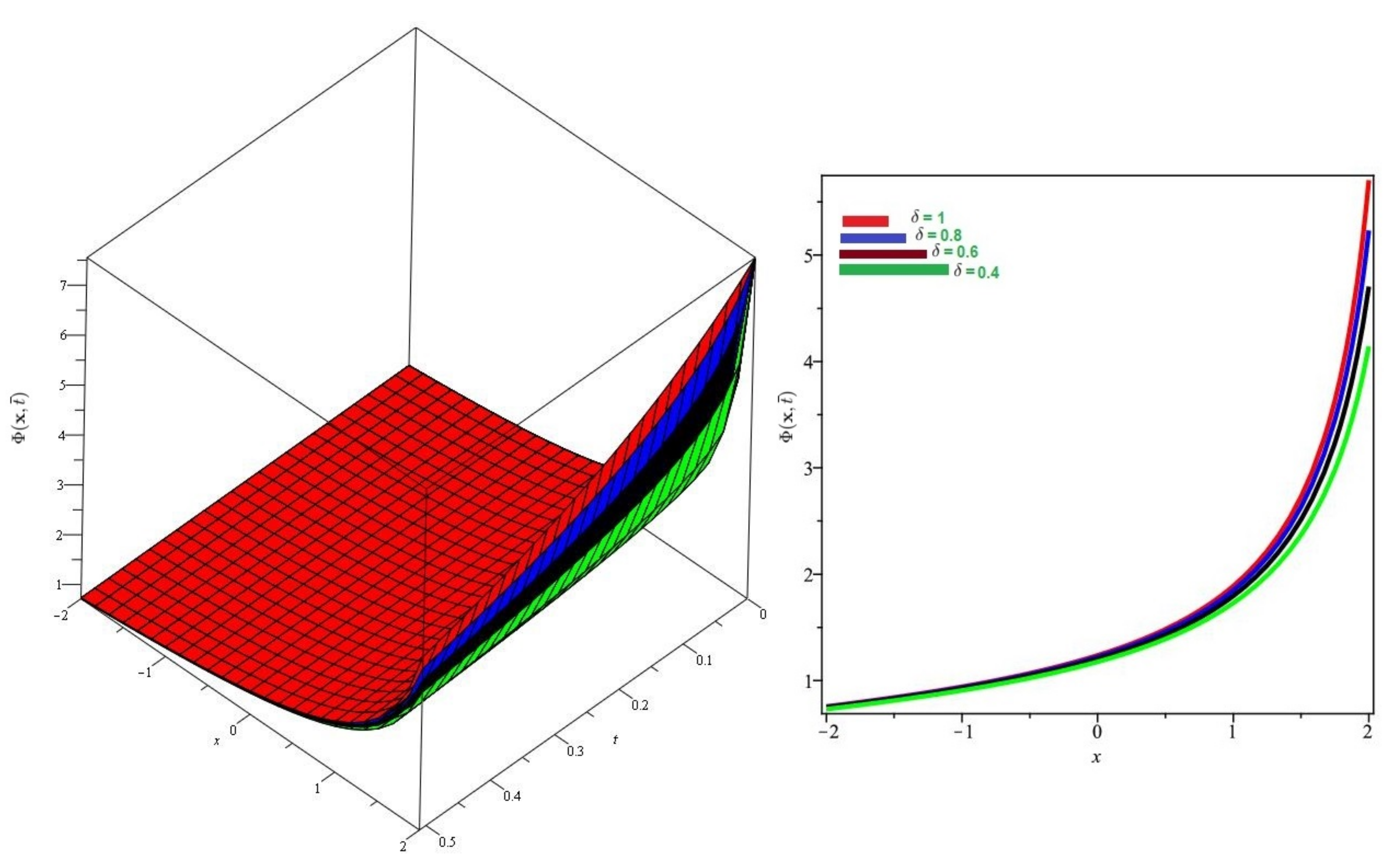
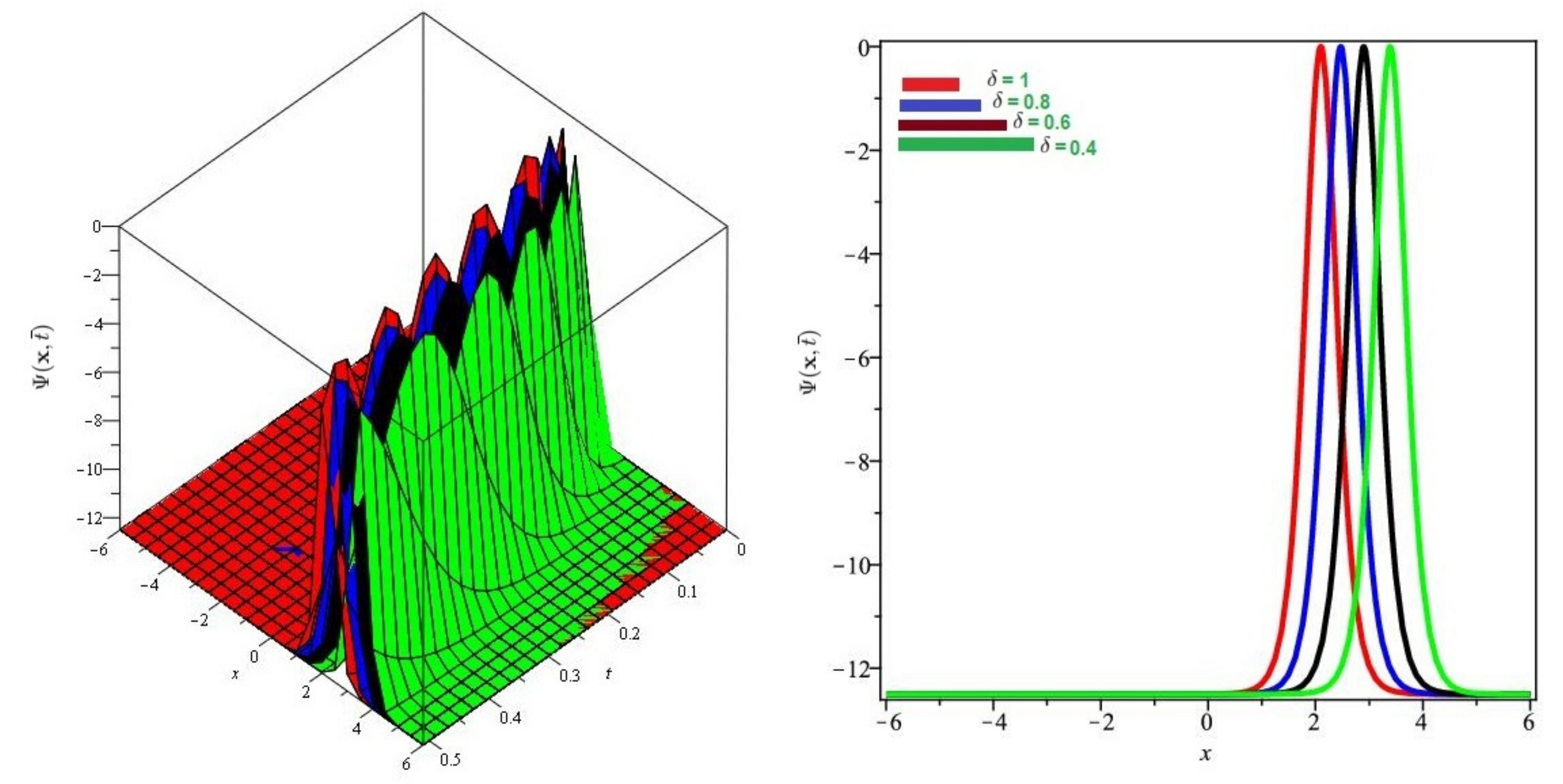
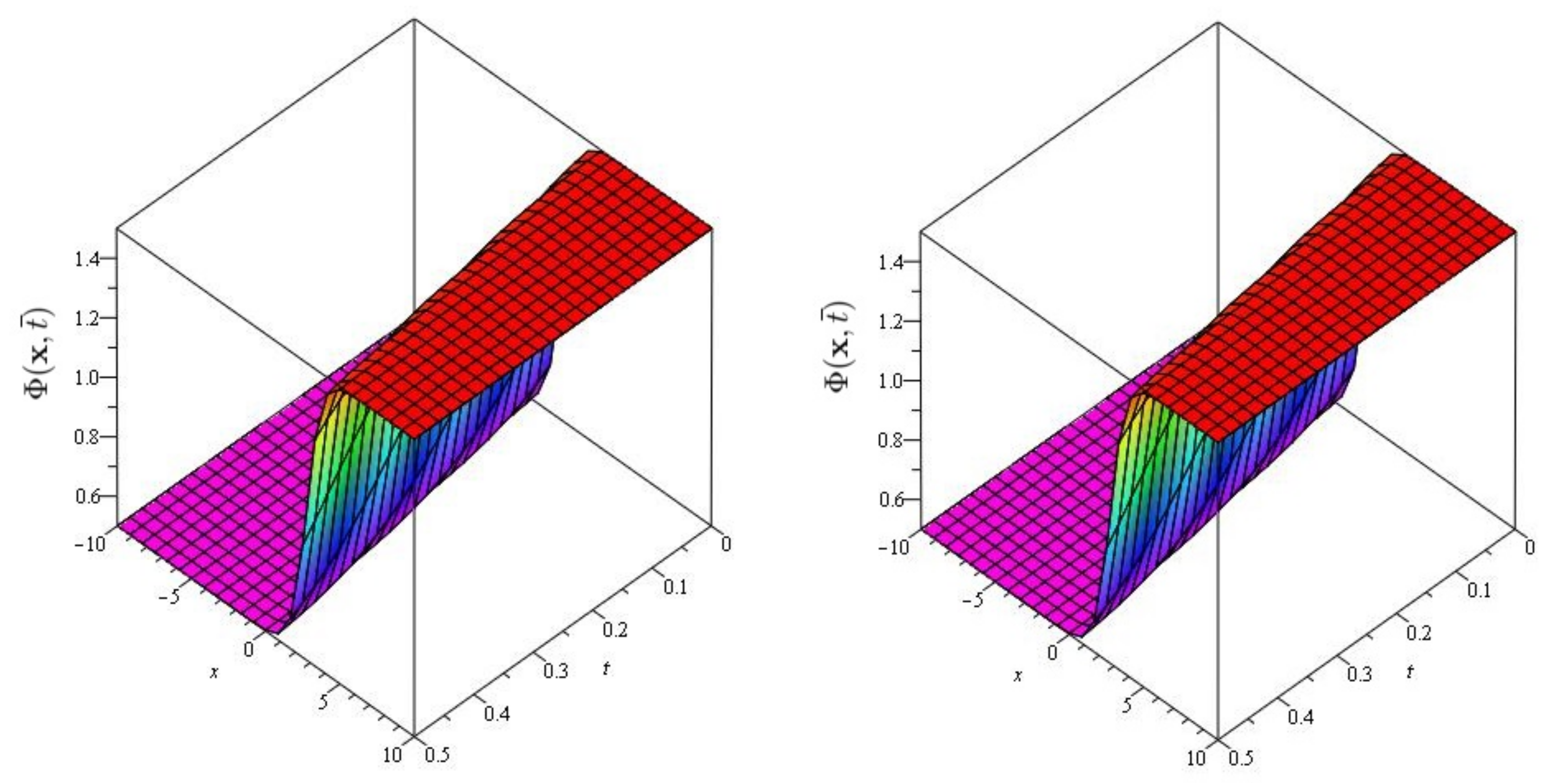
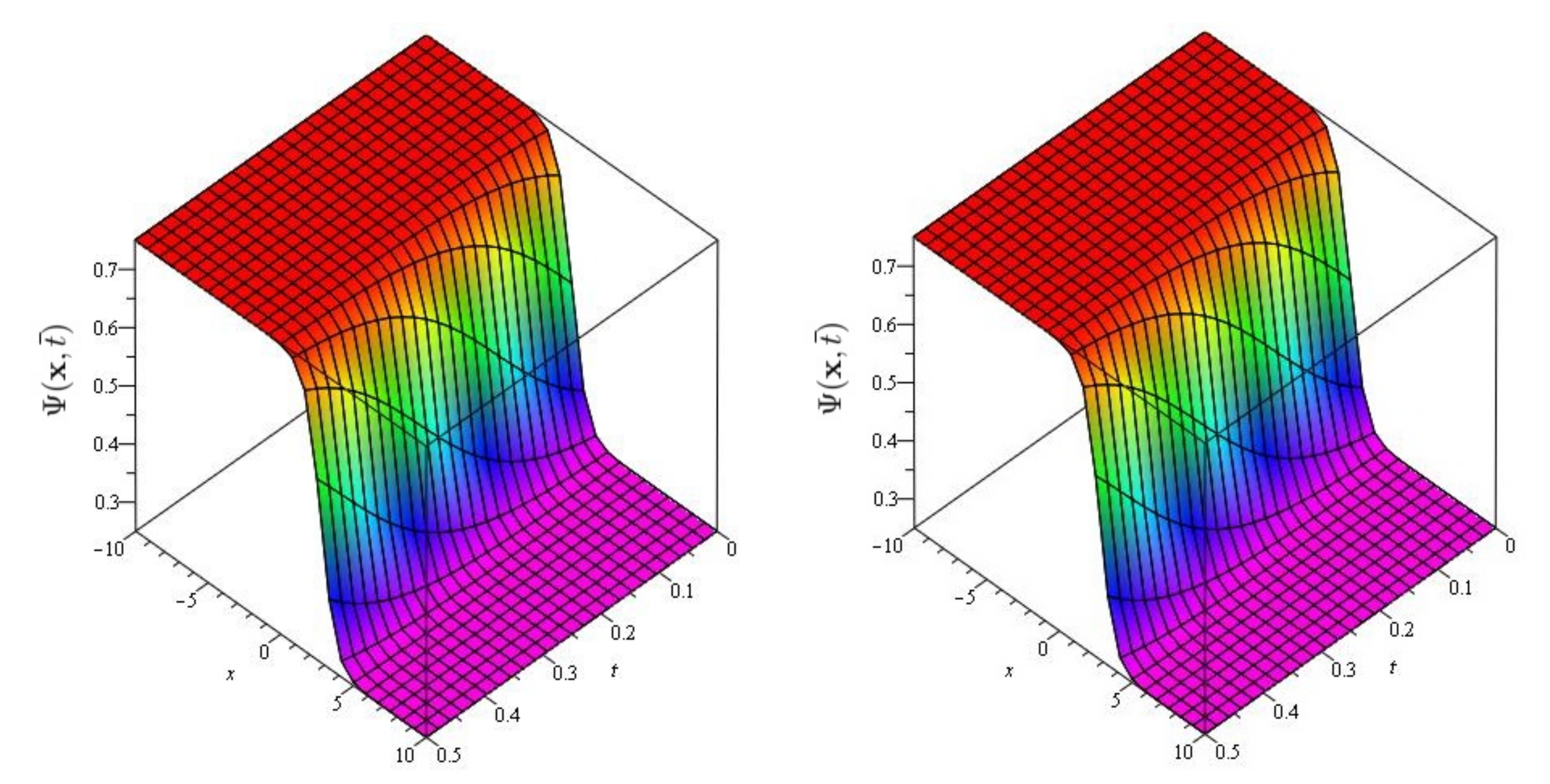
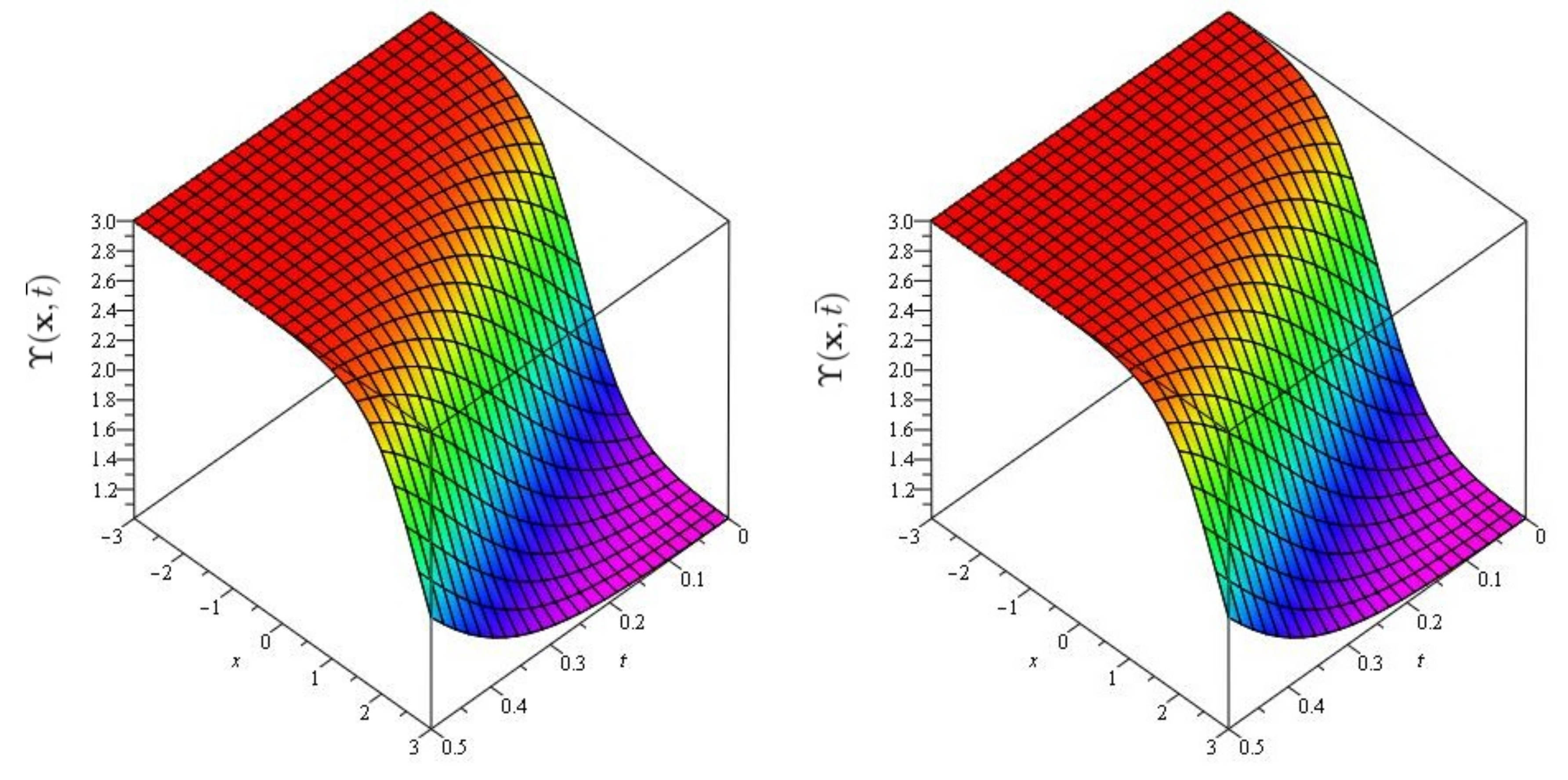
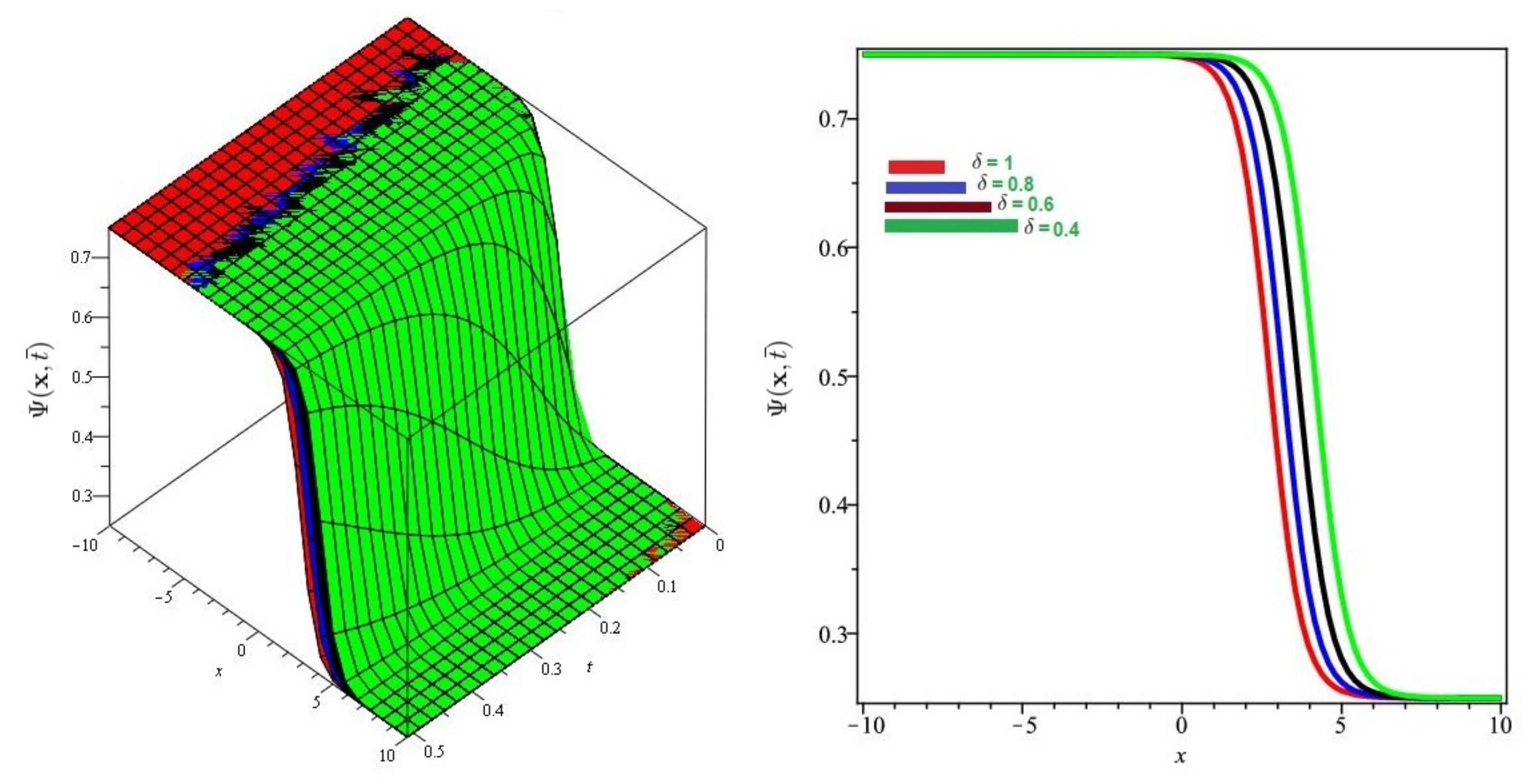
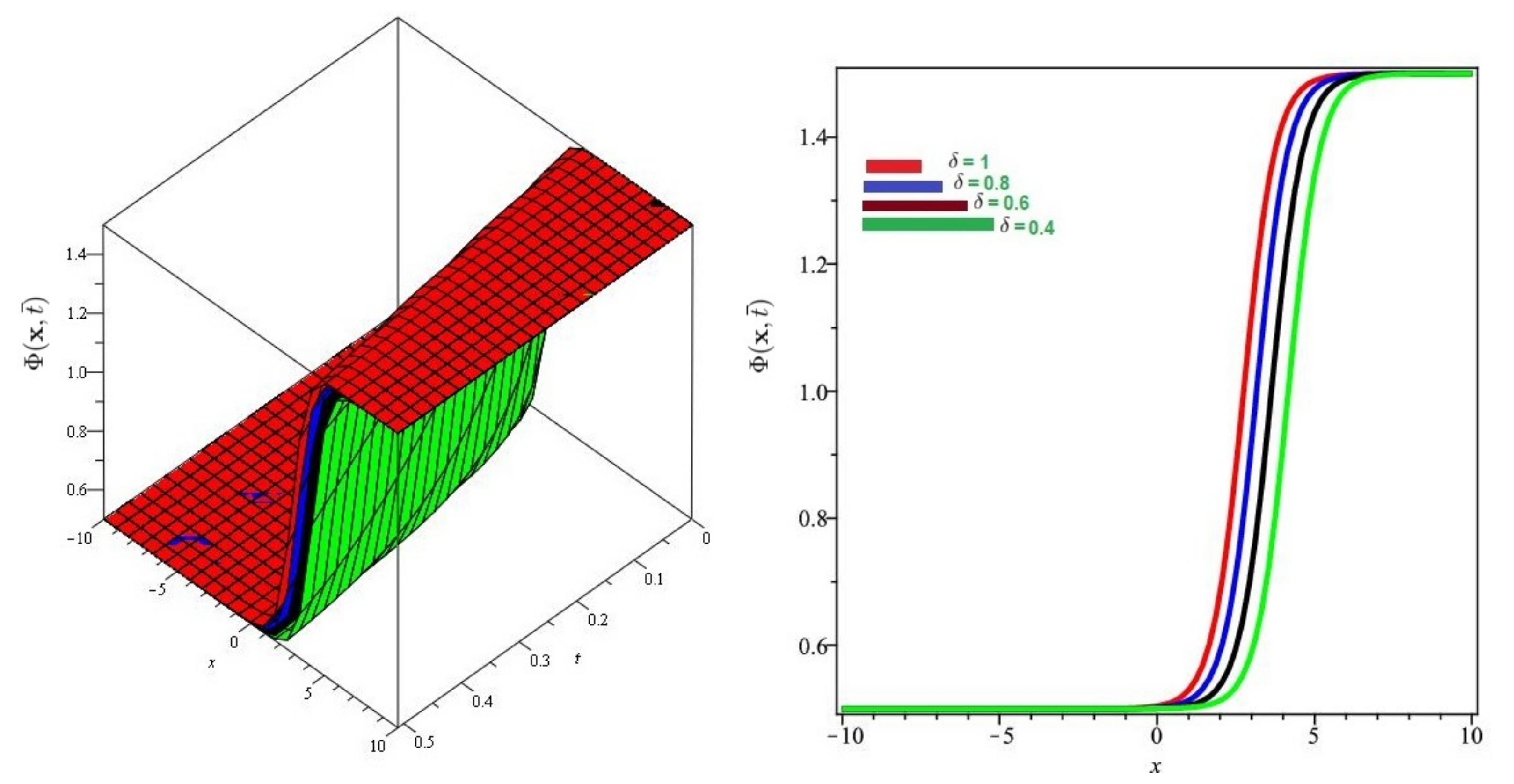
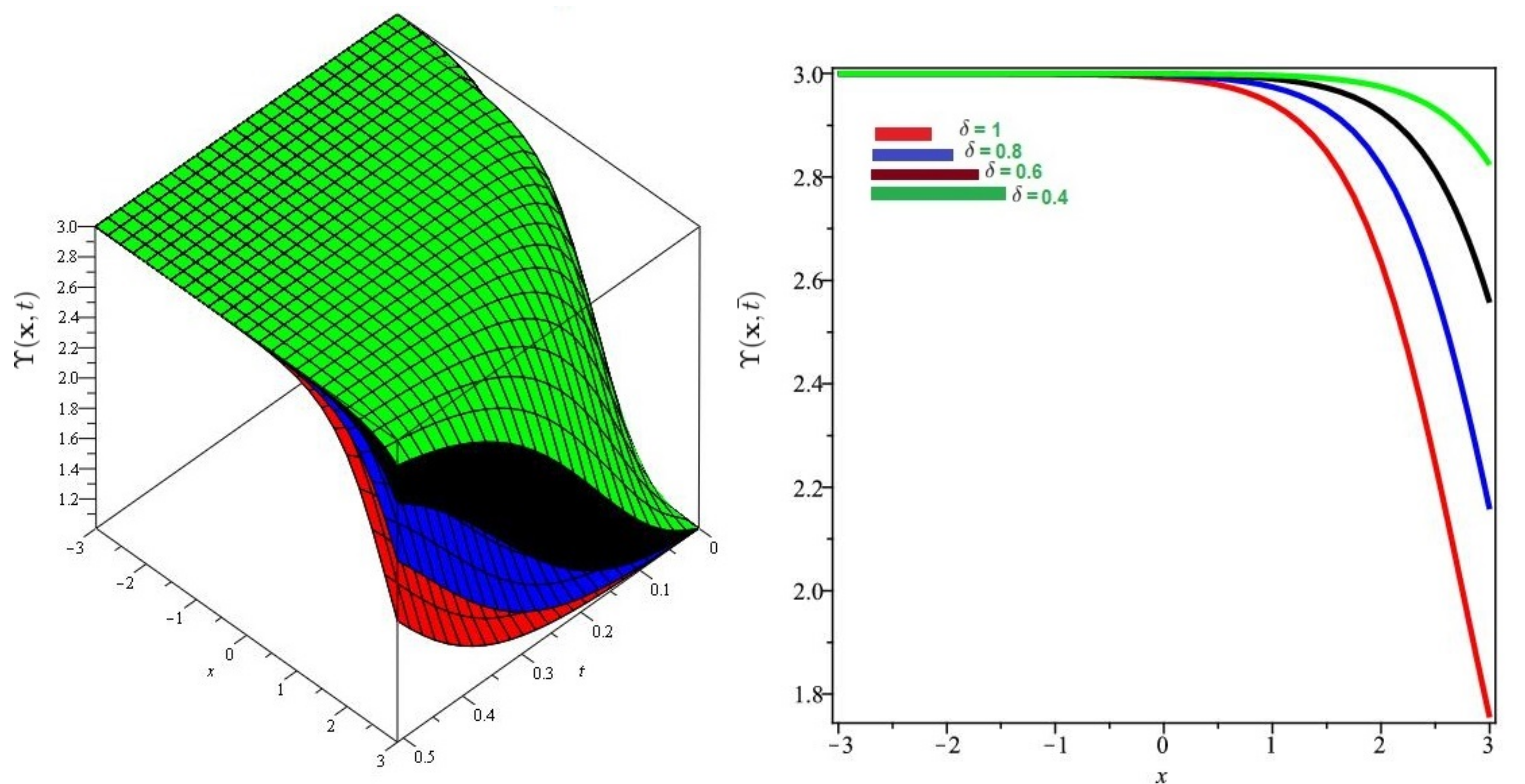
6. Evaluation of the Fractional KdV Model
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Geng, X.; Hu, X.; Zhu, S. A generalized Hirota-Satsuma coupled Korteweg-de Vries equation and Miura transformations. Phys. Lett. A 1999, 255, 259–264. [Google Scholar] [CrossRef]
- Abazari, R.; Abazari, M. Numerical simulation of generalized Hirota-Satsuma coupled KdV equation by RDTM and comparison with DTM. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 619–629. [Google Scholar] [CrossRef]
- Ganji, D.D.; Rafei, M. Solitary wave solutions for a generalized Hirota-Satsuma coupled KdV equation by homotopy perturbation method. Phys. Lett. A 2006, 356, 131–137. [Google Scholar] [CrossRef]
- Akinyemi, L.; Huseen, S.N. A powerful approach to study the new modified coupled Korteweg-de Vries system. Math. Comput. Simul. 2020, 177, 556–567. [Google Scholar] [CrossRef]
- Chen, C.K.; Ho, S.H. Solving partial differential equations by two-dimensional differential transform method. Appl. Math. Comput. 1999, 106, 171–179. [Google Scholar]
- Gao, Y.T.; Tian, B. Ion-acoustic shocks in space and laboratory dusty plasmas: Two dimensional and non-traveling-wave observable effects. Phys. Plasmas 2001, 8, 3146–3149. [Google Scholar] [CrossRef]
- Osborne, A. The inverse scattering transform: Tools for the nonlinear fourier analysis and filtering of ocean surface waves. Chaos Solitons Fract. 1995, 5, 2623–2637. [Google Scholar] [CrossRef]
- Ostrovsky, L.Y.; Stepanyants, A. Do internal solutions exist in the ocean. Rev. Geophys. 1989, 27, 293–310. [Google Scholar] [CrossRef]
- Wang, M.; Zhou, Y.; Li, Z. Application of a homogeneous balance method to exact solutions of non-linear equations in mathematical physics. Phys. Lett. A. 1996, 216, 67–75. [Google Scholar] [CrossRef]
- Gokdogan, A.; Yildirim, A.; Merdan, M. Solving coupled-KdV equations by differential transformation method. World Appl. Sci. J. 2012, 19, 1823–1828. [Google Scholar]
- Jafari, H.; Firoozjaee, M.A. Homotopy analysis method for solving KdV equations. Surv. Math. Appl. 2010, 5, 89–98. [Google Scholar]
- Rashid, S.; Kubra, K.T.; Rauf, A.; Chu, Y.-M.; Hamed, Y.S. New numerical approach for time-fractional partial differential equations arising in physical system involving natural decomposition method. Phys. Sci. 2021, 96, 105204. [Google Scholar] [CrossRef]
- Lu, D.; Suleman, M.; Ramzan, M.; Ul Rahman, J. Numerical solutions of coupled nonlinear fractional KdV equations using He’s fractional calculus. Int. J. Mod. Phys. B 2021, 35, 2150023. [Google Scholar] [CrossRef]
- Mohamed, M.A.; Torky, M.S. Numerical solution of non-linear system of partial differential equations by the Laplace decomposition method and the Padé approximation. Am. J. Comput. Math. 2013, 3, 175. [Google Scholar] [CrossRef] [Green Version]
- Seadawy, A.R.; El-Rashidy, K. Water wave solutions of the coupled system Zakharov-Kuznetsov and generalized coupled KdV equations. Sci. World J. 2014, 2014, 1–6. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, W.; Chen, N.; Dassios, I.; Shah, N.A.; Chung, J.E. Fractional System of Korteweg-De Vries equations via Elzaki transform. Mathematics 2021, 9, 673. [Google Scholar] [CrossRef]
- De la Rosa, R.; Recio, E.; Garrido, T.M.; Bruzón, M.S. Lie symmetry analysis of (2 + 1)-dimensional KdV equations with variable coefficients. Int. J. Comput. Math. 2019, 97, 1–13. [Google Scholar] [CrossRef]
- Kannan, R.; Wang, Z.J. A high order spectral volume solution to the Burgers’ equation using the Hopf-Cole transformation. Int. J. Numer. Meth. Fluids 2012, 69, 781–801. [Google Scholar] [CrossRef]
- Kannan, R. A high order spectral volume formulation for solving equations containing higher spatial derivative terms II: Improving the third derivative spatial discretization using the LDG2 method. Commun. Comput. Phy. 2012, 12, 767–788. [Google Scholar] [CrossRef]
- Fan, E. Using symbolic computation to exactly solve a new coupled MKdV system. Phys. Lett. A 2002, 299, 46–48. [Google Scholar] [CrossRef]
- Inc, M.; Cavlak, E. On numerical solutions of a new coupled MKdV system by using the Adomian decomposition method and He’s variational iteration method. Phys. Sci. 2008, 78, 1–7. [Google Scholar] [CrossRef]
- Inc, M.; Parto-Haghighi, M.; Akinlar, M.A.; Chu, Y.-M. New numerical solutions of fractional-order Korteweg-de Vries equation. Res. Phy. 2020, 19, 103326. [Google Scholar] [CrossRef]
- Lin, G.; Grinberg, L.; Karniadakis, G.E. Numerical studies of the stochastic Korteweg-de Vries equation. J. Comput. Phys. 2006, 213, 676–703. [Google Scholar] [CrossRef]
- Karczewska, A.; Szczeciński, M. Martingale solution to stochastic extended Korteweg-de Vries equation. Adv. Pure Math. 2018, 8. [Google Scholar] [CrossRef] [Green Version]
- Ghoreishi, M.; Ismail, A.I.; Rashid, A. The solution of coupled modifed KdV system by the homotopy analysis method. TWMS J. Pure Appl. Math. 2012, 3, 122–134. [Google Scholar]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus Models and Numerical Methods; Series on Complexity, Nonlinearity and Chaos; World Scientific: Singapore, 2012. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Atangana, A.; Secer, A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr. Appl. Anal. 2013, 2013, 279681. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Prog. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A.; Alkahtani, B.S.T. New model of groundwater flowing within a confine aquifer: Application of Caputo-Fabrizio derivative. Arab. J. Geosci. 2016, 9, 1–6. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N.J.; Freed, A.D. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Benson, D.A.; Scheffler, H.-P.; Baeumer, B. Stochastic solution of space-time fractional diffusion equations. Phys. Rev. E 2002, 65, 041103. [Google Scholar] [CrossRef] [Green Version]
- Fulger, D.; Scalas, E.; Germano, G. Monte Carlo simulation of uncoupled continuous-time random walks yielding a stochastic solution of the space-time fractional diffusion equation. Phys. Rev. E 2008, 77, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Maitama, S.; Zhao, W. New integral transform: Shehu transform a generalization of Sumudu and Laplace transform for solving differential equations. Int. J. Anal. Appl. 2019, 17, 167–190. [Google Scholar]
- Rani, D.; Mishra, V. Modification of Laplace adomian decomposition method for solving nonlinear Volterra integral and integro-differential equations based on Newton–Raphson formula. Eur. J. Pure Appl. Math. 2018, 11, 202–214. [Google Scholar] [CrossRef] [Green Version]
- Birajdar, G. Numerical solution of time fractional Navier–Stokes equation by discrete Adomian decomposition method. Nonlinear Eng. 2014, 3, 21–26. [Google Scholar] [CrossRef]
- Haq, F.; Shah, K.; Khan, A.; Shahzad, M.; Rahman, G. Numerical solution of fractional order epidemic model of a vector born disease by Laplace Adomian decomposition method. Punjab Univ. J. Math. 2017, 49, 13–22. [Google Scholar]
- Daftardar-Gejji, V.; Jafari, H. An iterative method for solving nonlinear functional equations. J. Math. Anal. Appl. 2006, 316, 753–763. [Google Scholar] [CrossRef] [Green Version]
- Jafari, H.; Nazari, M.; Baleanu, D.; Khalique, C.M. A new approach for solving a system of fractional partial differential equations. Comput. Math. Appl. 2013, 66, 838–843. [Google Scholar] [CrossRef]
- Ramadan, M.A.; Al-luhaibi, M.S. New iterative method for solving the Fornberg-Whitham equation and comparison with homotopy perturbation transform method. J. Adv. Math. Comput. Sci. 2014, 4, 1213–1227. [Google Scholar] [CrossRef]
- Alderremy, A.A.; Elzaki, T.M.; Chamekh, M. New transform iterative method for solving some Klein-Gordon equations. Res. Phys. 2018, 10, 655–659. [Google Scholar] [CrossRef]
- El-Kalla, I. Convergence of the Adomian method applied to a class of nonlinear integral equations. Appl. Math. Lett. 2008, 21, 372–376. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rashid, S.; Khalid, A.; Sultana, S.; Hammouch, Z.; Shah, R.; Alsharif, A.M. A Novel Analytical View of Time-Fractional Korteweg-De Vries Equations via a New Integral Transform. Symmetry 2021, 13, 1254. https://doi.org/10.3390/sym13071254
Rashid S, Khalid A, Sultana S, Hammouch Z, Shah R, Alsharif AM. A Novel Analytical View of Time-Fractional Korteweg-De Vries Equations via a New Integral Transform. Symmetry. 2021; 13(7):1254. https://doi.org/10.3390/sym13071254
Chicago/Turabian StyleRashid, Saima, Aasma Khalid, Sobia Sultana, Zakia Hammouch, Rasool Shah, and Abdullah M. Alsharif. 2021. "A Novel Analytical View of Time-Fractional Korteweg-De Vries Equations via a New Integral Transform" Symmetry 13, no. 7: 1254. https://doi.org/10.3390/sym13071254
APA StyleRashid, S., Khalid, A., Sultana, S., Hammouch, Z., Shah, R., & Alsharif, A. M. (2021). A Novel Analytical View of Time-Fractional Korteweg-De Vries Equations via a New Integral Transform. Symmetry, 13(7), 1254. https://doi.org/10.3390/sym13071254





