Implications of Noise on Neural Correlates of Consciousness: A Computational Analysis of Stochastic Systems of Mutually Connected Processes
Abstract
:1. Introduction
2. Materials and Methods
- Initialize the process state vector, , and set the initial time at 0.
- Calculate the propensities, .
- Generate a uniform random number, .
- Compute the time for the next event, .
- Generate a uniform random number, .
- Find which event is next, , if
- Update state vector, .
- Update time, .
- Repeat (2)–(8).
3. Results
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
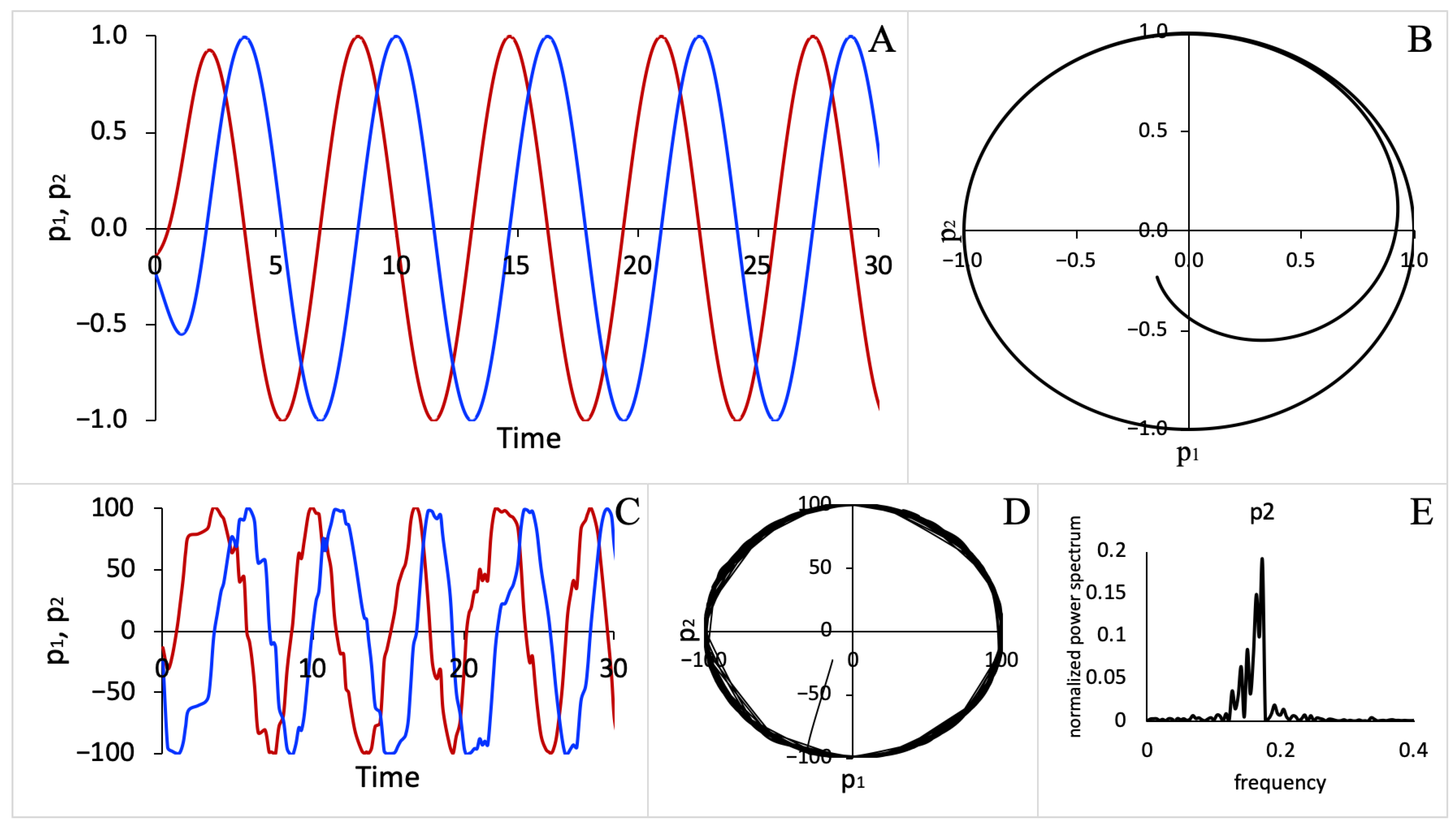
# code A par R=1 init p1=-0.1412 p2=-0.2316 p1’=-p2+p1*(R^2-p1^2-p2^2) p2’=p1+p2*(R^2-p1^2-p2^2) @ dt=.025, total=40, xplot=t,yplot=p1 @ xmin=0,xmax=30,ymin=-1,ymax=1 done
#code B par R=100 init p1=-14.12,p2=-23.16 # compute the sum of all event propensities x1=abs(p2) x2=x1+abs((R^2-p1*p1-p2*p2)*p1) x3=x2+abs(p1) x4=x3+abs((R^2-p1*p1-p2*p2)*p2) # choose random event s2=ran(1)*x4 y1=(s2<x1) y2=(s2<x2)&(s2>=x1) y3=(s2<x3)&(s2>=x2) y4=(s2>=x3) # time for next event tr’=tr-log(ran(1))/x4 p1’=p1-sign(p2)*y1+sign((R^2-p1*p1-p2*p2)*p1)*y2 p2’=p2+sign(p1)*y3+sign((R^2-p1*p1-p2*p2)*p2)*y4 @ bound=10000000000,meth=discrete,total=1000000,njmp=1000 @ xp=tr,yp=p1 @ xlo=0,ylo=-100,xhi=30,yhi=100 done
# code C init p1=1 p2=0 z1=0 z2=0 par eps=-1.0 p1’=eps*p2-z1-p1 z1’=p1 p2’=eps*p1-z2-p2 z2’=p2 @ dt=.025, total=40, xplot=t,yplot=p1 @ xmin=0,xmax=40,ymin=-1,ymax=1 done
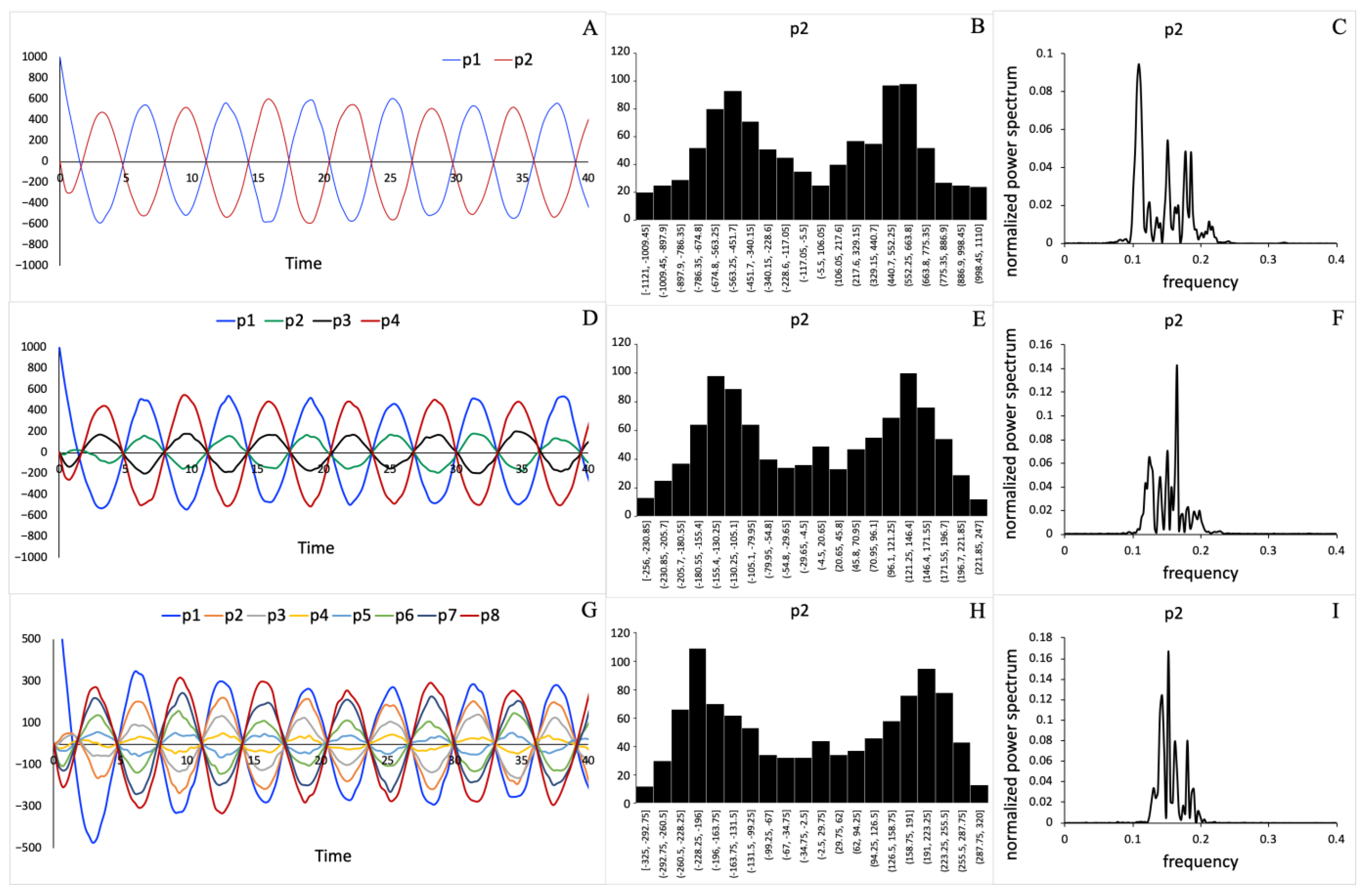
# code D par eps=-1 init p1=1000,p2=0, z1=0, z2=0 # compute the sum of all event propensities x1=abs(eps*p2) x2=x1+abs(eps*p1) x3=x2+abs(z1) x4=x3+abs(z2) x5=x4+abs(p1) x6=x5+abs(p2) # choose random event# s2=ran(1)*x6 y1=(s2<x1) y2=(s2<x2)&(s2>=x1) y3=(s2<x3)&(s2>=x2) y4=(s2<x4)&(s2>=x3) y5=(s2<x5)&(s2>=x4) y6=(s2>=x5) # time for the next event tr’=tr-log(ran(1))/x6 p1’=p1+sign(eps)*sign(p2)*y1-sign(z1)*y3-sign(p1)*y5 p2’=p2+sign(eps)*sign(p1)*y2-sign(z2)*y4-sign(p2)*y6 z1’=z1+sign(p1)*y5 z2’=z2+sign(p2)*y6 @ bound=100000000,meth=discrete,total=1000000,njmp=1000 @ xp=tr,yp=p1 @ xlo=0,ylo=-1000,xhi=40,yhi=1000 done
# code E par eps=-0.1 init p1=1000,p2=0, p3=0, p4=0, z1=0, z2=0, z3=0, z4=0 # compute the sum of all event propensities x11=abs(eps*p2) x12=x11+abs(4*eps*p3) x13=x12+abs(9*eps*p4) x21=x13+abs(eps*p1) x22=x21+abs(eps*p3) x23=x22+abs(4*eps*p4) x31=x23+abs(4*eps*p1) x32=x31+abs(eps*p2) x33=x32+abs(eps*p4) x41=x33+abs(9*eps*p1) x42=x41+abs(4*eps*p2) x43=x42+abs(eps*p3) x51=x43+abs(z1) x52=x51+abs(z2) x53=x52+abs(z3) x54=x53+abs(z4) x61=x54+abs(p1) x62=x61+abs(p2) x63=x62+abs(p3) x64=x63+abs(p4) # choose random event s2=ran(1)*x64 y1=(s2<x11) y2=(s2<x12)&(s2>=x11) y3=(s2<x13)&(s2>=x12) y4=(s2<x21)&(s2>=x13) y5=(s2<x22)&(s2>=x21) y6=(s2<x23)&(s2>=x22) y7=(s2<x31)&(s2>=x23) y8=(s2<x32)&(s2>=x31) y9=(s2<x33)&(s2>=x32) y10=(s2<x41)&(s2>=x33) y11=(s2<x42)&(s2>=x41) y12=(s2<x43)&(s2>=x42) y13=(s2<x51)&(s2>=x43) y14=(s2<x52)&(s2>=x51) y15=(s2<x53)&(s2>=x52) y16=(s2<x54)&(s2>=x53) y17=(s2<x61)&(s2>=x54) y18=(s2<x62)&(s2>=x61) y19=(s2<x63)&(s2>=x62) y20=(s2>=x63) # time for next event tr’=tr-log(ran(1))/x64 p1’=p1+sign(eps)*sign(p2)*y1+sign(eps)*sign(p3)*y2+sign(eps)*sign(p4)*y3-sign(z1)*y13-sign(p1)*y17 p2’=p2+sign(eps)*sign(p1)*y4+sign(eps)*sign(p3)*y5+sign(eps)*sign(p4)*y6-sign(z2)*y14-sign(p2)*y18 p3’=p3+sign(eps)*sign(p1)*y7+sign(eps)*sign(p2)*y8+sign(eps)*sign(p4)*y9-sign(z3)*y15-sign(p3)*y19 p4’=p4+sign(eps)*sign(p1)*y10+sign(eps)*sign(p2)*y11+sign(eps)*sign(p3)*y12-sign(z4)*y16-sign(p4)*y20 z1’=z1+sign(p1)*y17 z2’=z2+sign(p2)*y18 z3’=z3+sign(p3)*y19 z4’=z4+sign(p4)*y20 @ bound=100000000,meth=discrete,total=1000000,njmp=1000 @ xp=tr,yp=p1 @ xlo=0,ylo=-1000,xhi=40,yhi=1000 done
# code F par eps=-0.0119047619 init p1=1000,p2=0, p3=0, p4=0, p5=0, p6=0, p7=0, p8=0, z1=0, z2=0, z3=0, z4=0, z5=0, z6=0, z7=0, z8=0 # compute the sum of all event propensities x11=abs(eps*p2) x12=x11+abs(4*eps*p3) x13=x12+abs(9*eps*p4) x14=x13+abs(16*eps*p5) x15=x14+abs(25*eps*p6) x16=x15+abs(36*eps*p7) x17=x16+abs(49*eps*p8) x21=x17+abs(eps*p1) x22=x21+abs(eps*p3) x23=x22+abs(4*eps*p4) x24=x23+abs(9*eps*p5) x25=x24+abs(16*eps*p6) x26=x25+abs(25*eps*p7) x27=x26+abs(36*eps*p8) x31=x27+abs(4*eps*p1) x32=x31+abs(eps*p2) x33=x32+abs(eps*p4) x34=x33+abs(4*eps*p5) x35=x34+abs(9*eps*p6) x36=x35+abs(16*eps*p7) x37=x36+abs(25*eps*p8) x41=x37+abs(9*eps*p1) x42=x41+abs(4*eps*p2) x43=x42+abs(eps*p3) x44=x43+abs(eps*p5) x45=x44+abs(4*eps*p6) x46=x45+abs(9*eps*p7) x47=x46+abs(16*eps*p8) x51=x47+abs(16*eps*p1) x52=x51+abs(9*eps*p2) x53=x52+abs(4*eps*p3) x54=x53+abs(eps*p4) x55=x54+abs(eps*p6) x56=x55+abs(4*eps*p7) x57=x56+abs(9*eps*p8) x61=x57+abs(25*eps*p1) x62=x61+abs(16*eps*p2) x63=x62+abs(9*eps*p3) x64=x63+abs(4*eps*p4) x65=x64+abs(eps*p5) x66=x65+abs(eps*p7) x67=x66+abs(4*eps*p8) x71=x67+abs(36*eps*p1) x72=x71+abs(25*eps*p2) x73=x72+abs(16*eps*p3) x74=x73+abs(9*eps*p4) x75=x74+abs(4*eps*p5) x76=x75+abs(eps*p6) x77=x76+abs(eps*p8) x81=x77+abs(49*eps*p1) x82=x81+abs(36*eps*p2) x83=x82+abs(25*eps*p3) x84=x83+abs(16*eps*p4) x85=x84+abs(9*eps*p5) x86=x85+abs(4*eps*p6) x87=x86+abs(eps*p7) x91=x87+abs(z1) x92=x91+abs(z2) x93=x92+abs(z3) x94=x93+abs(z4) x95=x94+abs(z5) x96=x95+abs(z6) x97=x96+abs(z7) x98=x97+abs(z8) x101=x98+abs(p1) x102=x101+abs(p2) x103=x102+abs(p3) x104=x103+abs(p4) x105=x104+abs(p5) x106=x105+abs(p6) x107=x106+abs(p7) x108=x107+abs(p8) # choose random event# s2=ran(1)*x108 y1=(s2<x11) y2=(s2<x12)&(s2>=x11) y3=(s2<x13)&(s2>=x12) y4=(s2<x14)&(s2>=x13) y5=(s2<x15)&(s2>=x14) y6=(s2<x16)&(s2>=x15) y7=(s2<x17)&(s2>=x16) y8=(s2<x21)&(s2>=x17) y9=(s2<x22)&(s2>=x21) y10=(s2<x23)&(s2>=x22) y11=(s2<x24)&(s2>=x23) y12=(s2<x25)&(s2>=x24) y13=(s2<x26)&(s2>=x25) y14=(s2<x27)&(s2>=x26) y15=(s2<x31)&(s2>=x27) y16=(s2<x32)&(s2>=x31) y17=(s2<x33)&(s2>=x32) y18=(s2<x34)&(s2>=x33) y19=(s2<x35)&(s2>=x34) y20=(s2<x36)&(s2>=x35) y21=(s2<x37)&(s2>=x36) y22=(s2<x41)&(s2>=x37) y23=(s2<x42)&(s2>=x41) y24=(s2<x43)&(s2>=x42) y25=(s2<x44)&(s2>=x43) y26=(s2<x45)&(s2>=x44) y27=(s2<x46)&(s2>=x45) y28=(s2<x47)&(s2>=x46) y29=(s2<x51)&(s2>=x47) y30=(s2<x52)&(s2>=x51) y31=(s2<x53)&(s2>=x52) y32=(s2<x54)&(s2>=x53) y33=(s2<x55)&(s2>=x54) y34=(s2<x56)&(s2>=x55) y35=(s2<x57)&(s2>=x56) y36=(s2<x61)&(s2>=x57) y37=(s2<x62)&(s2>=x61) y38=(s2<x63)&(s2>=x62) y39=(s2<x64)&(s2>=x63) y40=(s2<x65)&(s2>=x64) y41=(s2<x66)&(s2>=x65) y42=(s2<x67)&(s2>=x66) y43=(s2<x71)&(s2>=x67) y44=(s2<x72)&(s2>=x71) y45=(s2<x73)&(s2>=x72) y46=(s2<x74)&(s2>=x73) y47=(s2<x75)&(s2>=x74) y48=(s2<x76)&(s2>=x75) y49=(s2<x77)&(s2>=x76) y50=(s2<x81)&(s2>=x77) y51=(s2<x82)&(s2>=x81) y52=(s2<x83)&(s2>=x82) y53=(s2<x84)&(s2>=x83) y54=(s2<x85)&(s2>=x84) y55=(s2<x86)&(s2>=x85) y56=(s2<x87)&(s2>=x86) y57=(s2<x91)&(s2>=x87) y58=(s2<x92)&(s2>=x91) y59=(s2<x93)&(s2>=x92) y60=(s2<x94)&(s2>=x93) y61=(s2<x95)&(s2>=x94) y62=(s2<x96)&(s2>=x95) y63=(s2<x97)&(s2>=x96) y64=(s2<x98)&(s2>=x97) y65=(s2<x101)&(s2>=x98) y66=(s2<x102)&(s2>=x101) y67=(s2<x103)&(s2>=x102) y68=(s2<x104)&(s2>=x103) y69=(s2<x105)&(s2>=x104) y70=(s2<x106)&(s2>=x105) y71=(s2<x107)&(s2>=x106) y72=(s2>=x107) # time for the next event tr’=tr-log(ran(1))/x108 p1’=p1+sign(eps)*sign(p2)*y1+sign(eps)*sign(p3)*y2+sign(eps)*sign(p4)*y3+sign(eps)*sign(p5)*y4+sign(eps)*sign(p6)*y5+sign(eps)*sign(p7)*y6+sign(eps)*sign(p8)*y7-sign(z1)*y57-sign(p1)*y65 p2’=p2+sign(eps)*sign(p1)*y8+sign(eps)*sign(p3)*y9+sign(eps)*sign(p4)*y10+sign(eps)*sign(p5)*y11+sign(eps)*sign(p6)*y12+sign(eps)*sign(p7)*y13+sign(eps)*sign(p8)*y14-sign(z2)*y58-sign(p2)*y66 p3’=p3+sign(eps)*sign(p1)*y15+sign(eps)*sign(p2)*y16+sign(eps)*sign(p4)*y17+sign(eps)*sign(p5)*y18+sign(eps)*sign(p6)*y19+sign(eps)*sign(p7)*y20+sign(eps)*sign(p8)*y21-sign(z3)*y59-sign(p3)*y67 p4’=p4+sign(eps)*sign(p1)*y22+sign(eps)*sign(p2)*y23+sign(eps)*sign(p3)*y24+sign(eps)*sign(p5)*y25+sign(eps)*sign(p6)*y26+sign(eps)*sign(p7)*y27+sign(eps)*sign(p8)*y28-sign(z4)*y60-sign(p4)*y68 p5’=p5+sign(eps)*sign(p1)*y29+sign(eps)*sign(p2)*y30+sign(eps)*sign(p3)*y31+sign(eps)*sign(p4)*y32+sign(eps)*sign(p6)*y33+sign(eps)*sign(p7)*y34+sign(eps)*sign(p8)*y35-sign(z5)*y61-sign(p5)*y69 p6’=p6+sign(eps)*sign(p1)*y36+sign(eps)*sign(p2)*y37+sign(eps)*sign(p3)*y38+sign(eps)*sign(p4)*y39+sign(eps)*sign(p5)*y40+sign(eps)*sign(p7)*y41+sign(eps)*sign(p8)*y42-sign(z6)*y62-sign(p6)*y70 p7’=p7+sign(eps)*sign(p1)*y43+sign(eps)*sign(p2)*y44+sign(eps)*sign(p3)*y45+sign(eps)*sign(p4)*y46+sign(eps)*sign(p5)*y47+sign(eps)*sign(p6)*y48+sign(eps)*sign(p8)*y49-sign(z7)*y63-sign(p7)*y71 p8’=p8+sign(eps)*sign(p1)*y50+sign(eps)*sign(p2)*y51+sign(eps)*sign(p3)*y52+sign(eps)*sign(p4)*y53+sign(eps)*sign(p5)*y54+sign(eps)*sign(p6)*y55+sign(eps)*sign(p7)*y56-sign(z8)*y64-sign(p8)*y72 z1’=z1+sign(p1)*y65 z2’=z2+sign(p2)*y66 z3’=z3+sign(p3)*y67 z4’=z4+sign(p4)*y68 z5’=z5+sign(p5)*y69 z6’=z6+sign(p6)*y70 z7’=z7+sign(p7)*y71 z8’=z8+sign(p8)*y72 @ bound=100,000,000,meth=discrete,total=1,000,000,njmp=1000 @ xp=tr,yp=p1 @ xlo=0,ylo=-1000,xhi=40,yhi=1000 done
References
- Jacobson, G.A.; Diba, K.; Yaron-Jakoubovitch, A.; Oz, Y.; Koch, C.; Segev, I.; Yarom, Y. Subthreshold voltage noise of rat neocortical pyramidal neurones. J. Physiol. 2005, 564, 145–160. [Google Scholar] [CrossRef] [PubMed]
- Faisal, A.A.; Selen, L.P.; Wolpert, D.M. Noise in the nervous system. Nat. Rev. Neurosci. 2008, 9, 292–303. [Google Scholar]
- Azouz, R.; Gray, C.M. Cellular mechanisms contributing to response variability of cortical neurons in vivo. J. Neurosci. 1999, 19, 2209–2223. [Google Scholar] [CrossRef] [Green Version]
- Deweese, M.R.; Zador, A.M. Shared and private variability in the auditory cortex. J. Neurophysiol. 2004, 92, 1840–1855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steinmetz, P.N.; Manwani, A.; Koch, C.; London, M.; Segev, I. Subthreshold voltage noise due to channel fluctuations in active neuronal membranes. J. Comput. Neurosci. 2000, 9, 133–148. [Google Scholar] [CrossRef] [PubMed]
- White, J.A.; Rubinstein, J.T.; Kay, A.R. Channel noise in neurons. Trends Neurosci. 2000, 23, 131–137. [Google Scholar] [CrossRef]
- Calvin, W.H.; Stevens, C.F. Synaptic noise and other sources of randomness in motoneuron interspike intervals. J. Neurophysiol. 1968, 31, 574–587. [Google Scholar] [CrossRef] [PubMed]
- Fellous, J.M.; Rudolph, M.; Destexhe, A.; Sejnowski, T.J. Synaptic background noise controls the input/output characteristics of single cells in an in vitro model of in vivo activity. Neuroscience 2003, 122, 811–829. [Google Scholar] [CrossRef]
- Faisal, A.A.; Laughlin, S.B. Stochastic simulations on the reliability of action potential propagation in thin axons. PLoS Comput. Biol. 2007, 3, e79. [Google Scholar]
- Van Rossum, M.C.; O’Brien, B.J.; Smith, R.G. Effects of noise on the spike timing precision of retinal ganglion cells. J. Neurophysiol. 2003, 89, 2406–2419. [Google Scholar] [CrossRef]
- Longtin, A.; Bulsara, A.; Moss, F. Time-interval sequences in bistable systems and the noise-induced transmission of information by sensory neurons. Phys. Rev. Lett. 1991, 67, 656–659. [Google Scholar] [CrossRef] [PubMed]
- Collins, J.J.; Imhoff, T.T.; Grigg, P. Noise-enhanced information transmission in rat SA1 cutaneous mechanoreceptors via aperiodic stochastic resonance. J. Neurophysiol. 1996, 76, 642–645. [Google Scholar] [CrossRef]
- Douglass, J.K.; Wilkens, L.; Pantazelou, E.; Moss, F. Noise enhancement of information transfer in crayfish mechanoreceptors by stochastic resonance. Nature 1993, 365, 337–340. [Google Scholar] [CrossRef] [PubMed]
- Kosko, B.; Mitaim, S. Stochastic resonance in noisy threshold neurons. Neural Netw. 2003, 16, 755–761. [Google Scholar] [CrossRef]
- Mitaim, S.; Kosko, B. Adaptive stochastic resonance in noisy neurons based on mutual information. IEEE Trans. Neural Netw. 2004, 15, 1526–1540. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bulsara, A.R.; Zador, A. Threshold detection of wideband signals: A noise-induced maximum in the mutual information. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics 1996, 54, R2185–R2188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Priplata, A.A.; Niemi, J.B.; Harry, J.D.; Lipsitz, L.A.; Collins, J.J. Vibrating insoles and balance control in elderly people. Lancet 2003, 362, 1123–1124. [Google Scholar] [CrossRef]
- Russell, D.F.; Wilkens, L.A.; Moss, F. Use of behavioural stochastic resonance by paddle fish for feeding. Nature 1999, 402, 291–294. [Google Scholar] [CrossRef]
- Seth, A.K.; Izhikevich, E.; Reeke, G.N.; Edelman, G.M. Theories and measures of consciousness: An extended framework. Proc. Natl. Acad. Sci. USA 2006, 103, 10799–10804. [Google Scholar] [CrossRef] [Green Version]
- Tononi, G.; Edelman, G.M. Consciousness and complexity. Science 1998, 282, 1846–1851. [Google Scholar] [CrossRef]
- Metzinger, T. Neural correlates of consciousness: Empirical and conceptual questions. In Bradford Bks; MIT Press: Cambridge, MA, USA, 2000; 350p. [Google Scholar]
- Crick, F.; Koch, C. A framework for consciousness. Nat. Neurosci. 2003, 6, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Koch, C.; Massimini, M.; Boly, M.; Tononi, G. Neural correlates of consciousness: Progress and problems. Nat. Rev. Neurosci. 2016, 17, 307–321. [Google Scholar] [CrossRef]
- Crick, F.; Koch, C. Consciousness and neuroscience. Cereb. Cortex 1998, 8, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Kraikivski, P. Systems of oscillators designed for a specific conscious percept. N. Math. Nat. Comput. 2020, 16, 73–88. [Google Scholar] [CrossRef] [Green Version]
- Kraikivski, P. Building systems capable of consciousness. Mind Matter 2017, 15, 185–195. [Google Scholar]
- Freeman, W.J. Neurodynamics: An exploration in mesoscopic brain dynamics. In Perspectives in Neural Computing; Springer: London, UK, 2000; 398p. [Google Scholar]
- Fingelkurts, A.A.; Fingelkurts, A.A.; Neves, C.F.H. Phenomenological architecture of a mind and operational architectonics of the brain: The unified metastable continuum. J. N. Math. Nat. Comput. 2009, 5, 221–244. [Google Scholar] [CrossRef] [Green Version]
- Fingelkurts, A.A.; Fingelkurts, A.A.; Neves, C.F.H. Consciousness as a phenomenon in the operational architectonics of brain organization: Criticality and self-organization considerations. Chaos Solitons Fractals 2013, 55, 13–31. [Google Scholar] [CrossRef]
- Freeman, W.J. A field-theoretic approach to understanding scale-free neocortical dynamics. Biol. Cybern. 2005, 92, 350–359. [Google Scholar] [CrossRef] [Green Version]
- Tononi, G. An information integration theory of consciousness. BMC Neurosci. 2004, 5, 42. [Google Scholar] [CrossRef] [Green Version]
- Northoff, G. What the brain’s intrinsic activity can tell us about consciousness? A tri-dimensional view. Neurosci. Biobehav. R 2013, 37, 726–738. [Google Scholar] [CrossRef]
- Northoff, G.; Huang, Z.R. How do the brain’s time and space mediate consciousness and its different dimensions? Temporo-spatial theory of consciousness (TTC). Neurosci. Biobehav. R 2017, 80, 630–645. [Google Scholar] [CrossRef] [PubMed]
- Reggia, J.A. The rise of machine consciousness: Studying consciousness with computational models. Neural Netw. 2013, 44, 112–131. [Google Scholar] [CrossRef]
- Laureys, S. The neural correlate of (un)awareness: Lessons from the vegetative state. Trends Cogn. Sci. 2005, 9, 556–559. [Google Scholar] [CrossRef]
- Chalmers, D.J. Absent qualia, fading qualia, dancing qualia. In Conscious Experience. Ferdinand Schoningh; Metzinger, T., Ed.; Imprint Academic: Exeter, UK, 1995. [Google Scholar]
- Martinez-Garcia, M.; Gordon, T. A new model of human steering using far-point error perception and multiplicative control. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 1245–1250. [Google Scholar]
- Zhang, Y.; Martinez-Garcia, M.; Gordon, T. Human response delay estimation and monitoring using gamma distribution analysis. In Proceedings of the 2018 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Miyazaki, Japan, 7–10 October 2018; pp. 807–812. [Google Scholar]
- Gillespie, D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Rao, C.V.; Arkin, A.P. Stochastic chemical kinetics and the quasi-steady-state assumption: Application to the Gillespie algorithm. J. Phys. Chem. 2003, 118, 4999–5010. [Google Scholar] [CrossRef] [Green Version]
- Tyson, J.J.; Laomettachit, T.; Kraikivski, P. Modeling the dynamic behavior of biochemical regulatory networks. J. Theor. Biol. 2019, 462, 514–527. [Google Scholar] [CrossRef]
- Bernstein, D. Simulating mesoscopic reaction-diffusion systems using the Gillespie algorithm. Phys. Rev. E 2005, 71, 041103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McKane, A.J.; Newman, T.J. Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 2005, 94, 218102. [Google Scholar] [CrossRef] [Green Version]
- Mather, W.H.; Hasty, J.; Tsimring, L.S. Fast stochastic algorithm for simulating evolutionary population dynamics. Bioinformatics 2012, 28, 1230–1238. [Google Scholar] [CrossRef] [Green Version]
- Prerau, M.J.; Brown, R.E.; Bianchi, M.T.; Ellenbogen, J.M.; Purdon, P.L. Sleep neurophysiological dynamics through the lens of multitaper spectral analysis. Physiology 2017, 32, 60–92. [Google Scholar] [CrossRef] [Green Version]
- Tuominen, J.; Kallio, S.; Kaasinen, V.; Railo, H. Segregated brain state during hypnosis. Neurosci. Conscious. 2021, 2021, niab002. [Google Scholar] [CrossRef]
- Thilakavathi, B.; Devi, S.S.; Malaiappan, M.; Bhanu, K. EEG power spectrum analysis for schizophrenia during mental activity. Australas. Phys. Eng. Sci. Med. 2019, 42, 887–897. [Google Scholar] [CrossRef]
- Helakari, H.; Kananen, J.; Huotari, N.; Raitamaa, L.; Tuovinen, T.; Borchardt, V.; Rasila, A.; Raatikainen, V.; Starck, T.; Hautaniemi, T.; et al. Spectral entropy indicates electrophysiological and hemodynamic changes in drug-resistant epilepsy—A multimodal MREG study. Neuroimage Clin. 2019, 22, 101763. [Google Scholar] [CrossRef]
- Yunusa-Kaltungo, A.; Sinha, J.K.; Elbhbah, K. An improved data fusion technique for faults diagnosis in rotating machines. Measurement 2014, 58, 27–32. [Google Scholar] [CrossRef]
- Luwei, K.C.; Yunusa-Kaltungo, A.; Sha’aban, Y.A. Integrated fault detection framework for classifying rotating machine faults using frequency domain data fusion and artificial neural networks. Machines 2018, 6, 59. [Google Scholar] [CrossRef] [Green Version]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Zhang, H.; Xu, W.; Zhang, H.; Yang, L.; Zheng, S.; Shi, Y. Spectral entropy can predict changes of working memory performance reduced by short-time training in the delayed-match-to-sample task. Front. Hum. Neurosci. 2017, 11, 437. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- James, W. Does ‘consciousness’ exist? J. Philos. Psychol. Sci. Methods 1904, 1, 477–491. [Google Scholar] [CrossRef]
- Dublanche, Y.; Michalodimitrakis, K.; Kummerer, N.; Foglierini, M.; Serrano, L. Noise in transcription negative feedback loops: Simulation and experimental analysis. Mol. Syst. Biol. 2006, 2, 41. [Google Scholar] [CrossRef] [Green Version]
- Nacher, J.C.; Ochiai, T. Transcription and noise in negative feedback loops. Biosystems 2008, 91, 76–82. [Google Scholar] [CrossRef]
- Austin, D.W.; Allen, M.S.; McCollum, J.M.; Dar, R.D.; Wilgus, J.R.; Sayler, G.S.; Samatova, N.F.; Cox, C.D.; Simpson, M.L. Gene network shaping of inherent noise spectra. Nature 2006, 439, 608–611. [Google Scholar] [CrossRef] [PubMed]
- Simpson, M.L.; Cox, C.D.; Sayler, G.S. Frequency domain analysis of noise in autoregulated gene circuits. Proc. Natl. Acad. Sci. USA 2003, 100, 4551–4556. [Google Scholar] [CrossRef] [Green Version]
- Boll, S. Suppression of acoustic noise in speech using spectral subtraction. IEEE Trans. Acoust. Speech Signal Process. 1979, 27, 113–120. [Google Scholar] [CrossRef] [Green Version]
- Yoshizawa, T.; Hirobayashi, S.; Misawa, T. Noise reduction for periodic signals using high-resolution frequency analysis. EURASIP J. Audio Speech Music Process. 2011, 2011, 5. [Google Scholar] [CrossRef] [Green Version]
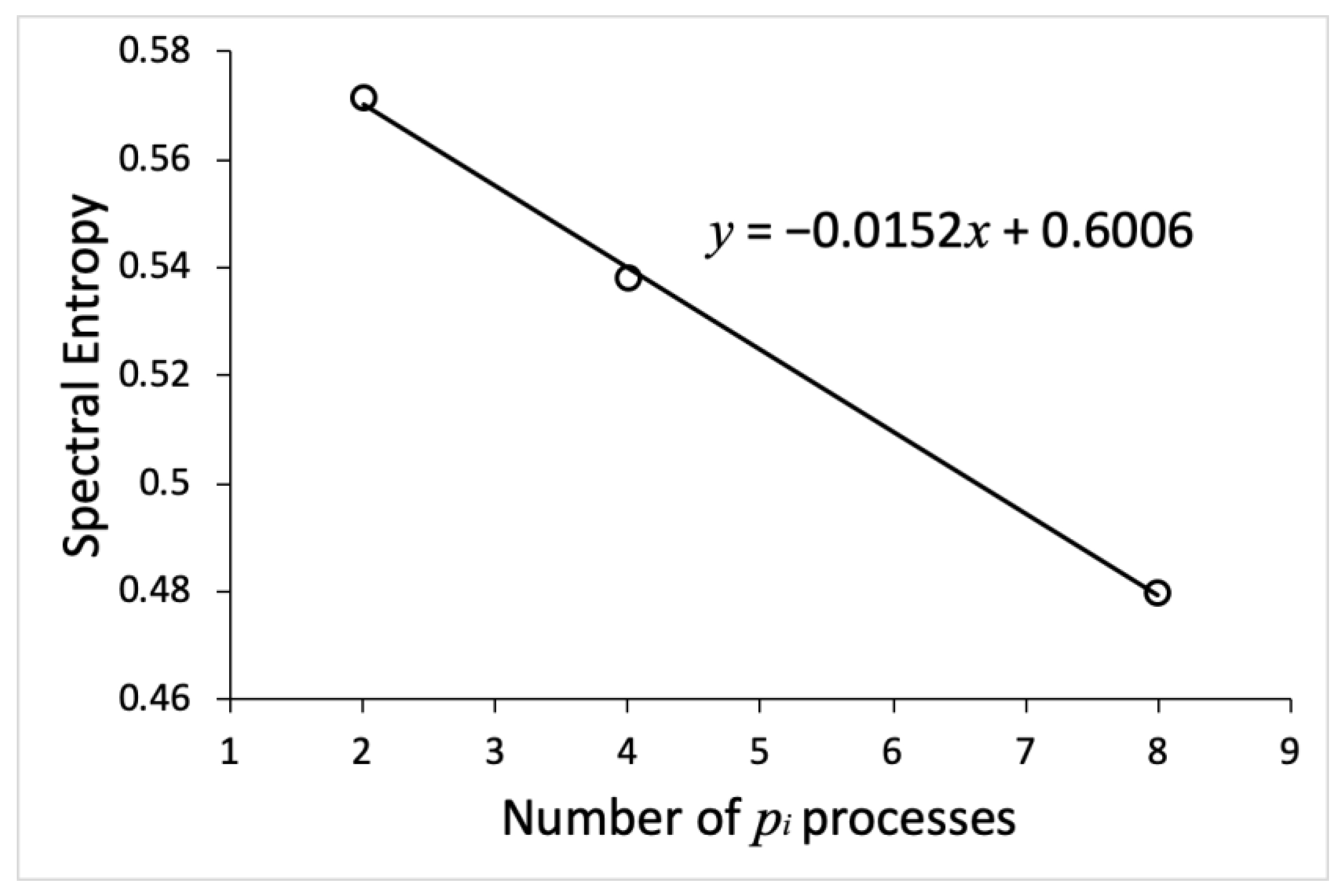
| The System of Two pi Processes | The System of Eight pi Processes | ||
| Process Name | Spectral Entropy | Process Name | Spectral Entropy |
| p1 | 0.5735 | p1 | 0.483 |
| p2 | 0.5693 | p2 | 0.466 |
| The average entropy value = 0.5714 | p3 | 0.474 | |
| The System of Four pi Processes | p4 | 0.512 | |
| Process Name | Spectral Entropy | p5 | 0.4986 |
| p1 | 0.539 | p6 | 0.4688 |
| p2 | 0.542 | p7 | 0.4686 |
| p3 | 0.5375 | p8 | 0.4664 |
| p4 | 0.5343 | The average entropy value = 0.48 | |
| The average entropy value = 0.538 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kraikivski, P. Implications of Noise on Neural Correlates of Consciousness: A Computational Analysis of Stochastic Systems of Mutually Connected Processes. Entropy 2021, 23, 583. https://doi.org/10.3390/e23050583
Kraikivski P. Implications of Noise on Neural Correlates of Consciousness: A Computational Analysis of Stochastic Systems of Mutually Connected Processes. Entropy. 2021; 23(5):583. https://doi.org/10.3390/e23050583
Chicago/Turabian StyleKraikivski, Pavel. 2021. "Implications of Noise on Neural Correlates of Consciousness: A Computational Analysis of Stochastic Systems of Mutually Connected Processes" Entropy 23, no. 5: 583. https://doi.org/10.3390/e23050583
APA StyleKraikivski, P. (2021). Implications of Noise on Neural Correlates of Consciousness: A Computational Analysis of Stochastic Systems of Mutually Connected Processes. Entropy, 23(5), 583. https://doi.org/10.3390/e23050583






