1. Introduction
Thermodiffusion natural convection is important in a variety of disciplines including oceanography, geology, material sciences, geophysics and chemical engineering. This topic has occupied increasing attention in the past two decades. Platten and Chavepeyer [
1] investigated the influence of thermodiffusion on the birth of free convection in Rayleigh-Benard configuration. They summarize the influence of thermodiffusion on free convection together with the way to use this mutual influence in order to experimentally deduce the value of the Soret effect. The Soret effet analysis in thermosolutal convection was investigated by Traore and Mojtabi [
2]. The calculation has been achieved in the particular case where the buoyancy forces are opposing and of equal intensity (
N=-1). They showed that the Soret effect can not be neglected in a double diffusion convection phenomena. Bennacer and Gobin [
3,
4] investigated the cooperating thermosolutal convection in enclosures. At first step, the scale analysis and mass transfer are studied [
3]. They showed, and numerically verified, that the distinction between heat transfer driven flows and mass transfer driven flows is dependent on different criteria which are expressed in terms of
N/
Le for heat transfer and
N/
Le1/3 for mass transfer. A general expression for the Sherwood number as a function of the main parameters of the problem is also proposed over a very wide range. At second step, heat transfer and flow strucure are investigated [
4]. They concluded that the thermosolutale convective flows may be classified in four different regimes: (i) unicellular regime, where the flow is dominated by the thermal effect; (ii) multicellular regime , where the thermal and the solutal effects are comparable in the central part of the cavity; (iii) flow globally driven by the solutal buoyancy force, with a persisting thermal cell in the centre; (iv) unicellular regime, where the solutal force is dominating. Bergman and Hyun [
5] investigated the simulation of two-dimensional thermosolutal convection in liquid metals induced by horizontal temperature and species gradients. Results show two distinct regimes of behavior, in which large solutal buoyancy forces lead to enhanced mass transfer rates. The regimes are separated by a transition region where thermal and solutal buoyancy forces can become balanced, resulting in a velocity reduction throughout the cavity and small mass transfer rates. Double diffusive steady natural convection in a vertical stack of square enclosures, with heat and mass diffusive walls was studied numerically by Costa [
6]. It has been established that changes on the buoyancy ratio are shown to affect seriously the temperature and concentration fields, the path followed by the heat and mass flows, and also the heat and mass transfer parameters. Mamou and Vasseur [
7] investigated the onset of double diffusive convective flows in an inclined fluid layer, when constants fluxes of heat and mass are applied on the two opposing boundary of the layer. It has been demonstrated, on the basis of the parallel flow approximation, the existence of a subcritical Rayleigh number, for the onset of finite amplitude convection. Transient double diffusive natural convection in a horizontal enclosure was investigated numerically and analytically by Bennacer and al. [
8]. It has been found that there are three distinct regimes, for lower buoyancy ratio (N) value the convective cell is essentially due to thermal forces, for high N value the transfer is diffusive and the stabilizing solutal stratification suppresses the flow and intermediate domain (moderate N value) the transfer decreases with N.Linear nonequilibrium thermodynamics (LNET) theory for coupled heat and mass transport was studied by Demirel and Sandler [
9]. It has been demonstrated that the theory of LNET can play crucial role in the proper definition of the coupled heat and mass flows. Also, it has been suggested the use of the resistance type of phenomenological coefficients in the phenomenological equations in which the conjugate forces and flows are identified by the dissipation function. Modeling Soret effect coefficient measurements in porous media considering thermal and solutal convection was investigated by Benano-Melly and al. [
10]. It has been found that multiple convection-roll flow patterns can develop when solutal and thermal buoyancy forces oppose each other, depending on the Soret number value. The effects of concentration and temperature on the coupled heat and mass transport in liquid mixtures are studied by Demirel and Sandler [
11]. Using published experimental data on the thermal conductivity, mutual diffusivity and heats of transport, the degree of coupling between heat and mass flows has been calculated for binary and ternary non ideal liquid mixtures. The extent of coupling and the thermal buoyancy ratio are expressed in terms of the transport coefficients to obtain a better understanting of the interactions between heat and mass flows in liquid mixtures. It was found that the composition of the heavy component bromobenzene changes the direction and magnitude of the two-flow coupling in ternary mixture. The influence of Grashof number on the double diffusive natural convection in a rectangular enclosures was investigated by Benissad and Afrid [
12]. Results allowed to observe complex and varied flow patterns with different conditions of numerical experimentations. In the traditional approach in numerical computation of double diffusive convection problems, the quantities to be computed are usually temperature, pressure, concentration, mass and heat flow rates, but infrequently involving entropy properties.
The contemporary trend in the field of heat transfer and thermal designs is the second Law (of thermodynamics) analysis and its design-related concept of entropy generation minimization [
13]. Entropy generation is associated with thermodynamic irreversibility, which is common in all types of heat transfer processes. Different sources of irreversibility are responsible for heat transfer’s generation of entropy like heat transfer across finite temperature gradient, characteristics of convective heat transfer, viscous effects, etc. Thus entropy generation depends functionally on the local values of velocity and temperature in the domain of interest. Energy conversion processes are accompanied by an irreversible increase in entropy, which leads to a decrease in exergy (available energy).
For a given system, a set of thermodynamic parameters, which optimize the operating conditions may be obtained. Nag and Kumar [
14] studied second Law optimization for convective heat transfer through a duct with constant heat flux. In their study, they plotted the variation of entropy generation versus the temperature difference of the bulk flow and the surface using a duty parameter. For this case [
14], the product of Stanton number and the temperature difference between bulk and surface is constant due to the constant heat flux imposed on the surface. Shuja and al. [
15] analyzed the entropy generation in an impinging jet and [
16,
17,
18] swirling jet impingement on an adiabatic wall for various flow conditions. The influence of fluid viscosity on the entropy generation due to turbulent pipe flow heated from the pipe wall at constant temperature is investigated by Al-Zaharnah and Yilbas [
19]. Sahin [
20], studied the entropy generation in a laminar viscous flow through a duct with constant wall heat flux. He showed that there could be an optimum size for heat exchangers and/or inlet temperature of fluid for which the total irreversibility due to heat transfer and pressure drop becomes the minimum. Narusawa [
21], studied the rate of entropy generation thoeritically and numerically for forced and mixed convection in rectangular duct heated at the bottom. In the theoritical study, he expressed the rate of entropy generation as a function of relevant non-dimensional thermal and hydrodynamic fields as well as interaction between the two fields. The flow structure and the rate of entropy generation were numerically investigated and the transition between two and four rolls occurs at the aspect ratio 3.02 and 2.95 for Rayleigh number,
Ra = 2427 and 3777 respectively. The transition of
Ra = 2427 is accompanied by a clear discontinuity of the entropy generation whereas for
Ra = 3777, the transition occurs without any discontinuity. Many other researches carried out studies on the entropy generation in various flow cases. Yapici and al. [
22], Hyder and Yilbas [
23], Abbassi and al. [
24] and Sahin [
25,
26] performed many studies on second Law analysis and the entropy generation due to heat transfer and fluid friction in duct flows under various conditions.
The dissipation of energy takes the form of a sum of products of conjugate forces and fluxes associated to the problem under consideration, this was presented by the text of the De Groot [
27]. The fluxes are expressed as linear functions of all forces, as constitutive equations, subjected to the reciprocal relations of Onsager. These lead to coupled field equations for the temperature and species concentrations in a given fluid mixture.
Interferences between heat and mass transport, at the level of constituve equations, and the linear theory of non-equilibrium thermodynamics had been formulated as a constitutive theory capable of fully expressing the dependence of all fluxes as a function of all thermodynamic forces.
Altough the varoius topics investigated about entropy generation and its minimization, the determination of total irreversibility in convective heat and mass transfer has not been encountered. In this context, the present paper reports a numerical determination of the entropy generation in doubly diffusive convection on 2D approximation in a square inclined cavity, filled with a fluid (assumed to be a perfect gas mixture).
2. Entropy generation for convective heat and mass transfer
The second law of thermodynamics states that the change in entropy for a given system can be written as the sum of two terms
des and
dis. The first is the entropy change due to exchange of matter and energy with the exterior, the second is the entropy due to “uncompensated transformations”, the entropy produced by the irreversible processes in the interior of the system [
28]:
where:
The entropy generation per unit time and volume, called local entropy generation rate is given by:
For an incompressible Newtonian fluid, the local entropy generation rate is given by Hirschfelder and al. [
29]:
On the right hand side of equation (3), the first term is due to fluid friction, the second is due to mass diffusion and the third is due to heat conduction. The fourth term is due to heat transfer induced by mass diffusion and the fifth is due to chemical reactions. In the case of non-reactive mixture, where the heat transfer due to diffusion is negligible, the entropy generation can be written as:
Assuming the fluid is a perfect gas mixture, the chemical potential of each species can be expressed in the following manner:
where
pα is given by the ideal gas equation state:
The mass diffusion flux, for the specie (
α), is given by the Fick’s law:
Using Eqs. (4–7) and the Fourier’s law, the local entropy generation rate in a two-dimensional flow with a single diffusing specie of concentration (
C) can be simplified as:
According to the Eq. (8), it is clear that the numerical calculation of the local entropy generation rate in a thermodynamics system requires the knowledge of the velocity, temperature and concentration fields in the system.
5. Results and discussions
In this study, four dimensionless numbers (
GrT,
N,
Pr and
Sc) are used in the governing combined heat and mass transfer equations. In order to keep the number of simulations manageable, the ranges of some of these parameters were reduced. The thermal Grashof number is varied from 10
2 to 10
4, only the cooperating situation is investigated, and the buoyancy ratio is kept positive and ranging between 0 and 10. The exploitation of the entropy generation equation limits the choices of the Prandtl and the Schmidt numbers to the case of a gaseous mixture only. For a gaseous mixture, the following definition of the Lewis number is used: (
Le =
D/
a ), both
Le ≥ 1 and
Le ≤ 1 are possible because (
D) is of the same order of magnitude as (
a). Furthermore the Prandtl and Schmidt numbers are fixed at 0.75 and 1.5 respectively. The parameter
λ1 is fixed at 10
−4. In the case of nonzero buoyancy ratio the terms
λ2 and
λ3 are fixed at 0.5 and 10
−2 respectively. The local entropy generation rate is a function of temperature and velocity gradients in the
x and
y directions in the entire calculation domain. It is then a good indicator of grid dependence. Grid refinement tests have been performed for the case 10
2 ≤
GrT ≤ 10
4 and 2 ≤
N ≤ 10. Results show that when we pass from a grid of 31x31 to a grid of 41x41, total entropy generation undergoes an increase of 3%. We conclude that the grid 31x31 is sufficient to carry out a numerical study of this flow. This grid is retained for all following investigations. The numerical simulations presented in this work has been conducted in order to study the effects of the inclination angle of the enclosure, the thermal Grashof number and the buoyancy ratio on entropy generation in steady state conditions. For comparison purposes, the presentation of results starts in
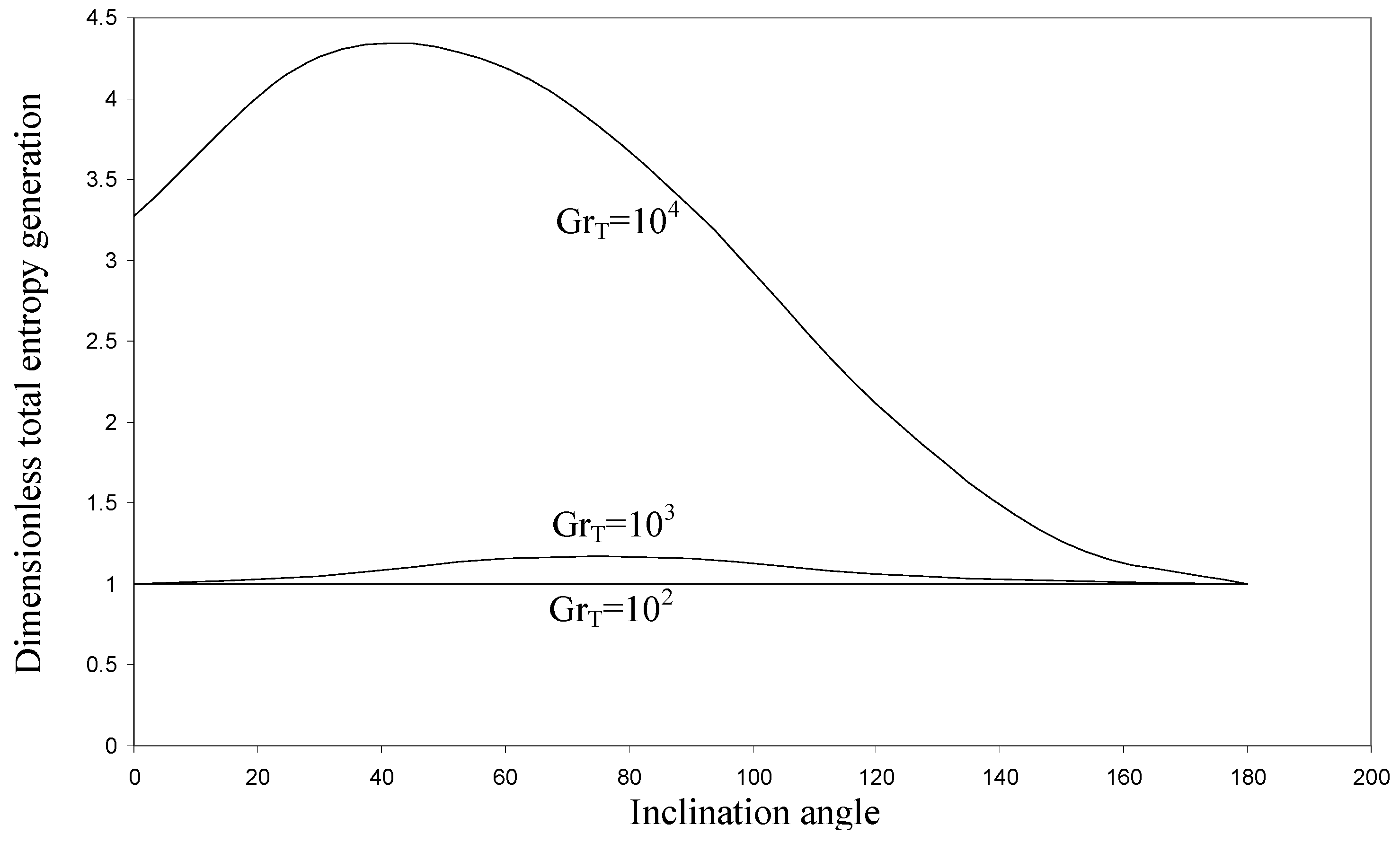
Fig.2 with the influence of the inclination angle at different thermal Grashof numbers on the total entropy generation, in the case of no solute transfer (
N = 0). In this case the solutal Grashof number is zero(
GrS = 0), the concentration difference between the walls W
1 and W
2 is zero(
ΔC = 0), and consequently the parameters
λ2 and
λ3 are zero (Eqs. (27,28)). Therefore the expression of the total entropy generation is reduced to the case of pure convective heat transfer that involves heat transfer and fluid friction irreversibilities given by the first and the second terms on the right hand side of equation (21) (σ
n = σ
n,h + σ
n,f). As can be seen in
Fig. 2, for a thermal Grashof number
GrT = 10
2 and inclination angle ranging between 0° and 180°, the total entropy generation is practically unity (
σn,T = 1 ). This value corresponds to the entropy generation of a system at rest (characterized by a conduction regime). This is due to the fact that for small thermal Grashof number, there is practically no convection and the entropy generation due to fluid friction is zero, consequently the total entropy generation is reduced to the entropy generation due to heat transfer. At a fixed value of inclination angle the total entropy generation increases with the thermal Grashof number. This is because at higher Grashof number heat transfer due to convection begins to play a significant role increasing the flow velocity and in turn the entropy generation due to the viscous effects. Also the isotherms are deformed increasing the temperature gradient and consequently the entropy generation due to heat transfer.
Fig.2 shows also, that the inclination angle has more pronounced effect for
GrT ≥ 10
4, the total entropy generation increases and reaches a maximum at the inclination angle
α ≈ 45°, then decreases and tends towards the value
σn,T = 1 for inclination angles near
α ≈ 180°. Indeed, for inclination angle near
α ≈ 45° buoyancy acts along both the active and adiabatic walls, there is more work done on the fluid by buoyancy thus increasing the total entropy generation via the augmentation of the convective heat transfer. As the inclination angle tends towards the value 180°, the velocity of the fluid diminishes because buoyancy and pressure oppose each other in the intrusion layer. This decreases entropy generation due to viscous effects. On the other hand, convective heat transfer decreases and the isotherms become nearly parallel to the active walls causing a decrease in the magnitude of the thermal gradient and consequently of the entropy generation due to heat transfer. Results concerning the entropy generation evolution versus inclination angle are in good agreement with those of Baytas [
37], who investigated the entropy generation for natural convection in an inclined porous cavity.
The inclination angle is marked between the horizontal and the adiabatic wall. It has been showed that flow is converted to a conduction regime for inclination angles from 240° to 300° for all Rayleigh numbers, which corresponds in our case to an inclination angle around
α ≈ 180°. It can be seen also that entropy generation has a maximum at inclination angle of 40° for Rayleigh number
Ra = 10
4 corresponding for our notation to an inclination angle
α ≈ 50°, which is close to the value found in
Fig.2 (
α ≈ 45°).
Fig.3 illustrates the effect of the buoyancy ratio (
N) on the total entropy generation for inclination angles
α = 60°, 90° and 120° and thermal Grashof numbres
GrT = 10
2, 10
3 and 10
4.
Fig.3 shows that the total entropy generation increases with the buoyancy ratio. This increasing is as important as the thermal Grashof number is higher. For thermal Grashof number
GrT = 10
2 and for buoyancy ratio 0 ≤
N ≤ 2.5.
Fig.3 shows that curves of total entropy generation are identical for
α = 60°, 90° and 120°, which indicates that the isotherms and isoconcentrations are nearly similar for the three considered inclination angles. It is important to note the linear behavior of the total entropy generation for relatively high thermal Grashof numbers (
GrT = 10
4). To understand why the total entropy generation increases with the buoyancy ratio, we have plotted in
Fig.4 the variation of the average Nusselt number on the heated wall and the total entropy generation versus the inclination angle. In this case, the viscous and diffusive irreversibilities are neglected (
λ1,
λ2 and
λ3 << 1) thus reducing the entropy generation to the heat transfer irreversibility only. Each pair of curves corresponds to a given value of the buoyancy ratio ranging from 0 to 10.
As can be seen from
Fig.4, curves of the total entropy generation and the average Nusselt number are nearly identical at fixed buoyancy ratio, and also the average Nusselt number increases with the buoyancy ratio
N. This result is consistent with the heat transfer correlations proposed, at low value of the Lewis number, by Trevisan and Bejan [
38] and Viskanta and Ranganathan [
39]. It can be concluded that the increase of the buoyancy ratio contribute to an augmentation of the energy exchanged between the flow and the walls, that induces an increase of the entropy generation via the augmentation of the temperature gradients near the walls. On the other hand, at low and moderate Lewis numbers and cooperating buoyancy ratio, the double diffusive convection numerical problem is close to the thermal convection problem (
N=0). This corresponds also to the fact that when the source term in the Navier-Stokes equation increases as the buoyancy forces increases through the solutal Grashof number, the convective flow is enhanced and the resulting heat transfer increases generating an increase of entropy generation.
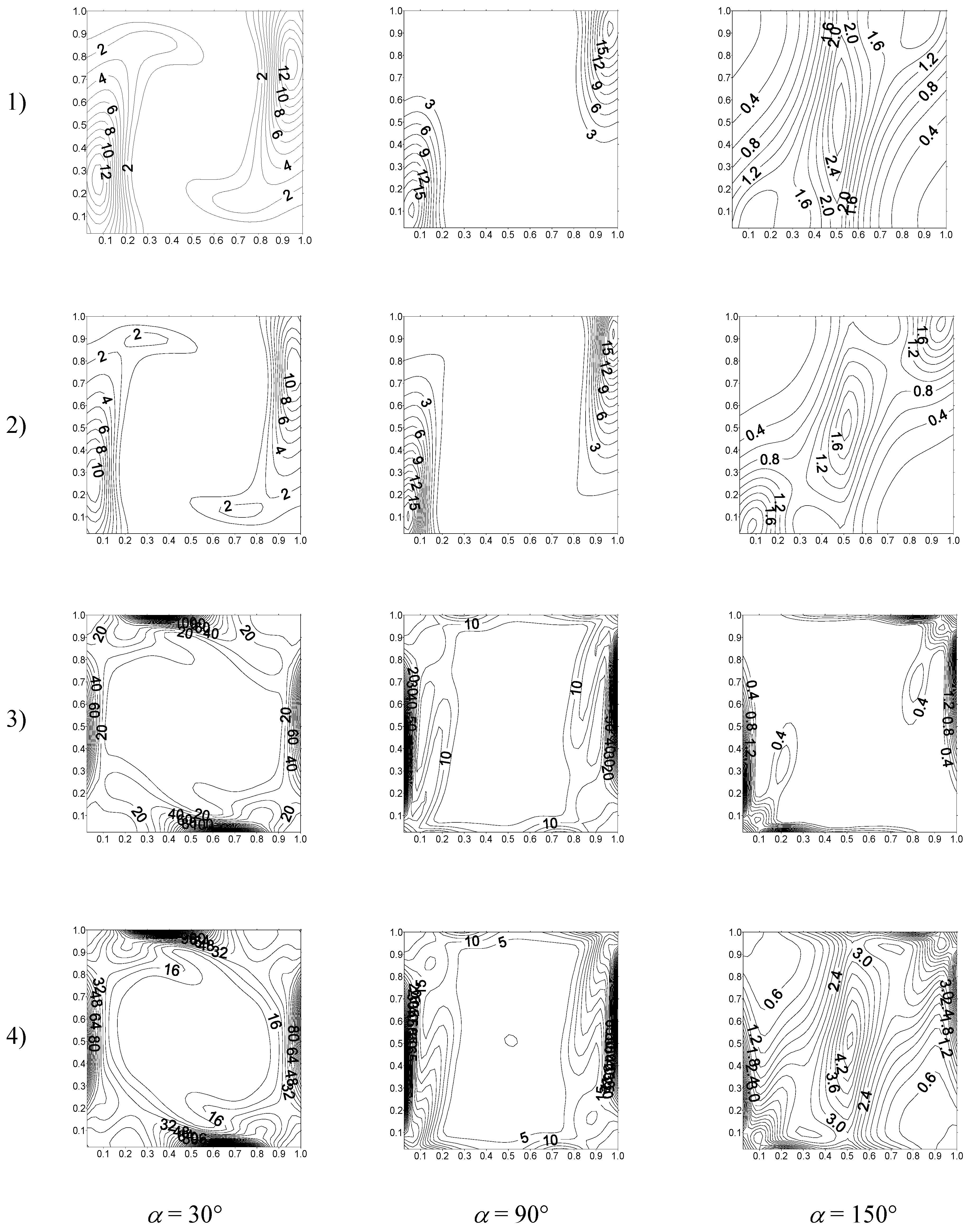
At local level, for a thermal Grashof number,
GrT = 10
4 and for three angles of inclination of the cavity set to be equal 30°, 90° and 150° respectively as an illustrative example, the heat transfer irreversibilities and the diffusive irreversibilities are found similar and mainly confined to the lower and the upper corners of the heated and the cooled walls respectively except for
α = 150° . As the buoyancy ratio increases, the indicated irreversibilities increase for
α = 30° and 90°, while at fixed buoancy ratio, they decrease gradually for increasing the inclination angle. Entropy generation due to viscous effect increases with the buoyancy ratio, its maximum is localized in the middle of the active and adiabatic walls for
α = 30° and in the middle of active walls for
α = 90°. At 150°, irreversibility due to viscous effect decreases considerably indicating that the flow velocity diminishes and convection becomes insignificant. Total entropy generation covers the whole domain except for the center of the cavity at
α = 30° and 90°. For
α = 150°, the total entropy generation takes on a small value even for moderately high value of the buoyancy ratio and is localized in the entire domain indicating that viscous irreversibility covers the top and the bottom of the cavity, while heat and diffusif irreversibilities cover the center.
Fig. 5 summarizes the local irreversibilities for a buoyancy ratio
N = 10 as an example.