Behavior of the Thermodynamic Properties of Binary Mixtures near the Critical Azeotrope
Abstract
:1. Introduction
1. Thermodynamic properties of binary mixtures
2. Investigation of the critical line
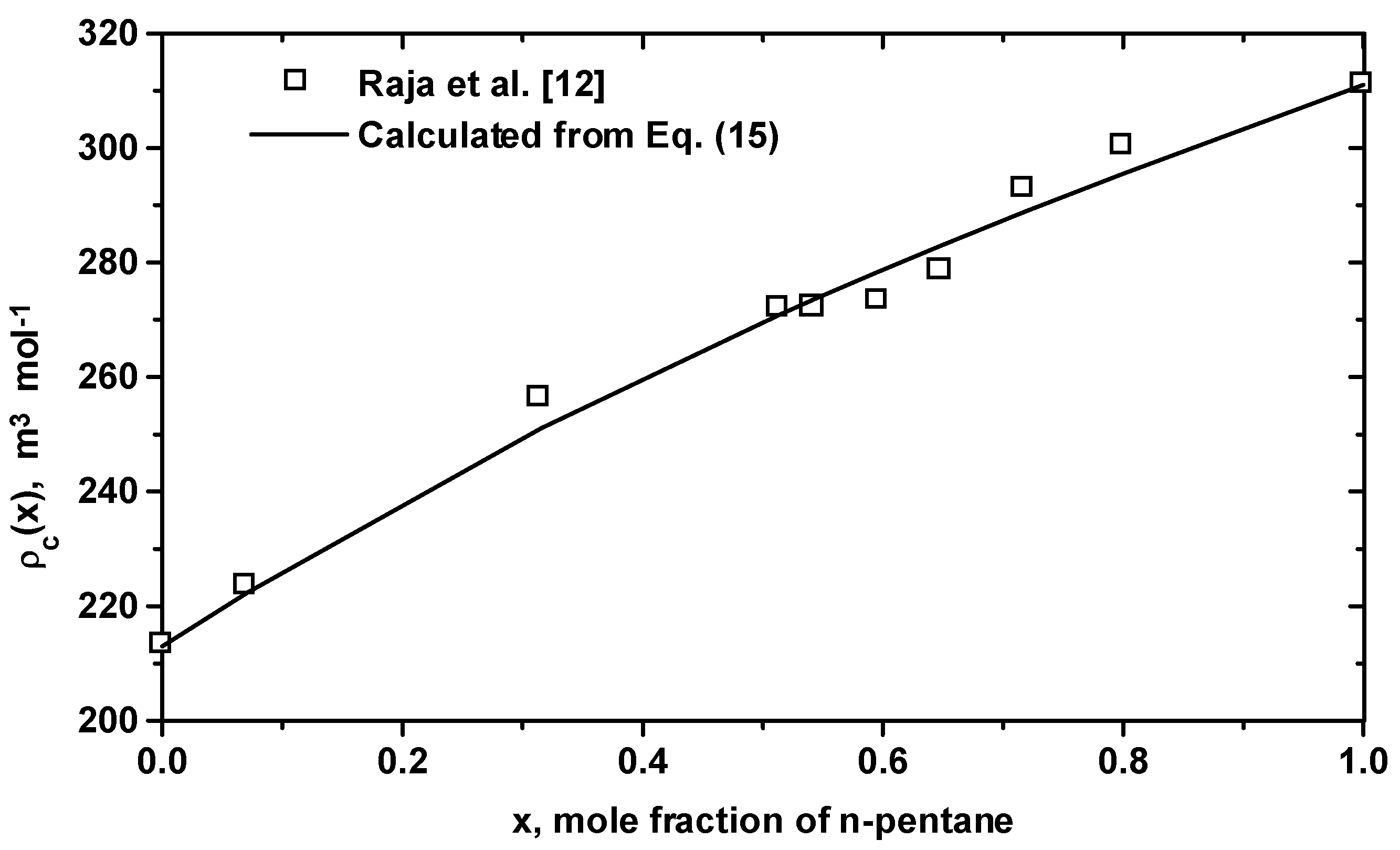
| Equation (16) for (m3/mol): (1)=311.0, (2)=213.0, =38.14, =-15.60 |
| Equation (17) for Tc(K): Tc(1)=469.80, Tc(2)=507.60, T1=-69.309, T2=87.175, T3=-204.59, T4=128.68 |
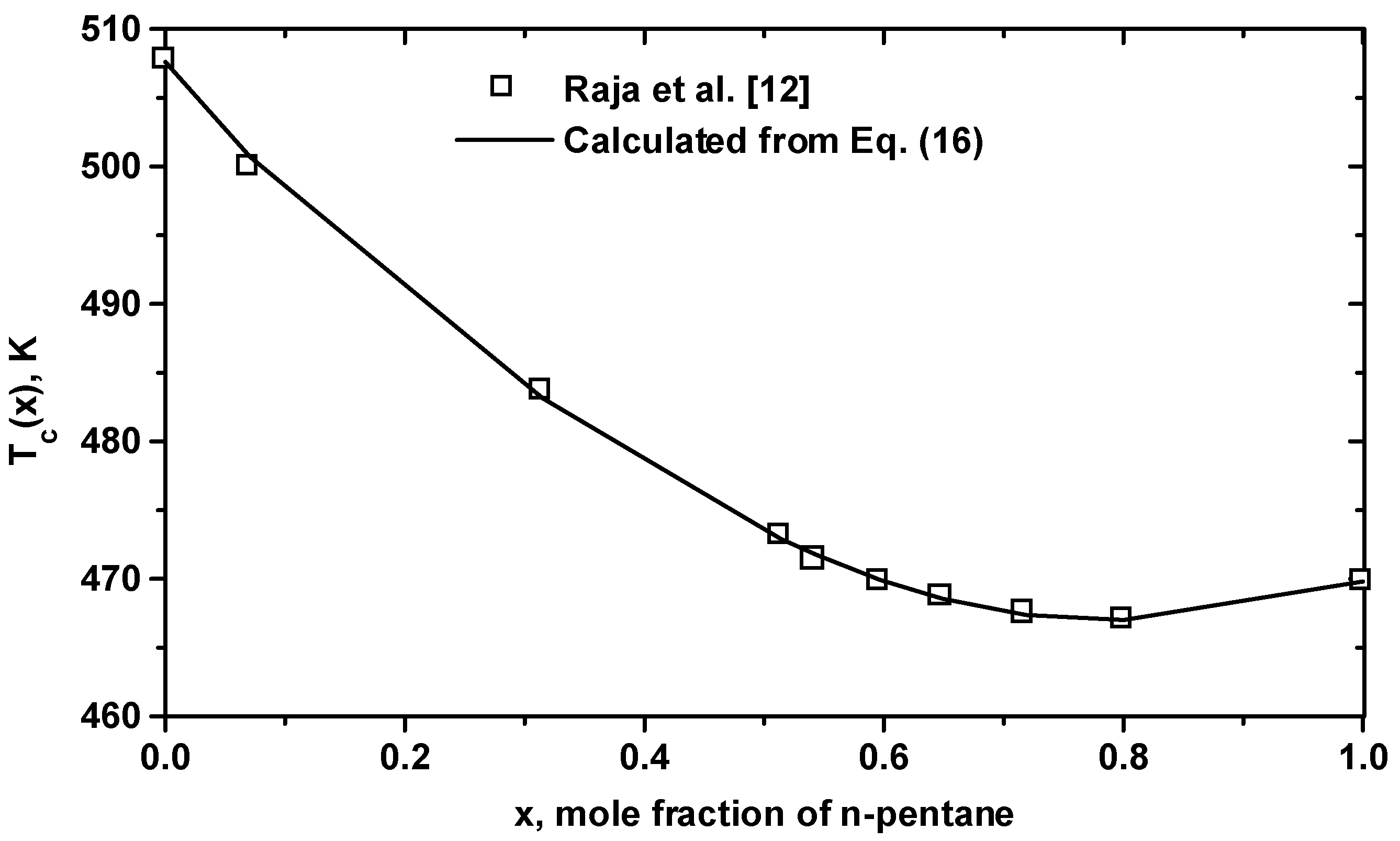
3 Conclusion
Acknowledgments:
References and notes
- van Konynenburg, J. P.; Scot, R. L. Critical Lines and Phase Equilibria in Binary van der Waals Mixtures. Phil. Trans. Roy. Soc. London. 1980, 298, 495–540. [Google Scholar] [CrossRef]
- Abbaci, A. Global Thermodynamic Behavior of Fluids and Fluid Mixtures in the Critical Region. Ph.D. Thesis, 1991. [Google Scholar]
- Rowlinson, J. S.; Swinton, F. L. Liquid and Liquid Mixtures; Butterworth, London, 1982. [Google Scholar]
- Griffiths, R. B.; Wheeler, J. C. Critical Points in Multi-Component Systems. Phys. Rev. A 1970, 2, 1047–1064. [Google Scholar] [CrossRef]
- Leung, S. S.; Griffiths, R. B. Thermodynamic Properties near the Liquid-Vapor Critical Line in Mixtures of He3 and He4. Phys. Rev. A 1973, 8, 2670–2683. [Google Scholar] [CrossRef]
- Moldover, M. R.; Gallagher, J. S. Critical Points of Mixtures: Analogy with Pure Fluids. AIChE J. 1978, 24, 267–278. [Google Scholar] [CrossRef]
- Levelt Sengers, J. M. H.; Greer, W. L.; Sengers, J. V. Scaled Equation of State Parameters for Gases in the Critical Region. J. Phys. Chem. Ref. Data 1976, 5, 1–49. [Google Scholar] [CrossRef]
- Khazanova, N. E.; Lesnevskaya, L. S. Phase and Volume Relations in the System Ethane- Carbon Dioxide. Russ. J. Phys. Chem. 1967, 41(9), 1279–1282. [Google Scholar]
- Khazanova, N. E.; Sominskaya, E. E. Abrupt Changes in Certain Derivatives at the Critical Point of the Azeotropic Mixture. Russ. J. Phys. Chem. 1968, 42(2), 300–301. [Google Scholar]
- Khazanova, N. E.; Lesnevskaya, L. S.; Rovoskii, M. B. Azeotropic Systems at High Pressures. Russ. J. Phys. Chem. 1978, 52(4), 521–524. [Google Scholar]
- Abbaci, A.; van den Berg, H. R.; Sakonidou, E.; Sengers, J. V. Critical Parameters of Mixtures of Carbon Dioxide and Ethane. Int. J. Thermophys. 1992, 13, 1043–1052. [Google Scholar] [CrossRef]
- Raja, F. H.; Cherry, R. H.; Kay, W. B. Critical Properties of the Vapor-Liquid Equilibria of the Binary System Acetone-n-Pentane. Fluid Phase Equilibria 1986, 25, 137–146. [Google Scholar]
- Mattedi, S.; Tavares, F. W.; Castier, M. Calculation of Mixtures Critical Diagrams Using an Equation of State Based on the Lattice Fluid Theory. Braz. J. Chem. Eng. 2000, N° 4-7. 17, 771–784. [Google Scholar] [CrossRef]
- Anisimov, M. A.; Sengers, J. V. Equations of State for Fluids and Fluid Mixtures. IUPAC, Elsevier; Sengers, J. V., Kaiser, R. F., Peters, C. J., White, J. R., Eds.; 2000; pp. 381–434. [Google Scholar]
- Cheng, H.; Anisimov, M. A.; Sengers, J. V. Prediction of Thermodynamic and Transport Properties in the One-Phase Region of Methane-n-Hexane Mixtures Near the Critical End Points. Physica 1997, 128, 67–96. [Google Scholar] [CrossRef]
© 2003 by MDPI (http://www.mdpi.org). Reproduction for noncommercial purposes permitted.
Share and Cite
Abbaci, A. Behavior of the Thermodynamic Properties of Binary Mixtures near the Critical Azeotrope. Entropy 2003, 5, 348-356. https://doi.org/10.3390/e5040348
Abbaci A. Behavior of the Thermodynamic Properties of Binary Mixtures near the Critical Azeotrope. Entropy. 2003; 5(4):348-356. https://doi.org/10.3390/e5040348
Chicago/Turabian StyleAbbaci, Azzedine. 2003. "Behavior of the Thermodynamic Properties of Binary Mixtures near the Critical Azeotrope" Entropy 5, no. 4: 348-356. https://doi.org/10.3390/e5040348
APA StyleAbbaci, A. (2003). Behavior of the Thermodynamic Properties of Binary Mixtures near the Critical Azeotrope. Entropy, 5(4), 348-356. https://doi.org/10.3390/e5040348




