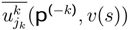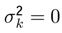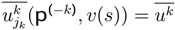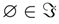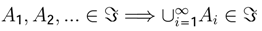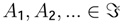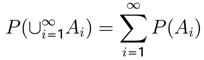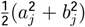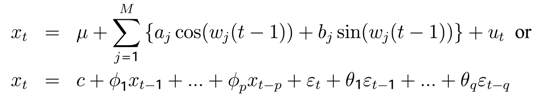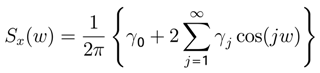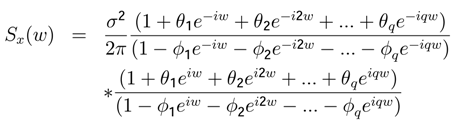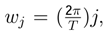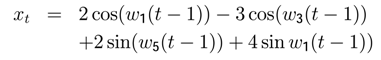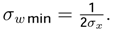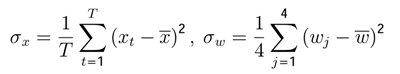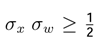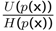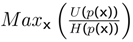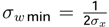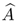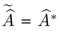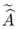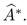4.1 Hermites’s Polynomials Application
Let Γ = (
K, S, v) be a 3−player game, with
K the set of players
k = 1, 2, 3. Thefinite set
Sk of cardinality
lk ∈
N is the set of pure strategies of each player where
k ∈
K,
skjk ∈
Sk, jk = 1, 2, 3 and
S =
S1 ×
S2 ×
S3 represent a set of pure strategy pro fi les with
s ∈
S as an element of that set and
l = 3 ∗ 3 ∗ 3 = 27 represents the cardinality of
S. The vectorial function
v :
S →
R3 associates with every profile
s ∈
S the vector of utilities
v(
s) = (
v1(
s),...,
v3(
s)), where
vk(
s) designates the utility of the player
k facing the profi le
s. In order to get facility of calculus we write the function
vk(
s) in an explicit way
vk(
s)=
vk (
j1, j2,...,
jn).The matrix
v3,27 represents all points of the Cartesian product Π
KSk see
Table 4. The vector
vk (
s) is the
k- column of
v. The graphic representation of the 3-player game is shown in
Figure 1.
In these games we obtain Nash’s equilibria in pure strategy (maximum utility MU,
Table 4) and mixed strategy (Minimum Entropy Theorem MET,
Table 5 and
Table 6). After finding the equilibria we carried out a comparison with the results obtained from applying the theory of quantum games developed previously.
Figure 1.
3-player game strategies
Figure 1.
3-player game strategies
Table 4.
Maximum utility (random utilities): maxp (u1 + u2 + u3)
Nash Utilities and Standard Deviations
Nash Utilities and Standard Deviations
| Maxp (u1 + u2 + u3) = 20.4 |
|---|
| | |
| u1 | u2 | u3 | |
| 8.7405 | 9.9284 | 1.6998 | |
| σ1 | σ2 | σ3 | |
| 6.3509 | 6.2767 | 3.8522 | |
| H1 | H2 | H3 | |
| 4.2021 | 4.1905 | 3.7121 | |
Nash Equilibria: Probabilities, Utilities
Nash Equilibria: Probabilities, Utilities
| Player 1 | Player 2 | Player 3 |
|---|
| p11 | p12 | p13 | p21 | p22 | p23 | p31 | p32 | p33 |
|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 00 | 1 |
| u11 | u12 | u13 | u21 | u22 | u23 | u31 | u32 | u33 |
| 8.7405 | 1.1120 | -3.8688 | 9.9284 | -1.2871 | -0.5630 | -1.9587 | 5.7426 | 1.6998 |
| p11u11 | p12u12 | p13u13 | p21u21 | p22u22 | p23u23 | p31u31 | p32u32 | p33u33 |
| 8.7405 | 0.0000 | 0.0000 | 9.9284 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 1.6998 |
Kroneker Products
| j1 | j2 | j3 | v1(j1,j2,j3) | v2(j1,j2,j3) | v3(j1,j2,j3) | p1j1 | p2j2 | p3j3 | p1j1p2j2 | p1j1p3j3 | p2j2p3j3 | u1(j1,j2,3) | u2(j1,j2,3) | u3(j1,j2,3) |
|---|
| 1 | 1 | 1 | 2.9282 | -1.3534 | -1.9587 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | -1.9587 |
| 1 | 1 | 2 | 6.2704 | 3.2518 | 5.7426 | 1.0000 | 1.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 5.7426 |
| 1 | 1 | 3 | 8.7405 | 9.9284 | 1.6998 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 8.7405 | 9.9284 | 1.6998 |
| 1 | 2 | 1 | 4.1587 | 6.9687 | 4.1021 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1 | 2 | 2 | 3.8214 | 2.7242 | 8.6387 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1 | 2 | 3 | -3.2109 | -1.2871 | -4.1140 | 1.0000 | 0.0000 | 1.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | -1.2871 | 0.0000 |
| 1 | 3 | 1 | 3.0200 | 2.3275 | 6.8226 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1 | 3 | 2 | -2.7397 | 3.0191 | 6.6629 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 1 | 3 | 3 | 1.1781 | -0.5630 | 5.3378 | 1.0000 | 0.0000 | 1.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | -0.5630 | 0.0000 |
| 2 | 1 | 1 | 3.2031 | -1.5724 | -0.9757 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 1 | 2 | 1.9478 | 2.9478 | 6.7366 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 1 | 3 | 1.1120 | 6.4184 | 5.0734 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 1.0000 | 1.1120 | 0.0000 | 0.0000 |
| 2 | 2 | 1 | 5.3695 | 5.7086 | -0.7655 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 2 | 2 | 2.4164 | 1.6853 | 7.1051 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 2 | 3 | 5.2796 | 2.5158 | -4.7264 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 3 | 1 | -4.0524 | -4.5759 | 5.8849 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 3 | 2 | 3.8126 | -1.2267 | 4.8101 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 2 | 3 | 3 | -1.4681 | 10.8633 | 0.2388 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 1 | 1 | -0.4136 | -2.6124 | 4.5470 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 1 | 2 | 2.6579 | 1.7204 | 0.7272 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 1 | 3 | -3.8688 | 4.0884 | 11.2930 | 0.0000 | 1.0000 | 1.0000 | 0.0000 | 0.0000 | 1.0000 | -3.8688 | 0.0000 | 0.0000 |
| 3 | 2 | 1 | 2.1517 | 4.8284 | 14.1957 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 2 | 2 | 6.8742 | -1.8960 | 7.4744 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 2 | 3 | 2.9484 | 2.1771 | 0.0130 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 3 | 1 | 3.9191 | -4.1335 | 7.4357 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 3 | 2 | -3.8252 | 3.0861 | 4.5020 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 3 | 3 | 3 | 3.6409 | 3.4438 | 5.4857 | 0.0000 | 0.0000 | 1.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
Table 5.
Minimum entropy (random utilities): minp(σ1 + σ2 + σ3) ⇒ minp (H1 + H2 + H3)
Nash Utilities and Standard Deviations
Nash Utilities and Standard Deviations
| Minp (σ1+σ2+σ3) = 1.382 |
|---|
| | |
| u1 | u2 | u3 | |
| 0.85 | 2.19 | 4.54 | |
| σ1 | σ2 | σ3 | |
| 1.19492 | 0.187 | 0.000 | |
| H1 | H2 | H3 | |
| 2.596 | 1.090 | 0.035 | |
Nash Equilibria: Probabilities, Utilities
Nash Equilibria: Probabilities, Utilities
| Player 1 | Player 2 | Player 3 |
|---|
| p11 | p12 | p13 | p21 | p22 | p23 | p31 | p32 | p33 |
| 0.0000 | 0.5188 | 0.4812 | 0.4187 | 0.0849 | 0.4964 | 0.2430 | 0.3779 | 0.3791 |
| u11 | u12 | u13 | u21 | u22 | u23 | u31 | u32 | u33 |
| 2.8549 | 1.1189 | 0.5645 | 2.3954 | 2.1618 | 2.0256 | 4.5421 | 4.5421 | 4.5421 |
| p11 u11 | p12 u12 | p13 u13 | p21 u21 | p22 u22 | p23 u23 | p31 u31 | p32 u32 | p33 u33 |
| 0.0000 | 0.5805 | 0.2717 | 1.0031 | 0.1835 | 1.0054 | 1.1036 | 1.7163 | 1.7221 |
Kroneker Products
| j1 | j2 | j3 | v1(j1,j2,j3) | v2(j1,j2,j3) | v3(j1,j2,j3) | p1j1 | p2j2 | p3j3 | p1j1p2j2 | p1j1p3j3 | p2j2p3j3 | u1(j1,j2,j3) | u2(j1,j2,j3) | u3(j1,j2,j3) |
|---|
| 1 | 1 | 1 | 2.93 | -1.35 | -1.96 | 0.0000 | 0.4187 | 0.2430 | 0.0000 | 0.0000 | 0.1017 | 0.2979 | 0.0000 | 0.0000 |
| 1 | 1 | 2 | 6.27 | 3.25 | 5.74 | 0.0000 | 0.4187 | 0.3779 | 0.0000 | 0.0000 | 0.1582 | 0.9922 | 0.0000 | 0.0000 |
| 1 | 1 | 3 | 8.74 | 9.93 | 1.70 | 0.0000 | 0.4187 | 0.3791 | 0.0000 | 0.0000 | 0.1588 | 1.3877 | 0.0000 | 0.0000 |
| 1 | 2 | 1 | 4.16 | 6.97 | 4.10 | 0.0000 | 0.0849 | 0.2430 | 0.0000 | 0.0000 | 0.0206 | 0.0858 | 0.0000 | 0.0000 |
| 1 | 2 | 2 | 3.82 | 2.72 | 8.64 | 0.0000 | 0.0849 | 0.3779 | 0.0000 | 0.0000 | 0.0321 | 0.1226 | 0.0000 | 0.0000 |
| 1 | 2 | 3 | -3.21 | -1.29 | -4.11 | 0.0000 | 0.0849 | 0.3791 | 0.0000 | 0.0000 | 0.0322 | -0.1034 | 0.0000 | 0.0000 |
| 1 | 3 | 1 | 3.02 | 2.33 | 6.82 | 0.0000 | 0.4964 | 0.2430 | 0.0000 | 0.0000 | 0.1206 | 0.3642 | 0.0000 | 0.0000 |
| 1 | 3 | 2 | -2.74 | 3.02 | 6.66 | 0.0000 | 0.4964 | 0.3779 | 0.0000 | 0.0000 | 0.1876 | -0.5139 | 0.0000 | 0.0000 |
| 1 | 3 | 3 | 1.18 | -0.56 | 5.34 | 0.0000 | 0.4964 | 0.3791 | 0.0000 | 0.0000 | 0.1882 | 0.2217 | 0.0000 | 0.0000 |
| 2 | 1 | 1 | 3.20 | -1.57 | -0.98 | 0.5188 | 0.4187 | 0.2430 | 0.2172 | 0.1260 | 0.1017 | 0.3259 | -0.1982 | -0.2119 |
| 2 | 1 | 2 | 1.95 | 2.95 | 6.74 | 0.5188 | 0.4187 | 0.3779 | 0.2172 | 0.1960 | 0.1582 | 0.3082 | 0.5778 | 1.4633 |
| 2 | 1 | 3 | 1.11 | 6.42 | 5.07 | 0.5188 | 0.4187 | 0.3791 | 0.2172 | 0.1967 | 0.1588 | 0.1765 | 1.2624 | 1.1021 |
| 2 | 2 | 1 | 5.37 | 5.71 | -0.77 | 0.5188 | 0.0849 | 0.2430 | 0.0440 | 0.1260 | 0.0206 | 0.1108 | 0.7196 | -0.0337 |
| 2 | 2 | 2 | 2.42 | 1.69 | 7.11 | 0.5188 | 0.0849 | 0.3779 | 0.0440 | 0.1960 | 0.0321 | 0.0775 | 0.3303 | 0.3129 |
| 2 | 2 | 3 | 5.28 | 2.52 | -4.73 | 0.5188 | 0.0849 | 0.3791 | 0.0440 | 0.1967 | 0.0322 | 0.1699 | 0.4948 | -0.2082 |
| 2 | 3 | 1 | -4.05 | -4.58 | 5.88 | 0.5188 | 0.4964 | 0.2430 | 0.2575 | 0.1260 | 0.1206 | -0.4887 | -0.5768 | 1.5153 |
| 2 | 3 | 2 | 3.81 | -1.23 | 4.81 | 0.5188 | 0.4964 | 0.3779 | 0.2575 | 0.1960 | 0.1876 | 0.7151 | -0.2405 | 1.2385 |
| 2 | 3 | 3 | -1.47 | 10.86 | 0.24 | 0.5188 | 0.4964 | 0.3791 | 0.2575 | 0.1967 | 0.1882 | -0.2763 | 2.1366 | 0.0615 |
| 3 | 1 | 1 | -0.41 | -2.61 | 4.55 | 0.4812 | 0.4187 | 0.2430 | 0.2015 | 0.1169 | 0.1017 | -0.0421 | -0.3055 | 0.9163 |
| 3 | 1 | 2 | 2.66 | 1.72 | 0.73 | 0.4812 | 0.4187 | 0.3779 | 0.2015 | 0.1819 | 0.1582 | 0.4206 | 0.3129 | 0.1465 |
| 3 | 1 | 3 | -3.87 | 4.09 | 11.29 | 0.4812 | 0.4187 | 0.3791 | 0.2015 | 0.1825 | 0.1588 | -0.6142 | 0.7460 | 2.2758 |
| 3 | 2 | 1 | 2.15 | 4.83 | 14.20 | 0.4812 | 0.0849 | 0.2430 | 0.0409 | 0.1169 | 0.0206 | 0.0444 | 0.5646 | 0.5800 |
| 3 | 2 | 2 | 6.87 | -1.90 | 7.47 | 0.4812 | 0.0849 | 0.3779 | 0.0409 | 0.1819 | 0.0321 | 0.2205 | -0.3448 | 0.3054 |
| 3 | 2 | 3 | 2.95 | 2.18 | 0.01 | 0.4812 | 0.0849 | 0.3791 | 0.0409 | 0.1825 | 0.0322 | 0.0949 | 0.3972 | 0.0005 |
| 3 | 3 | 1 | 3.92 | -4.13 | 7.44 | 0.4812 | 0.4964 | 0.2430 | 0.2389 | 0.1169 | 0.1206 | 0.4727 | -0.4833 | 1.7762 |
| 3 | 3 | 2 | -3.83 | 3.09 | 4.50 | 0.4812 | 0.4964 | 0.3779 | 0.2389 | 0.1819 | 0.1876 | -0.7175 | 0.5612 | 1.0754 |
| 3 | 3 | 3 | 3.64 | 3.44 | 5.49 | 0.4812 | 0.4964 | 0.3791 | 0.2389 | 0.1825 | 0.1882 | 0.6852 | 0.6284 | 1.3104 |
Table 6.
Minimum entropy (stone-paper-scissors): minp(σ1 + σ2 + σ3) ⇒ minp (H1 + H2 + H3)
Nash Utilities and Standard Deviations
Nash Utilities and Standard Deviations
| Minp (σ1+σ2+σ3) = 1.382 |
|---|
| |
| u1 | u2 | u3 | |
| 0.5500 | 0.5500 | 0.5500 | |
| σ1 | σ2 | σ3 | |
| 0.0000 | 0.0000 | 0.0000 | |
| H1 | H2 | H3 | |
| 0.0353 | 0.0353 | 0.0353 | |
Nash Equilibria: Probabilities, Utilities
Nash Equilibria: Probabilities, Utilities
| Player 1 | Player 2 | Player 3 |
|---|
| p11 | p12 | p13 | p21 | p22 | p23 | p31 | p32 | p33 |
| 0.3333 | 0.3333 | 0.3333 | 0.3333 | 0.3333 | 0.3333 | 0.3300 | 0.3300 | 0.3300 |
| u11 | u12 | u13 | u21 | u22 | u23 | u31 | u32 | u33 |
| 0.5500 | 0.5500 | 0.5500 | 0.5500 | 0.5500 | 0.5500 | 0.5556 | 0.5556 | 0.5556 |
| p11 u11 | p12 u12 | p13 u13 | p21 u21 | p22 u22 | p23 u23 | p31 u31 | p32u32 | p33u33 |
| 0.1833 | 0.1833 | 0.1833 | 0.1833 | 0.1833 | 0.1833 | 0.1833 | 0.1833 | 0.1833 |
Kroneker Products
| j1 | j2 | j3 | v1(j1,j2,j3) | v2(j1,j2,j3) | v3(j1,j2,j3) | p1j1 | p2j2 | p3j3 | p1j1p2j2 | p1j1p3j3 | p2j2p3j3 | u1(j1,j2,j3) | u2(j1,j2,j3) | u3(j1,j2,j3) |
|---|
| stone | stone | stone | 0 | 0 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.0000 | 0.0000 |
| stone | stone | paper | 0 | 0 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.0000 | 0.1111 |
| stone | stone | sccisor | 1 | 1 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.0000 |
| stone | paper | stone | 0 | 1 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.1100 | 0.0000 |
| stone | paper | paper | 0 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.1100 | 0.1111 |
| stone | paper | sccisor | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.1111 |
| stone | sccisor | stone | 1 | 0 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.0000 | 0.1111 |
| stone | sccisor | paper | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.1111 |
| stone | sccisor | sccisor | 1 | 0 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.0000 | 0.0000 |
| paper | stone | stone | 1 | 0 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.0000 | 0.0000 |
| paper | stone | paper | 1 | 0 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.0000 | 0.1111 |
| paper | stone | sccisor | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.1111 |
| paper | paper | stone | 1 | 1 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.0000 |
| paper | paper | paper | 0 | 0 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.0000 | 0.0000 |
| paper | paper | sccisor | 0 | 0 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.0000 | 0.1111 |
| paper | sccisor | stone | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.1111 |
| paper | sccisor | paper | 0 | 1 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.1100 | 0.0000 |
| paper | sccisor | sccisor | 0 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.1100 | 0.1111 |
| sccisor | stone | stone | 0 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.1100 | 0.1111 |
| sccisor | stone | paper | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.1111 |
| sccisor | stone | sccisor | 0 | 1 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.1100 | 0.0000 |
| sccisor | paper | stone | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.1111 |
| sccisor | paper | paper | 1 | 0 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.0000 | 0.0000 |
| sccisor | paper | sccisor | 1 | 0 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.0000 | 0.1111 |
| sccisor | sccisor | stone | 0 | 0 | 1 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.0000 | 0.1111 |
| sccisor | sccisor | paper | 1 | 1 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.1100 | 0.1100 | 0.0000 |
| sccisor | sccisor | sccisor | 0 | 0 | 0 | 0.3333 | 0.3333 | 0.3300 | 0.1111 | 0.1100 | 0.1100 | 0.0000 | 0.0000 | 0.0000 |
4.2 Time Series Application
The relationship between Time Series and Game Theory appears when we apply the entropy minimization theorem (EMT). This theorem (EMT) is a way to analyze the Nash-Hayek equilibrium in mixed strategies. Introducing the elements rationality and equilibrium in the domain of time series can be a big help, because it allows us to study the human behavior re fl ected and registered in historical data. The main contributions of this complementary focus on time series has a relationship with Econophysics and rationality.
Human behavior evolves and is the result of learning. The objective of learning is stability and optimal equilibrium. Due to the above-mentioned, we can affi rm that if learning is optimal then the convergence to equilibrium is faster than when the learning is sub-optimal. Introducing elements of Nash’s equilibrium in time series will allow us to evaluate learning and the convergence to equilibrium through the study of historical data (time series).
One of the branches of Physics called Quantum Mechanics was pioneered using Heisemberg’s uncer- tainty principle. This paper is simply the application of this principle in Game Theory and Time Series.
Econophysics is a newborn branch of the scientifi c development that attempts to establish the analogies between Economics and Physics, see
Mantenga and Stanley [
33]. The establishment of analogies is a creative way of applying the idea of cooperative equilibrium. The product of this cooperative equilibrium will produce synergies between these two sciences. From my point of view, the power of physics is the capacity of equilibrium formal treatment in stochastic dynamic systems. On the other hand, the power of Economics is the formal study of rationality, cooperative and non-cooperative equilibrium.
Econophysics is the beginning of a unifi cation stage of the systemic approach of scientifi c thought. I show that it is the beginning of a unifi cation stage but remains to create synergies with the rest of the sciences.
Let
![Entropy 05 00313 i221]()
be a covariance-stationary process with the mean
E[
xt] =
µ and
jth covariance
γjIf these autocovariances are absolutely summable, the population spectrum of
x is given by [
21].
If the
γj ’s represent autocovariances of a covariance-stationary process using the Possibility Theorem, then
and
Sx(
w) will be nonnegative for all
w. In general for an ARMA(
p,
q) process:
xt =
c +
ϕ1xt−1 +
ϕ2xt−2 + … +
ϕpxt−p +
εt +
θ1εt−2 + … +
θqεt−qThe population spectrum
Sx(
w) ∈ [
Sx(
w −
σw)
, Sx(
w +
σw)] is given by
Hamilton [
17].
where
![Entropy 05 00313 i189]()
and
w is a scalar.
Given an observed sample of
T observations denoted
x1,x2,.., xT , we can calculate up to
T − 1 sample autocovariances
γj from the formulas:
![Entropy 05 00313 i190]()
and
The sample periodogram can be expressed as:
When the sample size
T is an odd number,
xt will be expressed in terms of periodic functions with
M = (
T − 1)/2 representing different frequencies
![Entropy 05 00313 i193]()
The coefficients
![Entropy 05 00313 i195]()
can be estimated with OLS regression.
The sample variance of
xt can be expressed as:
The portion of the sample variance of
xt that can be attributed to cycles of frequency
wj is given by:
with
![Entropy 05 00313 i199]()
as the sample periodogram of frequency
wj.
Continuing with the methodology proposed by
Hamilton [
17]. we develop two examples that will allow us to verify the applicability of the Possibility Theorem.
In the second step, we find the value of the parameters
![Entropy 05 00313 i203]()
,
j = 1
,..., (
T − 1) for the time series
xt according to Q21 (
Table 7,
Figure 6).
In the third step, we find
![Entropy 05 00313 i204]()
(
Table 8,
Figure 7), only for the frequencies
w1, w3, w5, w12:
In the fourth step, we compute the values
σx,σw and
![Entropy 05 00313 i205]()
resp. for
y, z, u, (
Table 9).
In the fifth step, we verify that the Possibility Theorem is respected,
![Entropy 05 00313 i207]()
resp for
y,z,u, (
Table 9).
Example 6 Let {
vt}
t = 1,..,37 be a random variable, and w12 a random variable with gaussian probability density N (0, 1).
Both variables are related as continues By simplicity of computing, we suppose that
εv and
Et has gaussian probability density
N (0, 1). It is evident that
σw12 =
σε = 1 After a little computing we get the estimated value of
![Entropy 05 00313 i209]()
= 1.1334. The product
![Entropy 05 00313 i210]()
= 1.1334 verifi es the Possibility Theorem and permits us to compute:
![Entropy 05 00313 i211]()
The spectral analysis can not give the theoretical value of
E[
w12] = 2.037. The experimental value of
E[
w12] = 2.8 . You can see the results in
Figure 8,
Figure 9 and
Table 10.
Table 7.
Time series values of xt,yt,zt,ut
Table 7.
Time series values of xt,yt,zt,ut
| P a rame te rs o f xt |
|---|
| j = t | γj | ρj | E [wj] | γj·cos (E[w1]*j) | γj·cos (E[w3]*j) | γj·cos (E[w5]*j) | γj·cos (E[w12]*j) | xt | yt | zt | ut | cos(w1(t-1)) | cos(w3(t-1)) | sen(w5(t-1)) | sen(w12(t-1)) |
|---|
| 1 | 3,557 | 0,210 | 0,170 | 3,505 | 3,105 | 2,350 | -1,601 | -1,000 | 2,000 | 0,000 | 3,000 | 1,000 | 1,000 | 0,000 | 0,000 |
| 2 | -0,030 | -0,002 | 0,340 | -0,029 | -0,016 | 0,004 | 0,018 | 4,425 | 5,543 | 3,572 | 3,000 | 0,986 | 0,873 | 0,751 | 0,893 |
| 3 | 8,571 | 0,505 | 0,509 | 7,482 | 0,364 | -7,101 | 8,447 | -0,919 | -1,330 | -3,216 | 3,000 | 0,943 | 0,524 | 0,992 | -0,804 |
| 4 | -5,076 | -0,299 | 0,679 | -3,950 | 2,285 | 4,913 | 1,485 | 2,062 | 1,069 | -0,677 | 3,000 | 0,873 | 0,042 | 0,560 | -0,169 |
| 5 | -9,188 | -0,542 | 0,849 | -6,071 | 7,612 | 4,138 | 6,635 | 6,228 | 5,381 | 3,825 | 3,000 | 0,778 | -0,450 | -0,252 | 0,956 |
| 6 | 4,167 | 0,246 | 1,019 | 2,185 | -4,152 | 1,553 | 3,928 | -0,746 | -1,446 | -2,767 | 3,000 | 0,661 | -0,828 | -0,893 | -0,692 |
| 7 | -4,030 | -0,238 | 1,189 | -1,503 | 3,673 | -3,800 | 0,510 | 0,848 | -0,285 | -1,334 | 3,000 | 0,524 | -0,996 | -0,928 | -0,333 |
| 8 | -8,301 | -0,490 | 1,358 | -1,749 | 4,937 | -7,248 | 6,880 | 6,781 | 4,714 | 3,968 | 3,000 | 0,373 | -0,911 | -0,333 | 0,992 |
| 9 | 5,607 | 0,331 | 1,528 | 0,238 | -0,713 | 1,183 | 4,894 | 0,942 | -1,817 | -2,238 | 3,000 | 0,211 | -0,595 | 0,488 | -0,560 |
| 10 | -1,355 | -0,080 | 1,698 | 0,172 | -0,505 | 0,805 | -0,058 | 0,469 | -1,868 | -1,953 | 3,000 | 0,042 | -0,127 | 0,978 | -0,488 |
| 11 | -7,601 | -0,448 | 1,868 | 2,225 | -5,913 | 7,574 | 6,929 | 4,232 | 3,742 | 3,996 | 3,000 | -0,127 | 0,373 | 0,804 | 0,999 |
| 12 | 7,379 | 0,435 | 2,038 | -3,322 | 7,272 | -5,329 | 5,738 | -4,394 | -2,231 | -1,645 | 3,000 | -0,293 | 0,778 | 0,085 | -0,411 |
| 13 | 3,541 | 0,209 | 2,208 | -2,106 | 3,339 | 0,149 | 0,749 | -7,756 | -3,415 | -2,515 | 3,000 | -0,450 | 0,986 | -0,692 | -0,629 |
| 14 | -4,731 | -0,279 | 2,377 | 3,415 | -3,126 | -3,680 | 4,579 | -2,107 | 2,720 | 3,910 | 3,000 | -0,595 | 0,943 | -0,999 | 0,977 |
| 15 | 7,312 | 0,431 | 2,547 | -6,058 | 1,542 | 7,207 | 4,826 | -5,688 | -2,448 | -1,005 | 3,000 | -0,722 | 0,661 | -0,628 | -0,251 |
| 16 | 0,948 | 0,056 | 2,717 | -0,864 | -0,277 | 0,497 | 0,354 | -4,957 | -4,662 | -3,005 | 3,000 | -0,828 | 0,211 | 0,169 | -0,751 |
| 17 | -12,981 | -0,765 | 2,887 | 12,561 | 9,369 | 3,796 | 12,935 | 4,468 | 1,888 | 3,710 | 3,000 | -0,911 | -0,293 | 0,851 | 0,928 |
| 18 | -3,060 | -0,180 | 3,057 | 3,049 | 2,961 | 2,788 | -1,601 | 1,807 | -2,271 | -0,335 | 3,000 | -0,968 | -0,722 | 0,956 | -0,084 |
| 19 | -4,856 | -0,286 | - | 4,839 | 4,700 | 4,426 | -2,551 | -1,674 | -5,401 | -3,408 | 3,000 | -0,996 | -0,968 | 0,412 | -0,852 |
| 20 | -14,516 | -0,856 | - | 14,048 | 10,483 | 4,257 | 14,462 | 3,491 | 1,411 | 3,404 | 3,000 | -0,996 | -0,968 | -0,411 | 0,851 |
| 21 | 0,759 | 0,045 | - | -0,692 | -0,223 | 0,398 | 0,282 | -1,337 | -1,592 | 0,344 | 3,000 | -0,968 | -0,722 | -0,956 | 0,086 |
| 22 | 5,394 | 0,318 | - | -4,469 | 1,135 | 5,316 | 3,569 | -6,360 | -5,536 | -3,713 | 3,000 | -0,911 | -0,293 | -0,852 | -0,928 |
| 23 | -4,600 | -0,271 | - | 3,321 | -3,038 | -3,580 | 4,450 | 0,372 | 1,342 | 2,999 | 3,000 | -0,829 | 0,210 | -0,170 | 0,750 |
| 24 | 6,986 | 0,412 | - | -4,155 | 6,586 | 0,301 | 1,462 | -1,157 | -0,431 | 1,013 | 3,000 | -0,722 | 0,660 | 0,628 | 0,253 |
| 25 | 8,725 | 0,515 | - | -3,929 | 8,600 | -6,295 | 6,797 | -5,931 | -5,101 | -3,911 | 3,000 | -0,595 | 0,943 | 0,999 | -0,978 |
| 26 | -5,611 | -0,331 | - | 1,644 | -4,367 | 5,591 | 5,109 | 0,035 | 1,608 | 2,508 | 3,000 | -0,450 | 0,986 | 0,692 | 0,627 |
| 27 | 3,347 | 0,197 | - | -0,426 | 1,249 | -1,992 | 0,137 | -1,436 | 1,067 | 1,653 | 3,000 | -0,293 | 0,778 | -0,084 | 0,413 |
| 28 | 6,054 | 0,357 | - | 0,256 | -0,766 | 1,271 | 5,290 | -6,978 | -4,251 | -3,997 | 3,000 | -0,127 | 0,373 | -0,804 | -0,999 |
| 29 | -8,491 | -0,501 | - | -1,788 | 5,046 | -7,410 | 7,026 | 0,454 | 2,030 | 1,945 | 3,000 | 0,042 | -0,127 | -0,978 | 0,486 |
| 30 | 0,753 | 0,044 | - | 0,281 | -0,686 | 0,710 | -0,097 | 3,473 | 2,667 | 2,246 | 3,000 | 0,211 | -0,594 | -0,488 | 0,561 |
| 31 | 4,354 | 0,257 | - | 2,282 | -4,338 | 1,626 | 4,108 | 0,177 | -3,221 | -3,967 | 3,000 | 0,373 | -0,911 | 0,332 | -0,992 |
| 32 | -10,875 | -0,641 | - | -7,183 | 9,013 | 4,888 | 7,837 | 7,218 | 2,374 | 1,326 | 3,000 | 0,524 | -0,996 | 0,928 | 0,331 |
| 33 | -0,935 | -0,055 | - | -0,728 | 0,422 | 0,905 | 0,276 | 8,367 | 4,094 | 2,773 | 3,000 | 0,661 | -0,829 | 0,893 | 0,693 |
| 34 | 4,485 | 0,264 | - | 3,915 | 0,188 | -3,718 | 4,422 | -0,409 | -2,266 | -3,822 | 3,000 | 0,778 | -0,451 | 0,253 | -0,956 |
| 35 | -9,859 | -0,581 | - | -9,295 | -5,165 | 1,261 | 5,846 | 1,169 | 2,414 | 0,668 | 3,000 | 0,873 | 0,042 | -0,559 | 0,167 |
| 36 | 0,000 | - | - | - | - | - | - | 1,551 | 5,107 | 3,221 | 3,000 | 0,943 | 0,524 | -0,992 | 0,805 |
| 37 | - | - | - | - | - | - | - | -5,717 | -1,597 | -3,568 | 3,000 | 0,986 | 0,873 | -0,751 | -0,892 |
Table 8.
Frequencies, variances and sample periodogram of xt
Analysis of xt
| |
|---|
| Variance: st2 | |
|---|
| E[(xt-E[xt])2] | 16,958 |
| (a12+a32+b52+b1 | 16,500 |
| γ0 | 16,958 |
| T | 37,000 |
| Frequencies | Wavelength | Coefficients | (aj2+bj2)/2 | Sample Periodogram | (4*pj/T)sx(E[wj]) |
|---|
| E[w1] | 0,170 | l1 | 37,000 | a1 | 2,000 | a12 | 2,000 | Sx(E[w1]) | 4,961 | 1,685 |
| E[w3] | 0,509 | l2 | 12,333 | a3 | -3,000 | a32 | 4,500 | Sx(E[w3]) | 21,988 | 7,468 |
| E[w5] | 0,849 | l3 | 7,400 | b5 | 2,000 | b52 | 2,000 | Sx(E[w5]) | 8,350 | 2,836 |
| E[w12] | 2,038 | l4 | 3,083 | b12 | 4,000 | b122 | 8,000 | Sx(E[w12]) | 45,375 | 15,410 |
Table 9.
Verification of Possibility Theorem for series xt, yt, zt, ut
Table 9.
Verification of Possibility Theorem for series xt, yt, zt, ut
| Heisenberg's Uncertainty Principle |
| |
| σxσw = 3,348 >1/2 | | σyσw = 4,234 >1/2 | |
| | | | |
| E[xt] | 0,000 | σx=E[(xt-E[xt])2] | 4,118 | | E[yt] | 0,000 | E[(yt-E[yt])2] | 3,206 |
| E[w] | 0,892 | σw=E[(w-E[w])2] | 0,813 | | E[w] | 1,104 | E[(w-E[w])2] | 1,321 |
| | | | |
| σwmin | 0,121 | | σwmin | 0,156 | |
| | | | |
| | | Lower[w | Min[j] | Upper[wj] | Max[j] | | | | Lower[wj] | Min[j] | Upper[wj] | Max[j] |
| E[w1] | 0,170 | 0,048 | 0,285 | 0,291 | 1,715 | | |
| E[w3] | 0,509 | 0,388 | 2,285 | 0,631 | 3,715 | |
| E[w5] | 0,849 | 0,728 | 4,285 | 0,970 | 5,715 | | E[w1] | 0,170 | 0,014 | 0,082 | 0,326 | 1,918 |
| E[w12] | 2,038 | 1,916 | 11,285 | 2,159 | 12,715 | | E[w12] | 2,038 | 1,882 | 11,082 | 2,194 | 12,918 |
| |
| σzσw = 0,000 <1/2 | | σuσw = 0,000 <1/2 | |
| | | | |
| E[zt] | 0,000 | σz=E[(zt-E[zt])2] | 2,867 | | E[ut] | 3,000 | σu=E[(ut-E[ut])2] | 0,000 | |
| E[w12] | 2,038 | σw=E[(w-E[w])2] | 0,000 | | E[w] | ∞ | σw=E[(w-E[w])2] | − | |
| σwmin | 0,174 | | σwmin | ∞ | |
| |
| | | Lower[wMin[j] | Upper[wj] | Max[j] | | | | Lower[wj] | Min[j] | Upper[wj] | Max[j] |
| E[w12] | 2,038 | 1,863 | 10,973 | 2,038 | 12,000 | | E[wi] | 2,038 | 0,000 | 0,000 | ∞ | ∞ |
| |
Application of Possibility Theorem for time series vt
Application of Possibility Theorem for time series vt
| Heisenberg's Uncertainty Principle |
| |
| σvσw12= 1,1334 > 1/2 | |
| |
| |
| E[vt] | 0,0439 | σv=E[(vt-E[vt])2] | 1,1334 |
| E[w12] | 2,0377 | σw=E[(w12-E[w12])2] | 1,0000 |
| |
| σwmin | 0,4412 | T | 37 | γ0 | 1,1334 |
| |
| | | Lower[w12] | Min[j] | Upper[w12] | Max[j] |
| E[w12] | 2,0377 | 1,5966 | 9,4021 | 2,4789 | 14,5979 |
Figure 2.
yt = 2cos(w1(t − 1)) + 4 sin(w12(t − 1))
Figure 2.
yt = 2cos(w1(t − 1)) + 4 sin(w12(t − 1))
Figure 3.
zt = 4 sin(w12(t − 1))
Figure 3.
zt = 4 sin(w12(t − 1))
Figure 5.
Constitutive elements of time series xt
Figure 5.
Constitutive elements of time series xt
Figure 6.
Autocorrelations of time series xt
Figure 6.
Autocorrelations of time series xt
Figure 7.
Periodogram of time series xt
Figure 7.
Periodogram of time series xt
Figure 8.
Time series vt = sin(E[w12] + εt)(t − 1)) + εt
Figure 8.
Time series vt = sin(E[w12] + εt)(t − 1)) + εt
Figure 9.
Spectral analysis of vt
Figure 9.
Spectral analysis of vt
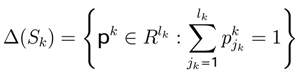
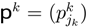 the probability vector. The set of pro fi les in mixed strategies is the polyhedron Δ with
the probability vector. The set of pro fi les in mixed strategies is the polyhedron Δ with 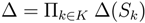 , where
, where 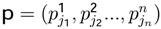 and
and 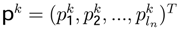 . Using the Kronecker product ⊗ it is possible to write1:
. Using the Kronecker product ⊗ it is possible to write1:
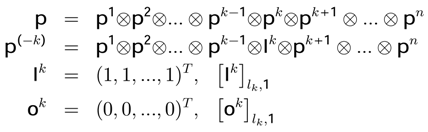
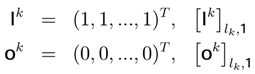
 associates with every pro fi le in mixed strategies the vector of expected utilities
associates with every pro fi le in mixed strategies the vector of expected utilities
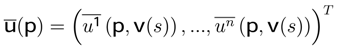
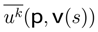 is the expected utility of the player k. Every
is the expected utility of the player k. Every 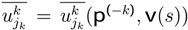 represents the expected utility for each player’s strategy and the vector uk is noted
represents the expected utility for each player’s strategy and the vector uk is noted 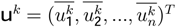 .
.
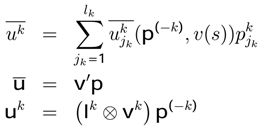
 designates the extension of the game Γ with the mixed strategies. We get Nash’s equilibrium (the maximization of utility [3,43,55,56,57]) if and only if, ∀k, p, the inequality
designates the extension of the game Γ with the mixed strategies. We get Nash’s equilibrium (the maximization of utility [3,43,55,56,57]) if and only if, ∀k, p, the inequality 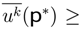
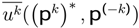 is respected.
is respected.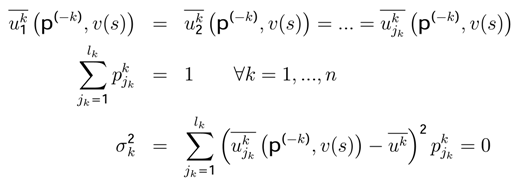
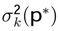 standard deviation and Hk(p∗) entropy of each player k.
standard deviation and Hk(p∗) entropy of each player k.
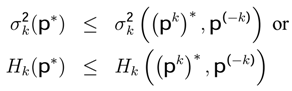
 has gaussian density function or multinomial logit.
has gaussian density function or multinomial logit.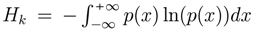 and p(x) the normal density function. Writing this entropy function in terms of minim−u∞m standard deviation we have.
and p(x) the normal density function. Writing this entropy function in terms of minim−u∞m standard deviation we have.
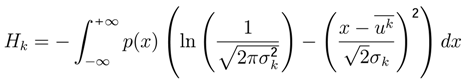
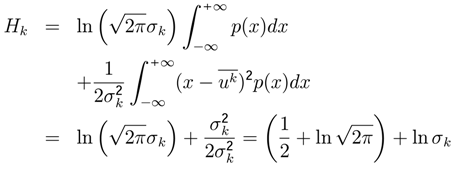
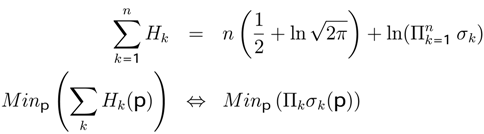
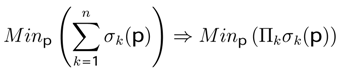
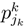 the probability for k ∈ K, jk = 1, ..., lk
the probability for k ∈ K, jk = 1, ..., lk
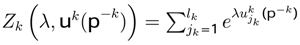 represents the partition utility function [1,45].
represents the partition utility function [1,45].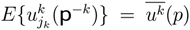 , and variance
, and variance 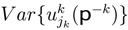 will be different for each player k.
will be different for each player k.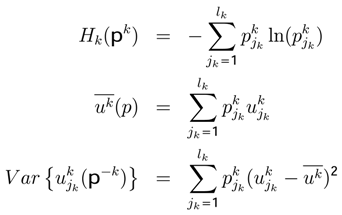
 , we can get the entropy, the expected utility and the variance:
, we can get the entropy, the expected utility and the variance:
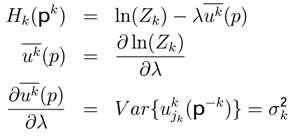
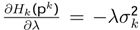 can be obtained using the last seven equations; it explains that, when the entropy diminishes, the parameter (rationality) λ increases.
can be obtained using the last seven equations; it explains that, when the entropy diminishes, the parameter (rationality) λ increases.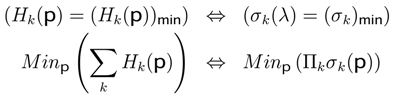
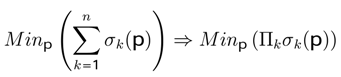
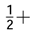
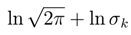 and
and 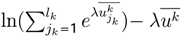
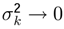 , the gaussian density function can be approximated by Dirac’s Delta
, the gaussian density function can be approximated by Dirac’s Delta 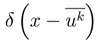 .
.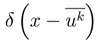 is called “Dirac’s function”. Dirac’s function is not a function in the usual sense. It represents an infinitely short, infinitely strong unit-area impulse. It satisfies
is called “Dirac’s function”. Dirac’s function is not a function in the usual sense. It represents an infinitely short, infinitely strong unit-area impulse. It satisfies 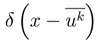 =
= 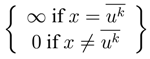 and can be obtained at the limit of the function
and can be obtained at the limit of the function
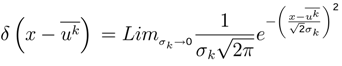
 ,then Nash’s equilibrium represents minimum standard deviation (σk)min , ∀k ∈ K.
,then Nash’s equilibrium represents minimum standard deviation (σk)min , ∀k ∈ K.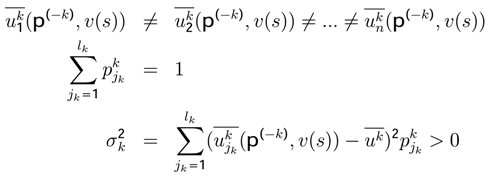
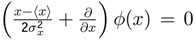 related to minimum dispersion of a lineal combination between the variable x, and a Hermitian operator
related to minimum dispersion of a lineal combination between the variable x, and a Hermitian operator 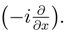
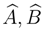 be Hermitian operators 2 which do not commute, because we can write,
be Hermitian operators 2 which do not commute, because we can write,

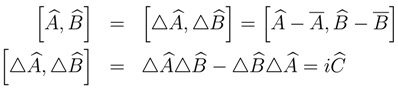
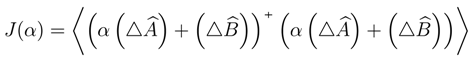
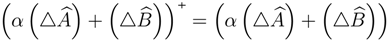 . Using this property,
. Using this property,
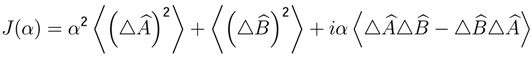
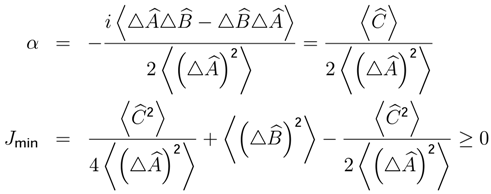
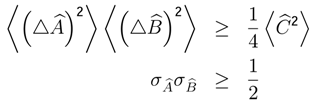
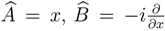 , where
, where 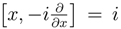 for which we need to solve the following differential equation.
for which we need to solve the following differential equation.
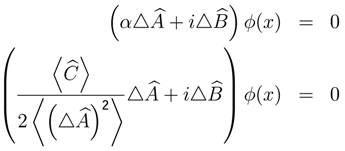
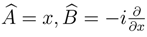 , and
, and 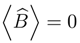 then
then  and
and
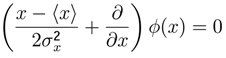
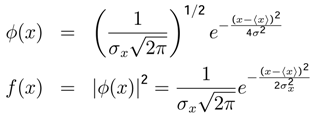
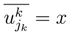 is a gaussian random variable with probability density fk (x), ∀k, and in order to calculate
is a gaussian random variable with probability density fk (x), ∀k, and in order to calculate 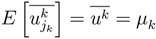 . We can write
. We can write
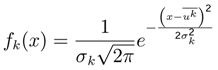
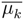 of the random variable
of the random variable 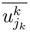 has normal density function”, is respected in the Minimum Entropy Method.
has normal density function”, is respected in the Minimum Entropy Method.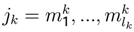 . According to the theorem of Minimum Dispersion, the utility
. According to the theorem of Minimum Dispersion, the utility 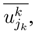 converges to Nash’s equilibria and follows a normal probability density
converges to Nash’s equilibria and follows a normal probability density 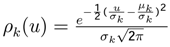 , where the expected utility is
, where the expected utility is 
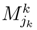 be the set of sub-strategies
be the set of sub-strategies 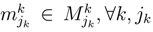 with a probabilitygiven by
with a probabilitygiven by 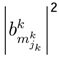 where
where 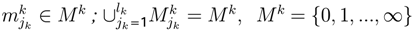 and
and 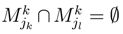 when k ≠ l. A strategy jk is constituted of several sub-strategies
when k ≠ l. A strategy jk is constituted of several sub-strategies 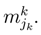
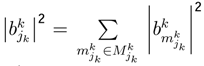 and we do not need any approximation of the function
and we do not need any approximation of the function 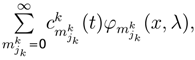 where:
where:
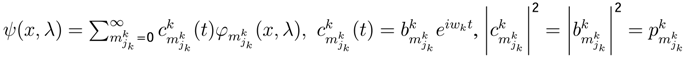
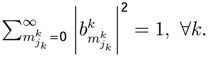
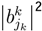 , indicates the probability value of playing jk strategy. The state function ϕk(x,λ) measuresthe behavior of jk strategy (jk one level in Quantum Mechanics [4,9,31]).The dynamic behavior of jk strategy can be written as
, indicates the probability value of playing jk strategy. The state function ϕk(x,λ) measuresthe behavior of jk strategy (jk one level in Quantum Mechanics [4,9,31]).The dynamic behavior of jk strategy can be written as 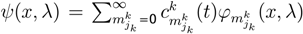 . One approximation is
. One approximation is 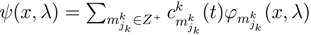
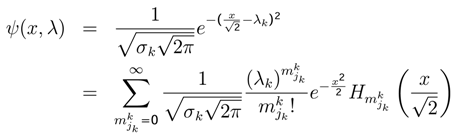
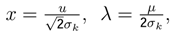 and
and
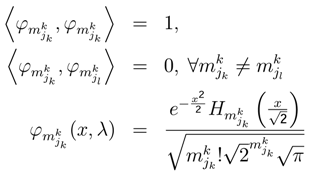
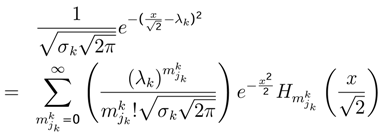
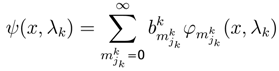
 with the equations (QG1, PH1, PH2) and:
with the equations (QG1, PH1, PH2) and:
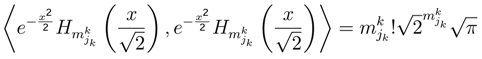
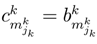 then wk = 0; we can write:
then wk = 0; we can write:
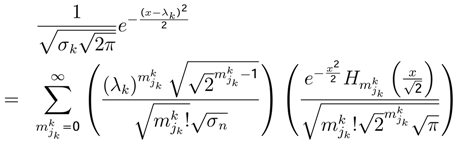

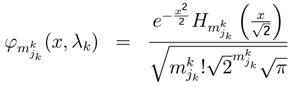
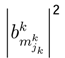 parameter represents the probability of
parameter represents the probability of 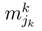 sub-strategy of each k player. The utility of vNM can be written as:
sub-strategy of each k player. The utility of vNM can be written as:
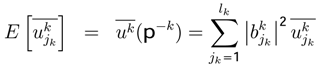
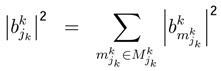
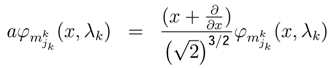
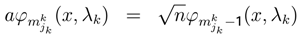
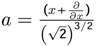 decreases the level of k player. The operator a can decrease the sub-strategy description
decreases the level of k player. The operator a can decrease the sub-strategy description 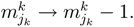
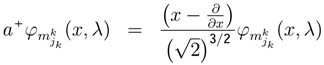

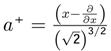 increases the level of k player [4,46]. The operator a+ can increase the sub-strategy description
increases the level of k player [4,46]. The operator a+ can increase the sub-strategy description 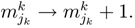
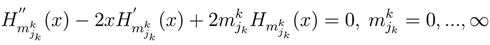
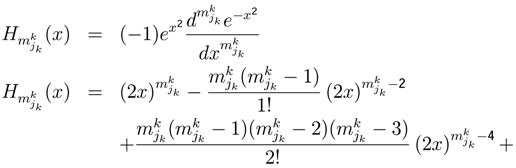
 −derivative of (PH1):
−derivative of (PH1):
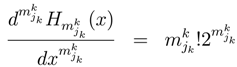
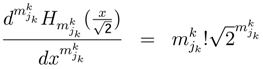
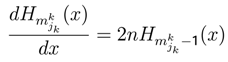
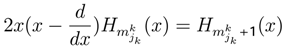
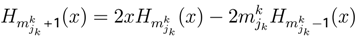
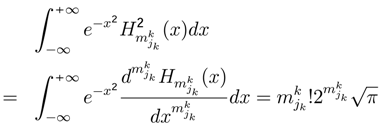
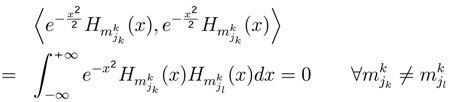
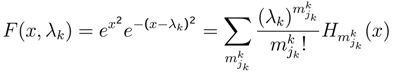
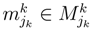 of each player k.
of each player k.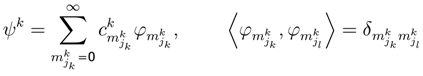
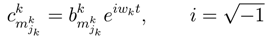
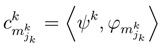
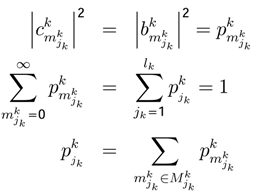
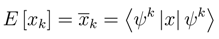
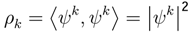
 , P) consisting of [10,13,30]:
, P) consisting of [10,13,30]:
of subsets of Ω with a structure of σ-algebra:
form a finite or countably infinite collection of disjointed sets (that is, Aj = Ø if i ≠ j) then
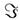 are called events and P is called a probability measure. A random variable is a function:
are called events and P is called a probability measure. A random variable is a function:
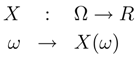
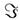 -measurable, that is,
-measurable, that is, 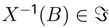 for all B in Borel’s σ algebra of R, noted ß(R).
for all B in Borel’s σ algebra of R, noted ß(R).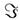 , P) the probability measure induced by X is the probability measure PX (called law or distribution of X) on ß(R) given by
, P) the probability measure induced by X is the probability measure PX (called law or distribution of X) on ß(R) given by
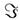 =ß(R), with P the Lebesgue-Stieltges measure corresponding to F.
=ß(R), with P the Lebesgue-Stieltges measure corresponding to F.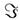 −measurable in ω ∈ Ω for each t ∈ T; henceforth we shall often follow established convention and write Xt for X(t). When T is a countable set, the stochastic process is really a sequence of random variables Xt1, Xt2, ..., Xtn, ..
−measurable in ω ∈ Ω for each t ∈ T; henceforth we shall often follow established convention and write Xt for X(t). When T is a countable set, the stochastic process is really a sequence of random variables Xt1, Xt2, ..., Xtn, ..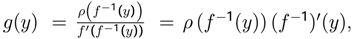 see Fudenberg and Tirole [12], (chapter 6).Thedensitiesρ(x) and g(y) show that “If X is a random variable and f−1(y) exists, then Y is a random variable and conversely.”
see Fudenberg and Tirole [12], (chapter 6).Thedensitiesρ(x) and g(y) show that “If X is a random variable and f−1(y) exists, then Y is a random variable and conversely.”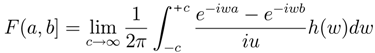
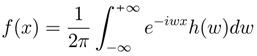
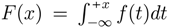 for all x; furthermore, F′ = f everywhere. Thus in this case, f and h are “Fourier transform pairs”:
for all x; furthermore, F′ = f everywhere. Thus in this case, f and h are “Fourier transform pairs”:
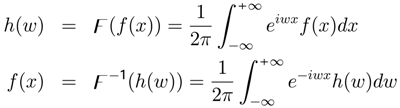
 ,
,  )] , then f(X) is an random variable [25]. If W is r.v., h(W) a Borel measurable function [on (
)] , then f(X) is an random variable [25]. If W is r.v., h(W) a Borel measurable function [on (  ,
,  )] , then h(W) is r.v.
)] , then h(W) is r.v.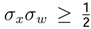 . “The more precisely the random variable VALUE x is determined, the less precisely the frequency VALUE w is known at this instant, and vice versa”. Let X = {X(t),t ∈ T} be the stochastic process with a density function f(x) and the random variable w with a characteristic function h(w). If the density functions can be written as f(x) = ψ(x)ψ(x)∗ and h(w) = φ(w)φ(w)∗, then:
. “The more precisely the random variable VALUE x is determined, the less precisely the frequency VALUE w is known at this instant, and vice versa”. Let X = {X(t),t ∈ T} be the stochastic process with a density function f(x) and the random variable w with a characteristic function h(w). If the density functions can be written as f(x) = ψ(x)ψ(x)∗ and h(w) = φ(w)φ(w)∗, then: 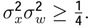
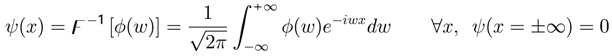

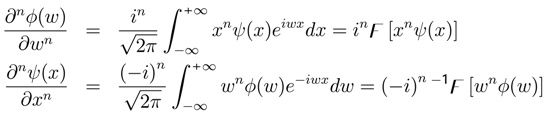

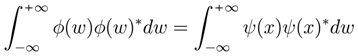
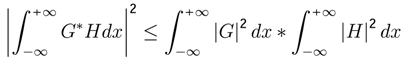
 , it is evident that:
, it is evident that:
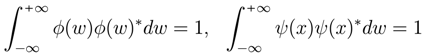
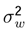 be the standard deviation of frequency w, and
be the standard deviation of frequency w, and 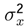 the standard deviation of the aleatory variable x
the standard deviation of the aleatory variable x
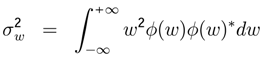
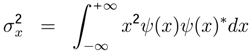
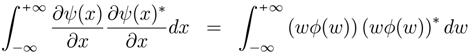
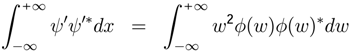
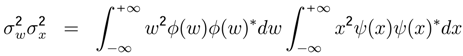
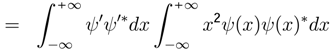
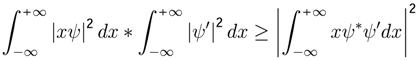
 . If the variable A is given by A =
. If the variable A is given by A =  then
then 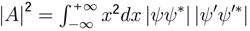 . By definition F′ = f = ψψ′
. By definition F′ = f = ψψ′
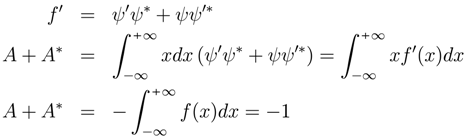
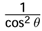 . Since −1 ≤ cosθ ≤ 1 then |A|2 ≥
. Since −1 ≤ cosθ ≤ 1 then |A|2 ≥ 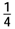 and therefore:
and therefore:
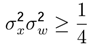
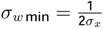 . The expected value E [wj] of each frequency can be determined experimentally.
. The expected value E [wj] of each frequency can be determined experimentally.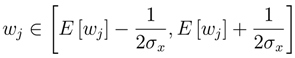
not as the portion of the variance of X that is due to cycles with frequency exactly equal to wj, but rather as the portion of the variance of X that is due to cycles with frequency near of wj, ” where:
![Entropy 05 00313 i178]()
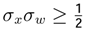 , because it includes the Minimum Entropy Theorem or equilibrium state theorem
, because it includes the Minimum Entropy Theorem or equilibrium state theorem 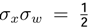 . It is necessary to analyze the different cases of the time series xt using the Possibility Theorem. A time series xt evolves in the dynamic equilibrium if and only if
. It is necessary to analyze the different cases of the time series xt using the Possibility Theorem. A time series xt evolves in the dynamic equilibrium if and only if 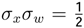 . A time series evolves out of the dynamic equilibrium if and only if
. A time series evolves out of the dynamic equilibrium if and only if 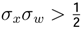 .
.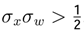 . In this table we can see the different changes in σx and σw.
. In this table we can see the different changes in σx and σw.
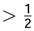
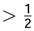
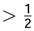
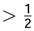
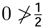
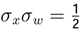 . In this table we can see the different changes in σx and σw.
. In this table we can see the different changes in σx and σw.
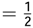
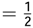
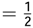
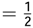
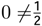
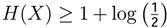 where:
where: 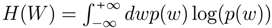 and
and 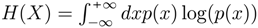 . When ψ(x) and φ(w) are gaussian H(W) = B + Log(σW) and H(X) = C + Log(σX), Hirschman’s inequality becomes Heisenberg’s principle, then inequalities are transformed in equalities and the minimum uncertainty is minimum entropy. In Quantum Mechanics the minimum uncertainty product also obeys a minimum entropy sum.
. When ψ(x) and φ(w) are gaussian H(W) = B + Log(σW) and H(X) = C + Log(σX), Hirschman’s inequality becomes Heisenberg’s principle, then inequalities are transformed in equalities and the minimum uncertainty is minimum entropy. In Quantum Mechanics the minimum uncertainty product also obeys a minimum entropy sum.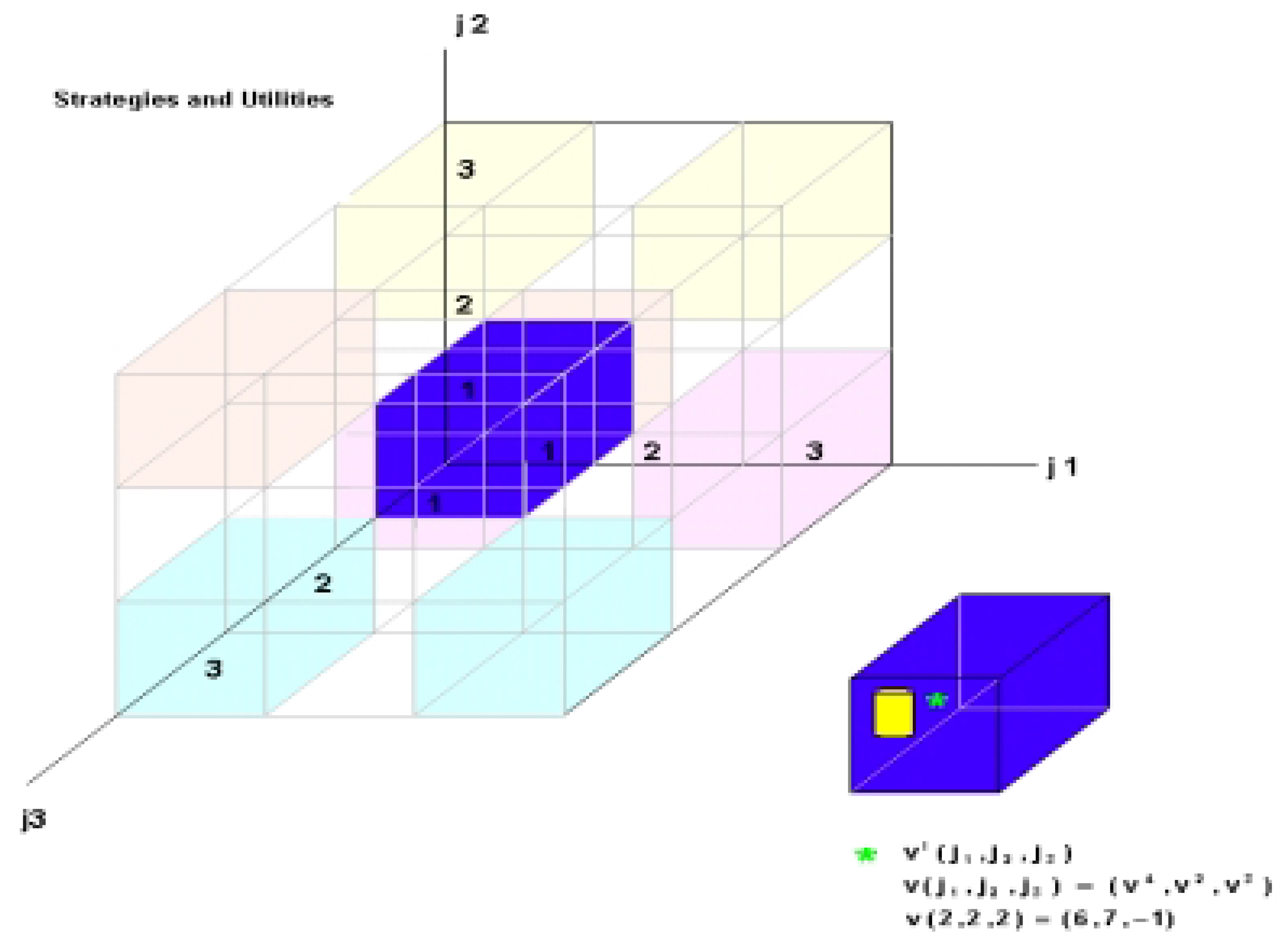
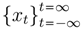 be a covariance-stationary process with the mean E[xt] = µ and jth covariance γj
be a covariance-stationary process with the mean E[xt] = µ and jth covariance γj
 and w is a scalar.
and w is a scalar.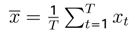 and
and
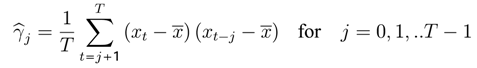
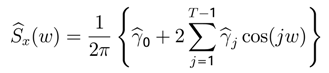
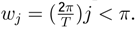
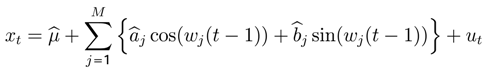
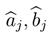 can be estimated with OLS regression.
can be estimated with OLS regression.
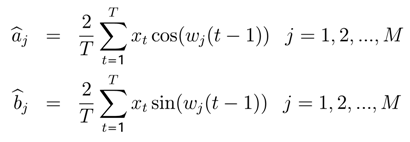
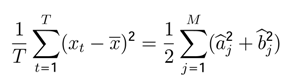
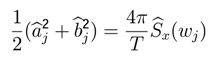
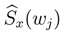 as the sample periodogram of frequency wj.
as the sample periodogram of frequency wj.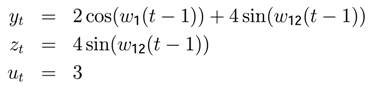
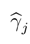 , j = 1,..., (T − 1) for the time series xt according to Q21 (Table 7, Figure 6).
, j = 1,..., (T − 1) for the time series xt according to Q21 (Table 7, Figure 6).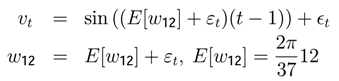
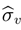 = 1.1334. The product
= 1.1334. The product 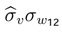 = 1.1334 verifi es the Possibility Theorem and permits us to compute:
= 1.1334 verifi es the Possibility Theorem and permits us to compute: 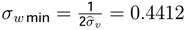

relationship is equivalent to the well-known bene fits/cost we present a new way to calculate equilibria:
, where p(x) represents probability function and x = (x1,x2,..., xn) represents endogenous or exogenous variables.
. “The more precisely the random variable VALUE x is determined, the less precisely the frequency VALUE w is known at this instant, and conversely”
have the next property:
, the transpose operator
is equal to complex conjugate operator