Physical and Statistical Pattern of the Thiva (Greece) 2020–2022 Seismic Swarm
Abstract
1. Introduction
2. Seismological Data
2.1. Relocation Using HypoDD
2.2. Catalogue Completeness
3. Analysis of Seismicity and Discussion
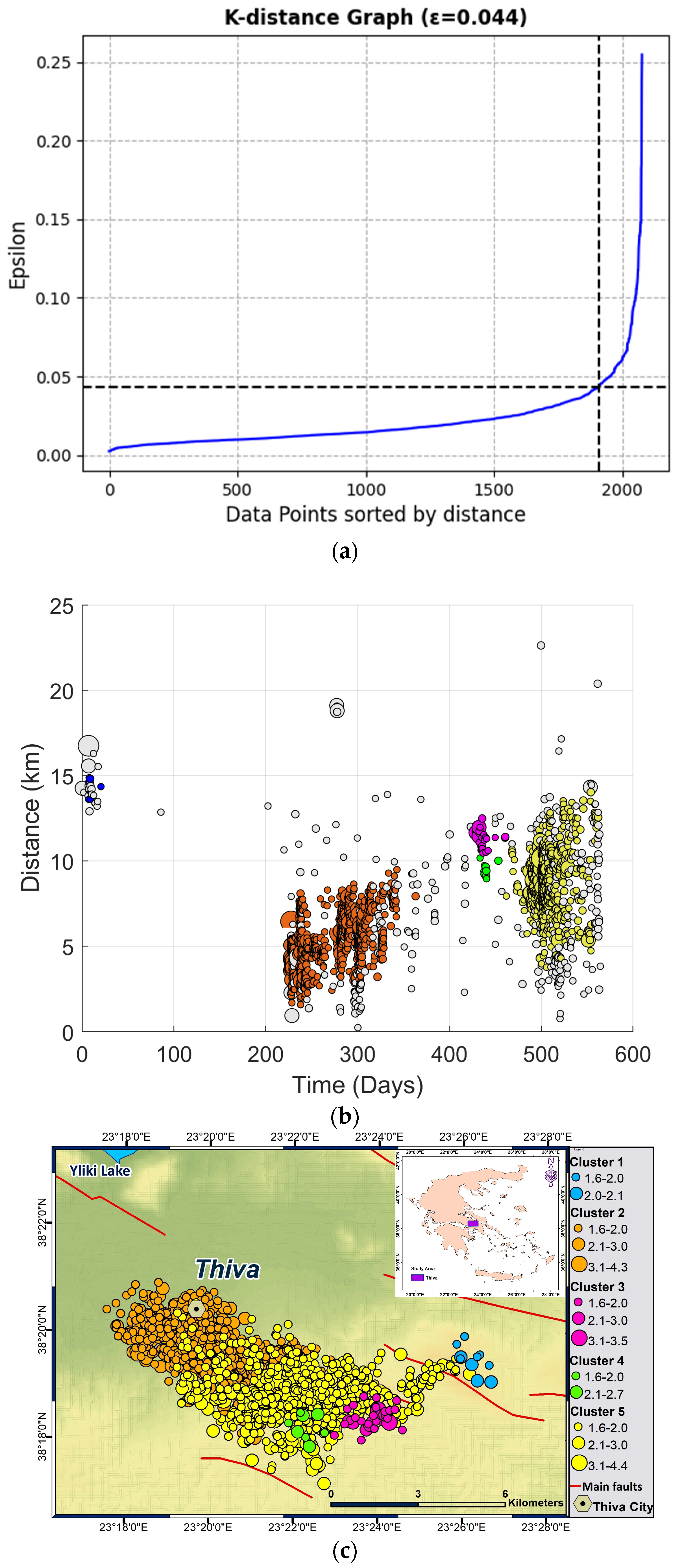
3.1. The DBSCAN Algorithm Results
3.2. A Non-Extensive Statistical Physics Approach (NESP)
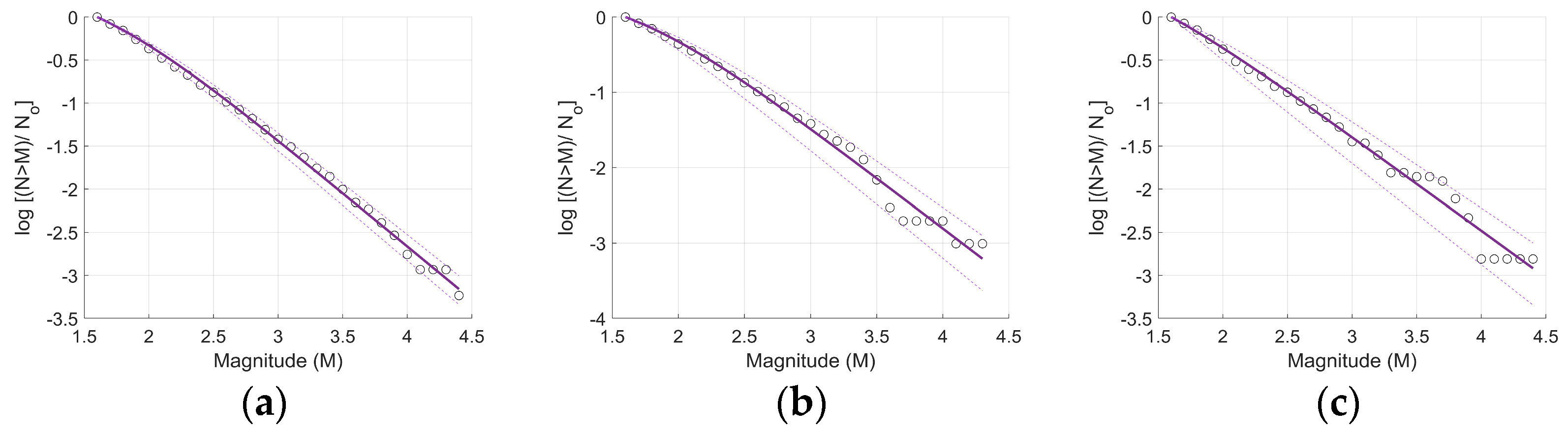
3.2.1. Frequency–Magnitude Distribution of Earthquake Clusters in Terms of NESP
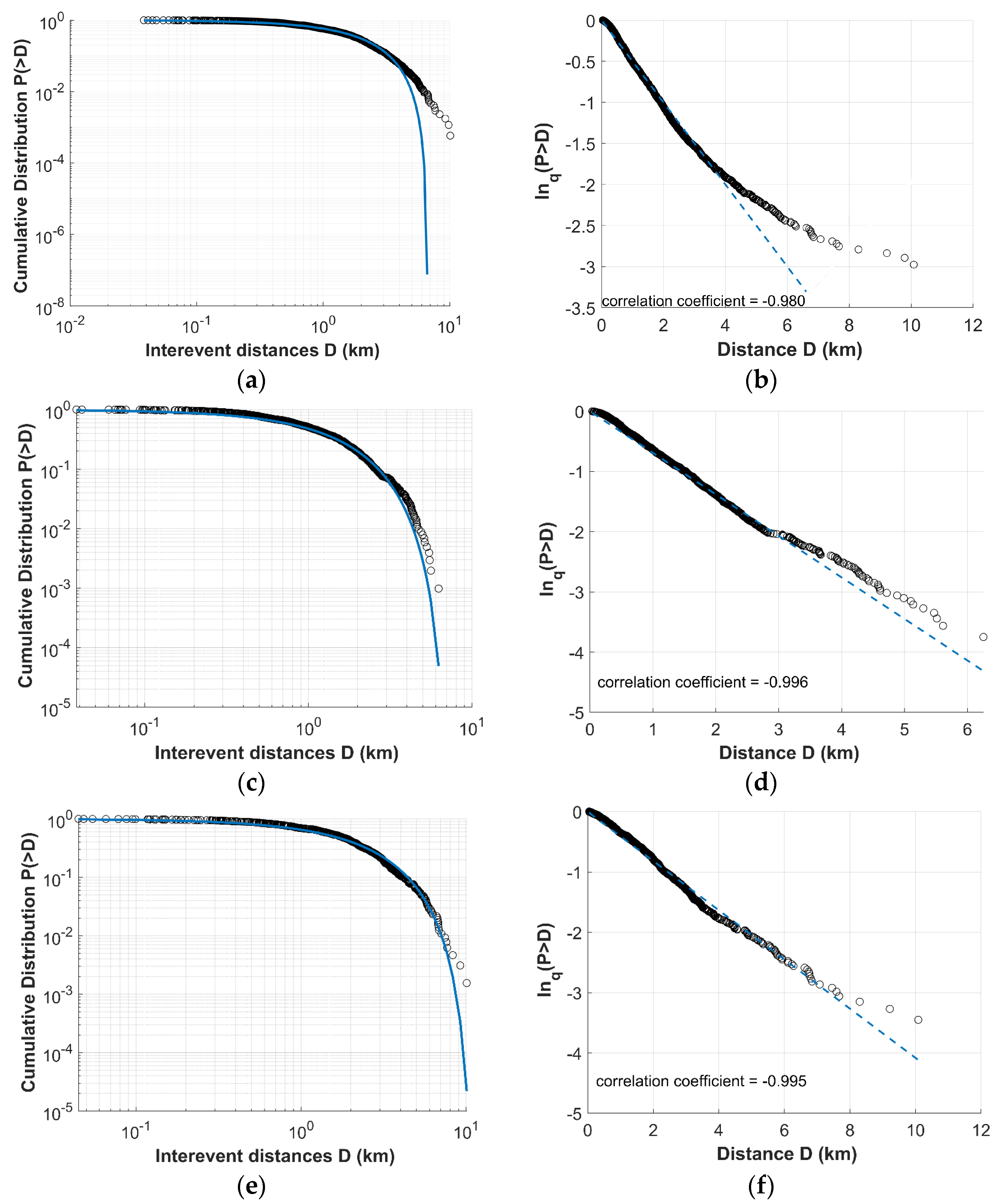
3.2.2. Spatiotemporal Scaling Properties of Earthquake Clusters in Terms of NESP
3.3. Physical Model of Cluster’s Evolution
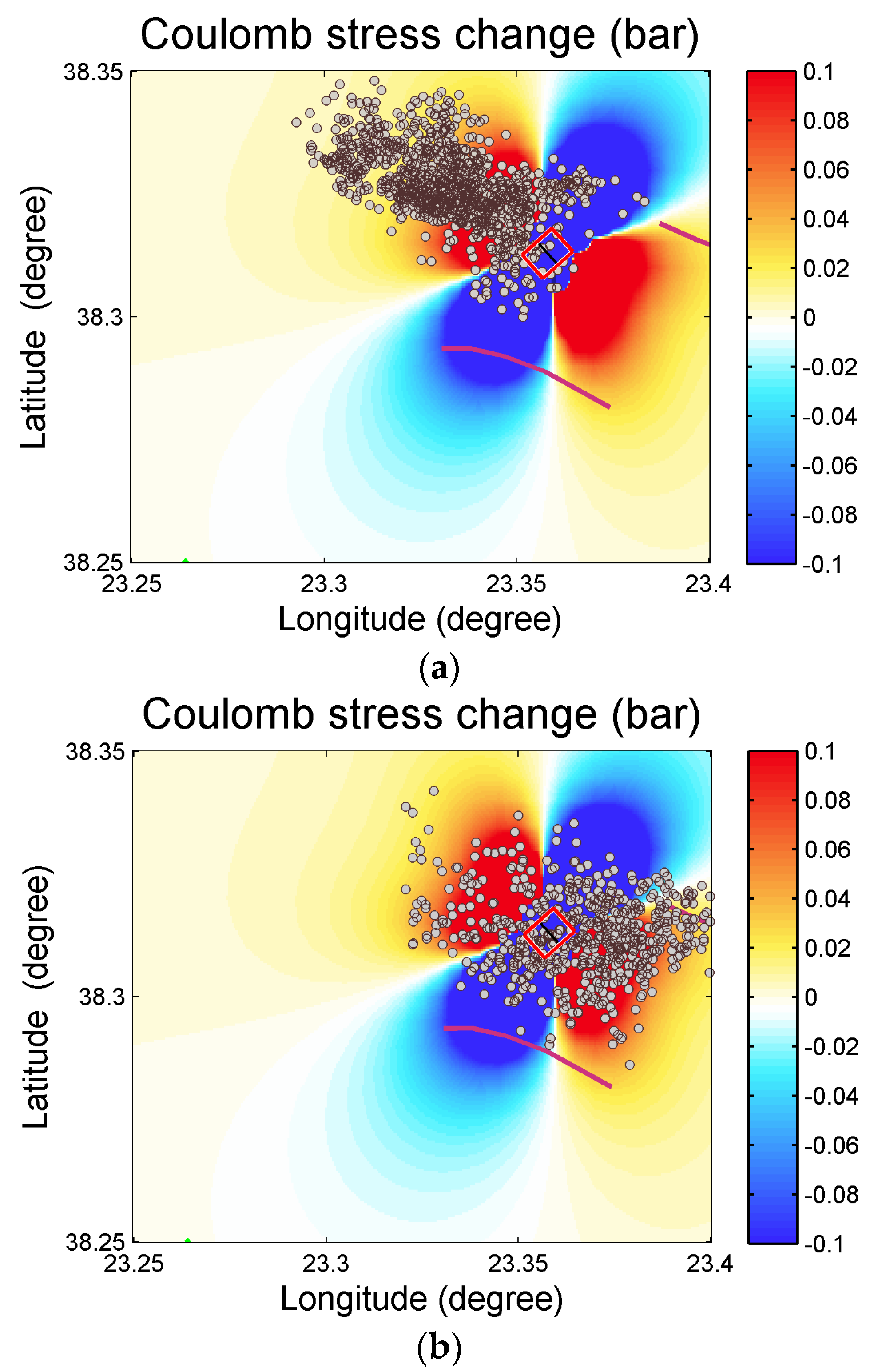
3.3.1. Coulomb Stress Changes
3.3.2. Evidence of Afterslip Migration of Seismicity in Cluster 2
3.3.3. Evidence of a Diffusion Process of Seismicity of Cluster 5
4. Discussion
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tsodoulos, I.M.; Koukouvelas, I.K.; Pavlides, S. Tectonic geomorphology of the easternmost extension of the Gulf of Corinth (Beotia, Central Greece). Tectonophysics 2008, 453, 211–232. [Google Scholar] [CrossRef]
- Sboras, S.; Ganas, A.; Pavlides, S. Morphotectonic Analysis of the Neotectonic and Active Faults of Beotia (Central Greece), Using G.I.S. Techniques. Bull. Geol. Soc. Greece 2017, 43, 1607–1618. [Google Scholar]
- Papazachos, B.C.; Papazachou, C. The Earthquakes of Greece; Ziti Publications: Thessaloniki, Greece, 2003. [Google Scholar]
- Ambraseys, N.N.; Jackson, J.A. Seismicity and Strain in the Gulf of Corinth (Greece) Since 1694. J. Earthq. Eng. 1997, 1, 433–474. [Google Scholar] [CrossRef]
- Ambraseys, N.N.; Jackson, J.A. Seismicity and associated strain of central Greece between 1890 and 1988. Geophys. J. Int. 1990, 101, 663–708. [Google Scholar] [CrossRef]
- Elias, P.; Spingos, I.; Kaviris, G.; Karavias, A.; Gatsios, T.; Sakkas, V.; Parcharidis, I. Combined Geodetic and Seismological Study of the December 2020 Mw = 4.6 Thiva (Central Greece) Shallow Earthquake. Appl. Sci. 2021, 11, 5947. [Google Scholar] [CrossRef]
- Ganas, A.; Oikonomou, I.A.; Tsimi, C. NOAfaults: A digital database for active faults in Greece. Bull. Geol. Soc. Greece 2017, 47, 518. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96), Portland, OR, USA, 2–4 August 1996; Volume 34, pp. 226–231. [Google Scholar]
- Waldhauser, F. HypoDD-A Program to Compute Double-Difference Hypocenter Locations; Open-File Report 01-113; U.S. Geological Survey: Menlo Park, CA, USA, 2001. [Google Scholar]
- Tsallis, C. Nonextensive Statistical Mechanics and Thermodynamics: Historical Backgroundand Present Status. In Nonextensive Statistical Mechanics and Its Applications; Abe, S., Okamoto, Y., Eds.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Telesca, L. Maximum Likelihood Estimation of the Nonextensive Parameters of the Earthquake Cumulative Magnitude Distribution. Bull. Seismol. Soc. Am. 2012, 102, 886–891. [Google Scholar] [CrossRef]
- Vallianatos, F.; Sammonds, P. Evidence of non-extensive statistical physics of the lithospheric instability approaching the 2004 Sumatran–Andaman and 2011 Honshu mega-earthquakes. Tectonophysics 2013, 590, 52–58. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P.A. Nonextensive Statistical Physics Analysis of the 1995 Kobe, Japan Earthquake. Pure Appl. Geophys. 2015, 172, 1923–1931. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F.; Sammonds, P. Non-extensivity and long-range correlations in the earthquake activity at the West Corinth rift (Greece). Nonlinear Process. Geophys. 2013, 20, 713–724. [Google Scholar] [CrossRef]
- Klein, F.W. User’s Guide to HYPOINVERSE-2000, a Fortran Program to Solve for Earthquake Locations and Magnitudes; Open-File Report 2002-171; United States Department of the Interior Geological Survey: Menlo Park, CA, USA, 2002. [Google Scholar]
- Karakonstantis, A. 3-D Simulation of Crust and Upper Mantle Structure in the Broader Hellenic Area through Seismic Tomography. Ph.D. Thesis, Department of Geophysics-Geothermics, Faculty of Geology, University of Athens, Athens, Greece, 2017. (In Greek). [Google Scholar]
- Waldhauser, F.; Ellsworth, W. A Double-Difference Earthquake Location Algorithm: Method and Application to the Northern Hayward Fault, California. Bull. Seismol. Soc. Am. 2000, 90, 1353–1368. [Google Scholar] [CrossRef]
- Paige, C.C.; Saunders, M.A. LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares. ACM Trans. Math. Softw. 1982, 8, 43–71. [Google Scholar] [CrossRef]
- Gutenberg, B.; Richter, C.F. Frequency of Earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Aki, K. Maximum lilkelihood estimate of b in the formula logN=a-bM and its confidence limits. Bull. Earthq. Res. Inst. 1965, 43, 237–239. [Google Scholar]
- Utsu, T. A statistical significance test of the difference in b-value between two earthquakes groups. J. Phys. Earth 1966, 14, 37–40. [Google Scholar] [CrossRef]
- Bender, B. Maximum likelihood estimation of b values for magnitude grouped data. Bull. Seismol. Soc. Am. 1983, 73, 831–851. [Google Scholar] [CrossRef]
- Utsu, T. Representation and analysis of the earthquake size distribution: A historical review and some new approaches. Pure Appl. Geophys. 1999, 155, 509–535. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Wyss, M.; Wiemer, S.; Zuniga, R. Zmap: A Tool for Analyses of Seismicity Patterns, Typical Applications and Uses: A Cookbook. 2001. Available online: https://www.researchgate.net/publication/261170802 (accessed on 2 July 2022).
- Sabermahani, S.; Frederiksen, A.W. Improved Earthquake Clustering Using a Density-Adaptive DBSCAN Algorithm: An Example from Iran. Seismol. Res. Lett. 2023, 95, 942–951. [Google Scholar] [CrossRef]
- Sharma, A.; Vijay, R.K.; Nanda, S.J. Identification and spatio-temporal analysis of earthquake clusters using SOM–DBSCAN model. Neural Comput. Applic. 2023, 35, 8081–8108. [Google Scholar] [CrossRef]
- Sardeli, E.; Michas, G.; Pavlou, K.; Zaccagnino, D.; Vallianatos, F. Spatiotemporal properties of the 2020–2021 Petrinja (Croatia) earthquake sequence. J. Seismol. 2024, 28, 899–920. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann-Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Tsallis, C. Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Sotolongo-Costa, O.; Posadas, A. Fragment-Asperity Interaction Model for Earthquakes. Phys. Rev. Lett. 2004, 92, 048501. [Google Scholar] [CrossRef]
- Matcharashvili, T.; Chelidze, T.; Javakhishvili, Z.; Jorjiashvili, N.; Fra Paleo, U. Non-extensive statistical analysis of seismicity in the area of Javakheti, Georgia. Comput. Geosci. 2011, 37, 1627–1632. [Google Scholar] [CrossRef]
- Papadakis, G.; Vallianatos, F.; Sammonds, P. Evidence of Nonextensive Statistical Physics Behavior of the Hellenic Subduction Zone Seismicity. Tectonophysics 2013, 608, 1037–1048. [Google Scholar] [CrossRef]
- Vincenty, T. Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations. Surv. Rev. 1975, 23, 88–93. [Google Scholar] [CrossRef]
- Vallianatos, F.; Papadakis, G.; Michas, G. Generalized statistical mechanics approaches to earthquakes and tectonics. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472, 20160497. [Google Scholar] [CrossRef] [PubMed]
- Picoli, S., Jr.; Mendes, R.S.; Malacarne, L.C.; Santos, R.P.B. q-distributions in complex systems: A brief review. Braz. J. Phys. 2009, 39, 468–474. [Google Scholar] [CrossRef]
- Sardeli, E.; Michas, G.; Pavlou, K.; Vallianatos, F.; Karakonstantis, A.; Chatzopoulos, G. Complexity of Recent Earthquake Swarms in Greece in Terms of Non-Extensive Statistical Physics. Entropy 2023, 25, 667. [Google Scholar] [CrossRef]
- King, G.C.; Stein, R.S.; Lin, J. Static stress changes and the triggering of earthquakes. Bull. Seismol. Soc. Am. 1994, 84, 935–953. [Google Scholar]
- Stein, R.S.; King, G.C.; Lin, J. Stress triggering of the 1994 M= 6.7 Northridge, California, earthquake by its predecessors. Science 1994, 265, 1432–1435. [Google Scholar] [CrossRef] [PubMed]
- Stein, R.S.; Barka, A.A.; Dieterich, J.H. Progressive failure on the North Anatolian fault since 1939 by earthquake stress triggering. Geophys. J. Int. 1997, 128, 594–604. [Google Scholar] [CrossRef]
- Stein, R.S. The role of stress transfer in earthquake occurrence. Nature 1999, 402, 605–609. [Google Scholar] [CrossRef]
- Harris, R.A.; Simpson, R.W. Suppression of large earthquakes by stress shadows: A comparison of Coulomb and rate-and-state failure. J. Geophys. Res. Solid Earth 1998, 103, 24439–24451. [Google Scholar] [CrossRef]
- Parsons, T.; Toda, S.; Stein, R.S.; Barka, A.; Dieterich, J.H. Heightened odds of large earthquakes near Istanbul: An interaction-based probability calculation. Science 2000, 288, 661–665. [Google Scholar] [CrossRef] [PubMed]
- Toda, S.; Lin, J.; Meghraoui, M.; Stein, R.S. 12 May 2008 M = 7.9 Wenchuan, China, earthquake calculated to increase failure stress and seismicity rate on three major fault systems. Geophys. Res. Lett. 2008, 35, L17305. [Google Scholar] [CrossRef]
- Vallianatos, F.; Pavlou, K. Scaling properties of the Mw7.0 Samos (Greece), 2020 aftershock sequence. Acta Geophys. 2021, 69, 1067–1084. [Google Scholar] [CrossRef]
- Kilb, D.; Gomberg, J.; Bodin, P. Triggering of earthquake aftershocks by dynamic stresses. Nature 2002, 408, 570–574. [Google Scholar] [CrossRef]
- Kilb, D.; Gomberg, J.; Bodin, P. Aftershock triggering by complete Coulomb stress changes. J. Geophys. Res. Solid Earth 2002, 107, ESE 2-1–ESE 2-14. [Google Scholar] [CrossRef]
- Scholz, C.H. The Mechanics of Earthquakes and Faulting, 3rd ed.; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Cocco, M. Pore pressure and poroelasticity effects in Coulomb stress analysis of earthquake interactions. J. Geophys. Res. 2002, 107, 2030. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Sevilgen, V.; Lin, J. Coulomb 3.3 Graphic-Rich Deformation and Stress-Change Software for Earthquake, Tectonic, and Volcano Research and Teaching-User Guide; Open-File Report 2011-1060; U.S. Geological Survey: Menlo Park, CA, USA, 2011; p. 63. [Google Scholar]
- Harris, R.A.; Simpson, R.W. In the shadow of 1857, an evaluation of the stress changes generated by the M8 Ft. Tejon, California, earthquake. Eos Trans. Am. Geophys. Union 1993, 74, 427. [Google Scholar]
- Harris, R.A.; Simpson, R.W. In the shadow of the 1857—The effect of the great Ft. Tejon earthquake on the subsequent earthquakes in southern California. Geophys. Res. Lett. 1996, 23, 229–232. [Google Scholar] [CrossRef]
- Kaviris, G.; Kapetanidis, V.; Spingos, I.; Sakellariou, N.; Karakonstantis, A.; Kouskouna, V.; Elias, P.; Karavias, A.; Sakkas, V.; Gatsios, T.; et al. Investigation of the Thiva 2020–2021 Earthquake Sequence Using Seismological Data and Space Techniques. Appl. Sci. 2022, 12, 2630. [Google Scholar] [CrossRef]
- Lippiello, E.; Giacco, F.; Marzocchi, W.; Godano, C.; De Arcangelis, L. Mechanical origin of aftershocks. Sci. Rep. 2015, 5, 15560. [Google Scholar] [CrossRef]
- Shapiro, S.A.; Rothert, E.; Rath, V.; Rindschwentner, J. Characterization of fluid transport properties of reservoirs using induced microseismicity. Geophysics 2002, 67, 212–220. [Google Scholar] [CrossRef]
- Perfettini, H.; Frank, W.B.; Marsan, D.; Bouchon, M. A Model of Aftershock Migration Driven by Afterslip. Geophys. Res. Lett. 2018, 45, 2283–2293. [Google Scholar] [CrossRef]
- Michas, G.; Pavlou, K.; Avgerinou, S.-E.; Anyfadi, E.-A.; Vallianatos, F. Aftershock patterns of the 2021 Mw 6.3 Northern Thessaly (Greece) earthquake. J. Seismol. 2022, 26, 201–225. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.-P. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. Solid Earth 2004, 109, 2003JB002488. [Google Scholar] [CrossRef]
- Pavlou, K.; Michas, G.; Vallianatos, F. Scaling Law Analysis and Aftershock Spatiotemporal Evolution of the Three Strongest Earthquakes in the Ionian Sea During the Period 2014–2019. Geosciences 2025, 15, 84. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Jeon, J.H.A.; Cherstvy, G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Bouchaud, J.P.; Georges, A. Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications. Phys. Rep. 1990, 195, 127–293. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Scaling properties and anomalous diffusion of the Florina micro-seismic activity: Fluid driven? Geomech. Energy Environ. 2020, 24, 100155. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Modelling earthquake diffusion as a continuous-time random walk with fractional kinetics: The case of the 2001 Agios Ioannis earthquake swarm (Corinth Rift). Geophys. J. Int. 2018, 215, 333–345. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Stochastic modeling of nonstationary earthquake time series with long-term clustering effects. Phys. Rev. E 2018, 98, 042107. [Google Scholar] [CrossRef]
- Michas, G.; Vallianatos, F. Stochastic modeling of injection induced seismicity based on the continuous time random walk model. Sci. Rep. 2024, 14, 4951. [Google Scholar] [CrossRef]
- McKernon, C.; Main, I.G. Regional variations in the diffusion of triggered seismicity. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Helmstetter, A.; Ouillon, G.; Sornette, D. Are aftershocks of large Californian earthquakes diffusing? J. Geophys. Res. Solid Earth 2003, 108, 2483. [Google Scholar] [CrossRef]
- Huc, M.; Main, I.G. Anomalous stress diffusion in earthquake triggering: Correlation length, time dependence, and directionality. J. Geophys. Res. Solid Earth 2003, 108, 2324. [Google Scholar] [CrossRef]
- Marsan, D.; Bean, C.J.; Steacy, S.; McCloskey, J. Observation of diffusion processes in earthquake populations and implications for the predictability of seismicity systems. J. Geophys. Res. Solid Earth 2000, 105, 28081–28094. [Google Scholar] [CrossRef]
- Shapiro, S.A.; Huenges, E.; Borm, G. Estimating the crust permeability from fluid-injection-induced seismic emission at the KTB site. Geophys. J. Int. 1997, 131, F15–F18. [Google Scholar] [CrossRef]
- Shapiro, S.A.; Audigane, P.; Royer, J. Large-scale in situ permeability tensor of rocks from induced microseismicity. Geophys. J. Int. 1999, 137, 207–213. [Google Scholar] [CrossRef]
- Parotidis, M.; Rothert, E.; Shapiro, S.A. Pore-pressure diffusion: A possible triggering mechanism for the earthquake swarms 2000 in Vogtland/NW-Bohemia, central Europe. Geophys. Res. Lett. 2003, 30, 20. [Google Scholar] [CrossRef]
- Antonioli, A.; Piccinini, D.; Chiaraluce, L.; Cocco, M. Fluid flow and seismicity pattern: Evidence from the 1997 Umbria-Marche (central Italy) seismic sequence. Geophys. Res. Lett. 2005, 32, 10. [Google Scholar] [CrossRef]
- Michas, G.; Kapetanidis, V.; Spingos, I.; Kaviris, G.; Vallianatos, F. The 2020 Perachora peninsula earthquake sequence (Εast Corinth Rift, Greece): Spatiotemporal evolution and implications for the triggering mechanism. Acta Geophys. 2022, 70, 2581–2601. [Google Scholar] [CrossRef]
- Kapetanidis, V.; Michas, G.; Kaviris, G.; Vallianatos, F. Spatiotemporal Properties of Seismicity and Variations of Shear-Wave Splitting Parameters in the Western Gulf of Corinth (Greece). Appl. Sci. 2021, 11, 6573. [Google Scholar] [CrossRef]
- Talwani, P.; Chen, L.; Gahalaut, K. Seismogenic permeability, ks. J. Geophys. Res. 2007, 112, B07309. [Google Scholar] [CrossRef]
- Chen, X.; Shearer, P.M.; Abercrombie, R.E. Spatial migration of earthquakes within seismic clusters in Southern California: Evidence for fluid diffusion. J. Geophys. Res. Solid Earth 2012, 117, B04301. [Google Scholar] [CrossRef]
- Lohman, R.B.; McGuire, J.J. Earthquake swarms driven by aseismic creep in the Salton Trough, California. J. Geophys. Res. Solid Earth 2007, 112. [Google Scholar] [CrossRef]
- Roland, E.; McGuire, J.J. Earthquake swarms on transform faults. Geophys. J. Int. 2009, 178, 1677–1690. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Law for the distance between successive earthquakes: A New Law for Distance Between Earthquakes. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Abe, S.; Suzuki, N. Scale-free statistics of time interval between successive earthquakes. Phys. A Stat. Mech. Its Appl. 2005, 350, 588–596. [Google Scholar] [CrossRef]





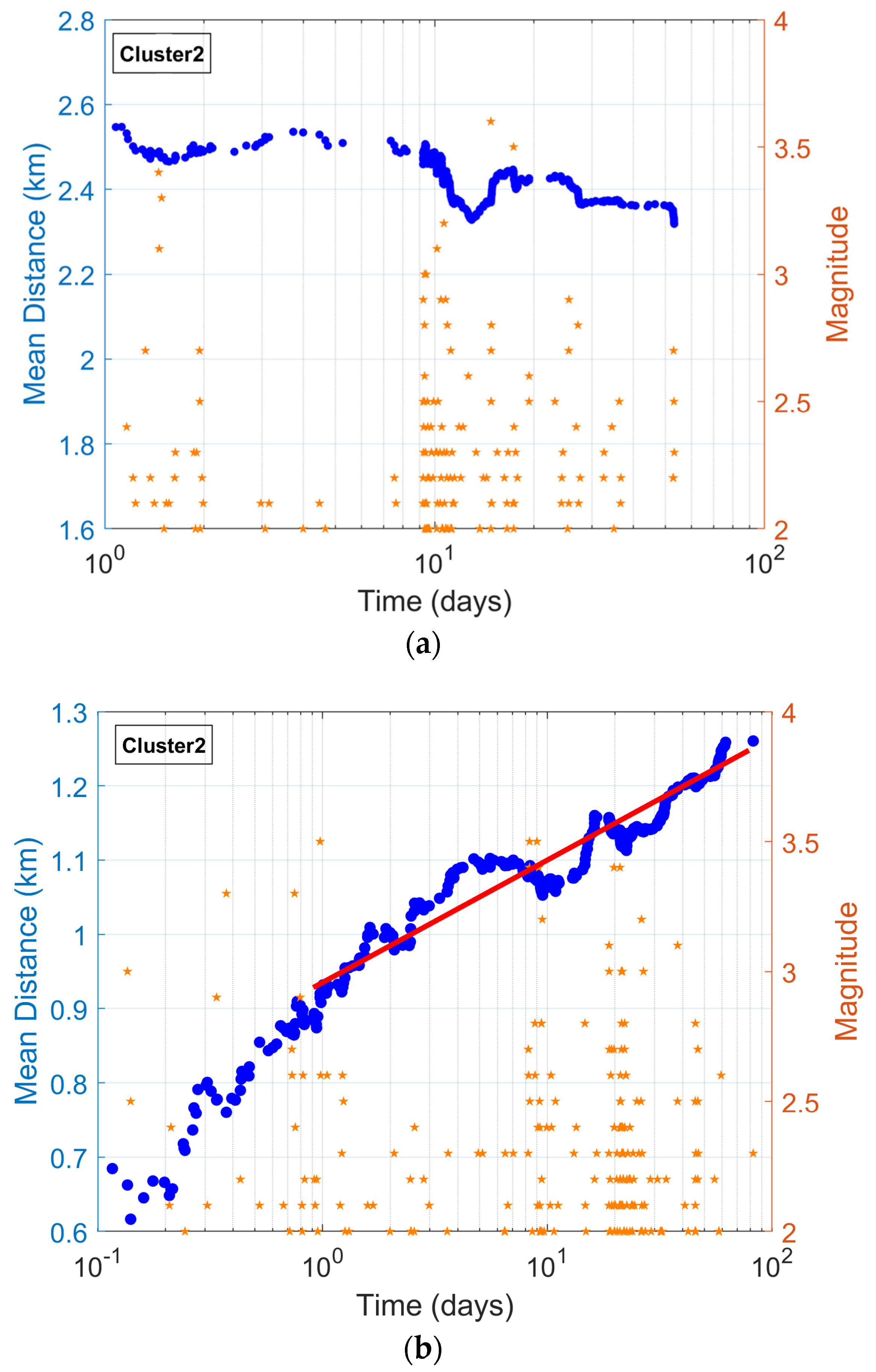
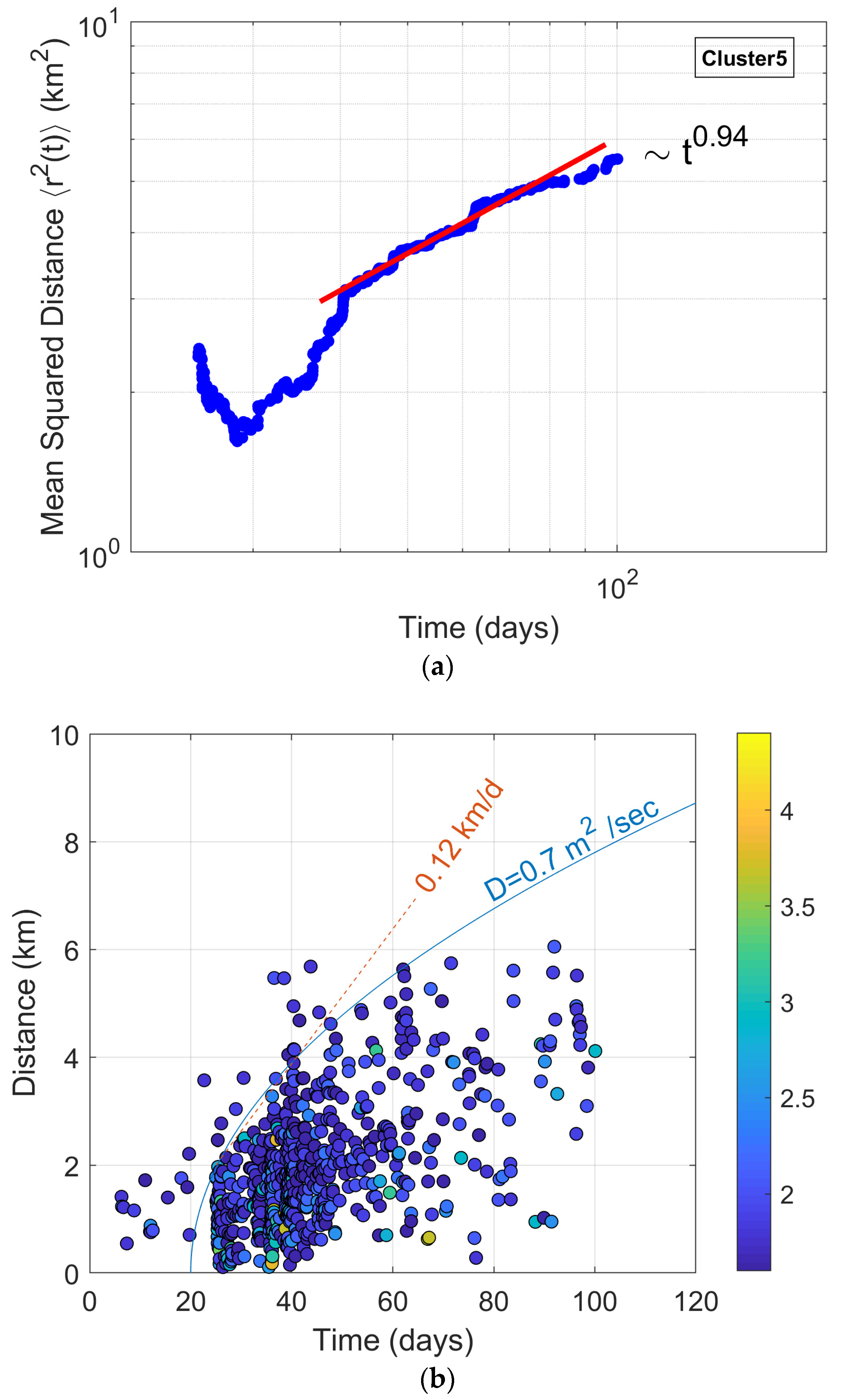
| Clusters | Period Time | Events |
|---|---|---|
| Cluster 1 | 2 December2020–15 December 2020 | 10 |
| Cluster 2 | 1 July 2021–23 November 2021 | 1018 |
| Cluster 3 | 28 January 2022–1 March 2022 | 32 |
| Cluster 4 | 1 February 2022–21 February 2022 | 9 |
| Cluster 5 | 2 March 2022–10 June 2022 | 644 |
| Clusters | qM |
|---|---|
| Unified Cluster | 1.65 ± 0.01 |
| Cluster 2 | 1.63 ± 0.02 |
| Cluster 5 | 1.68 ± 0.02 |
| Clusters | qT | Tq (s) | qD | Dq (km) |
|---|---|---|---|---|
| Unified Cluster | 1.50 | 1380 ± 4 | 0.70 | 2.00 ± 0.01 |
| Cluster 2 | 1.50 | 1095 ± 3 | 0.80 | 1.45 ± 0.01 |
| Cluster 5 | 1.44 | 2210 ± 13 | 0.78 | 2.45 ± 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallianatos, F.; Sardeli, E.; Pavlou, K.; Karakonstantis, A. Physical and Statistical Pattern of the Thiva (Greece) 2020–2022 Seismic Swarm. Entropy 2025, 27, 979. https://doi.org/10.3390/e27090979
Vallianatos F, Sardeli E, Pavlou K, Karakonstantis A. Physical and Statistical Pattern of the Thiva (Greece) 2020–2022 Seismic Swarm. Entropy. 2025; 27(9):979. https://doi.org/10.3390/e27090979
Chicago/Turabian StyleVallianatos, Filippos, Eirini Sardeli, Kyriaki Pavlou, and Andreas Karakonstantis. 2025. "Physical and Statistical Pattern of the Thiva (Greece) 2020–2022 Seismic Swarm" Entropy 27, no. 9: 979. https://doi.org/10.3390/e27090979
APA StyleVallianatos, F., Sardeli, E., Pavlou, K., & Karakonstantis, A. (2025). Physical and Statistical Pattern of the Thiva (Greece) 2020–2022 Seismic Swarm. Entropy, 27(9), 979. https://doi.org/10.3390/e27090979







