Multilayer Network Analysis of European Regional Flows
Abstract
1. Introduction
- R1
- How does a region’s importance transform when moving from an analysis of isolated flow types to a comprehensive multidimensional connectivity framework?
- R2
- What emergent functional relationships and regional clusters are revealed by the interplay of different flow types in a multilayer framework?
2. Materials and Methods
2.1. Data
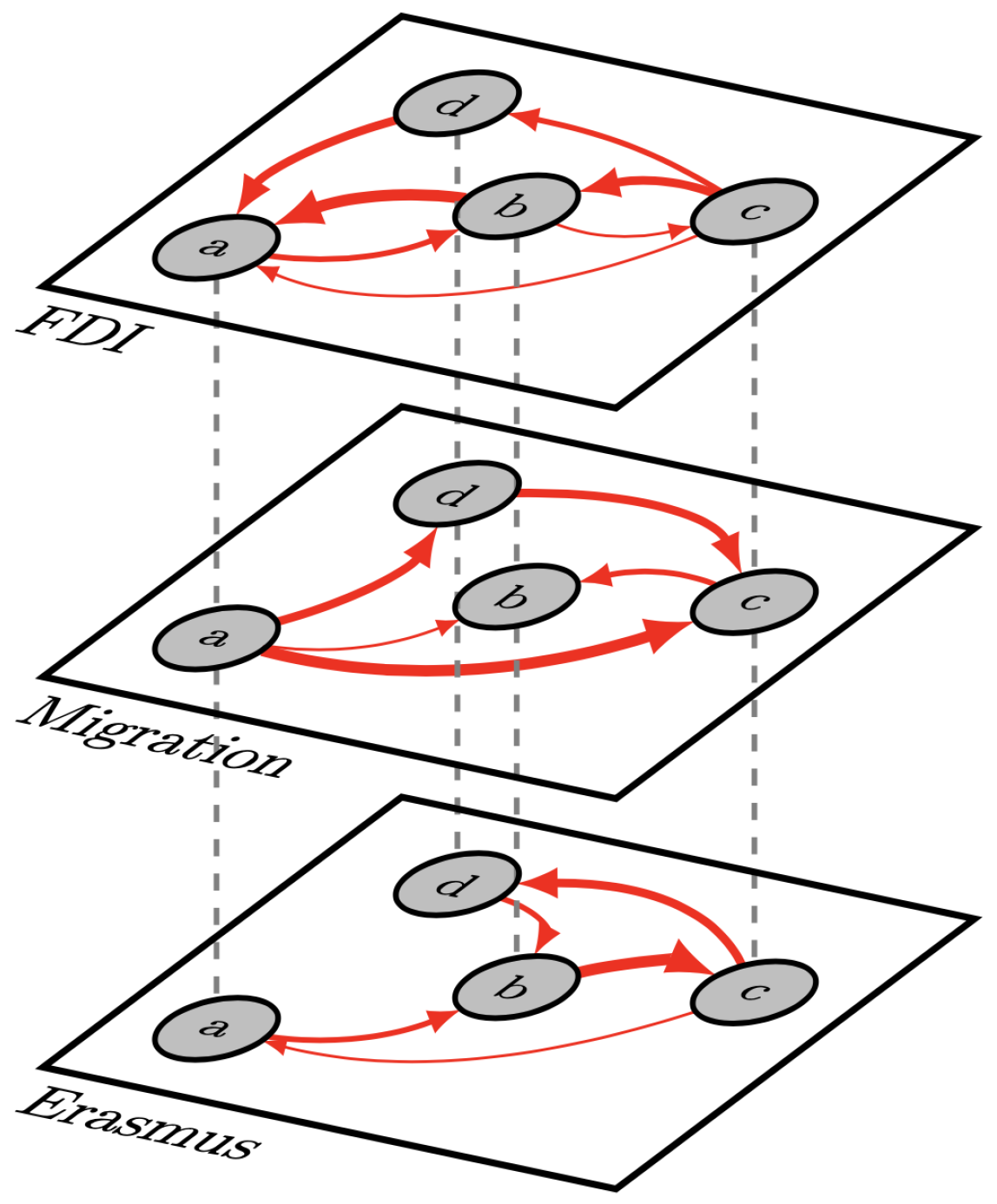
2.2. A Network Science Framework
2.3. Single-Layer Network Construction
2.4. Multilayer Network Construction
2.5. Analytical Techniques
2.5.1. Network Properties
2.5.2. Null Model: CReMA
2.5.3. Centrality Measure: PageRank
2.5.4. Community Detection: Infomap
3. Results
3.1. Single-Layer Networks
3.1.1. First-Order Properties
3.1.2. Second-Order Properties
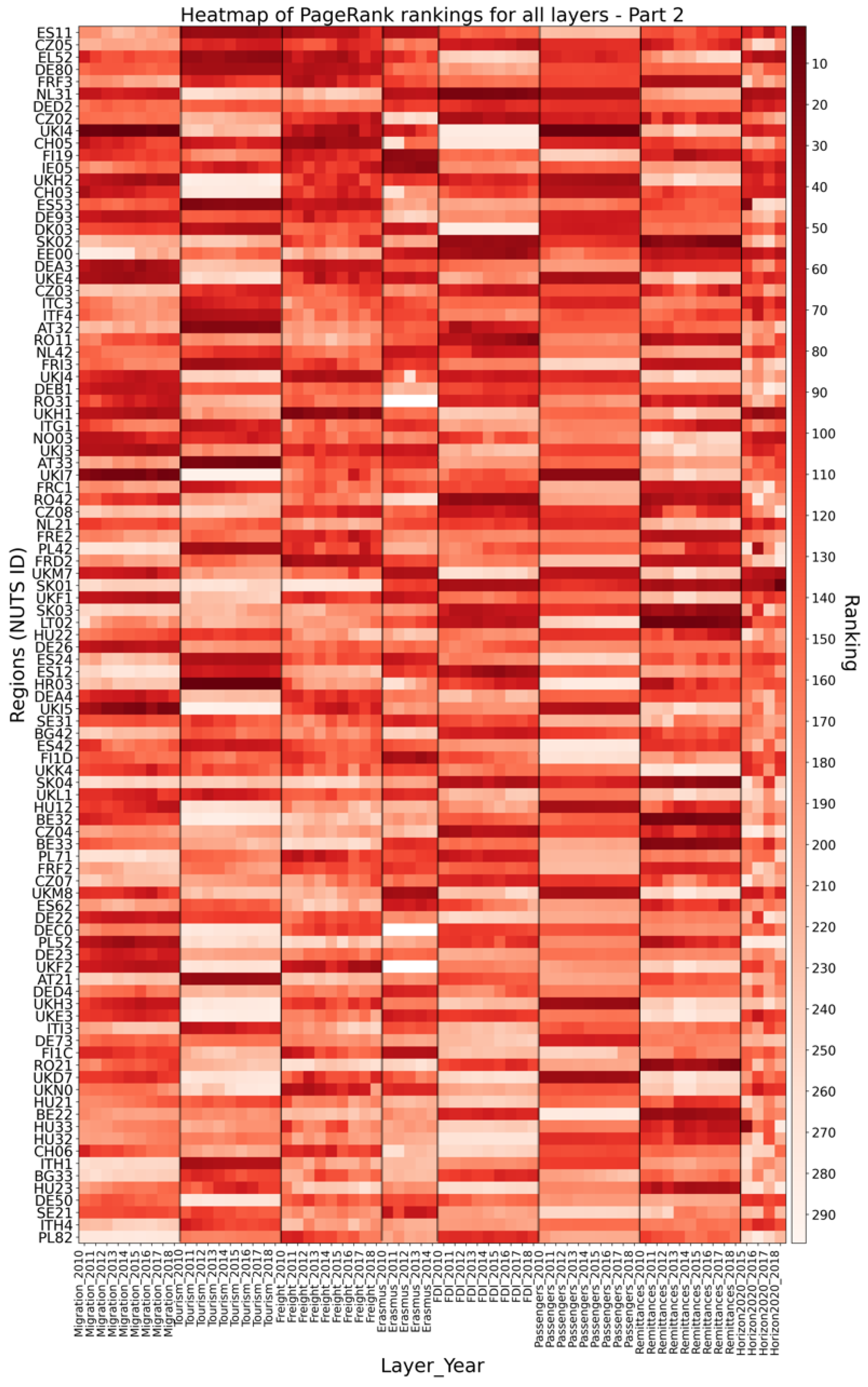
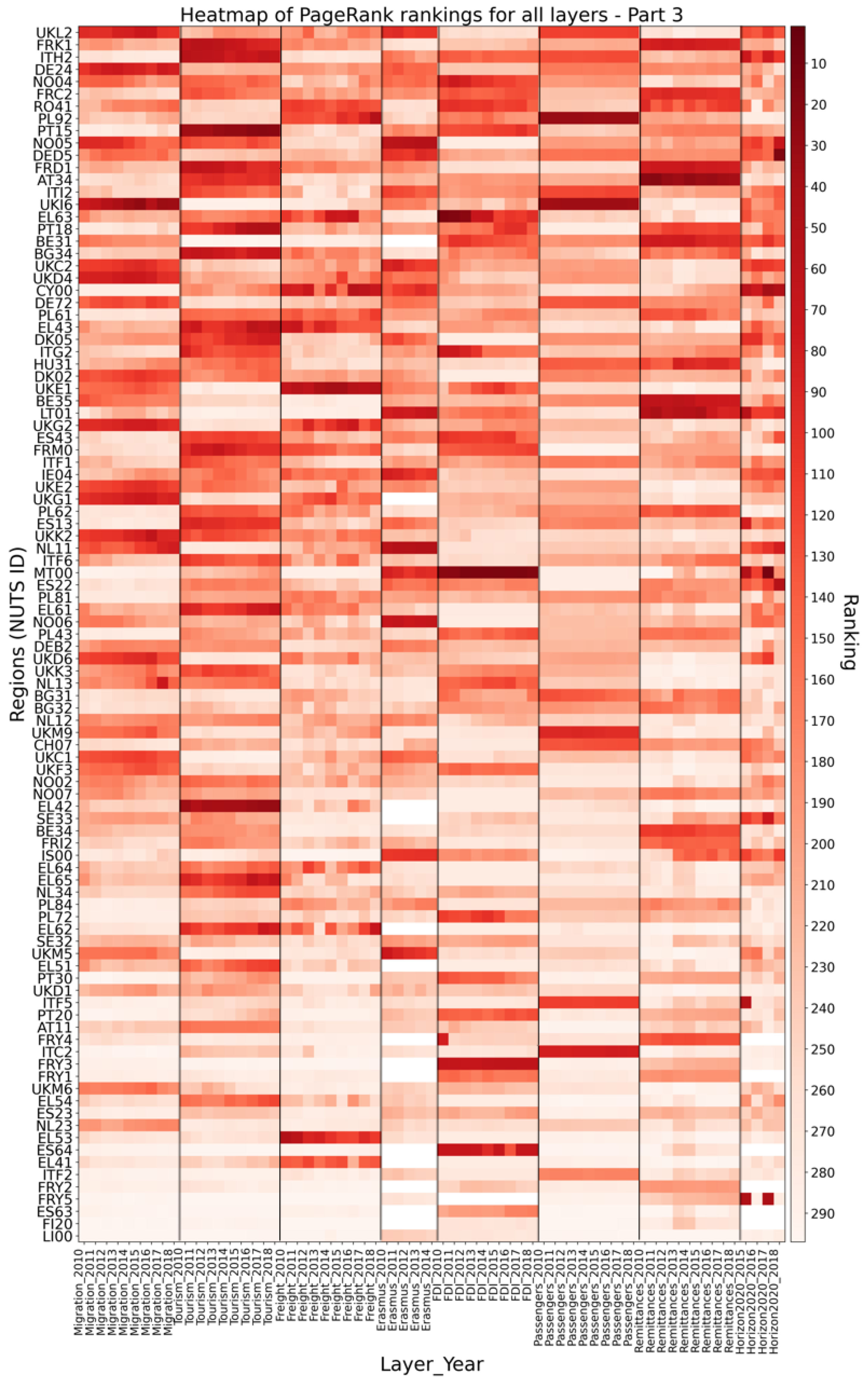
3.2. Centrality Measure: PageRank
Single-Layer vs. Multiplex
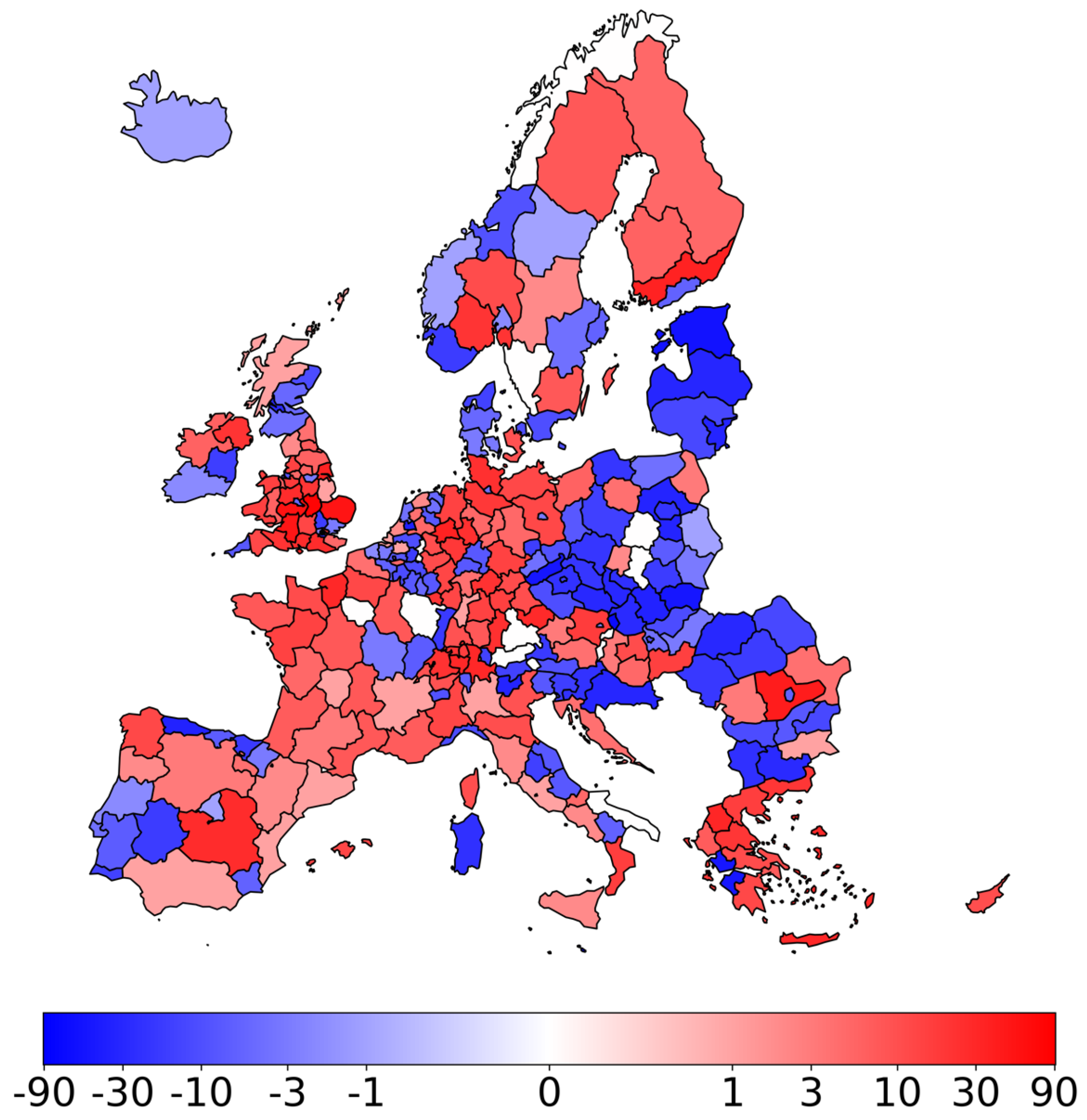
3.3. Community Detection: Infomap
- Belgium forms a community with Luxembourg and a neighboring Dutch region, suggesting strong economic and social ties in this cross-border area.
- The Czech Republic and Slovakia form a single community, reflecting their historical and ongoing close relations.
- A community comprises many English regions and Cyprus, indicating strong connections despite geographical distance.
- Several countries form predominantly self-contained communities, including Romania, Austria, Poland, Greece, Portugal, Hungary, Denmark, the Netherlands, Norway, Bulgaria, Finland, Malta, and Iceland. This suggests that these nations have stronger internal than external flows across the analyzed dimensions.
- Spain, France, and Italy each display a core community of multiple regions, with additional smaller communities, indicating complex internal structures.
- Cross-border communities are observed between Åland (Finland) and Sweden, as well as between Liechtenstein and Switzerland, highlighting strong regional ties that transcend national borders.
- The Baltic states (Lithuania, Estonia, and Latvia) form a cohesive community, reflecting their geographical proximity and shared historical background.
- Germany and the United Kingdom exhibit highly fragmented community structures, suggesting complex and diverse flow patterns within these countries.
- Slovenia, Croatia, and Malta form an unexpected community, potentially indicating strong economic or social ties among these Mediterranean and Adriatic regions.
- Northern Ireland and Ireland constitute a single community, aligning with their geographical proximity and historical connections.
4. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Flow Type | Description | Sources | Methodology | Our Analysis |
|---|---|---|---|---|
| Migration | Number of people migrating between NUTS 2 regions | EUROSTAT and NSI | Multi-step process: Base Data, Stock Gain estimation, In-Out-Cross estimation. Country-to-country matrices created, gaps filled using stock-gain method and linear models. Region-to-region flows estimated by decomposing country-level data | Applied floor function to ensure whole numbers. Divided by origin region population (see Supplementary Information) |
| Tourism | Number of tourists traveling between NUTS 2 regions | EUROSTAT and UNWTO for country-to-country; EUROSTAT for regional domestic arrivals | Completed gaps in country-to-country and disaggregated country-to-country to region-to-region. Methods include cross-referencing UNWTO indexes, interpolation/extrapolation, and gravity model analysis using GDP, arrivals, and distance data | Applied floor function. Divided by origin region population |
| FDI | Shareholders’ funds (thousand euros) in foreign-owned companies | AMADEUS database (Bureau van Dijk) | Aggregated firm-level data. Included intraregional and interregional intra-national flows | Summed FDI across all sectors. Divided by origin region GDP (see Supplementary Information) |
| Remittances | Regionalized bilateral remittance estimates (thousand euros) | EUROSTAT and World Bank | Estimated regional-level flows by regionalizing national-level data using ratio of regional to national migration flows | Divided by origin region GDP |
| Freight Transport | Total freight flow between NUTS-2 regions (thousand tons) | Various, for road, rail, maritime, and air transport | Performed consistency and plausibility checks. Developed disaggregation procedures where regionalized data unavailable | Divided by total outgoing flows from each region, multiplied by region’s relative economic importance |
| Erasmus Student Mobility | Higher education student mobility between partner countries | European Commission datasets | Geocoded individual movements to NUTS-2 regions based on sending and receiving institutions | Divided by origin region population |
| Horizon 2020 Partnerships | Number of H2020 partnerships between NUTS-2 regions | CORDIS project and participant organization lists | Geocoded organizations to NUTS-2 regions. Counted partnerships with coordinating partners as senders and other partners as receivers. | No additional processing |
| Passenger Transport | Passenger flows between NUTS-2 regions for air, maritime, and rail transport | Various Eurostat datasets | Implemented appropriate disaggregation procedures where regionalized data unavailable | Summed air, maritime, and rail (×1000) passenger flows. Divided by origin region population |
| Category | Erasmus | FDI | Freight | Horizon2020 |
|---|---|---|---|---|
| Highest Average: 1 | Comunidad de Madrid (ES) | Noord-Holland (NL) | Lombardia (IT) | Ile-de-France (FR) |
| Highest Average: 2 | Ile-de-France (FR) | Ile-de-France (FR) | Zuid-Holland (NL) | Comunidad de Madrid (ES) |
| Highest Average: 3 | Andalucía (ES) | Luxembourg (LU) | Cataluña (ES) | Oberbayern (DE) |
| Highest Average: 4 | Cataluña (ES) | Eastern and Midland (IE) | Ile-de-France (FR) | Région de Bruxelles (BE) |
| Highest Average: 5 | Berlin (DE) | Comunidad de Madrid (ES) | Nord-Pas de Calais (FR) | Lazio (IT) |
| Lowest Average: 1 | Sterea Ellada (EL) | Hovedstaden (DK) | Liechtenstein (LI) | Liechtenstein (LI) |
| Lowest Average: 2 | Yugoiztochen (BG) | Thessalia (EL) | Ísland (IS) | Valle d’Aosta (IT) |
| Lowest Average: 3 | Dytiki Makedonia (EL) | Espace Mittelland (CH) | Malta (MT) | Warmińsko-mazurskie (PL) |
| Lowest Average: 4 | Valle d’Aosta (IT) | Ticino (CH) | Sostinės regionas (LT) | Cumbria (UK) |
| Lowest Average: 5 | Warmińsko-mazurskie (PL) | Molise (IT) | Highlands and Islands (UK) | Opolskie (PL) |
| Largest Increase: 1 | Kontinentalna Hrvatska (HR) | Bretagne (FR) | Kontinentalna Hrvatska (HR) | Extremadura (ES) |
| Largest Increase: 2 | Jadranska Hrvatska (HR) | East Yorkshire (UK) | Ionia Nisia (EL) | Leipzig (DE) |
| Largest Increase: 3 | Wielkopolskie (PL) | Zachodniopomorskie (PL) | Střední Morava (CZ) | Zentralschweiz (CH) |
| Largest Increase: 4 | Podlaskie (PL) | Midi-Pyrénées (FR) | Jihovýchod (CZ) | Prov. West-Vlaanderen (BE) |
| Largest Increase: 5 | Pomorskie (PL) | Yugoiztochen (BG) | Östra Mellansverige (SE) | Nord-Vest (RO) |
| Largest Decrease: 1 | Nordjylland (DK) | Región de Murcia (ES) | N Ireland (UK) | Dél-Alföld (HU) |
| Largest Decrease: 2 | Inner London E (UK) | Sardegna (IT) | Nyugat-Dunántúl (HU) | Basilicata (IT) |
| Largest Decrease: 3 | Trentino (IT) | Dytiki Ellada (EL) | Peloponnisos (EL) | Moravskoslezsko (CZ) |
| Largest Decrease: 4 | Sjælland (DK) | Lancashire (UK) | Dél-Alföld (HU) | Malta (MT) |
| Largest Decrease: 5 | Liguria (IT) | Brandenburg (DE) | Etelä-Suomi (FI) | Jihovýchod (CZ) |
| Category | Migration | Passengers | Remittances | Tourism |
|---|---|---|---|---|
| Highest Average: 1 | Oberbayern (DE) | Ile-de-France (FR) | Ile-de-France (FR) | Jadranska Hrvatska (HR) |
| Highest Average: 2 | Stuttgart (DE) | Inner London W (UK) | Cataluña (ES) | Cataluña (ES) |
| Highest Average: 3 | Inner London E (UK) | Comunidad de Madrid (ES) | Luxembourg (LU) | Ile-de-France (FR) |
| Highest Average: 4 | Darmstadt (DE) | Inner London E (UK) | Comunidad de Madrid (ES) | Andalucía (ES) |
| Highest Average: 5 | Ile-de-France (FR) | Oberbayern (DE) | Rhône-Alpes (FR) | Rhône-Alpes (FR) |
| Lowest Average: 1 | Liechtenstein (LI) | Liechtenstein (LI) | Liechtenstein (LI) | Liechtenstein (LI) |
| Lowest Average: 2 | Valle d’Aosta (IT) | Ipeiros (EL) | Voreio Aigaio (EL) | Prov. Brabant Wallon (BE) |
| Lowest Average: 3 | Molise (IT) | Burgenland (AT) | Ionia Nisia (EL) | Outer London W-NW (UK) |
| Lowest Average: 4 | Malta (MT) | Corse (FR) | Highlands and Islands (UK) | Molise (IT) |
| Lowest Average: 5 | Basilicata (IT) | Dytiki Makedonia (EL) | NE Scotland (UK) | Outer London E-NE (UK) |
| Largest Increase: 1 | Vidurio ir vakarų Lietuvos (LT) | Etelä-Suomi (FI) | Ísland (IS) | Alentejo (PT) |
| Largest Increase: 2 | Sud-Vest Oltenia (RO) | Brandenburg (DE) | Nyugat-Dunántúl (HU) | Zuid-Holland (NL) |
| Largest Increase: 3 | Nord-Vest (RO) | Notio Aigaio (EL) | Pest (HU) | Jihovýchod (CZ) |
| Largest Increase: 4 | Sud-Est (RO) | Leicestershire (UK) | Västsverige (SE) | Overijssel (NL) |
| Largest Increase: 5 | Centru (RO) | Prov. Hainaut (BE) | Östra Mellansverige (SE) | Ísland (IS) |
| Largest Decrease: 1 | Zentralschweiz (CH) | Yugozapaden (BG) | Attiki (EL) | Sud-Est (RO) |
| Largest Decrease: 2 | Sicilia (IT) | Kontinentalna Hrvatska (HR) | Kentriki Makedonia (EL) | Lubuskie (PL) |
| Largest Decrease: 3 | Campania (IT) | Yugoiztochen (BG) | Zuid-Holland (NL) | Dorset and Somerset (UK) |
| Largest Decrease: 4 | Ostschweiz (CH) | Severoiztochen (BG) | Noord-Holland (NL) | Champagne-Ardenne (FR) |
| Largest Decrease: 5 | Calabria (IT) | Latvija (LV) | Jadranska Hrvatska (HR) | Bourgogne (FR) |

References
- Castells, M. The Information Age; Oxford Blackwell Publishers: Oxford, UK, 1996; Volume 1. [Google Scholar]
- Amin, A. Regions unbound: Towards a new politics of place. Geogr. Ann. Ser. B Hum. Geogr. 2004, 86, 33–44. [Google Scholar] [CrossRef]
- Bathelt, H.; Glückler, J. The Relational Economy: Geographies of Knowing and Learning; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Servillo, L.; Atkinson, R.; Russo, A.P. Territorial attractiveness in EU urban and spatial policy: A critical review and future research agenda. Eur. Urban Reg. Stud. 2012, 19, 349–365. [Google Scholar] [CrossRef]
- Russo, A.; Smith, I.; Atkinson, R.; Servillo, L.; Madsen, B.; Van der Borg, J. ATTREG. The Attractiveness of European Regions and Cities for Residents and Visitors-Scientific Report; ESPON: Luxembourg, 2013; Volume 1. [Google Scholar]
- Faludi, A. From European spatial development to territorial cohesion policy. Reg. Stud. 2006, 40, 667–678. [Google Scholar] [CrossRef]
- Cracolici, M.F.; Nijkamp, P. The attractiveness and competitiveness of tourist destinations: A study of Southern Italian regions. Tour. Manag. 2009, 30, 336–344. [Google Scholar] [CrossRef]
- Waltert, F.; Schläpfer, F. Landscape amenities and local development: A review of migration, regional economic and hedonic pricing studies. Ecol. Econ. 2010, 70, 141–152. [Google Scholar] [CrossRef]
- Jackson, S.; Markowski, S. The Attractiveness of Countries to Foreign Direct Investment. J. World Trade 1995, 29, 159. [Google Scholar] [CrossRef]
- Musolino, D.; Kotosz, B. A new territorial attractiveness index at the international scale: Design, application and patterns in Italy. Ann. Reg. Sci. 2024, 72, 1159–1187. [Google Scholar] [CrossRef]
- Measuring the Attractiveness of Regions. Available online: https://doi.org/10.1787/fbe44086-en (accessed on 5 December 2024).
- Kivelä, M.; Arenas, A.; Barthelemy, M.; Gleeson, J.P.; Moreno, Y.; Porter, M.A. Multilayer networks. J. Complex Netw. 2014, 2, 203–271. [Google Scholar] [CrossRef]
- Musolino, D. L’attrattività percepita di regioni e province del Mezzogiorno per gli investimenti produttivi. Riv. Econ. Mezzog. 2016, 30, 45–70. [Google Scholar]
- Reiner, C.; Meyer, S.; Sardadvar, S. Urban attraction policies for international academic talent: Munich and Vienna in comparison. Cities 2017, 61, 27–35. [Google Scholar] [CrossRef]
- Öner, Ö. Retail city: The relationship between place attractiveness and accessibility to shops. Spat. Econ. Anal. 2017, 12, 72–91. [Google Scholar] [CrossRef]
- Lee, K.H. The conceptualization of country attractiveness: A review of research. Int. Rev. Adm. Sci. 2016, 82, 807–826. [Google Scholar] [CrossRef]
- Page, L.; Brin, S.; Motwani, R.; Winograd, T. The Pagerank Citation Ranking: Bringing Order to the Web; Stanford Infolab: Stanford, CA, USA, 1999. [Google Scholar]
- Rosvall, M.; Axelsson, D.; Bergstrom, C.T. The map equation. Eur. Phys. J. Spec. Top. 2009, 178, 13–23. [Google Scholar] [CrossRef]
- IRiE Final Report. Available online: https://gis-portal.espon.eu/arcgis/sharing/rest/content/items/5d1239c0336041fdb87ef00454f61bb9/data (accessed on 5 December 2024).
- Komornicki, T.; Rosik, P.; Mazur, M. A Multilayer Vision of Regional Integration. Retrieved on 9 December 2024. COI: 20.500.12592/m7czwk. 2023. Available online: https://policycommons.net/artifacts/3458127/a-multilayer-vision-of-regional-integration/4258675/ (accessed on 9 December 2024).
- IRiE. Available online: https://gis-portal.espon.eu/arcgis/apps/sites/#/irie-hub? (accessed on 29 October 2024).
- Rauch, J.E.; Trindade, V. Ethnic Chinese networks in international trade. Rev. Econ. Stat. 2002, 84, 116–130. [Google Scholar] [CrossRef]
- Peri, G.; Requena-Silvente, F. The trade creation effect of immigrants: Evidence from the remarkable case of Spain. Can. J. Econ./Revue Canadienne D’économique 2010, 43, 1433–1459. [Google Scholar] [CrossRef]
- Docquier, F.; Lodigiani, E. Skilled migration and business networks. Open Econ. Rev. 2010, 21, 565–588. [Google Scholar] [CrossRef][Green Version]
- Santana-Gallego, M.; Ledesma-Rodríguez, F.; Pérez-Rodríguez, J.V. Tourism and trade in OECD countries. A dynamic heterogeneous panel data analysis. Empir. Econ. 2011, 41, 533–554. [Google Scholar] [CrossRef]
- Ishutkina, M.; Hansman, R.J. Analysis of Interaction between Air Transportation and Economic Activity. In Proceedings of the 26th Congress of ICAS and 8th AIAA ATIO, Anchorage, AK, USA, 14–19 September 2008; p. 8888. [Google Scholar]
- Fageda, X. International air travel and FDI flows: Evidence from Barcelona. J. Reg. Sci. 2017, 57, 858–883. [Google Scholar] [CrossRef]
- World Bank; KNOMAD. Leveraging Diaspora Finances for Private Capital Mobilization; Migration and Development Brief; World Bank: Washington, DC, USA, 2023. [Google Scholar]
- Boccaletti, S.; Bianconi, G.; Criado, R.; Del Genio, C.I.; Gómez-Gardenes, J.; Romance, M.; Sendina-Nadal, I.; Wang, Z.; Zanin, M. The structure and dynamics of multilayer networks. Phys. Rep. 2014, 544, 1–122. [Google Scholar] [CrossRef]
- Bonaccorsi, G.; Riccaboni, M.; Fagiolo, G.; Santoni, G. Country centrality in the international multiplex network. Appl. Netw. Sci. 2019, 4, 126. [Google Scholar] [CrossRef]
- Newman, M. Networks; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Barthélemy, M. Spatial networks. Phys. Rep. 2011, 499, 1–101. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Cimini, G.; Squartini, T.; Saracco, F.; Garlaschelli, D.; Gabrielli, A.; Caldarelli, G. The statistical physics of real-world networks. Nat. Rev. Phys. 2019, 1, 58–71. [Google Scholar] [CrossRef]
- Bianconi, G. Multilayer Networks: Structure and Function; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Gomez, S.; Diaz-Guilera, A.; Gomez-Gardenes, J.; Perez-Vicente, C.J.; Moreno, Y.; Arenas, A. Diffusion dynamics on multiplex networks. Phys. Rev. Lett. 2013, 110, 028701. [Google Scholar] [CrossRef] [PubMed]
- Kang, Y.; Gao, S.; Liang, Y.; Li, M.; Rao, J.; Kruse, J. Multiscale dynamic human mobility flow dataset in the US during the COVID-19 epidemic. Sci. Data 2020, 7, 390. [Google Scholar] [CrossRef]
- Provenzano, D.; Hawelka, B.; Baggio, R. The mobility network of European tourists: A longitudinal study and a comparison with geo-located Twitter data. Tour. Rev. 2018, 73, 28–43. [Google Scholar] [CrossRef]
- Parisi, F.; Squartini, T.; Garlaschelli, D. A faster horse on a safer trail: Generalized inference for the efficient reconstruction of weighted networks. New J. Phys. 2020, 22, 053053. [Google Scholar] [CrossRef]
- Squartini, T.; Mastrandrea, R.; Garlaschelli, D. Unbiased sampling of network ensembles. New J. Phys. 2015, 17, 023052. [Google Scholar] [CrossRef]
- Vallarano, N.; Bruno, M.; Marchese, E.; Trapani, G.; Saracco, F.; Cimini, G.; Zanon, M.; Squartini, T. Fast and scalable likelihood maximization for exponential random graph models with local constraints. Sci. Rep. 2021, 11, 15227. [Google Scholar] [CrossRef]
- De Domenico, M.; Porter, M.A.; Arenas, A. MuxViz: A tool for multilayer analysis and visualization of networks. J. Complex Netw. 2015, 3, 159–176. [Google Scholar]
- Anselin, L. Spatial Econometrics: Methods and Models; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1988; Volume 4. [Google Scholar]
- Taylor, P.; Derudder, B. World City Network: A Global Urban Analysis; Routledge: London, UK, 2015. [Google Scholar]
- Hanzl-Weiss, D.; Holzner, M.; Römisch, R. BRATISLAVA and VIENNA: Twin Cities with Big Development Potentials; The Vienna Institute for International Economic Studies (wiiw): Vienna, Austria, 2018. [Google Scholar]
- Cudny, W.; Kunc, J. Growth and Change in Post-Socialist Cities of Central Europe; Routledge, Taylor & Francis Group: Abingdon, UK, 2022. [Google Scholar]
- Scott, A.J. Global City-Regions: Trends, Theory, Policy; OUP Oxford: Oxford, UK, 2001. [Google Scholar]
- ESPON Database Portal. Available online: https://database.espon.eu/ (accessed on 17 June 2024).
- Calò, E. European Region-to-Region Origin Destination Matrices. 2025. Available online: https://zenodo.org/records/15401969 (accessed on 13 September 2025).





| Category | Region |
|---|---|
| Highest Average: 1 | Ile-de-France (FR) |
| Highest Average: 2 | Comunidad de Madrid (ES) |
| Highest Average: 3 | Noord-Holland (NL) |
| Highest Average: 4 | Cataluña (ES) |
| Highest Average: 5 | Lombardia (IT) |
| Lowest Average: 1 | Liechtenstein (LI) |
| Lowest Average: 2 | Molise (IT) |
| Lowest Average: 3 | La Rioja (ES) |
| Lowest Average: 4 | Flevoland (NL) |
| Lowest Average: 5 | Voreio Aigaio (EL) |
| Largest Increase: 1 | Bratislavský kraj (SK) |
| Largest Increase: 2 | Leipzig (DE) |
| Largest Increase: 3 | Alentejo (PT) |
| Largest Increase: 4 | Kypros (CY) |
| Largest Increase: 5 | Nord-Vest (RO) |
| Largest Decrease: 1 | Dytiki Ellada (EL) |
| Largest Decrease: 2 | Pohjois- ja Itä-Suomi (FI) |
| Largest Decrease: 3 | West Central Scotland (UK) |
| Largest Decrease: 4 | Northern Ireland (UK) |
| Largest Decrease: 5 | Länsi-Suomi (FI) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calò, E.; Facchini, A. Multilayer Network Analysis of European Regional Flows. Entropy 2025, 27, 978. https://doi.org/10.3390/e27090978
Calò E, Facchini A. Multilayer Network Analysis of European Regional Flows. Entropy. 2025; 27(9):978. https://doi.org/10.3390/e27090978
Chicago/Turabian StyleCalò, Emanuele, and Angelo Facchini. 2025. "Multilayer Network Analysis of European Regional Flows" Entropy 27, no. 9: 978. https://doi.org/10.3390/e27090978
APA StyleCalò, E., & Facchini, A. (2025). Multilayer Network Analysis of European Regional Flows. Entropy, 27(9), 978. https://doi.org/10.3390/e27090978








