An Extended Epistemic Framework Beyond Probability for Quantum Information Processing with Applications in Security, Artificial Intelligence, and Financial Computing
Abstract
1. Introduction
2. Related Works
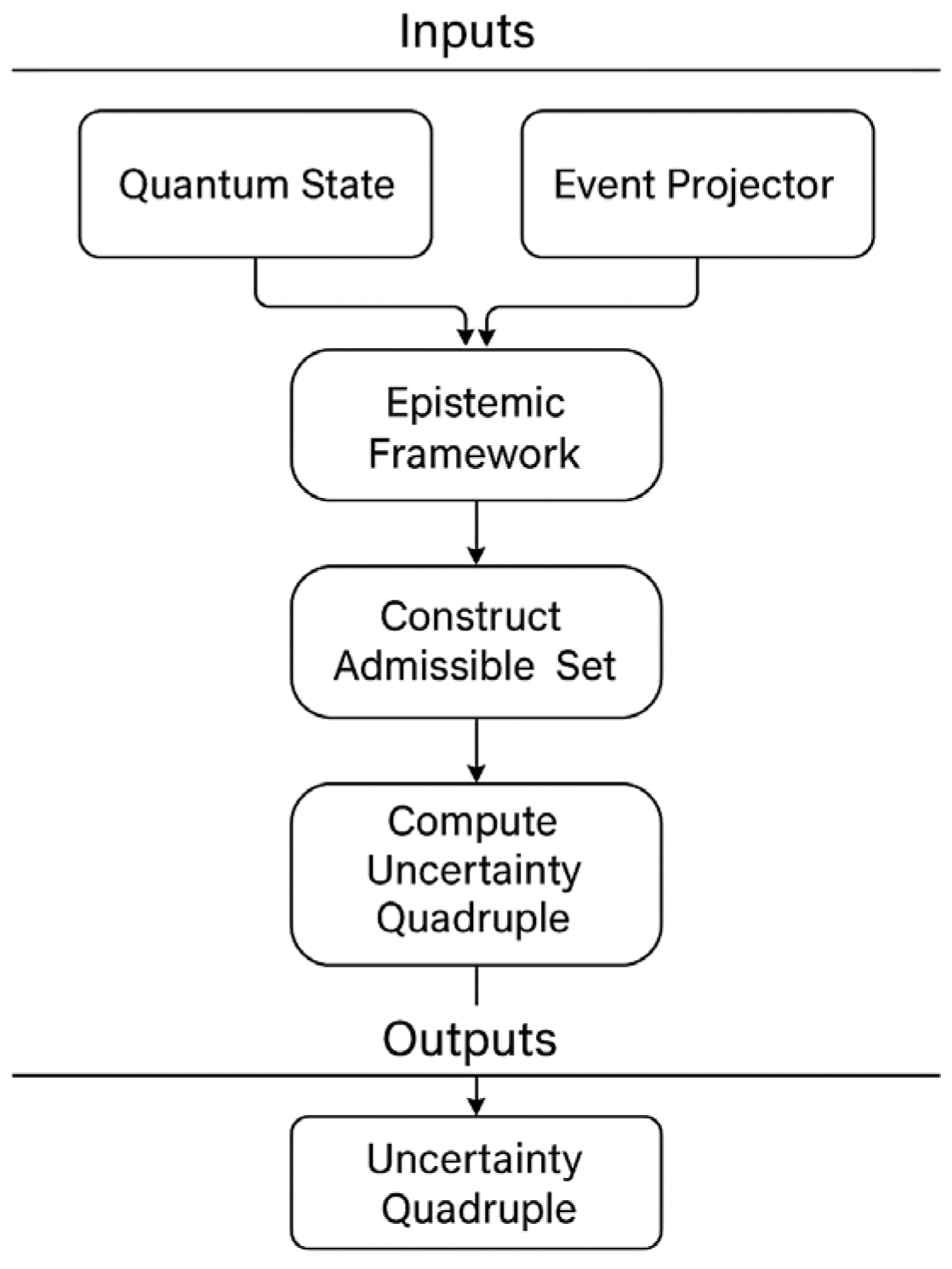
3. Materials, Methods and Model
- Data Processing Layer. Raw data from heterogeneous sources (e.g., network traffic, quantum sensors, financial time series) are pre-processed to extract features and events of interest. In quantum contexts, this includes tomography data, measurement outcomes and classical side information. The outcome space and event sigma-algebra are defined at this stage.
- Fusion Engine. Based on prior knowledge and the data, the engine constructs a family of admissible density matrices. This set may be defined by maximum-entropy constraints, confidence intervals on expectation values, or prior belief functions. Optimisation routines then compute and by solving semidefinite programs that maximise or minimise over . Possibility is obtained by minimising the support of the complement event. These optimisation problems can often be solved efficiently using convex programming techniques.
- Decision Module. The resulting quadruples feed into decision functions. For example, an anomaly detection system may trigger an alarm only if exceeds a threshold, while a portfolio manager may optimise expected returns under a risk measure defined by or . The module can implement decision policies that are robust to uncertainty by considering the interval and possibility constraints.
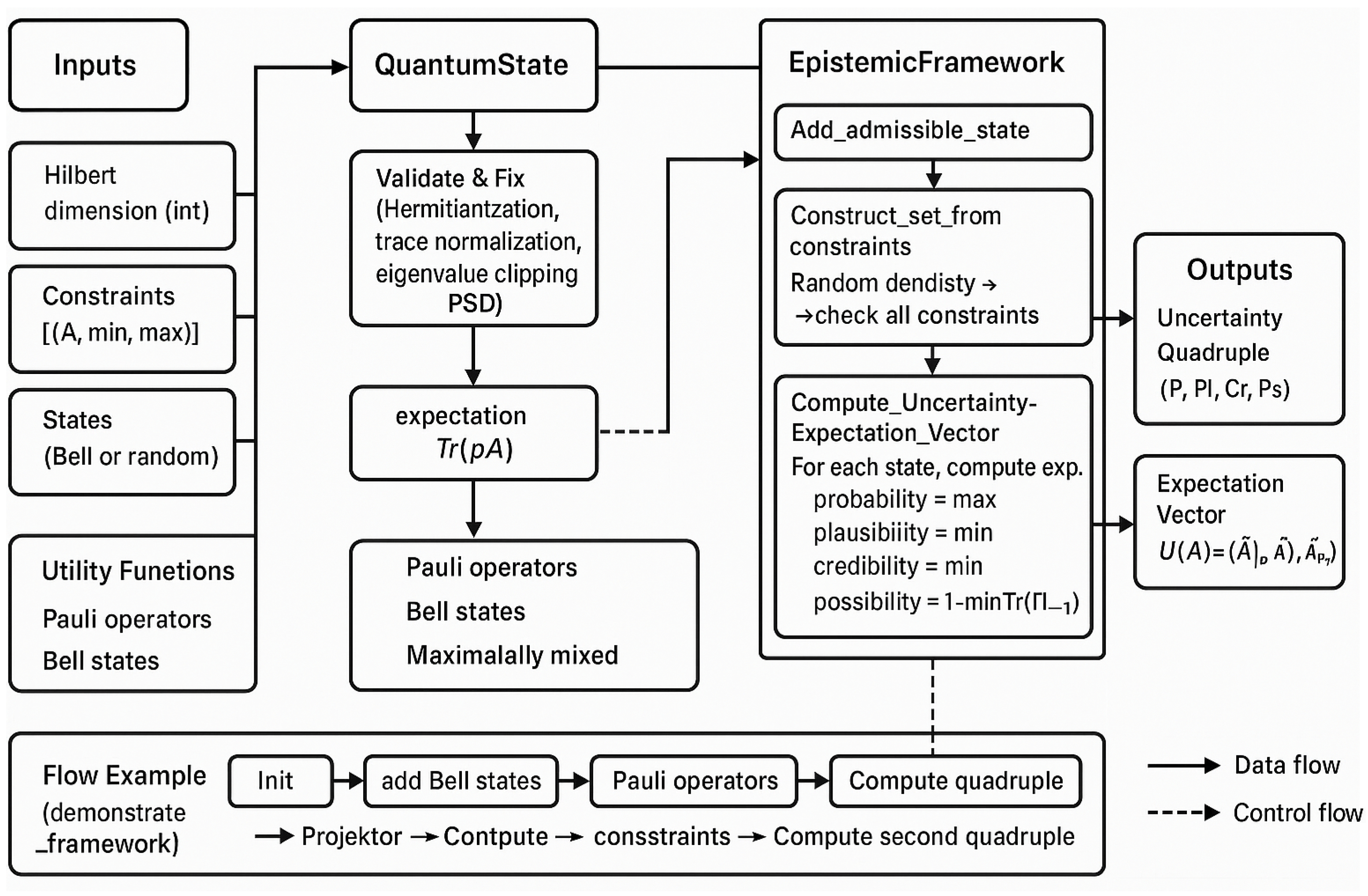
4. Implementation and Computational Architecture
| Algorithm 1: Generate_Random_Density_Matrix(d) |
|
- represents the probability-weighted expectation ,
- captures the maximum possible expectation value (plausibility),
- provides the minimum guaranteed expectation (credibility),
- represents the theoretical maximum achievable by any quantum state.
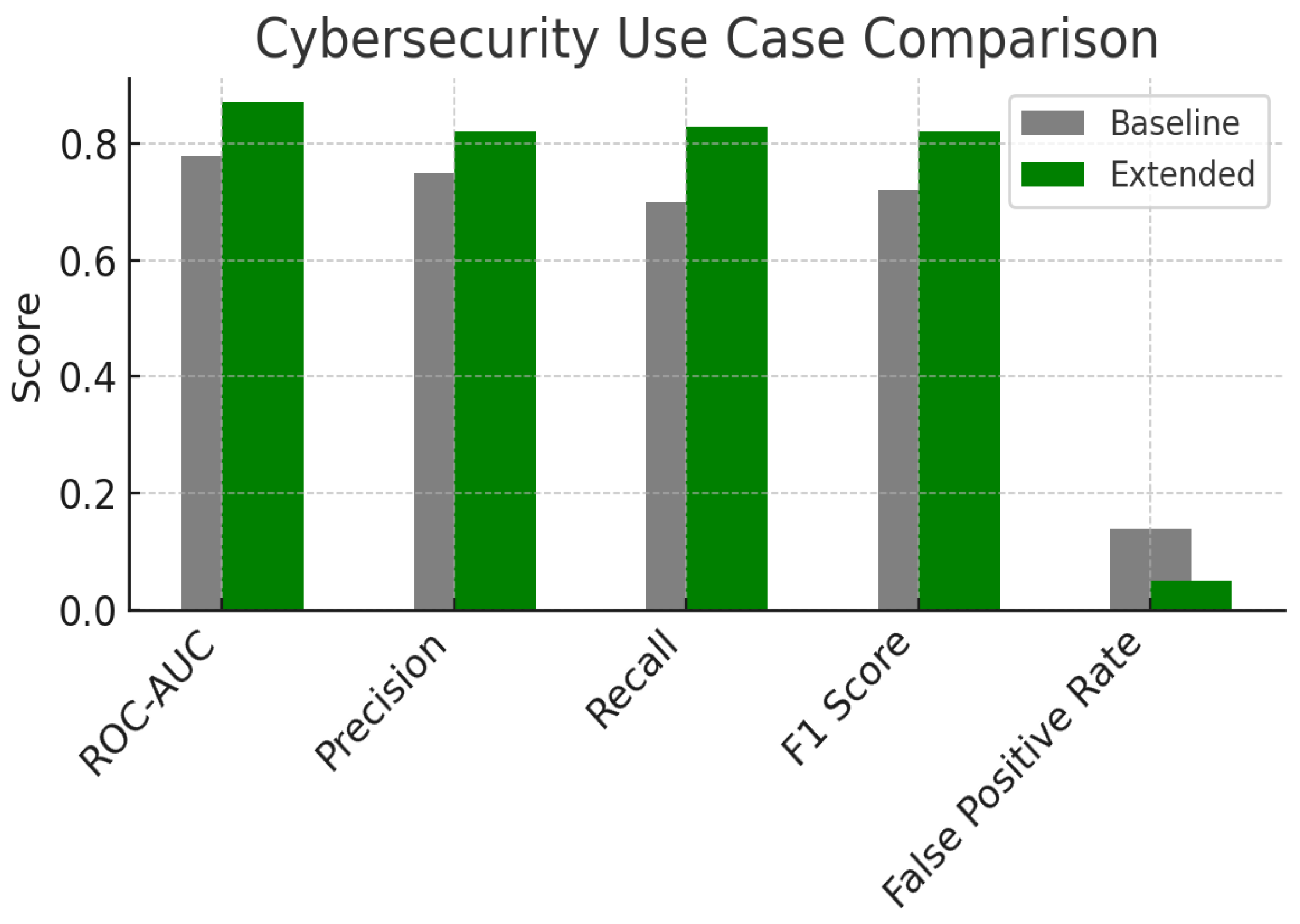
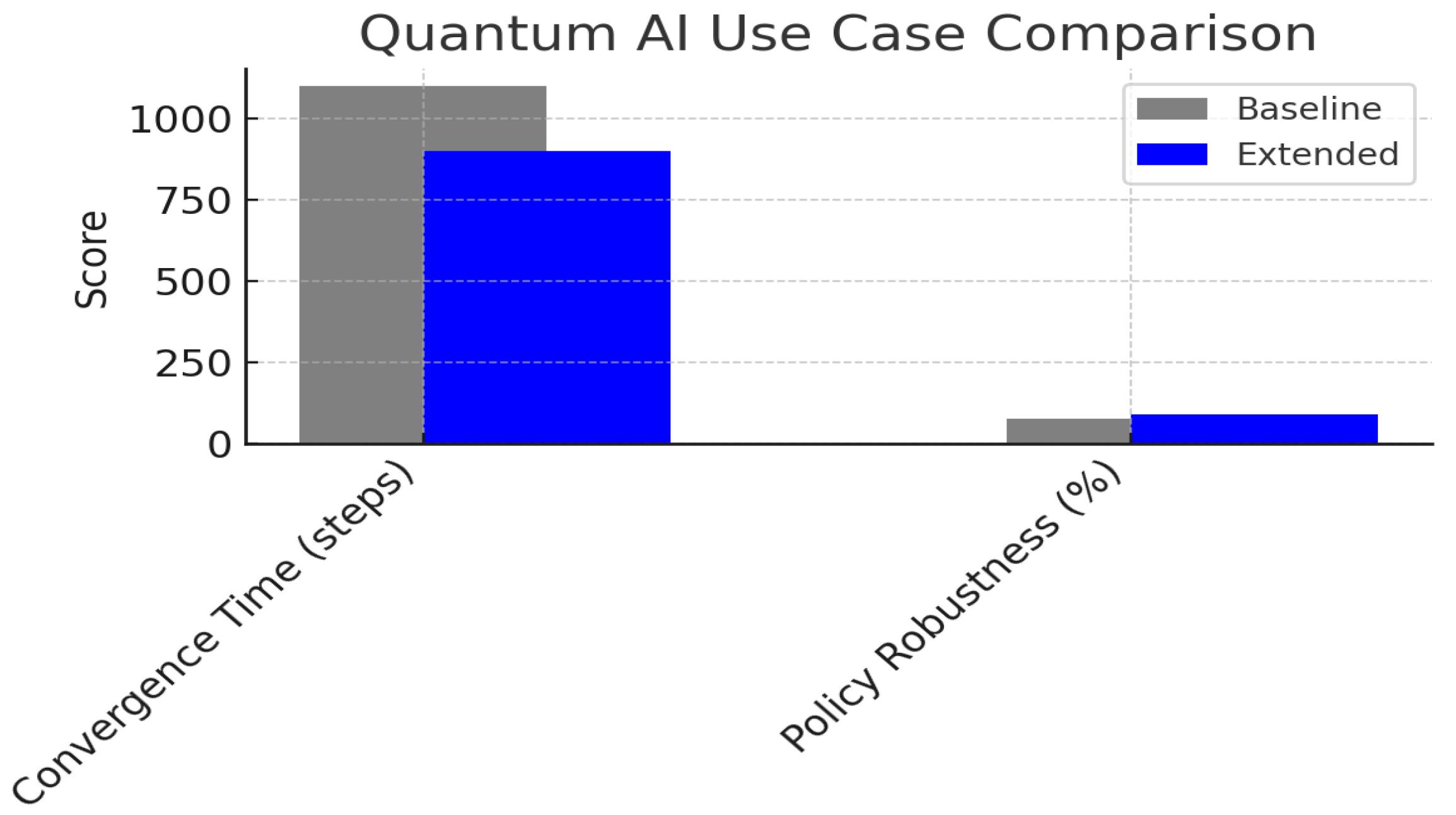
5. Results and Use Cases
6. Discussion and Perspectives
7. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Code
""" Extended Epistemic Framework Beyond Probability for Quantum Information Processing Core Implementation Author: Based on theoretical framework by Gerardo Iovane """ import numpy as np import cvxpy as cp from scipy.linalg import sqrtm, eigh from dataclasses import dataclass from typing import List, Tuple, Optional @dataclass class UncertaintyQuadruple: """Uncertainty quadruple U(E) = (P, Pl, Cr, Ps)""" probability: float # P(E) = Tr(ρΠ_E) plausibility: float # Pl(E) = sup_{ρ∈D} Tr(ρΠ_E) credibility: float # Cr(E) = inf_{ρ∈D} Tr(ρΠ_E) possibility: float # Ps(E) = 1 − inf_{ρ∈D} Tr(ρΠ_{¬E}) def __post_init__(self): """Enforce consistency: Cr(E) ≤ P(E) ≤ Pl(E) ≤ Ps(E)""" self.probability = max(0.0, min(1.0, self.probability)) self.plausibility = max(self.probability, min(1.0, self.plausibility)) self.credibility = min(self.probability, max(0.0, self.credibility)) self.possibility = max(self.plausibility, min(1.0, self.possibility)) def __str__(self) -> str: return f"U(E) = (P={self.probability:.3f}, Pl={self.plausibility:.3f}, Cr={self.credibility:.3f}, Ps={self.possibility:.3f})" class QuantumState: """Quantum density matrix with validation""" def __init__(self, rho: np.ndarray): self.rho = np.array(rho, dtype=complex) self._validate_and_fix() def _validate_and_fix(self): """Ensure valid density matrix""" # Make Hermitian and normalize trace self.rho = (self.rho + self.rho.T.conj()) / 2 self.rho = self.rho / np.trace(self.rho) # Ensure positive semidefinite eigenvals, eigenvecs = eigh(self.rho) eigenvals = np.maximum(eigenvals, 0) eigenvals = eigenvals / np.sum(eigenvals) self.rho = eigenvecs @ np.diag(eigenvals) @ eigenvecs.T.conj() def expectation(self, observable: np.ndarray) -> float: """Compute ⟨A⟩ = Tr(ρA)""" return np.real(np.trace(self.rho @ observable)) class EpistemicFramework: """Core epistemic framework implementation""" def __init__(self, hilbert_dimension: int): self.hilbert_dim = hilbert_dimension self.admissible_states: List[Tuple[QuantumState, float]] = [] def add_admissible_state(self, state: QuantumState, weight: float = 1.0): """Add quantum state to admissible set D""" self.admissible_states.append((state, weight)) def construct_admissible_set_from_constraints(self, constraints: List[Tuple[np.ndarray, float, float]], num_samples: int = 50) -> int: """ Construct admissible set from expectation constraints constraints: List of (observable, min_val, max_val) tuples """ self.admissible_states.clear() valid_states = 0 for _ in range(num_samples * 5): if valid_states >= num_samples: break # Generate random density matrix random_matrix = np.random.randn(self.hilbert_dim, self.hilbert_dim) + \ 1j * np.random.randn(self.hilbert_dim, self.hilbert_dim) rho = random_matrix @ random_matrix.T.conj() rho = rho / np.trace(rho) try: state = QuantumState(rho) # Check all constraints satisfies_all = True for observable, min_val, max_val in constraints: expectation = state.expectation(observable) if not (min_val <= expectation <= max_val): satisfies_all = False break if satisfies_all: self.add_admissible_state(state) valid_states += 1 except: continue return valid_states def compute_uncertainty_quadruple(self, projector: np.ndarray) -> UncertaintyQuadruple: """Compute U(E) = (P, Pl, Cr, Ps) for event projector Π_E""" if len(self.admissible_states) == 0: raise ValueError("No admissible states defined") # Compute expectation values for all admissible states expectations = [] weights = [] for state, weight in self.admissible_states: expectation = state.expectation(projector) expectations.append(expectation) weights.append(weight) expectations = np.array(expectations) weights = np.array(weights) normalized_weights = weights / np.sum(weights) # Compute the four measures probability = np.sum(expectations * normalized_weights) # P(E) plausibility = np.max(expectations) # Pl(E) = sup credibility = np.min(expectations) # Cr(E) = inf # Possibility: Ps(E) = 1 − inf Tr(ρΠ_{¬E}) complement_projector = np.eye(self.hilbert_dim) - projector complement_expectations = [state.expectation(complement_projector) for state, _ in self.admissible_states] possibility = 1.0 − np.min(complement_expectations) return UncertaintyQuadruple(probability, plausibility, credibility, possibility) def compute_observable_expectation_vector(self, observable: np.ndarray) -> np.ndarray: """Compute expectation vector U(A) = (⟨A⟩_P, ⟨A⟩_Pl, ⟨A⟩_Cr, ⟨A⟩_Ps)""" expectations = [] weights = [] for state, weight in self.admissible_states: expectation = state.expectation(observable) expectations.append(expectation) weights.append(weight) expectations = np.array(expectations) weights = np.array(weights) normalized_weights = weights / np.sum(weights) exp_P = np.sum(expectations * normalized_weights) # Weighted average exp_Pl = np.max(expectations) # Maximum exp_Cr = np.min(expectations) # Minimum exp_Ps = np.max(np.linalg.eigvals(observable)) # Maximum eigenvalue return np.array([exp_P, exp_Pl, exp_Cr, exp_Ps]) # UTILITY FUNCTIONS def create_pauli_operators() -> dict: """Create 2-qubit Pauli operators""" I = np.array([[1, 0], [0, 1]], dtype=complex) X = np.array([[0, 1], [1, 0]], dtype=complex) Y = np.array([[0, −1j], [1j, 0]], dtype=complex) Z = np.array([[1, 0], [0, −1]], dtype=complex) return { 'II': np.kron(I, I), 'IX': np.kron(I, X), 'IY': np.kron(I, Y), 'IZ': np.kron(I, Z), 'XI': np.kron(X, I), 'XX': np.kron(X, X), 'XY': np.kron(X, Y), 'XZ': np.kron(X, Z), 'YI': np.kron(Y, I), 'YX': np.kron(Y, X), 'YY': np.kron(Y, Y), 'YZ': np.kron(Y, Z), 'ZI': np.kron(Z, I), 'ZX': np.kron(Z, X), 'ZY': np.kron(Z, Y), 'ZZ': np.kron(Z, Z) } def create_bell_states() -> List[QuantumState]: """Create four Bell states""" bell_vectors = [ np.array([1, 0, 0, 1]) / np.sqrt(2), # |Φ+⟩ np.array([1, 0, 0, −1]) / np.sqrt(2), # |Φ−⟩ np.array([0, 1, 1, 0]) / np.sqrt(2), # |Ψ+⟩ np.array([0, 1, −1, 0]) / np.sqrt(2) # |Ψ−⟩ ] return [QuantumState(np.outer(psi, psi.conj())) for psi in bell_vectors] def create_maximally_mixed_state(dimension: int) -> QuantumState: """Create maximally mixed state I/d""" return QuantumState(np.eye(dimension) / dimension) # DEMONSTRATION EXAMPLE def demonstrate_framework(): """Basic demonstration of the epistemic framework""" print("Extended Epistemic Framework - Core Demonstration") print("=" * 50) # Create 2-qubit framework framework = EpistemicFramework(hilbert_dimension=4) # Add Bell states to admissible set bell_states = create_bell_states() for state in bell_states: framework.add_admissible_state(state) # Create measurement projector (first qubit in |0⟩) pauli_ops = create_pauli_operators() projector = (pauli_ops['II'] + pauli_ops['ZI']) / 2 # Compute uncertainty quadruple quad = framework.compute_uncertainty_quadruple(projector) print(f"Measurement: First qubit in |0⟩") print(f"Result: {quad}") print(f"Uncertainty interval: [{quad.credibility:.3f}, {quad.plausibility:.3f}]") print(f"Interval width: {quad.plausibility - quad.credibility:.3f}") # Test with constraints print("\nConstraint-based construction:") framework2 = EpistemicFramework(hilbert_dimension=4) # Constraint: ⟨ZZ⟩ ∈ [−0.5, 0.5] constraints = [(pauli_ops['ZZ'], −0.5, 0.5)] num_states = framework2.construct_admissible_set_from_constraints(constraints, num_samples=20) print(f"Generated {num_states} constrained states") if num_states > 0: quad2 = framework2.compute_uncertainty_quadruple(projector) print(f"Constrained result: {quad2}") print("\n  Framework demonstration") Framework demonstration")if __name__ == "__main__": demonstrate_framework() |
References
- Caticha, A. Entropic Inference and the Foundations of Physics; Brazilian Chapter of the International Society for Bayesian Analysis: São Paulo, Brazil, 2008; Available online: https://dl.icdst.org/pdfs/files1/77964f05542451c01e8e420e975dd664.pdf (accessed on 19 August 2025).
- Chaitin, G.J. Algorithmic Information Theory; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Buhrman, H.; Cleve, R.; Massar, S.; de Wolf, R. Nonlocality and communication complexity. Rev. Mod. Phys. 2010, 82, 665–698. [Google Scholar] [CrossRef]
- Werner, R.F. Quantum states with Einstein–Podolsky–Rosen correlations admitting a hidden-variable model. Phys. Rev. A 1989, 40, 4277–4281. [Google Scholar] [CrossRef] [PubMed]
- Vourdas, A. Quantum probabilities as Dempster–Shafer probabilities in the lattice of subspaces. J. Math. Phys. 2014, 55, 082107. [Google Scholar] [CrossRef]
- Metger, T.; Renner, R. Security of quantum key distribution from generalised entropy accumulation. Nat. Commun. 2023, 14, 5272. [Google Scholar] [CrossRef] [PubMed]
- Ishikawa, S.; Kikuchi, K. Quantum fuzzy logic and time. J. Appl. Math. Phys. 2021, 9, 2609–2622. [Google Scholar] [CrossRef]
- Ferrie, C. Quasi-probability representations of quantum theory with applications to quantum information science. Rep. Prog. Phys. 2011, 74, 116001. [Google Scholar] [CrossRef]
- Barkoutsos, P.K.; Nannicini, G.; Robert, A.; Tavernelli, I.; Woerner, S. Improving variational quantum optimization using CVaR. Quantum 2020, 4, 256. [Google Scholar] [CrossRef]
- Wu, S.; Jin, S.; Wen, D.; Han, D.; Wang, X. Quantum reinforcement learning in continuous action space. Quantum 2025, 9, 1660. [Google Scholar] [CrossRef]
- Iovane, G.; Di Gironimo, P.; Chinnici, M.; Rapuano, A. Decision and Reasoning in Incompleteness or Uncertainty Conditions. IEEE Access 2020, 8, 115109–115122. [Google Scholar] [CrossRef]
- Iovane, G.; Landi, R.E.; Rapuano, A.; Amatore, R. Assessing the Relevance of Opinions in Uncertainty and Info-Incompleteness Conditions. Appl. Sci. 2022, 12, 194. [Google Scholar] [CrossRef]
- Saatchi, R. Fuzzy Logic Concepts, Developments and Implementation. Information 2024, 15, 656. [Google Scholar] [CrossRef]
- Sudakov, V. Fuzzy Domination Graphs in Decision Support Tasks. Mathematics 2023, 11, 2837. [Google Scholar] [CrossRef]
- Brcko, T.; Luin, B. A Decision Support System Using Fuzzy Logic for Collision Avoidance in Multi-Vessel Situations at Sea. J. Mar. Sci. Eng. 2023, 11, 1819. [Google Scholar] [CrossRef]
- Tang, Y.; Wu, S.; Zhou, Y.; Huang, Y.; Zhou, D. A New Reliability Coefficient Using Betting Commitment Evidence Distance in Dempster–Shafer Evidence Theory for Uncertain Information Fusion. Entropy 2023, 25, 462. [Google Scholar] [CrossRef] [PubMed]
- Gentili, P.L. Establishing a New Link between Fuzzy Logic, Neuroscience, and Quantum Mechanics through Bayesian Probability: Perspectives in Artificial Intelligence and Unconventional Computing. Molecules 2021, 26, 5987. [Google Scholar] [CrossRef] [PubMed]
- Santana-Carrillo, R.; León-Montiel, R.d.J.; Sun, G.H.; Dong, S.H. Quantum Information Entropy for Another Class of New Proposed Hyperbolic Potentials. Entropy 2023, 25, 1296. [Google Scholar] [CrossRef] [PubMed]
- Bengtsson, I.; Życzkowski, K. Geometry of Quantum States: An Introduction to Quantum Entanglement, 2nd ed.; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1107026254. [Google Scholar]
- Shen, H.Z.; Shang, C.; Zhou, Y.H.; Yi, X.X. Unconventional single-photon blockade in non-Markovian systems. Phys. Rev. A 2018, 98, 2–023856. [Google Scholar] [CrossRef]
- Breuer, H.P.; Laine, E.M.; Piilo, J. Measure for the degree of non-Markovian behavior of quantum processes in open systems. Phys. Rev. Lett. 2009, 103, 210401. [Google Scholar] [CrossRef] [PubMed]
- Burenkov, I.A.; Annafianto, N.F.R.; Jabir, M.V.; Wayne, M.; Battou, A.; Polyakov, S.V. Experimental shot-by-shot estimation of quantum measurement confidence. Phys. Rev. Lett. 2022, 128, 040404. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.Y.; Rozpędek, F.; Hou, Z.; Wu, K.D.; Xiang, G.Y.; Li, C.F.; Guo, G.C. Experimental study of quantum uncertainty from lack of information. npj Quantum Inf. 2022, 8, 64. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iovane, G. An Extended Epistemic Framework Beyond Probability for Quantum Information Processing with Applications in Security, Artificial Intelligence, and Financial Computing. Entropy 2025, 27, 977. https://doi.org/10.3390/e27090977
Iovane G. An Extended Epistemic Framework Beyond Probability for Quantum Information Processing with Applications in Security, Artificial Intelligence, and Financial Computing. Entropy. 2025; 27(9):977. https://doi.org/10.3390/e27090977
Chicago/Turabian StyleIovane, Gerardo. 2025. "An Extended Epistemic Framework Beyond Probability for Quantum Information Processing with Applications in Security, Artificial Intelligence, and Financial Computing" Entropy 27, no. 9: 977. https://doi.org/10.3390/e27090977
APA StyleIovane, G. (2025). An Extended Epistemic Framework Beyond Probability for Quantum Information Processing with Applications in Security, Artificial Intelligence, and Financial Computing. Entropy, 27(9), 977. https://doi.org/10.3390/e27090977





