On the Storage–Communication Trade-Off in Graph-Based X-Secure T-Private Linear Computation
Abstract
1. Introduction
- The idea of exploiting MDS codes for the storage in graph-based PIR/PLC: Ref. [38] achieves a single point (minimum download cost) using replication codes that turn out to be storage-inefficient, while our scheme leverages MDS-coded storage to allow a storage–download trade-off. To the best of our knowledge, this is the first scheme to incorporate MDS codes in graph-based PIR/PLC.
- The technique used to handle the challenges introduced by the graph-based storage structure: Our work introduces a novel technique centered around the idea of a cross-subspace alignment (CSA) null shaper introduced in [27] to address the challenges introduced by the graph-based storage structure. The CSA null shaper was originally designed for storage-consistent private updates with unavailable servers. However, in this work, this idea is adapted to ensure that the overall storage conforms to valid CSA codewords under the graph-based storage constraints. This distinguishes our scheme from the scheme in [38], where the PLC under graph-based storage structure is enabled by a combination of techniques including CSA codes, dual Generalized Reed–Solomon (GRS) codes, and a Vandermonde decomposition of Cauchy matrices. Intuitively, CSA codes can be viewed as evaluation codes, and the CSA null shaper carefully places zeros at certain evaluation points, which correspond precisely to the servers prohibited by the graph-based storage pattern from storing codewords of a particular message. Consequently, the codewords for these servers are explicitly set to zero, requiring no storage at all, and the overall codewords (including zeros) remain valid CSA codewords. It should be noted that the idea of placing zeros in the storage construction for graph-based PIR/PLC may be profound, as the storage code of many known PIR/PLC schemes can be viewed as evaluation codes (e.g., polynomial codes based PIR/PLC in [12,24,46,47,48,49]). This idea may transform known PIR/PLC schemes into graph-based ones.
- Reduced decoding complexity and quantum adaptability: Unlike schemes based on dual GRS codes properties, where a pre-processing step of interference cancellation during decoding is generally necessary, in our scheme, the user can recover the desired linear combination by merely solving linear systems defined by Cauchy–Vandermonde matrices, hence the reduction in decoding complexity. Moreover, our scheme is compatible with the N-Sum Box abstraction of quantum “over-the-air” computing [44,50], enabling a direct transformation of our scheme into a quantum one to achieve the superdense coding gain.
2. Problem Statement
| Server 1 | Server 2 | Server 3 | Server 4 | Server 5 | Server 6 | Server 7 | Server 8 |
3. Main Result
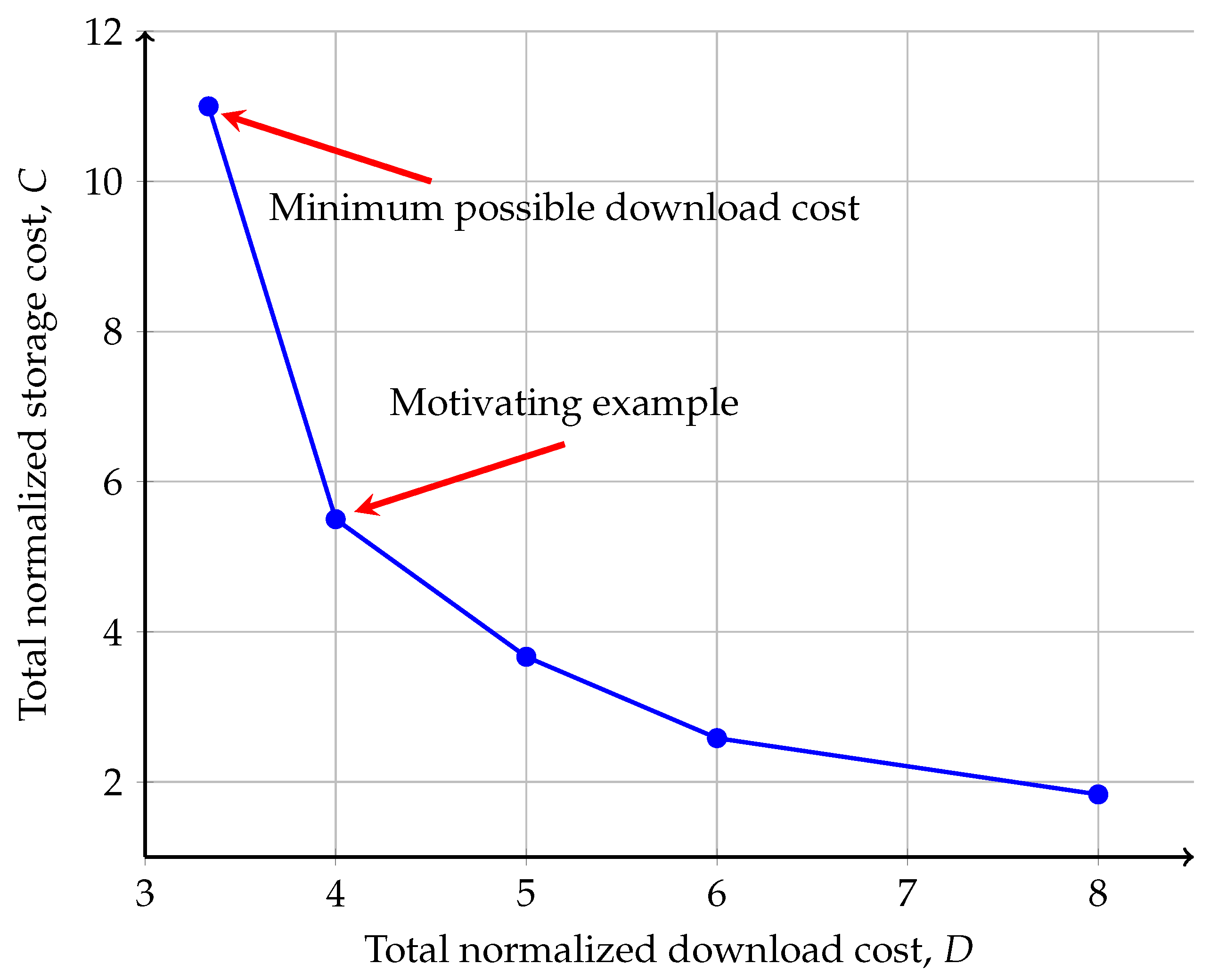
The Storage–Communication Trade-Off in the Proposed GXSTPLC Scheme
4. An Achievability Scheme for Asymmetric Setting
4.1. Preliminaries
4.2. Construction of the Storage
4.3. Construction of the Queries
4.4. Construction of the Answers
4.5. Motivating Example
5. Proof of Theorem 1
Motivating Example
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CSA | Cross-Subspace Alignment |
| GXSTPLC | Graph-Based X-Secure T-Private Linear Computation |
| GRS | Generalized Reed–Solomon |
| PIR | Private Information Retrieval |
| PLC | Private Linear Computation |
References
- Sun, H.; Jafar, S.A. The Capacity of Private Information Retrieval. IEEE Trans. Inf. Theory 2017, 63, 4075–4088. [Google Scholar] [CrossRef]
- Sun, H.; Jafar, S.A. The Capacity of Robust Private Information Retrieval with Colluding Databases. IEEE Trans. Inf. Theory 2018, 64, 2361–2370. [Google Scholar] [CrossRef]
- Sun, H.; Jafar, S.A. The Capacity of Private Computation. IEEE Trans. Inf. Theory 2019, 65, 3880–3897. [Google Scholar] [CrossRef]
- Tahmasebi, B.; Maddah-Ali, M.A. Private Function Computation. In Proceedings of the 2020 IEEE International Symposium on Information Theory (ISIT), Los Angeles, CA, USA, 21–26 June 2020; pp. 1118–1123. [Google Scholar] [CrossRef]
- Lu, Y.; Jia, Z.; Jafar, S.A. Double blind T-private information retrieval. IEEE J. Sel. Areas Inf. Theory 2021, 2, 428–440. [Google Scholar] [CrossRef]
- Raviv, N.; Karpuk, D.A. Private Polynomial Computation From Lagrange Encoding. IEEE Trans. Inf. Forensics Secur. 2020, 15, 553–563. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Jafar, S.A. The Asymptotic Capacity of Private Search. IEEE Trans. Inf. Theory 2020, 66, 4709–4721. [Google Scholar] [CrossRef]
- Yao, X.; Liu, N.; Kang, W. The Capacity of Private Information Retrieval Under Arbitrary Collusion Patterns for Replicated Databases. IEEE Trans. Inf. Theory 2021, 67, 6841–6855. [Google Scholar] [CrossRef]
- Banawan, K.; Ulukus, S. The Capacity of Private Information Retrieval From Coded Databases. IEEE Trans. Inf. Theory 2018, 64, 1945–1956. [Google Scholar] [CrossRef]
- Freij-Hollanti, R.; Gnilke, O.; Hollanti, C.; Karpuk, D. Private information retrieval from coded databases with colluding servers. SIAM J. Appl. Algebra Geom. 2017, 1, 647–664. [Google Scholar] [CrossRef]
- Sun, H.; Jafar, S.A. Private information retrieval from MDS coded data with colluding servers: Settling a conjecture by Freij-Hollanti et al. IEEE Trans. Inf. Theory 2018, 64, 1000–1022. [Google Scholar] [CrossRef]
- Tajeddine, R.; Gnilke, O.W.; Karpuk, D.; Freij-Hollanti, R.; Hollanti, C. Private Information Retrieval From Coded Storage Systems with Colluding, Byzantine, and Unresponsive Servers. IEEE Trans. Inf. Theory 2019, 65, 3898–3906. [Google Scholar] [CrossRef]
- Tajeddine, R.; Gnilke, O.W.; El Rouayheb, S. Private Information Retrieval From MDS Coded Data in Distributed Storage Systems. IEEE Trans. Inf. Theory 2018, 64, 7081–7093. [Google Scholar] [CrossRef]
- Wang, Q.; Skoglund, M. Symmetric Private Information Retrieval from MDS Coded Distributed Storage with Non-Colluding and Colluding Servers. IEEE Trans. Inf. Theory 2019, 65, 5160–5175. [Google Scholar] [CrossRef]
- Obead, S.A.; Lin, H.Y.; Rosnes, E.; Kliewer, J. Private Linear Computation for Noncolluding Coded Databases. IEEE J. Sel. Areas Commun. 2022, 40, 847–861. [Google Scholar] [CrossRef]
- Wang, Z.; Banawan, K.; Ulukus, S. Private Set Intersection: A Multi-Message Symmetric Private Information Retrieval Perspective. IEEE Trans. Inf. Theory 2022, 68, 2001–2019. [Google Scholar] [CrossRef]
- Kadhe, S.; Garcia, B.; Heidarzadeh, A.; El Rouayheb, S.; Sprintson, A. Private Information Retrieval with Side Information. IEEE Trans. Inf. Theory 2020, 66, 2032–2043. [Google Scholar] [CrossRef]
- Wei, Y.P.; Banawan, K.; Ulukus, S. Fundamental Limits of Cache-Aided Private Information Retrieval with Unknown and Uncoded Prefetching. IEEE Trans. Inf. Theory 2019, 65, 3215–3232. [Google Scholar] [CrossRef]
- Wei, Y.P.; Banawan, K.; Ulukus, S. The Capacity of Private Information Retrieval with Partially Known Private Side Information. IEEE Trans. Inf. Theory 2019, 65, 8222–8231. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, Z.; Jafar, S.A. The capacity of T-private information retrieval with private side information. IEEE Trans. Inf. Theory 2020, 66, 4761–4773. [Google Scholar] [CrossRef]
- Sun, H.; Jafar, S.A. Multiround private information retrieval: Capacity and storage overhead. IEEE Trans. Inf. Theory 2018, 64, 5743–5754. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, H.; Skoglund, M. The Capacity of Private Information Retrieval with Eavesdroppers. IEEE Trans. Inf. Theory 2019, 65, 3198–3214. [Google Scholar] [CrossRef]
- Yang, H.; Shin, W.; Lee, J. Private Information Retrieval for Secure Distributed Storage Systems. IEEE Trans. Inf. Forensics Secur. 2018, 13, 2953–2964. [Google Scholar] [CrossRef]
- Jia, Z.; Sun, H.; Jafar, S.A. Cross subspace alignment and the asymptotic capacity of X-secure T-private information retrieval. IEEE Trans. Inf. Theory 2019, 65, 5783–5798. [Google Scholar] [CrossRef]
- Jia, Z.; Jafar, S.A. X-secure T-private information retrieval from MDS coded storage with byzantine and unresponsive servers. IEEE Trans. Inf. Theory 2020, 66, 7427–7438. [Google Scholar] [CrossRef]
- Jia, Z.; Jafar, S.A. On the asymptotic capacity of X-secure T-private information retrieval with graph-Based replicated storage. IEEE Trans. Inf. Theory 2020, 66, 6280–6296. [Google Scholar] [CrossRef]
- Jia, Z.; Jafar, S.A. X-secure T-private federated submodel learning with elastic dropout resilience. IEEE Trans. Inf. Theory 2022, 68, 5418–5439. [Google Scholar] [CrossRef]
- Sun, H.; Jafar, S.A. The Capacity of Symmetric Private Information Retrieval. IEEE Trans. Inf. Theory 2019, 65, 322–329. [Google Scholar] [CrossRef]
- Zhu, J.; Yan, Q.; Tang, X.; Li, S. Symmetric private polynomial computation from Lagrange encoding. IEEE Trans. Inf. Theory 2022, 68, 2704–2718. [Google Scholar] [CrossRef]
- Banawan, K.; Ulukus, S. The Capacity of Private Information Retrieval from Byzantine and Colluding Databases. IEEE Trans. Inf. Theory 2019, 65, 1206–1219. [Google Scholar] [CrossRef]
- Banawan, K.; Ulukus, S. Asymmetry hurts: Private information retrieval under asymmetric traffic constraints. IEEE Trans. Inf. Theory 2019, 65, 7628–7645. [Google Scholar] [CrossRef]
- Sun, H.; Jafar, S.A. Optimal Download Cost of Private Information Retrieval for Arbitrary Message Length. IEEE Trans. Inf. Forensics Secur. 2017, 12, 2920–2932. [Google Scholar] [CrossRef]
- Jia, Z.; Sun, H.; Jafar, S.A. The Capacity of Private Information Retrieval with Disjoint Colluding Sets. In Proceedings of the GLOBECOM 2017—2017 IEEE Global Communications Conference, Singapore, 4–8 December 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Tian, C.; Sun, H.; Chen, J. Capacity-Achieving Private Information Retrieval Codes with Optimal Message Size and Upload Cost. IEEE Trans. Inf. Theory 2019, 65, 7613–7627. [Google Scholar] [CrossRef]
- Raviv, N.; Tamo, I.; Yaakobi, E. Private Information Retrieval in Graph-Based Replication Systems. IEEE Trans. Inf. Theory 2020, 66, 3590–3602. [Google Scholar] [CrossRef]
- Sadeh, B.; Gu, Y.; Tamo, I. Bounds on the Capacity of Private Information Retrieval Over Graphs. IEEE Trans. Inf. Forensics Secur. 2023, 18, 261–273. [Google Scholar] [CrossRef]
- Banawan, K.; Ulukus, S. Private Information Retrieval from Non-Replicated Databases. In Proceedings of the 2019 IEEE International Symposium on Information Theory (ISIT), Paris, France, 7–12 July 2019; pp. 1272–1276. [Google Scholar] [CrossRef]
- Jia, H.; Jia, Z. The Asymptotic Capacity of X-Secure T-Private Linear Computation with Graph Based Replicated Storage. IEEE Trans. Inf. Theory 2024, 70, 5269–5288. [Google Scholar] [CrossRef]
- Nomeir, M.; Vithana, S.; Ulukus, S. Asymmetric X-Secure T-Private Information Retrieval: More Databases is Not Always Better. In Proceedings of the 2024 58th Annual Conference on Information Sciences and Systems (CISS), Princeton, NJ, USA, 13–15 March 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Aytekin, A.; Nomeir, M.; Vithana, S.; Ulukus, S. Quantum Symmetric Private Information Retrieval with Secure Storage and Eavesdroppers. In Proceedings of the 2023 IEEE Globecom Workshops (GC Wkshps), Kuala Lumpur, Malaysia, 4–8 December 2023; pp. 1057–1062. [Google Scholar] [CrossRef]
- Song, S.; Hayashi, M. Capacity of Quantum Private Information Retrieval with Multiple Servers. IEEE Trans. Inf. Theory 2021, 67, 452–463. [Google Scholar] [CrossRef]
- Song, S.; Hayashi, M. Capacity of Quantum Private Information Retrieval with Colluding Servers. IEEE Trans. Inf. Theory 2021, 67, 5491–5508. [Google Scholar] [CrossRef]
- Allaix, M.; Song, S.; Holzbaur, L.; Pllaha, T.; Hayashi, M.; Hollanti, C. On the Capacity of Quantum Private Information Retrieval From MDS-Coded and Colluding Servers. IEEE J. Sel. Areas Commun. 2022, 40, 885–898. [Google Scholar] [CrossRef]
- Lu, Y.; Jafar, S.A. Quantum Cross Subspace Alignment Codes via the N-sum Box Abstraction. In Proceedings of the 2023 57th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 29 October–1 November 2023; pp. 670–674. [Google Scholar] [CrossRef]
- Lu, Y.; Jafar, S.A. Quantum X-Secure T-Private Information Retrieval From MDS Coded Storage with Unresponsive and Byzantine Servers. IEEE J. Sel. Areas Inf. Theory 2025, 6, 59–73. [Google Scholar] [CrossRef]
- Karpuk, D. Private Computation of Systematically Encoded Data with Colluding Servers. In Proceedings of the 2018 IEEE International Symposium on Information Theory (ISIT), Vail, CO, USA, 17–22 June 2018; pp. 2112–2116. [Google Scholar] [CrossRef]
- Obead, S.A.; Lin, H.Y.; Rosnes, E.; Kliewer, J. Private Polynomial Function Computation for Noncolluding Coded Databases. IEEE Trans. Inf. Forensics Secur. 2022, 17, 1800–1813. [Google Scholar] [CrossRef]
- Wang, Q.; Skoglund, M. On PIR and Symmetric PIR From Colluding Databases with Adversaries and Eavesdroppers. IEEE Trans. Inf. Theory 2019, 65, 3183–3197. [Google Scholar] [CrossRef]
- Yu, Q.; Li, S.; Raviv, N.; Kalan, S.M.M.; Soltanolkotabi, M.; Avestimehr, S.A. Lagrange coded computing: Optimal design for resiliency, security, and privacy. In Proceedings of the 22nd International Conference on Artificial Intelligence and Statistics, PMLR, Naha, Japan, 16–18 April 2019; Volume 89, pp. 1215–1225. [Google Scholar]
- Allaix, M.; Lu, Y.; Yao, Y.; Pllaha, T.; Hollanti, C.; Jafar, S.A. N-Sum Box: An Abstraction for Linear Computation Over Many-to-One Quantum Networks. IEEE Trans. Inf. Theory 2025, 71, 1121–1139. [Google Scholar] [CrossRef]
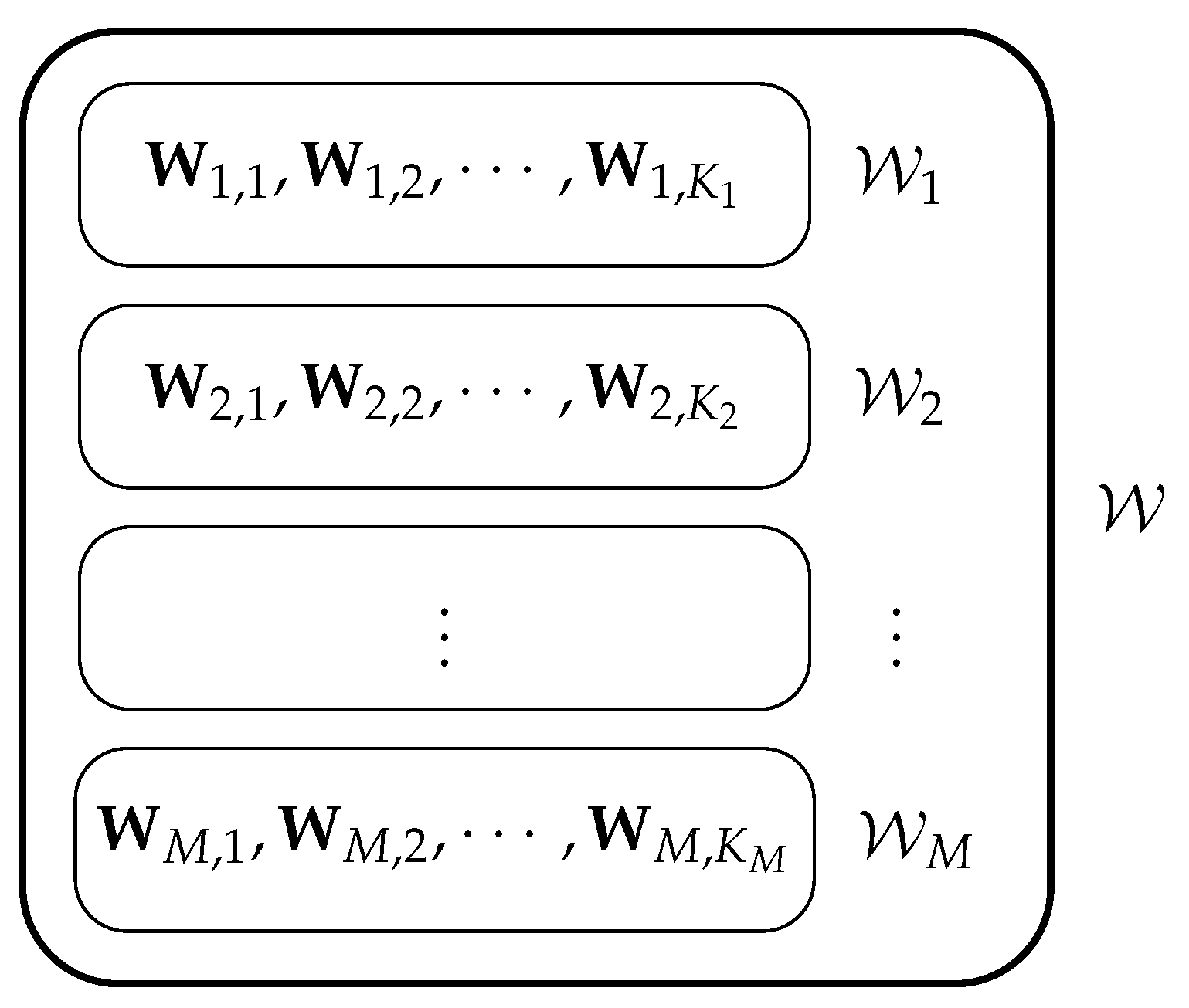
| Server | |||||||||
| 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | |
| Server | |||||||||
| 2 | 2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 2 | 2 | ||||||||
| Server | |||||||||
| 2 | 2 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jia, H.; Jia, Z. On the Storage–Communication Trade-Off in Graph-Based X-Secure T-Private Linear Computation. Entropy 2025, 27, 975. https://doi.org/10.3390/e27090975
Liu Y, Jia H, Jia Z. On the Storage–Communication Trade-Off in Graph-Based X-Secure T-Private Linear Computation. Entropy. 2025; 27(9):975. https://doi.org/10.3390/e27090975
Chicago/Turabian StyleLiu, Yueyang, Haobo Jia, and Zhuqing Jia. 2025. "On the Storage–Communication Trade-Off in Graph-Based X-Secure T-Private Linear Computation" Entropy 27, no. 9: 975. https://doi.org/10.3390/e27090975
APA StyleLiu, Y., Jia, H., & Jia, Z. (2025). On the Storage–Communication Trade-Off in Graph-Based X-Secure T-Private Linear Computation. Entropy, 27(9), 975. https://doi.org/10.3390/e27090975






