On the Coupling Between Cosmological Dynamics and Quantum Behavior: A Multiscale Thermodynamic Framework
Abstract
1. Introduction
2. The Recursive Thermodynamic Model
2.1. Internal Energy of the Universe
2.2. Further Consequences Resulting from the Recursive Model
3. Derivation of Newtonian Laws from Recursive Energy Structures
4. Hierarchical Energy Coupling and Local Observables
4.1. Thermodynamic Fluctuations Across Scales
Brownian Dynamics Under the Influence of Cosmological Fluctuations
4.2. Cosmic Effects on Quantum Systems
Quantitative Implications
4.3. Zero-Point Energy from Unresolved Recursive Thermodynamic Embedding
4.4. Remarks on the Uncertainty Principle of Quantum Physics
5. Constraining the Energy–Momentum Tensor Through Recursive Thermodynamic Structure
6. Conclusions and Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Structural Resolution and Wavefunction Compensation in Many-Body Approximations
The fewer interaction terms are explicitly resolved in the Hamiltonian, the more compensation is required by the wavefunction, effective potentials, or parametrized models.
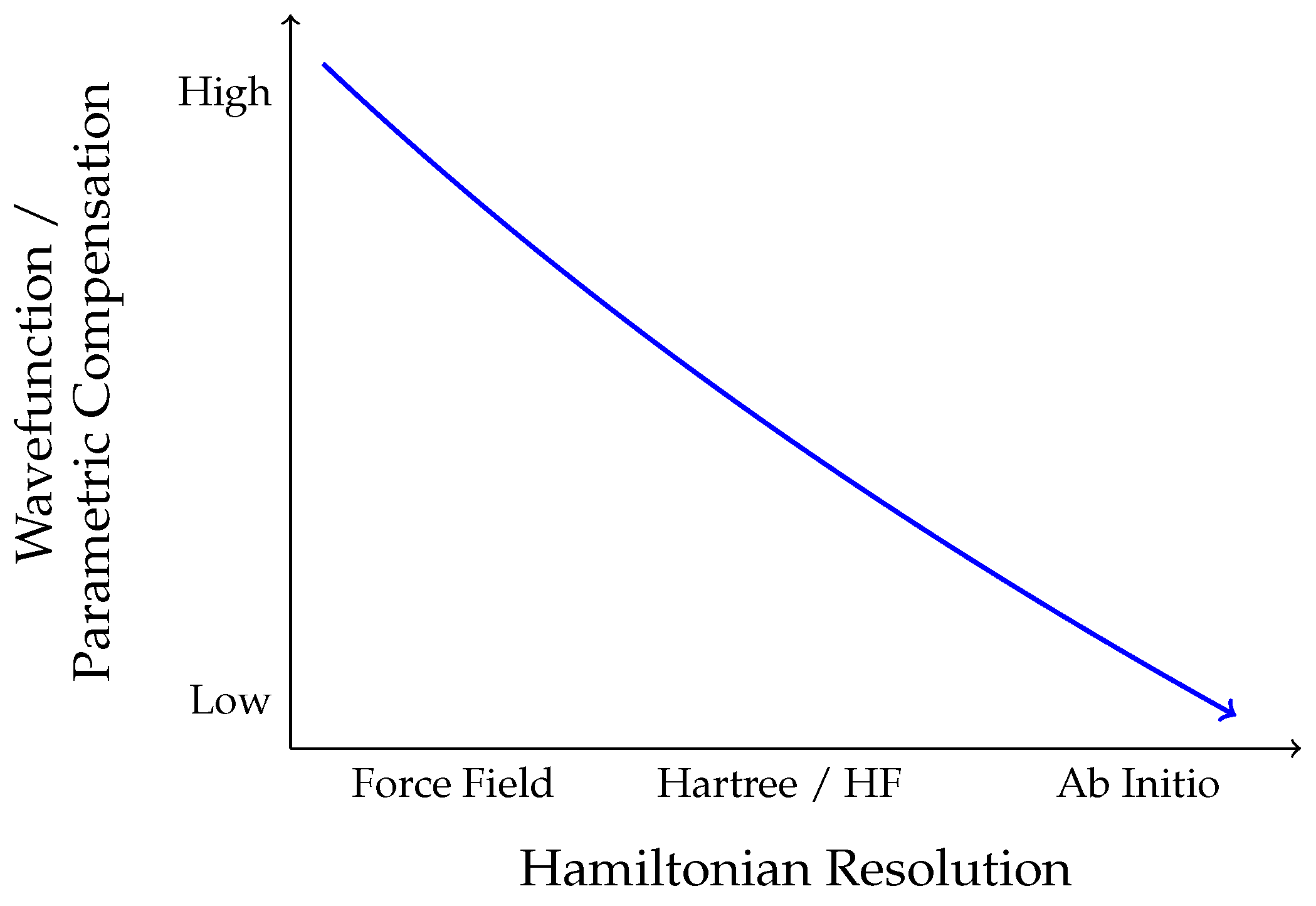
Appendix B. Experimental Testability
Appendix B.1. Quantitative Drift Estimates
Appendix B.2. Geochemical Barcoding
Appendix B.3. Brownian Motion
References
- Susskind, L. The anthropic landscape of string theory. In Universe or Multiverse? Carr, B., Ed.; Cambridge University Press: Cambridge, UK, 2007; pp. 247–266. [Google Scholar]
- Polchinski, J. String Theory; Cambridge University Press: Cambridge, UK, 1998; Volume 1. [Google Scholar]
- Polchinski, J. String Theory; Cambridge University Press: Cambridge, UK, 1998; Volume 2. [Google Scholar]
- Rovelli, C. Loop Quantum Gravity. Living Rev. Relativ. 1998, 1, 1. [Google Scholar] [CrossRef]
- Gielen, S.; Oriti, D. Quantum cosmology from group field theory condensates: A review. Front. Phys. 2016, 12, 082. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J.E. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406–3427. [Google Scholar] [CrossRef] [PubMed]
- Tsujikawa, S. Quintessence: A Review. Class. Quantum Gravity 2013, 30, 214003. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- Clifton, T.; Ferreira, P.G.; Padilla, A.; Skordis, C. Modified gravity and cosmology. Phys. Rep. 2012, 513, 1–189. [Google Scholar] [CrossRef]
- Reuter, M. Nonperturbative evolution equation for quantum gravity. Phys. Rev. D 1998, 57, 971–985. [Google Scholar] [CrossRef]
- Percacci, R. Asymptotic safety. In Approaches to Quantum Gravity: Toward a New Understanding of Space, Time and Matter; Oriti, D., Ed.; Cambridge University Press: Cambridge, UK, 2009; pp. 111–128. [Google Scholar] [CrossRef]
- Wetterich, C. Probing quintessence with time variation of couplings. J. Cosmol. Astropart. Phys. 2003, 10, 002. [Google Scholar] [CrossRef]
- Bonanno, A.; Reuter, M. Cosmology of the Planck era from a renormalization group for quantum gravity. Phys. Lett. B 2002, 527, 9–17. [Google Scholar] [CrossRef]
- Wetterich, C. Exact evolution equation for the effective potential. Nucl. Phys. B 1993, 301, 90–94. [Google Scholar] [CrossRef]
- Wetterich, C. Variable gravity Universe. Phys. Rev. D 2014, 89, 084007. [Google Scholar] [CrossRef]
- Verlinde, E.P. On the origin of gravity and the laws of Newton. J. High Energy Phys. 2011, 2011, 29. [Google Scholar] [CrossRef]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825–874. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- ’t Hooft, G. Dimensional Reduction in Quantum Gravity. arXiv 2009, arXiv:gr-qc/9310026. [Google Scholar] [CrossRef]
- Oppenheim, J. A Postquantum Theory of Classical Gravity? Phys. Rev. X 2023, 13, 041040. [Google Scholar] [CrossRef]
- ’t Hooft, G. The cellular automaton interpretation of quantum mechanics. Found. Phys. 2013, 43, 597–711. [Google Scholar] [CrossRef]
- Field, M.J.; Bash, P.A.; Karplus, M. A Combined Quantum Mechanical and Molecular Mechanical Potential for Molecular Dynamics Simulations. J. Comput. Chem. 1990, 11, 700–733. [Google Scholar] [CrossRef]
- Lyubartsev, A.; Tu, Y.; Laaksonen, A. Hierarchical Multiscale Modelling Scheme from First Principles to Mesoscale. J. Comput. Theor. Nanosci. 2009, 6, 951–959. [Google Scholar] [CrossRef]
- Karplus, M. Molecular Dynamics Simulations of Biomolecules. Accounts Chem. Res. 2002, 35, 321–323. [Google Scholar] [CrossRef]
- Levitt, M. Birth and Future of Multiscale Modeling for Macromolecular Systems (Nobel Lecture). Angew. Chem. Int. Ed. 2014, 53, 10006–10018. [Google Scholar] [CrossRef] [PubMed]
- Basar, Y.; Weichert, D. Nonlinear Continuum Mechanics of Solids; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar] [CrossRef]
- Lemaitre, G. Evolution of the Expanding Universe. Proc. Natl. Acad. Sci. USA 1934, 20, 12–17. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P.; Leighton, R.B.; Sands, M.L. The Feynman Lectures on Physics, definitive ed.; Pearson/Addison-Wesley: Boston, MA, USA, 2006. [Google Scholar]
- Watts, E.J.; Rees, R.; Jonathan, P.; Keir, D.; Taylor, R.N.; Siegburg, M.; Chambers, E.L.; Pagli, C.; Cooper, M.J.; Michalik, A.; et al. Mantle upwelling at Afar triple junction shaped by overriding plate dynamics. Nat. Geosci. 2025, 18, 661–669. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Warkentin, A. On the Coupling Between Cosmological Dynamics and Quantum Behavior: A Multiscale Thermodynamic Framework. Entropy 2025, 27, 976. https://doi.org/10.3390/e27090976
Warkentin A. On the Coupling Between Cosmological Dynamics and Quantum Behavior: A Multiscale Thermodynamic Framework. Entropy. 2025; 27(9):976. https://doi.org/10.3390/e27090976
Chicago/Turabian StyleWarkentin, Andreas. 2025. "On the Coupling Between Cosmological Dynamics and Quantum Behavior: A Multiscale Thermodynamic Framework" Entropy 27, no. 9: 976. https://doi.org/10.3390/e27090976
APA StyleWarkentin, A. (2025). On the Coupling Between Cosmological Dynamics and Quantum Behavior: A Multiscale Thermodynamic Framework. Entropy, 27(9), 976. https://doi.org/10.3390/e27090976





