b-Value Evaluation and Applications to Seismic Hazard Assessment
Abstract
1. Introduction
2. Methods to Estimate b-Value
| Method | Principle | Advantages | Limitations | Applicable Scenarios |
|---|---|---|---|---|
| Least Squares Method [1,2] | Best-fit line slope for earthquake distribution (minimizing distance) | Simple and straightforward | Easily biased by large earthquakes [47] | Relatively complete catalogs |
| Maximum Likelihood Estimation [35,36,38] | Best-fit distribution for earthquake (maximum likelihood function) | Not affected by specific large earthquake | Strongly dependent on the accurate assessment of | Relatively complete catalogs |
| B-Positive Estimator [34] | Estimation of temporal b-values of magnitude difference following the Laplace distribution | Robust, insensitive to changes in detection rate | Relies on positive magnitude difference | Temporal sequence with mainshocks |
| Classical Grid Search Method [31] | Search for events in nearby grid points to calculate b-value | Simple and straightforward | Requires a minimum sample size | Catalog including spatial and temporal heterogeneity |
| Objective Bayesian Method [28] | Addition of spatial/temporal derivative penalties to the likelihood function | High spatial resolution and coverage | Relatively complex calculation | Catalog including spatial and temporal heterogeneity |
| Data-Driven Method [33] | Average of top models from randomly generated models | Adaptive and objective | Complex calculation and computational consumption | Catalog including spatial and temporal heterogeneity |
2.1. B-Positive Estimator of b-Values for Aftershock Sequences
2.2. Classical Grid Search Method
2.3. Objective Bayesian Method
2.4. Data-Driven Method
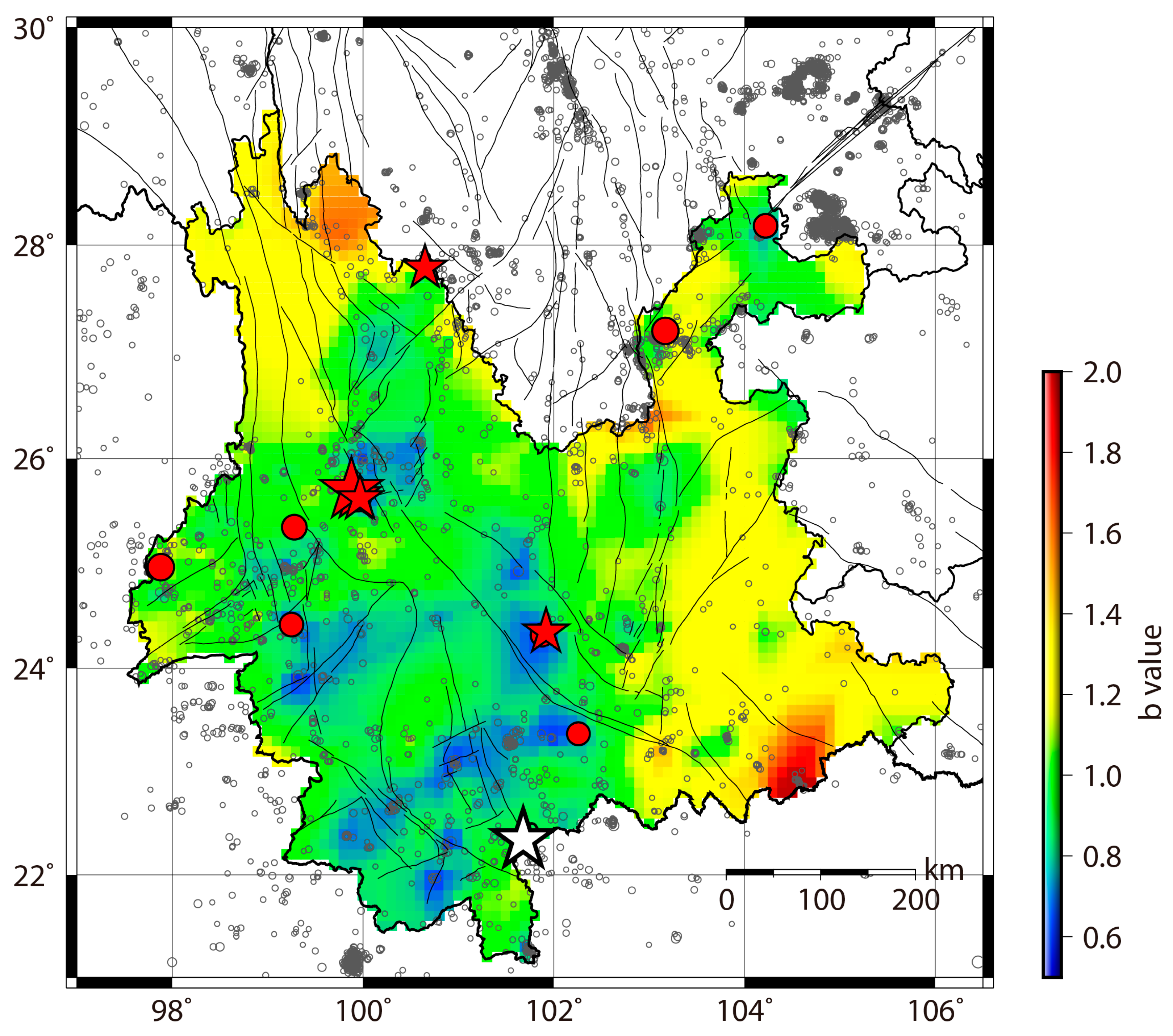
3. Applications of Spatiotemporal b-Value Estimation

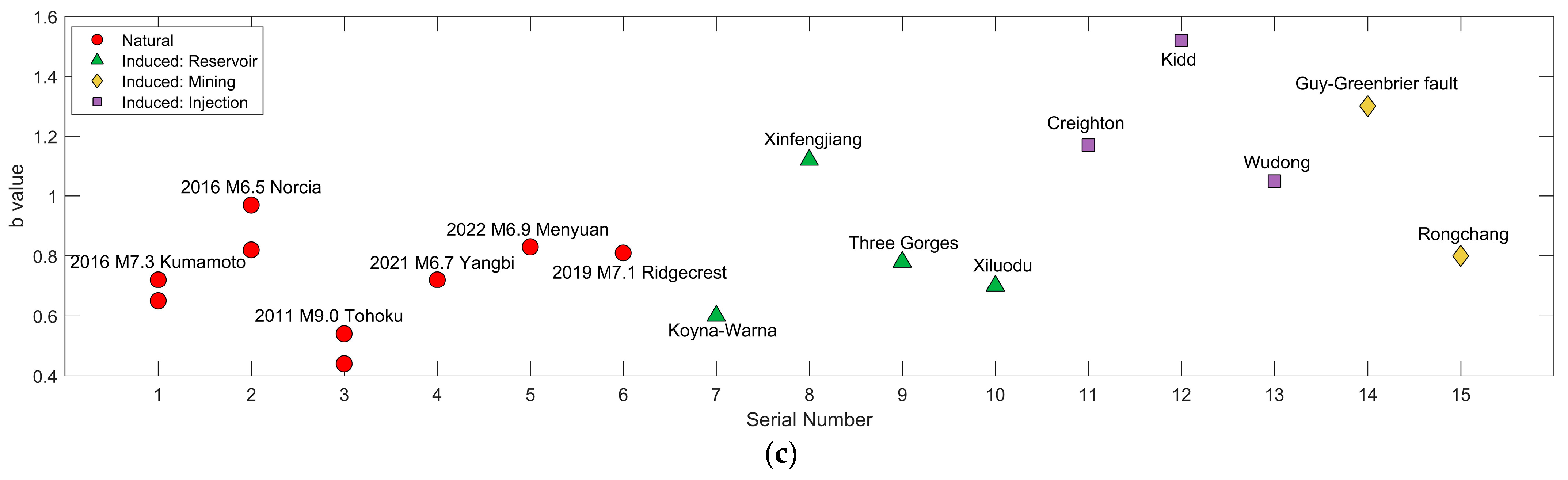
| Category | Key Applications | b-Value Characteristics | Reference |
|---|---|---|---|
| Foreshock–mainshock sequence | Real-time discrimination of sequence | b-value decrease before mainshock | [34,61,71,72,74,76,78,85,86] |
| Medium-to-long-term changes before large earthquakes | Stress concentration assessment in seismogenic zones, identification of potential nucleation zones | Significant b-value decrease near future epicenters pre-mainshock, low b-value zones in high-risk regions | [51,66,71,78,87,88,89,90,91,92,93,94,95,96] |
| Injection-triggered earthquakes | Real-time monitoring of injection impacts, early warning of small-to-moderate induced events | Higher b-values compared to natural earthquakes, b-value drop prior to main events and then rebounds, spatial heterogeneity linked to fault reactivation | [60,97,98,99,100,101,102,103,104,105,106,107,108] |
| Water reservoir-induced earthquakes | Assessing seismic response to impoundment/water level fluctuations | Slightly higher b-values than natural earthquakes, elevated b-value during initial impoundment | [79,80,81,82,109,110,111,112,113,114,115,116,117,118] |
| Mining-induced microseismicity | In situ stress evaluation, seismic hazard analyses | Generally higher b-values than natural earthquakes, b-value decreases before rockbursts | [8,45,46,83,96,119] |
3.1. Natural Earthquakes
3.1.1. Foreshock–Mainshock Sequence
3.1.2. Medium-to-Long-Term b-Value Change Before Large Earthquakes
3.2. Induced Seismicity
3.2.1. Injection-Triggered Earthquakes
3.2.2. Water Reservoir-Induced Earthquakes
3.2.3. Microseismicity in Mines
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Gutenberg, B.; Richter, C.F. Frequency of earthquakes in California. Bull. Seismol. Soc. Am. 1944, 34, 185–188. [Google Scholar] [CrossRef]
- Ishimoto, M. Observations sur les seismes enregistres par le microsismographe construit dernierement. Bull. Earthq. Res. Inst. Univ. Tokyo 1939, 17, 443–478. [Google Scholar]
- Pacheco, J.F.; Scholz, C.H.; Sykes, L.R. Changes in frequency–size relationship from small to large earthquakes. Nature 1992, 355, 71–73. [Google Scholar] [CrossRef]
- Frohlich, C.; Davis, S.D. Teleseismic b values; Or, much ado about 1.0. J. Geophys. Res. 1993, 98, 631–644. [Google Scholar] [CrossRef]
- Giardini, D. Frequency distribution and quantification of deep earthquakes. J. Geophys. Res. 1988, 93, 2095–2105. [Google Scholar] [CrossRef]
- Huang, J.; Turcotte, D.L. Fractal distributions of stress and strength and variations of b-value. Earth Planet. Sci. Lett. 1988, 91, 223–230. [Google Scholar] [CrossRef]
- Gerstenberger, M.; Wiemer, S.; Giardini, D. A systematic test of the hypothesis that the b value varies with depth in California. Geophys. Res. Lett. 2001, 28, 57–60. [Google Scholar] [CrossRef]
- Wang, C.; Wu, A.; Liu, X.; Li, R. Study on fractal characteristics of b value with microseismic activity in deep mining. Procedia Earth Planet. Sci. 2009, 1, 592–597. [Google Scholar] [CrossRef]
- Ritz, V.A.; Rinaldi, A.P.; Wiemer, S. Transient evolution of the relative size distribution of earthquakes as a risk indicator for induced seismicity. Commun. Earth Environ. 2022, 3, 249. [Google Scholar] [CrossRef]
- Bachmann, C.E.; Wiemer, S.; Woessner, J.; Hainzl, S. Statistical analysis of the induced Basel 2006 earthquake sequence: Introducing a probability-based monitoring approach for Enhanced Geothermal Systems. Geophys. J. Int. 2011, 186, 793–807. [Google Scholar] [CrossRef]
- Scholz, C.H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar] [CrossRef]
- Lei, X. Evolution of b-value and fractal dimension of acoustic emission events during shear rupture of an immature fault in granite. Appl. Sci. 2019, 9, 2498. [Google Scholar] [CrossRef]
- Scholz, C.H. On the stress dependence of the earthquake b value. Geophys. Res. Lett. 2015, 42, 1399–1402. [Google Scholar] [CrossRef]
- Spada, M.; Tormann, T.; Wiemer, S.; Enescu, B. Generic dependence of the frequency-size distribution of earthquakes on depth and its relation to the strength profile of the crust. Geophys. Res. Lett. 2013, 40, 709–714. [Google Scholar] [CrossRef]
- Amitrano, D. Brittle-ductile transition and associated seismicity: Experimental and numerical studies and relationship with the b value. J. Geophys. Res. 2003, 108, 2044. [Google Scholar] [CrossRef]
- Lei, X.; Kusunose, K.; Rao, M.V.M.S.; Nishizawa, O.; Satoh, T. Quasi-static fault growth and cracking in homogeneous brittle rock under triaxial compression using acoustic emission monitoring. J. Geophys. Res. 2000, 105, 6127–6139. [Google Scholar] [CrossRef]
- Goebel, T.H.W.; Schorlemmer, D.; Becker, T.W.; Dresen, G.; Sammis, C.G. Acoustic emissions document stress changes over many seismic cycles in stick-slip experiments. Geophys. Res. Lett. 2013, 40, 2049–2054. [Google Scholar] [CrossRef]
- van Stiphout, T.; Kissling, E.; Wiemer, S.; Ruppert, N. Magmatic processes in the Alaska subduction zone by combined 3-D b value imaging and targeted seismic tomography. J. Geophys. Res. 2009, 114, B11302. [Google Scholar] [CrossRef]
- El-Isa, Z.H.; Eaton, D.W. Spatiotemporal variations in the b-value of earthquake magnitude–frequency distributions: Classification and causes. Tectonophysics 2014, 615–616, 1–11. [Google Scholar] [CrossRef]
- Dempsey, D.; Suckale, J.; Huang, Y. Collective properties of injection-induced earthquake sequences: 2. Spatiotemporal evolution and magnitude frequency distributions. J. Geophys. Res. 2016, 121, 3638–3665. [Google Scholar] [CrossRef]
- Roberts, N.S.; Bell, A.F.; Main, I.G. Are volcanic seismic b-values high, and if so when? J. Volcanol. Geotherm. Res. 2015, 308, 127–141. [Google Scholar] [CrossRef]
- Lei, X.; Ma, S.; Chen, W.; Pang, C.; Zeng, J.; Jiang, B. A detailed view of the injection-induced seismicity in a natural gas reservoir in Zigong, southwestern Sichuan Basin, China. J. Geophys. Res. 2013, 118, 4296–4311. [Google Scholar] [CrossRef]
- Lei, X.; Yu, G.; Ma, S.; Wen, X.; Wang, Q. Earthquakes induced by water injection at ∼3 km depth within the Rongchang gas field, Chongqing, China. J. Geophys. Res. 2008, 113, B10310. [Google Scholar] [CrossRef]
- Wyss, M.; Hasegawa, A.; Nakajima, J. Source and path of magma for volcanoes in the subduction zone of northeastern Japan. Geophys. Res. Lett. 2001, 28, 1819–1822. [Google Scholar] [CrossRef]
- Wiemer, S.; Benoit, J.P. Mapping the b-value anomaly at 100 km depth in the Alaska and New Zealand subduction zones. Geophys. Res. Lett. 1996, 23, 1557–1560. [Google Scholar] [CrossRef]
- Schorlemmer, D.; Neri, G.; Wiemer, S.; Mostaccio, A. Stability and significance tests for b-value anomalies: Example from the Tyrrhenian Sea. Geophys. Res. Lett. 2003, 30, 1835. [Google Scholar] [CrossRef]
- Florez, M.A.; Prieto, G.A. Controlling factors of seismicity and geometry in double seismic zones. Geophys. Res. Lett. 2019, 46, 4174–4181. [Google Scholar] [CrossRef]
- Ogata, Y.; Imoto, M.; Katsura, K. 3-D spatial variation of b-values of magnitude-frequency distribution beneath the Kanto District, Japan. Geophys. J. Int. 1991, 104, 135–146. [Google Scholar] [CrossRef]
- Zhan, Z. Gutenberg-Richter law for deep earthquakes revisited: A dual-mechanism hypothesis. Earth Planet. Sci. Lett. 2017, 461, 1–7. [Google Scholar] [CrossRef]
- Gui, Z.; Bai, Y.; Wang, Z.; Dong, D.; Wu, S.; Li, T. Spatiotemporal Seismotectonic Implications for the Izu–Bonin–Mariana Subduction Zone from b-Values. Seismol. Res. Lett. 2020, 91, 1679–1693. [Google Scholar] [CrossRef]
- Wiemer, S. A software package to analyze seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Kamer, Y.; Hiemer, S. Data-driven spatial b value estimation with applications to California seismicity: To b or not to b. J. Geophys. Res. 2015, 120, 5191–5214. [Google Scholar] [CrossRef]
- Yin, F.; Jiang, C. Enhanced b-value time-series calculation method using data-driven approach. Geophys. J. Int. 2023, 236, 78–87. [Google Scholar] [CrossRef]
- van der Elst, N.J. B-Positive: A Robust Estimator of Aftershock Magnitude Distribution in Transiently Incomplete Catalogs. J. Geophys. Res. 2021, 126, e2020JB021027. [Google Scholar] [CrossRef]
- Utsu, T. A method for determining the value of “b” in a formula log n = a − bm showing the magnitude-frequency relation for earthquakes. Geophys. Bull. Hokkaido Univ. 1965, 13, 99–103. [Google Scholar]
- Aki, K. Maximum Likelihood Estimate of b in the Formula logN = a − bM and its Confidence Limits. Bull. Earthq. Res. Inst. Tokyo Univ. 1965, 43, 237–239. [Google Scholar]
- Shi, Y.; Bolt, B.A. The standard error of the magnitude-frequency b value. Bull. Seismol. Soc. Am. 1982, 72, 1677–1687. [Google Scholar] [CrossRef]
- Marzocchi, W.; Sandri, L. A review and new insights on the estimation of the b-valueand its uncertainty. Ann. Geophys. 2003, 46, 1271. [Google Scholar] [CrossRef]
- Wiemer, S.; Wyss, M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the Western United States, and Japan. Bull. Seismol. Soc. Am. 2000, 90, 859–869. [Google Scholar] [CrossRef]
- Cao, A.; Gao, S.S. Temporal variation of seismic b-values beneath northeastern Japan island arc. Geophys. Res. Lett. 2002, 29, 48-1–48-3. [Google Scholar] [CrossRef]
- Woessner, J.; Wiemer, S. Assessing the quality of earthquake catalogues: Estimating the magnitude of completeness and its uncertainty. Bull. Seismol. Soc. Am. 2005, 95, 684–698. [Google Scholar] [CrossRef]
- Mignan, A.; Woessner, J. Estimating the Magnitude of Completeness for Earthquake Catalogs. 2012. Available online: https://www.corssa.org/export/sites/corssa/.galleries/articles-pdf/Mignan-Woessner-2012-CORSSA-Magnitude-of-completeness.pdf (accessed on 24 July 2025).
- Lombardi, A.M. A normalized distance test for co-determining the completeness magnitude and b-value of earthquake catalogs. J. Geophys. Res. 2021, 126, e2020JB021242. [Google Scholar] [CrossRef]
- Taroni, M. Estimating the magnitude of completeness of earthquake catalogs using a simple random variable transformation. Seism. Rec. 2023, 3, 194–199. [Google Scholar] [CrossRef]
- Palgunadi, K.H.; Poiata, N.; Kinscher, J.; Bernard, P.; De Santis, F.; Contrucci, I. Methodology for full waveform near real-time automatic detection and localization of microseismic events using high (8 kHz) sampling rate records in mines: Application to the Garpenberg mine (Sweden). Seismol. Res. Lett. 2020, 91, 399–414. [Google Scholar] [CrossRef]
- Gulia, L.; Gasperini, P. Contamination of frequency–magnitude slope (b-value) by quarry blasts: An example for Italy. Seismol. Res. Lett. 2021, 92, 3538–3551. [Google Scholar] [CrossRef]
- Sandri, L.; Marzocchi, W. A technical note on the bias in the estimation of the b-value and its uncertainty through the Least Squares technique. Ann. Geophys. 2007, 50, 329–339. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; Dover: New York, NY, USA, 1972. [Google Scholar]
- Utsu, T. On Seismicity, Report of the Joint Research Institute for Statistical Mathematics; JPN: Tokyo, Japan, 1992; pp. 139–157. (In Japanese) [Google Scholar]
- Nishikawa, T.; Ide, S. Earthquake size distribution in subduction zones linked to slab buoyancy. Nat. Geosci. 2014, 7, 904–908. [Google Scholar] [CrossRef]
- Wang, R.; Chang, Y.; Miao, M.; Zeng, Z.; Chen, H.; Shi, H.; Li, D.; Liu, L.; Su, Y.; Han, P. Assessing Earthquake Forecast Performance Based on b Value in Yunnan Province, China. Entropy 2021, 23, 730. [Google Scholar] [CrossRef]
- Ogata, Y. Space-time model for regional seismicity and detection of crustal stress changes. J. Geophys. Res. 2004, 109, B03308. [Google Scholar] [CrossRef]
- Ogata, Y. Significant improvements of the space-time ETAS model for forecasting of accurate baseline seismicity. Earth Planets Space 2011, 63, 6. [Google Scholar] [CrossRef]
- Akaike, H. Likelihood and the Bayes procedure. Trab. Estad. Investig. Oper. 1980, 31, 143–166. [Google Scholar] [CrossRef]
- Si, Z.Y.; Jiang, C.S. Research on parameter calculation for the Ogata–Katsura 1993 model in terms of the frequency–magnitude distribution based on a data-driven approach. Seismol. Res. Lett. 2019, 90, 1318–1329. [Google Scholar] [CrossRef]
- Ogata, Y.; Katsura, K. Analysis of temporal and spatial heterogeneity of magnitude frequency distribution inferred from earthquake catalogues. Geophys. J. Int. 1993, 113, 727–738. [Google Scholar] [CrossRef]
- Tinti, S.; Mulargia, F. Confidence intervals of b values for grouped magnitudes. Bull. Seismol. Soc. Am. 1987, 77, 2125–2134. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Jiang, C.; Jiang, C.S.; Yin, F.L.; Zhang, Y.B.; Bi, J.; Long, F.; Si, Z.Y.; Yin, X. A new method for calculating b-value of time sequence based on data-driven (TbDD): A case study of the 2021 Yangbi MS6.4 earthquake sequence in Yunnan. Chin. J. Geophys. 2021, 64, 3126–3134. (In Chinese) [Google Scholar] [CrossRef]
- Jiang, C.S.; Han, L.B.; Long, F.; Lai, G.J.; Yin, F.L.; Bi, J.; Si, Z. Spatiotemporal heterogeneity of b values revealed by a data-driven approach for the 17 June 2019 MS 6.0 Changning earthquake sequence, Sichuan, China. Nat. Hazards Earth Syst. Sci. 2021, 21, 2233–2244. [Google Scholar] [CrossRef]
- Bi, J.; Yin, F.; Jiang, C.; Yin, X.; Ma, Y.; Song, C. Strong aftershocks traffic light system: A case study of the 8 January 2022 MS6.9 Menyuan earthquake, Qinghai Province, China. Front. Earth Sci. 2023, 10, 1. [Google Scholar] [CrossRef]
- Muntendam-Bos, A.G.; Grobbe, N. Data-driven spatiotemporal assessment of the event-size distribution of the Groningen extraction-induced seismicity catalogue. Sci. Rep. 2022, 12, 10119. [Google Scholar] [CrossRef]
- Nandan, S.; Ouillon, G.; Wiemer, S.; Sornette, D. Objective estimation of spatially variable parameters of epidemic type aftershock sequence model: Application to California. J. Geophys. Res. 2017, 122, 5118–5143. [Google Scholar] [CrossRef]
- Taroni, M.; Vocalelli, G.; De Polis, A. Gutenberg–Richter b-Value time series forecasting: A weighted likelihood approach. Forecasting 2021, 3, 561–569. [Google Scholar] [CrossRef]
- Fiedler, B.; Hainzl, S.; Zöller, G.; Holschneider, M. Detection of Gutenberg–Richter b-value changes in earthquake time series. Bull. Seismol. Soc. Am. 2018, 108, 2778–2787. [Google Scholar] [CrossRef]
- Nanjo, K.Z. Were changes in stress state responsible for the 2019 Ridgecrest, California, earthquakes? Nat. Commun. 2020, 11, 3082. [Google Scholar] [CrossRef]
- Nanjo, K.Z.; Yoshida, A. A b map implying the first eastern rupture of the Nankai Trough earthquakes. Nat. Commun. 2018, 9, 1117. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Ogwari, P.O.; Horton, S.P.; Langston, C.A. Spatio-temporal evolution of frequency-magnitude distribution and seismogenic index during initiation of induced seismicity at Guy-Greenbrier, Arkansas. Phys. Earth Planet. Inter. 2017, 267, 53–66. [Google Scholar] [CrossRef]
- Tan, Y.J.; Waldhauser, F.; Tolstoy, M.; Wilcock, W.S.D. Axial Seamount: Periodic tidal loading reveals stress dependence of the earthquake size distribution (b value). Earth Planet. Sci. Lett. 2019, 512, 39–45. [Google Scholar] [CrossRef]
- Xie, W.Y.; Hattori, K.; Han, P. Temporal variation and statistical assessment of the b value off the Pacific Coast of Tokachi, Hokkaido, Japan. Entropy 2019, 21, 249. [Google Scholar] [CrossRef] [PubMed]
- Nanjo, K.Z.; Hirata, N.; Obara, K.; Kasahara, K. Decade-scale decrease in b value prior to the M9-class 2011 Tohoku and 2004 Sumatra quakes. Geophys. Res. Lett. 2012, 39, L20304. [Google Scholar] [CrossRef]
- Nuannin, P.; Kulhanek, O.; Persson, L. Spatial and temporal b value anomalies preceding the devastating off coast of NW Sumatra earthquake of December 26, 2004. Geophys. Res. Lett. 2005, 32, L11307. [Google Scholar] [CrossRef]
- Xie, W.Y.; Hattori, K.; Han, P.; Shi, H. Temporal variation of b value with statistical test in Wenchuan area, China prior to the 2008 Wenchuan earthquake. Entropy 2022, 24, 494. [Google Scholar] [CrossRef]
- Shi, H.X.; Meng, L.Y.; Zhang, X.M.; Chang, Y.; Yang, Z.T.; Xie, W.Y.; Hattori, K.; Han, P. Decrease in b value prior to the Wenchuan earthquake (MS8.0). Chin. J. Geophys. 2018, 61, 1874–1882. (In Chinese) [Google Scholar] [CrossRef]
- Liu, Y.B.; Pei, S.P. Temporal and spatial variation of b-value before and after Wenchuan earthquake and its tectonic implication. Chin. J. Geophys. 2017, 60, 2104–2112. (In Chinese) [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S. Real-time discrimination of earthquake foreshocks and aftershocks. Nature 2019, 574, 193–199. [Google Scholar] [CrossRef]
- Nanjo, K.Z.; Yoshida, A. Anomalous decrease in relatively large shocks and increase in the p and b values preceding the April 16, 2016, M7.3 earthquake in Kumamoto, Japan. Earth Planets Space 2017, 69, 13. [Google Scholar] [CrossRef]
- Gulia, L.; Wiemer, S.; Vannucci, G. Pseudoprospective evaluation of the foreshock traffic-light system in Ridgecrest and implications for aftershock hazard assessment. Seismol. Res. Lett. 2020, 91, 2828–2842. [Google Scholar] [CrossRef]
- Mallika, K.; Gupta, H.; Shashidhar, D.; Rao, N.P.; Yadav, A.; Rohilla, S.; Satyanarayana, H.V.S.; Srinagesh, D. Temporal variation of b value associated with M ~4 earthquakes in the reservoir-triggered seismic environment of the Koyna–Warna region, Western India. J. Seismol. 2012, 17, 189–195. [Google Scholar] [CrossRef]
- Shen, C.-K.; Chang, C.-H.; Chen, H.-C.; Li, T.-C.; Hueng, L.; Wang, T.; Yang, C.; Lo, H. Earthquakes induced by reservoir impounding and their effect on the Hsinfengkiang Dam. Sci. Sin. 1974, 17, 239–272. [Google Scholar]
- Zhang, L.; Lei, X.; Liao, W.; Li, J.; Yao, Y. Statistical parameters of seismicity induced by the impoundment of the three gorges reservoir, central China. Tectonophysics 2019, 751, 13–22. [Google Scholar] [CrossRef]
- Zhao, C.; Zhao, C.; Lei, H.; Yao, M. Seismic activities before and after the impoundment of the Xiangjiaba and Xiluodu reservoirs in the lower Jinsha river. Earthq. Sci. 2022, 35, 355–370. [Google Scholar] [CrossRef]
- Ma, X.; Westman, E.; Slaker, B.; Thibodeau, D.; Counter, D. The b-value evolution of mining-induced seismicity and mainshock occurrences at hard-rock mines. Int. J. Rock Mech. Min. Sci. 2018, 104, 64–70. [Google Scholar] [CrossRef]
- Lai, X.; Yang, Y.; Zhang, L.; Liu, H. Research on structural evolution and microseismic response characteristics of overlying strata during repeated mining of steeply inclined and extra thick coal seams. Lithosphere 2021, 2021, 8047321. [Google Scholar] [CrossRef]
- Mignan, A. The debate on the prognostic value of earthquake foreshocks: A meta-analysis. Sci. Rep. 2014, 4, 4099. [Google Scholar] [CrossRef] [PubMed]
- Wang, R.; Chang, Y.; Han, P.; Miao, M.; Zeng, Z.Y.; Shi, H.X.; Li, D.N.; Liu, L.F.; Su, Y.J. Optimized Traffic Light System with AIC and Application to the 2021 M6.7 Yangbi Earthquake Sequence. Entropy 2023, 25, 759. [Google Scholar] [CrossRef]
- Suyehiro, S.; Asada, T.; Ohtake, M. Foreshocks and aftershocks accompanying a perceptible earthquake in central japan: On the peculiar nature of foreshocks. Pap. Meteorol. Geophys. 1964, 15, 71–88. [Google Scholar] [CrossRef] [PubMed]
- Suyehiro, S. Difference between aftershocks and foreshocks in the relationship of magnitude to frequency of occurrence for the great chilean earthquake of 1960. Bull. Seismol. Soc. Am. 1966, 56, 185–200. [Google Scholar] [CrossRef]
- Gibowicz, S.J. Variation of the frequency-magnitude relation during earthquake sequences in new zealand. Bull. Seismol. Soc. Am. 1973, 63, 517–528. [Google Scholar] [CrossRef]
- Papazachos, B.C. Foreshocks and earthquake prediction. Tectonophysics 1975, 28, 213–226. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Minadakis, G. Foreshock patterns preceding great earthquakes in the subduction zone of chile. Pure Appl. Geophys. 2016, 173, 3247–3271. [Google Scholar] [CrossRef]
- Dascher-Cousineau, K.; Lay, T.; Brodsky, E.E. Two foreshock sequences post gulia and wiemer (2019). Seismol. Res. Lett. 2020, 91, 2843–2850. [Google Scholar] [CrossRef]
- Wu, K.T.; Yue, M.S.; Wu, H.Y.; Cao, X.L.; Chen, H.; Huang, W.Q.; Tian, K.Y.; Lu, S.D. Certain characteristics of Haicheng earthquake sequence. Acta Geophys. Sin. 1976, 19, 95–109, (In Chinese with English Abstract). [Google Scholar]
- Nanjo, K.Z.; Izutsu, J.; Orihara, Y.; Furuse, N.; Togo, S.; Nitta, H.; Okada, T.; Tanaka, R.; Kamogawa, M.; Nagao, T. Seismicity prior to the 2016 Kumamoto earthquakes. Earth Planets Space 2016, 68, 187. [Google Scholar] [CrossRef]
- Görgün, E. Analysis of the b-values before and after the 23 october 2011 mw 7.2 van–erciş, turkey earthquake. Tectonophysics 2013, 603, 213–221. [Google Scholar] [CrossRef]
- Hu, N.; Han, P.; Wang, R.; Shi, F.; Chen, L.; Li, H. Spatial heterogeneity of b values in northeastern tibetan plateau and its interpretation. Entropy 2024, 26, 182. [Google Scholar] [CrossRef] [PubMed]
- Mahani, A.B.; Schultz, R.; Kao, H.; Walker, D.; Johnson, J.; Salas, C. Fluid injection and seismic activity in the northern montney play, british columbia, canada, with special reference to the 17 august 2015 Mw 4.6 induced earthquake. Bull. Seismol. Soc. Am. 2017, 107, 542–552. [Google Scholar] [CrossRef]
- Igonin, N.; Zecevic, M.; Eaton, D.W. Bilinear magnitude-frequency distributions and characteristic earthquakes during hydraulic fracturing. Geophys. Res. Lett. 2018, 45, 12866–12874. [Google Scholar] [CrossRef]
- British Columbia Oil and Gas Commission. Investigation of Observed Seismicity in the Montney Trend. Available online: https://oilandgasinfo.ca/wp-content/uploads/2017/03/Investigation-of-Observed-Seismicity-in-the-Montney-Trend.pdf (accessed on 24 July 2025).
- Hornbach, M.J.; DeShon, H.R.; Ellsworth, W.L.; Stump, B.W.; Hayward, C.; Frohlich, C.; Oldham, H.R.; Olson, J.E.; Magnani, M.B.; Brokaw, C.; et al. Causal factors for seismicity near Azle, Texas. Nat. Commun. 2015, 6, 6728. [Google Scholar] [CrossRef]
- Chen, H.; Meng, X.; Niu, F.; Tang, Y.; Yin, C.; Wu, F. Microseismic monitoring of stimulating shale gas reservoir in SW China: 2. Spatial clustering controlled by the preexisting faults and fractures. J. Geophys. Res. 2018, 123, 1659–1672. [Google Scholar] [CrossRef]
- Lei, X.; Wang, Z.; Su, J. Possible link between long-term and short-term water injections and earthquakes in salt mine and shale gas site in Changning, south Sichuan Basin, China. Earth Planet. Phys. 2019, 3, 510–525. [Google Scholar] [CrossRef]
- Sheng, M.; Chu, R.; Peng, Z.; Wei, Z.; Zeng, X.; Wang, Q.; Wang, Y. Earthquakes triggered by fluid diffusion and boosted by fault reactivation in weiyuan, China due to hydraulic fracturing. J. Geophys. Res. 2022, 127, e2021JB022963. [Google Scholar] [CrossRef]
- Yu, H.; Harrington, R.M.; Liu, Y.; Wang, B. Induced seismicity driven by fluid diffusion revealed by a near-field hydraulic stimulation monitoring array in the montney basin, british columbia. J. Geophys. Res. 2019, 124, 4694–4709. [Google Scholar] [CrossRef]
- Hu, J.; Chen, J.; Chen, Z.; Cao, J.; Wang, Q.; Zhao, L.; Zhang, H.; Xu, B.; Chen, G. Risk assessment of seismic hazards in hydraulic fracturing areas based on fuzzy comprehensive evaluation and AHP method (FAHP): A case analysis of shangluo area in yibin city, sichuan province, China. J. Pet. Sci. Eng. 2018, 170, 797–812. [Google Scholar] [CrossRef]
- Hu, J.; Xu, B.; Chen, Z.; Zhang, H.; Cao, J.; Wang, Q. Hazard and risk assessment for hydraulic fracturing induced seismicity based on the entropy-fuzzy-AHP method in southern sichuan basin, China. J. Nat. Gas Sci. Eng. 2021, 90, 103908. [Google Scholar] [CrossRef]
- Eaton, D.W.; Davidsen, J.; Pedersen, P.K.; Boroumand, N. Breakdown of the Gutenberg-Richter relation for microearthquakes induced by hydraulic fracturing: Influence of stratabound fractures. Geophys. Prospect. 2014, 62, 806–818. [Google Scholar] [CrossRef]
- Frohlich, C.; Hayward, C.; Stump, B.; Potter, E. The Dallas–Fort Worth Earthquake Sequence: October 2008 through May 2009. Bull. Seismol. Soc. Am. 2011, 101, 327–340. [Google Scholar] [CrossRef]
- Mandal, P.; Mabawonku, A.O.; Dimri, V.P. Self-organized fractal seismicity of reservoir triggered earthquakes in the Koyna-Warna seismic zone, Western India. Pure Appl. Geophys. 2005, 162, 73–90. [Google Scholar] [CrossRef]
- Singh, C.; Bhattacharya, P.M.; Chadha, R.K. Seismicity in the Koyna–Warna reservoir site in Western India: Fractal and b-value mapping. Bull. Seismol. Soc. Am. 2008, 98, 476–482. [Google Scholar] [CrossRef]
- Gupta, H.K. A review of recent studies of triggered earthquakes by artificial water reservoirs with special emphasis on earthquakes in koyna, India. Earth-Sci. Rev. 2002, 58, 279–310. [Google Scholar] [CrossRef]
- Gupta, H.K. Artificial water reservoir-triggered seismicity (RTS): Most prominent anthropogenic seismicity. Surv. Geophys. 2022, 43, 619–659. [Google Scholar] [CrossRef]
- Gupta, H.K. Are RIS events of M ≥5 preceded by a couple of foreshocks of M ≥ 4? Bull. Seismol. Soc. Am. 1992, 82, 517–520. [Google Scholar] [CrossRef]
- Gupta, H.K.; Rastogi, B.; Narain, H. Common features of the reservoir associated seismic activities. Bull. Seismol. Soc. Am. 1972, 62, 481–492. [Google Scholar] [CrossRef]
- Gupta, H.K.; Rastogi, B.K.; Narain, H. Some discriminatory characteristics of earthquakes near the Kariba, Kremasta, and Koyna artificial lakes. Bull. Seismol. Soc. Am. 1972, 62, 493–507. [Google Scholar] [CrossRef]
- Mahesh, P.; Gupta, S.; Rai, S.S.; Sarma, P.R. Fluid driven earthquakes in the Chamoli Region, Garhwal Himalaya: Evidence from local earthquake tomography. Geophys. J. Int. 2012, 191, 1295–1304. [Google Scholar] [CrossRef]
- Tao, W.; Masterlark, T.; Shen, Z.K.; Ronchin, E. Impoundment of the zipingpu reservoir and triggering of the 2008 Mw 7.9 wenchuan earthquake, China. J. Geophys. Res. 2015, 120, 7033–7047. [Google Scholar] [CrossRef]
- Yao, Y.-S.; Wang, Q.-L.; Liao, W.-L.; Zhang, L.-F.; Chen, J.-H.; Li, J.-G.; Yuan, L.; Zhao, Y.-N. Influences of the three gorges project on seismic activities in the reservoir area. Sci. Bull. 2017, 62, 1089–1098. [Google Scholar] [CrossRef] [PubMed]
- Vallejos, J.A.; McKinnon, S.D. Correlations between mining and seismicity for re-entry protocol development. Int. J. Rock Mech. Min. Sci. 2011, 48, 616–625. [Google Scholar] [CrossRef]
- Main, I.G.; Meredith, P.G.; Jones, C. A reinterpretation of the precursory seismic b-value anomaly from fracture mechanics. Geophys. J. Int. 1989, 96, 131–138. [Google Scholar] [CrossRef]
- Urbancic, T.I.; Trifu, C.I.; Long, J.M.; Young, R.P. Space-time correlations of b values with stress release. Pure Appl. Geophys. 1992, 139, 449–462. [Google Scholar] [CrossRef]
- Nuannin, P.; Kulhánek, O.; Persson, L. Variations of b-values preceding large earthquakes in the Andaman–Sumatra subduction zone. J. Asian Earth Sci. 2012, 61, 237–242. [Google Scholar] [CrossRef]
- Ashtari Jafari, M. Change of seismicity across the Ridgecrest earthquake area. J. Seismol. 2023, 27, 1067–1085. [Google Scholar] [CrossRef]
- Matsumoto, S. Large earthquake proximity indicated by seismic moment efficiency and frequency-number distribution of small earthquakes. Sci. Rep. 2025, 15, 17389. [Google Scholar] [CrossRef] [PubMed]
- Görgün, E. Reply to comments by Yavor Kamer and Stefan Hiemer on “Analysis of the b-values before and after the 23 october 2011 M 7.2 Van-Erciş, Turkey earthquake”. Tectonophysics 2014, 630, 313–318. [Google Scholar] [CrossRef]
- Kamer, Y.; Hiemer, S. Comment on “Analysis of the b-values before and after the 23 october 2011 Mw 7.2 Van–Erciş, Turkey, earthquake”. Tectonophysics 2013, 608, 1448–1451. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, R.; Shi, H.; Miao, M.; Zhuang, J.; Chang, Y.; Jiang, C.; Meng, L.; Li, D.; Liu, L.; et al. Earthquake Forecasting Based on b Value and Background Seismicity Rate in Yunnan Province, China. Entropy 2025, 27, 205. [Google Scholar] [CrossRef]
- Eaton, D.W. Seismicity induced by the development of unconventional oil and gas resources. In Environmental Impacts from the Development of Unconventional Oil and Gas Reserves; Cambridge University Press: Cambridge, UK, 2022; pp. 173–213. [Google Scholar]
- Mukuhira, Y.; Fehler, M.C.; Bjarkason, E.K.; Ito, T.; Asanuma, H. On the b-value dependency of injection-induced seismicity on geomechanical parameters. Int. J. Rock Mech. Min. Sci. 2024, 174, 105631. [Google Scholar] [CrossRef]
- Eaton, D.W.; Maghsoudi, S. 2b... or not 2b? Interpreting magnitude distributions from microseismic catalogs. First Break 2015, 33. [Google Scholar] [CrossRef]
- Huang, L.; Zhao, A.H.; Wu, Q.J.; Xu, Z.Y.; Pan, J.T.; Zhang, F.X.; Yao, Z.X. Characteristics of seismic b-value of Changning shale gas region, Sichuan, from a dense seismic array. Acta Seismol. Sin. 2024, 46, 825–843. (In Chinese) [Google Scholar] [CrossRef]
- Wessels, S.; Kratz, M.; De La Pena, A. Identifying fault activation during hydraulic stimulation in the Barnett shale: Source mechanisms, b values, and energy release analyses of microseismicity. In SEG Technical Program Expanded Abstracts 2011; Society of Exploration Geophysicists: Houston, TX, USA, 2011; pp. 1463–1467. [Google Scholar] [CrossRef]
- Yadav, A.; Bansal, B.K.; Pandey, A.P. Five decades of triggered earthquakes in Koyna-Warna region, western India—A review. Earth-Sci. Rev. 2016, 162, 433–450. [Google Scholar] [CrossRef]
- Zhai, Q.; Yin, J.; Yang, Y.; Atterholt, J.W.; Li, J.; Husker, A.; Zhan, Z. Comprehensive evaluation of DAS amplitude and its implications for earthquake early warning and seismic interferometry. J. Geophys. Res. 2025, 130, e2024JB030288. [Google Scholar] [CrossRef]
- Gu, Y.J.; Sun, W.; Yu, T.C.; Wang, J.; Wang, R.; Li, T.; Schultz, R. Peace River Induced Seismic Monitoring (PRISM) Nodal Seismic Array. Seismol. Res. Lett. 2024, 96, 562–575. [Google Scholar] [CrossRef]
- Ross, Z.E.; White, M.C.; Vernon, F.L.; Ben-Zion, Y. An improved algorithm for real-time S-wave picking with application to the (Augmented) ANZA network in Southern California. Bull. Seismol. Soc. Am. 2016, 106, 2013–2022. [Google Scholar] [CrossRef]
- Shen, H.; Shen, Y. Array-based convolutional neural networks for automatic detection and 4D localization of earthquakes in Hawai‘i. Seismol. Res. Lett. 2021, 92, 2961–2971. [Google Scholar] [CrossRef]
- Jia, K.; Zhou, S. Machine learning applications in seismology. Appl. Sci. 2024, 14, 7857. [Google Scholar] [CrossRef]
- Geffers, G.-M.; Main, I.G.; Naylor, M. Biases in estimating b-values from small earthquake catalogues: How high are high b-values? Geophys. J. Int. 2022, 229, 1840–1855. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, Y.; Wang, R.; Han, P.; Wang, J.; Miao, M.; Zeng, Z.; Wu, W.; Jiang, C.; Meng, L.; Shi, H.; et al. b-Value Evaluation and Applications to Seismic Hazard Assessment. Entropy 2025, 27, 958. https://doi.org/10.3390/e27090958
Chang Y, Wang R, Han P, Wang J, Miao M, Zeng Z, Wu W, Jiang C, Meng L, Shi H, et al. b-Value Evaluation and Applications to Seismic Hazard Assessment. Entropy. 2025; 27(9):958. https://doi.org/10.3390/e27090958
Chicago/Turabian StyleChang, Ying, Rui Wang, Peng Han, Jinhong Wang, Miao Miao, Zhiyi Zeng, Weiwei Wu, Changsheng Jiang, Lingyuan Meng, Haixia Shi, and et al. 2025. "b-Value Evaluation and Applications to Seismic Hazard Assessment" Entropy 27, no. 9: 958. https://doi.org/10.3390/e27090958
APA StyleChang, Y., Wang, R., Han, P., Wang, J., Miao, M., Zeng, Z., Wu, W., Jiang, C., Meng, L., Shi, H., & Hattori, K. (2025). b-Value Evaluation and Applications to Seismic Hazard Assessment. Entropy, 27(9), 958. https://doi.org/10.3390/e27090958









